bc (original) (raw)
Grammar
The grammar in this section and the lexical conventions in the following section shall together describe the syntax for_bc_ programs. The general conventions for this style of grammar are described in Grammar Conventions. A valid program can be represented as the non-terminal symbolprogram in the grammar. This formal syntax shall take precedence over the text syntax description.
%token EOF NEWLINE STRING LETTER NUMBER
%token MUL_OP /* '*', '/', '%' */
%token ASSIGN_OP /* '=', '+=', '-=', '*=', '/=', '%=', '^=' */
%token REL_OP /* '==', '<=', '>=', '!=', '<', '>' */
%token INCR_DECR /* '++', '--' */
%token Define Break Quit Length /* 'define', 'break', 'quit', 'length' */
%token Return For If While Sqrt /* 'return', 'for', 'if', 'while', 'sqrt' */
%token Scale Ibase Obase Auto /* 'scale', 'ibase', 'obase', 'auto' */
%start program
%%
program : EOF | input_item program ;
input_item : semicolon_list NEWLINE | function ;
semicolon_list : /* empty */ | statement | semicolon_list ';' statement | semicolon_list ';' ;
statement_list : /* empty */ | statement | statement_list NEWLINE | statement_list NEWLINE statement | statement_list ';' | statement_list ';' statement ;
statement : expression | STRING | Break | Quit | Return | Return '(' return_expression ')' | For '(' expression ';' relational_expression ';' expression ')' statement | If '(' relational_expression ')' statement | While '(' relational_expression ')' statement | '{' statement_list '}' ;
function : Define LETTER '(' opt_parameter_list ')' '{' NEWLINE opt_auto_define_list statement_list '}' ;
opt_parameter_list : /* empty */ | parameter_list ;
parameter_list : LETTER | define_list ',' LETTER ;
opt_auto_define_list : /* empty */ | Auto define_list NEWLINE | Auto define_list ';' ;
define_list : LETTER | LETTER '[' ']' | define_list ',' LETTER | define_list ',' LETTER '[' ']' ;
opt_argument_list : /* empty */ | argument_list ;
argument_list : expression | LETTER '[' ']' ',' argument_list ;
relational_expression : expression | expression REL_OP expression ;
return_expression : /* empty */ | expression ;
expression : named_expression | NUMBER | '(' expression ')' | LETTER '(' opt_argument_list ')' | '-' expression | expression '+' expression | expression '-' expression | expression MUL_OP expression | expression '^' expression | INCR_DECR named_expression | named_expression INCR_DECR | named_expression ASSIGN_OP expression | Length '(' expression ')' | Sqrt '(' expression ')' | Scale '(' expression ')' ;
named_expression : LETTER | LETTER '[' expression ']' | Scale | Ibase | Obase ;
Lexical Conventions in bc
The lexical conventions for bc programs, with respect to the preceding grammar, shall be as follows:
- Except as noted, bc shall recognize the longest possible token or delimiter beginning at a given point.
- A comment shall consist of any characters beginning with the two adjacent characters "/*" and terminated by the next occurrence of the two adjacent characters "*/". Comments shall have no effect except to delimit lexical tokens.
- The shall be recognized as the token NEWLINE.
- The token STRING shall represent a string constant; it shall consist of any characters beginning with the double-quote character ( ' )' and terminated by another occurrence of the double-quote character. The value of the string is the sequence of all characters between, but not including, the two double-quote characters. All characters shall be taken literally from the input, and there is no way to specify a string containing a double-quote character. The length of the value of each string shall be limited to {BC_STRING_MAX} bytes.
- A shall have no effect except as an ordinary character if it appears within a STRING token, or to delimit a lexical token other than STRING.
- The combination of a backslash character immediately followed by a shall have no effect other than to delimit lexical tokens with the following exceptions:
- It shall be interpreted as the character sequence "\" in STRING tokens.
- It shall be ignored as part of a multi-line NUMBER token.
- The token NUMBER shall represent a numeric constant. It shall be recognized by the following grammar:
NUMBER : integer
| '.' integer
| integer '.'
| integer '.' integer
;
integer : digit
| integer digit
;
digit : 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7
| 8 | 9 | A | B | C | D | E | F
;
8. The value of a NUMBER token shall be interpreted as a numeral in the base specified by the value of the internal registeribase (described below). Each of the digit characters shall have the value from 0 to 15 in the order listed here, and the period character shall represent the radix point. The behavior is undefined if digits greater than or equal to the value ofibase appear in the token. However, note the exception for single-digit values being assigned to ibase andobase themselves, in Operations in bc.
9. The following keywords shall be recognized as tokens:
auto break define ibase if for length obase quit return scale sqrt while 10. Any of the following characters occurring anywhere except within a keyword shall be recognized as the token LETTER: a b c d e f g h i j k l m n o p q r s t u v w x y z 11. The following single-character and two-character sequences shall be recognized as the token ASSIGN_OP: = += -= *= /= %= ^= 12. If an '=' character, as the beginning of a token, is followed by a '-' character with no intervening delimiter, the behavior is undefined. 13. The following single-characters shall be recognized as the token MUL_OP:
- / %
- The following single-character and two-character sequences shall be recognized as the token REL_OP:
== <= >= != < > - The following two-character sequences shall be recognized as the token INCR_DECR:
++ -- - The following single characters shall be recognized as tokens whose names are the character:
( ) , + - ; [ ] ^ { } - The token EOF is returned when the end of input is reached.
Operations in bc
There are three kinds of identifiers: ordinary identifiers, array identifiers, and function identifiers. All three types consist of single lowercase letters. Array identifiers shall be followed by square brackets ( "[]" ). An array subscript is required except in an argument or auto list. Arrays are singly dimensioned and can contain up to {BC_DIM_MAX} elements. Indexing shall begin at zero so an array is indexed from 0 to {BC_DIM_MAX}-1. Subscripts shall be truncated to integers. The application shall ensure that function identifiers are followed by parentheses, possibly enclosing arguments. The three types of identifiers do not conflict.
The following table summarizes the rules for precedence and associativity of all operators. Operators on the same line shall have the same precedence; rows are in order of decreasing precedence.
Table: Operators in bc
| Operator | Associativity |
|---|---|
| ++, -- | N/A |
| unary - | N/A |
| ^ | Right to left |
| *, /, % | Left to right |
| +, binary - | Left to right |
| =, +=, -=, *=, /=, %=, ^= | Right to left |
| ==, <=, >=, !=, <, > | None |
Each expression or named expression has a scale, which is the number of decimal digits that shall be maintained as the fractional portion of the expression.
Named expressions are places where values are stored. Named expressions shall be valid on the left side of an assignment. The value of a named expression shall be the value stored in the place named. Simple identifiers and array elements are named expressions; they have an initial value of zero and an initial scale of zero.
The internal registers scale, ibase, and obase are all named expressions. The scale of an expression consisting of the name of one of these registers shall be zero; values assigned to any of these registers are truncated to integers. The scale register shall contain a global value used in computing the scale of expressions (as described below). The value of the register scale is limited to 0 <= scale <= {BC_SCALE_MAX} and shall have a default value of zero. The ibase and obase registers are the input and output number radix, respectively. The value of ibaseshall be limited to:
2 <= ibase <= 16
The value of obase shall be limited to:
2 <= obase <= {BC_BASE_MAX}
When either ibase or obase is assigned a single digit value from the list in Lexical Conventions in bc , the value shall be assumed in hexadecimal. (For example, ibase=A sets to base ten, regardless of the current ibase value.) Otherwise, the behavior is undefined when digits greater than or equal to the value of ibase appear in the input. Both ibase and obase shall have initial values of 10.
Internal computations shall be conducted as if in decimal, regardless of the input and output bases, to the specified number of decimal digits. When an exact result is not achieved (for example, scale=0; 3.2/1), the result shall be truncated.
For all values of obase specified by this volume of IEEE Std 1003.1-2001, bc shall output numeric values by performing each of the following steps in order:
- If the value is less than zero, a hyphen ( '-' ) character shall be output.
- One of the following is output, depending on the numerical value:
- If the absolute value of the numerical value is greater than or equal to one, the integer portion of the value shall be output as a series of digits appropriate to obase (as described below), most significant digit first. The most significant non-zero digit shall be output next, followed by each successively less significant digit.
- If the absolute value of the numerical value is less than one but greater than zero and the scale of the numerical value is greater than zero, it is unspecified whether the character 0 is output.
- If the numerical value is zero, the character 0 shall be output.
- If the scale of the value is greater than zero and the numeric value is not zero, a period character shall be output, followed by a series of digits appropriate to obase (as described below) representing the most significant portion of the fractional part of the value. If s represents the scale of the value being output, the number of digits output shall be s ifobase is 10, less than or equal to s if obase is greater than 10, or greater than or equal to s ifobase is less than 10. For obase values other than 10, this should be the number of digits needed to represent a precision of 10_s_.
For obase values from 2 to 16, valid digits are the first obase of the single characters:
0 1 2 3 4 5 6 7 8 9 A B C D E F
which represent the values zero to 15, inclusive, respectively.
For bases greater than 16, each digit shall be written as a separate multi-digit decimal number. Each digit except the most significant fractional digit shall be preceded by a single . For bases from 17 to 100, bc shall write two-digit decimal numbers; for bases from 101 to 1000, three-digit decimal strings, and so on. For example, the decimal number 1024 in base 25 would be written as:
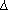 01
01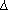 15
15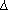 24
24
and in base 125, as:
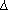 008
008 024
024
Very large numbers shall be split across lines with 70 characters per line in the POSIX locale; other locales may split at different character boundaries. Lines that are continued shall end with a backslash ( '\' ).
A function call shall consist of a function name followed by parentheses containing a comma-separated list of expressions, which are the function arguments. A whole array passed as an argument shall be specified by the array name followed by empty square brackets. All function arguments shall be passed by value. As a result, changes made to the formal parameters shall have no effect on the actual arguments. If the function terminates by executing a return statement, the value of the function shall be the value of the expression in the parentheses of the return statement or shall be zero if no expression is provided or if there is no return statement.
The result of sqrt( expression) shall be the square root of the expression. The result shall be truncated in the least significant decimal place. The scale of the result shall be the scale of the expression or the value of scale, whichever is larger.
The result of length( expression) shall be the total number of significant decimal digits in the expression. The scale of the result shall be zero.
The result of scale( expression) shall be the scale of the expression. The scale of the result shall be zero.
A numeric constant shall be an expression. The scale shall be the number of digits that follow the radix point in the input representing the constant, or zero if no radix point appears.
The sequence ( expression ) shall be an expression with the same value and scale as expression. The parentheses can be used to alter the normal precedence.
The semantics of the unary and binary operators are as follows:
-expression
The result shall be the negative of the expression. The scale of the result shall be the scale of expression.
The unary increment and decrement operators shall not modify the scale of the named expression upon which they operate. The scale of the result shall be the scale of that named expression.
++named-expression
The named expression shall be incremented by one. The result shall be the value of the named expression after incrementing.
--named-expression
The named expression shall be decremented by one. The result shall be the value of the named expression after decrementing.
named-expression++
The named expression shall be incremented by one. The result shall be the value of the named expression before incrementing.
_named-expression_--
The named expression shall be decremented by one. The result shall be the value of the named expression before decrementing.
The exponentiation operator, circumflex ( '^' ), shall bind right to left.
expression_^_expression
The result shall be the first expression raised to the power of the second expression. If the second expression is not an integer, the behavior is undefined. If a is the scale of the left expression and b is the absolute value of the right expression, the scale of the result shall be:
if b >= 0 min(a * b, max(scale, a)) if b < 0 scale
The multiplicative operators ( '*', '/', '%' ) shall bind left to right.
expression*expression
The result shall be the product of the two expressions. If a and b are the scales of the two expressions, then the scale of the result shall be:
min(a+b,max(scale,a,b))
expression/expression
The result shall be the quotient of the two expressions. The scale of the result shall be the value of scale.
expression%expression
For expressions a and b, a% b shall be evaluated equivalent to the steps:
- Compute a/ b to current scale.
- Use the result to compute:
a - (a / b) * b
to scale:
max(scale + scale(b), scale(a)) The scale of the result shall be:
max(scale + scale(b), scale(a))
When scale is zero, the '%' operator is the mathematical remainder operator.
The additive operators ( '+', '-' ) shall bind left to right.
expression+expression
The result shall be the sum of the two expressions. The scale of the result shall be the maximum of the scales of the expressions.
_expression_-expression
The result shall be the difference of the two expressions. The scale of the result shall be the maximum of the scales of the expressions.
The assignment operators ( '=', "+=", "-=", "*=", "/=", "%=","^=" ) shall bind right to left.
_named-expression_=expression
This expression shall result in assigning the value of the expression on the right to the named expression on the left. The scale of both the named expression and the result shall be the scale of expression.
The compound assignment forms:
named-expression <_operator_>= expression
shall be equivalent to:
named-expression=named-expression <_operator_> expression
except that the named-expression shall be evaluated only once.
Unlike all other operators, the relational operators ( '<', '>', "<=", ">=","==", "!=" ) shall be only valid as the object of an if, while, or inside a forstatement.
expression1<expression2
The relation shall be true if the value of expression1 is strictly less than the value of expression2.
_expression1_>expression2
The relation shall be true if the value of expression1 is strictly greater than the value of expression2.
expression1<=expression2
The relation shall be true if the value of expression1 is less than or equal to the value of expression2.
_expression1_>=expression2
The relation shall be true if the value of expression1 is greater than or equal to the value of expression2.
_expression1_==expression2
The relation shall be true if the values of expression1 and expression2 are equal.
expression1!=expression2
The relation shall be true if the values of expression1 and expression2 are unequal.
There are only two storage classes in bc: global and automatic (local). Only identifiers that are local to a function need be declared with the auto command. The arguments to a function shall be local to the function. All other identifiers are assumed to be global and available to all functions. All identifiers, global and local, have initial values of zero. Identifiers declared as auto shall be allocated on entry to the function and released on returning from the function. They therefore do not retain values between function calls. Auto arrays shall be specified by the array name followed by empty square brackets. On entry to a function, the old values of the names that appear as parameters and as automatic variables shall be pushed onto a stack. Until the function returns, reference to these names shall refer only to the new values.
References to any of these names from other functions that are called from this function also refer to the new value until one of those functions uses the same name for a local variable.
When a statement is an expression, unless the main operator is an assignment, execution of the statement shall write the value of the expression followed by a .
When a statement is a string, execution of the statement shall write the value of the string.
Statements separated by semicolons or s shall be executed sequentially. In an interactive invocation of_bc_, each time a is read that satisfies the grammatical production:
input_item : semicolon_list NEWLINE
the sequential list of statements making up the semicolon_list shall be executed immediately and any output produced by that execution shall be written without any delay due to buffering.
In an if statement ( if( relation) statement), the statement shall be executed if the relation is true.
The while statement ( while( relation) statement) implements a loop in which the relation is tested; each time the relation is true, the statement shall be executed and the relation retested. When the_relation_ is false, execution shall resume after statement.
A for statement( for( expression; relation; expression) statement) shall be the same as:
_first-expression_while (relation) { statement last-expression}
The application shall ensure that all three expressions are present.
The break statement shall cause termination of a for or while statement.
The auto statement ( auto identifier [, identifier ] ...) shall cause the values of the identifiers to be pushed down. The identifiers can be ordinary identifiers or array identifiers. Array identifiers shall be specified by following the array name by empty square brackets. The application shall ensure that the auto statement is the first statement in a function definition.
A define statement:
define LETTER ( optparameterlist ) { optautodefinelist statementlist}
defines a function named LETTER. If a function named LETTER was previously defined, the define statement shall replace the previous definition. The expression:
LETTER ( optargumentlist )
shall invoke the function named LETTER. The behavior is undefined if the number of arguments in the invocation does not match the number of parameters in the definition. Functions shall be defined before they are invoked. A function shall be considered to be defined within its own body, so recursive calls are valid. The values of numeric constants within a function shall be interpreted in the base specified by the value of the ibase register when the function is invoked.
The return statements ( return and return( expression)) shall cause termination of a function, popping of its auto variables, and specification of the result of the function. The first form shall be equivalent toreturn(0). The value and scale of the result returned by the function shall be the value and scale of the expression returned.
The quit statement ( quit) shall stop execution of a bc program at the point where the statement occurs in the input, even if it occurs in a function definition, or in an if, for, or while statement.
The following functions shall be defined when the -l option is specified:
s( expression )
Sine of argument in radians.
c( expression )
Cosine of argument in radians.
a( expression )
Arctangent of argument.
l( expression )
Natural logarithm of argument.
e( expression )
Exponential function of argument.
j( expression, expression )
Bessel function of integer order.
The scale of the result returned by these functions shall be the value of the scale register at the time the function is invoked. The value of the scale register after these functions have completed their execution shall be the same value it had upon invocation. The behavior is undefined if any of these functions is invoked with an argument outside the domain of the mathematical function.
The following sections are informative.
The bc utility is implemented historically as a front-end processor for dc; dc was not selected to be part of this volume of IEEE Std 1003.1-2001 because bc was thought to have a more intuitive programmatic interface. Current implementations that implement bc using dc are expected to be compliant.
The exit status for error conditions has been left unspecified for several reasons:
- The bc utility is used in both interactive and non-interactive situations. Different exit codes may be appropriate for the two uses.
- It is unclear when a non-zero exit should be given; divide-by-zero, undefined functions, and syntax errors are all possibilities.
- It is not clear what utility the exit status has.
- In the 4.3 BSD, System V, and Ninth Edition implementations, bc works in conjunction with dc. The _dc_utility is the parent, bc is the child. This was done to cleanly terminate bc if dc aborted.
The decision to have bc exit upon encountering an inaccessible input file is based on the belief that bc file1 file2 is used most often when at least file1 contains data/function declarations/initializations. Having_bc_ continue with prerequisite files missing is probably not useful. There is no implication in the CONSEQUENCES OF ERRORS section that bc must check all its files for accessibility before opening any of them.
There was considerable debate on the appropriateness of the language accepted by bc. Several reviewers preferred to see either a pure subset of the C language or some changes to make the language more compatible with C. While the bc language has some obvious similarities to C, it has never claimed to be compatible with any version of C. An interpreter for a subset of C might be a very worthwhile utility, and it could potentially make bc obsolete. However, no such utility is known in historical practice, and it was not within the scope of this volume of IEEE Std 1003.1-2001 to define such a language and utility. If and when they are defined, it may be appropriate to include them in a future version of IEEE Std 1003.1. This left the following alternatives:
- Exclude any calculator language from this volume of IEEE Std 1003.1-2001.
The consensus of the standard developers was that a simple programmatic calculator language is very useful for both applications and interactive users. The only arguments for excluding any calculator were that it would become obsolete if and when a C-compatible one emerged, or that the absence would encourage the development of such a C-compatible one. These arguments did not sufficiently address the needs of current application writers. - Standardize the historical dc, possibly with minor modifications.
The consensus of the standard developers was that dc is a fundamentally less usable language and that that would be far too severe a penalty for avoiding the issue of being similar to but incompatible with C. - Standardize the historical bc, possibly with minor modifications.
This was the approach taken. Most of the proponents of changing the language would not have been satisfied until most or all of the incompatibilities with C were resolved. Since most of the changes considered most desirable would break historical applications and require significant modification to historical implementations, almost no modifications were made. The one significant modification that was made was the replacement of the historical bc assignment operators "=+", and so on, with the more modern "+=", and so on. The older versions are considered to be fundamentally flawed because of the lexical ambiguity in uses like _a_=-1.
In order to permit implementations to deal with backwards-compatibility as they see fit, the behavior of this one ambiguous construct was made undefined. (At least three implementations have been known to support this change already, so the degree of change involved should not be great.)
The '%' operator is the mathematical remainder operator when scale is zero. The behavior of this operator for other values of scale is from historical implementations of bc, and has been maintained for the sake of historical applications despite its non-intuitive nature.
Historical implementations permit setting ibase and obase to a broader range of values. This includes values less than 2, which were not seen as sufficiently useful to standardize. These implementations do not interpret input properly for values of ibase that are greater than 16. This is because numeric constants are recognized syntactically, rather than lexically, as described in this volume of IEEE Std 1003.1-2001. They are built from lexical tokens of single hexadecimal digits and periods. Since s between tokens are not visible at the syntactic level, it is not possible to recognize the multi-digit "digits" used in the higher bases properly. The ability to recognize input in these bases was not considered useful enough to require modifying these implementations. Note that the recognition of numeric constants at the syntactic level is not a problem with conformance to this volume of IEEE Std 1003.1-2001, as it does not impact the behavior of conforming applications (and correct bc programs). Historical implementations also accept input with all of the digits '0' -'9' and 'A' - 'F' regardless of the value of ibase; since digits with value greater than or equal to ibase are not really appropriate, the behavior when they appear is undefined, except for the common case of:
ibase=8; /* Process in octal base. / ... ibase=A / Restore decimal base. */
In some historical implementations, if the expression to be written is an uninitialized array element, a leading and/or up to four leading 0 characters may be output before the character zero. This behavior is considered a bug; it is unlikely that any currently conforming application relies on:
echo 'b[3]' | bc
returning 00000 rather than 0.
Exact calculation of the number of fractional digits to output for a given value in a base other than 10 can be computationally expensive. Historical implementations use a faster approximation, and this is permitted. Note that the requirements apply only to values of obase that this volume of IEEE Std 1003.1-2001 requires implementations to support (in particular, not to 1, 0, or negative bases, if an implementation supports them as an extension).
Historical implementations of bc did not allow array parameters to be passed as the last parameter to a function. New implementations are encouraged to remove this restriction even though it is not required by the grammar.
End of informative text.