Reconstruction As a Set of Linear Equations (original) (raw)

Next: Attenuation Correction Up: Algebraic Reconstruction Methods Previous: Algebraic Reconstruction Methods

A different, and more general, approach to tomographic reconstruction is to formulate the problem in terms of a system of linear equations [4,5]. In order to accomplish this, the image is discretized and approximated by

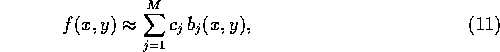
where the 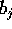are basis functions given by

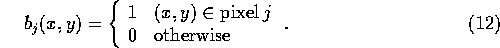
The projection data may now be written as

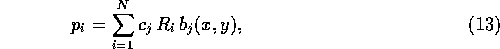
where 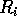is a projection operator that determines the contribution of each pixel to projection i. Since the 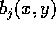are known, the numbers

may be calculated. This results in a matrix W, describing the contribution of each pixel to each projection as shown in Fig. 9, and since only a small number of pixels will contribute to a given projection, W will be a very sparse matrix.

The reconstruction problem is now the problem of solving the linear system of equations,

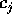where is a vector containing pixel intensities and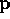 is a vector containing projection values .

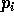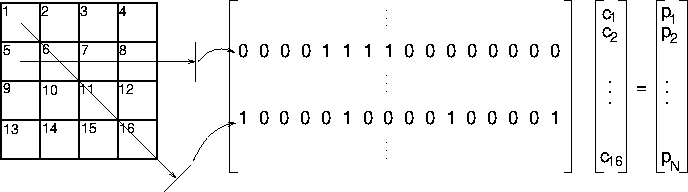
Figure 9: The sparse matrix W contains weighting factors for the contribution of each pixel to individual projection points.

Anders Johan Nygren Thu May 8 12:28:25 CDT 1997