four-level and three-level laser gain media (original) (raw)
Definition: laser gain media without/with reabsorption from the lower laser level
Categories:  optical materials,
optical materials,  laser devices and laser physics
laser devices and laser physics
- laser gain media
- ceramic laser gain media
- rare-earth-doped laser gain media
- transition-metal-doped laser gain media
- four-level and three-level laser gain media
- quasi-three-level laser gain media
- laser crystals
- laser glasses
Related: Ytterbium-doped 975-nm Fiber LasersErbium-doped Fiber Amplifier for Multiple SignalsDesigning a Double-clad Fiber Amplifierlaser physicsquasi-three-level laser gain medialaser gain mediaytterbium-doped laser gain mediarare-earth-doped laser gain medialaser transitionsStark level manifoldssolid-state lasersreciprocity methodeffective transition cross-sectionsUnderstanding Quasi-Three-Level Lasers
Page views in 12 months: 5954
DOI: 10.61835/aun Cite the article: BibTex BibLaTex plain textHTML Link to this page! LinkedIn
Content quality and neutrality are maintained according to our editorial policy.
Contents
Optical amplification in a laser gain medium (of a laser or laser amplifier) arises from stimulated emission, where the input light induces transitions of laser-active ions from some excited state to a lower state and acquires the energy related to the reduction in excitation energy. The characteristics of a gain medium depend substantially on the type of energy level scheme of the laser-active atoms or ions. Although the number of involved levels is not really the crucial aspect, it is common to distinguish profoundly different situations based on simplified schemes with three or four energy levels. In practice, a medium may have additional energy levels which do not necessarily affect the laser characteristics.
In the simplest cases, one is dealing with well-defined energy levels e.g. of isolated atoms or ions. In solid-state laser gain media, the situation is somewhat more complicated, involving Stark level manifolds. The explanations in this article start with simple energy levels, but also consider Stark level manifolds later on.
Three-Level Systems
It was realized early on that for laser amplification one requires at least three energy levels; two levels are not sufficient, since optical pumping can then never result in a population inversion as a requirement for positive laser gain (light amplification). Simultaneous pump absorption and signal amplification cannot occur in such a situation.
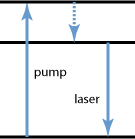
Figure 1: Energy level diagrams of a three-level system. The horizontal lines indicate energy levels; the higher a line, they higher the corresponding energy.
One more energy level is required for pumping, see the left part of Figure 1. Pumping transfers atoms (or ions) from the ground state into a level above the upper laser level, from which the atoms can (usually by non-radiative transitions) get into the upper laser level. An important aspect is that the atoms cannot be pushed back to the ground state by stimulated emission with pump radiation, since their excitation energy is too low for that — they cannot “see” the pump light anymore. Therefore, with sufficiently intense pumping it is possible to reach a population in the upper laser level which is well above 50%, and thus higher than that of the lower laser level (the ground state); a population inversion is reached. In that situation, stimulated emission at the laser wavelength dominates over re-absorption on that laser transition, so that a positive net gain results, which can be used for amplification or laser operation.
Because the population inversion requires that more than half of the atoms are in the upper laser level, pumping with fairly high optical intensity is required. In the case of a laser, the threshold pump power will be correspondingly high, which is often problematic.
A popular example of a three-level laser medium is ruby (Cr3+:Al2O3), as used by Maiman for the first laser, although the situation is in reality somewhat more complicated due to the Stark level manifolds (see below).
Pure three-level laser gain media are seldom used, while quasi-three-level media (see below) are quite common, particularly in the context of fiber lasers and fiber amplifiers.
Ytterbium-doped 975-nm Fiber Lasers
We explore how to realize Yb-doped fiber lasers emitting at the tricky wavelength of 975 nm. This turns out to be challenging for devices with double-clad fibers due to ASE at longer wavelengths.
Four-Level Systems
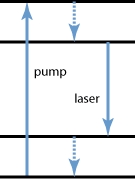
Figure 2: A typical four-level system. The laser transition ends on a level above the ground state, which is quickly depopulated.
A far lower threshold pump power can be achieved with a four-level laser medium, where the lower laser level is well above the ground state (see Figure 2) and is quickly depopulated e.g. by multiphonon transitions (in the case of a solid-state medium) or by collisions (in a gas). Ideally, no appreciable population density in the lower laser level can occur even during laser operation, since the lower laser level is very short-lived. In that way, reabsorption of the laser radiation is largely avoided (provided that there is no absorption on other transitions). This means that there is no absorption of the gain medium in the unpumped state, and a positive net gain is achieved already for a rather low population in the upper laser level. The gain usually rises linearly with the absorbed pump power.
The most popular four-level solid-state gain medium is Nd:YAG. All lasers based on neodymium-doped laser gain media, except those operated on the ground-state transition around 0.9–0.95 μm, are four-level lasers.
Neodymium ions can also be directly pumped into the upper laser level, e.g. with pump light around 880 nm for Nd:YAG. While this reduces the quantum defect and thus possibly increases the laser efficiency, it also opens the possibility of stimulated emission of pump radiation reducing the upper-state population. The latter is not necessarily a problem, since a quite low upper laser level population is sufficient. Even though effectively only three levels are involved, the term three-level system would not be used here.
Quasi-Three-Level Systems
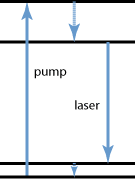
Figure 3: A quasi-three-level system.
A quasi-three-level laser medium is one with a kind of intermediate situation, where the lower laser level is so close to the ground state (see Figure 3) that an appreciable population in that level occurs in thermal equilibrium at the operating temperature. As a consequence, the unpumped gain medium causes some reabsorption loss at the laser wavelength, and transparency is reached only for some finite pump intensity. For higher pump intensities, there is gain, as required for laser operation.
For more details, see the article on quasi-three-level laser gain media.
Stark Level Manifolds
Atoms and ions as used in laser gain media exhibit Stark level manifolds. Depending on how strong the interactions of atoms with their neighborhood are, and how much the nature of that neighborhood varies between different atoms, one may or may not be able to spectroscopically resolve the different Stark levels.
Often, in laser models for solid-state laser gain media one deals with whole Stark level manifolds, rather than with all their sub-levels. The strength of optical transitions is then characterized by effective transition cross-sections, which are intrinsically temperature-dependent. One may still apply the basic reasoning concerning three-level or four-level transitions in such cases, but keeping in mind that some details get more complicated. For example, the effects of different level degeneracies may need to be taken into account. Also, it can happen e.g. that the ground state manifold has its degeneracy lifted so much that one obtains a quasi-three-level system instead of a three-level system: one exploits laser transitions ending on the highest sub-levels of the ground state manifold, which have only a limited thermal population.
Smooth Transition Between Four-level and Three-level Characteristics
There can actually be a smooth transition from three-level to four-level gain characteristics with increasing laser wavelength. For example, erbium-doped glass (see Figure 4) shows strong three-level behavior around 1535 nm but nearly four-level behavior for long wavelengths e.g. beyond 1600 nm. Similarly, ytterbium-doped glasses exhibit pronounced three-level characteristics for wavelengths below ≈ 1040 nm. For operation at such short wavelengths, a large inversion density is required for overcoming the reabsorption loss. For longer wavelengths, as sometimes used particularly in fiber lasers, there is hardly any reabsorption, and in a long fiber only a very low excitation density may be required to obtain sufficient gain.

Figure 4: Gain and absorption (negative gain) of erbium (Er3+) ions in germano-alumino-silicate glass for excitation levels from 0 to 100% in steps of 20%. Strong three-level behavior (with transparency reached only for > 50% excitation) occurs at 1530 nm. At longer wavelengths (e.g. 1580 nm), a lower excitation level is required for obtaining gain, but the maximum gain is smaller.
Pronounced three-level behavior is inevitable for gain media with a very small quantum defect because this enforces a small energy spacing between the lower laser level and the ground state, so that thermal population in the lower laser level is significant.
By reducing the temperature of the laser crystal, it is possible to obtain less pronounced three-level characteristics, i.e., a reduced degree of reabsorption on the laser wavelength. This is essentially because the population in higher-lying sublevels of the ground state manifold is reduced. As an example, Yb:YAG has pronounced three-level characteristics at 1030 nm when operated at room temperature, while essentially four-level characteristics are obtained for cryogenic operation at 77 K (the temperature of liquid nitrogen).
Note that the gain media of semiconductor lasers actually also behave like three-level lasers, exhibiting losses in the unpumped state and a shape of the gain spectrum which depends on the excitation density.
Frequently Asked Questions
This FAQ section was generated with AI based on the article content and has been reviewed by the article’s author (RP).
What is the main difference between three-level and four-level laser gain media?
In a three-level system, the laser transition terminates in the ground state, which requires high pump power to achieve population inversion. In a four-level system, the transition ends on a lower level that is well above the ground state and quickly depopulates, significantly reducing the pump threshold.
Why can't a simple two-level system be used for laser amplification?
A two-level system cannot achieve a population inversion with optical pumping. The rates of pump absorption and stimulated emission become equal when half the atoms are excited, preventing the upper level's population from exceeding the lower level's, which is required for net gain.
How does a four-level laser achieve a low pump threshold?
In a four-level laser, the lower laser level is quickly depopulated, keeping its population near zero. This minimizes reabsorption of the laser light, allowing positive net gain to be achieved with only a small population in the upper laser level, thus lowering the required pump power.
What is a quasi-three-level laser gain medium?
A quasi-three-level medium is an intermediate case where the lower laser level is an excited state but is very close to the ground state. At the operating temperature, this level has a significant thermal population, which causes some reabsorption loss that must be overcome by pumping.
Can a single gain medium exhibit both three-level and four-level characteristics?
Yes, the behavior can depend on the operating wavelength. For example, erbium-doped glass shows strong three-level behavior around 1535 nm but acts more like a four-level system at longer wavelengths beyond 1600 nm, where reabsorption is negligible.
How does temperature affect the behavior of a quasi-three-level laser?
Reducing the temperature can make a quasi-three-level medium behave more like a four-level one. Lowering the temperature reduces the thermal population in the higher sublevels of the ground state manifold, thereby decreasing reabsorption on the laser transition.
Bibliography
| [1] | P. P. Sorokin and M. J. Stevenson, “Stimulated infrared emission from trivalent uranium”, Phys. Rev. Lett. 5 (12), 557 (1960); doi:10.1103/PhysRevLett.5.557 (the first four-level laser) |
|---|---|
| [2] | W. P. Risk, “Modeling of longitudinally pumped solid-state lasers exhibiting reabsorption losses”, J. Opt. Soc. Am. B 5 (7), 1412 (1988); doi:10.1364/JOSAB.5.001412 |
| [3] | J. O. White, “Parameters for quantitative comparison of two-, three-, and four-level laser media, operating wavelengths, and temperatures”, IEEE J. Quantum Electron. 45 (10), 1213 (2009); doi:10.1109/JQE.2009.2020607 |
| [4] | Blog article: What is different for quasi-three-level lasers? |
(Suggest additional literature!)

Questions and Comments from Users
Here you can submit questions and comments. As far as they get accepted by the author, they will appear above this paragraph together with the author’s answer. The author will decide on acceptance based on certain criteria. Essentially, the issue must be of sufficiently broad interest.
Please do not enter personal data here. (See also our privacy declaration.) If you wish to receive personal feedback or consultancy from the author, please contact him, e.g. via e-mail.
By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.
