lstsq — SciPy v1.15.2 Manual (original) (raw)

scipy.linalg.

scipy.linalg.lstsq(a, b, cond=None, overwrite_a=False, overwrite_b=False, check_finite=True, lapack_driver=None)[source]#

Compute least-squares solution to equation Ax = b.

Compute a vector x such that the 2-norm |b - A x| is minimized.

Parameters:

a(M, N) array_like

Left-hand side array

b(M,) or (M, K) array_like

Right hand side array

condfloat, optional

Cutoff for ‘small’ singular values; used to determine effective rank of a. Singular values smaller thancond * largest_singular_value are considered zero.

overwrite_abool, optional

Discard data in a (may enhance performance). Default is False.

overwrite_bbool, optional

Discard data in b (may enhance performance). Default is False.

check_finitebool, optional

Whether to check that the input matrices contain only finite numbers. Disabling may give a performance gain, but may result in problems (crashes, non-termination) if the inputs do contain infinities or NaNs.

lapack_driverstr, optional

Which LAPACK driver is used to solve the least-squares problem. Options are 'gelsd', 'gelsy', 'gelss'. Default ('gelsd') is a good choice. However, 'gelsy' can be slightly faster on many problems. 'gelss' was used historically. It is generally slow but uses less memory.

Added in version 0.17.0.

Returns:

x(N,) or (N, K) ndarray

Least-squares solution.

residues(K,) ndarray or float

Square of the 2-norm for each column in b - a x, if M > N andrank(A) == n (returns a scalar if b is 1-D). Otherwise a (0,)-shaped array is returned.

rankint

Effective rank of a.

s(min(M, N),) ndarray or None

Singular values of a. The condition number of a iss[0] / s[-1].

Raises:

LinAlgError

If computation does not converge.

ValueError

When parameters are not compatible.

Notes

When 'gelsy' is used as a driver, residues is set to a (0,)-shaped array and s is always None.

Examples

import numpy as np from scipy.linalg import lstsq import matplotlib.pyplot as plt

Suppose we have the following data:

x = np.array([1, 2.5, 3.5, 4, 5, 7, 8.5]) y = np.array([0.3, 1.1, 1.5, 2.0, 3.2, 6.6, 8.6])

We want to fit a quadratic polynomial of the form y = a + b*x**2to this data. We first form the “design matrix” M, with a constant column of 1s and a column containing x**2:

M = x[:, np.newaxis]**[0, 2] M array([[ 1. , 1. ], [ 1. , 6.25], [ 1. , 12.25], [ 1. , 16. ], [ 1. , 25. ], [ 1. , 49. ], [ 1. , 72.25]])

We want to find the least-squares solution to M.dot(p) = y, where p is a vector with length 2 that holds the parametersa and b.

p, res, rnk, s = lstsq(M, y) p array([ 0.20925829, 0.12013861])

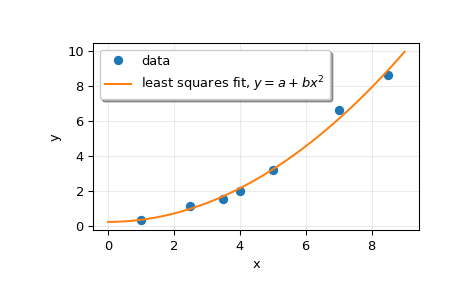
Plot the data and the fitted curve.

plt.plot(x, y, 'o', label='data') xx = np.linspace(0, 9, 101) yy = p[0] + p[1]*xx**2 plt.plot(xx, yy, label='least squares fit, y=a+bx2y = a + bx^2y=a+bx2') plt.xlabel('x') plt.ylabel('y') plt.legend(framealpha=1, shadow=True) plt.grid(alpha=0.25) plt.show()