Online signal extraction by robust regression in moving windows with data-adaptive width selection (original) (raw)

Abstract

Online (also ‘real-time’ or ‘sequential’) signal extraction from noisy and outlier-interfered data streams is a basic but challenging goal. Fitting a robust Repeated Median (Siegel in Biometrika 69:242–244, 1982) regression line in a moving time window has turned out to be a promising approach (Davies et al. in J. Stat. Plan. Inference 122:65–78, 2004; Gather et al. in Comput. Stat. 21:33–51, 2006; Schettlinger et al. in Biomed. Eng. 51:49–56, 2006). The level of the regression line at the rightmost window position, which equates to the current time point in an online application, is then used for signal extraction. However, the choice of the window width has a large impact on the signal extraction, and it is impossible to predetermine an optimal fixed window width for data streams which exhibit signal changes like level shifts and sudden trend changes. We therefore propose a robust test procedure for the online detection of such signal changes. An algorithm including the test allows for online window width adaption, meaning that the window width is chosen w.r.t. the current data situation at each time point. Comparison studies show that our new procedure outperforms an existing Repeated Median filter with automatic window width selection (Schettlinger et al. in Int. J. Adapt. Control Signal Process. 24:346–362, 2010).

Access this article

Log in via an institution

Subscribe and save

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

Discover the latest articles, news and stories from top researchers in related subjects.

References

Download references

Acknowledgements

The financial support of the Deutsche Forschungsgemeinschaft (SFB 823, Statistical modelling of nonlinear dynamic processes) is gratefully acknowledged. The authors thank the referees for their helpful comments.

Author information

Authors and Affiliations

  1. Faculty of Statistics, TU Dortmund University, 44221, Dortmund, Germany
    Matthias Borowski & Roland Fried

Authors

  1. Matthias Borowski
    You can also search for this author inPubMed Google Scholar
  2. Roland Fried
    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence toMatthias Borowski.

Appendices

Appendix A: Monte Carlo approximation of \(\hat{\mbox {V}} ( \ell,1 )\) and \(\hat{\mbox {V}} ( r,1 )\)

We approximate \(v_{n} := \hat{\mbox {V}} ( n,1 )\) for _n_=5,…,300 by the empirical variance of RM slopes which are estimated on samples coming from

Xt−n+i=mut+betatcdot(i−n)+varepsilont−n+i,quadi=1,ldots,n,X_{t-n+i} = \mu_t + \beta_t \cdot(i-n) + \varepsilon_{t-n+i},\quad i = 1,\ldots,n,Xt−n+i=mut+betatcdot(i−n)+varepsilont−n+i,quadi=1,ldots,n,

with standard normal i.i.d. errors ε t_−_n+i ∼N(0,1). W.l.o.g. we set μ t =β t =0 because of the regression equivariance of the RM slope (Rousseeuw and Leroy 1987), i.e. X t_−_n+i =ε t_−_n+i .

We generate time series (x t ) consisting of 100,000+300−1=100,299 observations. Then for each _n_=5,…,300 we move a time window {t_−_n+1…,t} over the time series, starting at time point _t_=300. Hence, for each n we obtain 100,000 RM slopes, and v n is the empirical variance computed on these 100,000 RM slopes. Due to this time series design the RM slopes are autocorrelated, as they are in practice. However, in another simulation study we also approximated the RM slope variance for independent samples. These estimates are comparable to those obtained by the time series design.

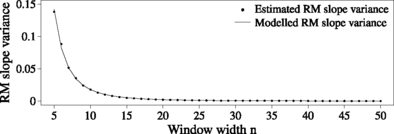
As was to be expected, the variance of the RM slope decreases monotonically with increasing window size n, see Fig. 9. In order to obtain approximations v n for _n_>300, we model the relationship between n and v n and find that the function

v(n)=4.77cdot10−7+17.71cdotn−3v(n)= 4.77 \cdot10^{-7} + 17.71 \cdot n^{-3}v(n)=4.77cdot10−7+17.71cdotn−3

gives an appropriate fit with standard error 0.0004 and coefficient of determination 0.9983.

Fig. 9

figure 9

Empirical variance of 100,000 RM slopes estimated on standard normal samples of size _n_=5,…,50

Full size image

Appendix B: The empirical distribution of the SCARM test statistic

This Monte Carlo study analyzes the distribution of the SCARM test statistic T t under the null hypothesis. That is, we compute T t on samples x t that come from model (4):

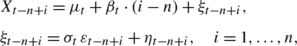
where we set μ t =β t =0 w.l.o.g. due to the regression equivariance of the RM slope. First of all we consider standard normal errors, as assumed in the theoretical development of the SCARM test, i.e. η t_−_n+i =0 and \(\sigma_{t} \, \varepsilon_{t-n+i} \sim N(0,\sigma_{t}^{2})\), and w.l.o.g. we set σ t =1. We generated 10,000 samples of length _n_=ℓ+r for _r_∈{5,10,…,100} and _ℓ_∈{r,r+5,…,100}. Thus, for any combination ℓ,r we obtained 10,000 realizations of the SCARM test statistic T t .

We find that the distribution of the SCARM test statistic can be well approximated by a _t_-distribution with f degrees of freedom, where f depends on ℓ and r. For each combination (ℓ,r), we compare the empirical α_- and (1−_α)-quantiles, _α_=0.01,0.02,…,0.05, of the SCARM test statistic to the corresponding theoretical quantiles of a _t_-distribution with degrees of freedom _f_=0.1,0.2,…,100, in order to find a suitable f for each combination (ℓ,r). For each (ℓ,r)-combination, we choose that f that minimizes the mean absolute difference between the empirical and the theoretical quantiles. Table 4 lists the suitable degrees of freedom f(ℓ,r) for _r_∈{5,10,…,50} and ℓ_∈{r,r+5,…,50}. The degrees of freedom f, and thus the quantiles t f,α/2 and t f,1−_α/2, are expected to be monotonically increasing in ℓ and r. However, this is not true for the approximations of f(ℓ,r) in Table 4. Therefore, for _r_∈{5,…,100} and _ℓ_∈{r,…,100} we set

f(ell,r)=minlimitsell′geqellminlimitsr′geqrbiglfbigl(ell′,r′bigr)bigr,f(\ell,r) = \min\limits _{\ell' \geq\ell} \min\limits _{r' \geq r} \bigl\{ f\bigl( \ell',r'\bigr) \bigr\},f(ell,r)=minlimitsell′geqellminlimitsr′geqrbiglfbigl(ell′,r′bigr)bigr,

(20)

with _r_′∈{5,10,…,50} and _ℓ_′∈{_r_′,r_′+5,…,50} to achieve monotonic degrees of freedom f and thus monotonic critical values t f,α/2 and t f,1−_α/2. By taking the minimum in (20) we decide for larger absolute critical values in order that the test keeps the chosen level of significance α. If ℓ or r is larger than 100, we use standard normal quantiles as critical values.

Table 4 Approximation of the SCARM test statistic distribution by a _t_-distribution: suitable degrees of freedom f(ℓ,r)

Full size table

2.1 B.1 Other error types

We further investigate the distribution of T t for heavy-tailed, skewed, and contaminated errors ξ t_−_n+i , in particular:

Table 5 gives the empirical (1−α/2)-quantiles, _α_=0.01,0.005,0.001, of the computed SCARM test statistics for the four noise types and for different combinations (ℓ,r). Furthermore, the table lists the quantiles of the t f(ℓ,r)-distribution which are used as critical values for test decision. The empirical quantiles are generally lower than the t f -quantiles that are used for test decision, except for (ℓ,r)=(10,10) and given the skewed noise type 2. That is, the test keeps the chosen level of significance, even if the noise is heavy-tailed or contaminated. However, if the noise is skewed, ℓ and r should both not be too small.

Table 5 Quantiles of a t f(ℓ,r) distribution and empirical quantiles of the SCARM test statistic computed on different types of noise

Full size table

Rights and permissions

About this article

Cite this article

Borowski, M., Fried, R. Online signal extraction by robust regression in moving windows with data-adaptive width selection.Stat Comput 24, 597–613 (2014). https://doi.org/10.1007/s11222-013-9391-7

Download citation

Keywords