Generic properties of combinatory maps: Neutral networks of RNA secondary structures (original) (raw)

Abstract

Random graph theory is used to model and analyse the relationship between sequences and secondary structures of RNA molecules, which are understood as mappings from sequence space into shape space. These maps are non-invertible since there are always many orders of magnitude more sequences than structures. Sequences folding into identical structures form_neutral networks_. A neutral network is embedded in the set of sequences that are_compatible_ with the given structure. Networks are modeled as graphs and constructed by random choice of vertices from the space of compatible sequences. The theory characterizes neutral networks by the mean fraction of neutral neighbors (λ). The networks are connected and percolate sequence space if the fraction of neutral nearest neighbors exceeds a threshold value (λ>λ*). Below threshold (λ<λ*), the networks are partitioned into a largest “giant” component and several smaller components. Structure are classified as “common” or “rare” according to the sizes of their pre-images, i.e. according to the fractions of sequences folding into them. The neutral networks of any pair of two different common structures almost touch each other, and, as expressed by the conjecture of_shape space covering_ sequences folding into almost all common structures, can be found in a small ball of an arbitrary location in sequence space. The results from random graph theory are compared to data obtained by folding large samples of RNA sequences. Differences are explained in terms of specific features of RNA molecular structures.

Access this article

Log in via an institution

Subscribe and save

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

Abbreviations

v[_G_]:

Vertex set of graph_G_

e[_G_]:

Edge set of graph_G_

ω(X):

Cardinality of_X_ as a set

δ v :

Vertex degree in a corresponding graph_G_

Q n α :

Generalized hypercube

\(\hat X\) :

X is a random variable

E[\(\hat X\)]:

Expectation value of the random variable\(\hat X\)

V[\(\hat X\)]:

Variance of\(\hat X\)

E[\(\hat X\)] r :

_r_th factorial moment of\(\hat X\)

μ n, λ,μ n :

Measure\(\mu _n (\Gamma _n )\mathop = \limits^{def} \lambda ^{\omega (v[\Gamma ])} (1 - \lambda )^{\omega (v[H]) - \omega (v[\Gamma ])} \)

Ω n :

Probability space ({Γ n },μ n, λ

\(\hat X_{n,k} \) :

Number of vertices in a random graph Γ n having degree_k_

\(\hat I_n (\Gamma _n )\) :

=ω({_v_∈v[Γ n ]|∂{v}∩v[Γ n ]=∅}), i.e., the number of isolated vertices in a random graph Γ n

\(\hat Z_n (\Gamma _n )\) :

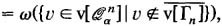
figure 1

i.e. the number of vertices inQ n α that are at least of distance 2 w.r.t. a random graph Γ n

\(M_{n,k}^{\upsilon ,\upsilon '} (\Gamma _n )\) :

Set of paths {π(υ1)|π(υ1)∈Π(Γ n )}

\(\hat Y_{n,k}^{\upsilon ,\upsilon '} \) :

\( = \omega (M_{n,k}^{\upsilon ,\upsilon '} (\Gamma _n ))\) and 0 otherwise

\(\hat \Lambda _{n,k} \) :

Random variable that is 1 if all pairs υ,υ′∈v[Γ n ] with_d(v, v′)<k_ occur in a path of_d_(υ,υ′)<k and 0 otherwise

∂ G V :

Set of adjacent vertices w.r.t. a vertex set_V_⊂v[G_] in a graph_G

\(\bar V\) :

v[V_]∪∂_V, i.e. the closure of_V_

ℬ r (v):

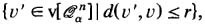
figure 2

the “ball” with radius_r_ and center_v_

n :

Chain length

n u ,n p :

Number of unpaired and paired based of a certain secondary structure

γ n :

(α−1)n, i.e. the vertex degrees ofQ n α

s :

RNA secondary structure in_n_ vertices

Π(s :

\(\mathop = \limits^{def} \left\{ {\left[ {i,k} \right]|a_{i,k} = 1,k \ne i - 1,i + 1} \right\}\) i.e. the set of contacts of the secondary structure_s_

L n :

Shape space, in particular, the space of RNA secondary structures in_n_ vertices

C[_s_]:

Graph of compatible sequences with respect to_s_

C[_s_]:

v[C[_s_]], the set of compatible sequences

S n :

Permutation group of_n_ letters

D m :

Dihedral group of order_2m_

Φ Γ x :

G 1 ×G 2{y_∈v[G 2]⋎(x, y)∈v[⩾s]}], the fiber in_x

Φ Γ y :

G 1 ×G 2[{x_∈v[G 1]⋎(x, y)∈v[⩽s]}], the fiber in_y

Γ A n [_s_]:

Random induced subgraph of

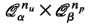
figure 3

according to model A

Γ B n [_s_]:

Random induced subgraph of

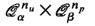
figure 4

according to model B

dist(Γ1, Γ2):

Minimum Hamming distance between the graph Γ1 and Γ2 considered as subgraph ofQ n α

References

Download references

Author information

Authors and Affiliations

  1. Santa Fe Institute, 87501, Santa Fe, NM, U.S.A.
    Christian Reidys, Peter F. Stadler & Peter Schuster
  2. Los Alamos National Laboratory, 87545, Los Alamos, NM, U.S.A.
    Christian Reidys, Peter F. Stadler & Peter Schuster
  3. Institut für Theoretische Chemie der Universität Wien, A-1090, Wien, Austria
    Peter Schuster
  4. Institut für Molekulare Biotechnologie, D-07708, Jena, Germany
    Peter Schuster

Authors

  1. Christian Reidys
    You can also search for this author inPubMed Google Scholar
  2. Peter F. Stadler
    You can also search for this author inPubMed Google Scholar
  3. Peter Schuster
    You can also search for this author inPubMed Google Scholar

Additional information

Deicated to professor Manfred Eigen

Rights and permissions

About this article

Cite this article

Reidys, C., Stadler, P.F. & Schuster, P. Generic properties of combinatory maps: Neutral networks of RNA secondary structures.Bltn Mathcal Biology 59, 339–397 (1997). https://doi.org/10.1007/BF02462007

Download citation

Keywords