Force can overcome object geometry in the perception of shape through active touch (original) (raw)

This is a preview of subscription content, access via your institution

References

1. Gibson, J. J. Observations on active touch. Psychol. Rev. 69, 477–491 (1962).
   Article CAS Google Scholar
2. Loomis, J. M. & Lederman, S. J. in Handbook of Perception and Human Performance Vol. 2 Cognitive Processes and Performance (ed. Boff, K. R. et al.) Ch. 31, 1–41 (New York, Wiley, 1986).
   Google Scholar
3. Lederman, S. J. & Klatzky, R. L. Hand movements: a window into haptic object recognition. Cogn. Psychol. 19, 342–368 (1987).
   Article CAS Google Scholar
4. Pont, S. C., Kappers, A. M. L. & Koenderink, J. J. Similar mechanisms underlie curvature comparison by static and dynamic touch. Percept. Psychophys. 61, 874–894 (1999).
   Article CAS Google Scholar
5. Robles-De-La-Torre, G. & Hayward, V. in Proc. ASME Dynamics Systems and Control Division Vol. 2 (ed. Nair, S. S.) 1081–1085 (The American Society of Mechanical Engineers, New York, 2000).
   Google Scholar
6. Gordon, I. E. & Morison, V. The haptic perception of curvature. Percept. Psychophys. 31, 446–450 (1982).
   Article CAS Google Scholar
7. Taylor, J. L. & McCloskey, D. I. Detection of slow movements imposed at the elbow during active flexion in man. J. Physiol. 457, 503–513 (1992).
   Article CAS Google Scholar
8. Hall, L. A. & McCloskey, D. I. Detections of movements imposed on finger, elbow and shoulder joints. J. Physiol. 335, 519–533 (1983).
   Article CAS Google Scholar
9. Clark, F. J., Burgess, R. C. & Chapin, J. W. Proprioception with the proximal interphalangeal joint of the index finger. Evidence for a movement sense without a static-position sense. Brain 109, 1195–1208 (1986).
   Article Google Scholar
10. Minsky, M. Computational Haptics: The Sandpaper System for Synthesizing Texture for a Force-Feedback Display. PhD dissertation. Massachusetts Institute of Technology (1995).
    Google Scholar
11. Coren, S. The Left-hander Syndrome (Maxwell Macmillan International, New York, 1992).
    Google Scholar

Download references

Acknowledgements

We thank M. Cynader, B. Frost and L. Requadt for helpful comments, and D. Pavlasek and J. Boka for help in designing/building the manipulandum and surfaces. The research was funded by Canada's Network of Centers of Excellence programme, Institute for Robotics and Intelligent Systems, and the Natural Sciences and Engineering Research Council of Canada.

Author information

Authors and Affiliations

1. McGill University, Center for Intelligent Machines, Montréal, H3A 2A7, Canada
   Gabriel Robles-De-La-Torre & Vincent Hayward

Authors

1. Gabriel Robles-De-La-Torre
   You can also search for this author inPubMed Google Scholar
2. Vincent Hayward
   You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence toGabriel Robles-De-La-Torre.

Supplementary information

Scatter plots of datasets used to compute tracking performance in Experiment 1, Conditions 6 and 7.

Figures 6 and 7 present all the data used to compute the correlations shown in Fig. 3c (Condition 6) and Fig. 3d (Condition 7). In Conditions 6 and 7, a force-masked physical shape and a control virtual shape were presented side by side. Subjects were asked to determine the location of the highest/deepest feature. Each panel in Figures 6 and 7 displays scatter plots of localization errors for one subject versus D = L FM − L V, the distance between the force-masked and virtual bumps (Fig. 5). One error (filled circles, Figs. 6 and 7) was E V = L V - L S, the difference between the position of the virtual bump, L V, and L S, the subject's perceived bump position (Fig. 5). The other error (empty circles, Figs. 6 and 7) was E FM = L FM − L S, the difference between the position of the force-masked physical bump, L FM, and the subject's perceived bump position, L S (Fig. 5). The panels in Figure 6 have been sorted in decreasing order by the value of the correlations between the location of control virtual bumps and subject's localization (Fig. 3c, Condition 6). The value of these correlations is indicated on top of each panel.

For most subjects (Fig. 6a-g), the localization error E V with respect to the virtual bump was consistently close to zero (filled circles), while the error E FM with respect to the force-masked physical bump (empty circles) grew as the distance between virtual and physical bumps increased. These subjects consistently tracked the virtual and not the force-masked bumps, as indicated also by the correlations (top of the panels) between subject's localization and the position of the virtual bumps (Fig. 3c, Condition 6, thick circles). The data of the subject exposed to stimuli with spurious correlations (main text, Fig. 3c, Condition 6, Force-masked physical bump) are shown in panel d. This subject also clearly tracked the virtual and not the force-masked bumps.

E V and E FM were frequently close to zero for some subjects (Fig. 6h-j). These subjects sometimes located the virtual bump and sometimes the force-masked physical bump. The data clustering below and above zero error in Fig. 6h-j suggests that these subjects were frequently not accurate when locating either virtual or force-masked stimuli.

Figure 7 shows equivalent error plots for all subjects exposed to virtual and force-masked holes. The error definitions and the order of the panels are the same as those used in Fig. 6. The top of each panel shows the correlations between the location of control virtual holes and subject's localization (Fig. 3d, Condition 7, thick circles). Most subjects (Fig. 7a-f and j) tracked the virtual holes. However, one subject consistently tracked virtual holes (Fig. 7j), but not virtual bumps (Fig. 6j), while a different subject consistently tracked virtual bumps (Fig. 6g) but not virtual holes (Fig. 7g). Also, one subject tracked the force-masked holes (Fig. 7h) and frequently tracked the force-masked bumps, too (Fig. 6h). Finally, one subject tracked both force-masked and virtual stimuli part of the time when presented either with bumps (Fig. 6i) or holes (Fig. 7i).

Figure 5

(GIF 5.88 KB)

The workspace positions of virtual (L V) and force-masked (L FM) shapes were compared in each trial to the subject's perceived position of the shape feature (L S) to compute localization errors.

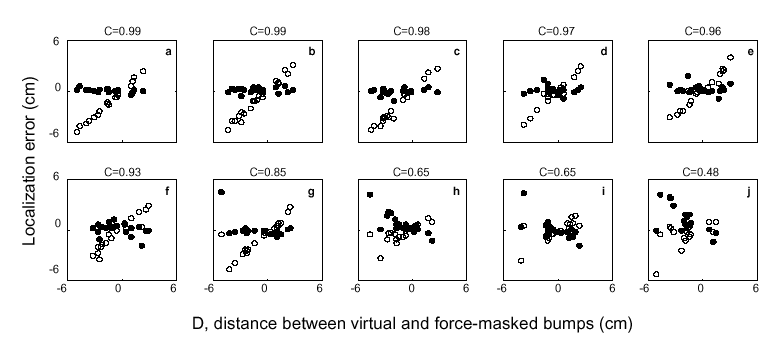
Figure 6

(GIF 12 KB)

Subjects' localization errors with respect to the position of virtual (filled circles) and force-masked bumps (empty circles). Each panel presents data from one subject. Most subjects (a-g) tracked the virtual bumps. Some subjects tracked force-masked bumps to a varying degree (h-j). Each circle represents a trial's error. The horizontal axis indicates the distance between the location of virtual and force masked stimuli (D=L FM -L V, Fig. 5). Panels are sorted by the correlations between subjects' localization and the position of the control virtual bump (Fig. 3c, Condition 6). These correlations are shown on top of each panel.

Figure 7

(GIF 11.4 KB)

Subjects' localization errors with respect to the position of virtual (filled circles) and force-masked holes (empty circles). Each panel presents data from one subject. Most subjects (a-f, j) tracked the virtual holes. Some subjects tracked force-masked holes to a varying degree (g-i). Each circle represents a trial's error. The order of panels is the same as that of Fig. 6. The horizontal axis indicates the distance between the location of virtual and force-masked stimuli (D=L FM -L V, Fig. 5). The correlations between subjects' localization and the position of the control virtual hole (Fig. 3d, Condition 7) are shown on top of each panel.

Rights and permissions

About this article

Cite this article

Robles-De-La-Torre, G., Hayward, V. Force can overcome object geometry in the perception of shape through active touch.Nature 412, 445–448 (2001). https://doi.org/10.1038/35086588

Download citation

• Received: 28 November 2000
• Accepted: 17 May 2001
• Issue Date: 26 July 2001
• DOI: https://doi.org/10.1038/35086588