Experimental realization of the topological Haldane model with ultracold fermions (original) (raw)
- Letter
- Published: 12 November 2014
- Michael Messer1,
- Rémi Desbuquois1,
- Martin Lebrat1,
- Thomas Uehlinger1,
- Daniel Greif1 &
- …
- Tilman Esslinger1
Nature volume 515, pages 237–240 (2014)Cite this article
- 40k Accesses
- 1670 Citations
- 191 Altmetric
- Metrics details
Subjects
Abstract
The Haldane model on a honeycomb lattice is a paradigmatic example of a Hamiltonian featuring topologically distinct phases of matter1. It describes a mechanism through which a quantum Hall effect can appear as an intrinsic property of a band structure, rather than being caused by an external magnetic field2. Although physical implementation has been considered unlikely, the Haldane model has provided the conceptual basis for theoretical and experimental research exploring topological insulators and superconductors2,3,4,5,6. Here we report the experimental realization of the Haldane model and the characterization of its topological band structure, using ultracold fermionic atoms in a periodically modulated optical honeycomb lattice. The Haldane model is based on breaking both time-reversal symmetry and inversion symmetry. To break time-reversal symmetry, we introduce complex next-nearest-neighbour tunnelling terms, which we induce through circular modulation of the lattice position7. To break inversion symmetry, we create an energy offset between neighbouring sites8. Breaking either of these symmetries opens a gap in the band structure, which we probe using momentum-resolved interband transitions. We explore the resulting Berry curvatures, which characterize the topology of the lowest band, by applying a constant force to the atoms and find orthogonal drifts analogous to a Hall current. The competition between the two broken symmetries gives rise to a transition between topologically distinct regimes. By identifying the vanishing gap at a single Dirac point, we map out this transition line experimentally and quantitatively compare it to calculations using Floquet theory without free parameters. We verify that our approach, which allows us to tune the topological properties dynamically, is suitable even for interacting fermionic systems. Furthermore, we propose a direct extension to realize spin-dependent topological Hamiltonians.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout
Additional access options:
Similar content being viewed by others
References
- Haldane, F. D. M. Model for a quantum Hall Effect without Landau levels: condensed-matter realization of the ‘parity’ anomaly. Phys. Rev. Lett. 61, 2015–2018 (1988)
Article ADS MathSciNet CAS Google Scholar - Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013)
Article ADS CAS Google Scholar - Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005)
Article ADS CAS Google Scholar - König, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007)
Article ADS Google Scholar - Hsieh, D. et al. A topological Dirac insulator in a quantum spin Hall phase. Nature 452, 970–974 (2008)
Article ADS CAS Google Scholar - Hasan, M. Z. & Kane, C. L. Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010)
Article ADS CAS Google Scholar - Oka, T. & Aoki, H. Photovoltaic Hall effect in graphene. Phys. Rev. B 79, 081406 (2009)
Article ADS Google Scholar - Tarruell, L., Greif, D., Uehlinger, T., Jotzu, G. & Esslinger, T. Creating, moving and merging Dirac points with a Fermi gas in a tunable honeycomb lattice. Nature 483, 302–305 (2012)
Article ADS CAS Google Scholar - Dunlap, D. & Kenkre, V. Dynamic localization of a charged particle moving under the influence of an electric field. Phys. Rev. B 34, 3625–3633 (1986)
Article ADS CAS Google Scholar - Lignier, H. et al. Dynamical control of matter-wave tunneling in periodic potentials. Phys. Rev. Lett. 99, 220403 (2007)
Article ADS CAS Google Scholar - Struck, J. et al. Tunable gauge potential for neutral and spinless particles in driven optical lattices. Phys. Rev. Lett. 108, 225304 (2012)
Article ADS CAS Google Scholar - Jiménez-García, K. et al. Peierls substitution in an engineered lattice potential. Phys. Rev. Lett. 108, 225303 (2012)
Article ADS Google Scholar - Parker, C. V., Ha, L.-C. & Chin, C. Direct observation of effective ferromagnetic domains of cold atoms in a shaken optical lattice. Nature Phys. 9, 769–774 (2013)
Article ADS CAS Google Scholar - Zenesini, A., Lignier, H., Ciampini, D., Morsch, O. & Arimondo, E. Coherent control of dressed matter waves. Phys. Rev. Lett. 102, 100403 (2009)
Article ADS Google Scholar - Struck, J. et al. Quantum simulation of frustrated classical magnetism in triangular optical lattices. Science 333, 996–999 (2011)
Article ADS CAS Google Scholar - Aidelsburger, M. et al. Experimental realization of strong effective magnetic fields in an optical lattice. Phys. Rev. Lett. 107, 255301 (2011)
Article ADS CAS Google Scholar - Struck, J. et al. Engineering Ising-XY spin-models in a triangular lattice using tunable artificial gauge fields. Nature Phys. 9, 738–743 (2013)
Article ADS CAS Google Scholar - Williams, R. A., Al-Assam, S. & Foot, C. J. Observation of vortex nucleation in a rotating two-dimensional lattice of Bose-Einstein condensates. Phys. Rev. Lett. 104, 050404 (2010)
Article ADS CAS Google Scholar - Aidelsburger, M. et al. Realization of the Hofstadter Hamiltonian with ultracold atoms in optical lattices. Phys. Rev. Lett. 111, 185301 (2013)
Article ADS CAS Google Scholar - Miyake, H., Siviloglou, G. A., Kennedy, C. J., Burton, W. C. & Ketterle, W. Realizing the Harper Hamiltonian with laser-assisted tunneling in optical lattices. Phys. Rev. Lett. 111, 185302 (2013)
Article ADS Google Scholar - Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013)
Article ADS CAS Google Scholar - Lim, L.-K., Fuchs, J.-N. & Montambaux, G. Bloch-Zener oscillations across a merging transition of Dirac points. Phys. Rev. Lett. 108, 175303 (2012)
Article ADS Google Scholar - Chang, M.-C. & Niu, Q. Berry phase, hyperorbits, and the Hofstadter spectrum. Phys. Rev. Lett. 75, 1348–1351 (1995)
Article ADS CAS Google Scholar - Dudarev, A. M., Diener, R. B., Carusotto, I. & Niu, Q. Spin-orbit coupling and Berry phase with ultracold atoms in 2D optical lattices. Phys. Rev. Lett. 92, 153005 (2004)
Article ADS Google Scholar - Price, H. M. & Cooper, N. R. Mapping the Berry curvature from semiclassical dynamics in optical lattices. Phys. Rev. A 85, 033620 (2012)
Article ADS Google Scholar - Dauphin, A. & Goldman, N. Extracting the Chern number from the dynamics of a Fermi gas: implementing a quantum Hall bar for cold atoms. Phys. Rev. Lett. 111, 135302 (2013)
Article ADS Google Scholar - Uehlinger, T. et al. Artificial graphene with tunable interactions. Phys. Rev. Lett. 111, 185307 (2013)
Article ADS Google Scholar - Varney, C. N., Sun, K., Rigol, M. & Galitski, V. Interaction effects and quantum phase transitions in topological insulators. Phys. Rev. B 82, 115125 (2010)
Article ADS Google Scholar - Neupert, T., Santos, L., Chamon, C. & Mudry, C. Fractional quantum Hall states at zero magnetic field. Phys. Rev. Lett. 106, 236804 (2011)
Article ADS Google Scholar - Grushin, A. G., Gómez-León, A. & Neupert, T. Floquet fractional Chern insulators. Phys. Rev. Lett. 112, 156801 (2014)
Article ADS Google Scholar - Greif, D., Tarruell, L., Uehlinger, T., Jördens, R. & Esslinger, T. Probing nearest-neighbor correlations of ultracold fermions in an optical lattice. Phys. Rev. Lett. 106, 145302 (2011)
Article ADS Google Scholar
Acknowledgements
We thank H. Aoki for drawing our attention to the relevance of their proposal for optical lattices and N. Cooper, S. Huber, L. Tarruell, L. Wang and A. Zenesini for discussions. We acknowledge the SNF, the NCCR-QSIT and the SQMS (ERC advanced grant) for funding.
Author information
Authors and Affiliations
- Institute for Quantum Electronics, ETH Zurich, 8093 Zurich, Switzerland,
Gregor Jotzu, Michael Messer, Rémi Desbuquois, Martin Lebrat, Thomas Uehlinger, Daniel Greif & Tilman Esslinger
Authors
- Gregor Jotzu
You can also search for this author inPubMed Google Scholar - Michael Messer
You can also search for this author inPubMed Google Scholar - Rémi Desbuquois
You can also search for this author inPubMed Google Scholar - Martin Lebrat
You can also search for this author inPubMed Google Scholar - Thomas Uehlinger
You can also search for this author inPubMed Google Scholar - Daniel Greif
You can also search for this author inPubMed Google Scholar - Tilman Esslinger
You can also search for this author inPubMed Google Scholar
Contributions
The data were measured by G.J., M.M., R.D. and D.G. and analysed by G.J., M.M., R.D., T.U. and D.G. The theoretical framework was developed by G.J. and M.L. All work was supervised by T.E. All authors contributed to planning the experiment, discussions and the preparation of the manuscript.
Corresponding author
Correspondence toTilman Esslinger.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Semi-classical simulations of the atomic motion.
The experiments shown in the main text in Fig. 2c and d are simulated using the semi-classical equations of motion (equations (6)–(9)). The band structure and the Berry curvature are those of the effective Haldane Hamiltonian (equation (1)). The atomic ensemble is modelled by a zero-temperature Fermi distribution. Data are mean ± s.d. of three simulations containing 4 × 104 trajectories. The differential drift 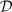 is computed when breaking either IS (a) or TRS (b). The former shows no differential drift, in agreement with the experimental data of Fig. 2c. For the latter, the different curves take into account the transfer to the higher band by excluding trajectories passing through regions where the bandgap lies below a certain threshold. If this transfer is not taken into account (purple line), the differential drift varies sharply around ϕ = 0° where the Chern number changes. However, as the threshold is raised to 0.5Δ_E_ (red line) and Δ_E_ (green line) where Δ_E_/h = 114.6 Hz is the energy offset per site driving the Bloch oscillation, this sharp feature progressively smoothens and qualitatively reproduces the experimental measurements. c, When TRS is maximally broken (ϕ = 90°) and Δ_AB varies, the transfer is also responsible for the differential drift extending beyond the topological phase. Without any transfer (purple line), the differential drift changes sharply around the topological phase transition (vertical dashed line), while it extends significantly in the topologically trivial phase when the threshold is set at Δ_E (green line) or 3Δ_E_ (blue line). d, Influence of the transverse trapping frequency ω x/2π. The frequency used in the experiment is indicated by a purple arrow. For much larger frequencies the differential drift can vanish, as the transverse oscillation time becomes comparable to the Bloch period.
is computed when breaking either IS (a) or TRS (b). The former shows no differential drift, in agreement with the experimental data of Fig. 2c. For the latter, the different curves take into account the transfer to the higher band by excluding trajectories passing through regions where the bandgap lies below a certain threshold. If this transfer is not taken into account (purple line), the differential drift varies sharply around ϕ = 0° where the Chern number changes. However, as the threshold is raised to 0.5Δ_E_ (red line) and Δ_E_ (green line) where Δ_E_/h = 114.6 Hz is the energy offset per site driving the Bloch oscillation, this sharp feature progressively smoothens and qualitatively reproduces the experimental measurements. c, When TRS is maximally broken (ϕ = 90°) and Δ_AB varies, the transfer is also responsible for the differential drift extending beyond the topological phase. Without any transfer (purple line), the differential drift changes sharply around the topological phase transition (vertical dashed line), while it extends significantly in the topologically trivial phase when the threshold is set at Δ_E (green line) or 3Δ_E_ (blue line). d, Influence of the transverse trapping frequency ω x/2π. The frequency used in the experiment is indicated by a purple arrow. For much larger frequencies the differential drift can vanish, as the transverse oscillation time becomes comparable to the Bloch period.
Extended Data Figure 2 Drift measurement for broken IS and TRS.
The measured drift used to obtain the differential drift 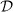 in Figs 2c, d and 4 of the main text is individually shown for positive and negative forces in the q y direction. Data for positive (negative) force is shown in blue (red). The central plot, showing the Haldane phase diagram, indicates the region which is scanned when breaking either IS (purple arrow) or TRS (brown arrow) in our system. a, We break IS by introducing a sublattice offset and show measurements with modulation frequency of 4.0 kHz and 3.75 kHz. Although the opposite Berry curvatures at the two Dirac points sum up to zero within the first Brillouin zone, we clearly see a drift depending on the size of _Δ_AB. Data show mean ± s.d. of at least 6 (4.0 kHz) or 2 (3.75 kHz) measurements. b, By changing the modulation phase difference ϕ we break TRS and the system enters the topologically non-trivial regime. Drift data for positive (negative) force is shown in blue (red) for a modulation frequency of 4.0 kHz and 3.75 kHz. Data show mean ± s.d. of at least 21 (4.0 kHz) or 6 (3.75 kHz) measurements. Schematics below show the expected orthogonal drifts caused by driving the atoms through the Berry curvature distribution. Red (blue) indicates positive (negative) Berry curvature. If only IS is broken (a) the Berry curvature distribution is point-antisymmetric and changes sign when changing the sign of the sublattice offset. For opposite forces this leads to the same direction of the drift, as indicated by the white arrows. If only TRS is broken (b) the Berry curvature distribution at each Dirac point has the same sign, which is changed when reversing the rotation direction. In this case the opposite forces lead to opposite directions of the drift.
in Figs 2c, d and 4 of the main text is individually shown for positive and negative forces in the q y direction. Data for positive (negative) force is shown in blue (red). The central plot, showing the Haldane phase diagram, indicates the region which is scanned when breaking either IS (purple arrow) or TRS (brown arrow) in our system. a, We break IS by introducing a sublattice offset and show measurements with modulation frequency of 4.0 kHz and 3.75 kHz. Although the opposite Berry curvatures at the two Dirac points sum up to zero within the first Brillouin zone, we clearly see a drift depending on the size of _Δ_AB. Data show mean ± s.d. of at least 6 (4.0 kHz) or 2 (3.75 kHz) measurements. b, By changing the modulation phase difference ϕ we break TRS and the system enters the topologically non-trivial regime. Drift data for positive (negative) force is shown in blue (red) for a modulation frequency of 4.0 kHz and 3.75 kHz. Data show mean ± s.d. of at least 21 (4.0 kHz) or 6 (3.75 kHz) measurements. Schematics below show the expected orthogonal drifts caused by driving the atoms through the Berry curvature distribution. Red (blue) indicates positive (negative) Berry curvature. If only IS is broken (a) the Berry curvature distribution is point-antisymmetric and changes sign when changing the sign of the sublattice offset. For opposite forces this leads to the same direction of the drift, as indicated by the white arrows. If only TRS is broken (b) the Berry curvature distribution at each Dirac point has the same sign, which is changed when reversing the rotation direction. In this case the opposite forces lead to opposite directions of the drift.
Extended Data Figure 3 Heating of a repulsively interacting Fermi gas.
a, Entropy increase associated with loading into the modulated lattice and reversing the loading procedure. b, Entropy increase rate in the modulated lattice for long holding times. The modulation frequency ω = 2π × 1,080 Hz opens a gap of h × 44 Hz in the non-interacting band-structure. This value, in units of the tunnelling, is similar to the measurements of the main text. The dashed lines show the measured heating in a lattice without modulation with identical interaction strengths.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data, Supplementary Figures 1-13, Supplementary Table 1 and additional references. (PDF 1531 kb)
PowerPoint slides
Source data
Rights and permissions
About this article
Cite this article
Jotzu, G., Messer, M., Desbuquois, R. et al. Experimental realization of the topological Haldane model with ultracold fermions.Nature 515, 237–240 (2014). https://doi.org/10.1038/nature13915
- Received: 19 June 2014
- Accepted: 29 September 2014
- Published: 12 November 2014
- Issue Date: 13 November 2014
- DOI: https://doi.org/10.1038/nature13915
This article is cited by
Editorial Summary
Lab demonstrations of the topological Haldane model
The quantum Hall effect leads to topologically protected edge states, and for a long time was thought to exclusively emerge in the presence of an external magnetic field. But in 1988, Duncan Haldane proposed a model in which this exotic electronics structure arises without this requirement. He proposed that, in a honeycomb lattice with a staggered flux, the necessary ingredients for a quantum Hall effect would be inherent in the material itself. The principles behind this concept were later recruited to design topological insulators, but in its original expression, the Haldane model has not been observed in the laboratory. In this issue of Nature, two groups report on progress connected to the Haldane model. Gregor Jotzu et al. report the first realization of the Haldane model and Pedram Roushan et al. show how it can be precisely measured. Jotzu et al. use ultracold fermions to realize the breaking of time-reversal and inversion symmetry — the two main requirements of the model — by implementing a circular modulation of the lattice position and an energy offset between neighbouring sites. Roushan et al. use superconducting quantum circuits — a Josephson junction sandwiched between superconducting electrodes — to realize a non-interacting form of the Haldane model with a single qubit and an interacting two-qubit model through a new experimental setup called 'gmon' coupling architecture. Their setup allows them to characterize both cases by measuring the Berry curvature, a feature that all topological structures have in common.