Topological and causal structure of the yeast transcriptional regulatory network (original) (raw)
In integrating genome-wide data on transcript abundance1 into a dynamic view of gene networks, recent studies have focused on abstracting the principles that underlie the architecture and causal interplay of these networks. At present, the yeast Saccharomyces cerevisiae is the most suitable eukaryotic organism for achieving this goal, as much information about its transcriptional regulations has been accumulated2,3. Of roughly 6,000 yeast genes, 124 have been shown through genetic and biochemical experiments to encode regulating proteins that can influence the expression of specific genes2. These data were obtained from a previous review2 and were validated and updated, until July 2001, by manual inspection of the websites of MIPS, SwissProt, Yeast Protein Database, S. cerevisiae Promoter Database and the Saccharomyces Genome Database (see Web Note A online). The elements of the general transcription initiation machinery were excluded from this study, although some have differential roles in transcription of large subsets of genes3. Some of the 124 regulatory genes transcriptionally control a set of 367 non-regulatory genes (Fig. 1) through 837 connections (see Web Table A online). Of the 124 regulatory genes, 52 interact with themselves or with other regulatory genes through 72 additional links (see Web Table A online). A transcriptional regulatory network can thus be represented as a graph where vertices are genes and directed edges denote activating or repressing effects on transcription. The graph of these 52 'interregulatory' genes comprises mainly several small disconnected components (Fig. 1).
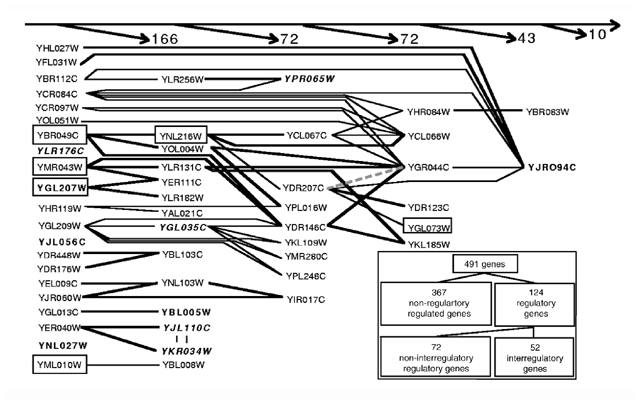
Figure 1: Data set on the experimentally established genetic interactions in yeast.
The graph shows causal relations among the 52 interregulatory genes. To indicate downstream causality (top arrow), genes lacking a known regulator other than mutual or self-regulation are listed in the left column. The other genes are then placed in the leftmost column so that all of their regulators locate to their left. Following the same rule, above are shown the numbers of nonregulatory genes (names omitted) regulated by genes from each column. From left to right, downstream causation emphasizes the consequences of altering a gene's activity for other genes. From right to left, upstream causation reveals the sources of a gene's perturbation. Bold type indicates self-activation, bold italics indicates self-inhibition and borders indicate essential genes. Thick lines represent activation, thin lines represent inhibition and the dashed gray line represents dual regulation.
Most networks fall into two major categories on the basis of their connectivity distribution, p k, which represents the probability that a vertex in the network is connected to k other vertices. One category of networks is characterized by a _p_k that peaks at an average _k_mean and decays exponentially for large k4,5. In these exponential networks, most vertices have approximately the same number of links. By contrast, metabolic pathways6,7,8 belong to a category of nonhomogeneous networks, where p k decays as a power law. As the connections are inherently oriented in a transcriptional regulatory network, we separately analyzed the number of regulating proteins per regulated gene (arriving connectivity) and the number of regulated genes per regulating protein (departing connectivity), to determine whether they were best described by the exponential or power-law models.
The arriving connectivity of the yeast network has an exponential distribution, with 93% of the genes being regulated by 1–4 regulating proteins (Fig. 2_a_). The probability_p_ k that a given target gene is regulated by k regulating proteins decreases roughly as C_e_−βk (C is a constant), with _β_∼0.45 for both the total set of regulated genes and its interregulatory subset. The available data for Escherichia coli9 are compatible with an exponential distribution of arriving connections, with _β_∼1.2; this higher β coefficient means that fewer targets have many regulators. This coefficient thus reflects the molecular limits on the number of regulating proteins that can combinatorially exert an effect on the target gene expression. Consequently, lower coefficients are predicted for multicellular organisms with a more sophisticated genetic regulatory machinery.
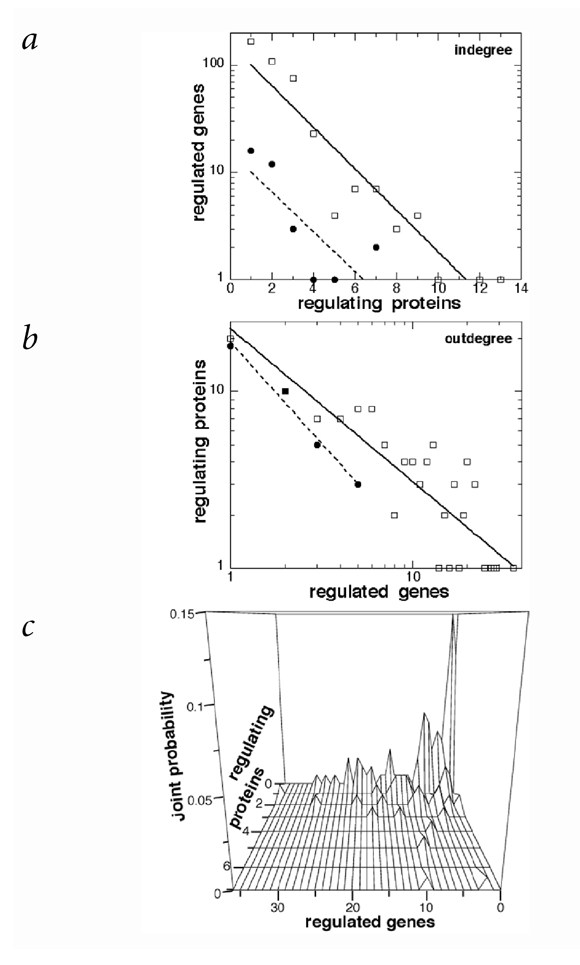
Figure 2: Connectivity of the yeast genetic network.
a, Arriving connectivity distribution (semi-log plot). The number of regulating proteins per regulated gene follows an exponential distribution (least-square method) both for all 402 regulated genes (367 nonregulatory and 35 interregulatory genes—17 interregulatory genes are excluded because they lack a known regulator; 909 connections; open squares, full line; _p_k=157e−0.45k; _R_=0.99) and for the subset of 35 interregulatory genes (72 connections; filled circles, broken line; _p_k=15e−0.43k; _R_=0.94). b, Departing connectivity distribution (log/log plot). The number of regulated genes per regulating protein better fits a power-law distribution both for all 124 regulating proteins (909 connections; open squares, full line; _P_k=23_k_−0.87; _R_=0.95) and for its subset of 37 regulating proteins that control regulatory genes (72 connections; filled circles, broken line; _P_k=19_k_−1.14; _R_=0.99). Opposite views (a versus b; exponential departing and power-law arriving connectivities) would give lower correlation coefficients (_R_=0.88, 0.91, 0.83 and 0.98, respectively) and very different slopes for global versus interregulatory genes. Null values were discarded. c, Joint distributions. The probability that a randomly chosen gene has in arriving and out departing connections is distributed on this linear plot as a function of in (regulating proteins) and out (regulated genes).
The departing connectivity of the yeast network does not seem to be distributed according to an exponential law (Fig. 2_b_). It fits better a power law, although there are insufficient data to rule out other possibilities. The probability p k that a given regulating protein regulates k target genes decreases as approximately C_k_−γ, with _γ_∼1 for both the global set of 124 regulatory proteins and its interregulatory subset. For E. coli as well, _γ_∼1 (our best fit computed from ref.9; see also refs 8,10). Because _γ_∼1, the number of departing connections (kp _k_∼_k_C_k_−1=C) is distributed almost equally over k, unlike the connections present in metabolic networks (_γ_∼1.5–3)6,7,8. Thus, bacterial and fungal genetic networks are free of a characteristic scale with respect to the distributions of both regulating proteins and departing connections.
The differing distribution laws for arriving and departing connectivities suggests that there is a correlation between them. A joint distribution (Fig. 2_c_) shows that genes with few regulators also tend to have few targets. Because there are many such genes, inactivating a gene selected at random has a low probability of altering the pathway structure of other genes. In contrast, inactivating one of the few highly connected genes would greatly decrease the communication between the remaining genes11 and could be lethal. Of 124 regulatory genes, 10 are essential, including 6 interregulatory genes that tend to be located upstream in the causal graph (Fig. 1). Indeed, their overall influence (direct and indirect targets) is twice as big on average as that of nonessential genes.
To evaluate the generality of the predicted topology, two things must be determined: (i) to what extent the present compilation differs from a complete yeast data set and (ii) whether the observed global topology is likely to hold true as more data accumulate. On the basis of sequence homology, at most, 77 additional yeast genes encode putative regulating proteins (see Web Note A online); however, recent work has investigated the genome-wide locations of 12 DNA-binding proteins, using chromatin immunoprecipitation and microarrays12,13,14,15. Depending on the laboratory, the number of targets thus obtained is on average 3.5-fold12,15 and 26-fold13,14 greater than the number found here for the same regulators (see Web Table A online). Although the exact number of targets depends on a somewhat arbitrary threshold, it is already clear that this new method has the potential to reveal many unsuspected links12,13,14,15. It is therefore essential to re-evaluate the topology of the yeast network once a sufficient set of regulatory genes has been studied with this genome-wide approach and universal threshold definitions. Moreover, theoretical considerations, consistent with the comparison of a subset to the whole set (Fig. 2_a_,b), suggest a way in which future data may affect the described network structure. If departing connectivity is free of a characteristic scale, future data should presumably not alter the power-law parameters. If arriving connectivity is shaped by the sophistication of the regulatory machinery, additional data would probably increase C while maintaining β.
To assess how accurately various models represent the biological situation, the actual yeast genetic network (a) was compared with directed random graphs modeled under three assumptions (see Web Note B online and Fig. 2): the connectivity distributions conform with (b) the empirical data (c) the laws deduced in Fig. 2 and (d) a Poisson law. A uniformly distributed connectivity (d) favors the emergence of a connected component that comprises the majority of the genes (Table 1), which is not observed. By contrast, both random graphs with constrained connectivity distributions (b or c; Fig. 2) reasonably approximate the average number of neighbors one or two steps away. At a more refined grain, however, they are no longer acceptable approximations. The local attribution of a few edges per vertex in a sparse graph is an important parameter that affects the network dynamics. It could be uniform, as in random graphs4, or highly clustered, as in small worlds5; extreme local clustering would result in global fragmentation, unlike small worlds, which still retain large connected components. Global fragmentation is observed (Fig. 1), beyond that expected from the empirical data or the deduced laws (b or c; Table 1). A clustering coefficient has been proposed to quantify the propensity of the links reaching an individual to involve him or her in local social interactions within 'cliques'5. Because genetic networks are directed, we introduce the notion of upstream or downstream 'semi-cliquishness' (see Web Note B online). The corresponding semi-clustering coefficients are approximately fivefold higher than those expected for the yeast network in a constrained random graph (Table 1). Along the same lines, the total number of observed feedback circuits is fivefold higher than that predicted by (b) or (c), and 14-fold higher for single-gene circuits(Table 1).
Table 1 Structure of the yeast transcriptional regulatory network.
These circuits are crucial to the dynamics of the system. Positive circuits comprise an even number of inhibitory interactions and contribute to multistationarity, whereas negative circuits comprise an odd number of inhibitory interactions and contribute to homeostasis16. In this view, higher organisms are expected to rely more heavily than lower ones on positive circuits, particularly to achieve cellular differentiation, with each cell type corresponding to one of several stationary states. We observed five negative and six positive circuits in 52 yeast interregulatory genes (Fig. 1). As expected, this is in marked contrast to the genes of E. coli, where 45 circuits (39 negative, 3 positive, 3 dual) were observed for 55 interregulatory genes9. Yeast positive circuits control switching processes, such as those leading to pseudohyphal growth (YJL110C/YKR034W, controlled by YER040W)17, sporulation (YJR094C)18 or multiple-drug resistance (YBL005W)19. Negative circuits are constituted by (self-) inhibitors that finely control responses to the absence of glucose (YGL035C)20, DNA damage (YLR176C)21 or oxygen (YPR065W)22.
As a whole, the yeast transcriptional regulatory network combines a small maximal diameter, an elevated local semi-clustering, a high number of feedback circuits and a global fragmentation. This departure from a random distribution must reflect functional constraints. Indeed, each small connected piece implements a biological function, and the global fragmentation may serve to limit inter-functional crosstalk at the transcriptional level. The elevated clustering and feedback content probably implement differentiative and homeostatic requirements. Single-gene feedback circuits are predominant (this study and ref. 9) and may have been selected through evolution for several reasons: (i) they decrease the biosynthetic cost (roughly proportional to the amount of transcripts and proteins to be produced), (ii) together with the small diameter, they reduce the response delay (often a consequence of macromolecular synthesis) and (iii) they stabilize the fluctuations of expression of the involved genes23. Similar laws seem to govern the local and global network topologies in eukaryotes and prokaryotes, notwithstanding the circuit sign. When prior knowledge of the specific transcriptional connections is limited, these laws may prove general enough to facilitate the integration of transcriptomic data into dynamic models of genetic networks.
Note: Supplementary information is available on the Nature Genetics website.