Biomarker-based prognosis in hepatocellular carcinoma: validation and extension of the BALAD model (original) (raw)

Main

The key features that influence prognosis in hepatocellular carcinoma (HCC) are now well recognised and can be broadly classified under the headings of tumour-related factors (such as tumour size or multiplicity), those that assess the severity of underlying liver dysfunction (such as conventional liver function tests or the Child–Pugh (C-P) classification (Child and Turcotte, 1964; Pugh et al, 1973)) and patient-related factors (such as symptoms or performance status). Several staging systems/prognostic scores that combine a number of these factors have been developed (Okuda et al, 1985; Group, 1998; Chevret et al, 1999; Leung et al, 2002; Kudo et al, 2003; Llovet et al, 2008) and, to varying degrees, validated and compared (Kudo et al, 2004; Marrero et al, 2005; Cho et al, 2008; Collette et al, 2008; Chen et al, 2009; Huitzil-Melendez et al, 2010; Chan et al, 2011). Some simply offer an estimate of prognosis, whereas others aim to indicate the appropriate therapy for specific disease stages (Llovet et al, 2008).

In an attempt to develop a more objective staging system, Toyoda et al (2006) have described the BALAD model that relies on two liver function tests (Bilirubin and Albumin) and three serological cancer biomarkers (AFP-L3, AFP, and DCP). They have shown that it is possible to achieve an excellent degree of discrimination between the proposed risk groups using such objective variables. However, the data analysis approach in the BALAD model utilised dichotomisation of the continuous variables, which raises a number of statistical issues.

In the present study, we aimed to validate the original BALAD model (built on a Japanese Cohort) in a geographically and aetiologically distinct HCC patient data set from the UK. We first confirmed that the variables in the BALAD model were identical to those independently identified in a UK data set, and assessed the discrimination achieved within the proposed prognostic groups. We then, in a collaborative Japan/UK study, took the raw data on which BALAD model was initially derived and applied a more sophisticated statistical method that treats the variables in a continuous manner and does not assume a linear relationship between predictors and outcome. The model developed here not only allows classification of patient risk, as with the original BALAD model, but also provides detailed estimation of patient-level survival in the Japanese cohort, and, with calibration, in UK patients.

A major challenge in applying the BALAD model to the UK population is the great difference in survival compared with the Japanese cohort. This problem is due to the difference in the underlying survivor function that describes hazard in relation to time; hazard could be greatest at diagnosis and then decrease over time or, conversely, the hazard at diagnosis may be low and then increase as time accumulates. Indeed, the hazard may be described by a more complicated, non-linear, and not necessarily monotonic function. To account for such differences, the methods applied in this analysis allowed interrogation of the scale and shape of the baseline hazard function.

The derived model is assessed in terms of discrimination and calibration. To assess discrimination, Harrell’s _C_-statistic was measured, as described by [Taktak et al (2007)](/articles/bjc2014130#ref-CR34 "Taktak AFG, Eleuteri A, Lake SP, Fisher AC (2007) Evaluation of prognostic models: discrimination and calibration performance. Comput Intell Med (Plymouth) Available at http://pcwww.liv.ac.uk/~afgt/CIMED07_1.pdf

              ."). This measures the proportion of patient pairs for which the model correctly assigns lower risk to the patient who truly survives longest (i.e. is at least risk). A model with good discriminative performance should have a high _C_\-statistic. To assess calibration, graphical methods were used. These assessments compare patient level survival with the predicted values.

Materials and methods

The study comprised two cohorts of patients. The first included 2599 Japanese patients previously reported by Toyoda et al (2006) and 319 UK patients, all with HCC (Table 1). The Japanese patients were recruited from five institutions in which a total of 3725 patients were initially diagnosed as having HCC between July 1994 and December 2004, and the UK patients from among 724 patients referred to the Queen Elizabeth, Birmingham, UK, between June 2007 and January 2012. The various aetiologies were classified as hepatitis B virus-related, hepatitis C virus-related, alcoholic-related, and ‘other’. The ‘other’ group comprised patients with hemochromatosis, primary biliary cirrhosis, non-alcoholic steatohepatitis, or cryptogenic cirrhosis. The diagnosis of chronic liver disease was made on the basis of liver biopsy and/or typical clinical and imaging features. The study protocol was approved by the institutional ethics review board at each of the institutions.

Table 1 Demographics and clinical data for the two cohorts

Full size table

Age and gender distributions were similar in the two populations, as was the distribution of liver dysfunction as assessed by the C-P classification (Table 1). However, there were striking differences in aetiological attribution, the Japanese patients having predominantly HCV-related HCC and the UK patients having multiple aetiologies. There were also major differences in disease stage (Table 1) and overall survival between the two cohorts. The median survival for those treated with palliative and curative therapy was 22.6 and 60.7 months for Japanese patients, respectively, with analogous figures for the UK of 13.9 and 27.5 months.

In all patients, the three serological cancer biomarkers of HCC (AFP, AFP-L3, and DCP) were measured at the time of diagnosis, and drugs that would influence the serum DCP levels, such as warfarin and vitamin K, were not taken. A standard operating procedure was applied to all blood collection. Samples were collected in the fasting state, before any treatment. Blood was allowed to clot at room temperature for 1–2 h, centrifuged at 3000 g for 20 min and the serum collected and stored at −80 °C until processing. Routine liver and renal function was measured by commercially available methods. Albumin was measured by the bromocresol green method in both UK and Japan. The severity of the liver disease was defined according to C-P classification.

Patients were staged by five systems: TNM 5, TNM 6 (Sobin and Fleming, 1997; Greene et al, 2002; UICC, 2002; Sobin et al, 2011), CLIP (Group, 1998), JIS or BCLC (Llovet et al, 2008), or by Milan criteria (Mazzaferro et al, 1996). However, for this analysis that focused on prognosis, we also grouped patients on the basis of whether or not the treatment received was curative or palliative. Curative treatments included transplantation, resection, radiofrequency ablation, and percutaneous ethanol injection. Palliative treatments included transarterial chemoembolisation, any form of chemotherapy, and supportive care. Where patients were listed for transplantation but had transarterial chemoembolisation as initial treatment as a ‘bridge’ to transplantation, they were classified as having potentially curative therapy. For the purpose of this analysis, UK patients who underwent liver transplantation were excluded, as the survival of this group would not be expected to be influenced by the baseline features included in the model (such as bilirubin and albumin).

Assays of AFP, AFP-L3%, and DCP

AFP, AFP-L3%, and DCP were all measured in the same serum sample. The measurements of hs-AFP-L3% and DCP were achieved by using a microchip capillary electrophoresis and liquid-phase binding assay on a μTASWako i30 auto analyzer (Wako Pure Chemical Industries, Ltd, Osaka, Japan) (Kagebayashi et al, 2009). Analytical sensitivity of μTASWako i30 is 0.3 ng ml−1 AFP, and the percentage of AFP-L3 can be measured when AFP-L3 is over 0.3 ng ml−1 (Kagebayashi et al, 2009).

Statistical methods

Discrimination

We assessed discriminatory performance using Harrell’s _C_-statistic, as described by [Taktak et al (2007)](/articles/bjc2014130#ref-CR34 "Taktak AFG, Eleuteri A, Lake SP, Fisher AC (2007) Evaluation of prognostic models: discrimination and calibration performance. Comput Intell Med (Plymouth) Available at http://pcwww.liv.ac.uk/~afgt/CIMED07_1.pdf

              ."). In brief, this measure reports the number of comparable pairs that are correctly ordered under the risk score. That is, for a pair of comparable patients PA and PB, if patient PA is known to have survived beyond PB’s time of event (death here), then PA should be subject to a lesser risk than PB, that is, should be assigned a lower-risk group. This method counts all the correctly ordered pairs from those that are comparable.

Flexible parametric models

Regression analyses utilised flexible parametric models (Royston and Lambert, 2011) that enable fitting of more appropriate baseline hazard functions. The baseline hazard describes risk over time when all covariates take the value zero (rather than the hazard at time zero as sometimes stated), and is described by a restricted cubic spline function (Royston and Lambert, 2011). Here all continuous covariates are centred about their mean, and so the interpretation of the function is the hazard at the mean of all covariates. Traditionally, the baseline hazard is assumed to have a simple constant or monotonic form, as in exponential or Weibull survival models, and Cox modelling does not directly model the baseline hazard function. The model as described here comprises two main components: the baseline hazard, which is described by a spline function consisting of a constant value and a function of log-time, and the covariate vector, which modifies risk based on the subject’s covariate values. Each of these components can be recalibrated (Van Houwelingen, 2000) should the model not perform as expected. Given our intention to apply the model in two geographically distinct cohorts, we assessed the baseline hazard function, as clinical insights led us to expect a difference.

Stata version 12 was used for all analyses.

Replication of BALAD results and model derivation

As an exploratory step, we validated the original BALAD model in both the Japanese and UK cohorts. Like Toyoda et al (2006), we fitted univariable Cox regression models to verify the set of prognostic parameters and confirmed that statistical significance was maintained when entered into a multivariable model. The steps taken by Toyoda to dichotomise the continuous data were not replicated. The BALAD score was calculated for each cohort and discrimination was assessed by fitting Kaplan–Meier (KM) curves and measuring Harrell’s C. A ‘training’ data set, which comprised 50% (Royston and Lambert, 2011) of the Japanese cohort, was used to derive the prognostic model, and the remainder was held back for validation. The random selection of the hold-back sample was stratified by treatment intention (potentially curative and palliative) such that each subset was equally represented in the training and validation data sets. A cohort of UK individuals was also used in the validation process.

New prognostic model

We then fitted flexible parametric survival models to the Japanese data, applying a more rigorous statistical approach in which the continuous form of the covariates was maintained and linearity of predictor–outcome relation was not assumed. Univariable and multivariable models were fitted to identify important prognostic factors with potential prognostic factors chosen from those that were not considered subjective. Martingale residuals were inspected to aid the choice of the appropriate covariate functional form and second-order fractional polynomials were explored, taking powers from the standard power set. Predictors were selected at the _P_=0.05 level in the multivariable modelling procedure that combined backward elimination with the selection of an FP function. Models were compared using Akaike information criteria (AIC); a 4-point reduction (per additional covariate) is indicative of an improved model. Having identified a preferred prognostic model, we then fitted a model keeping only the serological cancer biomarkers to see if similar performance could be obtained at less ‘cost’.

Development of scoring mechanisms

To assign risk groups ‘Cox cut-points’ were applied by splitting risk predictions, based on the relative part of the model only, in the training data at the 15th, 50th, and 85th percentiles. As a result, individuals were categorised into 1 of 4 levels of risk, ranging from low to high. We then calculated individual risk in the hold-back data and classified patients based on the cut-points established earlier. We refer to this discriminatory model as BALAD-2d. By incorporating risk as a function of time, that is, the baseline hazard function, we could estimate the probability of survival for each individual patient. We refer to this patient-level predictor as BALAD-2p.

Model validation

BALAD-2d: The prognostic model was validated using graphical methods (Royston and Lambert, 2011). A visual inspection of discrimination between the groups was performed and survival statistics were compared to assess the clinical relevance of the model. We assessed Harrell’s C of each model in a number of patient subgroups: stage of disease, treatment intention, tumour size, and BCLC (available only in UK patients).

BALAD-2p: Stata’s suite of flexible parametric modelling (stpm2) post-estimation tools were used to estimate population average survival for each validation cohort, thus allowing Kaplan–Meier curves depicting actual vs predicted survival to be plotted for each risk group. The similarity of the curves is indicative of the performance of the model. To determine if the model is appropriate for the estimation of patient-level survival in the UK validation set, or if recalibration was required, we assessed the similarity of the baseline hazard in each cohort by plotting the function. We also demonstrate the use of the BALAD-2p by example and report the results by graphical means.

Results

Replication of BALAD results

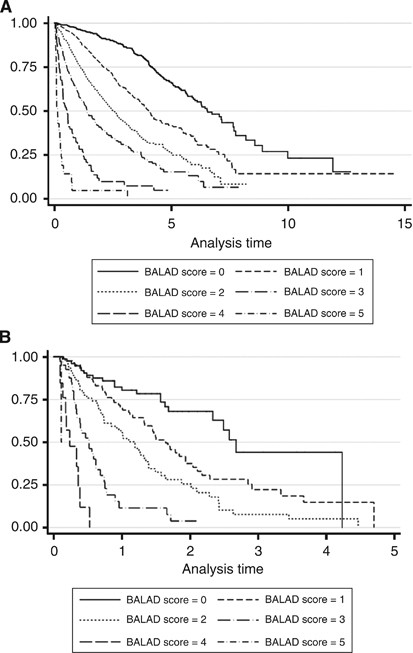
We confirmed that for both the Japanese and UK cohorts the measures of serological cancer biomarkers and bilirubin are associated with increased risk of mortality (results not shown); albumin is associated with a decreased risk. The Kaplan–Meier survival curves according to BALAD scores are shown in Figure 1A and B. For BALAD model in the Japanese and UK cohorts the respective Harrell’s _C-_statistics were 0.73 and 0.71, indicating similar discriminative performance. We note that for the BALAD model in the UK cohort there is overlap of the curves in the first 6 months and that there are very few patients in the highest-risk group. Table 2 reports the median survival with 95% confidence intervals; the estimates for the Japanese cohort are quite distinct; however, for the UK patients there is little difference in median survival for some of the groups, indicating that, from a clinical perspective, the BALAD model may have too many levels for use in the UK. The hazard ratio estimates for the BALAD score in the Japanese cohort ranged from 2.24 (95% CI, 1.85–2.72) in the lowest-risk group to 48.48 (95% CI, 30.52–77.02) in the highest-risk group. In the UK cohort, the corresponding figures were 1.93 (95% CI, 1.18–3.17) and 210.42 (95% CI, 20.87–2121.74). Between these two values, each cohort indicated an increasing trend in risk.

Figure 1

figure 1

Survival according to the BALAD model. Kaplan–Meier curves showing survival according to the original BALAD model in (A) Japanese and (B) UK cohorts.

Full size image

Table 2 Median survival times for BALAD and BALAD-2d in Japanese (validation) and UK cohorts

Full size table

New prognostic model

We split the 2599 Japanese patients into a ‘training’ set of 1327 patients and a hold-back set of 1272, and, as a result of stratification by treatment intent, each data set was approximately equal in terms of the proportion of curative (and therefore palliative) patients (33.5% training and 33.8% validation).

The univariable analysis confirmed that the variables in the original BALAD model are all highly prognostic (Table 3), and these factors maintained statistical significance in the resulting multivariable model (data not shown). The fractional polynomial transformations identified for the multivariable model were a log transform for DCP and a square-root for bilirubin. The AIC for this model was 2341. An increase in each of the markers, other than albumin, is associated with an increase in risk, and increased albumin has a beneficial effect on prognosis.

Table 3 Univariable analysis in Japanese training data

Full size table

The linear predictor resulting from the multivariable analysis considering the 5-serological cancer biomarkers – bilirubin, albumin, AFP-L3, AFP, and DCP – as potential prognostic factors is reported below. This function, the BALAD-2d score, calculates the log cumulative hazard for an individual:

Linear predictor (xb)=0.02*(afp_c−2.57)+0.012*(AFP-L3−14.19)+0.19*(ln(DCP)−1.93)+0.17*((bili(μmoll)1/2)−4.50)−0.09*(alb(gl)−35.11)

As part of the modelling procedure AFP was capped at 50 000 units. Both AFP and DCP are modelled as per 1000 units.

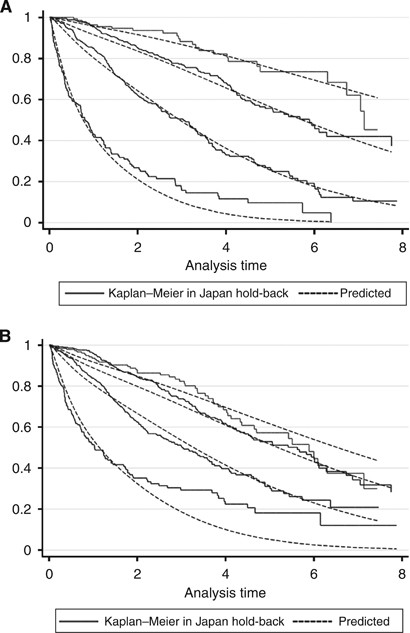
The multivariable model incorporating just the three serological cancer biomarkers had considerable overlap between the two lower-risk groups, indicating that the discriminative performance was considerably poorer than the 5-serological-cancer-biomarker model that included bilirubin and albumin (Harrell’s C of 0.69, AIC 2536) (Figure 2A and B).

Figure 2

figure 2

Comparison of five-marker and three-marker BALAD-2d model. Kaplan–Meier curves depicting actual (solid line) and predicted (dashed line) survival using a multivariable model incorporating (A) five serological cancer biomarkers and (B) three serological cancer biomarkers from the Japanese hold-back sample.

Full size image

BALAD-2d validation in the Japanese cohort

Application of the Cox cut-points for the linear predictor yielded four classes (1–4) of risk. These cut-points were as follows: xb>0.24 (risk 1, low), 0.24 to >−0.91 (risk 2), −0.91 to >−1.74 (risk 3) and ⩽−1.74 (risk 4, high). The KM survival curves depicting actual and predicted survival in the Japanese hold-back sample (Figure 2A) indicate that the risk groups are well discriminated (Harrell’s C 0.74). The logrank test indicates a statistically significant risk difference (P<0.001) and the differences in survival between the groups are clinically meaningful and distinct (Table 2). Harrell’s C was approximately equal in the subgroup comparisons detailed in the foregoing. Both BALAD and BALAD-2d models perform better in patients at greater risk.

Recalibration for use in the UK cohort

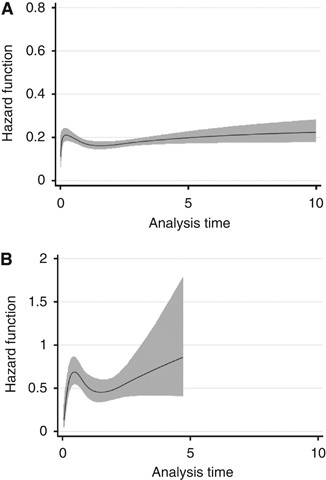
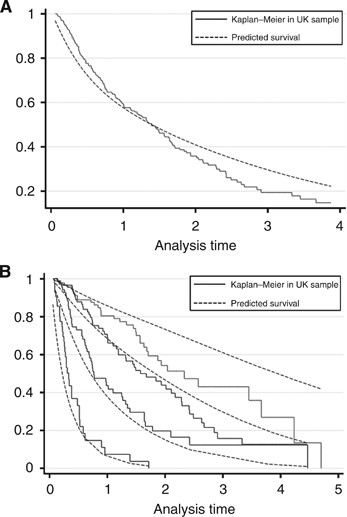
Figure 3A and B describe the baseline hazard function for each of the cohorts. The baseline hazards are similar in shape but differ in height or magnitude, indicating the need for recalibration (see Supplementary Data for methodology). Adjustment to the constant term in the spline function only was deemed sufficient. Figure 4A shows that for the recalibrated model the overall predicted survival curve approximates the true survival well; here we optimised the fit between 0 and 3 years. Survival is predicted best of all in the higher-risk groups, and there is some overestimation for patients in the lowest-risk group (Figure 4B). The model has an AIC of 827 compared with 1096 prior to recalibration, an improvement of 269 points. Note that the AIC in the Japanese cohort is not comparable to that in the UK.

Figure 3

figure 3

Baseline hazards. Plots illustrating the baseline hazard function with 95% confidence interval, CI (shaded region) for each of the (A) Japanese and (B) UK cohorts.

Full size image

Figure 4

figure 4

Kaplan–Meier curves of actual vs predicted survival in the UK cohort. Kaplan–Meier curves showing actual (solid line) vs predicted (dashed line) survival (A) overall and (B) by risk group, using the recalibrated model in the UK cohort.

Full size image

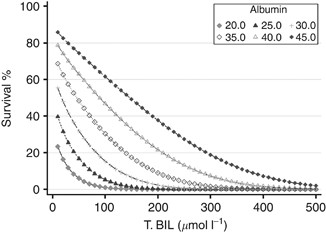
Figure 5 demonstrates patient-level survival estimation and reports predictions of 2-year survival for increasing levels of albumin and bilirubin; all other parameters are fixed (AFP 34, AFP-L3 16.1, and DCP 1.14). Each curve describes an incrementally different level of albumin, and each point along a curve represents a change in bilirubin. As observed in the regression analysis, increased bilirubin is associated with an increase in risk and albumin is negatively correlated with risk.

Figure 5

figure 5

Example of patient-level survival estimation. Reporting predictions of 2-year survival and describing the impact of increasing albumin and bilirubin; all other parameters are fixed (AFP 34, AFP-L3 16.1, and DCP 1.14).

Full size image

Discussion

We have confirmed that the biological factors identified in the original BALAD model, as described by Toyoda et al (2006), are highly prognostic. When applied to the UK patients, the BALAD model gave good discrimination, although performance appeared poorer among the UK cohort, particularly in groups 4 and 5, those with the worst survival (Figure 1B). Most likely the reason for the apparent limited degree of discrimination in these groups is related to the very small numbers (only 13 cases in group 4 and 20 in group 5), and the fact that survival for both these groups is only of the order of a few weeks indicates that there is little scope for clear discrimination. The overlap between risk groups is less evident for BALAD-2d, and the Harrell’s _C_-test is, in fact, similar, indicating that there is no major difference in discriminatory performance despite the new model using just four risk groups.

One of the concerns about current staging systems is that they encompass factors that are inherently subjective, leading to a potential lack of consistency between observers. For example, one of the most widely used, the CLIP (Group, 1998), system estimates the extent of tumour as > or <50% of the total liver volume, a measurement that, in clinical practice, is difficult to ascertain with any degree of certainty or consistency. Others such as CUPI (Leung et al, 2002) and BCLC (Llovet et al, 2008) demand a decision as to whether or not patients are symptomatic. Again, in practice this assessment may be highly variable between observers. Even widely used measures of liver function such as the C-P classification (Child and Turcotte, 1964; Pugh et al, 1973), which was developed for patients with cirrhosis rather than HCC, is remarkably subjective. Thus, presence/severity of ascites (one of the constituent variables in the C-P score) is, by some practitioners, based on whether or not subjects have ever developed ascites. Others may include ascites even when it is detectable only by radiological scanning and some may consider ascites to be ‘absent’ if it is controlled by diuretics. Encephalopathy may be equally difficult to grade, because of many of the early symptoms overlapping with those that may be attributable to the HCC. Such concerns have led to the development of objective measures of liver function such as the MELD score (Malinchoc et al, 2000; Botta et al, 2003), which is based solely on blood tests.

The second weakness of some of the current staging systems is that, perhaps in the pursuit of simplicity, they handle the relevant data in a categorical manner when it is, in fact, generated as a continuous variable. The loss of information consequent upon this approach is now increasingly well recognised, and it has been suggested that dichotomisation of continuous data in a multiple regression procedure may be associated with considerable loss of statistical power and introduction of bias (Del Priore et al, 1997; Royston et al, 2006). The most noticeable impact lies in those patients who fall around the ‘cut-point’, that is, just below or above the value used to define the two levels of the binary variable. They may be classified as having very different risk. Equally, in the C-P classification, a patient with a score based on a serum bilirubin level of 51 μmol l−1 has the same impact as one with a value of 500 μmol l−1 and a serum albumin of 24 g l−1, a similar impact as a serum albumin of 10 g l−1. Indeed, it has been shown that dichotomising (at the median) a normally distributed variable is equivalent to losing a third of the data. When the variable in question is exponentially distributed then such a conversion is equivalent to a loss of around half of the data (Royston et al, 2006). It has also been shown that in the case of logistic regression the chance of false positives is increased; as the sample size increases, so does the chance of such errors (Austin and Brunner, 2004).

Among the numerous biomarkers (Mann et al, 2007) that have been proposed for prognostication in HCC, the three used here have the advantage of being commercially available on a single platform and having regulatory approval in Japan, US, and Europe. All three are well documented to have prognostic significance when used individually, prognosis becoming poorer with increasing levels (Nagaoka et al, 2003; Toyoda et al, 2007; Nouso et al, 2011). AFP is also included in some staging systems such as CLIP (Group, 1998), where a level of >400 ng ml−1 is an adverse feature, and in the UK guidelines for liver transplantation levels of >10 000 are a contraindication to transplantation (NHSBT, 2013).

The BALAD model has an advantage over current staging systems in that it is entirely objective. The Toyoda model utilised a common method for determining the value at which continuous covariates were dichotomised, that is, multiple testing in search of the ‘optimal’ value. Altman et al (1994) appropriately refer to this approach as the ‘minimum _P_-value approach’, as the use of the term optimal is perhaps misleading. There are several issues with this approach. The value, if truly optimal, is likely to be such only in the derivation cohort. Furthermore, the values identified at the univariable level are not necessarily accurate in the multivariable setting. The Type I error rate is greatly increased, and as such there is a greater risk of incorrectly identifying prognostic factors. The extent of this increase is influenced by the number of values tested, and is reported to be in the region of 40% (Altman et al, 1994).

In this paper we have undertaken further detailed analyses of the data in its continuous form. The regression analyses were performed using flexible parametric models (Royston and Lambert, 2011), described earlier, with which we were able to examine the baseline hazard function and assess the need for model recalibration for use in cohorts outside Japan. By exploring fractional polynomials (Sauerbrei and Royston, 1999) (FPs) many of the issues associated with dichotomisation and data-driven cut-points are minimised or avoided. If appropriate, more intricate relationships between the outcome and explanatory variables can be fitted. Over-fitting of either the baseline hazard or the covariate functional form is a potential issue but is unlikely if the number of knots and the power-set for the FPs are sensibly chosen. Given the size of the Japanese cohort in particular, throughout our analyses we purposely avoided over-interpretation of _P_-values and considered more the clinical significance of the results.

At present, we cannot be certain of the reason for the markedly differing survival in the two cohorts. However, the most plausible explanation, and one supported by the data presented here, is that the Japanese patients are diagnosed at a much earlier stage, and hence are much more likely to receive potentially curative therapy. Again the most plausible explanation is that the Japanese population at risk of HCC (those with chronic liver disease) is more rigorously screened than that in the UK. Although we cannot rule out the influence of aetiology, we can be confident that ethnicity is unlikely to be responsible as survival in Japan was only 7 months in the decade 1975–85 and has risen steadily thereafter, coincidentally with the introduction of screening (Ikai et al, 2010).

Our analyses demonstrated that in both the Japanese and UK cohorts BALAD-2d model has a marginally better level of discrimination compared with the BALAD model despite the former having just four risk levels. Furthermore, visual inspection of the BALAD model suggested that, in the UK cohort at least, six risk levels is too many and that the BALAD-2d model is more appropriate. For risk grouping, such as BALAD or BALAD-2d, it is implicit that patients belonging to the same risk group have equal survival probability. This is of course not necessarily the case; patients at the extremes of each risk group are classified as equal but most likely have quite different chance of survival. BALAD-2p model does not suffer from this limitation.

We addressed the discrepancy in magnitude of the underlying hazard between the UK and Japanese patients through model recalibration. The relatively minor adjustments required are indicative of the transferability of the model, and we have shown that the covariate effects in the Japanese cohort are applicable in UK patients. Had recalibration beyond simple adjustment to the height of the baseline hazard been required (e.g. changes to the shape of the baseline hazard, or even the covariate vector), then the validity of BALAD-2p model would have been questionable. In this case we had no such concerns. Although the BALAD-2p model builds on the BALAD model’s concept by including the ability to predict patient-level survival (Figure 5) and as such is a more powerful prognostic device, validation in other regions of the world, especially where the aetiology is related to Hepatitis B, is still required.

Change history

This paper was modified 12 months after initial publication to switch to Creative Commons licence terms, as noted at publication

References

Download references

Acknowledgements

The analysis undertaken in this research was partly funded by Liverpool Health Partners.

Author information

Authors and Affiliations

  1. Cancer Research UK Clinical Trials Unit, School of Cancer Sciences, University of Birmingham, Birmingham, B15 2TT, UK
    R Fox
  2. Department of Molecular and Clinical Cancer Medicine, University of Liverpool, Liverpool, L69 3GA, UK
    S Berhane & P J Johnson
  3. Department of Oncology, Addenbrooke’s Hospital, University of Cambridge, Cambridge, CB2 0QQ, UK
    M Teng
  4. Liverpool Cancer Research UK Centre, Liverpool Cancer Trials Unit, University of Liverpool, Liverpool, L69 3GL, UK
    T Cox
  5. Department of Gastroenterology and Hepatology, Ogaki Municipal Hospital, Gifu, 503-8052, Japan
    T Tada, H Toyoda & T Kumada
  6. Wako Life Sciences, Inc., Mountain View, 94043-1829, CA, USA
    C Kagebayashi & S Satomura
  7. The Clatterbridge Cancer Centre NHS Foundation Trust, Clatterbridge Road, Bebington, Wirral, CH63 4JY, UK
    P J Johnson

Authors

  1. R Fox
    You can also search for this author inPubMed Google Scholar
  2. S Berhane
    You can also search for this author inPubMed Google Scholar
  3. M Teng
    You can also search for this author inPubMed Google Scholar
  4. T Cox
    You can also search for this author inPubMed Google Scholar
  5. T Tada
    You can also search for this author inPubMed Google Scholar
  6. H Toyoda
    You can also search for this author inPubMed Google Scholar
  7. T Kumada
    You can also search for this author inPubMed Google Scholar
  8. C Kagebayashi
    You can also search for this author inPubMed Google Scholar
  9. S Satomura
    You can also search for this author inPubMed Google Scholar
  10. P J Johnson
    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence toP J Johnson.

Additional information

This work is published under the standard license to publish agreement. After 12 months the work will become freely available and the license terms will switch to a Creative Commons Attribution-NonCommercial-Share Alike 3.0 Unported License.

Supplementary Information accompanies this paper on British Journal of Cancer website

Supplementary information

Rights and permissions

From twelve months after its original publication, this work is licensed under the Creative Commons Attribution-NonCommercial-Share Alike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/

Reprints and permissions

About this article

Cite this article

Fox, R., Berhane, S., Teng, M. et al. Biomarker-based prognosis in hepatocellular carcinoma: validation and extension of the BALAD model.Br J Cancer 110, 2090–2098 (2014). https://doi.org/10.1038/bjc.2014.130

Download citation

Keywords