Cell-to-cell variability in cell death: can systems biology help us make sense of it all? (original) (raw)
Facts
- Responses to apoptosis-inducing drugs or ligands are often heterogeneous.
- Single-cell measurements are key to accurate characterization and modeling of heterogeneous responses.
- State-space maps allow contextualization of protein function in cellular response.
- Single-cell signaling dynamics can encode information on cellular responses.
Questions
- Can computational models of cell death incorporate multiple sources of cell-to-cell variability?
- Can multivariate analysis approaches direct the design of effective combination therapies?
- Can we improve on current anticancer therapies by optimizing treatment sequence and dosing schedules?
Cell death in its various forms, including apoptosis and necrosis, has an essential role in development and in tissue homeostasis. When cell death regulation is derailed, disease ensues: too much cell death can lead to neurodegenerative diseases, while too little cell death can lead to autoimmune disorders or cancer. Nevertheless, when observing cell death under a microscope or plotting a dose-response curve to a drug or ligand, one observation recurs frequently, that some cells live and others die. How does this cell-to-cell variability affect our understanding of cell death? How does it impact human health and disease treatments? Although the concepts that we aim to cover are likely relevant to all forms of cell death and to the treatment of many diseases, we will focus largely on apoptosis in cancer, a context in which cell death has been heavily studied using a systems biology approach. Triggering programmed cell death or circumventing a defect in this process have been long-standing goals in cancer therapy and the systems biology of apoptosis is so far a pillar of the budding field of systems pharmacology.
How can systems biology help our efforts to understand and co-opt cell death in cancer? It may help by extracting mechanistic insights in cancer cell behavior and providing a broader view of signaling systems, while applying the iterative strategy to ‘measure, model, and manipulate’. Biologists have long applied this strategy, but systems biology makes it more explicit by bringing formalized, or mathematical, models to the forefront. Here we will discuss how we interpret measurements of cell death, how cell-to-cell variability impacts it, and how we build computational models to understand and predict cell death responses. We also explore the impact of what we have learned about the sources of cell-to-cell variability on our approaches to manipulating the biochemical state of cancer cells to induce cell death.
Interpreting Measurements of Cell Death in the Presence of Cell-to-Cell Variability
With its emphasis on quantitative results, one of the cornerstones of the systems biology of cell death is quantitative, or semiquantitative, measurements of various steps in the cell death process. Many assays developed to characterize programmed cell death since ‘apoptosis’ was coined1 have been leveraged for systems-level studies. Here we consider existing expertly cataloged assays,2 and the information they provide about cell-to-cell variability in cancer cell death.
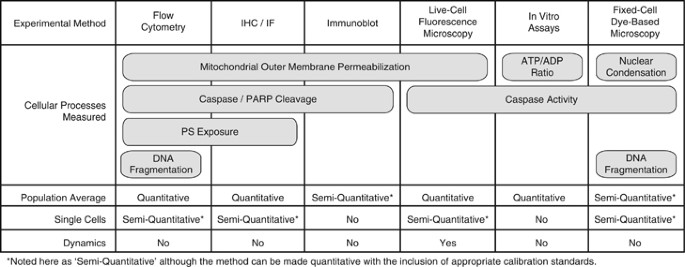
As Figure 1 illustrates, certain steps in apoptotic cell death can be measured by several techniques. These techniques vary significantly as to whether or not they can: (1) be quantitative, (2) yield single-cell measurements and (3) inform us about system dynamics. An illustrative example is to consider measurements of caspase activation. One option is to detect cleaved caspase substrates from cell lysates collected at specific end points by immunoblots. Immunoblots can be made semiquantitative – or even quantitative with proper calibration curves – and therefore are suitable to a systems biology approach (e.g., high-throughput microwesterns).3 However, because they measure protein abundance in homogenates of thousands of cells, by design they do not inform on cell-to-cell heterogeneity. With a series of measurements, one could effectively determine which conditions yielded more aggregate caspase activity in the cell population, but not how that activity was distributed across single cells within this population.
Figure 1
Different aspects of apoptosis can be assayed qualitatively or quantitatively at the single-cell level. For each experimental method listed, we note the apoptotic cell death processes that it measures as well as whether the measurements can be made in single cells or at the population level, whether they are quantitative or not, and whether they enable the tracking of response dynamics. IF, immunofluorescence; IHC, immunohistochemistry; PS, phosphatidylserine
Another common assay uses fluorogenic caspase substrates to quantify total caspase activity.4, 5 When used on sets of cellular lysates, this assay provides the same kind of aggregate, population-level information that immunoblots give us. However, if instead one labels intact cells with a fluorescent dye that accrues in the nucleus in response to caspase activation, the accumulation of caspase activity can be measured in single cells, revealing the extent of heterogeneity in the population.4, 5 By assessing a population of single cells the experimenter obtains semiquantitative information on caspase activation across this population and can determine whether the distribution of caspase activation is bimodal (some cells on, some cells off; Figure 2b), or unimodal (all cells activating caspases, with some variation around the average; Figure 2c). Taking it a step further, fluorescent protein-based biosensors designed to detect caspase activity enable measurements in individual living cells at multiple time points, providing information about the dynamics of caspase activation.6, 7, 8, 9, 10, 11, 12 Single-cell observations of activation dynamics accurately reflect dynamics in a single instance of the biochemical system – a cell undergoing a cell death decision process – and are therefore often the ultimate goal of system biology approaches.
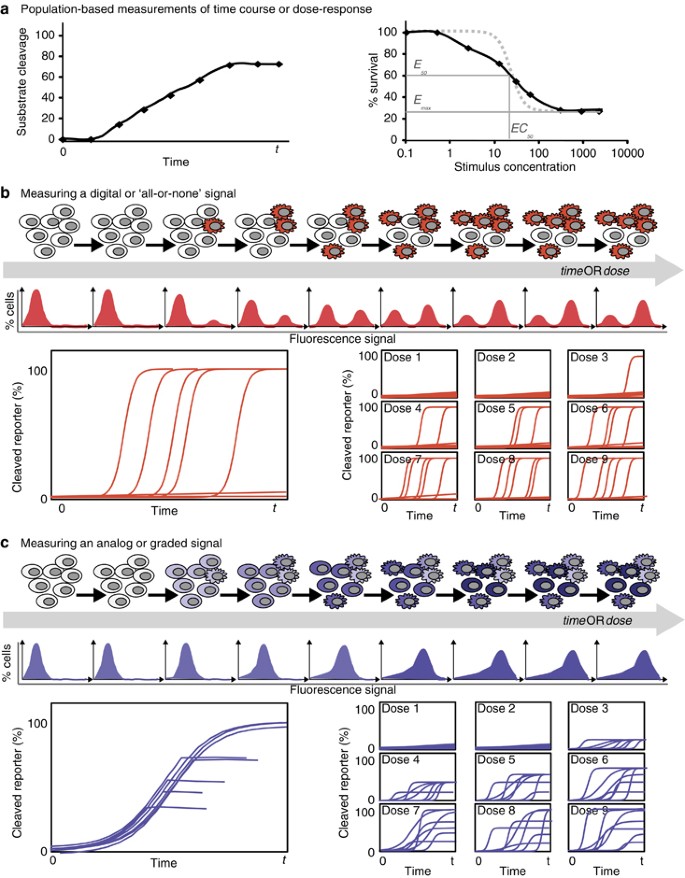
Figure 2
Characteristics of heterogeneous and homogeneous signaling responses for different forms of measurements. (a) Schematic representations of population-level measurements of signaling and apoptosis over time (left) or for a dose response (right). These are expected to be similar whether the cells respond heterogeneously or homogeneously. Dose-response curves can be characterized by the maximal effectiveness (_E_max), the half-point of effectiveness (_E_50) and the concentration at _E_50 (_EC_50). Recent work (Fallahi-Sichani et al.76) has shown that a shallow slope in a dose-response curve (black versus gray dotted line) may indicate heterogeneity in the response, see also Box 1. (b and c) Schematic representations of hypothetical results of various single-cell measurements – end point measurements such as flow cytometry (top) and dynamic measurements for time-dependent (bottom left) or dose-dependent (bottom right) data series. Although these are all consistent with the hypothetical population-level measurements shown in a, they illustrate how population-based measurements can fail to distinguish between heterogeneous all-or-none signals (b) and homogeneous graded signals (c)
How much information is missing from population-level measurements? That depends on the dynamics and the cell-to-cell variability of the process under study and, for the above examples, it depends on which caspase is assayed. During extrinsic apoptosis, death ligands bind to their receptors and, following assembly of a death-inducing signaling complex (DISC), activate initiator caspases-8/-10.13, 14, 15 Owing to cell-to-cell variations in the abundance of receptors, caspase-8, and protein components of the DISC, the timing and extent of caspase-8 activation can vary considerably between cells exposed to the same death ligand dose.6, 11 Thus, a population-level measurement of caspase-8 activity cannot distinguish between a small amount of caspase activation in most cells, and a large amount of activation in a few cells (Figures 2a and c). In contrast to caspase-8, population-level measurements of effector caspase-3 activity can effectively report on how many cells have activated the protease en route to apoptosis. This is because single-cell measurements of caspase-3 activation dynamics have already revealed that in extrinsic apoptosis, caspase-3 activation rapidly goes from nearly zero to maximal.6, 9 This rapid activation results in most cells having either no, or full, caspase-3 activation at any given time (also observable by flow cytometry; Figure 1 and detailed, for example, in Albeck et al.6). This knowledge of typical single-cell caspase-3 activation dynamics should influence our interpretation of population-level measurements of extrinsic apoptosis. For example, when observing twice as much caspase-3 activity in a sample, we can reasonably rule out that caspase activity doubled in each cell and instead conclude that there are twice as many apoptotic cells. This is a rather context-specific scenario and experimenters are still encouraged to use single-cell measurements, especially when their conclusions depend on knowing the distribution of responses within a population.
Importantly, the single-cell observations of caspase activation dynamics, coupled with computational models of caspase regulatory networks, have cemented our understanding of effector caspase regulation during apoptosis.6, 7, 8, 10, 16 Caspase-3 is normally under the tight control of the inhibitory protein XIAP (X-linked inhibitor of apoptosis protein). However, after mitochondrial outer membrane permeabilization (MOMP), a key ‘point of no return’ event in both intrinsic and extrinsic apoptosis,17, 18 XIAP is disabled and caspase-9, an activator of caspase-3, is activated. This, in effect, is as if the cell simultaneously releases the brake (disabling XIAP) and presses on the accelerator (activating caspase-9). MOMP is therefore an event that promotes the ‘snap-action’, rapid increase in caspase-3 activity characterized in single-cell assays.6, 9, 12 Computational modeling predicted, and subsequent experiments validated, that feedback mechanisms (e.g., via XIAP cleavage, or caspase-6 activation) are not required for the ‘snap-action’ dynamics.7
Implications of Cell-to-Cell Variability for the Computational Modeling of Cell Death
Systems biology models of cell signaling and cellular behaviors have been built using several strategies.19 For computational models of both extrinsic (ligand-induced) and intrinsic (damage-induced) apoptosis, strategies include Boolean or fuzzy logic,20, 21, 22 data-driven23, 24, 25, 26, 27, 28, 29, 30 or Bayesian algorithms.31 Each method is suited to a specific type of question, but the modeling approach that can most easily relate to the underlying molecular mechanisms is the use of a system of ordinary differential equations (ODEs). The system of ODEs mathematically encodes the biochemical reactions that are understood, or assumed, to take place in a cell death/survival decision.32, 33 Many ODE models of ligand-induced cell death have been published, simulating and predicting the cell death response to Fas ligand (FasL), TNF-related apoptosis-inducing ligand (TRAIL) or tumor necrosis factor (TNF) with various degrees of details.7, 10, 34, 35, 36, 37, 38
Most ODE models recapitulate a series of biochemical reactions that take place over time, and therefore simulate response dynamics in a signaling network. It is worth noting that one instance of the model represents one instance of the biochemical network, and thus represents one cell. Accordingly, simulation results should be compared with experimental measurements characterizing the dynamic behavior of single cells.
Which cell should a model attempt to recapitulate: a cell matching population-averaged measurements or, perhaps, a ‘typical’ cell? Although seemingly fastidious, this is a crucial decision in the context of models of cell death, principally because certain measurable steps of the cell death process, like caspase-3 activation, have an ‘all-or-none’ character, as we discussed in the previous section. In general, if there is substantial cell-to-cell variability in the cell death process being modeled, especially if the cellular responses are asynchronous, there may not exist any individual cell within the population that responds with a behavior that tracks the measured average (Figure 2b). One clear example of the risk of relying on population-based measurements when developing ODE models of cell death lies with the concept of an ‘_EC_50’ (or half-maximal effective concentration). At the _EC_50 for a certain cell death-inducing drug or ligand, half of the treated cells die but, in all likelihood, no cell ‘half-dies’. Therefore, matching a model solely to a population-average measurement can be a foiled exercise and may yield a model that does not behave like any cell in the population.
What if the only accessible quantitative data are from population-based assays? As we discuss in Box 1, recent work points to ways to analyze population-based data to infer whether there is heterogeneity in the cellular responses of interest. This could be done by interpreting a dose-response curve or by statistical analysis of repeated measurements on small numbers of cells (Box 1). Nevertheless, how should we then compare model simulation results to population-based data? One promising approach to modeling heterogeneous cell responses is to run ‘populations’ of models, to recapitulate the behavior of populations of cells. In this approach, sets of many simulations of the same model with variations in parameters representative of cell-to-cell variability sources (the sources of this variability are discussed in the next section) are used to approximate the behavior of an ensemble of cells.11, 39, 40, 41, 42, 43, 44 Averaged simulation results can be compared with population-average measurements, or when single-cell data are available, sets of simulations can be directly compared with sets of single-cell data. Toward this end, the recent development of Bayesian and Monte Carlo Markov Chain approaches for parameter estimation, where the distributions of possible parameter values are derived by calculating the best fits to distributions of single-cell measurements, should prove particularly useful.45
In conclusion, when comparing results from simulations and experiments, computational modelers should ask: are the data semiquantitative, quantitative or qualitative? Do the data provide single-cell information? If so, do they provide information about single-cell dynamics? Any type of measurement can be useful, but knowledge of its information content will allow the modeler to compare the data with the appropriate modeling results. One final point that we have not yet addressed is that to accurately predict experimental results, we need to understand, with precision, what activity each assay measures. Going back to our example of caspase activation discussed in the previous section, one must know: (1) whether the assay measures the activity of a specific caspase or whether it is a measurement of total caspase activity (even ‘caspase-specific’ substrates tend to have cross-reactivity with other caspases),46 and (2) whether the assay measures caspase cleavage, caspase activity or accumulated caspase cleavage product. For example, it is known that cleaved poly (ADP-ribose) polymerase, a product of effector caspase activity is relatively stable, and therefore can perdure as evidence of past caspase activity. By contrast, cleaved caspase-3 itself is relatively unstable, and evidence of its activation can disappear over time if monitored solely via cleaved caspase-3 abundance. In fact, modeling predicted, and experiments validated, that the short half-life of caspase-3 is important to the dynamics of cell death: if one deletes the E3 ubiquitin ligase domain of XIAP responsible for tagging caspase-3 for degradation, cells can lose the ‘snap-action’ cell death dynamics and may survive with damaged proteins and DNA.8 Just as crucial as comparing population averages with simulation averages and comparing single-cell data sets to sets of single model instances, accurate pairing of measured and modeled entities is key to the development of high-quality models.
Sources of Cell-to-Cell Variability in Cell Death Responses
As we remarked in our introduction, the motivation for single-cell approaches to measurements arose from the observation that, more often than not, the response to death-inducing stimuli is variable. What are the sources of this cell-to-cell variability? Which sources are relevant when building systems biology models of cancer cell death?
Perhaps the most obvious source of variation in a population of cancer cells is genetic changes. Almost 100 years ago, the idea of mutations being at the origins of cancer first emerged (reviewed in Wunderlich47), and so did the observation that cancer cells tend to lose or gain chromosomes.48 It is well established that chromosomal or mutational genomic instability is one of the hallmarks of cancer, an idea first proposed nearly 40 years ago (Nowell49; reviewed in Negrini et al.50). As a result of this genomic instability, tumors are heterogeneous and even cancer cells in culture accumulate mutations, including mutations that lead to anticancer drug resistance. For example, treatment with epidermal growth factor receptor (EGFR) kinase inhibitors selects for cells with mutations in EGFR,51 ABL (Abelson murine leukemia viral oncogene homolog 1) kinase mutations lead to resistance of leukemia cells treated with imatinib52 and mutations in the pro-apoptotic protein Bax (B-cell lymphoma 2 (Bcl-2)-associated X protein) emerge when selecting for cells resistant to TRAIL.53
When genetic changes directly impinge on the signaling events and cellular responses represented in a systems biology model, they must be implemented to obtain accurate predictions. Different types of mutations require different changes to a model: (1) if a tumor-suppressor protein species is lost, it can be removed from the model; (2) if a mutation instead affects binding or enzymatic activity, the appropriate reaction rate constants should be modified; (3) if a mutation affects protein stability, it can be implemented by changing the parameters for synthesis or degradation or, in a less detailed model, by changing the concentration of the protein to reflect a new equilibrium value.
But what if one is modeling a cell population heterogeneous for a mutation? Then it will become relevant to model a population of cells, using a mixture of ‘wild-type’ and ‘mutant’ models, as we introduced in the previous section. Another plausible scenario is that mutations arise as a consequence of treatment (as they do for the examples listed above). In that scenario, one could model a population of cells and assign to each cell a probability for a switch to the mutant phenotype. Such an approach has been effectively applied to model the evolution of pancreatic tumors and a model prediction, later experimentally validated, correctly inferred the effect of dosing schedule on the acquisition of resistance in lung cancer.54, 55 Efforts such as the Cancer Cell Line Encyclopedia project, aiming to catalog genetic mutations and drug sensitivity, will help customize our computational models to each experimental model cell line.56
Although ‘fractional kill’, the concept that one round of chemotherapy generally does not kill all cells in a tumor, can be partly explained by genetic heterogeneity, we now also appreciate the importance of non-genetic heterogeneity. A common idea for a non-genetic cause of fractional kill is that rapidly dividing cancer cells exhibit different drug sensitivity in different cell cycle phases. This explanation makes sense for cytotoxic drugs that target cell cycle processes − taxanes that target microtubules could preferentially act on mitotic cells and DNA-damaging agents could be especially toxic for cells replicating their DNA or already committed to mitosis. Indeed, rapidly proliferating cells in the body, such as bone marrow or hair cells, are specifically targeted by these drugs. However, although tumor cells do inappropriately proliferate, the fraction of cells in mitosis at any time within a solid tumor can be very small, likely too small to explain the amount of cell death observed with anti-mitotic drug treatment (reviewed in Mitchison57 and Komlodi-Pasztor et al.58). Therefore, although cell cycle phase impacts the response of cancer cells to cytotoxic treatment, other non-genetic sources of variability are required to explain the observed response of tumors.
Are other inducers of cancer cell death similarly affected by variability in cell cycle phase? For apoptosis-inducing ligands, the cell cycle effect hypothesis has been disproved for TRAIL,11 but the question is unresolved for FasL and TNF. Early work had reported that TNF lengthened the G2 phase and induce death preferentially during or soon after mitosis in mouse L929 fibroblasts,59 while a later study reported that B lymphoma cells preferentially die at exit from S phase, and are more sensitive to TNF-induced apoptosis if treated during G1.60 The use of single-cell and more quantitative approaches should allow us to elucidate whether the cell cycle-associated variability in response to TNF is cell type-specific or whether there is a generalizable effect.
When cell cycle effects are observed, or hypothesized, accurate models of the cellular responses to apoptosis-inducing treatments will have to include them. A rigorous approach would be to integrate cell-cycle driving pathways into the model, as was done to investigate the interplay between cell cycle and DNA-damage response pathways regulating cell cycle arrest.44 This model predicted, and experiments confirmed, that knocking out p21 would allow endoduplication of DNA in about 50% of _γ_-irradiated cells, showing that the model successfully captured the cell cycle and DNA-damage response pathway crosstalk.44 A simpler approach to integrate cell cycle effects would be to simulate a population of models with a data-based distribution of cell cycle phases while including, for each cell cycle phase, a probability that quantifies the likelihood of pathway activation.
Cell cycle phase is an example of a potential source of variability outside the cell death signaling networks, but what about variability within these networks? It is now appreciated that the general biochemical ‘state’ of all cells is somewhat plastic, because transcription occurs in stochastic bursts.61, 62 This ultimately results in variability in the abundance of all proteins both across a cell population and in the same cell over time (e.g., as observed in Cohen et al.63). Therefore, even a deterministic cell death process – which always has the same outcome if starting conditions are the same – can have a variable outcome because each cell starts with different initial protein concentrations. Notably, because the state of each cell changes over time, this plasticity actually allows cell populations decimated by a death-inducing stimulus to repopulate and recapitulate the sensitivity profile of the original population after a few days.11, 64
How can this noise in gene expression be incorporated into models of cell death? The most faithful, if cumbersome, representation would be to model the synthesis of each protein from first principles, with bursts of transcription. An effective alternative approach is to model a population of cells, as introduced above, by sampling from measured distributions of protein concentrations to build a ‘population’ of models.11, 39, 40, 41, 42 This approach can be used to mimic any measurable, or hypothesized, cell-to-cell variability in protein abundance, whether from noise in gene expression or, for example, from longer-lasting chromatin-encoded epigenetic changes, which have been shown to impact the response of genetically equivalent tumor cells to chemotherapeutics in vitro65, 66 and in xenograft models (Kreso et al.67; reviewed in Marusyk and Polyak68).
In summary, both genetic and non-genetic sources of cell-to-cell variability that impact the response to anticancer agents have already been identified. Additional sources of variability certainly exist in vivo; for example, the microenvironment differences across different regions of a solid tumor that could influence how cancer cells respond to anticancer drugs (reviewed in Hanahan and Weinberg69). To design effective cancer treatments, we will have to account for these diverse forms of variability and incorporate them into our systems biology models of cancer treatments. Although this may seem like a daunting task, as long as we can measure the source of variability we can also model its impact on cellular responses, whether the variability arises from outside or inside the signaling network of interest.
Master Regulator versus Multifactorial Regulation – A Road to Combinatorial Anticancer Therapies
Above, we discussed possible sources of cell-to-cell heterogeneity and examples of approaches to account for them in systems biology models. But is that complexity necessary? What if there was a single master regulator of the cell death decision process, a single source of variability? In the apoptosis literature, there are countless examples of correlating cell fate with the abundance of a key protein. When Khaider et al.70 reviewed factors contributing to TRAIL resistance, they found articles citing the importance of receptor abundance, receptor trafficking, abundance of Bcl-2, Bim (Bcl2-interacting mediator gamma), BID (BH3 interacting-domain death agonist), PUMA (p53 upregulated modulator of apoptosis), Noxa, BAD (Bcl-2 antagonist of cell death), Mcl-1 (myeloid leukemia cell sequence 1), Bcl-xl (B-cell lymphoma-extra large), FLIP (FLICE (FADD-like IL-1_β_-converting enzyme)-inhibitory protein), STAT5 (signal transducer and activator of transcription 5), pro-caspase-8, pro-caspase-3, FADD (Fas-associated protein with death domain), p53 and even constitutive Akt activation. Which, if any, of these cited studies identified the correct ‘master regulator’ of TRAIL-induced cell death versus survival decisions? Perhaps tellingly, several implicated two or more regulators. Taken together, these studies suggest that the regulation of cell death is highly context dependent and multifactorial. Although purely experimental approaches often necessarily take a reductionist view to identify a key regulator in a specific context, systems biology models that formalize our accumulated knowledge will enable a multivariate view of the system, and ultimately allow reconciliation of many experimental findings.
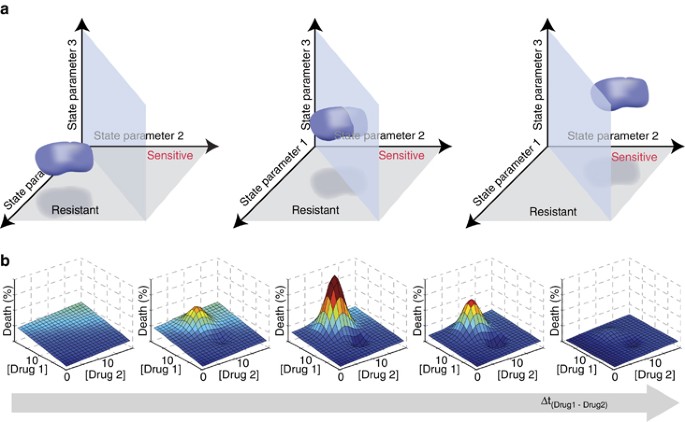
The multifactorial nature of cell death decisions is a powerful rationale for pursuing combinatorial anticancer therapies, where one drug sensitizes cancer cells to the action of the other. For example, although TRAIL-based monotherapies have proven unsuccessful, many different co-drugging strategies are being investigated (reviewed in Hellwig and Rehm71). Essentially, each drug changes the biochemical ‘state’ of each cell over a period of time. This ‘state’ is determined by factors such as the relative abundance of signaling proteins or cell cycle phase and the values of these factors can be used to plot the location of each cell in a multidimensional ‘state-space’. Co-drugging chemotherapeutic strategies aim for one drug to shift cancer cells from a state-space region where they are resistant to the second drug to one where they are sensitive (Figure 3a). Models and experiments can help us map this state-space and predict the most promising co-drugging interventions.
Figure 3
Multivariate and dynamic analyses of cell state to predict synergistic effects of drug regimens on cellular responses. (a) Hypothetical three-parameter ‘state-space’ maps showing the position of a population of cells (blue), as well as the plane separating regions of state-space leading to sensitivity (back) or resistance (front) to treatment. Here ‘parameters’ could quantify the abundance or activity of certain proteins, for example. In the scenario illustrated here, the values of parameters 1 and 2 are found to govern the sensitivity of the cells to a given drug. The middle graph shows the results of a moderately successful intervention, which results in many cells becoming sensitive to the drug. The graph on the right shows a successful intervention where the entire population becomes sensitive. Note that interventions can also lead to changes in other parameters, such as parameter 3, which do not affect the sensitivity of the population. (b) Graphs showing hypothetical cell death response surfaces for treatment with various concentrations of drugs 1 and 2. The time interval between administration of drug 1 and drug 2 increases to the right, potentially leading to much stronger or weaker effects than the simple additive effect achieved by the simultaneous administration seen in the leftmost panel. The vertical axis (death (%)) and the color scale (from blue (0%), to cyan, green, yellow, orange and red (100%)) both indicate the fraction of cells dying in the population
State-space mapping of cellular responses to death-inducing stimuli will necessitate predictive, well-validated models. For ligand-induced apoptosis, high-quality models exist and mapping results are emerging. For example, Howells et al.72 created a model to identify which cellular parameters determine whether abundance and phosphorylation of BAD, a pro-apoptotic Bcl-2 family protein, influence MOMP and ultimately cell fate. Although not yet experimentally validated, this model helps predict scenarios where BAD-mimicking drugs would increase sensitivity to death-inducing ligands. In this study, a cellular response map was derived from bifurcation analysis, a mathematical method that maps where steady-state cellular responses transition from one to another (e.g., to map the blue plane separating ‘resistant’ and ‘sensitive’ states in Figure 3a). However, not all apoptosis-inducing signals evolve to a steady state. When transient events dominate the cell death decision, bifurcation analysis becomes inadequate. For the response of cells to CD95 (cluster of differentiation 95, also known as Fas receptor) activation, Neumann et al.36 aptly used forward model simulations, predicting system behavior within a multidimensional grid of initial conditions, to map regions of the cellular FLIP (c-FLIP) versus pro-caspase-8 space that lead to strong activation of pro-survival (NF-_κ_B) nuclear factor kappa-light-chain-enhancer of activated B cells signaling versus pro-apoptotic caspase-3. This map predicted how to manipulate c-FLIP and/or caspase-8 abundance or activity to promote cell death, and these predictions were confirmed experimentally using genetic manipulations to vary protein abundance and small molecule inhibitors of caspases to manipulate caspase activity.36
A third method, the calculation of Lyapunov exponents, can similarly be applied to highlight where system (or cellular) behavior diverges in state-space (see also overview in Box 2 of Aldridge et al.8). Lyapunov exponents were applied to a seven-dimensional state-space of a computational model of TRAIL-induced cell death and predicted that the cellular concentration of several proteins, namely ligand, receptor, initiator caspases-8 (and -10), XIAP and caspase-3 influenced whether or not cells required MOMP to commit to extrinsic apoptosis.8 Experiments confirmed that, indeed, XIAP to caspase-3 ratio and ligand concentration were major determinants of the requirement for MOMP. Interestingly, another prediction from this analysis was that while in certain biochemical contexts (or regions of state-space), cell-to-cell variability in XIAP and caspase-3 concentration should cause phenotypic cell-to-cell variability, in other contexts all cells were predicted to have the same phenotype. This was validated experimentally by showing that whereas the fraction of MOMP-dependent cells in the T47D breast carcinoma line was ligand concentration dependent, other cell lines, such as the SKW6.4 B-cell lymphoma line, had no phenotypic heterogeneity and were even insensitive to overexpression of XIAP.8 This context dependence of the impact of variability in protein abundance on cellular responses likely arises in part from the underlying network topology and can be explored using state-space maps (see also Gaudet et al.39).
Using these mapping approaches and others, we can start to understand how to maximize the impact of co-drugging strategies by re-positioning cancer cells into region of the ‘state-space’ where the entire population is drug sensitive (Figure 3a). As discussed above, in concept, drug treatments shift the biochemical ‘state’ of a cell. This shift is dynamic and thus the position of cells will depend on time since drug addition. Lee et al.23 expertly demonstrated this principle, a process they refer to as dynamic network rewiring. They optimized relative timing and sequence of drug addition (Figure 3b); over time, the first drug ‘rewires’ the signaling network, by moving cells within state-space, maximizing responses to subsequent drugs. They found that treatment with the EGFR inhibitor erlotinib 4 h before addition of doxorubicin, a conventional DNA-damaging chemotherapy, markedly enhanced killing of triple-negative breast cancer cells compared with either drug alone, both drugs added simultaneously, or doxorubicin preceding erlotinib.23 A data-driven model was built from systematic time-dependent measurements within the responsive signaling networks following EGFR inhibition by erlotinib, and the model identified a key predictive dynamic biomarker for cell sensitization. Late increase in cleaved caspase-8 was specifically associated with synergistic effects of sequential erlotinib–doxorubicin treatment, likely indicating reactivation of otherwise dysregulated extrinsic apoptosis.23 Although no simple systematic way exists to probe whether synergy could arise from specific sequential or co-drugging regimens, it is clearly a promising frontier for the systems biology of anticancer treatments.
The shape of cleaved caspase-8 accumulation over time is a biomarker for the synergistic response to sequential erlotinib and doxorubicin treatment, and there are other examples where signaling dynamics encode information for cellular responses. One striking example involves the p53 tumor suppressor: in single cells, _γ_-irradiation induces oscillations in p53 nuclear abundance and cell-cycle arrest, while ultraviolet treatment induces sustained p53 nuclear localization and apoptosis (reviewed in Purvis and Lahav73). Could pharmacological interventions that manipulate signaling dynamics be used to induce specific cell fates? Purvis et al.74 showed that this could be done for p53: as predicted by their model, timed treatments with nutlin-3, an inhibitor of MDM2 (mouse double minute 2 homolog)-directed degradation of p53, forced sustained elevated nuclear abundance of p53 after _γ_-irradiation, resulting in cell death. Such manipulations could also apply to other well-characterized systems, as enticingly proposed by Behar et al.75 They used computational models to virtually screen for conditions yielding specific dynamics, then applied their findings to NF-_κ_B-driven transcription. They found that, as predicted by their analysis, different inhibitor treatments yielded stimulus-specific effects on early versus late NF-_κ_B target gene expression.75 By combining accurate measurements of cell ‘states’ and single-cell response dynamics, we can learn how signaling dynamics encode cell fate, and use models to predict how to manipulate these dynamics to obtain the desired cellular outcomes.
Conclusion
There is an oft-quoted phrase from George EP Box, a British statistician, stating that ‘all models are wrong, but some are useful’. As models are by necessity an approximation of reality, all models are ‘wrong’. However, when carefully developed and solidly anchored in high-quality data, models can be predictive, leading to testable and falsifiable hypotheses and thereby allowing us to learn about the system under study. Here we have discussed the frequently observed phenotypic heterogeneity in the response of human cells to various death-inducing stimuli as well as the sources of this variability and implications for measuring and modeling cell death. We are entering an era of ‘biology in the second moment’ where the focus is not the average, or dominant, behavior exhibited by a population of cells, but rather the focus is on the variance, and we anticipate that this new focus will continue to contribute to our understanding of the regulation of cell death in health and disease.
Abbreviations
BAD:
Bcl-2 antagonist of cell death
Bcl-2:
B-cell lymphoma 2
c-FLIP:
cellular FLIP
DISC:
death-inducing signaling complex
E 50 :
half-point of effectiveness
EC 50 :
concentration at half-point of effectiveness
EGFR:
epidermal growth factor receptor
E max :
maximum effect
FADD:
Fas-associated protein with death domain
FasL:
Fas ligand
FLIP:
FLICE (FADD-like IL-1_β_-converting enzyme)-inhibitory protein
HS:
hill slope coefficient
MOMP:
mitochondrial outer membrane permeabilization
NF-_κ_B:
nuclear factor kappa-light-chain-enhancer of activated B cells
ODE:
ordinary differential equation
PI3K:
phosphatidylinositol-4,5-bisphosphate 3-kinase
TNF:
tumor necrosis factor
TRAIL:
TNF-related apoptosis-inducing ligand
XIAP:
X-linked inhibitor of apoptosis protein
References
- Kerr JF, Wyllie AH, Currie AR . Apoptosis: a basic biological phenomenon with wide-ranging implications in tissue kinetics. Br J Cancer 1972; 26: 239–257.
Article CAS PubMed PubMed Central Google Scholar - Galluzzi L, Aaronson SA, Abrams J, Alnemri ES, Andrews DW, Baehrecke EH et al. Guidelines for the use and interpretation of assays for monitoring cell death in higher eukaryotes. Cell Death Differ 2009; 16: 1093–1107.
Article CAS PubMed Google Scholar - Ciaccio MF, Wagner JP, Chuu C-P, Lauffenburger DA, Jones RB . Systems analysis of EGF receptor signaling dynamics with microwestern arrays. Nat Methods 2010; 7: 148–155.
Article CAS PubMed PubMed Central Google Scholar - Komoriya A, Packard BZ, Brown MJ, Wu ML, Henkart PA . Assessment of caspase activities in intact apoptotic thymocytes using cell-permeable fluorogenic caspase substrates. J Exp Med 2000; 191: 1819–1828.
Article CAS PubMed PubMed Central Google Scholar - Köhler C, Orrenius S, Zhivotovsky B . Evaluation of caspase activity in apoptotic cells. J Immunol Methods 2002; 265: 97–110.
Article PubMed Google Scholar - Albeck JG, Burke JM, Aldridge BB, Zhang M, Lauffenburger DA, Sorger PK . Quantitative analysis of pathways controlling extrinsic apoptosis in single cells. Mol Cell 2008; 30: 11–25.
Article CAS PubMed PubMed Central Google Scholar - Albeck JG, Burke JM, Spencer SL, Lauffenburger DA, Sorger PK . Modeling a snap-action, variable-delay switch controlling extrinsic cell death. PLoS Biol 2008; 6: e299.
Article CAS PubMed Central Google Scholar - Aldridge BB, Gaudet S, Lauffenburger DA, Sorger PK . Lyapunov exponents and phase diagrams reveal multi-factorial control over TRAIL-induced apoptosis. Mol Syst Biol 2011; 7: 1–21.
Article CAS Google Scholar - Rehm M . Single-cell fluorescence resonance energy transfer analysis demonstrates that caspase activation during apoptosis is a rapid process. ROLE OF CASPASE-3. J Biol Chem 2002; 277: 24506–24514.
Article CAS PubMed Google Scholar - Rehm M, Huber HJ, Dussmann H, Prehn JHM . Systems analysis of effector caspase activation and its control by X-linked inhibitor of apoptosis protein. EMBO J 2006; 25: 4338–4349.
Article CAS PubMed PubMed Central Google Scholar - Spencer SL, Gaudet S, Albeck JG, Burke JM, Sorger PK . Non-genetic origins of cell-to-cell variability in TRAIL-induced apoptosis. Nature 2009; 459: 428–432.
Article CAS PubMed PubMed Central Google Scholar - Tyas L, Brophy VA, Pope A, Rivett AJ, Tavaré JM . Rapid caspase-3 activation during apoptosis revealed using fluorescence-resonance energy transfer. EMBO Rep 2000; 1: 266–270.
Article CAS PubMed PubMed Central Google Scholar - Barnhart BC, Peter ME . The TNF receptor 1. Cell 2003; 114: 148–150.
Article CAS PubMed Google Scholar - Hengartner MO . The biochemistry of apoptosis. Nature 2000; 407: 770–776.
Article CAS PubMed Google Scholar - Micheau O, Tschopp J . Induction of TNF receptor I-mediated apoptosis via two sequential signaling complexes. Cell 2003; 114: 181–190.
Article CAS PubMed Google Scholar - Rehm M, Huber HJ, Hellwig CT, Anguissola S, Dussmann H, Prehn JHM . Dynamics of outer mitochondrial membrane permeabilization during apoptosis. Cell Death Differ 2009; 16: 613–623.
Article CAS PubMed Google Scholar - Kroemer G, Galluzzi L, Brenner C . Mitochondrial membrane permeabilization in cell death. Physiol Rev 2007; 87: 99–163.
Article CAS PubMed Google Scholar - Tait SWG, Green DR . Mitochondria and cell death: outer membrane permeabilization and beyond. Nat Rev Mol Cell Biol 2010; 11: 621–632.
Article CAS PubMed Google Scholar - Kholodenko B, Yaffe MB, Kolch W . Computational approaches for analyzing information flow in biological networks. Sci Signal 2012; 5: re1.
Article PubMed Google Scholar - Saez-Rodriguez J, Alexopoulos LG, Epperlein J, Samaga R, Lauffenburger DA, Klamt S et al. Discrete logic modelling as a means to link protein signalling networks with functional analysis of mammalian signal transduction. Mol Syst Biol 2009; 5: 1–19.
Article CAS Google Scholar - Aldridge BB, Saez-Rodriguez J, Muhlich JL, Sorger PK, Lauffenburger DA . Fuzzy logic analysis of kinase pathway crosstalk in TNF/EGF/insulin-induced signaling. PLoS Computational Biol 2009; 5: e1000340.
Article CAS Google Scholar - Morris MK, Saez-Rodriguez J, Clarke DC, Sorger PK, Lauffenburger DA . Training signaling pathway maps to biochemical data with constrained fuzzy logic: quantitative analysis of liver cell responses to inflammatory stimuli. PLoS Computational Biol 2011; 7: e1001099.
Article CAS Google Scholar - Lee MJ, Ye AS, Gardino AK, Heijink AM, Sorger PK, MacBeath G et al. Sequential application of anticancer drugs enhances cell death by rewiring apoptotic signaling networks. Cell 2012; 149: 780–794.
Article CAS PubMed PubMed Central Google Scholar - Janes KA . A systems model of signaling identifies a molecular basis set for cytokine-induced apoptosis. Science 2005; 310: 1646–1653.
Article CAS PubMed Google Scholar - Janes KA, Gaudet S, Albeck JG, Nielsen UB, Lauffenburger DA, Sorger PK . The response of human epithelial cells to TNF involves an inducible autocrine cascade. Cell 2006; 124: 1225–1239.
Article CAS PubMed Google Scholar - Lau KS, Juchheim AM, Cavaliere KR, Philips SR, Lauffenburger DA, Haigis KM . In vivo systems analysis identifies spatial and temporal aspects of the modulation of TNF- induced apoptosis and proliferation by MAPKs. Sci Signal 2011; 4: ra16.
PubMed PubMed Central Google Scholar - Miller-Jensen K, Janes KA, Brugge JS, Lauffenburger DA . Common effector processing mediates cell-specific responses to stimuli. Nature 2007; 448: 604–608.
Article CAS PubMed Google Scholar - Kreeger PK . Using partial least squares regression to analyze cellular response data. Sci Signal 2013; 6: tr7.
Article PubMed PubMed Central CAS Google Scholar - Prasasya RD, Tian D, Kreeger PK . Analysis of cancer signaling networks by systems biology to develop therapies. Sem Cancer Biol 2011; 21: 200–206.
Article Google Scholar - Passante E, Wurstle ML, Hellwig CT, Leverkus M, Rehm M . Systems analysis of apoptosis protein expression allows the case-specific prediction of cell death responsiveness of melanoma cells. Cell Death Differ 2013; 20: 1521–1531.
Article CAS PubMed PubMed Central Google Scholar - Sachs K . Causal protein-signaling networks derived from multiparameter single-cell data. Science 2005; 308: 523–529.
Article CAS PubMed Google Scholar - Rehm M, Prehn JHM . Systems modelling methodology for the analysis of apoptosis signal transduction and cell death decisions. Methods 2013; 61: 165–173.
Article CAS PubMed Google Scholar - Aldridge BB, Burke JM, Lauffenburger DA, Sorger PK . Physicochemical modelling of cell signalling pathways. Nat Cell Biol 2006; 8: 1195–1203.
Article CAS PubMed Google Scholar - Fussenegger M, Bailey JE, Varner J . A mathematical model of caspase function in apoptosis. Nat Biotechnol 2000; 18: 768–774.
Article CAS PubMed Google Scholar - Wurstle ML, Laussmann MA, Rehm M . The caspase-8 dimerization/dissociation balance is a highly potent regulator of caspase-8, -3, -6 signaling. J Biol Chem 2010; 285: 33209–33218.
Article PubMed PubMed Central CAS Google Scholar - Neumann L, Pforr C, Beaudouin J, Pappa A, Fricker N, Krammer PH et al. Dynamics within the CD95 death-inducing signaling complex decide life and death of cells. Mol Syst Biol 2010; 6: 1–17.
Article CAS Google Scholar - Bentele M . Mathematical modeling reveals threshold mechanism in CD95-induced apoptosis. J Cell Biol 2004; 166: 839–851.
Article CAS PubMed PubMed Central Google Scholar - Hua F, Cornejo MG, Cardone MH, Stokes CL, Lauffenburger DA . Effects of Bcl-2 levels on Fas signaling-induced caspase-3 activation: molecular genetic tests of computational model predictions. J Immunol 2005; 175: 985–995.
Article CAS PubMed Google Scholar - Gaudet S, Spencer SL, Chen WW, Sorger PK . Exploring the contextual sensitivity of factors that determine cell-to-cell variability in receptor-mediated apoptosis. PLoS Computational Biol 2012; 8: e1002482.
Article CAS Google Scholar - Hasenauer J, Heinrich J, Doszczak M, Scheurich P, Weiskopf D, Allgöwer F . A visual analytics approach for models of heterogeneous cell populations. EURASIP J Bioinform Syst Biol 2012; 2012: 4.
Article PubMed PubMed Central Google Scholar - Schliemann M, Bullinger E, Borchers S, Allgöwer F, Findeisen R, Scheurich P . Heterogeneity reduces sensitivity of cell death for TNF-stimuli. BMC Syst Biol 2011; 5: 204.
Article CAS PubMed PubMed Central Google Scholar - Feinerman O, Veiga J, Dorfman JR, Germain RN, Altan-Bonnet G . Variability and robustness in T cell activation from regulated heterogeneity in protein levels. Science 2008; 321: 1081–1084.
Article CAS PubMed PubMed Central Google Scholar - Lee RE, Walker SR, Savery K, Frank DA, Gaudet S . Fold change of nuclear NF-kappaB determines TNF-induced transcription in single cells. Mol Cell 2014; 53: 867–879.
Article CAS PubMed PubMed Central Google Scholar - Toettcher JE, Loewer A, Ostheimer GJ, Yaffe MB, Tidor B, Lahav G . Distinct mechanisms act in concert to mediate cell cycle arrest. Proc Natl Acad Sci USA 2009; 106: 785–790.
Article CAS PubMed PubMed Central Google Scholar - Eydgahi H, Chen WW, Muhlich JL, Vitkup D, Tsitsiklis JN, Sorger PK . Properties of cell death models calibrated and compared using Bayesian approaches. Mol Syst Biol 2013; 9: 1–17.
Article CAS Google Scholar - Stennicke HR, Renatus M, Meldal M, Salvesen GS . Internally quenched fluorescent peptide substrates disclose the subsite preferences of human caspases 1, 3, 6, 7 and 8. Biochem J 2000; 350 (Pt 2): 563–568.
Article CAS PubMed PubMed Central Google Scholar - Wunderlich V . Early references to the mutational origin of cancer. Int J Epidemiol 2007; 36: 246–247.
Article PubMed Google Scholar - Boveri T . Zur Frage der Entstehung Maligner Tumoren. Gustav Fischer: Jena, Germany, 1914: p64.
- Nowell PC . The clonal evolution of tumor cell populations. Science 1976; 194: 23–28.
Article CAS PubMed Google Scholar - Negrini S, Gorgoulis VG, Halazonetis TD . Genomic instability—an evolving hallmark of cancer. Nat Rev Mol Cell Biol 2010; 11: 220–228.
Article CAS PubMed Google Scholar - Pao W, Miller VA, Politi KA, Riely GJ, Somwar R, Zakowski MF et al. Acquired resistance of lung adenocarcinomas to gefitinib or erlotinib is associated with a second mutation in the EGFR kinase domain. PLoS Med 2005; 2: e73.
Article PubMed PubMed Central CAS Google Scholar - Deininger M, Buchdunger E, Druker BJ . The development of imatinib as a therapeutic agent for chronic myeloid leukemia. Blood 2005; 105: 2640–2653.
Article CAS PubMed Google Scholar - LeBlanc H, Lawrence D, Varfolomeev E, Totpal K, Morlan J, Schow P et al. Tumor-cell resistance to death receptor—induced apoptosis through mutational inactivation of the proapoptotic Bcl-2 homolog Bax. Nat Med 2002; 8: 274–281.
Article CAS PubMed Google Scholar - Foo J, Chmielecki J, Pao W, Michor F . Effects of pharmacokinetic processes and varied dosing schedules on the dynamics of acquired resistance to erlotinib in EGFR-mutant lung cancer. J Thorac Oncol 2012; 7: 1583–1593.
Article CAS PubMed PubMed Central Google Scholar - Haeno H, Gonen M, Davis MB, Herman JM, Iacobuzio-Donahue CA, Michor F . Computational modeling of pancreatic cancer reveals kinetics of metastasis suggesting optimum treatment strategies. Cell 2012; 148: 362–375.
Article CAS PubMed PubMed Central Google Scholar - Barretina J, Caponigro G, Stransky N, Venkatesan K, Margolin AA, Kim S et al. The Cancer Cell Line Encyclopedia enables predictive modelling of anticancer drug sensitivity. Nature 2012; 483: 603–607.
Article CAS PubMed PubMed Central Google Scholar - Mitchison TJ . The proliferation rate paradox in antimitotic chemotherapy. Mol Biol Cell 2012; 23: 1–6.
Article CAS PubMed PubMed Central Google Scholar - Komlodi-Pasztor E, Sackett D, Wilkerson J, Fojo T . Mitosis is not a key target of microtubule agents in patient tumors. Nat Rev Clin Oncol 2011; 8: 244–250.
Article CAS PubMed Google Scholar - Darzynkiewicz Z, Williamson B, Carswell EA, Old LJ . Cell cycle-specific effects of tumor necrosis factor. Cancer Res 1984; 44: 83–90.
CAS PubMed Google Scholar - Shih SC, Stutman O . Cell cycle-dependent tumor necrosis factor apoptosis. Cancer Res 1996; 56: 1591–1598.
CAS PubMed Google Scholar - Chubb JR, Trcek T, Shenoy SM, Singer RH . Transcriptional pulsing of a developmental gene. Curr Biol 2006; 16: 1018–1025.
Article CAS PubMed PubMed Central Google Scholar - Cisse II, Izeddin I, Causse SZ, Boudarene L, Senecal A, Muresan L et al. Real-time dynamics of RNA polymerase II clustering in live human cells. Science 2013; 341: 664–667.
Article CAS PubMed Google Scholar - Cohen AA, Geva-Zatorsky N, Eden E, Frenkel-Morgenstern M, Issaeva I, Sigal A et al. Dynamic proteomics of individual cancer cells in response to a drug. Science 2008; 322: 1511–1516.
Article CAS PubMed Google Scholar - Flusberg DA, Roux J, Spencer SL, Sorger PK . Cells surviving fractional killing by TRAIL exhibit transient but sustainable resistance and inflammatory phenotypes. Mol Biol Cell 2013; 24: 2186–2200.
Article CAS PubMed PubMed Central Google Scholar - Sharma SV, Lee DY, Li B, Quinlan MP, Takahashi F, Maheswaran S et al. A chromatin-mediated reversible drug-tolerant state in cancer cell subpopulations. Cell 2010; 141: 69–80.
Article CAS PubMed PubMed Central Google Scholar - Marusyk A, Almendro V, Polyak K . Intra-tumour heterogeneity: a looking glass for cancer? Nat Rev Cancer 2012; 12: 323–334.
Article CAS PubMed Google Scholar - Kreso A, O'Brien CA, van Galen P, Gan OI, Notta F, Brown AM et al. Variable clonal repopulation dynamics influence chemotherapy response in colorectal cancer. Science 2013; 339: 543–548.
Article CAS PubMed Google Scholar - Marusyk A, Polyak K . Cancer. Cancer cell phenotypes, in fifty shades of grey. Science 2013; 339: 528–529.
Article CAS PubMed Google Scholar - Hanahan D, Weinberg RA . Hallmarks of cancer: the next generation. Cell 2011; 144: 646–674.
Article CAS PubMed Google Scholar - Khaider NG, Lane D, Matte I, Rancourt C, Piche A . Targeted ovarian cancer treatment: the TRAILs of resistance. Am J Cancer Res 2012; 2: 75–92.
CAS PubMed Google Scholar - Hellwig CT, Rehm M . TRAIL signaling and synergy mechanisms used in TRAIL-based combination therapies. Mol Cancer Ther 2012; 11: 3–13.
Article CAS PubMed Google Scholar - Howells CC, Baumann WT, Samuels DC, Finkielstein CV . The Bcl-2-associated death promoter (BAD) lowers the threshold at which the Bcl-2-interacting domain death agonist (BID) triggers mitochondria disintegration. J Theor Biol 2010; 271: 114–123.
Article PubMed CAS Google Scholar - Purvis JE, Lahav G . Encoding and decoding cellular information through signaling dynamics. Cell 2013; 152: 945–956.
Article CAS PubMed PubMed Central Google Scholar - Purvis JE, Karhohs KW, Mock C, Batchelor E, Loewer A, Lahav G . p53 dynamics control cell fate. Science 2012; 336: 1440–1444.
Article CAS PubMed PubMed Central Google Scholar - Behar M, Barken D, Werner SL, Hoffmann A . The dynamics of signaling as a pharmacological target. Cell 2013; 155: 448–461.
Article CAS PubMed Google Scholar - Fallahi-Sichani M, Honarnejad S, Heiser LM, Gray JW, Sorger PK . Metrics other than potency reveal systematic variation in responses to cancer drugs. Nat Chem Biol 2013; 9: 708–714.
Article CAS PubMed PubMed Central Google Scholar - Wang L, Janes KA . Stochastic profiling of transcriptional regulatory heterogeneities in tissues, tumors and cultured cells. Nat Protoc 2013; 8: 282–301.
Article CAS PubMed Google Scholar - Janes KA, Wang CC, Holmberg KJ, Cabral K, Brugge JS . Identifying single-cell molecular programs by stochastic profiling. Nat Methods 2010; 7: 311–317.
Article CAS PubMed PubMed Central Google Scholar - Bajikar SS, Fuchs C, Roller A, Theis FJ, Janes KA . Parameterizing cell-to-cell regulatory heterogeneities via stochastic transcriptional profiles. Proc Natl Acad Sci USA 2014; 111: E626–E635.
Article CAS PubMed PubMed Central Google Scholar
Acknowledgements
This work was funded by NIH grants P01-CA139980, R01-GM104247 and a Barr investigator award to SG. SG is a Kimmel Scholar and RECL is a CIHR research fellow.
Author information
Author notes
- X Xia and M S Owen: These authors contributed equally to this work.
Authors and Affiliations
- Department of Cancer Biology and Center for Cancer Systems Biology, Dana Farber Cancer Institute, Boston, 02215, MA, USA
X Xia, M S Owen, R E C Lee & S Gaudet - Department of Genetics, Harvard Medical School, Boston, 02115, MA, USA
X Xia, M S Owen, R E C Lee & S Gaudet
Authors
- X Xia
- M S Owen
- R E C Lee
- S Gaudet
Corresponding author
Correspondence toS Gaudet.
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Edited by B Zhivotovsky
Rights and permissions
Cell Death and Disease is an open-access journal published by Nature Publishing Group. This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Xia, X., Owen, M., Lee, R. et al. Cell-to-cell variability in cell death: can systems biology help us make sense of it all?.Cell Death Dis 5, e1261 (2014). https://doi.org/10.1038/cddis.2014.199
- Received: 23 December 2013
- Revised: 24 February 2014
- Accepted: 25 February 2014
- Published: 29 May 2014
- Issue Date: May 2014
- DOI: https://doi.org/10.1038/cddis.2014.199