Second-order free-riding problem solved? (original) (raw)
Suppose a population shows two types of behaviour. In each period, ‘cooperators’ pay a cost C to contribute to a public good and receive a benefit B. ‘Defectors’ also receive benefit B but do not pay the cost. Assuming growth of each type in the population is proportional to mean pay-offs, how can we explain the emergence and persistence of cooperators?
Panchanathan and Boyd propose that a first-round public-goods game is followed by a second-round ‘mutual-aid’ game. In this game, each ‘shunner’ cooperates in the first round and then pays a cost c to generate a benefit b to one randomly chosen shunner, which yields a pay-off of B_−_C+b_−_c. Shunners can invade and dominate a population of defectors if _b_−_c_>C. In other words, shunners will prevail if they can create an in-group net surplus from mutual aid in the second round that exceeds the cost of cooperation in the first round. However, this is only possible if shunners can exclude second-round defectors from mutual aid. Although Panchanathan and Boyd include in their model individuals who receive a benefit without paying the cost in the first round (defectors), they do not consider such a type for the second round. Thus, rather than solving the second-order free-rider problem, their model merely assumes it away.
To see why, suppose that ‘second-round defectors’ enter the population. These individuals receive the same pay-off as shunners in the first round and are eligible to receive aid in the second round. However, they do not give aid to others. If we denote the proportion of shunners in the population by p, then the average pay-off for second-round defectors is B_−_C+bp and the average pay-off to shunners changes to B+C+bp_−_c. If second-round defectors invade a population of shunners, then second-round cooperation collapses, pay-offs to second-round defectors fall, and eventually ordinary defectors can invade and dominate the population — leaving us back where we started.
Panchanathan and Boyd implicitly acknowledge this problem when they note that each individual must have perfect information about the cooperation and aid-giving histories of all other members of the population in order for mutual aid to be sustained. In other words, shunners must be able to recognize and exclude second-round defectors from receiving aid. They do incorporate an error term into their model, but they do not consider errors in which individuals mistakenly help a recipient of bad reputation during the mutual-aid game1.
Suppose that e is the probability that shunners mistakenly aid a second-round defector or withhold aid from a shunner. Cooperation can only be maintained when the pay-off to shunners, B_−_C+bp(1−e)−c_[p(1−_e)+e(1−p)], is greater than the pay-off to second-round defectors, B_−_C+ebp, or
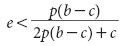
This means a population of shunners (_p_=1) is only evolutionarily stable if the error is sufficiently small
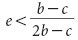
In other words, cooperation will unravel if second-round defectors cannot be detected most of the time. In contrast, a population of second-round defectors (_p_=0) is stable for any positive error rate and can resist invasion even when shunners are common. Thus, the emergence of shunners when they are rare cannot be explained by the authors' model1.
Note that the simple model presented here raises a broader concern with all models of indirect reciprocity3,4,5 and related experimental results6. Previous work has already shown that indirect reciprocity is stable only when donors have very reliable information about the behavioural histories of all individuals in the population4,7. But even this assumes that there is no evolutionary pressure on the reliability of information. If at least some acts of giving are not observable, then individuals may have an incentive to misrepresent their behavioural histories in order to secure the benefits of indirect reciprocity without paying the costs. Considering a human context in particular, what keeps these individuals from evolving deceptive behaviours that would reduce the reliability of information and allow them to benefit from aid without providing it?