Protein structure prediction from sequence variation (original) (raw)
In the past 50 years, there has been tremendous progress in experimental determination of protein three-dimensional structures, but this has not kept pace with the explosive growth of sequence information that results from massively parallel sequencing technology. We therefore know many more protein sequences than protein three-dimensional structures, and the gap is widening rather than diminishing. Yet as the Anfinsen legacy suggests1,2, many proteins contain enough information in their amino acid sequence to determine their three-dimensional structure, thus opening the possibility of predicting three-dimensional structure from sequence.
Computational prediction of protein structures, which has been a long-standing challenge in molecular biology for more than 40 years, may be able to fill this gap, if done with sufficient accuracy. Many useful and quite accurate three-dimensional models have been computed from amino acid sequences by using the similarity of the protein sequence of interest to another protein whose three-dimensional structure is known, often called template or homology model building3,4. However, correct de novo predictions from sequence, when not a single structure in a protein family is known, have been hard to achieve, as the pioneering Critical Assessment of Techniques for Protein Structure Prediction (CASP) evaluation of blinded predictions has demonstrated over the past two decades5,6. Some of the best recent state-of-the-art approaches to de novo folding, such as Rosetta, are based on searching for sequence-similar fragments in three-dimensional structure databases followed by fragment assembly using empirical intermolecular force fields7. Such approaches have worked favorably in cases for smaller proteins that have fewer than ∼90 amino acids7 and need to be combined with experimental data for larger proteins8,9. Other approaches attempt to predict residue contacts using three-dimensional information with machine-learning techniques, such as support vector machines, random forests and neural networks, but contact prediction accuracy remained “still quite low”10 with substantial improvements to models achieved only for some small proteins11,12. Clearly, and unfortunately, the de novo structure prediction problem does not scale13, the conformational search space increases exponentially as the size of the protein increases, presenting a fundamental computational challenge, even for fragment-based methods14. In this sense, the general problem of de novo three-dimensional structure prediction has remained unsolved.
Covariation and the problem of transitive correlations
A substantial step forward in protein-structure prediction is now on the horizon based on the power of evolutionary information found in patterns of correlated mutations in protein sequences (Fig. 1a). The extraordinary improvements in DNA sequencing technology, aided by advanced statistical analysis, have now provided the keys to unlock this evolutionary information. Several groups have demonstrated that extracting covariation information from sequences is sufficient not only to estimate which pairs of residues are close in three-dimensional space15,16,17,18,19,20,21 but also to fold a protein to reasonable accuracy15,22,23,24,25 (Table 1). In addition to being predictive of contacts in a protein, these pairs of covarying residues should also be predictive of functional sites (Fig. 1b), protein interactions and alternative conformations15,16,22.
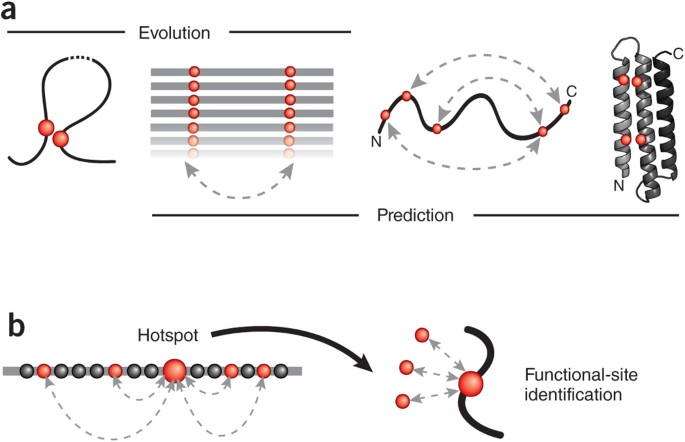
Figure 1: Reading the sequence record for evolutionary constraints.
(a) Evolutionary pressure (left) to maintain favorable interactions between physically interacting amino acid residues (red circles) in the three-dimensional fold of a protein (curved line) leaves a visible record of residue covariation (double-headed, dashed arrow) in related protein sequences (aligned horizontal lines). The inverse problem of inferring (right) directly causative residue couplings (evolutionary couplings) from the covariation record is challenging because of transitive correlations and other confounding effects, but once evolutionary couplings are determined (double-headed dashed arrows on curved protein chain), they can be used to predict the unknown three-dimensional structure of a protein (ribbon, right) from a set of sequences alone. (b) Residues subject to a high number of evolutionary pair constraints (double-headed, dashed arrows; left) represent likely functional hotspots (large red dot). Such highly constrained residues include residues in functional sites (for example, interaction with external ligands, red dots on right) that may not be detectable by analysis of single-residue conservation.
Table 1 Statistical models for predicting coevolution between protein residues
The most successful approaches deal with a well-known statistical problem, as elegantly stated in the 1920s by Sewall Wright26: “The ideal method of science is the study of the direct influence of one condition on another in experiments in which all other possible causes of variation are eliminated.” For the problem of correlated mutation analysis, to find true evolutionary covariation between residues, one must minimize the effect of transitive correlations—that is, false positive correlations that are observed, for example, when two residues contact the same third residue but do not actually contact each other. For example, if residues A and B contact each other, as do residues B and C, then there is in general, a transitive influence observed between residues A and C ('chaining effect'17,27). As residues can contact many other residues (not just one), transitive effects occur across the network, and pairs of residues that are correlated as computed using a 'local' statistical model, such as mutual information scores, are not necessarily functionally constrained or close in space (Fig. 2). Local statistical models (below referred to as local models or local methods) assume that pairs of residue positions are statistically independent of other pairs of residues (Table 1 and Fig. 2). In real proteins, however, residues can contact many other residues, and their cooperative interaction is crucial to the protein structure and function. In the 18-year history of contact-prediction methods using correlated mutations, all methods used local mutual information or other local statistical models28,29,30,31,32,33, with one notable but unnoticed exception17.
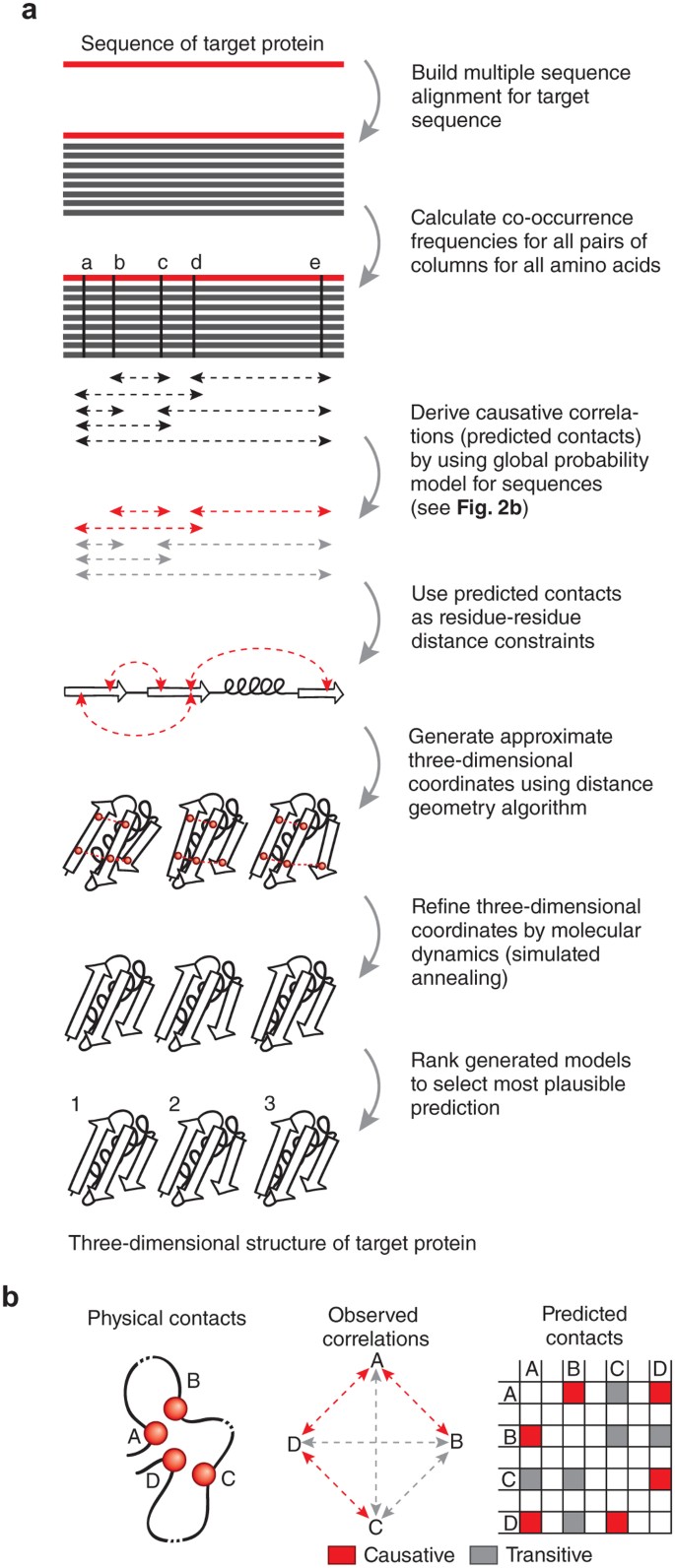
Figure 2: Deriving folded three-dimensional structure for a target protein sequence.
(a) Workflow as implemented on the publicly available web server EVfold.org. Related methods (Table 1) follow similar steps, but details differ. The amino acid sequence of the target protein is used to perform a database search for putative structural homologs, with attention to the optimal cutoff in sequence similarity so that sufficient sequences are available yet they are not too far diverged to lose subfamily specificity. Minimally, hundreds of sequences are needed to derive plausible causative evolutionary couplings. For ten candidate structures for a medium-sized protein (∼200 residues), the computation takes less than an hour on a typical laptop computer. (b) The principal confounding effect dealt with by global probability models, but not by the local models, is that of transitive (indirect) correlations that do not reflect causative evolutionary constraints on interactions. For example, correlations between residues A and B, residues A and D, and residues D and C are causative because they reflect direct interactions, whereas residues A and C show transitive correlation owing to their mutual direct interactions with residue D. The transitive correlations, in special cases, can have numerically stronger correlation values than causative correlation, for example, if two noninteracting residues have in common several neighbors27, thereby confounding structure prediction.
Although these local methods have been used to make some improvements in contact prediction or identification of functional residues, they have not been used successfully to predict three-dimensional structures from sequence information alone presumably for two main reasons. First, local statistical models do not deal with transitive correlations, and second, such models do not adequately take into account important information in conserved positions33. Other confounding effects that have prevented high-accuracy prediction of residue contacts include uneven representation of family members in sequence space, statistical-noise as the result of an inadequate number of sequences in the family as well as phylogenetic effects. Whether or not explicit removal of quantifiable phylogenetic effects can be productively added to the suppression of transitive correlations in global models remains an open question.
In contrast, a 'global' modeling approach treats correlated pairs of residues as dependent on each other, rather than as statistically independent, thereby minimizing the effects of transitivity and spurious noise. This approach also uses globally consistent single-residue marginals, which takes into account effects from conservation of single residue positions. Global approaches yield high coupling scores only for pairs or residue positions that are likely to be causative of all the observed correlations. Residue pairs with high globally derived coupling scores are most likely to represent the true interactions between residues deduced from the evolutionary history of the protein. In contrast, local information–based methods, which treat each pair of residue positions independently, will have high ranking correlations that are not necessarily causative and such correlations can be even greater than the causative correlations. Noncausal correlation is well understood in statistical physics; it includes, for instance, long-range order observed in spin systems, where in fact the spins only have short-range direct interactions, and is called 'chained covariation'27,34. In essence, global statistical approaches for analysis of protein sequences address this question: given all pair correlations, which ones best explain all the others? Or, as in other areas of statistics, how does one go from correlation to causation26?
Transitive correlations removed by global statistical approaches
One global statistical approach is known as entropy maximization under data constraints, a classic inference method connecting information theory and Boltzmann statistics35. Maximizing entropy under constraints36 has been successfully used in statistical physics and other areas of statistical inference37,38,39, and the conditional mutual information derived from correlations between positions in a protein sequence is a discrete, nonlinear analog of partial correlation analysis40. In contrast to simple mutual information, the conditional mutual information can be thought of as the degree of covariation between residues at positions a and b that is due solely to direct effects of a on b, factoring out contributions to the correlation that are caused by interaction of both a and b with the rest of the network of residues.
The first step in the practical application of such global approaches is to create a multiple sequence alignment between many members of an evolutionarily related protein family (Fig. 2). Next, one calculates the covariance matrix (the observed minus expected pair counts) of dimension (20_L_)2, where L is the length of the protein sequence, by counting how often a given pair of the 20 amino acids, say alanine and lysine, occurs in a particular pair of positions, say position 15 and 67, in any one sequence, summing over all sequences in the multiple-sequence alignment. This large matrix contains the raw data capturing all residue pair relationships across evolution up to second order (pairs, not triplets or higher). One can then compute a measure of causative correlations, the conditional mutual information, in the global statistical approaches by taking the inverse of the covariance matrix. That such a matrix inversion results in a measure of causative correlations is well known in the statistical theory of Gaussian multivariate distributions of continuous variables40.
An analogous derivation for discrete-state biological sequence analysis is, for example, based on a mean-field expansion in analogy to statistical physics16. The resulting explicit probability model for a sequence in the particular protein family resulting from inversion of the covariation matrix contains numerical estimates of direct pair interactions. These are directly and simply computed from the raw data in the covariation matrix, in contradistinction to machine-learning methods that rely on parameter fitting in learning sets and cross-validation in test sets. The pair interaction terms can also be interpreted as residue-residue pair energies, in analogy to pair terms in a Hamiltonian energy expression in statistical physics. The conditional mutual information between a pair of positions derived using the global statistical approach becomes a useful predictor of residue-residue contacts.
The maximum-entropy approach to potentially solving the problem of protein structure prediction from residue covariation patterns was first described by Lapedes and collaborators17,27. However, instead of inversion of the covariance matrix, they used a more computationally demanding Monte Carlo method (that is, iterative exploration of the best set of pair interactions values) to derive the probability terms in conditional mutual information. Although Lapedes and Jarzynski did not compute three-dimensional structures, they reached a first breakthrough in contact prediction in 2002 for 11 small proteins and reported 50–70% accuracy for top 20 contact predictions, in contrast to 35–45% accuracy with the previous best methods available17.
A more recent independently derived implementation of the maximum-entropy approach used an iterative parameter-estimation technique for deriving the pair-interaction parameters known as belief propagation21. This was superseded by a much more efficient mean-field approximation, in which the parameter estimation problem was solved by inverting the correlation matrix15,16, as currently used by the EVfold and DCA-fold structure-prediction methods. Other implementations have used derivatives of partial correlation approaches, where 'partial' refers to computing direct residue-residue correlations after removal of transitive effects. These methods used Bayesian network inference19 and sparse inverse covariance estimation20, which leads to equations that are similar to those derived with the maximum-entropy approach in the mean-field approximation to eliminate the effect of transitive correlations. After removal of transitive correlations and other confounding effects, predicted contacts based on the global probability models provide a base for the computation of three-dimensional folds.
From contact predictions to protein folding
To what extent does improved contact prediction lead to improved de novo prediction of three-dimensional structures? We developed (D.S.M. and colleagues15), a folding protocol, EVfold, in which predicted residue contacts from coevolution patterns are translated into detailed atomic coordinates by using distance restraints placed on an extended polypeptide (Fig. 2). In this method, a three-dimensional structure is calculated by constraining the distance between pairs of residues with high covariance scores using a standard distance geometry algorithm, first pioneered and then ubiquitously used to solve three-dimensional structures with experimental constraints deduced from NMR spectroscopy data41. This is then followed by simulated annealing by molecular dynamics to ensure the correct bond lengths and plausible side-chain conformations. In a benchmark test on known structures, all-atom three-dimensional coordinates were predicted from sequence alone for 15 diverse globular folds of up to 220 amino acids and for eight folds with 100 or more residues15. The predicted structural elements were correctly placed in three-dimensional space, with an overall accuracy of as low as 2.8–5.1 Å Ca r.m.s. deviation relative to the experimentally determined structures. Predictions for enzymatic proteins were the most accurate, and the quality of prediction was robust to false positive predicted contacts.
To compare alternative global statistical methods, we (D.S.M. and colleagues15) also have folded proteins using residue contacts predicted by a Bayesian network model19, reporting three-dimensional structure error between 4 and 6 Ca r.m.s. deviation, at somewhat lower accuracy than with contacts predicted by the maximum-entropy formalism15. Using EVfold contacts and folding protocol, the accuracy of atomic coordinates were reported to be best (down to ∼1 Å all-atom over 5–10 residues) around active sites. Plausibly, this reflects strong functional requirements for protein-ligand interaction, such that active-site residues are multiply constrained by interactions between pairs of residues (Fig. 1b).
The quality of the predicted folds, and the number of cases in which this works, is likely to improve in time, given the observation15 that more sequence information tends to lead to higher accuracy of distance constraints. And the currently limited atomic accuracy (in the range of 2–5 Å Ca r.m.s. deviation) of the successful de novo structures is likely to improve with advanced molecular dynamics refinement methods resulting in more accurate atomic coordinates (for example, using the molecular dynamics and refinement software Cystallography and NMR System (CNS)42, Rosetta43, the deformable elastic network (DEN) approach44 or the Anton massively parallel special purpose computer45).
The structures of membrane proteins are notoriously difficult to determine by crystallography or NMR spectroscopy. Using a maximum-entropy approach, one of our groups (T.H. and colleagues22) recently has tested the ability to predict the three-dimensional structures of membrane proteins on 25 membrane proteins with up to 487 residues (up to 14 transmembrane helices) from 23 structurally diverse families, excluding information from homologous three-dimensional structures and sequence-similar fragments. The protein set included examples from important functional classes, such as G protein–coupled receptors (GPCRs) and membrane transporters22. The EVfold-membrane protocol provides a ranked set of predicted structures for each protein, which was then compared with the corresponding crystal structure. Accuracy results ranged from Ca r.m.s. deviation of 2.6 Å to 4.8Å over >70% of the length and template modeling scores46 of 0.5–0.7, which are notable for de novo predictions of proteins of this size (Fig. 3).
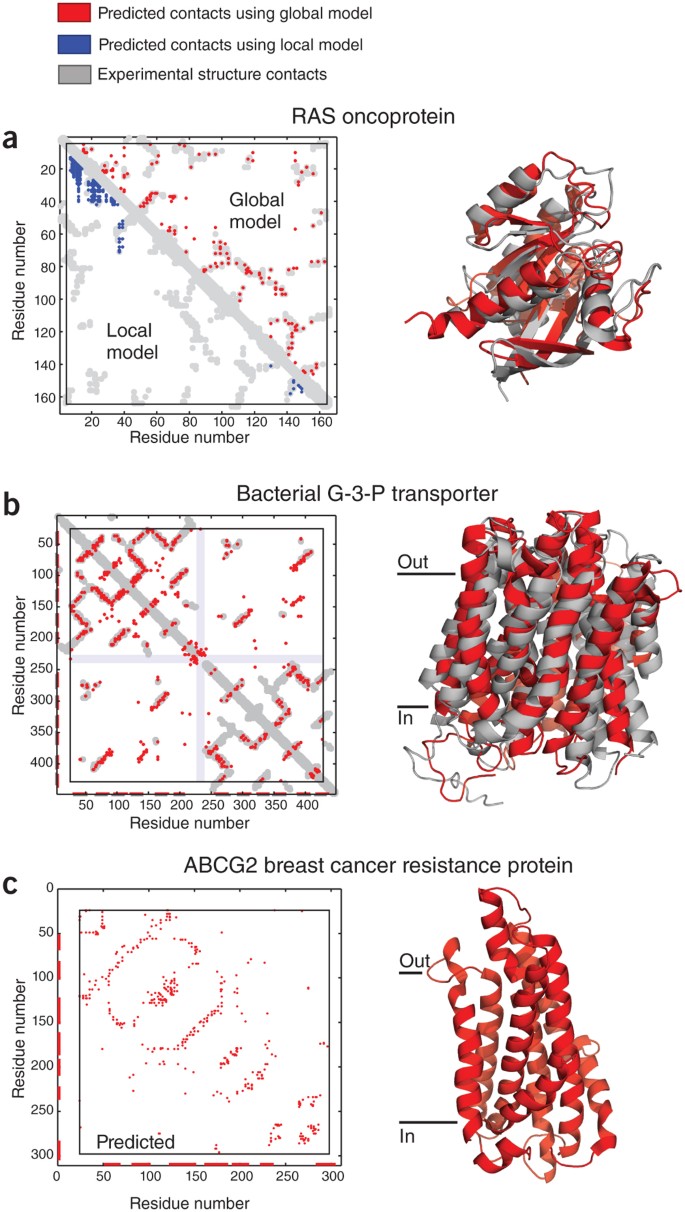
Figure 3: High-ranking evolutionary constraints correspond well to experimental structure contacts in blinded tests, encouraging prediction of unknown structures.
(a) Blinded prediction test for a globular protein. Dots in plots on left represent contacts between residues in a protein. Residue pairs with high coevolution scores from local models based on mutual information are mostly not close in three dimensions (blue dots), whereas high-ranking evolutionary constraints (red dots) correspond well to experimental structure contacts (gray). The same number of predictions are shown in each triangle (same number of blue and red dots). The high accuracy of prediction of evolutionary constraints allows the prediction of the all-atom three-dimensional structures of globular proteins, shown as a ribbon diagram of the human oncoprotein RAS (red, evolutionary coupling–based prediction; gray, crystal structure; Uniprot identifier RASH_HUMAN; PDB identifier 5p21)15. (b) Blinded prediction test as in a for a transmembrane protein (Uniprot identifier GLPT_ECOLI; PDB identifier, 1pw4 (ref. 22). (c) Example of prediction of a medically important protein of unknown three-dimensional structure, ATP-binding cassette sub-family G member 2 (alias, breast cancer resistance protein, Uniprot identifier ABCG2_HUMAN)22.
Several other global statistical modeling approaches have since been used to predict residue contacts for use in folding protocols. The Jones group24, using a method called FILM3, predicted accurate all-atom three-dimensional structures of membrane proteins using an evolutionary coupling term added to an earlier fragment-based prediction method. They predicted the structure of 32 known membrane proteins with template modeling scores of ∼0.25–0.75 (folds with scores >0.5 are considered essentially correct). From a first set of results on known structures they derived an empirical ranking protocol that can be used to objectively select structures such that template modeling scores are likely to exceed 0.47. This level of accuracy is comparable with that of the EVfold method, although unlike FILM3, EVfold uses no experimentally determined protein fragments nor known membrane protein _Z_-plane coordinates.
The Onuchic group23, using a protocol called DCAfold, predicted three-dimensional structures of 15 bacterial protein domains up to 133 residues (in their test set) using the information content in evolutionary couplings, with or without assumed native (experimental) secondary structure and statistical potentials derived from a set of known proteins unrelated to those folded. The derivation of predicted contacts uses essentially the same maximum-entropy approach as EVfold, and the structures are generated from a one-bead-per-residue representation, followed by generation of all-atom coordinates. The results generated with known or predicted secondary structure are comparable to those of EVfold, at least for smaller-length proteins reported.
Each of these three approaches to folding from evolutionary constraints predicted residue contacts from correlated mutations at much higher accuracy than did previous contact prediction methods (Box 1). They often reached the correct fold (that is, correct topography of secondary structure elements in three dimensions; 2–6 Å Ca r.m.s. deviation), which is unprecedented without the use of three-dimensional fragments and unprecedented for any proteins over 100 residues, even with the use of three-dimensional fragments. The three approaches differ in details of the statistical models, the use of predicted secondary structure and the protocol for generating atomic coordinates of predicted folded three-dimensional structures, for example, with or without the use of sequence-similar database fragments and in all-atom or residue-center representation. EVfold uses the least existing structural information of all three approaches and therefore showed the potential for the prediction of unknown folds. DCAfold showed how using evolutionary constraints with very detailed experimental information about secondary structure can predict native-like three-dimensional structures. FILM3, for membrane proteins, showed that using fragments from globular proteins and information from membrane protein secondary structure may increase prediction accuracy. It is reasonable to expect that use of any independent empirical information or advanced refinement protocols can improve the accuracy of predicted coordinates from the new covariation methods. Taken together, these global approaches for calculating sequence-derived constraints show the power of evolutionary information and the potential to increase the accuracy of predicted three-dimensional structures by adding limited experimental data. Going all the way from multiply aligned sequence families via predicted residues couplings and contacts to often well-folded predicted three-dimensional structures has now been achieved in several reports (Table 1)15,22,23,24. These implementations may be broadly applied over the next few years and will benefit from the continuing rapid growth in the number of sequences in protein families and of known protein families.
Applications of improved structure-prediction methods
Beyond benchmarks, the value of three-dimensional structure prediction methods is best established over time by making biological discoveries, in unknown territory. Notably, evolutionary couplings, even with transitive correlation effects removed, can be caused by diverse functional effects, of which the formation and stability of the folded three-dimensional structure is only one (Fig. 4a). Several applications are possible.
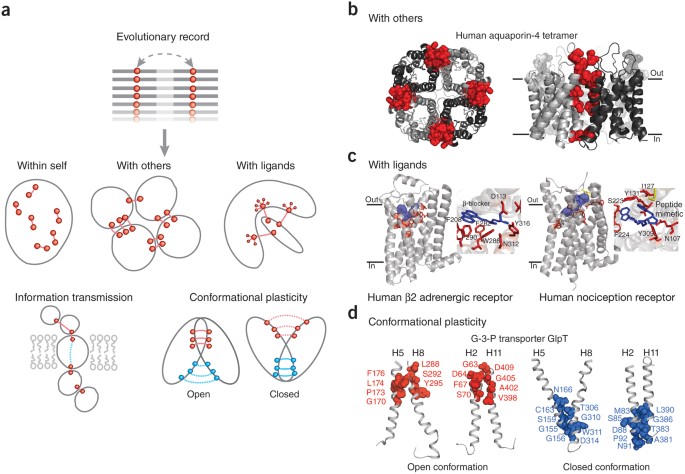
Figure 4: Beyond three-dimensional folds: predicting protein complexes and functional interactions.
(a) Besides the prediction of monomer three-dimensional structure ('within self'), in principle, evolutionary couplings can be used to deduce additional functional interactions (between a target protein and other proteins or ligands), the transmission of information and conformational plasticity. (b) Evolutionary constraints reflect the coevolution of residues in homomultimer interaction interfaces (red spheres, residues participating in interprotein evolutionary couplings; monomeric subunits, ribbons in different shades of gray), allowing the prediction of both tertiary and quaternary (oligomeric) structures from correlated mutations. (c) Residues (red sticks, predicted from summed evolutionary couplings) involved in ligand (blue sticks, position known in crystal structure) binding of transmembrane receptors are often affected by multiple high-ranking evolutionary constraints, which reflect the requirements of a particular spatial arrangement of binding residues, even in the presence of diverse ligand specificities in subfamilies. (d) In proteins with conformational plasticity, evolutionary constraints may reflect the proximity of residues in alternative conformations and can be used to fold structural models of the different states. Transmembrane helices H5-H8 H5 and H8, and H2 and H11, form two pairs that rock between the alternative conformations of the glycerol-3-phosphate transporter GlpT. The 'closed conformation' (closed to cytoplasm) was predicted by EVfold22; the 'open conformation' is known from X-ray crystallography data (PDB identifier 1pw4).
Proteins with unknown structures. The first published exercise of prediction in unknown territory using the EVfold method focused on medically interesting transmembrane proteins (Fig. 2c) associated with diabetes, obesity, Crohn's disease, breast cancer, a hereditary optic neuropathy, Alzheimer's disease or Parkinson's disease. The predicted several hundred all-atom three-dimensional models for each protein were ranked according to an empirical score, with the top ranking thought to be more likely to be correct. Such predicted structures can be used for functional interpretation and design of targeted experiments (all three-dimensional coordinates available at http://www.EVfold.org/). A particularly interesting application is the identification of putative binding and interaction sites and possibly computational drug screening, which is not unreasonable in light of the higher accuracy near active sites in the benchmarks (Fig. 4). A search of predicted structures against experimentally known structures in the Protein Data Bank (PDB) for similar folds can be used to determine whether a predicted structure is a new fold or to discover unexpected evolutionary relationships. Such unexpected 'remote homologies' are either indicative of remote evolutionary relatedness not easily detectable at the sequence level, or indicative of convergent evolution to particularly advantageous or easily accessible folds22.
Protein oligomers and complexes. Functional constraints have an effect on a protein sequence through interactions, but not all of these are internal to the protein. Thus, analysis of evolutionary covariation may also reveal constraints imposed by protein oligomers or complexes made of identical (homo-oligomers) or different (hetero-oligomers) types of proteins. For homo-oligomers, interactions between monomers can be false positives when considering intramonomer contacts. In de novo structure prediction, one needs an algorithm that disambiguates between intramonomer and intermonomer contacts in an oligomer, as is needed in structure determination of oligomers by NMR spectroscopy.
A recent example has shown the accuracy of the evolutionary constraints in identifying multimer contacts (Fig. 4b), including dimer contacts for an Escherichia coli methioinine transporter, tetramer contacts for a cataract disease protein and predicted dimer contacts for the _de novo_–predicted structure of the adiponectin receptor22. Similarly, another report16 has demonstrated that three of the top 20 predicted contacts for an ATPase domain were false positives for the monomer but true positives for the multimer. Both reports showed that ∼50–70% of the top predicted contacts that are not intradomain contacts, are inter-domain contacts from multimeric assemblies.
Such an algorithm can help with monomer folding accuracy, if the conflicting oligomer contacts are removed in the process of computing the monomer structure. A related but actually simpler problem is that of predicting pairwise protein–protein interactions21,47,48. Assembly of protein complexes from evolutionary couplings should also be possible, in analogy to the computation of the higher-order structure of the nuclear pore complex49 from interactions between pairs of residues deduced for mass spectrometry data.
Functional sites and signal transmission. As prediction accuracy using evolutionary couplings is generally higher near active sites and binding sites, it is reasonable to hypothesize that strong pair constraints are a signature of functional constraints. This can be generalized and applied to the prediction of functional elements in two ways. First, one can use the cumulative strength of evolutionary couplings for a particular residue as a measure of the effect of functional selective pressure on one residue (that as a single residue does not have to be strongly conserved). Second, one can identify chains of residue pairs with high evolutionary coupling values as potential chains of transmission of information, which is particularly interesting in transmembrane receptors. Such predictions of functional information for proteins (with either known or unknown three-dimensional structures) may be useful for multiple biological applications, including basic protein mechanism, interpretation of genotypic differences across the human population and evolution, somatic mutations in cancers, and the synthetic design of functionally altered proteins.
In one of our papers (D.S.M. and colleagues15) we illustrated the first principle by demonstrating that the predicted active sites of trypsin and Ras were particularly accurate relative to the accuracy of the rest of the protein when compared with the crystal structures, following the spirit of earlier work that used a weighted local mutual information method50,51. Morcos et al.16 also showed that a long-distance high-scoring pair of predicted contacts in a metallo-enzyme was more than 14 Å apart in the monomer, so seemed as if the pair prediction was a false positive, but the residues are in principle in contact through a catalytic manganese ion in the respective monomer units of the dimer16.
The second principle of functional interpretation is illustrated in a subsequent paper (T.A.H. and colleagues22), where we systematically mapped the cumulative strength of all high-ranking evolutionary couplings onto all residues to predict functional sites and functional chains over and above single-residue conservation. Mapping these highly evolutionary constrained residues onto two GPCRs, adrenergic beta-2 receptor and an opioid receptor, highlights known ligand-binding residues (Fig. 4c) and the G-protein binding residues on the cytoplasmic interface (data not shown).
Alternative conformations and allostery. Many proteins can adopt different distinct conformations as part of their function. An interesting example of covariation analysis of conformational changes is the derivation from computed evolutionary constraints of the alternative three-dimensional conformations in the large 'major facilitator' superfamily of transmembrane proteins22,52,53. In general, for some proteins with functional conformational flexibility, the record of functional constraints in multiple sequence alignments may be sufficiently strong to permit modeling not just of one structure, but of alternate structures, for example, of the end points of functional conformational transitions (Fig. 4d)22.
Limitations. Although evolutionary couplings show promise for the identification of functional sites, homomultimer contacts, alternative conformations and functional sites, many of the predicted contacts involved in these protein features may appear as false positives in the prediction of intradomain residue contacts. Therefore, a challenge for the field will be to develop algorithms that can disambiguate the different functional constraints. In addition, protein sequences that are confidently aligned will not necessarily have the same three-dimensional conformations, and methods should be developed to identify those protein families that are likely to be more varied in their three-dimensional structure. An objective measure has been described22 to choose the optimal alignment depth for accurate prediction of three-dimensional structure, but such measures will need to be developed further to be more rigorously applicable and yield better predictions.
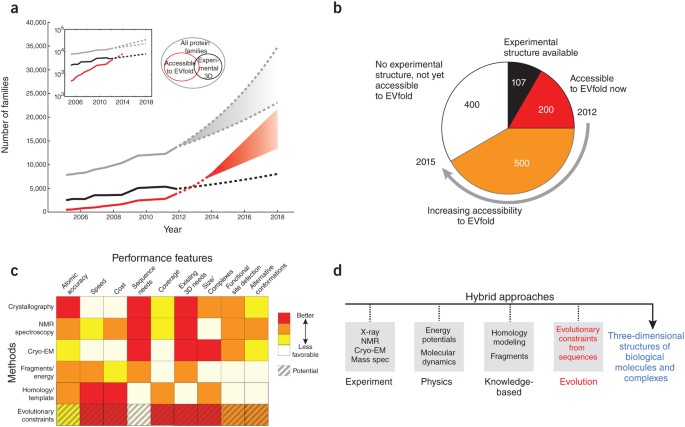
The detection of evolutionary couplings between residues requires a substantially diverse set of sequences, which is not yet available for many families. For instance, to obtain a good fold, EVFold needs about 5_L_ (rough estimate) sequences in the multiple alignment, where L is the length of the protein. However, this shortcoming may be addressed simply over time, and more sophisticated use of family and subfamily information54 may improve the accuracy of the algorithms. Given the massive throughput capacity of current sequencing technology, the growth of protein family information is primarily limited by the acquisition of genomic samples from a diverse set of species. A reasonable extrapolation predicts that within a few years most of the current 15,000 protein families (as defined by PFAM-A55) will have sufficiently many known sequences to yield a robust evolutionary coupling signal (Fig. 5a). In addition, conservative extrapolation suggests that another 500 of the ∼1,300 currently known transmembrane protein families will be amenable to folding with evolutionary constraints (Fig. 5b). Of course, new families will also join the known universe of sequences, at a rate that is hard to predict56, but it is likely that the absolute number of correctly predictable protein folds will rise sharply into the many thousands over the next few years. None of the methods reviewed here have been tested yet in the CASP competition (http://predictioncenter.org/casp10/) but one can assume researchers using the new methods will enter the CASP competition in the future.
Figure 5: Future applications.
(a) Although experimental structure-determination in structural biology laboratories or structural genomics centers is highly productive (solid black line), it cannot keep up with the pace at which new protein families are being discovered by high-throughput sequencing (solid gray line). The number of three-dimensional structures that can be reasonably predicted using evolutionary conservation (solid red line) was estimated by a linear extrapolation in the log plot of the exponential growth inset. We expect the growth curves to saturate in the future (dashed lines), but there is no indication this will happen in the next couple of years, and indications are that a large increase in the number of protein families may be apparent from multispecies (metagenomic) sequencing58. (b) Of the 1,250 alpha-helical transmembrane protein families known in mid-2012, 107 have solved experimental three-dimensional structures and another 200 are accessible to solution by evolutionary constraints in 2012. By 2015, we estimate an additional 500 of these 2012 families will become accessible to fold prediction by coevolution methods (Pfam numbers courtesy of J. Mistry and M. Punta). Similar extrapolations can be made for other protein structure classes, such as β-sheet transmembrane proteins or globular water-soluble proteins. (c) A comparison of methods for three-dimensional protein structure determination showing the complementary nature of various features from different approaches. 'Sequence needs' refers to the number of sequnces needed to solve the three-dimensional structure; 'Existing 3D needs' refers to the number of homologous sequences needed to solve structure. 'Coverage' refers to the ability to solve a large fraction of existing proteins given sufficient sequence information. Not included in our comparison matrix are large specialized hardware computational methods for protein structures such as Anton, which though providing insights into protein dynamics and folding are not yet easily reproducible59. (d) Hybrid methods using all three computational approaches in c, with easier to produce experimental data, may greatly increase the number of protein structures and complexes, which are currently not in reach of experimental methods alone. EM, electron microscopy.
Signatures of evolutionary constraints may be left in sequences as a result of forces other than natural evolution. Guided evolution or selection in the laboratory is a potentially powerful tool for focused expansion of the sequence repertoire in any particular protein family57. After generating partially randomized large sequence sets, one can use a selection or screening method to identify sequences that are the result of strong functional constraints. Sequence-constraint experiments in the laboratory, coupled with massively parallel sequencing, have the promise of generating tens or hundreds of thousands of diverse sequences, permitting a robust derivation of evolutionary couplings.
Combine experimental and computational structural biology
With the steep rise in the amount of sequence information, a rapid scan of the universe of protein folds at reasonable prediction accuracy appears to be within reach. Such a survey would provide insight into the diversity of protein structures that have evolved to perform a wide range of specific molecular functions. Obtaining higher-accuracy structures will take more time, even if experimental structural genomics technology is further accelerated.
A particularly productive approach may be the combination of computational and experimental methods (Fig. 5c). Protein-structure determination by NMR spectroscopy is ideally suited for a hybrid approach8, as it is based on the determination of distance constraints. Combining distance constraints derived from evolutionary couplings with those from NMR spectroscopy could reduce the amount of experimental effort needed to obtain a correct structure or facilitate the solution of larger structures than possible using NMR spectroscopy alone. A similar increase in overall efficiency could be obtained using X-ray crystallography if a molecular replacement search of a predicted three-dimensional structure against just a native data set can be made to work. This would save the effort of obtaining additional derivative or anomalous diffraction data sets. Combining reduced X-ray and NMR spectroscopy data sets with predicted three-dimensional models may open a new phase for structural biology with much more rapid determination of high-accuracy protein structures (Fig. 5d).
Experimental and computational structural biology has made tremendous progress since the first elucidation of the intricate details of protein three-dimensional structures and the first in vitro protein-folding experiments. We are now entering a phase in which the evolutionary information in the genetic sequences of the living system is being rapidly read using advanced sequencing technology. Using the resulting massive sequence data sets, successful decoding of the molecular record of evolutionary constraints could now reveal structural and functional information about proteins at an unprecedented rate.