Towards sound epistemological foundations of statistical methods for high-dimensional biology (original) (raw)
The challenge we face
High-dimensional biology (HDB) encompasses the 'omic' technologies1 and can involve thousands of genetic polymorphisms, sequences, expression levels, protein measurements or combination thereof. How do we derive knowledge about the validity of statistical methods for HDB? A shared understanding regarding this second-order epistemological question seems to be lacking in the HDB community. Although our comments are applicable to HDB overall, we emphasize microarrays, where the need is acute. “The field of expression data analysis is particularly active with novel analysis strategies and tools being published weekly” (ref. 2; Fig. 1), and the value of many of these methods is questionable3. Some results produced by using these methods are so anomalous that a breed of 'forensic' statisticians4,5, who doggedly detect and correct other HDB investigators' prominent mistakes, has been created.
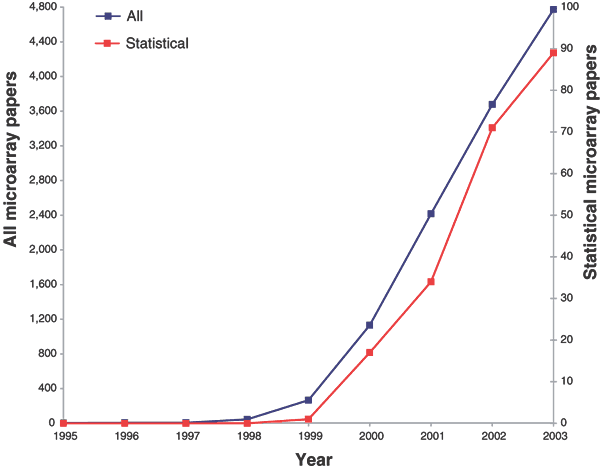
Figure 1: Growth of microarray and microarray methodology literature listed in PubMed from 1995 to 2003.
The category 'all microarray papers' includes those found by searching PubMed for microarray* OR 'gene expression profiling'. The category 'statistical microarray papers' includes those found by searching PubMed for 'statistical method*' OR 'statistical techniq*' OR 'statistical approach*” AND microarray* OR 'gene expression profiling'.
Here we offer a 'meta-methodology' and framework in which to evaluate epistemological foundations of proposed statistical methods. On the basis of this framework, we consider that many statistical methods offered to the HDB community do not have an adequate epistemological foundation. We hope the framework will help methodologists to develop robust methods and help applied investigators to evaluate whether statistical methods are valid.
Our vantage point: from samples to populations
We study samples and data to understand populations and nature. From this perspective (Table 1), the sampling units are cases (e.g., mice) and not genes. Although this may seem obvious, methods in which inferences about differences in gene expression between populations are made by comparing observed sample differences with an estimated null distribution of differences based on technical rather than biological replicates have been proposed6. Measurement error should not be confused with true biological variability among cases in a population. This conflates the standard error of measurement with the standard error of the sample statistic; it takes observations from Level I (Table 1), makes an inference to Level II and conflates this inference with the desired inference to Level III. This is one example of a common class of mistakes that can be avoided by considering the sample-to-population perspective.
Table 1 Iconic representation of levels of observation and inference
What is validity?
Assessing validity requires explicit standards for evaluating methods. This requires an explanation of what a method is supposed to do or what properties it is supposed to have. A full description of various properties that a statistical procedure should have is beyond our scope. There is inherent subjectivity in choosing which properties are of interest or desired, but once criteria are chosen, methods can and should be evaluated objectively. Validity can be relative and situation-specific. This is noteworthy in considering the merit of a newly proposed procedure when one or more procedures already exist for similar purposes. In such cases, it may be important to ask not only whether the new method is valid in an absolute sense, but whether and under what circumstances it confers any relative advantage with respect to the chosen properties. Table 2 outlines four common statistical activities in HDB, how validity might be defined in each and special issues with their application to HDB.
Table 2 Four common statistical activities in HDB and issues in the validation of their methods
The search for proof: deduction
A proof is a logical argument proceeding from axioms to eventual conclusion through an ordered deductive process. Its certainty stems from the deductive nature by which each step follows from an earlier step. As things proven and methods of their proof have become more complex, certainty is not always easy to achieve and what is obvious to one person may not be to another7. The key structure that we should seek in a proof that a method has a certain property has three parts: precise formulation of axioms, statement of the method's purported property and logical steps connecting the two.
Proofs begin with axioms or postulates (i.e., assumptions) and are valid only when the assumptions hold. The proof's practical conclusions may hold across broader circumstances, but additional evidence is required to support this. Therefore, it is important to state and appreciate the assumptions underlying any method's validity. This allows assessment of whether those assumptions are plausible and, if not, what the effect of violations might be.
Many methods assume that residuals from some fitted model are normally distributed. It is unclear, however, whether transcriptomic or proteomic data are normally distributed even after the familiar log transformation. For least squares–based procedures, the central limit theorem guarantees robustness with large sample sizes. But HDB sample sizes are typically small. Some analyses allow the enormous numbers of measurements to compensate for the few cases8, but the extent to which such procedures compensate for robustness to departures from distributional assumptions is unclear.
An equally important Gauss-Markov assumption9, homoscedasticity (homogeneity of variance), is crucial for most least squares–based tests. Violation can greatly affect power and type 1 error levels. Here, it is important to highlight a common misconception about nonparametric statistics. Nonparametric statistics, including permutation tests, are distribution-free. Their validity does not depend on any particular data distribution. But distribution-free is not assumption-free. Many HDB methodologists use nonparametric, particularly permutation or bootstrap, testing as though it eliminates all assumptions and is universally valid. This is not so10,11. For example, conventional permutation tests assume homoscedasticity and can be invalidated by outliers10. Moreover, conducting inference for one's method by permutation, even if this yields correct type 1 error rates, may not be optimal for all purposes. For example, in some transcriptomic studies, investigators may primarily wish to rank genes by their 'importance' or the magnitude of their effect. In such cases, permutation tests may yield valid type 1 error rates but may be outperformed by parametric tests in terms of ranking genes by magnitude of effect12.
Another common assumption about statistical techniques is that certain elements of the data are independent9, and violations can markedly invalidate tests. This includes permutation and bootstrap tests, unless the dependency is built into the resampling process, as some have done13. Thus, we should ask whether dependency is accommodated in our methods. A popular approach in microarray data is to calculate a test statistic for each gene and then permute the data multiple times, each time recalculating and recording the test statistics, thereby creating a pseudonull distribution against which observed test statistics can be compared for statistical significance. If one uses only the distribution of test statistics in each gene, then, given the typically small samples, there are insufficient possible permutations and the distribution is coarse and minimally useful14,15. Some investigators16 pool the permutation-based test statistics across all genes to create a pseudonull distribution with lesser coarseness. But this approach treats all genes as independent, which is not the case. Therefore, P values derived from such permutations may not be strictly valid17.
Statements about proposed approaches can be supported by referring to proofs already published. For example, those proposing a particular mixed model approach18 correctly realized that they did not need to prove that (under certain conditions) this model is asymptotically valid for frequentist testing, because this has already been shown. They needed only to cite those references. Recognizing the limits of what has been previously shown is important, and mixed models exemplify an acute concern in HDB. Certain mixed model tests are asymptotically valid but can be invalid under some circumstances with samples as small as 20 per group19, far larger than those typically used in HDB. Thus, validating methods with small samples when their validity relies on asymptotic approximations is vital.
Finally, we note that mathematical description of some process is not equivalent to proof that the result of the process has any particular properties. Methodological papers in HDB often present new algorithms with exquisite mathematical precision. Those who are less comfortable with mathematics may mistake this for proof. Writing an equation may define something, but it does not prove anything.
The proof of the pudding is in the eating: induction
In induction, there is no proof that a method has certain properties. Instead we rely on extra-logical information20,21. If a method performs in a particular manner across many instances, we assume it will probably do so in the future. We therefore seek to implement methods in situations that can provide feedback about their performance22. Simulation and plasmode studies (below) are two such methods.
Many methodologists use simulation to examine methods for HDB8,14. Because the data are simulated, one knows the right answers and can unequivocally evaluate the correspondence between the underlying 'truth' and estimates, conclusions or predictions derived with the method. Moreover, once a simulation is programmed, one can generate and analyze many data sets and, thereby, observe expected performance across many studies. Furthermore, one can manipulate many factors in the experiment (e.g., sample size, measurement reliability, effect magnitude) and observe performance as a function. There are two key challenges to HDB simulation: computational demand and representativeness.
Regarding computational demand, consider that we need to analyze many variables (e.g., genes) and may use permutation tests that necessitate repeating analyses many times per data set. This demand is compounded when we assess method performance across many conditions and wish to work at α levels around 10−4 or less, necessitating on the order of 106 simulations per condition to accurately estimate (i.e., with 95% confidence to be within 20% of the expected value) type 1 error rates. Simulating at such low α levels is important, because a method based on asymptotic approximations may perform well at higher α levels but have inflated type 1 error rates at lower α levels. In such situations, even a quick analysis for an individual variable becomes a computational behemoth at the level of the simulation study. Good programming, ever-increasing computational power and advances in simulation methodology (e.g., importance sampling)23 are, therefore, essential.
The second challenge entails simulating data that reasonably represent actual HDB data, despite limited knowledge about the distribution of individual mRNA or protein levels and the transcriptome- or proteome-wide covariance structure. Consequently, some investigators believe that HDB simulation studies are not worthwhile. This extreme and dismissive skepticism is ill-founded.
First, although we have limited knowledge of the key variables' distributions, this is not unique to HDB24, and we can learn about such distributions by observing real data. We rarely know unequivocally the distribution of biological variables, yet we are able to develop and evaluate statistical tests for these. One can simulate data from an extraordinarily broad variety of distributions25. If tests perform well across this variety, we can be relatively confident of their validity. Moreover, if we identify specific 'pathological' distributions for which our statistical procedures perform poorly, then by using them in practice, we can attempt to ascertain whether the data have such distributions.
Regarding correlation among genes, it is easy to simulate a few, even non-normal, correlated variables26. In HDB, the challenge is simulating many correlated variables. Using block diagonal correlation matrices14 oversimplifies the situation. 'Random' correlation matrices27 are unlikely to reflect reality. Alternatively, one can use real data to identify a correlation structure from which to simulate. This can be done by using the observed expression values and simulating other values (e.g., group assignments, quantitative outcomes) in hypothetical experiments or by generating simulated expression values from a correlation matrix that is based in some way on the observed matrix28 using factoring procedures. Exactly how to do this remains to be elucidated, but the challenge seems to be surmountable. Investigators are addressing this challenge29,30,31, and several microarray data simulators exist (refs. 32–34 and the gene expression data simulator at http://bioinformatics.upmc.edu/GE2/index.html).
Another challenge in simulation is to make the covariance structure 'gridable', meaning that the theoretically possible space of a parameter set can be divided into a reasonably small set of mutually exclusive and exhaustive adjacent regions. Typically, simulation is used when we are unable to derive a method's properties analytically. Therefore, it is usually desirable to evaluate performance across the plausible range of a key factor. If that factor is the correlation between two variables, one can easily simulate along the possible range (−1,1) at suitably small adjacent intervals (a grid). With multiple variables under study, the infinite number of possible correlation matrices is not obviously represented by a simple continuum, and it is not obvious how to establish a reasonably sized grid. But if one could extract the important information from a matrix in a few summary metrics, such as some function of eigenvalues, it might be possible to reduce the dimensionality of the problem and make it 'gridable'. This is an important topic for future research.
A plasmode is a real data set whose true structure is known35. As in simulations, the right answer is known a priori, allowing the inductive process to proceed. Plasmodes may represent actual experimental data sets better than simulations do. In transcriptomics, the most common type of plasmode is the 'spike-in' study. For example, real cases from one population are randomly assigned to two groups and then known quantities of mRNA for specific genes (different known quantities for each group) are added to the mRNA samples. In this situation, the null hypothesis of no differential expression is known to be true for all genes except those that were spiked, and the null hypothesis is known to be false for all those that are spiked. One can then evaluate a method's ability to recover the truth.
Plasmode studies have great merit and are being used15,36, but there is a need for greater plurality. Because statistical science deals with random variables, we cannot be certain that a method's performance in one data set will carry over to another. We can only make statements about expected performance, and estimating expected or average performance well requires multiple realizations. Analysis of a single plasmode is minimally compelling. Because plasmode creation can be expensive and laborious, it is difficult for investigators to create many. Additionally, although plasmodes might offer better representations of experimental data sets, there is no guarantee. For example, in spike-in studies, it is unclear how many genes should be spiked or what the distribution of spike-created effects should be to reflect reality.
Combined modes
One can also combine the approaches above15. When two or more modes yield consistent conclusions, confidence is strengthened. One could also creatively combine deduction and induction. For example, suppose there were two alternative inferential tests, A and B, which could be proven deductively to have the correct type 1 error rate under the circumstances of interest. If one applied the tests to multiple real data sets and consistently found that test A rejected more null hypotheses than did test B, one could reasonably conclude that test A was more powerful than test B. This makes sense only if both tests have correct type 1 error rates.
Data sets of unknown nature: circular reasoning
Authors often purport to demonstrate a new method's validity in HDB by applying it to one real data set of unknown nature. A new method is applied to a data set, and a new interesting finding is reported; for example, a gene previously not known to be involved in disease X is found to be related to the disease, and the authors believe that the finding shows their method's value. The catch is this: if the gene was previously not known to be involved in disease X, how do the authors know that they got the right answer? If they do not know that the answer is right, how do they know that this validates their method? If they do not know that their method is valid, how do they know that they got the right answer? We are in a loop (circular argument). Illustration of a method's use is not demonstration of its value. Illustration with single data sets of unknown nature, though interesting, is not a sound epistemological foundation for method development.
Where to from here? We offer four suggestions for progress:
(i) Vigorous solicitation of rigorous substantiation. Guidelines have been offered or requested for genome scan inference37, transcriptomic data storage38, specimen preparation and data collection39, and result confirmation40. We agree that these should remain guidelines and not rules41. Such guidelines help evaluate evidential strength of claims. But there are no guidelines for presentation and evaluation of methodological developments22. Thus, we offer the guidelines in Box 1 to be used in evaluating proffered methods.
(ii) 'Meta-methods'. For methodologists to strive for high standards of rigor, they must have the tools to do so. An important area for new research is HDB 'meta-methodology', methodological research about how to do methodological research. Such second-order methodological research could address how to simulate realistic data and how to meet computational demands. Public plasmode database archives would also be valuable.
(iii) Qualified claims? A risk in requesting more rigorous evidential support for new HDB statistical techniques is that if such requests became inflexible demands, progress might be slowed. 'Omic' sciences move fast, and investigators need new methodology. Therefore, although we hope methodologists publish new methods with the most rigorous validation possible, public scientific conjecture has an illustrious history, and it is in the interests of scientific progress and intellectual freedom that compelling methods, though merely conjectured to be useful, be published. But, as Bernoulli wrote, “In our judgments we must beware lest we attribute to things more than is fitting to attribute...and lest we foist this more probable thing upon other people as something absolutely certain”42. Thus, it is reasonable to publish methods without complete evidence regarding their properties, provided we follow Bernoulli: state the claims we are making for our proffered methods and whether such claims are supported by simulations, proofs, plasmode analyses or merely conjecture.
(iv) Caveat emptor. Ultimately, we offer the ancient wisdom, “_caveat emptor_”. Statistical methods are, by definition, probabilistic, and in using them, we will err at times. But we should have the opportunity to proceed knowing how error-prone we will be, and we appeal to methodologists to provide that knowledge.