Directed acyclic graphs: a tool for causal studies in paediatrics (original) (raw)
Introduction
A wide variety of studies are undertaken with the aim of understanding and improving paediatric health, and in particular to identify the causal processes that lead to the development of health outcomes or disease. To achieve this, it is helpful to define a number of variables (for the benefit of the reader unacquainted with the technical language that follows, we have created a Supplemental Glossary available online). For example, in a study looking at the relationship between screen time (time spent watching television, using computers or games consoles) and childhood obesity,1 the authors hypothesised that more screen time (the exposure) may lead to an increased risk of childhood obesity (the outcome). The exposure may cause the outcome not directly but through an intermediate process—a direct reduction in physical activity (the intermediate variable or mediator). Finally, we want to identify factors that influence both the exposure and the outcome, but are not directly in the causal pathway. An example is low parental education, which is a cause of both increased screen time and an increased risk of obesity/overweight.2,3 In this situation, low parental education acts as what is called a confounder. If not recognised and controlled for, this could lead to a false interpretation of the true relationship between the two variables, for example by falsely attributing obesity solely to increased screen time.
We will not attempt to summarise the history, philosophy and applications of causal inference, but instead in this review focus on the use of a graphical tool, causal directed acyclic graphs (DAGs). DAGs provide a simple way of graphically representing, communicating and understanding key concepts of relevance to practising clinicians and researchers, and are particularly helpful in delineating and understanding confounders and potential sources of bias in exposure–outcome relationships. A bias is a systematic, incorrect interpretation of the true relationship between the exposure and the outcome. Biases differ from random error in that they distort our interpretation of true causal relationships in a non-random way: repeating a study, or increasing the sample size, will not lead to the elimination of bias. Confounders and biases may distort our interpretations in a variety of ways. If the researcher is not aware of confounders, and does not appropriately control for them, a variable may erroneously appear to cause the outcome where there is no causal relationship, or the magnitude of this relationship may be distorted. Conversely, if a researcher treats variables associated with both exposure and outcome as confounders when they in fact are not (see below), and inappropriately controls for them, this too may cause bias.
We first discuss how to create and interpret DAGs, using paediatric examples to demonstrate how they can identify, and appropriately correct for, confounders and biases in observational studies that can affect our ability to draw correct conclusions about causal relationships. We then outline how they can be helpful in interpreting interventional studies, and understanding potential threats to validity in these. After outlining some of the limitations of DAGs, we conclude with some thoughts on how they might prove useful for researchers and clinicians.
Creating and interpreting a DAG
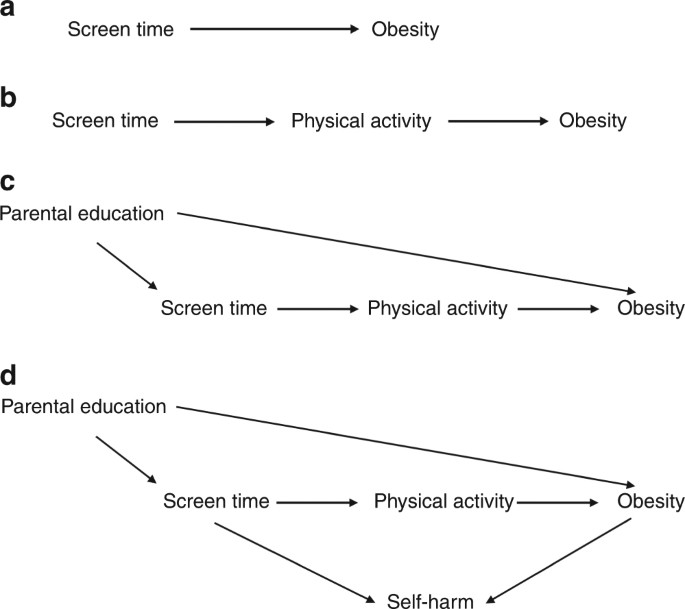
Diagrams have been used to represent causal relationships for many years, in a variety of fields ranging from genetics to sociology.4,5,6,7 However, in recent years an epidemiological literature outlining a standard terminology and set of rules,8 has grown around DAGs. In a DAG, causal relationships are represented by arrows between the variables, pointing from cause to effect. As seen in Fig. 1a, an arrow from screen time to obesity means that we hypothesise that a change in screen time causes a change in adiposity. DAGs must obey two rules. First, they must be acyclic, which means that it is impossible to start at any variable in the DAG, follow the directed arrows forward, and end up at the same variable. In other words, a DAG must not contain a feedback loop where a variable causes itself. A corollary of this is that a causal relationship between two variables must be unidirectional: they cannot cause each other. Bidirectional arrows, often used to depict feedback loops, are in fact a simple graphical expedient to show as a single variable what in reality is a sequence of variables.9 Second, for a DAG to be complete, the shared cause of any two variables in the DAG must be included.10
Fig. 1
a Screen time (the exposure) causes obesity (the outcome). b Screen time acts on obesity through the mediator of physical activity. c Low parental education increases both screen time and obesity, and is therefore a confounder. d Self-harm is a collider in the path from screen time to obesity
In a DAG, two variables can be connected by what is called a “path” between them. Open “paths” represent statistical associations between two variables; closed “paths” represent the absence of such associations (the correspondence between path “openness” and associations in DAGs derives from mathematics).8 Variables and arrows can be combined into three main types of paths as follows:
- Directed paths: all arrows point in the same direction, and the association between these variables reflects a causal relationship. Such a path is open. Increased screen time leads directly to reduced physical activity, which in turn leads to an increased risk of obesity (Fig. 1b).
- Backdoor paths: this is where two variables share the same cause. Looking at Fig. 1c, increased screen time and childhood obesity are influenced by low parental education. In the terminology of DAGs, screen time and childhood adiposity are said to be connected by a backdoor path through low parental education. This path (one that connects exposure and outcome through a third variable, including an arrow entering rather than emanating from the exposure) is open, and depicts a statistical association between screen time and adiposity, through low parental education. However, the association transmitted by this backdoor path is non-causal, and represents the basic structure of confounding.
- Closed (or blocked) paths: this is when two variables have the same effect, called a collider (Fig. 1d). For example, both screen time and obesity have been found to increase the risk of low self-esteem, self-harm and suicidal ideation in adolescents,11,12,13 that is self-harm is a collider between physical activity and obesity. In this situation, unlike directed and backdoor paths, this path is closed: there is no association between screen time and adiposity transmitted through self-harm.
Researchers can change the status of a path from open to closed, or vice versa, by acting on (conditioning on, or controlling for) a variable, which can occur through study design or statistical adjustments such as restriction, stratification, matching, standardisation, or multivariable regression. Controlling for parental education (a confounder) in our example will close this backdoor path, and lead to a less biased relationship in the directed path between screen time and adiposity. Conversely, conditioning on a variable in a directed path between two variables (a mediator), physical activity in our example, closes this path, and could lead to an incorrect estimate of the true overall association between the variables. Finally, conditioning on a variable in a closed path (a collider) opens this path and leads to transmission of a non-causal association. If we were to mistakenly identify self-harm as a confounder, and condition on it, this would distort the true relationship between the exposure and the outcome. Equally, if a study examined the relationship between screen time and obesity in a group of adolescents selected because they had a history of self-harm, this would again represent conditioning on a collider, in this case by restriction (see “selection bias” below).
Using DAGs to understand confounding: paracetamol and wheeze
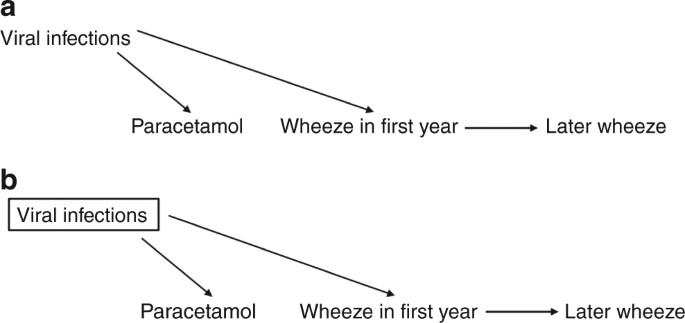
In the language of DAGs, a confounder is defined as a common cause of the exposure and the outcome. This situation occurs in nature; it is not created by the researcher. Confounders, if not identified and appropriately adjusted for (conditioned on), can distort the true causal relationship between an exposure and an outcome. As an example, a number of observational studies14,15 found an association between receiving paracetamol in the first year of life and later risk of developing wheeze/asthma. DAGs have proven useful in examining this relationship.16
In fact, the increased risk of later wheezing may not be due to paracetamol, but to confounding. Viral respiratory tract infections—for which paracetamol is prescribed—are common in children, trigger wheezing and might increase the risk of later wheeze.17,18 That is, viral infections act as a confounder in the relationship between paracetamol usage and wheezing (Fig. 2a) (so-called confounding by indication).19,20 Therefore we might expect these two variables (paracetamol use and wheeze) to be statistically associated through a common cause, even if there is no direct causal association. To identify the true causal relationship between paracetamol use and later wheeze, one should condition on viral infections. Conditioning in a DAG is generally shown as a box around the variable, and as described previously changes an open path (in this case a backdoor path) to a closed path (Fig. 2).
Fig. 2
a Viral infections cause both paracetamol use and wheeze, acting as a confounder. b This bias can be controlled by conditioning on the confounder (shown by a box around viral infections)
Once we have closed this backdoor path by making the appropriate statistical adjustments, and assuming there are no other confounders, we should be able to identify the true magnitude, if any, of the relationship between paracetamol use and wheeze. Supporting this hypothesis, studies which have conditioned on respiratory tract infections in early life find a diminished relationship between paracetamol use and later wheeze, suggesting that part of this apparent relationship may be due to confounding.16,21,22
Risks of inappropriate adjustment: overadjustment
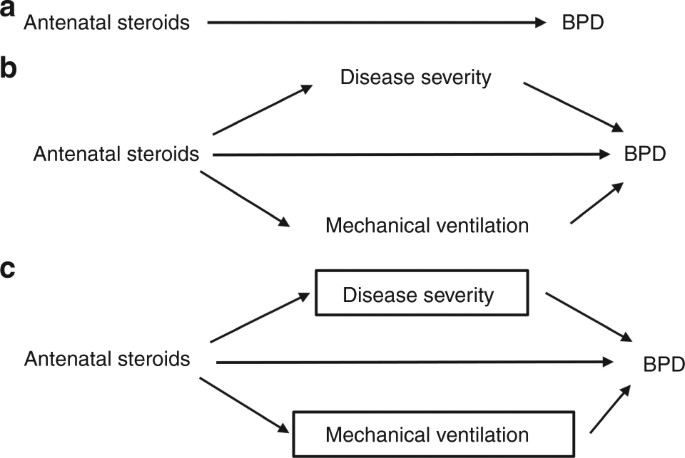
Whilst failing to identify confounders can threaten the validity of findings, the converse, inappropriately identifying other variables as confounders, can also be problematic.23 Take the relationship between the administration of antenatal steroids (the exposure) and the outcome of bronchopulmonary dysplasia (BPD) (Fig. 3a). A number of studies found that administration of antenatal steroids was not associated with a decreased risk of BPD,24,25,26 despite reducing several known risk factors for BPD. These studies adjusted for variables such as severity of neonatal disease,24 and need for mechanical ventilation,24,25,26 the rationale being that these factors are associated with both the administration of antenatal steroids and an increased risk of BPD.
Fig. 3
a Antenatal steroids affect the risk of bronchopulmonary dysplasia (BPD). b Antenatal steroids also have indirect effects. c By controlling for disease severity and mechanical ventilation, we underestimate the true overall effect of the antenatal steroids
However, these variables do not fulfil the definition of a confounder (they are not causes of both exposure and outcome), but act as mediators between the exposure (antenatal steroids) and the outcome (BPD) (Fig. 3b). Conditioning on a mediator closes one of the causal paths between antenatal steroids and BPD and distorts the overall relationship between the two. This is represented in Fig. 3c by the boxes surrounding the two intermediate variables. Adjusting for (conditioning on) an intermediate results in overadjustment. With this process we remove the part of the association between antenatal steroids and BPD mediated through the reduction of severe illness, or the reduced need for mechanical ventilation.27 This adjustment can attenuate the true causal effect of the exposure or even reverse it, leading to counterintuitive results.
Supporting the interpretation that overadjustment might explain the apparent lack of effect of antenatal steroids on the development of BPD, a cohort study28 found a negative (protective) association between antenatal steroid administration and mediators (severity of neonatal disease and the need for mechanical ventilation), and a positive association between the mediators and the risk of the BPD. The authors found a protective effect of steroids on BPD when intermediate factors were not adjusted for, but not when they adjusted for these intermediate variables (Fig. 3c). That is, inappropriately conditioning on mediators led to a distortion of the true (likely protective) relationship between antenatal steroids and risk of developing BPD. Of note, whilst conditioning on mediators distorts the overall relationship between an exposure and an outcome, Fig. 3c also shows that this should reveal the direct effect of steroids on BPD (with the highly simplified assumption that there are no other common causes of steroid administration, BPD, or the mediators); this concept underlies the field of mediation analysis.29,30
Selection bias in the language of DAGs
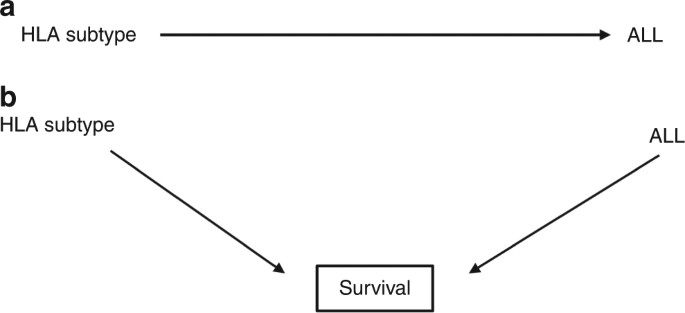
In observational or interventional studies, selection bias occurs when both the exposure and the outcome affect whether an individual is included in the analyses. In the language of DAGs, selection bias occurs due to inappropriate conditioning on a collider. An example are studies that examined HLA subtypes (the exposure) as risk factors for the development of acute lymphoblastic leukaemia (ALL, the outcome). Initial cross-sectional studies using prevalent (i.e. already diagnosed) cases and matched controls31,32,33 found an increased risk of developing ALL in individuals with the HLA-A2 serotype (Fig. 4a).
Fig. 4
a A possible relationship: HLA subtypes affect the risk of acute lymphoblastic leukaemia (ALL). b The true causal structure, showing selection bias: both HLA subtype and ALL influence survival, and the study is conducted in survivors
However, a subsequent study34 examined patients presenting with a new diagnosis of ALL (incident cases), and found that the frequency of HLA-A2 in these individuals matched that of the general population. When examining survivors at the time of typing, they found that the frequency of HLA-A2 was higher than in the general population, and that length of survival appeared to be associated with the HLA-A2 serotype. That is, HLA-A2 was not associated with an increased risk of developing ALL, but rather with an increased chance of survival. Because previous studies had examined a prevalent population (patients with a previous diagnosis of ALL) rather than an incident one (those presenting with a new diagnosis), they had examined the relationship between HLA-A2 and leukaemia in a sample restricted to survivors, and an incorrect association was inferred between the exposure and the outcome.
Presented as a DAG, the source of this bias, also called “incidence-prevalence” or Neyman’s bias,35,36 can be seen to be due to conditioning on a collider. In this case, both the exposure and the outcome influence a third variable, survival, which acted as a collider (Fig. 4b). If we consider all patients—surviving or not—by including newly diagnosed patients, the two variables are not associated (the path is closed). Conditioning on survival (by restricting the inclusion to patients surviving a certain time, as shown by the box surrounding survival in the figure), opens the path through the collider, and we enrich the sample for individuals with HLA-A2 among ALL patients, creating a (spurious) association.
Overadjustment and selection bias
Overadjustment and selection bias can also coexist. Take the relationship between maternal pre-eclampsia (the exposure) and subsequent cerebral palsy (the outcome): pre-eclampsia is hypothesised to be directly causative of cerebral palsy. However, pre-eclampsia is also associated with a higher risk of medically indicated preterm birth, which in turn is associated with a higher risk of cerebral palsy (Fig. 5a). We might think to examine the effect of pre-eclampsia after adjusting for preterm birth or gestational age (as if this represented confounding) (Fig. 5b), shown by the box around this variable. However, here preterm birth is an intermediate between pre-eclampsia and cerebral palsy, and not a common cause of both.
Fig. 5
a Pre-eclampsia increases the risk of cerebral palsy directly, and indirectly by increasing preterm birth. b By adjusting for preterm birth, we underestimate the overall effect of pre-eclampsia on cerebral palsy. c Adjusting for preterm birth causes the estimated effect of pre-eclampsia on cerebral palsy to suffer from both overadjustment and selection bias
By (over)adjusting, we take away part of the detrimental effect of pre-eclampsia, that mediated through preterm birth. This adjustment can attenuate the true effect of the exposure and even reverse it. An early study found that maternal pre-eclampsia was protective in very preterm infants, but detrimental to those born at a later gestation.37 This was a surprising result—as a pathologic condition, we would expect pre-eclampsia to be detrimental across the entire spectrum of gestations.38,39 Visualised as a DAG, this finding could be due to the conditioning on gestational age at birth. In this case, conditioning does not take place through statistical adjustment, but by stratification (performing separate analyses in two groups) based on the criterion of gestational age at birth (preterm birth). This closes the causal path from pre-eclampsia to cerebral palsy via preterm birth, and could lead to bias.
However, the true situation is probably more complex. Examining a more realistic DAG, to which chorioamnionitis (as another cause of both preterm birth and cerebral palsy) has been added (Fig. 5c), one can see that gestational age, as the shared effect of both pre-eclampsia and chorioamnionitis, also acts as a collider. Critically, closing one path between two variables may lead to a change in other potential paths between the two. Conditioning on gestational age opens a previously closed path, from pre-eclampsia to cerebral palsy through preterm birth and chorioamnionitis. This creates a new source of bias, and another reason for the counterintuitive association found in our example. If we analyse the relationship between pre-eclampsia and the outcome within the group of preterm infants, a faulty comparison group and a spurious association will be created. If a preterm baby is born to a mother who has pre-eclampsia, the baby will be less likely to have chorioamnionitis and vice versa. Among preterm infants the effect of pre-eclampsia on cerebral palsy will be compared with the effect of another significant cause of cerebral palsy, chorioamnionitis, and pre-eclampsia will falsely appear to be protective. Thus, the estimated direct causal effect of pre-eclampsia on the outcome will be biased (through the effect of chorioamnionitis). Although widely used, conditioning on gestational at birth in studies of prenatal exposures and their relationship to postnatal outcomes may not reduce but actually lead to bias through overadjustment and faulty comparisons as illustrated above,40,41,42,43 and generate counterintuitive results and apparent changes of effect in different groups of patients.
Disentangling confounders from mediators and colliders can prove challenging. Statistical tests reveal only the strength of an association between two variables, not the causal relationship between them, and in this context the researcher must rely on causal reasoning.44 Here, DAGs, supported by subject-matter knowledge, can be helpful as they illustrate a modern definition of confounding:45,46 a common cause of both the exposure and the outcome under study. This demonstrates how older definitions,47,48 focusing on factors associated with the exposure and also related to the risk of disease in the unexposed, and not being an intermediate (i.e. on associations rather than presumed causal relationships), may lead to biased statistical estimates due to inappropriate adjustment for a common effect of two variables (conditioning on a collider).
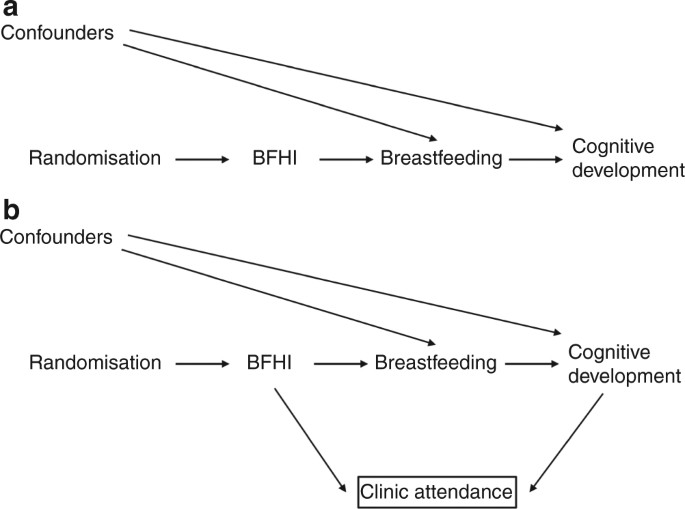
The language of DAGs as applied to interventional studies
The DAG in Fig. 6a shows the causal structure of a randomised controlled trial (RCT) randomising women to an intervention promoting breastfeeding, the Baby Friendly Hospital Initiative (BFHI),49 to examine cognitive development in childhood.50 Random assignment determines the exposure (BFHI) which in turn influences the outcome (cognitive development) via mediators such as breastfeeding (and probably others, not shown). Even if there are confounders that influence both the chance of breastfeeding and the outcome, they do not bias the causal effect of the random assignment on the outcome, as breastfeeding is a collider in the path between random assignment and cognitive development via potential confounders, and blocks this path. Therefore, as regards confounding, an intention-to-treat analysis (according to how a mother was randomised) is likely to be unbiased, and DAGs demonstrate the critical value of randomisation in inferring unbiased causal relationships. A per-protocol analysis of whether a mother actually breastfed is not immune to confounding, as it resembles an observational study where a backdoor path exists between breastfeeding and the outcome via any confounders.51 Of course, the effect of treatment actually received may be of interest, and a per-protocol analysis, carefully controlled for confounders, may be justified to extract the maximum of information from clinical trials.52
Fig. 6
a The structure of a randomised controlled trial (RCT); BFHI refers to the Baby Friendly Hospital Initiative. b Loss to follow-up in an RCT creates selection bias
Whilst RCTs and intention-to-treat analyses minimise threats to validity posed by confounding, they are not immune to other biases, including information bias (see glossary) and bias due to differential loss to follow-up. It is plausible that the BFHI might lead to differences in health awareness in the intervention group, leading to a different likelihood of follow-up clinic attendance. In addition, mothers with a child exhibiting signs of impaired cognitive development could also be more likely to attend follow-up to find out whether their child was developing normally. Seen as a DAG (Fig. 6b), both the BFHI and the outcome have a causal effect on the chance of follow-up. Examining data only on children who attend follow-up (conditioning on follow-up, represented by the box around clinic attendance), introduces bias into the relationship between the intervention and cognitive development via a faulty comparison, opening an otherwise closed path. Conditioning on a collider leads to what is called collider stratification bias.53,54 This example illustrates that whilst RCTs minimise confounding, they are still susceptible to bias such as that introduced by loss to follow up.
Limitations of DAGs and some caveats on their use
One limitation of DAGs is their non-parametric nature: they neither specify the form of the causal relationships, nor depict the size of the associations, and remain qualitative in nature. A DAG shows that uncontrolled confounding might bias the results, but does not give a quantitative measure of this.10,55 Another is that a DAG can only be as good as the background information used to create it;56 a DAG is complete and therefore has a causal interpretation only if it contains all common causes of any two variables (all confounders), including both measured and unmeasured variables. A further limitation is the inability of DAGs to depict random, as opposed to systematic, error. For instance, randomisation allocates known and unknown confounders equally between groups in the “average” ideal case. This does not always happen in real-world RCTs, where confounding, due to random differences at baseline, can—and indeed often does—occur, but is not shown by DAGs. Ignoring random error also means that when examining misclassification (information) bias, concepts such as non-differential measurement error (where error is randomly distributed across the groups being studied) cannot be incorporated into a DAG.
More subtly, and of relevance not only to DAGs but to any analytical approach, the research question influences how we consider variables and therefore analyse the data. A variable may be simultaneously a mediator, a collider or a confounder, can be interpreted differently in separate research questions using the same data, and these will dictate different analytical strategies. For example, in the study looking at the relationship between antenatal steroids and BPD, one could ask about the effect of steroids (exposure) on the outcome. Here the need for mechanical ventilation is a mediator and should not be conditioned on. However, if one were to investigate the effect of mechanical ventilation (treating it as an exposure) on the risk of BPD, antenatal steroids are a confounder in the backdoor path between mechanical ventilation and the outcome, and should be conditioned on. In addition, it is possible that two researchers might ask the same research question, using the same variables in their analyses, but choose to condition on different variables because they have different opinions regarding the underlying causal relationship. Representing their analyses as DAGs allows an explicit comparison between the two approaches should their findings differ.
Finally, throughout this article we have, of necessity, presented simple examples to illustrate our key points. Partly, this is inherent to the approach: any graphical method is likely to over-simplify the complex biological reality being investigated. DAGs have for this reason attracted criticism because they may lead to oversimplification in the field of causal inference.57,58 DAGs however do not lead per se to oversimplified analyses, but only explicitly present their underlying assumptions. There are also a number of theoretical points, such as the exact distinction between selection bias and confounding, that remain contested.59,60 We therefore direct interested readers to more in-depth reviews about the theory and limitations of DAGs.8,10,61,62
Conclusion
The aim of much clinical research is to elucidate and test causal relationships. In epidemiological terms, we want to establish exposures that might be amenable to modification, and test interventions acting on these leading to an improvement in health outcomes. Critical to a correct interpretation of causal relationships is correctly identifying and appropriately adjusting for confounders and potential sources of bias. In this review we have shown that DAGs can illustrate threats to validity found to greater or lesser extents in virtually all clinical research: confounding, selection (or collider-stratification) bias and overadjustment. We believe that DAGs are useful for practising clinicians in interpreting research that deals with proposed causal relationships, by allowing them to frame research questions and findings using the concepts of exposures, outcomes, intermediates, confounders and colliders. They remind those planning observational studies to collect sufficient data to condition on possible confounders, and to appropriately adjust for these in analyses, whilst refraining from inappropriate adjustments. Finally, they show that whilst randomisation does minimise the risks of confounding in interventional studies, possibilities for bias remain, for example through loss to follow-up.
References
- Nightingale, C. M., Rudnicka, A. R. & Donin, A. S. et al. Screen time is associated with adiposity and insulin resistance in children. Arch. Dis. Child 102, 612–616 (2017).
Article Google Scholar - Nagel, G., Wabitsch, M. & Galm, C. et al. Determinants of obesity in the Ulm Research on Metabolism, Exercise and Lifestyle in Children (URMEL-ICE). Eur. J. Pediatr. 168, 1259–1267 (2009).
Article Google Scholar - Falbe, J., Rosner, B., Willett, W. C., Sonneville, K. R., Hu, F. B. & Field, A. E. Adiposity and different types of screen time. Pediatrics 132, e1497–e1505 (2013).
Article Google Scholar - Wright, S. Correlation and causation. J. Agric. Res. 20, 557–585 (1921).
Google Scholar - Wright, S. The theory of path coefficients a reply to Niles’s criticism. Genetics 8, 239–255 (1923).
CAS PubMed PubMed Central Google Scholar - Holland, P. W. Causal inference, path analysis, and recursive structural equations models. Sociol. Methodol. 18, 449 (1988).
Article Google Scholar - Freedman, D. A. As others see us: a case study in path analysis. J. Educ. Stat. 12, 101 (1987).
Article Google Scholar - Pearl, J. Causal diagrams for empirical research. Biometrika 82, 669–688 (1995).
Article Google Scholar - Hernán, M., Schisterman, E. F. & Hernández-Díaz, S. Invited commentary: composite outcomes as an attempt to escape from selection bias and related paradoxes. Am. J. Epidemiol. 179, 368–370 (2014).
Article Google Scholar - Glymour, M. & Greenland, S. Causal Diagrams. Modern Epidemiology pp. 183–212 (Lippincott Williams & Wilkins, Philadelphia, 2008).
- Oshima, N., Nishida, A. & Shimodera, S. et al. The suicidal feelings, self-injury, and mobile phone use after lights out in adolescents. J. Pediatr. Psychol. 37, 1023–1030 (2012).
Article Google Scholar - Liu, M., Wu, L. & Yao, S. Dose-response association of screen time-based sedentary behaviour in children and adolescents and depression: a meta-analysis of observational studies. Br. J. Sports Med. 50, 1252–1258 (2016).
Article Google Scholar - Maras, D., Flament, M. F. & Murray, M. et al. Screen time is associated with depression and anxiety in Canadian youth. Prev. Med. 73, 133–138 (2015).
Article Google Scholar - Beasley, R., Clayton, T. & Crane, J. et al. Association between paracetamol use in infancy and childhood, and risk of asthma, rhinoconjunctivitis, and eczema in children aged 6–7 years: analysis from Phase Three of the ISAAC programme. Lancet 372, 1039–1048 (2008).
Article CAS Google Scholar - Etminan, M., Sadatsafavi, M., Jafari, S., Doyle-Waters, M., Aminzadeh, K. & FitzGerald, J. M. Acetaminophen use and the risk of asthma in children and adults. Chest 136, 1316–1323 (2009).
Article Google Scholar - Rusconi, F., Gagliardi, L. & Galassi, C. et al. Paracetamol and antibiotics in childhood and subsequent development of wheezing/asthma: association or causation? Int. J. Epidemiol. 40, 662–667 (2011).
Article Google Scholar - Blanken, M. O., Rovers, M. M. & Molenaar, J. M. et al. Respiratory syncytial virus and recurrent wheeze in healthy preterm infants. N. Engl. J. Med. 368, 1791–1799 (2013).
Article CAS Google Scholar - Jartti, T. & Gern, J. E. Role of viral infections in the development and exacerbation of asthma in children. J. Allergy Clin. Immunol. 140, 895–906 (2017).
Article Google Scholar - Bosco, J. L. F., Silliman, R. A. & Thwin, S. S. et al. A most stubborn bias: no adjustment method fully resolves confounding by indication in observational studies. J. Clin. Epidemiol. 63, 64–74 (2010).
Article Google Scholar - Kyriacou, D. N. & Lewis, R. J. Confounding by indication in clinical research. JAMA 316, 1818 (2016).
Article Google Scholar - Wickens, K., Ingham, T. & Epton, M. et al. The association of early life exposure to antibiotics and the development of asthma, eczema and atopy in a birth cohort: confounding or causality? Clin. Exp. Allergy 38, 1318–1324 (2008).
Article CAS Google Scholar - Lowe, A. J., Carlin, J. B. & Bennett, C. M. et al. Paracetamol use in early life and asthma: prospective birth cohort study. BMJ 341, c4616 (2010).
Article Google Scholar - Ananth, C. V. & Schisterman, E. F. Confounding, causality, and confusion: the role of intermediate variables in interpreting observational studies in obstetrics. Am. J. Obstet. Gynecol. 217, 167-175 (2017)
Article Google Scholar - Egreteau, L., Pauchard, J. Y. & Semama, D. S. et al. Chronic oxygen dependency in infants born at less than 32 weeks’ gestation: incidence and risk factors. Pediatrics 108, E26 (2001).
Article CAS Google Scholar - Van Marter, L. J., Allred, E. N. & Leviton, A. et al. Antenatal glucocorticoid treatment does not reduce chronic lung disease among surviving preterm infants. J. Pediatr. 138, 198–204 (2001).
Article Google Scholar - Marshall, D. D., Kotelchuck, M., Young, T. E., Bose, C. L., Kruyer, L. & O’Shea, T. M. Risk factors for chronic lung disease in the surfactant era: a North Carolina population-based study of very low birth weight infants. North Carolina Neonatologists Association. Pediatrics 104, 1345–1350 (1999).
Article CAS Google Scholar - Roberts, D., Brown, J., Medley, N. & Dalziel, S. R. Antenatal corticosteroids for accelerating fetal lung maturation for women at risk of preterm birth. Cochrane Database Syst. Rev. 3, CD004454 (2017).
- Gagliardi, L., Bellù, R., Rusconi, F., Merazzi, D. & Mosca, F. Antenatal steroids and risk of bronchopulmonary dysplasia: a lack of effect or a case of over-adjustment? Paediatr. Perinat. Epidemiol. 21, 347–353 (2007).
Article Google Scholar - MacKinnon, D. P., Fairchild, A. J. & Fritz, M. S. Mediation analysis. Annu. Rev. Psychol. 58, 593–614 (2007).
Article Google Scholar - Richiardi, L., Bellocco, R. & Zugna, D. Mediation analysis in epidemiology: methods, interpretation and bias. Int. J. Epidemiol. 42, 1511–1519 (2013).
Article Google Scholar - Rogentine, G. N., Yankee, R. A., Gart, J. J., Nam, J. & Trapani, R. J. HL-A antigens and disease. J. Clin. Invest. 51, 2420–2428 (1972).
Article Google Scholar - Lawler, S. D., Klouda, P. T., Hardisty, R. M. & Till, M. M. Histocompatibility and acute lymphoblastic leukaemia. Lancet 1, 699 (1971).
Article CAS Google Scholar - Walford, R. L., Finkelstein, S., Neerhout, R., Konrad, P. & Shanbrom, E. Acute childhood leukaemia in relation to the HL-A human transplantation genes. Nature 225, 461–462 (1970).
Article CAS Google Scholar - Rogentine, G. N., Trapani, R. J., Yankee, R. A. & Henderson, E. S. HL-A antigens and acute lymphocytic leukemia: the nature of the HL-A2 association. Tissue Antigens 3, 470–476 (1973).
Article CAS Google Scholar - Sackett, D. L. Bias in analytic research. J. Chronic Dis. 32, 51–63 (1979).
Article CAS Google Scholar - Neyman, J. Statistics; servant of all sciences. Science (80-) 122, 401–406 (1955).
Article CAS Google Scholar - Murphy, D. J., Sellers, S., MacKenzie, I. Z., Yudkin, P. L. & Johnson, A. M. Case-control study of antenatal and intrapartum risk factors for cerebral palsy in very preterm singleton babies. Lancet 346, 1449–1454 (1995).
Article CAS Google Scholar - Mann, J. R., McDermott, S., Griffith, M. I., Hardin, J. & Gregg, A. Uncovering the complex relationship between pre-eclampsia, preterm birth and cerebral palsy. Paediatr. Perinat. Epidemiol. 25, 100–110 (2011).
Article Google Scholar - Blair, E. & Watson, L. Cerebral palsy and perinatal mortality after pregnancy-induced hypertension across the gestational age spectrum: observations of a reconstructed total population cohort. Dev. Med. Child Neurol. 58, 76–81 (2016).
Article Google Scholar - Wilcox, A. J., Weinberg, C. R. & Basso, O. On the pitfalls of adjusting for gestational age at birth. Am. J. Epidemiol. 174, 1062–1068 (2011).
Article Google Scholar - Kramer, M. S., Zhang, X. & Platt, R. W. Commentary: Yerushalmy, maternal cigarette smoking and the perinatal mortality crossover paradox. Int. J. Epidemiol. 43, 1378–1381 (2014).
Article Google Scholar - VanderWeele, T. J., Mumford, S. L. & Schisterman, E. F. Conditioning on intermediates in perinatal epidemiology. Epidemiology 23, 1–9 (2012).
Article Google Scholar - Snowden, J. M. & Basso, O. Causal inference in studies of preterm babies: a simulation study. BJOG 125, 686–692 (2018).
Article Google Scholar - Pearl, J. Causality: Models, Reasoning, and Inference pp. 173–82 (Cambridge University Press, Cambridge, 2009).
- Weinberg, C. R. Toward a clearer definition of confounding. Am. J. Epidemiol. 137, 1–8 (1993).
Article CAS Google Scholar - Howards, P. P., Schisterman, E. F., Poole, C., Kaufman, J. S. & Weinberg, C. R. Toward a clearer definition of confounding revisited with directed acyclic graphs. Am. J. Epidemiol. 176, 506–511 (2012).
Article Google Scholar - Breslow, N. & Day, N. Statistical Methods in Cancer Research: The Analysis of Case-Control Studies. IARC Scientific Publications No. 32 (International Agency for Research on Cancer, Lyon, 1980).
- Morabia, A. History of the modern epidemiological concept of confounding. J Epidemiol Community Health 65, 297–300 (2011).
Article Google Scholar - World Health Organization & UNICEF. Protecting, Promoting and Supporting Breast-feeding: the Special Role of Maternity Services (World Health Organization, Geneva, 1989).
- Kramer, M. S., Aboud, F. & Mironova, E. et al. Breastfeeding and child cognitive development. Arch. Gen. Psychiatry 65, 578 (2008).
Article Google Scholar - Hernán, M. A. A definition of causal effect for epidemiological research. J. Epidemiol. Community Health 58, 265–271 (2004).
Article Google Scholar - Hernán, M. A. & Robins, J. M. Per-protocol analyses of pragmatic trials. N. Engl. J. Med. 377, 1391–1398 (2017).
Article Google Scholar - Greenland, S. Quantifying biases in causal models: classical confounding vs collider-stratification bias. Epidemiology 14, 300–306 (2003).
PubMed Google Scholar - Liu, W., Brookhart, M. A., Schneeweiss, S., Mi, X. & Setoguchi, S. Implications of M bias in epidemiologic studies: a simulation study. Am. J. Epidemiol. 176, 938–948 (2012).
Article Google Scholar - VanderWeele, T. J. & Robins, J. M. Directed acyclic graphs, sufficient causes, and the properties of conditioning on a common effect. Am. J. Epidemiol. 166, 1096–1104 (2007).
Article Google Scholar - Pearce, N. & Lawlor, D. A. Causal inference-so much more than statistics. Int. J. Epidemiol. 45, 1895–1903 (2016).
Article Google Scholar - Vandenbroucke, J. P., Broadbent, A. & Pearce, N. Causality and causal inference in epidemiology: the need for a pluralistic approach. Int. J. Epidemiol. 45, 1776–1786 (2016).
Article Google Scholar - Krieger, N. & Davey Smith, G. The tale wagged by the DAG: broadening the scope of causal inference and explanation for epidemiology. Int. J. Epidemiol. 45, dyw114 (2016).
Article Google Scholar - Haneuse, S. Distinguishing selection bias and confounding bias in comparative effectiveness research. Med. Care 54, e23–e29 (2016).
Article Google Scholar - Rothman, K. J., Gallacher, J. E. & Hatch, E. E. Why representativeness should be avoided. Int. J. Epidemiol. 42, 1012–1014 (2013).
Article Google Scholar - Greenland, S., Pearl, J. & Robins, J. M. Causal diagrams for epidemiologic research. Epidemiology 10, 37–48 (1999).
Article CAS Google Scholar - Shrier, I. & Platt, R. W. Reducing bias through directed acyclic graphs. BMC Med. Res. Methodol. 8, 70 (2008).
Article Google Scholar
Acknowledgements
We thank Professor Mark Klebanoff and the two reviewers for their careful reading of our manuscript and constructive comments.
Funding
T.C.W. is the recipient of a Wellcome Trust Grant [204802/Z/16/Z].
Author information
Author notes
- These authors contributed equally: Thomas C. Williams, Cathrine C. Bach, Niels B. Matthiesen
Authors and Affiliations
- Epidemiology Section, European Society for Paediatric Research, Edinburgh, UK
Thomas C Williams, Tine B Henriksen & Luigi Gagliardi - MRC Human Genetics Unit, Institute for Genetics and Molecular Medicine, University of Edinburgh, Edinburgh, UK
Thomas C Williams - Paediatrics and Adolescent Medicine, Randers Regional Hospital, Randers, Denmark
Cathrine C Bach & Niels B Matthiesen - Perinatal Epidemiology Research Unit, Paediatrics and Adolescent Medicine, Aarhus University Hospital, Aarhus, Denmark
Cathrine C Bach, Niels B Matthiesen & Tine B Henriksen - Division of Pediatrics and Neonatology, Ospedale Versilia, Azienda USL Toscana Nord Ovest, Pisa, Italy
Luigi Gagliardi
Authors
- Thomas C Williams
You can also search for this author inPubMed Google Scholar - Cathrine C Bach
You can also search for this author inPubMed Google Scholar - Niels B Matthiesen
You can also search for this author inPubMed Google Scholar - Tine B Henriksen
You can also search for this author inPubMed Google Scholar - Luigi Gagliardi
You can also search for this author inPubMed Google Scholar
Contributions
All authors made substantial contributions to the conception, design and drafting of this review, and approved the final manuscript as submitted.
Corresponding author
Correspondence toLuigi Gagliardi.
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Williams, T.C., Bach, C.C., Matthiesen, N.B. et al. Directed acyclic graphs: a tool for causal studies in paediatrics.Pediatr Res 84, 487–493 (2018). https://doi.org/10.1038/s41390-018-0071-3
- Received: 19 December 2017
- Revised: 27 April 2018
- Accepted: 10 May 2018
- Published: 04 June 2018
- Issue Date: October 2018
- DOI: https://doi.org/10.1038/s41390-018-0071-3