Statistical implications of pooling RNA samples for microarray experiments (original) (raw)
- Methodology article
- Open access
- Published: 24 June 2003
- Constance L Wood1,
- Eric M Blalock2,
- Kuey Chu Chen2,
- Philip W Landfield2 &
- …
- Arnold J Stromberg1
BMC Bioinformatics volume 4, Article number: 26 (2003)Cite this article
- 28k Accesses
- 242 Citations
- Metrics details
Abstract
Background
Microarray technology has become a very important tool for studying gene expression profiles under various conditions. Biologists often pool RNA samples extracted from different subjects onto a single microarray chip to help defray the cost of microarray experiments as well as to correct for the technical difficulty in getting sufficient RNA from a single subject. However, the statistical, technical and financial implications of pooling have not been explicitly investigated.
Results
Modeling the resulting gene expression from sample pooling as a mixture of individual responses, we derived expressions for the experimental error and provided both upper and lower bounds for its value in terms of the variability among individuals and the number of RNA samples pooled. Using "virtual" pooling of data from real experiments and computer simulations, we investigated the statistical properties of RNA sample pooling. Our study reveals that pooling biological samples appropriately is statistically valid and efficient for microarray experiments. Furthermore, optimal pooling design(s) can be found to meet statistical requirements while minimizing total cost.
Conclusions
Appropriate RNA pooling can provide equivalent power and improve efficiency and cost-effectiveness for microarray experiments with a modest increase in total number of subjects. Pooling schemes in terms of replicates of subjects and arrays can be compared before experiments are conducted.
Background
Researchers are increasingly realizing the importance of true biological replicates for assessing statistical confidence in microarray experiments [1–6], but replication is often hindered by financial or technical constraints. One problem is that large, prefabricated microarray chips can be relatively expensive, driving up the total cost of an experiment. (In fact, the cost of a subject is often lower.) Another obstacle to using replicates is that the biological tissues from which RNA is extracted can often be of such small quantity by nature that it is technically difficult to get enough RNA sample from one subject for hybridization to one array [3]. Either or both of these problems have motivated biologists to pool RNA samples together before hybridization. Many research papers using this method have been published [3–5], but the statistical properties of pooling have not been explicitly addressed. There are two different approaches of sample pooling. One is dubbed "complete pooling", where all samples from one treatment group are pooled onto one chip and there is no replication of chips for one treatment. This approach does not provide an estimate of variability among chips and therefore can not be used for statistical analysis. The other approach is dubbed "sub-pooling", where subsets of samples are randomly selected and pooled onto one chip but there are still multiple chips within each group. Here we investigated the statistical properties and the technical and financial implications of the second, sub-pooling approach.
Results
Simulation study of statistical characteristics
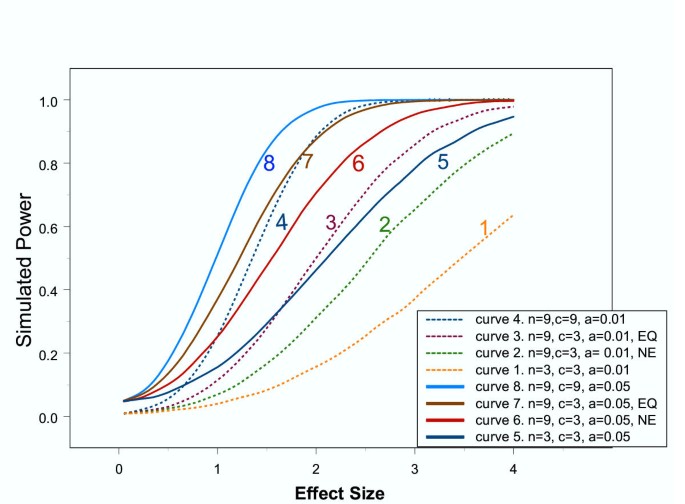
First, simulated microarray data were used to investigate the statistical properties (see Methods for details). Figure 1 shows the simulated power curves (for two-sample t tests) with respect to different α levels (i.e. type I error rates), effect sizes (i.e. differences of the means divided by common standard deviation), and sample sizes. Some well-known statistical properties are shown here: power increases with effect size and/or sample size when other conditions are fixed (e.g. curve 8 vs. curve 5, or curve 4 vs. curve 1); but it decreases when α level is lowered with other conditions being fixed (e.g. curve 8 vs. curve 4). However, the main purpose of Figure 1 is to demonstrate the effect of pooling. Consider curves 5 to 8, all of which have α level fixed at 0.05. Without pooling, nine replicates per group (curve 8) give much higher power than three replicates per group (curve 5). With pooling, power curves are intermediate. Both curve 6 and curve 7 reveal the power of pooling nine samples onto three chips each. The difference between them is that equal pooling with replicates in the same pool contributing equally (curve 7) has better power than non-equal pooling (curve 6). See methods section for statistical justification. Notice that power curve 7 is not very far from power curve 8, with only one third the number of chips being used.
Figure 1
Relationships among type I error rate, sample size, effect size, and power with or without pooling. Note: n is the number of biological replicates per treatment group; c is the number of gene chips per group; a is the type I error rate; EQ means that samples are pooled with equal contribution; NE means samples do not contribute equally when pooled together (weights assigned randomly to each chip: 0.7, 0.2, and 0.1).
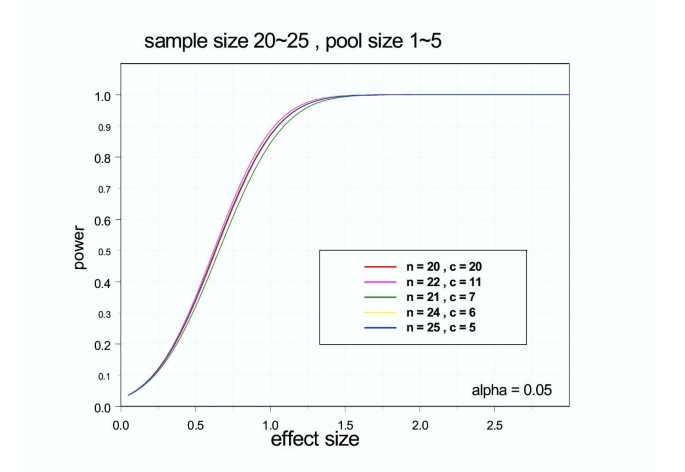
Figure 2 shows that approximately equivalent power to non-pooling can be achieved if the number of gene chips is reduced but the number of samples is increased. The simulated power curves for two-sample t tests for different pooling schemes under the same type I error rate control are very similar. In this figure, n25c5 means that RNA samples from 25 subjects are randomly pooled onto 5 chips with 5 subjects contributing equally to each pool. Specifically, the power of (n25c5) ≈ power of (n24c6) ≈ power of (n22c11) ≈ power of (n21c7) ≈ power of (n20c20). Notice that power of (n25c5) ≈ power of (n20c20), which suggests that by randomly pooling RNA samples from 5 subjects onto one chip with equal contributions, we can decrease number of chips needed per group from 20 to 5 while number of subjects per group only needs to be increased from 20 to 25. As will be shown later, this may have great financial consequences.
Figure 2
Approximately equivalent power curves under different pooling schemes. Power curves generated for two-sample t tests. Equal pooling assumed. Legend: n is the number of subjects per treatment group; c is the number of arrays per group. The five pooling schemes with different choices of number of subjects and number of arrays have approximately equivalent power curves when type I error rate is controlled at 0.05.
"Virtual" pooling example using data from an Affymetrix microarray experiment
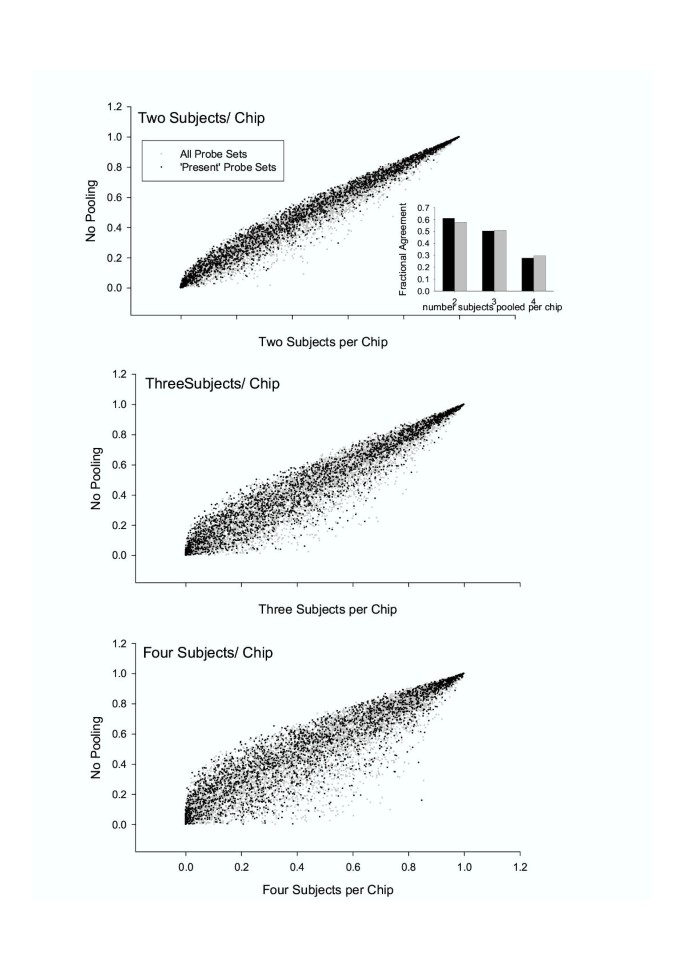
Blalock et al [2] investigated the correlation of gene expression with cognitive impairment in rats of different ages. Original data were from 29 Affymetrix microarrays. To further study the effect of pooling, we used 24 of the 29 arrays to do "virtual pooling". Namely, we first randomly selected 24 arrays and assigned them to two groups. P-values from two-sample t-tests on individual genes were recorded. Next, in each of the two groups, we "virtually" pooled the 12 samples onto 6, 4, 3 arrays respectively (assuming equal contribution in each pool). The statistical tests were then conducted on the "pooled" data with degrees of freedom being reduced to 10 (i.e. 2*(6-1)), 6 (i.e. 2*(4-1)), or 4 (i.e. 2*(3-1)), respectively. The P-values from the "pooled" data were then plotted against the original P-values. As shown in Figure 3, there is a good agreement of the P-values among the pooling schemes for the majority of the genes among the pooling and no pooling schemes. Table 1 shows that a moderate percentage of those genes that are found to be significant at a fixed α (0.05) level can be picked up by designs with pooling at the same α level. Multiple-testing adjustment was not considered here because it is a separate statistical issue. Note that "virtual" pooling serves as indirect evidence only.
Figure 3
Scatter plots of the P-values with different "virtual" pooling schemes. On Y-axis are the P-values from two-sample t-tests for 8799 genes on the RGU34A gene chip with no pooling (12 subjects, 12 arrays per group). On X axis are the P-values from two-sample t-tests for pool size 2 (12 subjects, 6 arrays per group), pool size 3 (12 subjects, 4 arrays per group), and pool size 4 (12 subjects, 3 arrays per group), respectively.
Table 1 Agreement of significant genes between "virtual" pooling and no pooling with data from one real experiment. Note: total number of "genes" on the chip = 8799, α = 0.05. _Pool size_=number of subjects per chip (# subjects per group/ # chips per group)
Effect size considerations
Because we are testing hundreds or thousands of genes at the same time, it is not easy to determine the effect size needed for power or sample size estimation. Effect size can vary from experiment to experiment, from one kind of biological sample to another, as well as from gene to gene. If we set the goal of an experiment to detect all genes that are differentially expressed at any scale, then the sample size needed to do so would be prohibitively large. Therefore, we need to set up a realistic goal, say, to detect genes with effect size ≥ 0.5. For a two-sample t test, this means the true difference between the means is one half of the common standard deviation. Empirical data from many experiments suggest that this goal is often achievable. A pilot study is also desirable to obtain an estimate of approximate effect size for specific experiments and genes. To assist researchers in making such estimates, we include here some empirical results from several experiments conducted in our core facility, which may provide a rough idea regarding the range of effect sizes that might be realistically expected with one type of microarray – the Affymetrix oligonucleotide GeneChip® array. Of course, the reader should be cautious in relying on these numbers, as they are estimates based on pilot studies from only one microarray core facility.
Financial implications of sample pooling and optimal pooling design
Since a microarray chip often costs more than a biological subject and we have more than one pooling design to achieve the same statistical control, it is possible for us to search for the most cost effective pooling design while maintaining the desired statistical properties. For a given combination of maximal type I error rate, minimal power, and the estimated or expected effect size to be detected, there are multiple pooling designs that may satisfy these conditions. We can compare the total cost of chips and subjects for each design and choose the one with minimal total cost, provided it is technical feasible. While this is a simplified economic framework (because it does not consider other cost in the experiment), it manifests the major point of the financial efficiency with pooling. An example function written in R language used to automate the searching and comparing process is attached as an additional file.
Discussion
Assessing variability on a per gene basis is an increasingly important aspect of microarray analysis. In the present paper we demonstrate that variance could be estimated accurately with different pooling schemes, and that the chip cost (and therefore experimental cost) can be dramatically affected by decisions regarding the pooling scheme employed. Many researchers are aware that replicates of biological samples are needed to assess experimental error. Even though thousands of genes are interrogated simultaneously on each chip, estimates of variance based on these measures do not of course include biological variance for any single gene in question. In this paper, we addressed the question of how many replicates are needed to achieve adequate power while considering an efficient technical procedure that is applicable in microarray experiments.
Since the specific design and data processing of microarrays can cause some confusion about what constitutes true replicates, it is important to distinguish technical replicates from biological replicates. In the Affymetrix microarray, 11 to 20 probe pairs are used to measure expression level of a probe set. It is important to note that these duplicated probe pairs are different measurement units rather than experimental units. The true biological replicates are the arrays (provided that they do not measure the same biological sample). An estimate of variability among the probe pairs reveals the precision of the measurement at the probe level but not the variability among biological samples. The latter is usually what is needed when conducting statistical hypothesis testing in order to make inferences about differential gene expression under various treatment or environmental conditions. Confusion between technical duplicates and biological replicates can sometimes lead to misconceptions in conducting and interpreting statistical tests. Based on the intensity readings on the probe pairs, Affymetrix Microarray Suite Version 5.0 gives a "change P-value" for the comparison analysis of each probe set ("gene") between a baseline chip and an experiment chip (MAS V 5.0 manual) based on Wilcoxon signed rank test. According to the manual, the change P-value indicates the significance of the difference between the experimental chip and the baseline chip. However, it should be noted that a significant difference of gene expression between a single chip from the experimental group and a single chip from the baseline group can not provide statistical evidence to show that the two groups are different. Often the goal of comparing a treatment group to a control group is to detect the true difference of the population means, and the "change P-value" is not the appropriate P-value for that goal.
To overcome the difficulty of estimating the variance of microarray data with few or no biological replicates, so-called "cross-gene models", "global error models" or "local error models" have been proposed [[7](/articles/10.1186/1471-2105-4-26#ref-CR7 " GeneSpring:[ http://www.silicongenetics.com
]"), [8](/articles/10.1186/1471-2105-4-26#ref-CR8 "
Clontech:[
http://www.clontech.com/techinfo/manuals/AtlasNavHelp/GlobalErrorModel.shtml
][
http://www.clontech.com/techinfo/manuals
]")\]. According to such models, genes with similar expression levels from the same chip can be "borrowed" to construct a pseudo sample as the basis to estimate the "global" or "local" errors for each individual gene. This is very appealing because "Statistical group comparisons can now be done on experiments without replicates by using the global error model"\[[8](/articles/10.1186/1471-2105-4-26#ref-CR8 "
Clontech:[
http://www.clontech.com/techinfo/manuals/AtlasNavHelp/GlobalErrorModel.shtml
][
http://www.clontech.com/techinfo/manuals
]")\]. However, these algorithms are based on two implicit assumptions that are difficult to support:(1). The measurement of the expression of a gene on one single chip can be used to estimate the true population mean expression of that gene. This assumption is often false because an observed intensity can be far from the true mean with moderate or high probability. For example, even if gene expression measurements follow a perfect normal distribution, the chance that a measurement falls beyond one standard deviation from the mean on either side is as large as 32%.
(2). Genes with similar measurement values "share" the same variance within the treatment group. This assumption may be reasonably accurate for some genes (e.g. those with low expression intensities), but empirical observations show that it is clearly not true for all genes, especially for those with high intensity.
The cross gene error model references for support the two component error model proposed by Rocke et al [9] and Durbin et al [10] but those papers made it very clear that true replication could not be circumvented, especially to estimate variances for genes with high expression. (For additional discussion on different sources of error in microarray experiments, see [10–13].)
Except under very restrictive models, duplicate observations per chip do not provide valid estimates of variability among subjects. Hence, multiple chips per treatment group, each measuring an RNA sample from a separate biological subject or pooled groups of subjects, are required for statistical analysis. However, this approach often entails financial and/or technical difficulties. To address these issues, we tested RNA sample pooling and showed that it provides an efficient alternative solution. Because arrays are usually more expensive than subjects, sample pooling frequently may help defray the total cost of an experiment. The larger the difference between the cost of a single array and that of a single subject, the more the sub-pooling strategy will save. Simulated microarray data and "virtual pooling" of actual data utilized here as well as statistical theory suggest that the underlying principles of this proposal are sound. Note that even with pooling, we still show a requirement for reasonable replication of (pooled) arrays because there is no other way to assess biological variation.
A limitation of our current study is that we have yet to conduct a definitive experiment in which the same biological samples are compared with or without pooling. Although this has not been done, we nevertheless have indirect supporting evidences from multiple actual microarray experiments. After analyzing data from over 50 research projects (with replications) done in our facility, we have consistently seen smaller within-group variability (and more genes with significant differences) in experiments using appropriate RNA pooling strategies than those with approximately the same number of arrays that did not employ pooling. This observation implies that experiments with pooling have greater power than those without pooling for a fixed number of chips, when conditions are comparable (i.e. similar experimental conditions, statistical methods and multiple testing correction procedures, etc.). In addition, a recent study [5] found high correlation between the intensities from the calculated pool and those from the actual pool using the same samples, (although in that study the pooling effect on reducing variance was not explicitly addressed).
RNA pooling may also have adverse consequences, and can be inappropriate in some cases. Pooling should not be used if inferences are needed for single subjects. For example, when the goal of the research is to correlate gene expression with some other variables measured at the subject level [2] or to identify gene profiles that help classify individual subjects and predict their membership in groups (e.g. cancer patients vs. normal patients). Pooling will also prevent later analysis of the data on variables that may have been ignored initially. As an example, suppose that we pooled all samples from the same gender and compared the differential expression of some genes between the two genders. This would make it impossible to subsequently analyze differential gene expression related to aging effects since samples from different ages would have been pooled together. The researcher must decide at the outset whether the potential loss of information is outweighed by the increased statistical power and cost-efficiency of the design. Similarly, pooling will prevent users from finding differences in expression that might divide only one set of samples. For example, if the goal of the experiment is to find genes that help differentiate subtypes of colon cancers rather than between colon cancer and healthy tissues, then it is inappropriate to pool cancer subtypes.
As pointed out by one reviewer, sample pooling is able to reflect group-specific variance, but assumes that residual individual variance is not influenced by the group variable. While this assumption may be a reasonable first approximation, it does not allow for the possibility of a cross-product relationship in which a group-specific variable (for example, toxic exposure) might lead to informative sub-states that exhibit separate groups of coordinately regulated responsive genes as a function of the extent to which the individual responds. Thus, there may also be loss of information regarding possible cross-product relationships by pooling. The experimenter should be aware of this caveat before deciding to pool samples.
There are also a few technical concerns with pooling. Theoretically, the more samples pooled, the greater the improvement in power. Practically, however, researchers may be reluctant to pool more than five samples to one chip due to technical limitations, and here we restricted our comparisons among pool sizes to no more than five. Further, we recommend pooling RNA samples instead of tissue or cell samples, because the variability at the tissue level is usually larger than at the RNA level. However, as long as equal contribution is assured, pooling at the tissue level should not make a big difference.
Finally, although we used only Affymetrix oligonucleotide data models as examples in this paper, the same principles should be readily applicable to two color cDNA arrays as well. In general, pooling should have similar advantages for more complex experimental designs (such as factorial designs, time course designs, etc.), when inferences are being made at the group level.
Conclusions
Appropriately designed RNA sample pooling can provide adequate statistical power, and improve efficiency and cost-effectiveness, for many types of microarray experiments when inferences are made at the group level. However, researchers have to consider the pros and cons of pooling for their experimental objectives. Designing optimal pooling schemes to achieve statistical control with minimal total cost is readily possible before the experiments are conducted.
Methods
Mixtures of Individual Gene Expressions
Gene expression levels for a single gene for n subjects will be denoted as X1,...,Xn. If the RNA samples from p subjects are randomly selected and pooled, then we can model the resulting gene expression level as 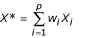 , where w1,...,w p are the mixing coefficients. These coefficients may be random. If the original gene expression levels, X1,...,Xn, are identically and independently distributed random variables with mean μ and variance σ2 and the mixing coefficients are independent of the individual gene expression levels, then we have
, where w1,...,w p are the mixing coefficients. These coefficients may be random. If the original gene expression levels, X1,...,Xn, are identically and independently distributed random variables with mean μ and variance σ2 and the mixing coefficients are independent of the individual gene expression levels, then we have
σ2 / p ≤ Var (X*) ≤ σ2. (1)
This result follows immediately from the fact that
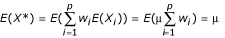
and
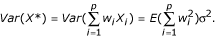
Since
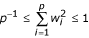
, (1) follows. Note that the lower bound is achieved when the mixing coefficients are equal; i.e., uniform mixing. This shows that RNA pooling reduces variance and the minimal variance of the mixture is achieved with equal pooling.
Relative Efficiency
As far as the number of chips needed is concerned, the relative efficiency of pooling n subject to n/p chips with uniform mixing can be computed as:
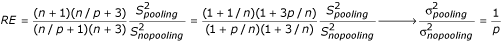
as n → ∞ and p/n → 0. Hence, when p samples are equally mixed, we need approximately 1/p of the original number of chips to achieve similar power with pooling when both n is large and p/n is small. This is a large sample result and does not take into account the loss of degrees of freedom for the test. Next, we consider the effects of both aspects on statistical power.
Power Equivalence
Although pooling RNA samples with uniform mixing substantially reduces the variability among chips within a group, this may not result in an increase in power while testing differences among groups with a fixed number of subjects. Here we investigate the power of the two-sample t-test. Let X1,...,Xn be identically and independently distributed with N(μ1, σ1 2) and Y1,...,Yn be identically and independently distributed with N(μ2, σ2 2). For simplicity, let σ1 2 = σ2 2 = σ2. Suppose we use two-sample t-test to test H0: μ1 = μ2 against Ha: μ1<μ2. Without pooling, the t statistic follows the central t distribution f(t, df 1) with df 1 = 2(n - 1) under H0; while under Ha, it follows a non-central t distribution with df 1 and non-centrality parameter 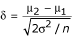 , which is inversely related to the standard deviation σ. For a fixed α level, we can find a critical value t0 under H0 such that
, which is inversely related to the standard deviation σ. For a fixed α level, we can find a critical value t0 under H0 such that 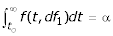 . To compute the power, we only need to find the rejection region corresponding to t0 under the alternative non-central t distribution g(t, df 1, δ):
. To compute the power, we only need to find the rejection region corresponding to t0 under the alternative non-central t distribution g(t, df 1, δ): 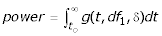 . Now when the n samples are randomly assigned into pools of size p with equal mixing, power is decreased because the degrees of freedom are reduced to df 2 = 2(n/p - 1), which makes the tails of the central t distribution under H0 heavier and thus the critical value t0* will be further from 0, while the non-centrality parameter is unchanged:
. Now when the n samples are randomly assigned into pools of size p with equal mixing, power is decreased because the degrees of freedom are reduced to df 2 = 2(n/p - 1), which makes the tails of the central t distribution under H0 heavier and thus the critical value t0* will be further from 0, while the non-centrality parameter is unchanged: 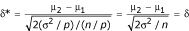 (since the variance is reduced to σ2/p and the number of chips reduced to n/p). However, if n + k subjects with pool size p are compared to n subjects without pooling, then the power change is not monotonic. The loss of power due to reduction of degrees of freedom will be partially compensated by gain of power due to increase of effect size. This can be seen by noting that the non-centrality parameter for pooling is now
(since the variance is reduced to σ2/p and the number of chips reduced to n/p). However, if n + k subjects with pool size p are compared to n subjects without pooling, then the power change is not monotonic. The loss of power due to reduction of degrees of freedom will be partially compensated by gain of power due to increase of effect size. This can be seen by noting that the non-centrality parameter for pooling is now 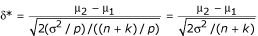 , which is non-trivially larger than
, which is non-trivially larger than 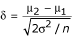 . This shifts the alternative distribution further away from the null distribution and thus increases power. Hence we have heuristically shown that the power change is not monotonic when decreasing replication of chips while simultaneously increasing number of subjects. This implies that power can be preserved with the right choice of (subject) sample size and pool size. Many statistical software packages, such as R, S Plus or SAS, have built-in functions for both central and non-central t distributions and thus we can write programs to evaluate the power change or equivalent power curves under different pooling schemes. For two sided two-sample t test or experiments with more than 2 treatment groups, we can use the central and non-central F distributions rather than t distributions. The power equivalence should be very similar. Readers not very familiar with the above statistical concepts are referred to [14–16].
. This shifts the alternative distribution further away from the null distribution and thus increases power. Hence we have heuristically shown that the power change is not monotonic when decreasing replication of chips while simultaneously increasing number of subjects. This implies that power can be preserved with the right choice of (subject) sample size and pool size. Many statistical software packages, such as R, S Plus or SAS, have built-in functions for both central and non-central t distributions and thus we can write programs to evaluate the power change or equivalent power curves under different pooling schemes. For two sided two-sample t test or experiments with more than 2 treatment groups, we can use the central and non-central F distributions rather than t distributions. The power equivalence should be very similar. Readers not very familiar with the above statistical concepts are referred to [14–16].
Simulation study
To investigate the above properties, we generated random samples based on two-treatment design and then compared the performance of different pooling schemes. We simulated microarray data as follows: randomly generate a data matrix of 5000 rows and 2_n_ columns, with each row represents one gene and each column represents one subject. The first n subjects are random samples from a normal distribution with mean μ1 and standard deviation σ; the last n subjects are random samples from a normal distribution with mean μ2 and standard deviation σ, where 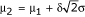 . For each row, μ1 was generated from a uniform distribution U(0, 30000) and standard deviation σ is set to be 0.2 * μ1. The effect size δ was specified for every data matrix.
. For each row, μ1 was generated from a uniform distribution U(0, 30000) and standard deviation σ is set to be 0.2 * μ1. The effect size δ was specified for every data matrix.
Simulation of power curves without pooling: for δ from 0 to 4.0, n from 3 to 30, we generated data matrices and then performed two-sample t tests on each row between the first n observations and the last n observations. For each specified δ, n and α level (0.05 or 0.01), we repeated the above simulation 1000 times and recorded the proportion of rejections, R α, δ, n , for each iteration. We then calculated the averaged R α, δ, n as the simulated power.
Simulation of power curves with pooling: similar to the above with the only difference being that the two-sample t tests were performed on first m pools and last m pools, where each of the m pools is the average of p subjects randomly selected from the original n subjects. Note that n = m*p and we used sampling without replacement. This is to simulate the scenario of equal pooling.
Table 2 Observed effect sizes of data from some experiments with Affymetrix microarrays.
Table 3 Comparison of different pooling schemes and total cost using model data. Several pooling designs that can achieve power at least 0.8 while controlling type I error rate at 0.01 for an effect size of 1.0 are shown. Assuming a microarray chip costs 1000andasubjectcosts1000 and a subject costs 1000andasubjectcosts300, the total cost for each design is also computed and the optimal design with the minimal total cost is underlined. A function written in R (a free statistical software downloadable at http://www.r-project.org) to perform the above search automatically is attached as additional file.
References
- Lee MLT, Kuo FC, Whitmore GA, Sklar J: Importance of replication in microarray gene expression studies: Statistical methods and evidence from repetitive cDNA hybridizations. Proc Nat Acad Sci 2000, 97: 9834–9839. 10.1073/pnas.97.18.9834
Article PubMed Central CAS PubMed Google Scholar - Blalock EM, Chen KC, Sharrow K, Foster TC, Landfield PW: Gene microarray analyses of hippocampal aging: statistical profiling reveals novel expression programs correlated with cognitive impairment. Journal of Neuroscience 2003, 23: 3807–3819.
CAS PubMed Google Scholar - Pletcher SD, Macdonald SJ, Marguerie R, Certa U, Stearens SC, Goldstein DB, Partridge L: Genome-wide transcript Profiles in aging and calorically restricted drosophila melanogaster. Current Biology 2002, 12: 712–723. 10.1016/S0960-9822(02)00808-4
Article CAS PubMed Google Scholar - Miller RA, Galecki A, Shmookler-Reis RJ: Interpretation, design, and analysis of gene array expression experiments. J of Gerontol A Biol Sci Med Sci 2001, 56: B52–57.
Article CAS Google Scholar - Agrawal D, Chen T, Irby R, Quackenbush J, Chambers AF, Szabo M, Cantor A, Coppola D, Yeatman TJ: Osteopontin identified as a lead marker of colon cancer progression, using pooled sample expression profiling. J Natl Cancer Inst 2002, 94(7):513–521. 10.1093/jnci/94.7.513
Article CAS PubMed Google Scholar - Pan W, Lin J, Le CT: How many replicates of arrays are required to detect gene expression changes in microarray experiments? A mixture model approach. Genome Biol 2002, 3(5):research0022. 10.1186/gb-2002-3-5-research0022
Article PubMed Central PubMed Google Scholar - **GeneSpring:**[http://www.silicongenetics.com]
- **Clontech:**[http://www.clontech.com/techinfo/manuals/AtlasNavHelp/GlobalErrorModel.shtml][http://www.clontech.com/techinfo/manuals]
- Rocke DM, Lorenzato S: A two-component model for measurement error in analytical chemistry. Technometrics 1995, 37(2):176–185.
Article Google Scholar - Durbin BP, Hardin JS, Hawkins DM, Rocke DM: A variance-stabilizing transformation for gene-expression microarray data. Bioinformatics 2002, 18(Suppl 1):S105-S110.
Article PubMed Google Scholar - Nadon R, Shoemaker J: Statistical issues with microarrays: processing and analysis. Trends Genet 2002, 18(5):265–271. 10.1016/S0168-9525(02)02665-3
Article CAS PubMed Google Scholar - Bakay M, Chen YW, Borup R, Zhao P, Nagaraju K, Hoffman E: Sources of variability and effect of experimental approach on expression profiling data interpretation. BMC Bioinformatics 2002, 3: 4. 10.1186/1471-2105-3-4
Article PubMed Central PubMed Google Scholar - Welle S, Brooks AI, Thornton CA: Computational methods for reducing variance with Affymetrix microarrays. BMC Bioinformatics 2002, 3: 23. 10.1186/1471-2105-3-23
Article PubMed Central PubMed Google Scholar - Casella G, Berger RL: Statistical Inference. Duxbury Press 2 Edition 2002.
Google Scholar - Snedecor GW, Cochran WG: Statistical Methods. Iowa University Press 8 Edition 1989.
Google Scholar - Douglas C: Montgomery: Design and Analysis of Experiments. John Willy & Sons 5 Edition 2000.
Google Scholar
Acknowledgement
Aspects of this study were supported by AG-10836 and AG-04542 from NIA to PWL and NIH-1P20RR16481-01 and NSF-EPS-0132295 to AJS. The authors thank the reviewers and editors for their helpful comments. We also thank Ms Donna Wall for her excellent technical support.
Author information
Authors and Affiliations
- Department of Statistics, University of Kentucky, Lexington, KY, 40506, USA
Xuejun Peng, Constance L Wood & Arnold J Stromberg - Department of Molecular and Biomedical Pharmacology, University of Kentucky, Lexington, KY, 40536, USA
Eric M Blalock, Kuey Chu Chen & Philip W Landfield
Authors
- Xuejun Peng
You can also search for this author inPubMed Google Scholar - Constance L Wood
You can also search for this author inPubMed Google Scholar - Eric M Blalock
You can also search for this author inPubMed Google Scholar - Kuey Chu Chen
You can also search for this author inPubMed Google Scholar - Philip W Landfield
You can also search for this author inPubMed Google Scholar - Arnold J Stromberg
You can also search for this author inPubMed Google Scholar
Corresponding author
Correspondence toXuejun Peng.
Additional information
Authors' Contributions
XP carried out the study. CLW and AJS supervised the study. EMB, KC, and PWL contributed discussions. All authors contributed to writing the manuscript. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Rights and permissions
This article is published under license to BioMed Central Ltd. This is an Open Access article: Verbatim copying and redistribution of this article are permitted in all media for any purpose, provided this notice is preserved along with the article's original URL.
About this article
Cite this article
Peng, X., Wood, C.L., Blalock, E.M. et al. Statistical implications of pooling RNA samples for microarray experiments.BMC Bioinformatics 4, 26 (2003). https://doi.org/10.1186/1471-2105-4-26
- Received: 02 December 2002
- Accepted: 24 June 2003
- Published: 24 June 2003
- DOI: https://doi.org/10.1186/1471-2105-4-26