Zooprophylaxis or zoopotentiation: the outcome of introducing animals on vector transmission is highly dependent on the mosquito mortality while searching (original) (raw)
- Research
- Open access
- Published: 19 September 2003
Malaria Journal volume 2, Article number: 32 (2003)Cite this article
- 17k Accesses
- 142 Citations
- Metrics details
Abstract
Background
Zooprophylaxis, the diversion of disease carrying insects from humans to animals, may reduce transmission of diseases such as malaria. However, as the number of animals increases, improved availability of blood meals may increase mosquito survival, thereby countering the impact of diverting feeds.
Methods
Computer simulation was used to examine the effects of animals on the transmission of human diseases by mosquitoes. Three scenarios were modelled: (1) endemic transmission, where the animals cannot be infected, eg. malaria; (2) epidemic transmission, where the animals cannot be infected but humans remain susceptible, e.g. malaria; (3) epidemic disease, where both humans and animals can be infected, but develop sterile immunity, eg. Japanese encephalitis B. For each, the passive impact of animals as well as the use of animals as bait to attract mosquitoes to insecticide was examined. The computer programmes are available from the author. A teaching model accompanies this article.
Results
For endemic and epidemic malaria with significant searching-associated vector mortality, changing animal numbers and accessibility had little impact. Changing the accessibility of the humans had a much greater effect. For diseases with an animal amplification cycle, the most critical factor was the proximity of the animals to the mosquito breeding sites.
Conclusion
Estimates of searching-associated vector mortality are essential before the effects of changing animal husbandry practices can be predicted. With realistic values of searching-associated vector mortality rates, zooprophylaxis may be ineffective. However, use of animals as bait to attract mosquitoes to insecticide is predicted to be a promising strategy.
Background
The role of animals in diverting mosquitoes from feeding on, and transmitting disease to humans has long been appreciated [1]. The concept of diverting insect blood feeding from humans to other animals has been named zooprophylaxis [2, 3] and has been regarded as an important tool in environmental management of vector-borne diseases [4]. For example, changing agricultural practices resulting in more effective zooprophylaxis has been one of the reasons given for the disappearance of malaria from Europe [5]. In more recent times, major development projects in areas endemic for mosquito-borne disease, such as the Mahawali irrigation scheme in Sri Lanka [6], demonstrate how disease-risk may be exacerbated by changes in the environment. Such environmental changes impacts on disease transmission to humans in four ways:
By affecting the number of adult insects feeding
This can occur through an impact on the environment which changes the number and capacity of larval habitats, and through changes in adult survival and, thus, more mosquitoes survive to feed and lay eggs a second time or more. This aspect of the presence of animals was examined by Sota and Mogi [7]. However the relationship between increased number of eggs laid, and a changing equilibrium in the number of adult mosquitoes is likely to be a complex relationship. In contrast to the model presented by Sota and Mogi [7], it is often assumed that the major effect is on the capacity of the larval habitat and that the number of emerging adults is largely independent of the number of eggs laid.
By diverting insect blood feeding from people to animals that are not the reservoir hosts of the disease
The impact on human transmission rates is complex. For anthrophagic vectors with a low propensity to bite non-human hosts, doubling the number of animals would have little impact, while vectors with a low human blood index would respond better. In the latter case, doubling the number of animals available would halve the human biting rate and halve the human blood index. This would reduce the human inoculation by a factor of ≤ 4. Therefore, the expectation is that zooprophylaxis would have the greatest impact on disease transmitted by zoophilic vectors. However, several authors have shown that, in situations where livestock is kept close to humans, animals may actually increase the risk of individual humans being bitten by attracting mosquitoes to the general proximity [8–10].
By affecting the survival of the vector
More animals should lead to less time spent by the mosquitoes searching for a blood meal with a corresponding lower vector mortality while searching. This has a double impact, resulting in more vectors surviving the extrinsic incubation period, and an increase in the number of blood meals by these infectious vectors. There is little data available on searching-related vector mortality and this aspect of transmission has attracted little theoretical treatment. Randolph et al. [11] examined the effect of feeding-related vector mortality on the feeding strategy of tsetse. Although they identified feeding-related vector mortality as an important factor in transmission, they had no experimental data on the relative importance of searching-related vector mortality and "background" vector mortality.
4. In some diseases, such as Japanese encephalitis B, the animals could act as a source of infection. Therefore, introduction ofanimals may create an amplification of the cycle, but the importance of this may change with time as the level of immunity increases in animal population.
In a real situation, all four effects are operating simultaneously, resulting in a very complex interplay between changing numbers of animals, or in the ways in which they are housed as well as changing the potential for transmission of human disease.
The passive effect of livestock on vector abundance and feeding propensities, and the efficacy of zooprophylaxis may be enhanced by using livestock not just to divert insects from humans but to attract them to contact with insecticide treated livestock and livestock premises. For example, such approaches have been attempted for the control of Anopheles quadrimaculatus and Psorophora columbiae populations in the USA, through the use of permethrin treatment of cattle [12], and for the control of malaria and filariasis in the Philippines through the use of buffalo-baited traps treated with K-orthine [13].
General computer models are presented in this paper for analysing the interaction between attraction rate of vectors to humans and animals on the potential of vectors to transmit disease under conditions of stable endemicity and epidemic outbreaks. The modelling highlights the importance of vector mortality while searching for a blood meal and shows that the use of bait animals to attract vectors to their death during this phase may have major impacts in slowing-down the build-up of cases during an epidemic.
Methods
Models
Two deterministic models were developed: an equilibrium model, where the proportion of infected people or animals remains constant over time (e.g. for malaria in sub-Saharan Africa), and a simulation model for investigating the rate at which outbreaks of disease occur (e.g. an epidemic of malaria or Japanese encephalitis B). Both are based on the cyclic feeding model presented by Saul, Graves, and Kay [14], rather than the continuous models developed by Macdonald [1]. The cyclic feeding model assumes that mosquitoes will not feed again for some time after a feed, whereas the Macdonald model assumes a constant feeding rate, regardless of where a mosquito lies in its gonadotrophic cycle. As a result of the different assumption underlying the model, estimates for a number of parameters differ from similar estimates based on the Macdonald model. For example, the cyclic feeding model gives the following estimate for vectorial capacity (c),
c = H bt Q h vkP e /(1 - P f ) (1)
compared with
c = H bt Q h vkP e /(-ln_P_ f ) (2)
for the Macdonald model, reformulated in the same symbols as defined in Table 1. Not only does the cyclic model give a more realistic description of the feeding process, but also it has the advantage that the cyclic nature of the model readily lends itself to iterative computer simulations.
Table 1 Symbols used in equations
Two models are used in this paper. The first model presented below has been formulated in general terms to allow a large range of control measures to be investigated. The second model is a combination of the above model with an extension of the simulation model presented by Saul [15] to examine the rates at which epidemics will occur.
Equilibrium model
Mosquitoes (including those newly emerged) seek a blood meal. During this searching phase, they are exposed to risks and have a zero order vector mortality rate constant, M s . The time it takes the vectors to find a suitable blood meal depends upon the number of animals present (Y) and their attraction rate constant, A (a first order rate constant). A similar attraction rate constant and underlying assumptions were used in the model of Sota and Mogi [7]. Killeen et al. [16] used a similar rate constant that they defined as "availability". "Attraction rate constant" has been retained in this paper since it emphasises that this defines a rate. Several biological factors will have an effect on the size of A. These include the intrinsic propensity of the animals to emit mosquito attractants and their accessibility. For example, humans sleeping under an untreated bednet would have a lower A than those not protected by a net; animals housed near mosquito breeding sites would have a higher A than animals housed further away. As shown below, relative values of A can be calculated from blood meal analysis. These relative values correspond to the Feeding Index as define by Kay, Boreham, and Edman [[17](/articles/10.1186/1475-2875-2-32#ref-CR17 "Kay BH, Boreham PFL, Edman JD: Application of the "Feeding index" concept to studies of mosquito host-feeding patterns. Mosquito News. 1979, 39: 68-72.")]. However, for this model, absolute values are required. These can be calculated from both the relative values and from the time taken by mosquitoes to find a meal.
This model can accommodate up to 3 types of blood source: the host of the disease (h) (humans in the case of Plasmodium falciparum); refractory or strongly immune animals (a) (eg. cattle for human malaria); and a population of "bait" animals (b). The bait animals may or may not be susceptible to the disease. Vectors feeding on these animals have a probability of being killed M f while attempting to feed. The "bait" could be humans sleeping under a permethrin-treated bednet or cattle sprayed with permethrin. Where the bait animals are susceptible, the model makes the appropriate adjustment for vectors that die before or after feeding. Since two human diseases, malaria and Japanese encephalitis B are being used to illustrate the model, in the remainder of this paper the host population will always be assumed to be human, and the source of alternative blood meals will be assumed to be 'animal', and both populations will be referred to as such. However, the model is general and for other diseases, the host of the disease (h population) could be an animal, and the alternative blood meal, human (e.g. in the case of Dirofilaria in domestic dogs).
The proportion of humans that is infected is x and for vectors feeding on infectious people, the probability of actually becoming infected is k. After feeding, it takes T ov days for egg maturation and oviposition before the vector starts searching for another blood meal. There is a probability, P ov , that the vector will survive during this time. Vectors that have been infected and survive for at least the extrinsic incubation period have a probability, v, of actually becoming infectious and transmitting to a new host [14].
Using these basic assumptions and definitions, a number of parameters can be derived. The overall attraction rate of the mosquitoes (Σ_AY_) depends on the numbers of each blood source and their attraction rate constants
Σ_AY_ = A h Y h + A b Y b + A a Y a (3)
(using the symbols defined in Table 1).
The human blood index Q h will depend on the relative attraction rate of vectors to humans (A h Y h ) compared to all animals (Σ_AY_), and allowing for those attracted to, and killed feeding on bait animals.
Q h = A h Y h /(Σ_AY_ - A b Y b M f ) (4)
Similarly
Q b = A b Y b (1 - M f )/(Σ_AY_ - A b Y b M f ) (5)
and
Q a = A a Y a /(Σ_AY_ - A b Y b M f ) (6)
Where there are only 2 blood meal sources, eg. humans and animals, then
Q h /Q a = A h Y h /A a Y a (7)
and the relative attraction rates can be calculated from a blood meal analysis and an estimate of the numbers of sources of blood meals in an area. In principle, this method could be extended to any number of different types of blood meal sources.
The average time it takes a vector that survives the search phase to find a suitable source of blood meal is:
T s = -(ln0.5)/(Σ_AY_ + M s ) (8)
In all situations examined in this paper, M s is small compared to A h Y h + A b Y b + A a Y a . Therefore, an estimate of T s with estimates of relative attraction rates and numbers of animals and humans present will allow the absolute values of A h , A a etc. to be calculated. For a situation with just 2 classes of blood meals,
A a = (-ln0.5 - T s M s )/[T s Y a (Q h /Q a + 1)] (9)
Because vector feeding and egg laying usually occur at a particular time of day, changes in the length of this searching phased may or may not alter the length of the feeding cycle. In this model we assume that the length of the feeding cycle (T f ) will equal T ov if the search phase is shorter than the maximum possible contiguous time (T max ) spent searching (eg. all night), but T f will increase by one day for each complete T max spent searching. The probability of surviving a feeding cycle (P f ) can be divided into several phases: the probability of surviving the search phase
Σ_AY_/(Σ_AY_ + M s ) (10)
the probability of surviving the feed
- 1
- A b Y b M f /Σ_AY_ (11)
and P ov the probability of surviving the period from one feed to the commencement of the next search phase. P f is the product of these terms, ie.
P f = P ov (Σ_AY_ - A b Y b M f )/(Σ_AY_ + M s ) (12)
In this model, it is assumed that other than the extra vector mortality associated with deliberate efforts to kill mosquitoes on bait animals, that vector mortality normally associated with actually feeding is part of P ov . It is also assumed that the extrinsic incubation period will be an integral number of feeding cycles. For example, if the minimum time that sporozoites are found in mosquito salivary glands in a particular situation is 10 d, but T f = 3 d, then the extrinsic incubation period will be 12 d or 4 feeding cycles (F) since these vectors will not transmit until their next feed. The probability of surviving the extrinsic incubation period (P e ) is then

As shown previously [14], in situations where N 0 vectors emerge each day, the number of vectors starting to search for a meal on each day is N 0</(1 - P f ). The number of these surviving and feeding on each human per day is:
H bt = N 0 A h /[(Σ_AY_ + M s )(1 - P f )] (14)
The number feeding on each bait animal or person depends on whether they die before or after feeding.
If they die after feeding,
B bt = N 0 A b /[(Σ_AY_ + M s )(1 - P f )] (15)
if before,
B bt = N 0(1 - M f )A b /[(Σ_AY_ + M s )(1 - P f )] (16)
These parameters can be used in the equations previously defined to calculate the proportion of mosquitoes that are infectious (S), the human inoculation rate (EIR h ) and the vectorial capacity (c).
S = xkvQ h P e /1 - P f + xkQ h P f ) (bait not susceptible) (17)
or
S = xkv(Q h + Q b )P e /(1 - P f + xk(Q h + Q b )P f ) (bait susceptible) (17a)
(assuming an equal proportion of human and bait are infectious)
EIR h = SH bt (18)
EIR b = SB bt (19)
c = H bt Q h kvP e /(1 - P f ) (bait not susceptible) (20)
or
c = (Y h H bt + Y b B bt )(Q h + Q b )kvP e /[(1 - _P_ _f_ )(_Y_ _h_ + _Y_ _b_ )](bait susceptible) (20a)
Where feeding is tightly linked with egg laying, then the number of vectors ovipositing per day will be:
N 0 (Σ_AY_ - A b Y b M f )P f /[(Σ_AY_ + M s )(1 - P f )] (21)
Thus the model is defined by equations 12 to 21.
There are five important assumptions in this model.
- The number of adult mosquitoes emerging each day is constant and, therefore, independent of the number of eggs previously laid. Thisassumption would not be true if changing seasonal conditions altered the availability and capacity of the larval habitat, or if here was excess capacity in the larval habitat.
- All mosquitoes genuinely feed at random. That is, there are no sub-populations of mosquito present which differ in their propensity to feed on humans or animals (eg., because some oviposition sites are closer to animals and further from humans than other oviposition sites), or that certain individual mosquitoes are not more likely than expected to feed on a particular group of humans and animals (eg. because of genetic polymorphisms within the mosquito population which influences feeding behaviour).
- There is no interaction between animals or animals and humans in the attraction rate. For example, this assumption would not be true if two people together did not attract twice as many mosquitoes as a single person, or if placing a highly attractive animal in close proximity to a person, resulted in higher than expected bites on the person. Such interactions between humans and animals have been observed in the Philippines for water buffalo [8] and Afghanistan for cattle and goats [9].
- Other than changes in vector mortality while searching for a feed, the probability of surviving the remainder of the feeding cycle is not changed by altering the number of animals, ie. P ov is independent of Y a . Effectively, this assumes that theprobability of being killed while actually feeding is the same for a feed on humans and on animals (other than bait animals) and that the ease of finding an oviposition site is not altered by changing animal numbers.
- The proportion of the population that is infectious (humans in the case of malaria) is not determined by the inoculation rate. In areas of stable malaria for example, control of this level may be dominated by levels of immunity and availability of treatment.
The consequences of these assumptions are examined in the discussion. The model as described, explicitly links feeding cycles with egg maturation, ie. feeding is linked to the gonotrophic cycle. This is not a required assumption, as a feeding cycle is the time from one feed to the next as originally defined [14]. If feeding is not linked to the gonotrophic cycle, then P ov is the probability of surviving from one feed to the start of the next search phase.
Epidemic models
The second model is a modification of the deterministic simulation model described in Saul [14] to describe epidemics of malaria. It also uses the same assumptions in the time taken for a mosquito to find a blood meal and vector mortality during the feeding cycle estimates P f , used in the equilibrium model described above. Unlike the equilibrium model, only two classes of blood meal, animals and humans, are used and the animals may be infected where appropriate (i.e. k a is not always zero). Briefly, separate arrays store the number of animals, bait, humans and mosquitoes in each state (non-infected, infected, infectious and immune) for each day of the simulation period. The model starts with the introduction of a single infected animal, human or mosquito. The programme calculates the number of animals, humans and mosquitoes that change state each day (eg. become infected, infectious or immune) and the number of each category of mosquito that die. In this model, it is assumed that the animal and human populations are static, i.e. no recruitment or losses, and that the size of the mosquito population remains constant. The number of mosquitoes dying each day is determined by equation 11 for P f . The model uses specific values for k h , k a , v h , v a , the probability that a mosquito will become infected after feeding on an infectious human or animal, and the probability that a potentially infectious mosquito will actually infect a human or animal respectively. If v = 0, then the animal or human cannot be infected (eg. v a = 0 for malaria).
As for the equilibrium model, the epidemic model assumes constant numbers of emerging mosquitoes, no sub-structuring of the mosquito population, that the attraction rates of individual animals and humans are independent and that changing animals has no effect on P ov .
Results
Endemic malaria
Initially, a wide range for each of the input parameters was examined for the equilibrium model [P ov from 0.3 to 0.9, ratio of Y a A a to Y h A h from 0:1 to 40:1, M s 0 to 0.08 h-1]. These values were chosen to give a realistic range of the survival per feeding cycle, P f , ranging from <0.3 to a maximum of 0.9 (i.e. average daily survival from about 0.67 to 0.97 for a three day feeding cycle), and to cover a range of Q h expected for malaria vectors (0.024 to 1). In this equilibrium model, the vectorial capacity the human inoculation rate and the number of mosquitoes ovipositing each day are directly proportional to the number of female mosquitoes emerging each day, N 0. Although different values of N 0 will change the scale of the output, it will not alter the relationship between the output and the input parameters. From this initial sensitivity analysis, a smaller range, characteristic of the transmission in the Madang region of Papua New Guinea [18, 19], but broadly compatible with transmission in most endemic regions, including Africa, was examined in more detail.
Three situations were examined. First, a constant rate at which mosquitoes found humans (ie. the product, A h Y h , of the number of humans and their attraction rate constant held constant) and the rate at which mosquitoes were attracted to animals varied. This was modelled as a constant attraction rate constant, A a and varying number of animals, Y a , or vice versa. Only the results for the former are shown here since both gave identical results. Second, the rate at which mosquitoes found animals was held constant (e.g. constant number of animals and attraction rate constant) and the rate at which mosquitoes found humans varied (A h Y h varied, for example, as would occur if the size of the human population changed or humans started to use untreated bednets). Third, the relative rates at which mosquitoes found both animals and humans was kept constant, but the absolute values varied, as would happen if local oviposition sites were removed. As expected from the equations underlying this model, in the absence of killing on bait animals or humans (discussed below), and where the searching-related vector mortality rate, M s , is small compared with the rate at which blood meals are found (M s < the sum of AY for all sources of blood meal), then the human inoculation rate is proportional to Q h 2 and the sporozoite rate is directly proportional to Q h . In practical terms, doubling the number of animals when the human blood index is close to 1 had little effect, but doubling the number of animals for a low human blood index will reduce the human inoculation rate by a factor of four.
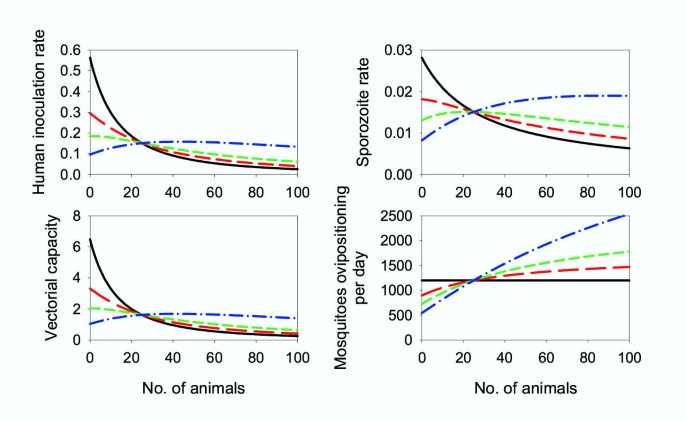
For all three cases, the effect of search-related vector mortality rate become noticeable when M s is greater than about 10% of the overall attraction rate and is illustrated in Fig. 1 for a constant rate at which mosquitoes find humans, but varying A a Y a . The starting combination of parameters (Table 2) for this set of simulations gives an overall attraction rate of 0.2 h-1 and an average time to find a blood meal of ~3.5 h. A vector mortality rate of 0.02 h-1 (i.e. 2% of the mosquitoes die per hour while searching) causes a marked flattening of the relationship between added animals, human inoculation rate, vectorial capacity and particularly, in the sporozoite rate. At higher vector mortality rates, eg. M s 0.08 h-1 or 40% of the attraction rate, there is a reversal of the expected relationship between added animals and human inoculation rates. In this model, the number of mosquitoes emerging as adults is assumed to be fixed by the availability of larval habitat. However, where there is a significant M s , the total number of mosquitoes feeding will change as the number or attraction rate constant of the animal changes, resulting in more mosquitoes surviving to feed again. These changes will partially compensate for the diversion of mosquitoes from people to animals. For example, if M s = 0 h-1, then for the conditions modelled, changing the number of animals from zero to 100 decreases the bites per person per 24 h from 20 to 4, or a 5-fold change. However, for M s = 0.08 h-1, the bites per person per 24 h change from 11.7 to 7 or only a 1.67-fold change, for zero and 100 animals, respectively.
Figure 1
Simulation of endemic malaria. The effect of altering numbers of animals on the human inoculation rate, the sporozoite rate, the vectorial capacity, and the number of mosquitoes ovipositing per day. Parameters used are shown in Table 2. Black line: M s = 0 h-1; red line: M s = 0.02 h-1; green line: M s = 0.04 h-1; blue line: M s = 0.08 h-1.
Table 2 Parameters for modelling endemic malaria
Where M s is appreciable, changing the number of animals will have a marked effect on the number of mosquitoes surviving to lay eggs. In the example used above for human biting rate with M s of 0.08 h-1, changing the number of animals from zero to 100 would increase egg production by a factor of 4.7, although there would be no change at all for M s = 0 h-1 (Fig. 1).
To investigate the use of animals to attract vectors to insecticide, the model was re-run using the combinations on Fig. 1 using M s of 0.04 h-1, but considering the animals as bait with varying probabilities of killing associated with feeding on these animals (Y b varied from 0 to 100, A b 0.004 h-1, Y h 100, A h 0.001 h-1, N 0 960, P ov 0.72, M f of 0, 0.2, 0.4 and 0.6). In this simulation, the animals are not a host for malaria, and the outcome of the numerical simulation is identical if the mosquitoes die before or after feeding on the bait animals (Fig. 2).
Figure 2
Simulation of endemic malaria with varying numbers of animals used as bait to attract mosquitoes to insecticide. Black line: M f = 0; red line: M f = 0.2; green line: M f = 0.4; blue line: M f = 0.6 (ie. a 0, 20, 40 or 60% chance of being killed as a result of feeding on animals respectively). M s = 0.04 h-1, P ov = 0.72, N 0 = 960. Other parameters are those used for Fig. 1 (Table 2). The black line (M f = 0) is the same as the green line in Fig. 1.
The model predicts that insecticide treatment of livestock would have a major impact on the human inoculation rate for malaria. For example, with the standard conditions for the model shown (animal to human ratio of 1:4 and a corresponding human blood index of 0.5), treating the livestock (or their stalls) with a non-repellent insecticide so that 20, 40 or 60% of mosquitoes feeding on them are killed would reduce the human inoculation rate for malaria by 44, 69 or 83%, respectively. Under these conditions, changing animal numbers or their accessibility has a major additional impact on malaria transmission. For example, a 4-fold increase in the number of animals (or a 4-fold increase in the attraction rate constant) would produce 60% decrease in the human inoculation rate if the animals were untreated, but there would be an 86, 95 or 99% decrease if 20, 40 or 60%, mosquitoes died while feeding on animals, respectively. Conversely, should the insecticide treatment also have a repellent effect, then the benefits of attracting mosquitoes to the bait animals would be offset, or in extreme cases, reversed, by making humans relatively more attractive.
Epidemic malaria
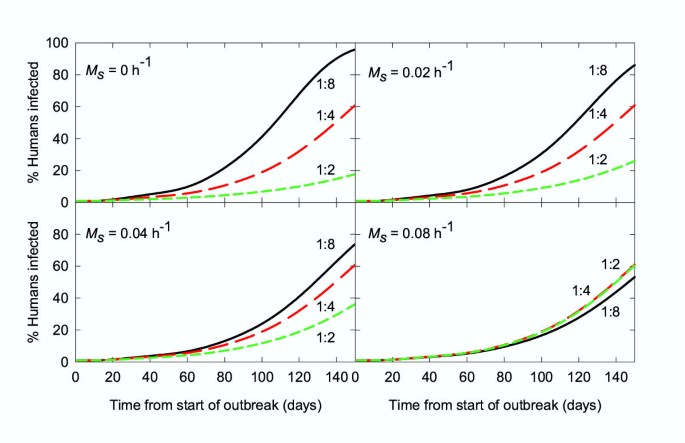
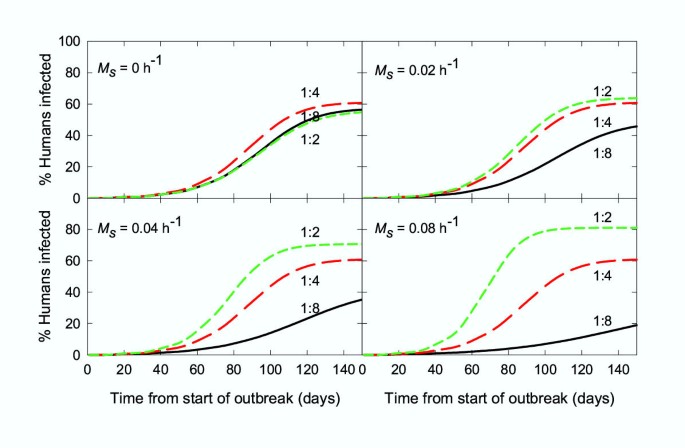
The effect of animals on the rate at which an epidemic of malaria would spread was modelled using the starting parameters listed in Table 3, assuming the outbreak was initiated by the introduction of an infected human. In these simulations, for each value of M s , P 0 and the number of new adults mosquitoes emerging each day was adjusted, so that the overall number of mosquitoes feeding each day and their probability of surviving a feeding cycle, P f , was the same for each simulation for an animal to human ratio of 1:4. For each value of M s , the model was run three times with ratios animals to humans of 1:2, 1:4 and 1:8. In this simulation, it is assumed that people becoming infected with malaria but remain untreated for the duration of the outbreak. Therefore, this represents a 'worst case scenario'. In this model, changing the accessibility of animals (i.e. modelled by changing the attraction rate constant, A a ) has the same impact as changing the number of animals (Y a ). For example, keeping the animal to human ratio at 1:4 and changing the attraction rate constant (A a = 0.002 h-1, 0.004 h-1, 0.008 h-1) produces the same output as A a = 0.004 h-1 and changing the animal to human ratio from 1:8 to 1:4 and to 1:2. Although both cases were modelled, only the effect of a 4 fold range of animal numbers is shown. At these animal to human ratios, the corresponding values for the human blood index were 0.33, 0.5 and 0.67 respectively. The effect of changing numbers of animals on the rate at which a malaria epidemic spread was markedly dependent on the searching-related vector mortality rate (Fig. 3). At low or zero values of M s , increasing the number of animals decreased the rate at which the epidemic spread and vice versa. However, as larger values of M s were modelled, the effect of changing animal numbers on the rate at which the epidemic spread was markedly dampened. At the highest value of M s modelled, 0.08 h-1, increasing the number of animals slightly increased the predicted rate at which the epidemic spread.
Table 3 Parameters for modelling epidemics
Figure 3
Simulation of a malaria epidemic: effect of altering the number of animals. The parameters used are shown in Table 3. Black line: animal to human ratio of 1:8; red line: animal to human ratio of 1:4; green line: animal to human ratio of 1:2 (or an equivalent of 12.5, 25 and 50 animals respectively, for a village of 100 people).
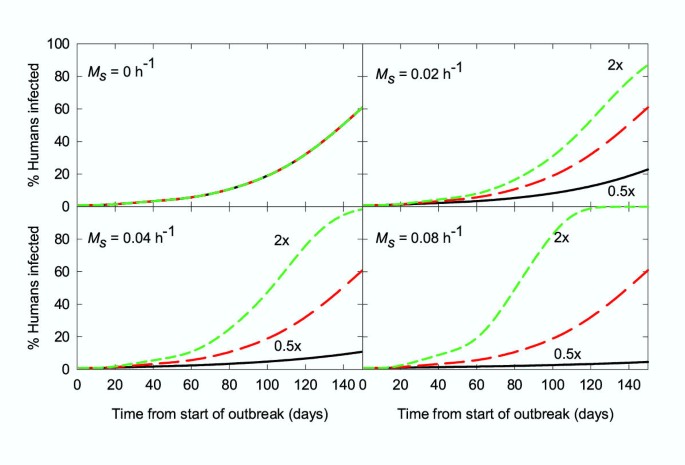
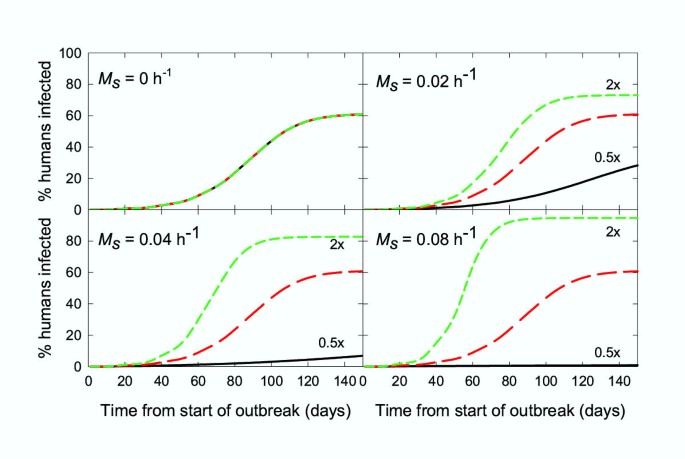
The situation was also modelled where the numbers of animals and humans and their relative attraction rate constants were held constant, but the absolute attraction rate constants were changed, eg. as would occur if the distance between oviposition sites and a village was changed, using the basic conditions used for Fig. 3 with an animal to human ratio of 1:4 (Q h = 0.5). As shown in Fig. 4, the effect of this change depends markedly on the searching-related vector mortality. Where there is no searching-related vector mortality, changing the absolute attraction rate constant (A) has no effect. On the other hand, even a 2-fold decrease in A had a major impact on the rate at which an epidemic would spread if there is a significant searching-related vector mortality rate.
Figure 4
Simulation of a malaria epidemic: effect of altering the accessibility of both humans and animals. Ratio of animals to humans 1: 4 used for each curve (25 animals and 100 humans). Black line: A a = 0.002 h-1, A h = 0.0005 h-1 (ie. both 0.5 times as accessible as the standard conditions); red line: A a = 0.004 h-1, A h = 0.001 h-1 (standard conditions); green line: A a = 0.008 h-1, A h = 0.002 h-1 (ie. both 2 times as accessible as the standard conditions). Other parameters were those used in Fig. 3 (Table 3).
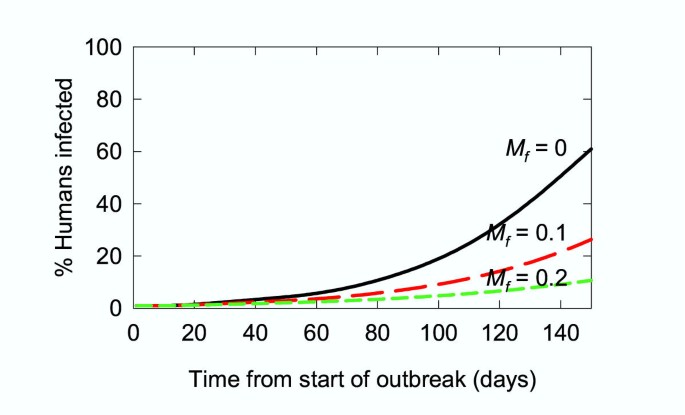
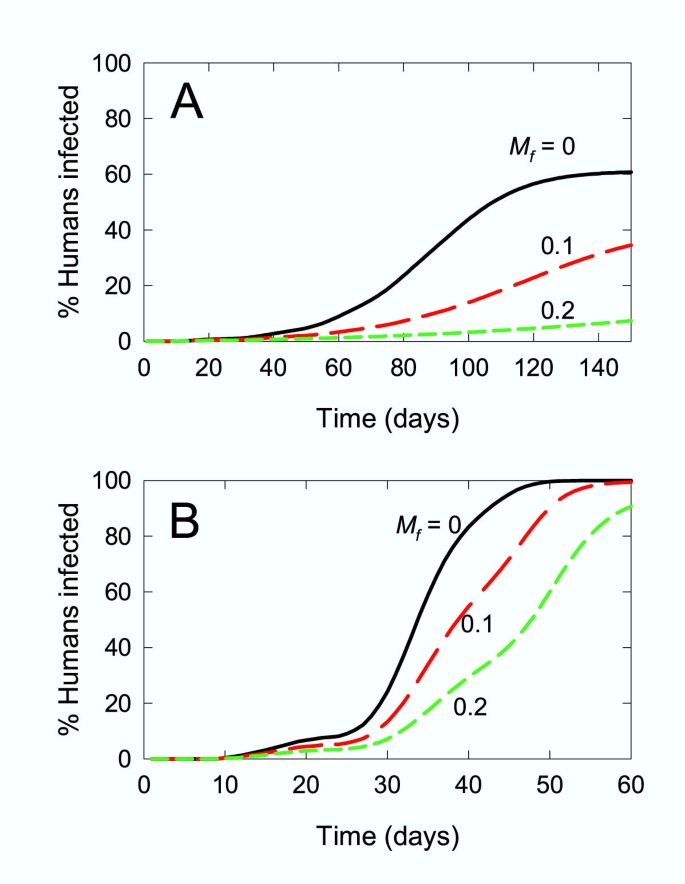
As for the models of endemic malaria, the epidemic model was also used to assess the impact of using animals to attract mosquitoes to an insecticide. The model was run with a range of probabilities that mosquitoes attracted to animals would be killed and again, since animals are not hosts for malaria, identical results are obtained if the mosquitoes die before or after feeding on animals. The model was run with the same parameters used for Fig. 3. Although the absolute rates at which the outbreak occurred were different, similar relative impacts were seen on the evolution of the malaria outbreak at all values of M s tested. Only the results obtained for an M s of 0.04 h-1 are shown (Fig. 5). In all cases, a major impact on the spread of malaria occurred when even a small proportion of the mosquitoes attracted to animals were killed.
Figure 5
Simulation of a malaria epidemic: use of animals to attract mosquitoes to insecticide. Black line: M f = 0; red line: M f = 0.1; green line: M f = 0.2 (ie. a 0, 10, or 20% chance of being killed as a result of feeding on animals respectively). M s = 0.04 h-1, P ov = 0.72, N 0 = 960, A a = 25. Other parameters are those used for Fig. 3 (Table 3). The black line is the same as the red line in Fig. 3 for M s = 0.04 h-1.
Arbovirus Epidemic
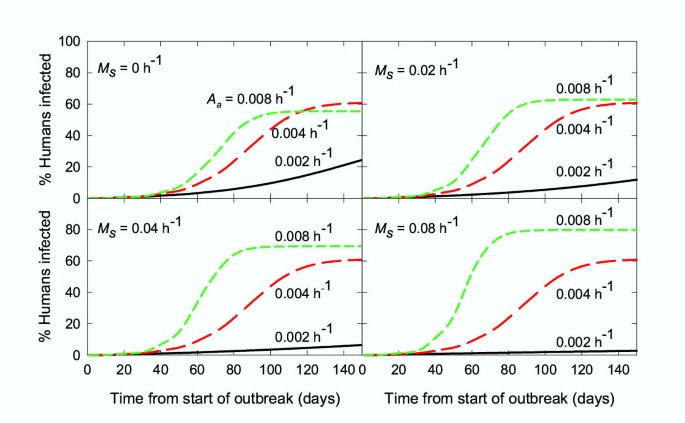
The effect of changing the number of animals, or their accessibility, on the rate at which an epidemic of an arbovirus, such as Japanese encephalitis B, would spread was modelled (Fig. 6) using the parameters used parameters listed in Table 3. In this analysis it is assumed that animals can amplify the infection but then become immune following recovery. It is also assumed that humans can be infected but are not infectious to mosquitoes. As for the malaria model, for each M s simulated, the values of P 0 and N 0 were adjusted to keep the overall number of mosquitoes, and their probability of surviving a feeding cycle, constant for an animal to human ratio of 1:4.
Figure 6
Simulation of an arbovirus epidemic: effect of altering the number of animals. The parameters used are shown in Table 3. Black line: animal to human ratio of 1:8; red line: animal to human ratio of 1:4; green line: animal to human ratio of 1:2 (or an equivalent of 12.5, 25 and 50 animals respectively, for a village of 100 people).
Unlike the malaria model, the effect of changing the number of animals had little effect if there was no searching-related vector mortality, as the increased reservoir of infection in the community was offset by a decrease in the number of bites per person per day. However, as M s increased, the speed at which an epidemic would spread through the human population became very dependant on the number of animals present. Interestingly, the total number of humans infected at the end of the epidemic also depended on the interaction between M s and the ratio of animals to humans. The spread of the epidemic is limited by the increase in the number of immune animals in the environment. With a higher M s , more animals resulted in higher mosquito survival and more mosquitoes feeding, thus allowing the epidemic to be sustained at a higher proportion of immune animals in the community.
Because of the increased complexity of the transmission cycle, changing the number of animals is not equivalent to changing their accessibility. With the conditions modelled, decreasing the relative attraction rate constant of the animals resulted in a substantial decrease in the number of people infected, even at a zero searching-related vector mortality rate (Fig. 7). At realistic searching-related vector mortality rates, decreasing the accessibility of animals to decrease the attraction rate constant by 2-fold nearly abolished the epidemic. This occurred because a decrease in animal accessibility resulted in both a lower survival of mosquitoes, and a shift in feeding from animals to humans. If infected humans could transmit the virus to mosquitoes, the effect would not have been as great.
Figure 7
Simulation of an arbovirus epidemic: effect of altering theaccessibility (attractive rate constant) of animals. The parameters used are shown in Table 3. Black line: A a 0.002 h-1; red line: A a 0.004 h-1 (standard conditions: red lines in Fig. 6); green line: A a 0.008 h-1.
As for the malaria epidemic model, where there is some feeding associated vector mortality, then decreasing the accessibility of both animals and humans had a major impact on the rate at which an epidemic spread (Fig. 8).
Figure 8
Simulation of an arbovirus epidemic: effect of altering the accessibility of both humans and animals. Ratio of animals to humans 1: 4 used for each curve (25 animals and 100 humans). Black line: A a = 0.002 h-1, A h = 0.0005 h-1 (ie. both 0.5 times as accessible as the standard conditions); red line: A a = 0.004 h-1, A h = 0.001 h-1 (standard conditions); green line: A a = 0.008 h-1, A h = 0.002 h-1 (ie. both 2 times as accessible as the standard conditions). Other parameters were those used in Fig. 6 (Table 3).
As for the malaria epidemic model, using animals to attract mosquitoes to an insecticide was predicted to be a highly effective means of slowing the rate at which an epidemic of arbovirus would spread (Fig. 9A). The input parameters chosen for the simulations shown in this figure give an R 0 close to 1 with a 20% feeding related vector mortality. As a result, this simulation illustrates the maximum impact that such a treatment would have. Nevertheless, at a 10-fold higher level of transmission, the impact is still highly significant (Fig. 9B) with an initial 54% decrease in the number of human cases, rising to 72% decrease at day 30.
Figure 9
Simulation of an arbovirus epidemic: use of animals to attract mosquitoes to insecticide. Black line: M f = 0; red line: M f = 0.1; green line: M f = 0.2 (ie. a 0, 10, or 20% chance of being killed as a result of feeding on animals respectively). M s = 0.04 h-1, P m = 0.72, A a = 25. Top graph (A): N 0 = 96; lower graph (B): N 0 = 960. Other parameters are those used for Fig. 6 (Table 3). In Fig. 9A, the black line is the same as the red line in Figs. 6 and 7 for M s = 0.04 h-1.
Discussion
This study extends the conclusions reached by Sota and Mogi [7] for modelling endemic malaria and to malaria and arbovirus epidemics. It highlights the potential importance of the time taken for a mosquito to find a blood meal and the corresponding searching-related vector mortality rate in evaluating the impact of livestock on the transmission of human diseases. Unlike the Sota and Mogi model, the much simpler model examined in this paper concentrates only on the direct effect of animals on the transmission cycle, and not the longer term affects on the rate at which adult mosquitoes are produced, nor on the equilibrium levels of malaria that would result. By using a model that assumes no change in these parameters, the impact of mosquito searching-related vector mortality rate is easier to determine. Because of the importance of the searching-related vector mortality rate on the outcome, highlighted in the present study and in the earlier work of Sota and Mogi, models of multiple host disease transmission [20, 21] that do not include this factor, need to be interpreted with caution and are unlikely to be useful for predicting the effect of changing the relative numbers of different animal species.
The modelling shows that even low values of the searching-related vector mortality rate has a major dampening impact on the effect of changing numbers of animals and higher values can completely reverse the expected relationship. This buffering is consistent with the small effect seen in some studies that have looked at the presence of animals as risk factors for malaria [22].
Although this model highlights the importance of this factor, there is a dearth of information available to estimate its size realistically. A mosquito with a 3 d feeding cycle and a survival per cycle of 0.6 has an average death rate of 0.0071 per hour [ie. -(ln0.6)/72]. It seems highly likely that the risks associated with finding a meal would be much higher than the average risks of death and so an estimate of M s of 0.02 per hour, or approximately 3 times the average, would be a conservative estimate. An upper estimate of the death rate is fixed by the average survival per feeding cycle. For a P f of 0.6 and where the mosquitoes take about 3 h to feed, if it is assumed that all vector mortality occurs while searching then the maximum value of M s is about 0.17 per hour [-(ln0.6)/3]. Besides searching for a feed, other high-risk activities for a mosquito include taking a meal, finding a suitable resting place, finding an oviposition site and the actual egg laying. Therefore, a practical upper limit to M s for a mosquito under these conditions may be about half this absolute maximum, ie. 0.08 per hour.
The impact of M s is closely related to the time it takes a mosquito to find a blood meal, and there is little information from field data on such searching rates, with the critical parameter being the relative rate at which mosquitoes are killed and at which they find a blood meal. Mark-release-recapture experiments of the Anopheles punctulatus complex in the Madang area of Papua New Guinea show that most mosquitoes feed every third evening [19]. Laboratory experiments suggest that under these conditions the shortest possible time is 2 d, so it is likely that most mosquitoes find a blood meal on the first night of searching following egg laying. Since feeding often takes place with a broad peak of several hours, the estimate of an average searching time of several hours is likely. Such estimates would also be consistent with delays seen in indoor biting catches compared with outdoor biting catches for vectors without a strong preference for feeding indoors or outdoors. For example, Torres et al. [23] found that the mean capture time for Anopheles flavirostris was 0:40 AM in outdoor landing catches and 1:40 AM in indoor landing catches.
Where animals act as alternative blood meals for the mosquitoes and can also be infected with organisms that cause humans disease, predicting the outcome of changing numbers of animals becomes even more complicated. In this situation, increasing numbers of animals divert blood feeding from humans but also increase vector survival and may act as an amplifier of the virus. In this situation, the impact of the searching-related vector mortality rate has the opposite effect to that observed in the malaria epidemic model. As expected, decreasing the number of animals will decrease the risks associated with an epidemic, but unlike the malaria epidemic model, the impact of changing animal numbers becomes much greater if there is a feeding associated vector mortality associated with feeding. Unlike the malaria epidemic model, because of the amplification cycle in the animals, changing animal attraction rate constant is not equivalent to changing the number of animals. This model predicts that changing the attraction rate constant of animals to mosquitoes, for example, by moving them further from a mosquito breeding site, or screening their enclosure will have a major impact on the amount of human disease, especially for realistic values of M s .
Several simplifying assumptions were used in developing the model. Although the magnitude of the errors introduced by these simplifying assumptions is difficult to predict with certainty, the direction of the error can be determined by reference to the underlying model. Four important assumptions common to both the endemic and epidemic model and their impacts on the conclusions are:
- No change in the number of emerging adult mosquitoes per day. Since increasing the number of animals will always increase mosquito survival, the number of eggs laid will always increase and this will generally result in the same number (as assumed here) or an increase in the number of adult mosquitoes feeding. Therefore, the number of feeds per person will normally be as high, or higher than the number of bites predicted by this model and may underestimate the transmission that would occur in nature. Thus, adding more animals will not be as effective as expected (where a reduction occurs), orworse than expected (where increases in transmission occurs). This transition may occur at fewer animals than predicted. In rarer situations, increased egg production may lead to a decreased or more unstable adult production through intense larval competition or through changing predator-prey dynamics. As an output of this model, the number of vectors ovipositing per day is calculated and where a more complex larval dynamic is warranted, could be used as the basis for a more sophisticated model.
- All mosquitoes have an equal probability of feeding on a human or animal. In the extreme case, where there are two completely separate populations of mosquitoes feeding on humans and animals, changing the number of animals will not affect transmission in humans. Therefore, if some structuring of the mosquito population occurred, this would decrease the impact of changing animal numbers on human disease transmission, i.e. structuring will not result in more effective zooprophylaxis than that predicted by this model.
- Attraction rate constant is independent of interactions between people and animals. The consequence of two people together being less or more attractive than two separate people, has no major impact on this model since it only changes the average attraction rate to humans and animals, respectively. A more important complication is where an animal and a person together attract mosquitoes at a different rate than they attract mosquitoes to each independently. There is a possibility that this occurred in the Afghan refugee settlements studied by Bouma and Rowland [10] where people who kept cattle had higher malaria rates than the general population. In this situation, animals would have two effects: a general effect simulated by this model on the whole human population (ie. either reducing transmission through the diversion of feeds, or increasing transmission through increased vector life expectancy) and an increased risk for that sub-section of the human population in close contact with the cattle. Therefore, the model would not predict that livestock will have a greater zooprophylactic effect than that which would occur under field conditions, but may underestimate the harmful effects of additional livestock.
- Other than during the searching phase, mosquito survival is independent of the number of blood meal sources. There are two situations where this may not be true. Besides using animals as bait for killing by insecticide, there is likely to be a significant vector mortality associated with the actual feed. The impact on the simulations will depend on the relative death rates associated with feeding on the different types of blood meal sources. If humans are better at killing mosquitoes as they feed than animals, then increasing animal numbers will result in an additional increase in mosquito survival. Again, the model would not predict that livestock will have a greater zooprophylactic effect than would occur under field conditions, but may underestimate the harmful effects of additional livestock. A second effect may be on survival during the search for oviposition sites. Increasing or decreasing the number of livestock in a particular location would not be expected to change the rate at which mosquitoes found an oviposition site (unless there were accompanying ecological changes from more cattle). On the other hand, changes to the attraction rate constant (eg. moving animals further away) could mean a corresponding change in time taken to find an oviposition site, and a corresponding change in survival. Where significant, the impact of changing oviposition searching time could be readily incorporated in the model. In analysing the direction of errors this is likely to introduce, the effect would be similar to underestimating the size of M s , and again this model will overestimate the beneficial effect, and underestimate the harmful effects of additional animals.
Hence, all four assumptions are likely to lead to the beneficial effects of zooprophylaxis being overestimated. Where the model predicts that additional livestock would decrease transmission, the actual decrease will be equal or less than predicted. Where the model predicts additional animals will make transmission worse then the actual transmission will be equal or worst than predicted. A change from a beneficial to a detrimental effect will occur where the number of animals is the same or less than predicted.
For the endemic model, an additional assumption was that the changes in transmission rates did not result in changes in the proportion of the human population that was infectious. Since one would expect that a deceased transmission would result in the same or lower proportion of the population infectious, and vice versa. This assumption should not alter whether livestock are harmful or beneficial but would result in the size of the effect being underestimated.
Besides highlighting the importance of the searching-related vector mortality rate, the simulations in this study predict that using animals as bait to attract mosquitoes to insecticide should be an effective way of decreasing disease transmission. This was especially true for decreasing the rate at which an epidemic occurred and in the conditions modelled has less impact on transmission in endemic areas. In the epidemic situation, this results from a compound effect: decreased transmission results in a smaller infectious reservoir and still lower transmission.
The results presented in this paper show that plausible situations can be found where the presence of animals will be either have a smaller effect than expected, or may even potentiate transmission. At realistic values for M s , the modelling suggests different strategies would be more effective for using animals to reduce transmission of malaria or arboviruses. For malaria, the effects of changing the numbers or accessibility of animals will be buffered by increased mosquito survival. The most effective strategy will be to minimize breeding sites in the vicinity of humans and animals. Since altering animal accessibility had comparatively little impact, this effect is primarily mediated by making the humans as inaccessible as possible.
By contrast, for an arbovirus epidemic, making animals as inaccessible as possible (eg. moving them as far from the breeding site as possible) will have a pronounced effect on transmission. As for the malaria epidemic, the best option would be to remove breeding sites from the vicinity of both animals and humans.
The modelling also shows that the use of animals as bait may be highly effective especially for slowing the rate at which a malaria or an arbovirus outbreak will occur, even where changing animals numbers or their accessibility has little effect through the buffering effects of M s .
While the examples used this paper are indicative of several common situations for malaria and arboviruses, there is a complex relationship between the addition of extra sources of blood meal and the impact on transmission. For any particular situation, the programmes presented in this paper should provide a tool for investigating both the best estimate of the impact of changing the mixture of hosts and other blood meal sources and changing their accessibility.
This paper explores the use of the model to analyse zooprophylaxis. However, the transmission model also directly applicable to a variety of other situations. For example, by regarding people sleeping under insecticide treated bednets as the "bait" population, the model can be used without modification to estimate the impact of insectide treated bednets.
The detailed programmes used for the modelling and instructions on their use are available from the author. An Excel spreadsheet, Vector Transmission Model.xls that models the simpler endemic situations described in this paper is available for downloading as an accompanying file to this paper. The instructions for use of the spreadsheet, Vector Tranmission Model Instructions.pdf also give examples of the use of this model for a variety of vector control approaches. This spreadsheet been designed particularly for teaching purposes.
Conclusions
This model suggests that predicting the impact of alternative sources of blood meals for disease carrying vectors is not straightforward. Specifically:
- Decreased transmission by feeding on animals is likely to be offset by the increased survival of vectors stemming from greater success in feeding
- Beside the number and relative attraction rate of vectors to animals, the key factor in determining the magnitude of zooprophylaxis is the rate at which vectors die while searching for a blood meal, for which there is little quantitative data available. More research in this area is important.
- Reduction of vector breeding sites (thus reducing the number of mosquitoes) and keeping both animals and humans as far as possible from breeding sites (thus maximizing mortality while searching for both oviposition sites and blood meals) are important, practical control measures. In particular, as part of a zooprophylaxis strategy, it is important that addition of animals does not lead to an increase in breeding sites.
- In addition to removing humans from the proximity of breeding sites, further steps to make humans as inaccessible as possible, e.g. through the use of bednets, provides an optimal strategy. For simplicity, this model considers the attractive effect of each animal or human independently. However, over longer distances, the presence of animals may attract vectors to humans thus increasing the rate at which vectors find humans, so it would be prudent to separate animals and humans.
- Use of animals to attract vectors to insecticide may lead to substantial reductions in vectorial capacity.
References
- Macdonald G: The epidemiology and control of malaria. 1957, London: Oxford University Press
Google Scholar - Service MW: Mosquito ecology: Field sampling Methods. 1976, London: Applied Science Publishers
Google Scholar - WHO: Manual on environmental management for mosquito control with special emphasis on mosquito vectors. W.H.O offset publication No. 66. Geneva, Sw: W.H.O. 1982
Google Scholar - Ault SK: Environmental management: a re-emerging vector control strategy. Am J Trop MedHyg. 1994, 50: 35-49.
CAS Google Scholar - Bruce-Chwatt LJ: Essential Malariology. 1985, London: Heinemann, second
Google Scholar - Amerasinghe FP, Ariyasena TG: Survey of adult mosquitoes (Diptera: Culicidae) during irrigation development in the Mahaweli Project, SriLanka. J Med Entomol. 1991, 28: 387-393.
Article CAS PubMed Google Scholar - Sota T, Mogi M: Effectiveness of zooprophylaxis in malaria control: a theoretical inquiry, with a model for mosquito populations with two bloodmeal hosts. Med Vet Entomol. 1989, 3: 337-345.
Article CAS PubMed Google Scholar - Schultz GW: Animal influence on man-biting rates at a malarious site in Palawan, Philippines. Southeast Asian J Trop Med Public Health. 1989, 20: 49-53.
CAS PubMed Google Scholar - Hewitt S, Kamal M, Muhammad N, Rowland M: An entomological investigation of the likely impact of cattle ownership on malaria in an Afghan refugee camp in the North West Frontier Province of Pakistan. Med Vet Entomol. 1994, 8: 160-164.
Article CAS PubMed Google Scholar - Bouma M, Rowland M: Failure of passive zooprophylaxis: cattle ownership in Pakistan is associated with a higher prevalence of malaria. Trans R Soc Trop Med Hyg. 1995, 89: 351-353.
Article CAS PubMed Google Scholar - Randolph SE, Williams BG, Rogers DJ, Conner H: Modelling the effects of feeding-related mortality on the feeding strategy of tsetse (Diptera: Glossinidae). Med Vet Entomol. 1992, 6: 231-240.
Article CAS PubMed Google Scholar - Nasci RS, Mclaughlin RE, Focks D, Billodeaux J: Effects of topically treating cattle with permethrin on Psorophora columbiae (Diptera: Culicidae) blood feeding in a Southwest Louisiana rice-pasture ecosystem. J Med Entomol. 1990, 27: 1031-1034.
Article CAS PubMed Google Scholar - delas Llagas LA, Hernandez L, Samaniego J: Insecticidal zooprophylaxis. ENHR Executive Brief (Philippines). 1996, 2: 3-7.
Google Scholar - Saul AJ, Graves PM, Kay BH: A cyclical feeding model for pathogen transmission and its application to determine vectorial capacity from vector infection rates. J Appl Ecology. 1990, 27: 123-133.
Article Google Scholar - Saul A: Minimal efficacy requirements for malarial vaccines to significantly lower transmission in epidemic or seasonal malaria. Acta Trop. 1993, 52: 283-296. 10.1016/0001-706X(93)90013-2.
Article CAS PubMed Google Scholar - Killeen GF, McKenzie FE, Foy BD, Bogh C, Beier JC: The availability of potential hosts as a determinant of feeding behaviours and malaria transmission by African mosquito populations. Trans R Soc Trop Med Hyg. 2001, 95: 469-476.
Article PubMed Central CAS PubMed Google Scholar - Kay BH, Boreham PFL, Edman JD: Application of the "Feeding index" concept to studies of mosquito host-feeding patterns. Mosquito News. 1979, 39: 68-72.
Google Scholar - Graves PM, Burkot TR, Saul AJ, Hayes RJ, Carter R: Estimation of anopheline survival rate, vectorial capacity and mosquito infection probability from malaria vector infection rates in villages near Madang, Papua New Guinea. J Appl Ecology. 1990, 27: 134-147.
Article Google Scholar - Saul A: Estimation of survival rates and population size from mark-recapture experiments of bait-caught haematophagous insects. Bull Entomol Res. 1987, 77: 589-602.
Article Google Scholar - Lord CC, Woolhouse MEJ, Heesterbeek JAP, Mellor PS: Vector-borne diseases and the basic reproduction number: a case study of the African horse sickness. Med Vet Entomol. 1996, 10: 19-28.
Article CAS PubMed Google Scholar - Rogers DJ: A general model for the African trypanosomiases. Parasitology. 1988, 97: 193-212.
Article PubMed Google Scholar - van der Hoek W, Amerasinghe FP, Konradsen F, Amerasinghe PH: Characteristics of malaria vector breeding habitats in Sri Lanka: relevance for environmental management. Southeast Asian J Trop Med Publ Hlth. 1998, 29: 168-172.
CAS Google Scholar - Torres EP, Salazar NP, Belizario VY, Saul A: Vector abundance and behaviour in an area of low malaria endemicity in Bataan, the Philippines. Acta Trop. 1997, 63: 209-220. 10.1016/S0001-706X(96)00622-5.
Article CAS PubMed Google Scholar
Acknowledgements
This study was undertaken in part, while the author was a staff member of the Australian Centre for International and Tropical Health and Nutrition at the Queensland Institute of Medical Research and supported by funding from the Australian National Health and Medical Research Council.
Author information
Authors and Affiliations
- Malaria Vaccine Development Unit, NIAID, NIH, Rockville, MD, 20852, USA
Allan Saul
Authors
- Allan Saul
You can also search for this author inPubMed Google Scholar
Corresponding author
Correspondence toAllan Saul.
Electronic supplementary material
12936_2003_51_MOESM1_ESM.pdf
Additional File 1: Vector Transmission Model Instructions.pdf. This pdf file contains a background to modelling, the instructions on the use of the accompanying Vector Transmission Model spreadsheet and a series of instructions for use of the spreadsheet to model transmission in the presence of larvicide programmes, spraying programmes, the use of repellents, insecticide treated bednets, natural and vaccine induced immunity, zooprophylaxis and in the use of feeding catches to assess transmission. (PDF 148 KB)
12936_2003_51_MOESM2_ESM.xls
Additional File 2: Vector Transmission Model.xls This spreadsheet has been created in Microsoft Excel 2002 but saved as an Excel 5.0 worksheet. Thus it should be compatible with all subsequent versions of Excel (95, 97 and 2000). The spreadsheet allows the calculation of the endemic models detailed in this paper (XLS 3 MB)
Authors’ original submitted files for images
Rights and permissions
This article is published under license to BioMed Central Ltd. This is an Open Access article: Verbatim copying and redistribution of this article are permitted in all media for any purpose, provided this notice is preserved along with the article's original URL.
About this article
Cite this article
Saul, A. Zooprophylaxis or zoopotentiation: the outcome of introducing animals on vector transmission is highly dependent on the mosquito mortality while searching.Malar J 2, 32 (2003). https://doi.org/10.1186/1475-2875-2-32
- Received: 13 July 2003
- Accepted: 19 September 2003
- Published: 19 September 2003
- DOI: https://doi.org/10.1186/1475-2875-2-32