Estimating Daily Land Surface Temperatures in Mountainous Environments by Reconstructed MODIS LST Data (original) (raw)
Author / Affiliation / Email
Article Menu
/ajax/scifeed/subscribe
Font Type:
Arial Georgia Verdana
Open AccessArticle
IASMA Research and Innovation Centre, Environment and Natural Resources Area, Fondazione Edmund Mach, 38010 S. Michele all'Adige, TN, Italy
Submission received: 1 December 2009 /Revised: 8 January 2010 /Accepted: 11 January 2010 /Published: 18 January 2010
Abstract
:
Continuous monitoring of extreme environments, such as the European Alps, is hampered by the sparse and/or irregular distribution of meteorological stations, the difficulties in performing ground surveys and the complexity of interpolating existing station data. Remotely sensed Land Surface Temperature (LST) is therefore of major interest for a variety of environmental and ecological applications. But while MODIS LST data from the Terra and Aqua satellites are aimed at closing the gap between data demand and availability, clouds and other atmospheric disturbances often obscure parts or even the entirety of these satellite images. A novel algorithm is presented in this paper, which is able to reconstruct incomplete MODIS LST maps. All nine years of the available daily LST data (2000–2008) have been processed, allowing the original LST map resolution of 1,000 m to be improved to 200 m, which means the resulting LST maps can be applied at a regional level. Extracted time series and aggregated data are shown as examples and are compared to meteorological station time series as an indication of the quality obtained.
Graphical Abstract
1. Introduction
In complex terrain such as the Central European Alps, meteorological stations and ground surveys are usually sparsely and/or irregularly distributed and often favor agricultural areas. The application of traditional geospatial interpolation methods in complex terrain remains challenging [1] and difficult to optimize. Remote sensing is an alternative data source [2] since remotely sensed imagery is intrinsically spatialized. The use of time series provided by modern remote sensing platforms in particular improves the quality of derived ecological indicators [3,4]. These indicators can be generated on a global scale from optical/thermal remote sensing data (with the exception of cloud dominated areas). The quality of ecological indicators, especially in complex terrain, is determined by thorough pre- and postprocessing of the data in order to minimize artifacts in the resulting maps [5,6]. The MODIS sensor is currently the optimal match between temporal and spatial resolution [7] and is an excellent data source for both local and global change research [8].
Daily time series of satellite data have been successfully used since the advent of the Advanced Very High Resolution Radiometer (AVHRR) instrument on board the NOAA series of satellites in the 1970s [9,10,11,12,13]. In 2000, the MODIS (Moderate-resolution Imaging Spectroradiometer) instrument was launched as a payload on the Terra satellite, and in 2002 a second MODIS instrument was launched on the Aqua satellite. MODIS improves upon the performance of AVHRR by providing both higher spatial resolution and greater spectral resolution. The polar-orbiting MODIS sensors, like AVHRR, produce daily Land Surface Temperature (LST) maps with global coverage [14]. These time series are used to monitor actual conditions but they are also routinely aggregated to extract annual or monthly minimum/maximum temperatures in order to identify late frost periods and unusual hot summer temperatures or to accumulate growing degree days. The latter indicator is important in agriculture, since aggregated LST maps could be used to predict crop maturing or insect development [15,16]. Habitat seasonality on a continental scale has been assessed with Temporal Fourier Analysis (TFA) applied to AVHRR satellite maps by Rogers [17]. The Temporal Fourier Analysis technique was later expanded to MODIS LST 8-day composites by Scharlemann [13], while Jönsson and Eklundh [18] applied non-linear least squares fits of asymmetric Gaussian model functions to AVHRR time-series. LST time series have been used for estimating cooling degree-days for buildings or for urban heat island analysis, as carried out in a few studies with NOAA-AVHRR thermal infrared data and MODIS LST [19].
A central problem with optical/thermal satellite data is cloud contamination as clouds hinder the observation of land and sea surfaces. In the case of LST maps, land/sea surface temperatures in cloud covered areas are simply unavailable since cloud-top temperatures are measured instead. In the case of thin cloud cover (cirrus, etc.), cloud detection is rather difficult [20]. Statistically, greater cloud contamination is found in night-time LST maps because at night only thermal infrared (TIR) band data can be used in the spectral tests needed for cloud mask production. During the daytime other channels may also be used. Most cloud-contaminated LST pixels which remain undetected by the NASA LST map production algorithms appear to occur near cloudy areas, i.e., at the fringes of cloud fields [6]. Outliers in MODIS V005 LST data typically appear only in the negative degree Celsius range due to the cold surfaces of undetected clouds.
When deriving climatic parameters from remotely sensed time series, one should ideally work with complete data sets. Typically, this requires reconstruction of the void map areas. Since the amount of available data is huge (to date more than 11,000 MODIS maps have been generated for each MODIS map tile), reconstruction requires the data processing to be automated. This paper focuses on the reconstruction of Land Surface Temperatures (LST) time series from MODIS. Validation of the reconstructed time series can be done by ground stations. While LST data are not directly comparable to air temperatures, which are measured at 2 m above ground, it can be assumed that the general temperature profile/patterns are very similar [21].
The purpose of the paper is to:
- present a novel approach to reconstructing MODIS LST data, including rejection of poor quality pixels by application of MODIS quality maps, low-range temperature outlier elimination based on histogram data, and temperature gradient-based map reconstruction with volumetric spline interpolation to fill all void map areas paying special attention to complex terrain;
- compare the reconstructed LST map time series to instantaneous and aggregated meteorological temperature measurements in order to assess the quality of the reconstruction;
- derive climatic parameters from reconstructed LST time series as maps, to be used as input variables for ecological and epidemiological modeling.
2. Materials and Methods
2.1. Study Region
The area under study is located in the central-eastern Alps in Northern Italy (see Figure 1) includes the provinces of Trento, Bolzano and Belluno, and also parts of the regions of Friuli-Venezia Giulia, Lombardia and Veneto. The area covers 24,240 km2, its boundaries being: north latitude: 46:45:00N, south latitude: 45:36:50N, west longitude: 10:06:33E, and east longitude: 12:46:30E. It is divided by several dominant wide river valleys, for example the territory of the Autonomous Provinces of Trento and Bolzano is bisected from north to south by the Adige river valley, following the south-eastern drainage pattern in this area. This is a predominantly mountainous region (more than 70% of the territory lies 1,000 m above sea level and about 55% of the territory is covered by coniferous and deciduous forests), encompassing a large part of the Dolomites and the Southern Alps, although it also includes small parts of the Po river plain. The complex terrain has an elevation range from slightly above sea level to 3,900 m. The climate is temperate-oceanic with four main areas: sub-Mediterranean (close to Lake Garda, which has mild winters), sub-continental (the main valleys, which have harsher winters), continental (the alpine valleys) and alpine (the areas above the tree line). The annual rainfall is above 1,000 mm except in some parts of the province of Bolzano. The region has a wide variety of habitats providing suitable environments for Mediterranean tree species, sub-alpine species, alpine species and mountain grasses. The human population density in the region is low compared with the rest of Italy, the total number of inhabitants being 1,231,000 (498,000 in the province of Bolzano, 519,000 in the province of Trento and 214,000 in province of Belluno, as of 2008). Up to 50% of the population is concentrated in the valley floors.
2.2. Available Data
A set of official GIS maps was obtained for the study area, which included a high resolution digital elevation model and political boundary maps of the provinces, municipalities, rivers and lakes. A set of meteorological time series was also obtained. Meteorological data for the Autonomous Province of Trento were obtained from Meteotrentino and from the Fondazione Edmund Mach-Consulting and Services Center; for the Autonomous Province of Bolzano they were obtained from the province’s Hydrographical Service. Due to the costs involved, data for the Province of Belluno were limited to a single time series from ARPAV Veneto.
Terra-MODIS data are available from 3/2000 onwards, MODIS-Aqua data from 8/2002 onwards, with daily resolution. Besides “Base Level Swath Data”, MODIS data are also provided as “gridded data”. Grid data are originally obtained in equal-area Sinusoidal projection (SIN) and delivered in HDF data format. In the present work, the recent MODIS product level V005 was used. This level offers significantly improved data quality compared to previous levels, especially for inland water pixels [22,23], as well as other, product-specific improvements. In addition to each HDF file, an XML file is provided with metadata (of interest are the fields “RangeBeginningTime”, “RangeEndingTime”, “QAPercentCloudCover”, “DayNightflag”, “QAPercentMissingData”, “PGEVersion”). The processed MODIS data are usually made available for download on a NASA FTP server less than one week after image acquisition.
2.3. MODIS LST Map Reconstruction Method
The traditional approach using direct interpolation of (often sparse) meteorological point data has been replaced here by the elaboration of already spatialized satellite maps. Medium spatial resolution satellite data (MRRS) are nowadays available at low cost from the Terra and Aqua satellites. MODIS Land Surface Temperature and Emissivity products (LST/E; MOD11A1 from Terra satellite and MYD11A1 from Aqua satellite) map land surface temperatures and emissivity values ideally under clear-sky conditions [22]. The underlying algorithms use other MODIS data and further auxiliary maps for input, including geolocation, radiance, cloud masking, atmospheric temperature, water vapor, snow, and land cover [24]. Temperatures are provided in Kelvin. The MODIS LST algorithm is aimed at reaching a better accuracy than 1 Kelvin (+/− 0.7 K stddev.) for areas with known emissivities in the range −10 °C to 50 °C [24,25]. LST is observed by the two MODIS sensors four times per day (01:30, 10:30, 13:30, 22:30, local solar time) originally at 1,000 m pixel resolution. Clouds and other atmospheric disturbances, which may obscure parts of or even the entire satellite image, constitute a significant obstacle for continuous LST monitoring; the low quality pixels of each LST map are marked in an accompanying quality assessment (QA) layer.
In this paper, we present a self-contained LST reconstruction algorithm (implemented in the Open Source software GRASS GIS Version 6.4.0, [26]) which does not depend on meteorological data since they are often unavailable. The procedure developed includes re-projection of the MODIS LST maps and the application of the accompanying quality assessment map layer to filter out invalid pixels. The MODIS Reprojection Tool software (MRT V4.0, [27]) was used to reproject from the original Sinusoidal (SIN) to the Universal Transverse Mercator projection (UTM Zone 32N, WGS84 ellipsoid). MRT allows for geographical subsetting, and it exports the resulting maps to standard GIS data formats such as GeoTIFF. The MRT software supports Nearest Neighbor, Bilinear, and Cubic Convolution resampling. For this work, Nearest Neighbor (NN) resampling was chosen for two reasons: (1) only NN is able to maintain the bit-pattern encoded structure of the quality maps during resampling as it does not interpolate between existing bit values; (2) tests with the Bilinear and Cubic Convolution (CC) resampling revealed that artifacts were introduced to the resulting maps; in particular, CC tends to add error at cloud mask boundaries (i.e., excessively high values are introduced apparently due to numerical instability in the underlying MRT algorithm). To minimize data loss during the reprojection, spatial oversampling was performed to increase the target raster cell resolution: the LST data with nominal resolution of 1000 m × 1000 m were resampled at 200 m × 200 m resolution to reduce artifacts and pixel shifts due to the use of the Nearest Neighbor resampling method.
For the LST maps, pixels with the following labels indicated in the QA bitmap layer were rejected: “clouds”, “other error”, “cirrus cloud”, “missing pixel”, “poor quality”, “Average emissivity error >0.04”, “LST error 2K−3K”, and “LST error >3K”. The bit patterns of interest were combined into logical conditions and applied to the LST map using map algebra. The maps are originally provided in Kelvin and were transformed to degrees Celsius. To each resulting filtered LST map, a temperature color table was assigned and the metadata (as extracted from the XML file) was stored as GIS metadata for each map.
The filter step was followed by the application of several histogram and temperature gradient-based outlier filters. Outliers in MODIS V005 LST data typically appear only in the negative degree Celsius range as they are usually caused by undetected clouds. To overcome this problem, a post-import outlier detector was applied in order to eliminate the remaining cloud-contaminated pixels. The detector is based on an image-based histogram analysis that finds and remove pixels which show unusually low LST values, when quartiles are considered [5]. The equation is given as (1):
l o w e r _ b o u n d a r y = 1 s t _ q u a r t i l e − 1.5 × ( 3 r d _ q u a r t i l e − 1 s t _ q u a r t i l e )
(1)
This outlier detection is only applied to the lower temperature range (since high temperature outliers are uncommon). Only LST maps with a sufficient number of pixels (25% valid LST pixels after the application of QA map filtering) were considered in this calculation to avoid maps with only few pixels negatively influencing the overall outlier statistics. For each map, equation (1) was determined by calculating the univariate statistics of the map. Then, for each month, the mean lower boundary value was calculated and used as a filter threshold. If the entire month was below the minimum number of valid LST pixels, a fixed mean lower boundary value was set to −20 °C. Then all LST maps for that month were filtered with the mean lower boundary threshold by setting pixels below the threshold to zero. All available Terra and Aqua scenes were processed separately by satellite and for day and night overpasses because data from Terra are available for a longer period and, because missing data (arising from cloud coverage etc.) would lead, in the case of processing a single pass, to undesirable shifts of the daily minimum and maximum in missing maps. Instead, constraining the calculations to the day or night was found to significantly reduce the error added to the lower boundary threshold estimate.
From each outlier-filtered LST map a preliminary temperature gradient was calculated if 10% or more pixels were valid, otherwise all gradient parameters (i.e., the linear regression formula) were set to zero; these gradients were subsequently removed from the set of valid gradients in a later step. All LST maps were then filtered again based on the 1st and 3rd quartiles of the intercepts and slopes of the 16-day period mean gradients to identify and remove remaining LST outliers. From the filtered maps the final set of gradients was generated, again setting a minimum of 10% valid LST pixels per map to maintain statistical significance. The statistics were calculated separately for each overpass (01:30, 10:30, 13:30, 22:30 hs). For each original LST map, the resulting set of 16-day mean gradients was used to generate a synthetic LST map used to fill holes in the original LST maps. Rather than interpolating over map holes it considered more correct to fill these holes with typical values for a given 16-day period/overpass time in order to stabilize the interpolation. To avoid artifacts at the confluence of actual and synthetic maps, a random sampling approach was used to extract 10% of the pixels as samples from each patched map for the subsequent volumetric splines interpolation step in order to obtain a smooth map. In this interpolation step, an elevation model was used as an additional variable. Splines have been used extensively in the interpolation of various climate variables including regions with complex topography ([28,29]; among others). Splines are robust in areas with sparse or irregularly spaced data points [30]. If an insufficient number of pixels was available in the filtered LST map, a purely synthetic map was generated based on the periodical mean gradient model which was derived earlier. A number of physical and meteorological constraints were implemented to avoid unusual results, especially for the minimum and maximum slope values of the gradients. The overall simplified procedure is shown in Figure 2.
Various quality measures were subsequently applied to validate the LST map reconstruction:
- Cross-checking of Land Surface Temperature against elevation (analysis of relationship);
- Comparison with meteorological measurements (instantaneous meteorological measurements; comparison of periodical, monthly and annual averages; comparison of short term trends);
- Comparison with LANDSAT-TM thermal maps.
2.4. Time Series Aggregation
A series of indicators relevant to ecological or epidemiological studies can be derived from the reconstructed MODIS LST daily data time series by time series aggregation. In particular, daily/monthly/annual mean value maps of minimum/mean/maximum are relevant ecological indicators [31]. In addition, the well known BIOCLIM set of variables [32] can be taken into consideration, which has been done in previous studies. Temperature-related indicators include the annual mean temperature and range, mean diurnal range, isothermality, temperature seasonality, the maximum temperature of warmest month, the minimum temperatures of coldest month, the mean temperature of warmest and coldest quarters. Input data include the four daily MODIS LST observations from the reconstructed LST data set, which can be easily aggregated pixelwise in a GIS framework.
Another indicator that was considered was the growing degree days (GDD) which is a temperature-based index mostly used in phenology to predict flowering of plants or insect molting [15]. GDD estimates heat accumulation with a simple formula from the daily mean temperature minus a base temperature, calculated year-wise from the winter minimum to the end of a year. Before calculating the mean, any temperature below Tbase is set to Tbase. A maximum cut-off temperature is also defined, acknowledging that no further increase in the plant's or insect's growth rate is expected above that temperature. The use of reconstructed daily MODIS LST data as a temperature data source is superior to the use of the 8-day MODIS LST product where the GDD values were systematically overestimated [16].
The identification of exceptional warm/cold seasons can be done by applying temperature thresholds to multi-annual temperature maps. Then if the number of events over a given period (i.e., pixels over or under the indicated threshold) is significant, the season can be defined as unusual. In mountainous areas exceptional seasons are not necessarily evenly distributed over the terrain, hence remote sensing offers the opportunity to localize the deviations.
Aggregation of daily MODIS LST maps over several months allows intra-annual short term trends to be determined, for example the ecologically relevant spring temperature increase gradient (“spring warming”) and autumnal temperature decrease gradient (“autumnal cooling”). The latter has already been used in studies on tick-borne encephalitis [6,33,34]. The temperature decrease in autumn (“autumnal cooling”) is assessed with a year-wise linear regression of the monthly LST mean values of August, September and October. In addition, the annual maximum of the monthly mean LST values per pixel is selected. The cooling rate is the relationship between this monthly temperature decrease and the maximum LST value [33]. The spring warming rate is calculated likewise: February, March and April monthly LST mean values are subjected to linear regression with the winter minimum temperature as a difference value.
With the increasing availability of daily satellite data, inter-annual short- and long-term trends can also be analyzed. From the nine years of available reconstructed MODIS LST time series (potentially extendible by daily AVHRR data to cover previous years), the first trends can be identified (for example: winter minimum temperature trends). However, this MODIS-only series is as yet too short to deliver reasonable statistics.
3. Results and Discussion
3.1. MODIS QA Statistics
Analysis of the average percentage of valid LST pixels has been done on both daily data and aggregated data which does not overly to emphasize outliers. A statistical analysis of the spatial distribution of “good quality” pixels with respect to altitude is shown in Table 1. This analysis revealed that the low altitude zones (planes and mountain valleys) are subject to slightly more haze or cloud effects than higher altitudes. Overall, between 32% and 41.5% of each altitudinal zone has good pixel coverage per altitude zone between 2000 and 2008 for the study region; no significant spatial clustering could be observed.
This situation improves when aggregating the MODIS LST data set to 16-day periods (in temporal agreement with the MODIS vegetation index product) as it minimizes cloud cover problems. Figure 3 shows the average percentage of valid pixels (average good pixels/total pixels) separately for day and night overpasses.
On average, 54.3% good pixels in the two day overpasses and 51.2% in the two night overpasses are found. Surprisingly, during the winter period, the mean percentage of valid pixels is slightly higher for maps processed from nighttime versus daytime overpasses in the study region. Future research will be aimed at exploring these differences by analyzing the spatial distribution of valid pixels with respect to the overpass time.
3.2. Reconstructed LST Maps
A total of 11,179 MODIS LST maps were processed for the study area: 8,017 maps were reconstructed from the actual map gradients and 3,162 maps from a 16-day periodical model since insufficient pixels were available to derive a map based on a gradient model. The approach developed delivers reasonable results even in cases where 75% of the filtered LST map are void; in any case, the actual map gradient can be used to reconstruct the map due to the gradient-based model. Figure 4 and Figure 5 show two examples of reconstructed LST maps. Re-projection and other artifacts have been smoothed out in the LST map reconstruction process.
During the early night of 11 April 2003 (01:30 hs), in Trento-Sud an air temperature of 6.2 °C was measured at 02:00 local solar time; 6.8 °C in Arco. Figure 4 shows the original, filtered and reconstructed LST maps as well as differences and the temperature gradients. The final LST map shows systematically a few degree Celsius less than the air temperature. The final gradient (green) results as slightly different with respect to the raw LST map gradient since outliers were removed.
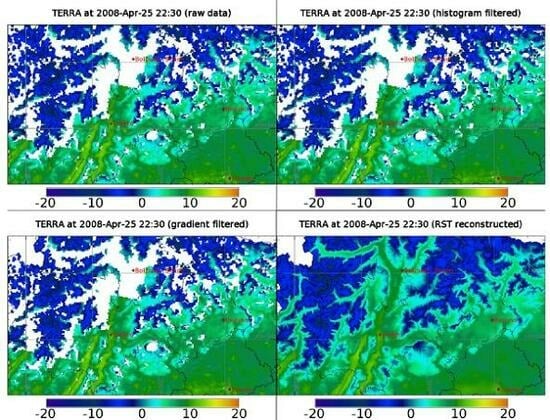
Figure 5 shows the situation of 25 April 2008 (22:30 hs); the low temperatures in higher altitudes are due to snow cover and contrast with the significantly warmer valley floors. Air temperature of 14.5 °C was reported for Trento-Sud at 23:00 local solar time, about 30 minutes later than the satellite overpass, and 16.4 °C in Arco, while the respectively LST map value is approximately 2 °C lower. The final gradient (green) differs slightly from the raw LST map gradient since outliers have been removed.
3.3. Quality of the Reconstructed Daily MODIS LST Maps
The resulting maps were thoroughly compared with various data sources such as meteorological data measurements (0.70 ≤ R2 ≤ 0.98 for Tair/LST linear regression) and with datalogger field measurements in EDEN Project sites (data not shown here). A Wilcoxon rank sum test performed on the two daily mean temperature curves (Arco meteorological station and LST time series of the station pixel, see Figure 6) confirmed that they do not differ statistically (W = 63775.5, p-value = 0.6232). Some differences in the daily data plot can be observed which are less evident in the 16-day aggregated data plot. As a tendency, in winter the LST appears to be lower than the air temperature while it is slightly higher in summer. Comparison of annual temperatures at the meteorological stations at Arco and Trento-Sud in the province of Trento showed differences between meteorological data and LST aggregation (1,460 maps) of ≤0.5 K.
The results show that annual mean temperatures derived from aggregated LST data are very similar to those generated from meteorological stations. No systematic shift can be observed. The advantage of LST data is that the study area is completely covered (hence each LST map pixel time series can be considered as a “virtual meteorological station” for temperature data).
Uncertainty in the processed MODIS LST data as proposed in this paper is of two types: (1) intrinsic uncertainty in the downloaded MODIS data; (2) error introduced by processing. The former includes error in the radiometric and geometric precision of the MODIS instrument, and uncertainties in the known emissivity values of land surfaces, cirrus or other atmospheric phenomena. The latter is a potential error added during reprojecting from Sinusoidal to UTM projection with nearest-neighbor resampling. However, in this step, such artifacts are minimized by spatial oversampling (200 m) which reduces the potential pixel offset to a fraction of the original pixel size (1,000 m). A major source of error is unavoidably added when long term cloud coverage means that, for certain pixels, a gradient must be selected from the mean 16-day periodical model rather than from the MODIS LST map itself. This error may be reduced in the future by using additional data sources.
3.4. Derived Indicators: Exceptional Months and Seasons
Univariate statistics on the LST maps aggregated by season identified the particularly outstanding warm winter of 2006/2007: comparison of the monthly minimum LST values compared to the related monthly mean of minimum values from reconstructed daily MODIS LST (base 2002–2009) shows that the monthly minimum temperatures of this winter were several degrees Celsius above the average (December 2006: mean = 3.07 °C, stddev = 0.706; January 2007: mean = 2.92 °C, stddev = 0.773; February 2007: mean = 3.57 °C, stddev = 0.753). The low standard deviation indicates a rather homogeneous distribution of these higher minimum temperatures in the study area for the period indicated. A similar test for the monthly maximum temperatures shows them to be exceptionally high, especially for January 2007 (December 2006: mean = 2.47 °C, stddev = 2.093; January 2007: mean = 5.22 °C, stddev = 1.434; February 2007: mean = 1.83 °C, stddev = 1.198). The high standard deviation here indicates that the maximum temperatures were not evenly distributed in the study area. The LST maps show that in December 2006 and January 2007 the valley floors were closer to the “normal” (limited to the base 2002–2009), while in February 2007 the valley floors are relatively warmer than higher altitudes (reverse effect; maps not shown here). Climatic 30-year air temperature mean values could not be obtained for comparison. Although data are not shown here, we can report that winter 2006/2007 and summer 2007 were exceptionally warm seasons, while the winters of 2001/2002 and 2005/2006 were colder than average, which is also reflected in the meteorological station observations.
3.5. Derived Indicators: Growing Degree Days
To compare the annual GDD performance from MODIS to field data, minimum and maximum air temperature data were obtained from FEM-CTT for the years 2003–2008 (10 °C baseline temperature, 30 °C cut-off temperature). The same values were used to calculate GDD from the LST. Although the differences are small (see Figure 7), the GDD curves from reconstructed daily MODIS LST are systematically slightly higher than those calculated from the meteorological station in spring time, while they coincide in summer and are slightly lower in autumn. The mean shift is −7.7 GDD (2003) and −16.1 GDD (2006), in fact less than 5% of the error obtained in a similar study in Canada, which was based on the 8-day MODIS LST product instead of daily MODIS LST as used here. In the Canadian study, the GDD values were systematically overestimated by 511 GDD [16]. With reconstructed daily MODIS LST the fact that neither the daily night minimum nor the day maximum are well represented is apparently averaged out to some extent.
Growing degree day threshold maps were used to assess insect development. The typical GDD maximum for an area can be also used to indicate if a disease vector can survive and become established, since all life stages need to be completed, or if crop can mature. Accepting the LST-GDD maps produced earlier, threshold maps can be generated by counting pixelwise the number of days needed to reach a certain GDD threshold. A series of threshold maps was produced for the second case study.
As in Pasotti et al.’s paper [15], various maps can be generated but in this case from satellite data rather than from meteorological data. It is assumed that MODIS LST-based GDD maps preserve microhabitat-like effects better than maps obtained from interpolated meteorological station data. Figure 8 shows for the year 2003 the day of year (DOY) when a certain GDD threshold (here: 440 GDD, compare [15]) was reached. The threshold is reached earlier on the valley floors and in the Po river plain due to higher radiation, compared with higher altitudes where it is reached later or where it cannot be reached at all.
4. Conclusions
The availability of new satellite data with high temporal resolution offers fresh opportunities for remote sensing in ecology, epidemiology and other fields. The new reconstructed LST time series are reducing the gap between high spatial resolution (with typically low temporal resolution) and high temporal resolution (originally with low spatial resolution, although this is now significantly enhanced).
We propose that these reconstructed daily LST time series be substituted for meteorological observations, especially in modeling approaches where data are typically aggregated. Indicators derivable from these daily LST map series include: (1) minimum, mean and maximum temperatures for annual/monthly/16-day periods; (2) unusually hot summers; (3) calculation of growing degree days, and (4) spring temperature increases or autumnal temperature decreases. Since more than 8 years of MODIS LST data are now available, even preliminary gradients can be extracted to assess multi-annual temperature trends.
While remote sensing data are currently more easily available (especially from data providers in the USA), the important preparatory steps are still very time consuming. Nonetheless, as described in this paper, processing can be almost entirely automated and can run even on large grid or cluster infrastructures for parallel computing. These results show that reconstructed daily LST time series constitute a valid data set which in many cases can substitute meteorological temperature observations, especially when the distribution of the stations is irregular or sparse. The indicators developed are not only of relevance to epidemiology but can also be used in agriculture or forest research.
In total, more than 11,000 maps were reprocessed. The modeling approach enabled the original LST map resolution of 1,000 m to be increased to 200 m. The typical method for obtaining temperature maps from meteorological stations is rather challenging for the study area due to its complex terrain (Central European Alps) as well as the irregularly distributed meteorological stations and ground surveys which favor agricultural zones. In this paper, it has been shown that reconstructed daily MODIS LST data can be used to substitute aggregated meteorological data for many purposes. An additional advantage is the fact that satellite data are already spatialized, thus helping to identify the effects of microhabitats which are typically lost in classical meteorological data spatial interpolation methods.
Acknowledgements
This thesis was partially funded by the Fondazione E. Mach and the EU project “Emerging Diseases in a Changing European Environment” (GOCE-2003-010284 EDEN). This paper is cataloged by the EDEN Steering Committee as EDEN0185 (http://www.eden-fp6project.net/). The contents of this publication are the sole responsibility of the author and can in no way be taken to reflect the views for the European Union.
References and Notes
- Steinacker, R.; Ratheiser, M.; Bica, B.; Chimani, B.; Dorninger, M.; Gepp, W.; Lotteraner, C.; Schneider, S.; Tschannett, S. A mesoscale data analysis and downscaling method over complex terrain. Mon. Weather Rev. 2006, 134, 2758–2771. [Google Scholar] [CrossRef]
- Hassan, Q.; Bourque, C. Potential species distribution of balsam fir based on the integration of biophysical variables derived with remote sensing and process-based methods. Remote Sens. 2009, 1, 393–407. [Google Scholar] [CrossRef]
- Kerr, J.T.; Ostrovsky, M. From space to species: ecological applications for remote sensing. Trend. Ecol. Evolut. 2003, 18, 299–305. [Google Scholar] [CrossRef]
- Hais, M.; Kučera, T. The influence of topography on the forest surface temperature retrieved from Landsat TM, ETM+ and ASTER thermal channels. ISPRS J. Photogramm. Remote Sens. 2009, 64, 585–591. [Google Scholar] [CrossRef]
- Neteler, M. Time series processing of MODIS satellite data for landscape epidemiological applications. Int. J. Geoinf. 2005, 1, 133–138. [Google Scholar]
- Rizzoli, A.; Neteler, M.; Rosà, R.; Versini, W.; Cristofolini, A.; Bregoli, M.; Buckley, A.; Gould, E. Early detection of TBEv spatial distribution and activity in the Province of Trento assessed using serological and remotely-sensed climatic data. Geospatial Health 2007, 1, 169–176. [Google Scholar] [CrossRef]
- Tatem, A.J.; Goetz, S.J.; Hay, S.I. Terra and Aqua: new data for epidemiology and public health. Int. J. Appl. Earth Obs. Geoinf. 2004, 6, 33–46. [Google Scholar] [CrossRef]
- Justice, C.O.; Vermote, E.; Townshend, J.R.G.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; Lucht, W.; Myneni, R.B.; Knyazikhin, Y.; Running, S.W.; Nemani, R.R.; Wan, Z.; Huete, A.R.; van Leeuwen, W.; Wolfe, R.E.; Giglio, L.; Muller, J.; Lewis, P.; Barnsley, M.J. The Moderate Resolution Imaging Spectroradiometer (MODIS): land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]
- Holben, B. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Myneni, R.; Tucker, C.; Asrar, G.; Keeling, C. Interannual variations in satellite-sensed vegetation index data from 1981 to 1991. J. Geophys. Res. 1998, 103, 6145–6160. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trend. Ecol. Evolut. 2005, 20, 503–510. [Google Scholar] [CrossRef]
- Beck, P.S.; Atzberger, C.; Hogda, K.A.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: a new method using MODIS NDVI. Remote Sens. Environ. 2006, 100, 321–334. [Google Scholar] [CrossRef]
- Scharlemann, J.P.; Benz, D.; Hay, S.I.; Purse, B.V.; Tatem, A.J.; Wint, G.R.; Rogers, D.J. Global data for ecology and epidemiology: a novel algorithm for temporal fourier processing MODIS data. PLoS ONE 2008, 3, e1408. [Google Scholar] [CrossRef]
- Justice, C.O.; Townshend, J.R.G.; Vermote, E.F.; Masuoka, E.; Wolfe, R.E.; Saleous, N.; Roy, D.P.; Morisette, J.T. An overview of MODIS Land data processing and product status. Remote Sens. Environ. 2002, 83, 3–15. [Google Scholar] [CrossRef]
- Pasotti, L.; Maroli, M.; Giannetto, S.; Brianti, E. Agrometeorology and models for the parasite cycle forecast. Parassitologia 2006, 48, 81–83. [Google Scholar]
- Hassan, Q.K.; Bourque, C.P.; Meng, F.R.; Richards, W. Spatial mapping of growing degree days: an application of MODIS-based surface temperatures and Enhanced Vegetation Index. J. Appl. Remote Sens. 2007, 1, 013511. [Google Scholar] [CrossRef]
- Rogers, D.J.; Hay, S.I.; Packer, M.J. Predicting the distribution of tsetse flies in West Africa using temporal Fourier processed meteorological satellite data. Ann. Trop. Med. Parasitol. 1996, 90, 225–241. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
- Tran, H.; Uchihama, D.; Ochi, S.; Yasuoka, Y. Assessment with satellite data of the urban heat island effects in Asian mega cities. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 34–48. [Google Scholar] [CrossRef]
- Ackerman, S.; Strabala, K.; Menzel, P.; Frey, R.; Moeller, C.; Gumley, L. Discriminating clear sky from clouds with MODIS. J. Geophys. Res. 1998, 103, 141–157. [Google Scholar] [CrossRef]
- Colombi, A.; De Michele, C.; Pepe, M.; Rampini, A. Estimation of daily mean air temperature from MODIS LST in Alpine areas. EARSeL eProc. 2007, 6, 38–46. [Google Scholar]
- Wan, Z. MODIS Land-Surface Temperature Products Users' Guide. 2003. Available online: http://www.icess.ucsb.edu/modis/LstUsrGuide/usrguide.html (accessed on 8 January 2010).
- Wan, Z. New refinements and validation of the MODIS land-surface temperature/emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- Wan, Z. MODIS Land-Surface Temperature. Algorithm Theoretical Basis Document (LST ATBD): LST Calculations. 1999. Available online: http://modis.gsfc.nasa.gov/data/atbd/atbd_mod11.pdf (accessed on 8 January 2010).
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z.L. Quality assessment and validation of the MODIS global land surface temperature. Int. J. Remote Sens. 2004, 25, 261–274. [Google Scholar] [CrossRef]
- Neteler, M.; Mitasova, H. Open Source GIS: A GRASS GIS Approach; Springer: New York, NY, USA, 2008. [Google Scholar]
- MODIS Reprojection Tool V4.0 Software. Available online: https://lpdaac.usgs.gov/lpdaac/tools/modis_reprojection_tool (accessed on 8 January 2010).
- Hutchinson, M.F. Interpolating mean rainfall using thin plate smoothing splines. Int. J. Geogr. Inf. Sci. 1995, 9, 385–403. [Google Scholar] [CrossRef]
- Hofierka, J.; Parajka, J.; Mitasova, H.; Mitas, L. Multivariate interpolation of precipitation using regularized spline with tension. Trans. GIS 2002, 6, 135–150. [Google Scholar] [CrossRef]
- New, M.; Hulme, M.; Jones, P. Representing twentieth-century space-time climate variability. Part I: Development of a 1961-90 mean monthly terrestrial climatology. J. Climate 1999, 12, 829–856. [Google Scholar] [CrossRef]
- Hay, S.I.; Tucker, C.J.; Rogers, D.J.; Packer, M.J. Remotely sensed surrogates of meteorological data for the study of the distribution and abundance of arthropod vectors of disease. Ann. Trop. Med. Parasitology 1996, 90, 1–19. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Randolph, S.E.; Green, R.M.; Peacey, M.F.; Rogers, D.J. Seasonal synchrony: the key to tick-borne encephalitis foci identified by satellite data. Parasitology 2000, 121, 15–23. [Google Scholar] [CrossRef]
- Carpi, G.; Cagnacci, F.; Neteler, M.; Rizzoli, A. Tick infestation on roe deer in relation to geographic and remotely sensed climatic variables in a tick-borne encephalitis endemic area. Epidemiol. Infect. 2008, 1416–1424. [Google Scholar] [CrossRef]
Figure 1. Study region in Northern Italy.
Figure 1. Study region in Northern Italy.

Figure 2. Simplified sketch of MODIS LST reconstruction processing chain.
Figure 2. Simplified sketch of MODIS LST reconstruction processing chain.

Figure 3. Average percentage of valid pixels in outlier filtered MODIS LST time series maps aggregated to 16-day periods (average good pixels/total pixels) separately for day and night overpasses. All available maps from 3/2000–2/2009 are included, with the exception of maps containing less than 10% valid pixels, based on 11,179 LST maps (spatial extent is the study region in Northern Italy).
Figure 3. Average percentage of valid pixels in outlier filtered MODIS LST time series maps aggregated to 16-day periods (average good pixels/total pixels) separately for day and night overpasses. All available maps from 3/2000–2/2009 are included, with the exception of maps containing less than 10% valid pixels, based on 11,179 LST maps (spatial extent is the study region in Northern Italy).

Figure 4. Spring MODIS LST night map reprocessing (11 April 2003 at 01:30 hs, all maps in UTM32/WGS84 metric grid, map scale 1:2,600,000): Raw LST map (upper left), map outlier filtered via histogram (upper right), outlier filtered via gradient (central left), volumetric splines reconstructed (RST, central right), differences map between the raw and RST maps (lower left), scatterplots of raw (black), histogram & gradient filtered (yellow) and RST (green) maps including linear regression gradients (lower right). For explanations, see text.
Figure 4. Spring MODIS LST night map reprocessing (11 April 2003 at 01:30 hs, all maps in UTM32/WGS84 metric grid, map scale 1:2,600,000): Raw LST map (upper left), map outlier filtered via histogram (upper right), outlier filtered via gradient (central left), volumetric splines reconstructed (RST, central right), differences map between the raw and RST maps (lower left), scatterplots of raw (black), histogram & gradient filtered (yellow) and RST (green) maps including linear regression gradients (lower right). For explanations, see text.


Figure 5. Spring MODIS LST night map reprocessing (25 April 2008 at 22:30 hs, all maps in UTM32/WGS84 metric grid, map scale 1:2,600,000): Raw LST map (upper left), map outliers filtered via histogram (upper right), outliers filtered via gradient (central left), volumetric splines reconstructed (RST, central right), difference map between the raw and RST maps (lower left), scatter plots of raw (black), histogram & gradient filtered (yellow) and RST (green) maps including linear regression gradients (lower right). For explanations, see text.
Figure 5. Spring MODIS LST night map reprocessing (25 April 2008 at 22:30 hs, all maps in UTM32/WGS84 metric grid, map scale 1:2,600,000): Raw LST map (upper left), map outliers filtered via histogram (upper right), outliers filtered via gradient (central left), volumetric splines reconstructed (RST, central right), difference map between the raw and RST maps (lower left), scatter plots of raw (black), histogram & gradient filtered (yellow) and RST (green) maps including linear regression gradients (lower right). For explanations, see text.


Figure 6. Comparison of daily mean temperature and 16-day aggregated mean temperatures in Arco, Italy: time series of the meteorological station (blue dashed) versus MODIS LST values (red) as extracted from 1,460 reconstructed Aqua/Terra scenes at the pixel position of the Arco station in Trentino (10.887125E, 45.910415N).
Figure 6. Comparison of daily mean temperature and 16-day aggregated mean temperatures in Arco, Italy: time series of the meteorological station (blue dashed) versus MODIS LST values (red) as extracted from 1,460 reconstructed Aqua/Terra scenes at the pixel position of the Arco station in Trentino (10.887125E, 45.910415N).

Figure 7. Comparison of accumulated growing degree day curve from FEM-CTT meteorological station and MODIS LST for 2003 and 2006: time series of the meteorological station (blue dashed) versus MODIS LST values (red) as extracted from 1,460 reconstructed Aqua/Terra scenes at the pixel position of the Trento-Sud station in the Autonomous Province of Trento (11.126386E, 46.021841N; baseline temperature 10 °C, cut-off temperature 30 °C).
Figure 7. Comparison of accumulated growing degree day curve from FEM-CTT meteorological station and MODIS LST for 2003 and 2006: time series of the meteorological station (blue dashed) versus MODIS LST values (red) as extracted from 1,460 reconstructed Aqua/Terra scenes at the pixel position of the Trento-Sud station in the Autonomous Province of Trento (11.126386E, 46.021841N; baseline temperature 10 °C, cut-off temperature 30 °C).

Figure 8. Number of days of the year (DOY) to reach 440 accumulated growing degree days in the year 2003 (baseline temperature: 10 °C, cut-off temperature: 30 °C). The threshold is reached earliest in the year on the valley floors and the Po river plain, later or not at all in higher altitudes (uncolored zones; map scale 1:1,400,000).
Figure 8. Number of days of the year (DOY) to reach 440 accumulated growing degree days in the year 2003 (baseline temperature: 10 °C, cut-off temperature: 30 °C). The threshold is reached earliest in the year on the valley floors and the Po river plain, later or not at all in higher altitudes (uncolored zones; map scale 1:1,400,000).

Table 1. Spatial distribution analysis of good quality pixels in daily MODIS LST after applying all filters with respect to altitude. The values indicate the percentage of “good” pixels (*: only observations from MODIS on Terra satellite; °: MODIS on Aqua data only available from 8 July 2002). The overall number of input maps is 11,179.
Table 1. Spatial distribution analysis of good quality pixels in daily MODIS LST after applying all filters with respect to altitude. The values indicate the percentage of “good” pixels (*: only observations from MODIS on Terra satellite; °: MODIS on Aqua data only available from 8 July 2002). The overall number of input maps is 11,179.
| Year | 0–499 m | 500–1,499 m | >1,500 m |
|---|---|---|---|
| 2000* | 30.0 | 36.0 | 36.1 |
| 2001* | 32.4 | 40.3 | 40.5 |
| 2002° | 27.0 | 33.6 | 35.9 |
| 2003 | 35.5 | 46.1 | 47.6 |
| 2004 | 31.5 | 39.2 | 41.6 |
| 2005 | 35.1 | 44.7 | 45.1 |
| 2006 | 34.7 | 43.8 | 46.1 |
| 2007 | 38.2 | 46.6 | 46.5 |
| 2008 | 28.3 | 33.4 | 34.0 |
| Mean | 32.5 | 40.4 | 41.5 |
| Stddev | 3.68 | 5.21 | 5.17 |
© 2010 by the authors. licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
MDPI and ACS Style
Neteler, M. Estimating Daily Land Surface Temperatures in Mountainous Environments by Reconstructed MODIS LST Data. Remote Sens. 2010, 2, 333-351. https://doi.org/10.3390/rs1020333
AMA Style
Neteler M. Estimating Daily Land Surface Temperatures in Mountainous Environments by Reconstructed MODIS LST Data. Remote Sensing. 2010; 2(1):333-351. https://doi.org/10.3390/rs1020333
Chicago/Turabian Style
Neteler, Markus. 2010. "Estimating Daily Land Surface Temperatures in Mountainous Environments by Reconstructed MODIS LST Data" Remote Sensing 2, no. 1: 333-351. https://doi.org/10.3390/rs1020333
Article Metrics
Article Access Statistics
For more information on the journal statistics, click here.
Multiple requests from the same IP address are counted as one view.
We use cookies on our website to ensure you get the best experience.
Read more about our cookies here.