Performance Assessment of Multi-Source Weighted-Ensemble Precipitation (MSWEP) Product over India (original) (raw)
Author / Affiliation / Email
Article Menu
/ajax/scifeed/subscribe
Font Type:
Arial Georgia Verdana
Open AccessArticle
by
Akhilesh S. Nair
and
J. Indu
*
Department of Civil Engineering, Indian Institute of Technology Bombay, Mumbai 400076, India
*
Author to whom correspondence should be addressed.
Submission received: 18 October 2016 /Revised: 20 December 2016 /Accepted: 4 January 2017 /Published: 11 January 2017
Abstract
:
Error characterization is vital for the advancement of precipitation algorithms, the evaluation of numerical model outputs, and their integration in various hydro-meteorological applications. The Tropical Rainfall Measuring Mission (TRMM) Multi-satellite Precipitation Analysis (TMPA) has been a benchmark for successive Global Precipitation Measurement (GPM) based products. This has given way to the evolution of many multi-satellite precipitation products. This study evaluates the performance of the newly released multi-satellite Multi-Source Weighted-Ensemble Precipitation (MSWEP) product, whose temporal variability was determined based on several data products including TMPA 3B42 RT. The evaluation was conducted over India with respect to the IMD-gauge-based rainfall for pre-monsoon, monsoon, and post monsoon seasons at daily scale for a 35-year (1979–2013) period. The rainfall climatology is examined over India and over four geographical extents within India known to be subject to uniform rainfall. The performance evaluation of rainfall time series was carried out. In addition to this, the performance of the product over different rainfall classes was evaluated along with the contribution of each class to the total rainfall. Further, seasonal evaluation of the MSWEP products was based on the categorical and volumetric indices from the contingency table. Upon evaluation it was observed that the MSWEP products show large errors in detecting the higher quantiles of rainfall (>75th and > 95th quantiles). The MSWEP precipitation product available at a 0.25° × 0.25° spatial resolution and daily temporal resolution matched well with the daily IMD rainfall over India. Overall results suggest that a suitable region and season-dependent bias correction is essential before its integration in hydrological applications. While the MSWEP was observed to perform well for daily rainfall, it suffered from poor detection capabilities for higher quantiles, making it unsuitable for the study of extremes.
Graphical Abstract
1. Introduction
Precipitation is a crucial variable that drives the atmosphere’s general circulation through latent heat release. Hence, quantifying its spatiotemporal variability holds paramount importance in fields of hydrology, atmospheric and environmental science, etc. Examining precipitation variability by maintaining a dense network of ground-based rain gauges or Doppler weather radar networks can often be prohibitively costly, especially for developing nations. This gap is duly filled by satellite-based precipitation products made available at a high spatial and temporal resolution. Precipitation estimation from satellites are either based on the indirect relationship of cloud-top temperature by infrared sensors, cloud characteristics of reflectivity by visible sensors, or the sources and sinks of microwave radiations during interaction with atmospheric hydrometeors. While the visible and infrared sensors provide fine temporal resolution data by exploiting the cloud-top temperature and surface precipitation, the microwave sensors provide direct and accurate rainfall estimates but at the cost of coarse temporal resolution. Therefore, the algorithms for multi-satellite precipitation combine observations from the infrared and microwave on a global scale at high temporal resolutions. These high-resolution precipitation data from multi-satellite products have immensely advanced our existing knowledge by providing useful worldwide precipitation estimates [1]. Some of the global products available to date are: Tropical Rainfall Measuring Mission (TRMM) Multisatellite Precipitation Analysis (TMPA; not presently operational)near-real-time TMPA, gauge-adjusted TMPA version 7 products [2,3,4]; the National Oceanic and Atmospheric Administration (NOAA) Climate Prediction Center (CPC) morphing technique (CMORPH) [5,6]; the Global Satellite Mapping of Precipitation Microwave-IR Combined Product (GSMaP-MVK) and gauge-adjusted (GSMaP-Gauge) datasets [7,8]; the Integrated Multisatellite Retrievals for GPM (IMERG) [9]; etc.
These products fail to fully resolve the evolution of hourly high intensity rainfall cells occurring at smaller spatial scales. Hence, along with the widespread utility of the multi-satellite precipitation products, it has also been recognized that multi-satellite precipitation products suffer from large uncertainties. Uncertainty analysis of satellite-based precipitation is a complex problem requiring statistical information [9]. To date, studies have investigated satellite-based precipitation uncertainty by evaluating the precipitation products themselves, exemplified by the uncertainty analysis between monthly satellite rainfall estimates and rain gauge data over Pacific [10], the validation of the Global Precipitation Climatology Project (GPCC-1DD) [11], evaluation of satellite based precipitation products over the USA [12,13], analysis of high-resolution rainfall products over the Continental United States(CONUS) [14], global analysis of high-resolution satellite-based precipitation [15], and performance evaluation of high-resolution precipitation product over China [16]. More recent examples include Anagnoustou et al. [17], who have studied the error properties of CMORPH and TRMM 3B42 precipitation products in the Midwestern USA; Stampoulis and Anagnostou [18], who have evaluated the CMORPH and TRMM 3B42 over Europe; Habib et al. [19], who have studied the performance of the high-resolution satellite precipitation product over a watershed in south Louisiana; Kirstetter et al. [20], who evaluated the performance of the precipitation from TRMM TMI using the Bayesian Rain retrieval Algorithm Including Neural Network (BRAIN) over West Africa; Chen et al. [21], who studied the spatial error structure of precipitation products from TRMM Multi-satellite Precipitation Analysis (TMPA) for two successive versions 6 and 7 over CONUS.
Similar studies have been conducted over India to elucidate the accuracy of precipitation products over various geographical regions. Such as, Joshi et al. [22], performed the validation of TMPA and GPCC-1DD over India. Nair et al. [23] evaluated the performance of the TMPA product over the western states of India and found that this product fails to detect the heavy convective precipitation, particularly over the windward side of the Western Ghats. Further studies such as Prakash et al. [24] examined the performance of high-resolution precipitation products such as TMPA, CMORPH, and PERSIANN over India and found that these products perform poor over the rain-shadow region of southeast peninsular India, the semi-arid northwest parts of India, and hilly northern parts over from their six years of analysis results. Prakash et al. [25] compared the TMPA and Global Satellite Mapping of Precipitation (GSMaP) products over India with IMD observations and found that the products show poor performance over the Western Ghats and over southeast peninsular India. Indu and Kumar [26] also found that the TMPA product shows poor performance over India at higher quantiles for the monsoon season (JJAS).
For skillful application of precipitation products, studies have been conducted to model the associated errors. For example, Alemohammad et al. [27] used an ensemble-based Bayesian method for the characterization of uncertainties pertaining to satellite-based precipitation retrieval for land data assimilation over a part of central CONUS; Aghakouchak et al. [28] studied the feasibility of using the copula-based method to model the uncertainty of multisensory-based rainfall estimates; Tian et al. [29] studied the suitability of the additive error model and multiplicative error model for uncertainty representation of satellite precipitation products; Seyyedi [30] performed an uncertainty assessment of precipitation estimates for hydrological modeling; and Maggioni et al. [31] proposed a framework for precipitation uncertainties from satellite precipitation to provide global estimates of errors at temporal resolution.
Performance evaluations of these products over varying geographical extents equip algorithm developers to examine the underlying complex error characteristics [32,33,34]. From a data producer’s perspective, error estimate is crucial information used towards creating a better product with higher spatial and temporal resolution. Also, error estimates empower data users with an expected range of uncertainty for various applications. With the release of new blended precipitation data products, each aiming to outperform existing products, uncertainty analysis dictates our choice of data products. As uncertainty directly points to the information content, it becomes that much more imperative to understand the efficiency of a newly released multi-satellite precipitation product. Comprehensive uncertainty analyses studies enable develop error correction procedures.
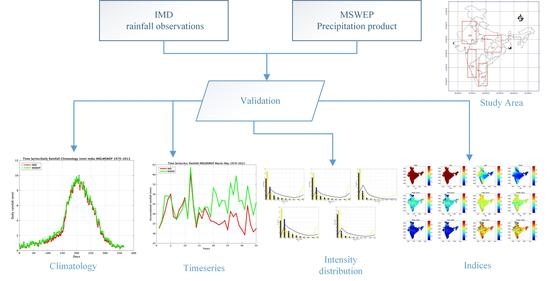
This study furthers existing knowledge by examining the uncertainty of the newly released daily 0.25° × 0.25° Multi-Source Weighted Ensemble Precipitation (MSWEP) [35] research-quality product over the Indian subcontinent. A thorough evaluation of its performance is being assessed for daily precipitation for the pre-monsoon, monsoon, and post-monsoon seasons over India. The performance of MSWEP is also studied for higher quantiles of rainfall (>75th and>95th). The paper is organized as follows: the details of the study area and datasets are provided in Section 2. Evaluation methodology is presented in Section 3, followed by results and discussion in Section 4. The conclusions and recommendations for future research are outlined in Section 5.
2. Data Used
This study examines the daily 0.25° × 0.25° MSWEP research-quality product that combines observations from a wide range of data sources like gauge, satellite, and reanalysis data. MSWEP involves a long-term bias-corrected climatic mean derived from the Climate Hazards Group Precipitation Climatology (CH-Pclim) dataset, PRISM climatic precipitation data, and stream flow data from USGS Geospatial Attributes of Gages for Evaluating stream flow (GAGES)-II database and the Global Runoff Data Centre (GRDC).Afterwards, several gridded satellite precipitation products such as CMORPH, GSMaPMVK, TMPA 3B42RT, PERSIANN, SM2RAIN-ASCAT and the reanalysis precipitation datasets of NCEP-CFSR, ERA-Interim, and JRA-55 were evaluated in terms of their temporal variability to assess their potential inclusion in MSWEP. The long-term climatic mean was subsequently temporally downscaled first to a monthly timescale, then to a daily timescale and finally to a three-hourly timescale using weighted averages of precipitation anomalies obtained from gauge, satellite, and reanalysis datasets to yield the final MSWEP dataset. More details on this data product can be found in Beck et al. [35].
The reference dataset used is a daily gridded rainfall product available at 0.25° latitude × 0.25° longitude resolution developed by the Indian Meteorological Department (IMD), which is prepared using the daily rainfall data from the archive of National Data Centre, IMD, Pune for the period 1901–2013. Over India, a total of 547 IMD observatory stations, 494 hydro-meteorology observatories, and 74 Agromet observatories, along with rainfall reporting stations maintained by State Governments, adds up to 6955 stations. A rainy day is defined by IMD as when the daily rainfall exceeds 2.5 mm and a heavy rain event is defined if the same exceeds 64.5 mm. This gauge-based gridded rainfall data set is known to reproduce the sharp gradient of orographic rainfall in a realistic manner while still representing finer scale monsoon rainfall features.
3. Methodology
As MSWEP and IMD gauge-based precipitation data are available at 0.25° × 0.25° spatial resolution, in the present study evaluation is conducted at the same grid resolution on a daily temporal scale. The grid points over the Indian subcontinent are extracted using a land mask. It should be noted that the density of IMD rain gauges are not uniformly distributed over India. They are especially sparse over the Jammu and Kashmir region. The performance evaluation of MSWEP datasets are being conducted over a 35-year period (1979–2013) for the seasons of pre-monsoon (March, April, May-MAM), monsoon (June, July, August, September-JJAS), and post-monsoon (October, November-ON), which comprises 92, 122, and 61 days each year, respectively.
To quantitatively compare MSWEP precipitation with IMD rain gauge observations, widely used validation statistical indices are used in this study. The correlation coefficient (CC) reflects the degree of linear correlation between satellite-based precipitation and gauge observations, the root mean square error (RMSE) quantifies the average error magnitude, which is slightly biased towards larger error, and the relative bias (BIAS) is used to measure the systematic bias of the MSWEP precipitation.
C C = ∑ i = 1 n ( R i − R ¯ ) ( P i − P ¯ ) ∑ i = 1 n ( R i − R ¯ ) 2 . ∑ i = 1 n ( P i − P ¯ ) 2 ,
(1)
R M S E = 1 n ∑ i = 1 n ( P i − R i ) 2 ,
(2)
B I A S = ∑ i = 1 n ( P i − R i ) ∑ i = 1 n G i ,
(3)
where n is the number of samples, R i are the reference IMD observations, P i are MSWEP precipitation, and P ¯ and R ¯ are mean MSWEP and IMD precipitation, respectively.
In addition, performance evaluation is conducted based on the widely used 2 × 2 contingency table as shown in Table 1, which provides information about hits, misses, or false alarms using several categorical skill metrics such as probability of detection (POD), false alarm ratio (FAR), miss rate (MISS), and critical success index (CSI).The capability of MSWEP datasets was also examined using the volumetric skill scores derived by AghaKouchak and Mehran [36], which are the volumetric equivalents like volumetric hit index (VHI), volumetric false alarm ration (VFAR), volumetric miss index (VMI), and volumetric critical success index (VCSI).The skill scores range from 0 to 1 for POD, FAR, MISS, CSI, VHI, VFAR, VMI, and VCSI with 1 being the perfect score for POD, CSI, VHI, and VCSI and 0 being the perfect score for FAR, VFAR, and VMI. Metrics used for the present study have been summarized in Table 2. MSWEP and IMD represent the daily rainfall in mm/day from the MSWEP precipitation product and the reference IMD rain gauge observations, respectively; t stands for the threshold (which can be 75th or 95thrainfall quantile). A seasonal analysis was conducted for the Indian summer monsoonal months of June, July, August, September (JJAS), pre-monsoonal months, and post-monsoonal months for the 35-year data record over India. It should be noted that the results of this analysis are presented for pixels with more than 50 concurrent pairs of IMD precipitation and MSWEP precipitation in order to avoid unreliable statistics.
4. Results
The variability of mean seasonal rainfall from a 35-year period (1979–2013) over India is for both IMD and MSWEP datasets for summer, monsoon and retreating monsoonal months. The Indian summer monsoonal months contribute nearly 70% of annual rainfall to the country, whereas the pre-monsoon and post-monsoonal months are responsible for nearly 25% of total rainfall. The winter season is not being considered in the present study. As mentioned, this is mainly because of a lack of sufficient rain gauge data over the Jammu and Kashmir region and owing to the low intensity of winter rainfall over India.
4.1. Rainfall Climatology
To examine the rainfall climatology over India, four different geographical regions are selected based on the uniformity of precipitation over them. The regions are the southwest (11.5° N–21.5° N, 73.5° E–76.5° E), southeast (8.5° N–16.5° N, 77.5° E–80.5° E), central (20.5° N–26.5° N, 79.5° E–85.5° E), and northwest (23.5° N–31.5° N, 71.5° E–76.5° E) regions [37] as shown in Figure 1. Figure 2 shows the climatology of data for the period of analysis over the four geographical extents for MSWEP and IMD rainfall. The time series area-averaged rainfall from IMD for all India and its subregions is found to be in accordance with the existing results by Krishnamurthy and Shukla [37]. Figure 2 shows a good correspondence by the MSWEP datasets over all regions except southwest India. Figure 3 shows the time series of annual rainfall for the 35-year period for both IMD and MSWEP. It can be observed that while there seems to be a good match during the JJAS season, for the post-monsoon and pre-monsoon seasons, the MSWEP tends to overestimate the annual mean rainfall. Further analysis for the southwest Indian region shows that MSWEP depicts slight underestimation (in the period from 150 to 250 days); this may be caused due to the southwest region receiving heavy rain during the monsoon season (JJAS) from orographic rainfall caused due to the Western Ghats. From the evaluation of MSWEP precipitation under different rainfall intensity in Section 4.2, it has been found that MSWEP underestimates the heavy rainfall class (>50 mm/day), which makes a significant contribution total rainfall, as shown in Figure 4. Furthermore, the product depicts a slight overestimation (in the period from 90 to 150 days) for the same region; this may be due to the overestimation of the light rainfall class (3 mm/day–15 mm/day) by MSWEP product, which makes a significant contribution total rainfall during the pre-monsoon season, as is evident in Figure 5. For southeast India, the MSWEP dataset exhibited a very slight overestimation (in the period from 250 to 300 days). This may be caused by the overestimation of the medium rainfall class (3 mm/day–25 mm/day), which has high contribution in total rainfall for MSWEP during post-monsoon as shown in Figure 6. Furthermore, it can be seen that the southeast region attains its peak during the post-monsoon season due to higher rainfall during the months of October, November, and December, generally referred to as the winter monsoon, compared to the low rainfall during JJAS.
Further, the statistical parameters of all India and its subregions’ daily climatological rainfall for the analysis period (1979–2013) have been tabulated in Table 3. The spatial average of the climatological mean rainfall over all India, southwest, southeast, central, and northwest, is 3.135 mm/day, 3.501 mm/day, 2.408 mm/day, 3.114 mm/day, and 1.372 mm/day, respectively, from IMD reference observations; that from MSWEP is 3.31 mm/day, 3.234 mm/day, 2.639 mm/day, 3.358 mm/day, and 1.530 mm/day, respectively. This shows that the spatial average of climatological mean from MSWEP is in accordance with the IMD rain gauge observations over the heavy/moderate rainfall regions of southwest/central regions and with low/less rainfall occurring northwest/southeast regions, though it slightly underestimates precipitation over the southwest region and slightly overestimates it over the remaining regions. The correlation coefficient (CC) for all India, southwest, southeast, central, and northwest regions is 0.8605, 0.8625, 0.8589, 0.8690, and 0.8628, respectively.
4.2. Evaluation of the Rainfall Data under Different Rainfall Intensity
This analysis has been conducted to evaluate the performance of MSWEP precipitation product under different daily rainfall intensities. The comparative evaluation of MSWEP precipitation has been done over all India and its subregions for MAM, JJAS, and ON months by calculating the intensity distribution of daily rainfall in different classes and their contributions to the total rainfall in different grids. Figure 4 shows the intensity distributions of daily rainfall in different classes and their contributions to total rainfall during monsoon (JJAS) season. It is seen that non-rainy and weak rain (<3 mm/day) has the largest occurrence, occurring about 60%–80% of the total days, in all regions. Furthermore, MSWEP overestimates precipitation compared with IMD observations for rainfall intensity of 25 mm/day, then has excellent correspondence with observations up to 50 mm/day; finally it underestimates precipitation for higher rainfall intensities (>50 mm/day) over all India. It can also be seen that, although the occurrence of the first class is around 48% for MSWEP and 65% for IMD observations, their contribution to the total rainfall amount was very small. The rainfall makes a higher contribution in lower precipitation bins (3–10 mm/day) and heavy precipitation bins (>50 mm/day) over all India. Similar trends have been observed in other subregions, where the occurrence of the middle rainfall class (15 mm/day < rainfall < 50 mm/day) estimated by MSWEP was equivalent to that of IMD observations with slight variations; further, for the lower rainfall class (3 mm/day < rainfall < 15 mm/day), MSWEP overestimates rainfall, whereas for the heavy rainfall class (rainfall > 50 mm/day) it underestimates rainfall compared with the IMD observations.
Figure 5 shows the intensity distributions of daily rainfall and their contributions to total rainfall during the post-monsoon season (ON). During this season southern India receives high rainfall, which is evident from Figure 5, and the southeast and southwest regions show high contribution from heavy rainfall class (rainfall > 50 mm/day). MSWEP precipitation in the post-monsoon season follows a similar trend as in the monsoon season, where the low rainfall classes are overestimated, the middle rainfall class is estimated equivalent to IMD observations with slight variations, and the MSWEP product underestimates the heavy rainfall class (rainfall > 50 mm/day).
Figure 6 shows the intensity distributions of daily rainfall and their contributions to total rainfall during the pre-monsoon (MAM) season. During this season southern India receives prominent rainfall, which is evident in the distribution—with large contribution from the heavy rainfall class (rainfall > 50 mm/day) in the southeast and southwest regions. MSWEP follows the same trend as in other seasons by overestimating the low and medium rainfall classes and underestimating the high rainfall class.
In order to further elucidate the efficiency of MWSEP precipitation prediction over India, a rain event detection analysis using contingency table metrics has been performed for the pre-monsoon (MAM), monsoon (JJAS), and post-monsoon (ON) seasons, as discussed below.
4.3. Results for the Monsoon Season
Results of comparative evaluation of MSWEP precipitation data using the contingency table metrics are presented for daily and higher quantiles of rainfall during monsoon season in present section, post-monsoon in Section 4.4 and pre-monsoon in Section 4.5. It should be noted that the MSWEP precipitation has been evaluated for higher quantiles (daily rainfall > 75th and >95th quantiles) by computing quantiles independently for each 0.25° × 0.25° grid cell, as shown in Figure 7. Furthermore, all the analyses have been conducted for pixels having a minimum of 50 observations to avoid unreliable statistics. Figure 7b shows the 95th quantile for the monsoon season, which indicates that the northwest region (indicated in gray) does not receive heavy rainfall during this season. Similarly, Figure 7d shows the 95th quantile for summer (MAM), which indicates that only the southwest, north, and northeast regions receive heavy rainfall during this season. The spatial distributions of the categorical and volumetric skill scores are studied for MSWEP precipitation product during the monsoon, pre-monsoon, and post-monsoon periodsfor 35 years from 1979 to 2013. Results are shown for daily rainfall and for higher quantiles of rainfall (> 75th and > 95th quantile). Here, the ratio of number of correct identifications of MSWEP to the total number of reference (IMD) precipitation occurrences is shown by the Probability of Detection (POD) and the volume of correctly detected precipitation is given by the volumetric hit index (VHI). From Figure 7, for the JJAS rainfall, the POD and VHI values lie close to 1 (slightly less for the regions of Jammu Kashmir and northern Rajasthan, which are significant exceptions). The incorrectly detected precipitation denoted by the False Alarm Ratio (FAR) shows very low values (close to 0) over the northeast region and the Western Ghats. In the study by Li et al. [38], it has been stated that for the Indian summer monsoonal season, the proportion of stratiform precipitation attains a maximum value during the summer. This implies that for the seasonal rainfall over India, most of the missed events in MSWEP are light rainfall events/stratiform rainfall. However, for higher rainfall quantiles (i.e., Q75 and Q95), POD and VHI from Figure 8 indicate that as the threshold for heavy rain rate increases, both POD and VHI tend to decrease. Both FAR and VFAR were found to increase at higher thresholds of Q75 and Q95 (Figure 8).The critical success index (CSI) values (Figure 9) over the majority of Indian regions show that the overall performance score of MSWEP over India is between 0 and 1.0, whereas the overall measure of volumetric performance given by the volumetric critical success index (VCSI) (Figure 8) indicates a higher performance score (between 0.6 and 1.0). It can be observed from the MISS index (Figure 9) that MSWEP fails to detect a large fraction of precipitation for the monsoon season at higher quantiles. However, the volumetric miss index (VMI) (Figure 9) suggests that the volume of precipitation that MSWEP does not detect is relatively small.
In a study by Prakash et al. [39], two regions over India were shown to be subject to rainfall extremes: the west coast, including Gujarat state; and the western parts of northeast India, including Sikkim and Meghalaya states. The windward side of the Western Ghats is known to be subjected to higher rainfall intensities during the southwest monsoon, while its leeward side typically stays as a rain-shadow region. The regions of the east coast, central India, and the Himalayas are known to get 3%–5% of conditional heavy rainfall events, as per IMD data. The MSWEP shows rather higher POD over most parts of the country except northern India (e.g., Jammu and Kashmir states). Although MSWEP can detect heavy rainfall along the windward side of the Western Ghats, it has a rather large FAR along the leeward side (e.g., southeast peninsular India), a rain-shadow region. Lower POD and CSI with higher FAR and MISS over northern and northwest India suggest that the performance of the MSWEP product gets affected while detecting heavy rainfall over these regions. The spatial distributions of volumetric skill metrics are similar to categorical skill metrics; however, their magnitude is different. VHI indicates that MSWEP captures most of the rainfall volume in the detected rainy days. We also note that the gauge density is not sufficient over the Jammu and Kashmir regions for a valid comparison. Hence, the results over these regions have more uncertainty.
4.4. Comparison for the Post-Monsoon Season
During the retreating monsoon season, a higher fraction of rainy days are mainly concentrated over southern India, mainly over the southeastern and western coastlines. Figure 10 and Figure 11 show the spatial distribution of indices values from daily rainfall for the post-monsoon season of India from 1979 to 2013 with a near-perfect POD and VHI values obtained from total rainfall (Figure 10a,b). Comparative analysis with the FAR and VFAR plots suggests that the MSWEP tends to falsely detect the precipitation over parts of central and northern India. For higher quantiles of rainfall (mainly > 75th quantile), MSWEP depicts an excellent detection rate over the northeastern region. It correctly captures the precipitation variability over space for the post-monsoon season. Comparative analysis with Figure 11 shows that for the post-monsoon season, the MSWEP depicts a MISS rate of ~0 for daily rainfall (for all of India), between 0.4 and 0.8 for rainfall > 75th quantile (covering most of south and southeastern India), and between 0.8 and 1 for rainfall > 95th quantile (covering a few parts of southern India).
4.5. Comparative Analysis for the Pre-Monsoon Season
The fraction of rainy days for MAM seasons are less than 10 for the majority of the central and western parts of India. During MAM seasons, rainfall frequently occurs mainly in the southern states and on the eastern coast of India. From Figure 12 and Figure 13, for daily rainfall the MAM season shows higher correspondence for the entire country for daily rainfall with respect to POD and VHI. The CSI and VCSI plots show the high ability of MSWEP to capture the daily precipitation over the eastern extent of India and over northern India. The results also indicate its ability to better capture the daily rainfall occurring over the southern coastline of Kerala and the eastern regions. However, the increased values of FAR (between 0.6 and 0.8) over the majority of India suggest that MSWEP is falsely detecting the daily precipitation. Though the pattern of MAM rainfall is being correctly captured spatially by the MSWEP products, there is a tendency for MSWEP to slightly overestimate the MAM precipitation values, as indicated by their high FAR and MISS values. Comparative analysis with Figure 13 shows that for the pre-monsoon season, the MSWEP depicts a MISS rate of 0–0.2 for daily rainfall (for entire India), between 0.4 and 1 for rainfall > 75th quantile (covering parts of southern, northern, and southeastern India) and between 0.6 and 1 for rainfall > 95th quantile (covering a few parts of southwestern, northeastern, and northern India).
To summarize, graphical and statistical evaluation of MSWEP precipitation for daily rainfall and for higher quantiles shows that, as the threshold of detection is increased, the indices of CSI, VCSI, MISS, and VMI lose power over India, especially over parts of the southwestern coastline, indicating that the MSWEP data product fails to detect rainfall extremes (above Q75 and Q95). Overall, for daily rainfall estimates, the volumetric indicators show good performance by MSWEP data when compared with IMD precipitation estimates.
5. Conclusions
The capability of the research quality product of MSWEP is assessed against the IMD gauge-based observations across the Indian subcontinent. An initial assessment of the MSWEP research-quality product for detecting daily rainfall across India for the 35-year data period (1979–2013) during monsoon, post-monsoon, and pre-monsoon seasons shows good agreement with the reference gauge-based IMD rainfall. Rainfall climatology was also studied for four different geographical regions of India. The climatological mean statistics shows that the MSWEP product has a low RMSE of 0.1788 mm/day, a low negative bias of 0.0499 mm/day, and a high correlation coefficient (CC) of 0.8605 over all India; similar results were obtained for the four subregions, as summarized in Table 3.
The daily precipitation from MSWEP was assessed separately for the pre-monsoon, monsoon, and post-monsoon periods. In the study region, the MSWEP precipitation overestimated the rainfall amount contribution rates in the middle rainfall class ranges (3 mm/day < rainfall < 20 mm/day) but underestimated it in the heavy rainfall class (>50 mm/day). The precipitation classes that contribute the most to the total rainfall are key to understanding the overestimation/under-estimation. The detection of heavy rainfall classes is very important in the study of extreme hydro-meteorological events such as floods, but the overall MSWEP underestimates this class throughout the study region. However, it estimates middle rainfall classes in a fairly similar manner to the IMD gauge observations, as is evident from Figure 4, Figure 5 and Figure 6.
Performance evaluation was conducted using the categorical and volumetric indices derived from the contingency table. The seasonal variations of daily rainfall over 75th and 95th percentile are plotted spatially using various categorical and volumetric metrics derived using the contingency table. An initial assessment of this product shows promising results for daily precipitation estimates over all India and the chosen geographical extents of central, southwestern and northeastern India. However, the performance of the MSWEP data product was affected when detecting precipitation extremes (>75th and >95th quantiles of rainfall) in this evaluation as well.
Land–atmosphere interactions are known to influence the weather and climate. A study of the energy and water exchanges between the atmosphere and the land requires the use of Land Surface Models (LSMs). The forcing data made available for LSM prediction acts as one of the main contributors that dictate the prediction uncertainty. In this regard, the utility of the present study is to validate a newly released precipitation product and thereby establish its reliability to be used as a forcing data within the LSM. This also aids in land data assimilation because a realistic estimation of precipitation uncertainty is crucial to improve the assimilation skill.
The MSWEP precipitation product evaluated in the present study was obtained by merging multiple high-resolution rainfall products, as explained in Section 2. In comparison with existing studies, it can be concluded that over India the MSWEP product performs poorly in detecting higher rainfall quantiles. This study furthers the existing literature by presenting the initial performance evaluation of the newly released MSWEP precipitation product. Results from such studies need to be carefully examined before employing any data product in application-oriented studies. As a future extension of this work, we plan to conduct a comprehensive analysis focusing on the comparison of several multi-satellite precipitation products in different rainfall regimes.
Acknowledgments
Author Contributions
Akhilesh S. Nair and J. Indu have conceived and designed the experiment; Akhilesh performed the experiments, Akhilesh and Indu have analyzed the data and have contributed to writing the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ebert, E.; Janowiak, J.; Kidd, C. Comparison of near-real-time precipitation estimates from satellite observations and numerical models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.J.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The TRMM multi-satellite precipitation analysis (TMPA). In Satellite Rainfall Applications for Surface Hydrology; Springer: Dordrecht, The Netherlands, 2010; pp. 3–22. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. Integrated Multi-Satellite Retrievals for GPM (IMERG) Technical Documentation; NASA/GSFC: Greenbelt, MD, USA, 2014.
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Xie, P.; Chen, M.; Shi, W. CPC unified gauge-based analysis of global daily precipitation. In Proceedings of the 24th Conference on Hydrology, Atlanta, GA, USA, 18 January 2010.
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K.; et al. Global precipitation map using satellite-borne microwave radiometers by the GSMaP project: Production and validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Ushio, T.; Tashima, T.; Kubota, T.; Kachi, M. Gauge adjusted global satellite mapping of precipitation (GSMaP_Gauge). In Proceedings of the 29th ISTS (International Symposium on Space Technology and Science), Nagoya-Aichi, Japan, 2–9 June 2013.
- Huffman, G.J.; Adler, R.F.; Arkin, P.; Chang, A.; Ferraro, R.; Gruber, A.; Janowiak, J.; McNab, A.; Rudolf, B.; Schneider, U. The global precipitation climatology project (GPCP) combined precipitation dataset. Bull. Am. Meteorol. Soc. 1997, 78, 5–20. [Google Scholar] [CrossRef]
- Morrissey, M.; Greene, J. Uncertainty analysis of satellite rainfall algorithms over the tropical Pacific. J. Geophys. Res. Atmos. 1998, 103, 19569–19576. [Google Scholar] [CrossRef]
- McPhee, J.; Margulis, S.A. Validation and error characterization of the GPCP-1DD precipitation product over the contiguous United States. J. Hydrometeorol. 2005, 6, 441–459. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.; Eylander, J.; Joyce, R.; Huffman, G.; Adler, R.; Hsu, K.; Turk, F.; Garcia, M.; Zeng, J. Component analysis of errors in satellite-based precipitation estimates. J. Geophys. Res. 2009, 114, D24101. [Google Scholar] [CrossRef]
- Habib, E.; Henschke, A.; Adler, R.F. Evaluation of TMPA satellite-based research and rea-time rainfall estimates during six tropical related heavy rainfall events over Louisiana, USA. Atmos. Res. 2009, 94, 373–388. [Google Scholar] [CrossRef]
- Sapiano, M.R.P.; Arkin, P.A. An intercomparison and validation of high-resolution satellite precipitation estimates with 3-hourly gauge data. J. Hydrometeorol. 2009, 10, 149–166. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D. A global map of uncertainties in satellite-based precipitation measurements. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.Y.; Wang, Y.; Xie, P.P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Anagnostou, E.N.; Maggioni, V.; Nikolopoulos, E.I.; Meskele, T.; Hossain, F.; Papadopoulos, A. Benchmarking high-resolution global satellite rainfall products to radar and rain-gauge rainfall estimates. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1667–1683. [Google Scholar] [CrossRef]
- Stampoulis, D.; Anagnostou, E.N. Evaluation of global satellite rainfall products over continental Europe. J. Hydrometeorol. 2012, 13, 588–603. [Google Scholar] [CrossRef]
- Habib, E.; Haile, A.T.; Tian, Y.; Joyce, R.J. Evaluation of the high-resolution CMORPH satellite rainfall product using dense rain gauge observations and radar-based estimates. J. Hydrometeorol. 2012, 13, 1784–1798. [Google Scholar] [CrossRef]
- Kisrtetter, P.E.; Viltard, N.; Gosset, M. An error model for instantaneous satellite rainfall estimates: Evaluation of BRAIN-TMI over West Africa. Q. J. R. Meteorol. Soc. 2012, 139, 894–911. [Google Scholar]
- Chen, S.; Hong, Y.; Gourley, J.J.; Huffman, G.J.; Tian, Y.; Cao, Q.; Yong, B.; Kirstetter, P.E.; Hu, J.; Hardy, J. Evaluation of the successive V6 and V7 TRMM multisatellite precipitation analysis over the Continental United States. Water Resour. Res. 2013, 49, 8174–8186. [Google Scholar] [CrossRef]
- Joshi, M.K.; Rai, A.; Pandey, A.C. Validation of TMPA and GPCP 1DD against the ground truth rain-gauge data for Indian region. Int. J. Climatol. 2013, 33, 2633–2648. [Google Scholar] [CrossRef]
- Nair, S.; Srinivasan, G.; Nemani, R. Evaluation of multi-satellite TRMM derived rainfall estimates over a western state of India. J. Meteorol. Soc. Jpn. 2009, 87, 927–939. [Google Scholar] [CrossRef]
- Prakash, S.; Sathiyamoorthy, V.; Mahesh, C.; Gairola, R.M. An evaluation of high-resolution multisatellite rainfall products over the Indian monsoon region. Int. J. Remote Sens. 2014, 35, 3018–3035. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Rajagopal, E.N.; Pai, D.S. Assessment of TRMM-based TMPA-3B42 and GSMaP precipitation products over India for the peak southwest monsoon season. Int. J. Climatol. 2015, 36, 1614–1631. [Google Scholar] [CrossRef]
- Indu, J.; Kumar, D.N. Evaluation of precipitation retrievals from orbital data products of TRMM over a subtropical basin in India. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6429–6442. [Google Scholar] [CrossRef]
- Alemohammad, S.H.; McLaughlin, D.B.; Entekhabi, E. Quantifying precipitation uncertainty for land data assimilation applications. Mon. Weather Rev. 2015, 143, 3276–3299. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Bardossy, A.; Habib, E. Copula-based uncertainty modelling: application to multisensory precipitation estimates. Hydrol. Process. 2010, 24, 2111–2124. [Google Scholar] [CrossRef]
- Tian, Y.; Huffman, G.J.; Adler, R.F.; Tang, L.; Sapiano, M.; Maggioni, V.; Wu, H. Modeling errors in daily precipitation measurements: Additive or multiplicative? Geophys. Res. Lett. 2013, 40, 2060–2065. [Google Scholar] [CrossRef]
- Seyyedi, H. Performance Assessment of Satellite Rainfall Products for Hydrologic Modeling. Ph.D. Thesis, University of Connecticut, Storrs, CT, USA, 2014. [Google Scholar]
- Maggioni, V.; Sapiano, M.R.P.; Adler, R.F.; Tian, Y.; Huffman, G.J. An error model for uncertainty quantification in high-time-resolution precipitation products. J. Hydrometeorol. 2014, 15, 1274–1292. [Google Scholar] [CrossRef]
- Petty, G.W.; Krajewski, W.F. Satellite estimation of precipitation over land. Hydrol. Sci. J. 1996, 41, 433–451. [Google Scholar] [CrossRef]
- Anagnostou, E.N. Assessment of satellite rain retrieval error propagation in the prediction of land surface hydrologic variables. In Measuring Precipitation from Space: EURAINSAT and the Future; Levizzani, V., Bauer, P., Turk, F.J., Eds.; Springer: New York, NY, USA, 2007; pp. 357–368. [Google Scholar]
- Tian, Y.; Peters-Lidard, C.D.; Choudhury, B.J.; Garcia, M. Multitemporal analysis of TRMM-based satellite precipitation products for land data assimilation applications. J. Hydrometeorol. 2007, 8, 1165–1183. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. MSWEP: 3-hourly 0.25° global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. Discuss. 2016. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Mehran, A. Extended contingency table: Performance metrics for satellite observations and climate model simulations. Water Resour. Res. 2013, 49, 7144–7149. [Google Scholar] [CrossRef]
- Krishnamurthy, V.; Shukla, J. Intraseasonal and interannual variability of rainfall over India. J. Clim. 2000, 13, 4366–4377. [Google Scholar] [CrossRef]
- Li, J.; Zheng, Y.; Li, F.; Guo, F.; Li, W. The structural characteristics of precipitation in Asian-Pacific’s three monsoon regions measured by tropical rainfall measurement mission. Acta Oceanol. Sin. 2014, 33, 111–117. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Pai, D.S. Error characterization of TRMM Multisatellite Precipitation Analysis (TMPA-3B42) products over India for different seasons. J. Hydrol. 2015, 529, 1302–1312. [Google Scholar] [CrossRef]
Figure 1. Study area and geographical subregions chosen for the study. The subregions are: subregion a, southwest (11.5° N–21.5° N, 73.5° E–76.5° E); subregion b, southeast (8.5° N–16.5° N, 77.5° E–80.5° E); subregion c, central (20.5° N–26.5° N, 79.5° E–85.5° E); and subregion d, northwest (23.5° N–31.5° N, 71.5° E–76.5° E).
Figure 1. Study area and geographical subregions chosen for the study. The subregions are: subregion a, southwest (11.5° N–21.5° N, 73.5° E–76.5° E); subregion b, southeast (8.5° N–16.5° N, 77.5° E–80.5° E); subregion c, central (20.5° N–26.5° N, 79.5° E–85.5° E); and subregion d, northwest (23.5° N–31.5° N, 71.5° E–76.5° E).

Figure 2. Rainfall climatology for (a) all India; (b) central India; (c) northwest India; (d) southeast India; and (e) southwest India.
Figure 2. Rainfall climatology for (a) all India; (b) central India; (c) northwest India; (d) southeast India; and (e) southwest India.

Figure 3. Time series of annual accumulated rainfall over India from IMD and MSWEP datasets from 1979 to 2013 for (a) MAM; (b) JJAS; and (c) ON.
Figure 3. Time series of annual accumulated rainfall over India from IMD and MSWEP datasets from 1979 to 2013 for (a) MAM; (b) JJAS; and (c) ON.

Figure 4. Distribution of daily rainfall in different rainfall classes and their relative contributions to the total rainfall in different grids for monsoon season (June, July, August, September) (JJAS): (a) all India; (b) southwest India; (c) southeast India; (d) central India; (e) northwest India.
Figure 4. Distribution of daily rainfall in different rainfall classes and their relative contributions to the total rainfall in different grids for monsoon season (June, July, August, September) (JJAS): (a) all India; (b) southwest India; (c) southeast India; (d) central India; (e) northwest India.

Figure 5. Distribution of daily rainfall in different rainfall classes and their relative contributions to the total rainfall in different grids for the pre-monsoon season (March, April, May) (MAM): (a) all India; (b) southwest India; (c) southeast India; (d) central India; (e) northwest India.
Figure 5. Distribution of daily rainfall in different rainfall classes and their relative contributions to the total rainfall in different grids for the pre-monsoon season (March, April, May) (MAM): (a) all India; (b) southwest India; (c) southeast India; (d) central India; (e) northwest India.

Figure 6. Distribution of daily rainfall in different rainfall classes and their relative contributions to the total rainfall in different grids for the post-monsoon season (October and November) (ON): (a) all India; (b) southwest India; (c) southeast India; (d) central India; (e) northwest India.
Figure 6. Distribution of daily rainfall in different rainfall classes and their relative contributions to the total rainfall in different grids for the post-monsoon season (October and November) (ON): (a) all India; (b) southwest India; (c) southeast India; (d) central India; (e) northwest India.

Figure 7. Spatial distribution of higher quantile rainfall intensities over India using IMD precipitation data from 1979 to 2013: (a) JJAS (Q > 75); (b) JJAS (Q > 95); (c) MAM (Q > 75); (d) MAM (Q > 95); (e) ON (Q > 75); (f) ON (Q > 95).
Figure 7. Spatial distribution of higher quantile rainfall intensities over India using IMD precipitation data from 1979 to 2013: (a) JJAS (Q > 75); (b) JJAS (Q > 95); (c) MAM (Q > 75); (d) MAM (Q > 95); (e) ON (Q > 75); (f) ON (Q > 95).

Figure 8. (a–l) Spatial distribution of categorical indices for the JJAS months over India for daily and higher quantiles of precipitation using MSWEP and IMD daily precipitation data from 1979 to 2013 showing POD (a,e,i); VHI (b,f,j); FAR (c,g,k); and VFAR (d,h,l).
Figure 8. (a–l) Spatial distribution of categorical indices for the JJAS months over India for daily and higher quantiles of precipitation using MSWEP and IMD daily precipitation data from 1979 to 2013 showing POD (a,e,i); VHI (b,f,j); FAR (c,g,k); and VFAR (d,h,l).

Figure 9. (a–l) Spatial distribution of categorical indices for the JJAS months over India for daily and higher quantiles of precipitation using MSWEP and IMD daily precipitation data from 1979 to 2013 showing CSI (a,e,i); VCSI (b,f,j); MISS (c,g,k); and VMI (d,h,l).
Figure 9. (a–l) Spatial distribution of categorical indices for the JJAS months over India for daily and higher quantiles of precipitation using MSWEP and IMD daily precipitation data from 1979 to 2013 showing CSI (a,e,i); VCSI (b,f,j); MISS (c,g,k); and VMI (d,h,l).

Figure 10. (a–l) Spatial distribution of categorical indices for the ON months over India for daily and higher quantiles of precipitation using MSWEP and IMD daily precipitation data from 1979 to 2013 showing POD (a,e,i); VHI (b,f,j); FAR (c,g,k); and VFAR (d,h,l).
Figure 10. (a–l) Spatial distribution of categorical indices for the ON months over India for daily and higher quantiles of precipitation using MSWEP and IMD daily precipitation data from 1979 to 2013 showing POD (a,e,i); VHI (b,f,j); FAR (c,g,k); and VFAR (d,h,l).

Figure 11. (a–l) Spatial distribution of categorical indices for the ON months over India for daily and higher quantiles of precipitation using MSWEP and IMD daily precipitation data from 1979 to 2013 showing CSI (a,e,i); VCSI (b,f,j); MISS (c,g,k); and VMI (d,h,l).
Figure 11. (a–l) Spatial distribution of categorical indices for the ON months over India for daily and higher quantiles of precipitation using MSWEP and IMD daily precipitation data from 1979 to 2013 showing CSI (a,e,i); VCSI (b,f,j); MISS (c,g,k); and VMI (d,h,l).

Figure 12. (a–l) Spatial distribution of categorical indices for the MAM months over India for daily and higher quantiles of precipitation using MSWEP and IMD daily precipitation data from 1979 to 2013 showing POD (a,e,i); VHI (b,f,j); FAR (c,g,k); and VFAR (d,h,l).
Figure 12. (a–l) Spatial distribution of categorical indices for the MAM months over India for daily and higher quantiles of precipitation using MSWEP and IMD daily precipitation data from 1979 to 2013 showing POD (a,e,i); VHI (b,f,j); FAR (c,g,k); and VFAR (d,h,l).

Figure 13. (a–l) Spatial distribution of categorical indices for the MAM months over India for daily and higher quantiles of precipitation using MSWEP and IMD daily precipitation data from 1979 to 2013 showing CSI (a,e,i); VCSI (b,f,j); MISS (c,g,k); and VMI (d,h,l).
Figure 13. (a–l) Spatial distribution of categorical indices for the MAM months over India for daily and higher quantiles of precipitation using MSWEP and IMD daily precipitation data from 1979 to 2013 showing CSI (a,e,i); VCSI (b,f,j); MISS (c,g,k); and VMI (d,h,l).

Table 1. Contingency table for comparing MSWEP with IMD rain gauge data.
Table 1. Contingency table for comparing MSWEP with IMD rain gauge data.
| | Rain Detected by IMD (Yes) | No Rain Detected by IMD (No) | | | ----------------------------------- | ---------------------------- | ------------- | | Rain detected by MSWEP data (Yes) | Hit (H) | False (F) | | No rain detected by MSWEP data (No) | Miss(M) | Null event(T) |
Table 2. List of performance metrics used in the study.
Table 2. List of performance metrics used in the study.
| Serial No. | Performance Measure | Formula | ||
|---|---|---|---|---|
| 1. | Probability of Detection (POD) | H H + M | ||
| 2. | False Alarm Ratio (FAR) | H H + M | ||
| 3. | Critical Success index (CSI) | H ( H + M + F ) | ||
| 4. | Volumetric hit index (VHI) | ∑ i = 1 n ( M S W E P t | ( M S W E P t > t & I M D t > t ) ) ∑ i = 1 n ( M S W E P t | ( M S W E P t > t & I M D t > t ) ) + ∑ i = 1 n ( M S W E P t | ( M S W E P t ≤ t & I M D t > t ) ) |
| 5. | Volumetric False alarm ratio (VFAR) | ∑ i = 1 n ( M S W E P t | ( M S W E P t > t & I M D t ≤ t ) ) ∑ i = 1 n ( M S W E P t | ( M S W E P t > t & I M D t > t ) ) + ∑ i = 1 n ( M S W E P t | ( M S W E P t > t & I M D t ≤ t ) ) |
| 6. | Volumetric miss index (VMI) | ∑ i = 1 n ( M S W E P t | ( M S W E P t ≤ t & I M D t > t ) ) ∑ i = 1 n ( M S W E P t | ( M S W E P t > t & I M D t > t ) ) + ∑ i = 1 n ( M S W E P t | ( M S W E P t ≤ t & I M D t > t ) ) |
| 7. | Volumetric Critical Success index (VCSI) | ∑ i = 1 n ( M S W E P t | ( M S W E P t > t & I M D t > t ) ) ∑ i = 1 n ( M S W E P t | ( M S W E P t > t & I M D t > t ) ) + ∑ i = 1 n ( M S W E P t | ( M S W E P t ≤ t & I M D t > t ) ) |
Table 3. Statistics of daily rainfall over 1979–2013.
Table 3. Statistics of daily rainfall over 1979–2013.
| Region | Climatological Mean Rainfall (mm/Day) | Daily Rainfall Mean for Monsoon Season (mm) | Root Mean Square Error (RMSE) (mm) | BIAS (mm) | Correlation Coefficient (CC) | ||
|---|---|---|---|---|---|---|---|
| IMD | MSWEP | IMD | MSWEP | ||||
| All India | 3.135 | 3.3096 | 7.1615 | 6.9751 | 0.1788 | −0.049 | 0.8605 |
| Southwest | 3.5006 | 3.2336 | 8.7101 | 7.3426 | 0.1953 | −0.043 | 0.8625 |
| Southeast | 2.4082 | 2.6388 | 3.0937 | 3.2343 | 0.1890 | −0.055 | 0.8589 |
| Central | 3.114 | 3.3577 | 8.1905 | 8.596 | 0.1947 | −0.060 | 0.8690 |
| Northwest | 1.3716 | 1.5297 | 3.595 | 3.9681 | 0.1901 | −0.056 | 0.8628 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Nair, A.S.; Indu, J. Performance Assessment of Multi-Source Weighted-Ensemble Precipitation (MSWEP) Product over India. Climate 2017, 5, 2. https://doi.org/10.3390/cli5010002
AMA Style
Nair AS, Indu J. Performance Assessment of Multi-Source Weighted-Ensemble Precipitation (MSWEP) Product over India. Climate. 2017; 5(1):2. https://doi.org/10.3390/cli5010002
Chicago/Turabian Style
Nair, Akhilesh S., and J. Indu. 2017. "Performance Assessment of Multi-Source Weighted-Ensemble Precipitation (MSWEP) Product over India" Climate 5, no. 1: 2. https://doi.org/10.3390/cli5010002
APA Style
Nair, A. S., & Indu, J. (2017). Performance Assessment of Multi-Source Weighted-Ensemble Precipitation (MSWEP) Product over India. Climate, 5(1), 2. https://doi.org/10.3390/cli5010002
Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.
Article Metrics
Article Access Statistics
For more information on the journal statistics, click here.
Multiple requests from the same IP address are counted as one view.
We use cookies on our website to ensure you get the best experience.
Read more about our cookies here.