Passive Microwave Remote Sensing of Snow Depth: Techniques, Challenges and Future Directions (original) (raw)
Author / Affiliation / Email
Article Menu
/ajax/scifeed/subscribe
Font Type:
Arial Georgia Verdana
Open AccessReview
by
Srinivasarao Tanniru
RAAJ Ramsankaran
1
Hydro-Remote Sensing Applications (H-RSA) Group, Department Civil Engineering, Indian Institute of Technology Bombay, Mumbai 400076, India
2
Interdisciplinary Program in Climate Studies, Indian Institute of Technology Bombay, Mumbai 400076, India
*
Author to whom correspondence should be addressed.
Submission received: 28 November 2022 /Revised: 13 January 2023 /Accepted: 19 January 2023 /Published: 15 February 2023
Abstract
:
Monitoring snowpack depth is essential in many applications at regional and global scales. Space-borne passive microwave (PMW) remote sensing observations have been widely used to estimate snow depth (SD) information for over four decades due to their responsiveness to snowpack characteristics. Many approaches comprised of static and dynamic empirical models, non-linear, machine-learning-based models, and assimilation approaches have been developed using spaceborne PMW observations. These models cannot be applied uniformly over all regions due to inherent limitations in the modelling approaches. Further, the global PMW SD products have masked out in their coverage critical regions such as the Himalayas, as well as very high SD regions, due to constraints triggered by prevailing topographical and snow conditions. Therefore, the current review article discusses different models for SD estimation, along with their merits and limitations. Here in the review, various SD models are grouped into four types, i.e., static, dynamic, assimilation-based, and machine-learning-based models. To demonstrate the rationale behind these drawbacks, this review also details various causes of uncertainty, and the challenges present in the estimation of PMW SD. Finally, based on the status of the available PMW SD datasets, and SD estimation techniques, recommendations for future research are included in this article.
Graphical Abstract
1. Introduction
Snow cover is a critical component of the earth’s climate system, exerting both positive and negative impacts on human and natural ecosystems at various regional and local scales [1,2,3]. Snow and ice in their many forms collectively constitute distinct cryosphere components. Seasonal snow cover, together with permanent snow, constitutes the second-greatest component of the cryosphere, with an average aerial extent of more than 45 million square kilometres in peak winter [4,5]. Snow, with its very high albedo, affects the earth’s energy budget [6]. In addition, snow is an important water source for many water bodies. Knowledge of snow cover and its depth is required in many applications of meteorology, hydrology, and climate change studies, such as estimating seasonal runoff from streams [7,8], avalanche monitoring [9], global climate warming [10,11], etc.
Generally, in-situ measurements, air and space-borne remote sensing observations, and snowpack modelling approaches are extensively used for understanding the spatiotemporal snow depth information. In-situ measurements for snow depth are comprised of direct and indirect techniques. Direct techniques are invasive and rely on snow stakes and snow gauges for providing snow depth data, whereas indirect techniques such as observations from automatic weather stations, ultraviolet and gamma sensors, etc., are non-invasive and do not disturb the snowpack [12]. In-situ methods offer the most accurate observations for assessing snow depth, along with other physical characteristics such as snow density, snow grain dimension, etc. Automatic weather stations, snow gauges, snow stakes, ground-penetrating radar, and various other field equipment are commonly used in field investigations to measure and monitor snow depth, along with other physical attributes [13]. Though highly accurate observations can be made using these methods, the instrument’s calibration, field personnel, and methodology used can generate errors in the measurements. Inclement weather, complex terrain, lack of facilities, improper equipment maintenance, and risks such as avalanches all contribute to a decrease in the number of ground observation stations and field studies used for obtaining snow observations [14]. Further, many of the snow observatory stations are located over flat terrains that are shielded from wind and other turbulence, and are not representative of complex high mountain terrains. Snow cover and snow depth exhibit strong heterogeneity in both spatial and temporal scales, rendering the sparsely distributed existing snow monitoring network insufficient to adequately characterize snow depth variation at a larger scale [14,15,16,17]. These limitations, if not addressed, can potentially impact the usability of various hydrological and climate models. Different methods comprised of numerical and spatial interpolation schemes [18,19], unmanned aerial vehicle (UAV)-based techniques [20,21], space-borne remote sensing observations [22,23,24,25], and machine learning techniques [26,27], etc., are developed for estimating snow depth. The application of these techniques can greatly augment and complement the limited amount of ground observations available for snow depth.
Over the last four decades, space-borne remote sensing datasets have been used extensively to collect various types of snow data. Remote sensing can provide spatially and temporally continuous snow observations, and thereby can account for the spatial and temporal discontinuity issues present with the in-situ snow measurements [28]. Optical and infrared remote sensing datasets are mainly used for snow cover area and albedo. Inferences about snow depth with optical remote sensing are made using photogrammetric techniques and digital elevation model datasets over the region of interest [21,29,30,31,32]. However, because of the intrinsic properties of snowpack in the visible and infrared portions of the electromagnetic spectrum, optical remote sensing is not very effective in acquiring snow depth information. Further, optical remote sensing observations are hindered by cloud cover, weather conditions, and poor temporal resolution. Due to these limitations, the use of optical remote sensing data in estimating snow depth is rather constrained and is limited to augmenting other snowpack information (such as albedo, snow cover area, surface temperature, etc.) in different approaches of snow depth estimation. As opposed to visible and infrared energy, microwaves can penetrate snowpack and respond to its bulk properties, as well as to the variation in surface and subsurface aspects of the snowpack [33,34]. Thus, microwave remote sensing offers valuable insights on various snowpack properties such as snow density, snow depth, snow water equivalent, snow wetness, and so on [30]. Discernible sensitivity to snowpack characteristics, all-weather capability, worldwide coverage with good temporal resolution, and availability of a long archive of time series observations make passive microwave (PMW) remote sensing highly promising for researchers in various applications of the cryosphere.
Active microwave remote sensing (AMW) also offers valuable information for deriving snow depth at higher spatial resolution, which is highly useful, particularly in mountainous regions [35,36,37,38,39,40]. However, the revisit period of AMW sensors varies from 2 days to 14 days depending on the region. The smaller frequency bands present in the AMW satellites, such as C-band, L-band, and X-band, penetrate very deep into the snowpack and are less scattered if snow volume is less when compared to higher frequencies i.e., above 10 GHz [30,41,42,43]. Further, geometrical distortion, snow wetness, and weather factors affect the snow depth retrievals, as reported in several studies [36,39,44]. Thus, AMW has limitations in detecting the shallow snow depth. Though similar limitations i.e., saturation of signal in wet snow conditions and problems in very shallow and deep snowpacks, are present for PMW observations, the wide area coverage, large temporal archive of collected data, and numerous operational and planned satellites make PMW a preferable choice for the researchers for snow depth estimation.
The microwave radiation emitted from the earth surface can be scattered or occluded by interposed snow before it reaches the satellite sensor. The interaction of PMW radiation and its attenuation with the snowpack generally increases with the volume of the snowpack. Therefore, snow depth can be estimated using extinction characteristics of multifrequency PMW radiation observations. Initial models for snow depth estimation from spaceborne PMW data were developed in the mid-1980s using inversion schemes and radiative transfer modelling of observations [22]. Since then, many algorithms have been developed using PMW remote sensing for the estimation of snow depth and improving its accuracy and spatial resolution.
This article presents the scientific accomplishments and current advances in snow depth estimation using PMW remote sensing observations. Multiple review articles have previously explored the merits and drawbacks of various PMW techniques for estimating snow water equivalent (SWE), snow cover, etc. [45,46,47,48]. These reviews are mainly focused on the SWE rather than snow depth. Though reviews of PMW remote sensing of SWE can be related to snow depth due to the direct relationship between snow depth and SWE, relatively few papers have focused entirely on PMW remote sensing of snow depth. Many of the SWE estimation techniques reported in different studies require the knowledge of snow density [49,50,51,52,53]. However, there is a dearth of precise large-scale snow density information on both spatial and temporal scales. Consequently, many studies [22,54,55] have used constant snow density values, or values based on snow class [56] to estimate SWE. The dearth of snow density information, and inherent assumptions made with regard to grain size, snow class, etc., while developing SWE products can restrict the derivation of accurate snow depth information from SWE products. Nevertheless, snow depth is an important snowpack characteristic and is directly used in many applications, such as avalanche studies, climate change, estimation of melt discharge for snow fed streams, etc. Further, the existing review articles have provided little emphasis on issues that lead to uncertainties in PMW snow depth estimates. Therefore, the current article presents a detailed discussion on several important factors that contribute to the uncertainties in snow depth estimates from different approaches. Further, the recent advances in the snow depth models comprised of machine learning schemes, forward radiance models, and assimilation schemes and downscaling are appropriately discussed. To begin with, Section 2 summarises the theoretical foundations for using passive microwave remote sensing to determine snow depth and a short review of existing PMW datasets. Section 3 highlights distinct approaches for snow depth estimation that are classified based on model development. Section 4 reviews various globally used PMW snow depth products. Numerous critical aspects that contribute to the complexity and accuracy of the snow depth inversion are discussed in Section 5. Finally, the review concludes with presenting an overall summary and different recommendations for possible future research in Section 6.
2. Physical and Spectral Characterization of Snowpack in Microwave Wavelength Region for Snow Depth Inversion and PMW Missions
Microwaves can penetrate into snowpack and are least affected by the weather. Thermal microwave radiation exhibits unique interaction with snow which offers promising prospects for observation of various snow characteristics. The PMW response from a snowpack varies with the frequency of microwave. Further, the dynamically changing physical attributes of snowpack can result in a heterogeneous response from the snowpack under different conditions. The physical and spectral characteristics that are essential in understanding the PMW response of the snowpack, and required for the inversion of snow depth, are discussed in the following section.
2.1. Physical Characterization of Snow
The ice crystals deposited on the earth’s surface as a result of precipitation or wind will melt seasonally or remain throughout the year, resulting in the formation of temporary and permanent snow. Snow is primarily composed of ice particles, air, and liquid water. If snowpack temperature is less than 0 °C, generally liquid water content is absent, and snow is termed as dry. However, in saline conditions and regions where the temperature is slightly above 0 °C, water also coexists along with snow, resulting in wet snow. The dielectric properties of wet snow are significantly different compared to dry snow and affect the PMW response from a snowpack. Snow density typically varies between 0.1 to 0.6 kg/m3, with fresh snow having a density of 0.1 kg/m3. However, owing to metamorphism and internal adjustment of snow grains, the density increases as the snowpack matures. Snow grain size is another important physical characteristic of the snowpack that depicts the interior structure of snow. A typical snow grain size varies from 0.1 to 3 mm. However, an aged snowpack can exhibit inhomogeneous grain size distribution due to metamorphism caused by recrystallization. These physical properties strongly affect the interaction between microwaves and snowpack, and thereby impact the PMW response of a snowpack.
2.2. Spectral Characterisation of Snow
Microwave radiation has a spectral range of 0.1 to 100 cm (i.e., 300 to 0.3 GHz frequency) in the electromagnetic spectrum. According to Rayleigh’s principle, energy having larger wavelengths has very little scattering intensity. Clouds, fog, aerosol, and other gaseous molecules have a relatively tiny particle size compared to the microwave wavelength, resulting in less interference with the emitted microwave radiation. Hence, the atmosphere is nearly transparent in certain microwave parts of the electromagnetic spectrum, and less radiation is dispersed as a result of scattering interactions. These advantages make microwave sensors the most suitable choice for monitoring the emitted signal from earth surface objects under all weather conditions. PMW sensors detect the upwelling PMW radiation from the snowpack to generate a signal, which in turn is transformed to brightness temperature, and analysed further to retrieve various information.
Microwave emission from a snowpack typically consists of two major components, i.e., (1) emission from snow volume, and (2) emission from underlying ground. The emission from the snowpack and the underlying ground is recorded by the radiometers onboard various platforms in the form of brightness temperature (TB) in PMW remote sensing. Dry snow has low emissivity, hence the ground beneath the snowpack acts as a major source of PMW radiation. The physical basis for detection of snow with PMW radiation is characterized by intrinsic scattering of the snowpack, which is affected by snow grain distribution, snow thickness, particle size, and wetness, etc. In a snowpack, the dielectric properties of snow grains and the presence of liquid water have a significant impact on the propagation, scattering, and attenuation aspects of PMW radiation [57,58]. The study by Chang and others [59] using Nimbus-5 Scanning Multichannel Microwave Radiometer (SMMR) has provided early insights on the physical basis for determining microwave properties of snow. The snow grains were assumed to be randomly spaced spherical particles and cause non-coherent scattering. Moreover, the dimension of snow grains is typically comparable to various microwave wavelengths, hence Mie scattering theory can be applied for understanding the energy redistribution and scattering within a snowpack [59].
Depending on the condition of a snowpack, PMW radiation from the underlying ground is subjected to both volume scattering and absorption while it is passing through it. In dry snow, scattering is caused due to discontinuity in the dielectric properties of snow grains and air [33]. Hence, in dry snow for wavelengths comparable to grain size, internal volume scattering caused primarily by the snow grains takes place, resulting in reduced PMW emission. Whereas, at longer wavelengths such as 1.4 cm and above (18 GHz or less) there exists less interaction between snow particles and PMW energy regardless of the snow depth, resulting in increased transmission and higher emissivity. Snowpacks with more thickness and density consist of a higher number of snow grains and can attenuate more energy even at shorter wavelengths resulting in lesser emissions [60].
The brightness temperature of a snowpack for a given frequency decreases with an increase in snowpack thickness as shown in Figure 1. Hence, several inversion algorithms have used brightness temperatures (and brightness temperature differences) at different frequencies for the inversion of snow depth. Brightness temperature at longer wavelengths is generally used as a background against shorter wavelengths for retrieving snow depth in such algorithms [22,23,61]. However, the brightness temperature difference which is widely used in many empirical models saturates with an increase in snow density as shown in Figure 2. In case of wet snowpack, large particle size and the presence of liquid water cause attenuation of energy even at longer wavelengths resulting in significantly lesser penetration depth [60,62,63,64]. Depending on snowpack conditions i.e., liquid water content, density, snow grain shape, and size, etc., the penetration depth varies from 10 to 100 times the wavelength of the microwave. Thus, a 37 GHz (0.8 cm wavelength) channel of PMW sensors can penetrate close to 80 cm deep and SWE of approximately 250 mm in dry snow [65]. If snowpack depth is less than the microwave penetration the underlying ground affects the signal generated by the PMW sensor which causes difficulty in shallow snow estimation [66]. The sensitivity of PMW energy to snow depth and other snowpack characteristics motivated many researchers to develop various approaches for retrieving snow depth using PMW remote sensing.
2.3. Passive Microwave Remote Sensing Missions
The first spaceborne passive microwave experiments for earth observation were flown on the two Russian spacecrafts Cosmos-243, and 384, in 1968 and 1970, respectively [67]. Following those experiments, the Nimbus-5’s Electrically Scanning Microwave Radiometer (ESMR) which was onboard the Nimbus-5 (launched in December 1972), paved the way for more sophisticated missions later. ESMR has collected the observations at a frequency of 19 GHz and with horizontal polarisation. Nimbus-7 had a more sophisticated SMMR sensor, which collected data at five different microwave frequencies and in both horizontal and vertical polarizations. One of the primary objectives of the Nimbus mission was to provide observations for the monitoring and research of cryosphere components. Following Nimbus, many missions have provided useful observations for monitoring the cryosphere globally. The Defense Meteorological Satellite Programme (DMSP) accommodated Special Sensor Microwave/Imager (SSM/I) and Special Sensor Microwave Imager/Sounder (SSMIS) sensors and has provided data in four different microwave frequencies. The Advanced Microwave Scanning Radiometer for Earth observation (AMSR-E) and AMSR-2 mounted on the Aqua and GCOM-W satellites, respectively, are more advanced compared to their predecessors and have provided observations in fourteen channels operating at seven different frequencies. Key characteristics of different PMW sensors onboard various satellites from few selected missions, and a timeline of various PMW satellites are mentioned in Appendix A (See in Table A1, Figure A1). More PMW missions and their detailed sensors information is available to the readers in the portal (http://database.eohandbook.com/database/missiontable.aspx, accessed on 10 November 2022) and are not shown in the current review.
3. Snow Depth Estimation from PMW Observations
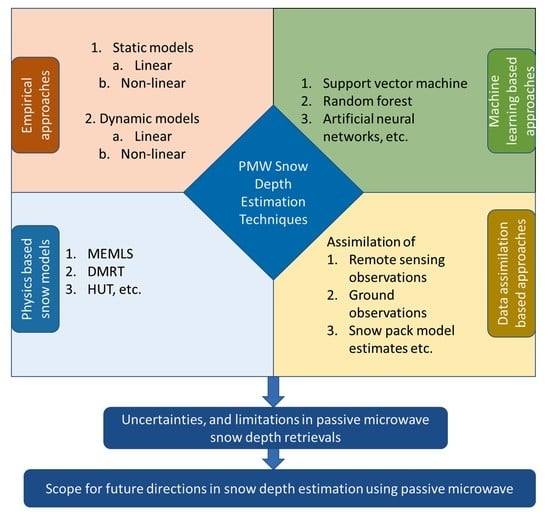
Significant progress has been made in the PMW estimation of snow depth since the launch of Nimbus-5 in 1972. With the growing archive of time series PMW data from a wide range of microwave instruments, researchers have developed various approaches for retrieving and improving snow depth estimates. Different approaches adopted by various researchers consist of linear and non-linear empirical models, semi-empirical models, physics-based models, models based on a priori information and statistics, etc. These methods adopted by the researchers are categorized into four main types, as shown in Figure 3, and are discussed in the current review article.
Despite the development of several techniques, much uncertainty prevails in the snow depth data retrieved from PMW due to the coarse footprint of the PMW instruments, the complex relationship between snowpack characteristics and microwaves, and limitations in the algorithms’ approaches. Some of the recent approaches, along with the most commonly used models for estimation of snow depth based on the PMW radiometry, are grouped into four categories and presented in Section 3.1 to 3.4. In Section 3.5, different approaches for downscaling of PMW snow depth are discussed. An overview of different types of snow depth estimation models is given in Table 1.
3.1. Static Linear and Non-Linear Inversion Algorithms
Different inversion models, ranging from simple to complex, have been developed to establish the relationship between PMW observations, topographic variables, and snow depth. Simple empirical models are developed based on the choice of various combinations of PMW brightness temperature difference between lower and higher frequencies as the independent variable to estimate snow depth. Other models have used combinations of several brightness temperatures and their differences, along with the topographic variables such as elevation, land-cover, etc., with different model coefficients in different schemes for retrieval of snow depth.
Static linear algorithms are very popular due to their simplicity and have been extensively used since the 1980s for various regional and global studies by researchers across the world. These models were developed based on the philosophy that PMW emissivity observed from a snowpack at various frequencies is sensitive to snow depth. Many static models [22,23] were developed by performing regression analysis between the recorded snow depth from ground stations and PMW brightness temperature difference (BTD) of various frequencies. Early insights on the importance and sensitivity of TB at 19 GHz and 37 GHz in retrieving snow depth were reported by [68,69]. The temperature gradient between multiple microwave frequencies was widely used for the inversion of snow depth. Chang and others (1987) [22], demonstrated a brightness temperature gradient approach for Nimbus-7 SMMR data, which was widely adopted, modified, and evaluated for other PMW platforms, as well as by many researchers [23,66,70,71]. Chang’s (1987) model [22] employed regression between in-situ snow depth and BTD from horizontally polarized 19 GHz and 37 GHz frequency observations for inversion of snow depth. The general form of the statistical relation used in brightness temperature gradient models for snow depth formulation is given in Equation (1).
where SD = snow depth, BTD = Brightness temperature difference between the selected frequencies and, a = slope coefficient (cm/K), c = offset constant (mm).
Table 1. Overview of different types of models for estimating snow depth.
Table 1. Overview of different types of models for estimating snow depth.
| S. No. | Type of Model | Modelling Approach | Studies | Observations |
|---|---|---|---|---|
| 1 | Static Empirical models (Linear and Non-linear) | Static models use a fixed relationship between snow depth and model variables. | [22,23,65,72,73,74] | Linear and non-linear models are used for representing the relationship between snow depth and PMW TB, with other factors. Many models used static values of snow density, grainsize while formulating the snow depth model. The performance of models is mainly constrained to study region. |
| 2 | Dynamic models | Dynamic models use a varying relationship between snow depth and model parameters. | [66,75,76,77]; | These models adopted dynamic values of different model parameters such as regression coefficient, snow grain size, snow density, etc., for estimation of snow depth. Look-up tables are developed for dynamic approaches in few studies. |
| 3 | Semi-empirical and physically based models | The physical relation between various snowpack characteristics is taken into account using different snow emission models such as MEMLS, HUT, DMRT. | [64,78,79,80]; | Depending on data availability, requirements, either semi-empirical or fully physical snow emission models are used for forward simulation of TB, and estimating snow depth. |
| 4 | Non-linear models based on machine learning | PMW data and other various observations used for training the models using different machine learning and deep learning frameworks. | [26,27,81,82,83,84,85]; | Due to naive representation of relationship between snowpack characteristics, the transferability and reliability of developed models is always a concern. |
| 5 | Data assimilation models | Assimilation models use or provide a framework for integrating variety of data such as in-situ, remote sensing, model simulations data, etc., from different sources. | [86,87,88,89,90,91,92,93] | Different types of snowpack parameters are assimilated into LSM models such as CLSM, SSiB for snow depth estimations. The estimates rely mainly on the forcing parameters of LSM. The limitation of these approaches is: the observed climatological and weather forcing parameters are often not available in many places and not consistent on varying scales. |
In a BTD approach, TB from a longer wavelength (ex:19 GHz frequency) offers an unattenuated response, while the TB from a shorter wavelength (ex: 37 GHz frequency) provides an attenuated response. Many simplified models have considered constant density and grain size while estimating snow depth. Chang’s popular model (1987) [22] (given in Equation (2)) was developed assuming the snow density at 300 kg/m3 and snow grain size as 0.3 mm. However, these parameters can have high spatio-temporal variation resulting in uncertainties in model estimates at different regions. However, as density increases, the BTD saturates, limiting the potential utility of such static models (for example Chang’s model) as given in Figure 2. As a result, Chang’s model, and many other similar models with snowpack generalizations have shown decent performance at the regional level for which the model was developed. However, poor results have been observed outside the model region, in mountainous areas and forest regions, where snowpack characteristics can be more heterogenous and differ from model assumptions.
SD = 1.59 × TB 18 H − TB 36 H cm
(2)
where TB18H, TB 36H denote the horizontally polarized brightness temperatures (K) at 18 and 36 GHz
The coefficient value of 1.59 considered in Chang’s model [22] as given in Equation (2) is applicable only when snow grain size is 0.3; if snow grain size becomes 0.4, the coefficient value changes to 0.78 [23]. Further, the interception of signal by forest cover is considered by Foster [23] while estimating snow depth, as given in Equation (3).
SD = a × TB 18 H − TB 36 H cm 1 − f c
(3)
where fc = fractional forest cover, a = coefficient (1.59 or 0.78 depending on the grain size, i.e., 0.3 or 0.4, respectively).
Therefore, it is very difficult to develop a single algorithm for snow depth that provides satisfactory performance at the global level; hence, several regional level snow depth models have been developed by various researchers [66,77,94]. Che and others [66] have improved Chang’s model [22] by accounting for the effects of rain, wet snow, vegetation, frozen ground, etc., by using various brightness temperature filters. The coefficients in Chang’s model are calibrated separately for SMMR and SSM/I data, and temporal offset corrections are carried out according to the snow conditions of China region [66]. Their study results show that 65% of the estimated retrievals have absolute error of less than 5 cm. In algorithms which rely only on brightness temperature difference, the effect of physical temperature of the snowpack can be neglected due to signal difference (i.e., subtraction of brightness temperature). However, the saturation effect of microwave signal cannot be alleviated. Saturation of 19 GHz radiation in the deep snow was reported in various studies [95,96,97] which can result in underestimation of snow depth at many places. To account for this limitation, a few researchers have investigated the utility of TBs at additional PMW frequencies (ex: 10 GHz) with different combinations [98] in spectral gradient algorithms. Because of the coarse resolution of PMW observations, many times, pure snow pixels are not present and hybrid land covers features; for example, snow and forest often coexist in a single pixel. In forested regions, PMW emission from snow is overwhelmed by the radiation from forest canopies resulting in underestimation of snow depth [10,23]. Several algorithms have been developed to account for the forest cover present within the coarse PMW pixel [23,65,70]. Jiang and others [70], have developed different regression models based on land-cover type using multifrequency BTD and snow depth. In another approach, Jiang and others [54] have used linear unmixing method to account for the effects of different types of vegetation while deriving SD. In [54], SD for a pixel with different land-cover classes is obtained by combining weighted SD of each land-cover class calculated using empirical approaches. The SD is then converted into SWE using a density value of 180 kg/m3.
Though linear algorithms are widely popular, the potential of static non-linear algorithms has also been examined in few studies [73,74,99]. In the multifactor approach in addition to in-situ snow depth and PMW data, multiple ancillary information such as topographic data, land-cover data, and location details were used for estimating snow depth. Various multifactor linear and non-linear empirical models are compared in different studies [73,74,99] over Tibetan plateau. The results of these studies [73,74,99] indicate that non-linear regression models developed using logarithmic, exponential and power functions have shown better performance over linear models when multiple factors were considered.
3.2. Dynamic Models
Static models consider snow characteristics such as snow density and grain size to be constant over the entire space and snow season. Thus, the primary limitation of the static approaches is that they do not account for the sensitivity of snowpack emission to variation in other snowpack characteristics such as density, grain size, underlying ground temperature, etc. Due to these limitations, the model’s performance was not uniform across different locations and is generally constrained to render the specific locations/regions for which the model was built [22,61]. These limitations have been addressed to a certain extent by implementing dynamic models which treat snowpack as a scattering medium with varying complexity.
Dynamic models for snow depth estimation are developed by integrating snowpack microstructure information (such as density, grain size, etc.) derived from different sources using empirical/semi-empirical snow emission models, data assimilation techniques, etc. [71,74,87]. Section 3.2.1 and Section 3.2.2 outline how empirical and semi-empirical/physical approaches were utilized to develop dynamic models. Section 3.3 and Section 3.4 discuss assimilation strategies and machine learning models, respectively, in detail.
3.2.1. Dynamic Models Built upon the Empirical Methods or Statistical Analysis
There are multiple factors that vary dynamically and impact the PMW response of snowpack affecting the accuracy of snow depth retrievals from the model. Many of the dynamic snow depth models tried to account for variation in vegetation and grain sizes at different regions. Grain size metamorphism in a snowpack is mainly controlled by the aging of snowpack and changes in the bulk temperature gradient.
In very cold regions where soil temperature is higher than the outside air temperature, thin snowpacks will often have a higher temperature gradient than the thick snowpacks, causing rapid grain size metamorphism (crystal growth) in thin snow [75]. This leads to saturation of shorter wavelength TB, resulting in increased spectral gradient. Josberger and Mognard [75] have observed an increase of TB spectral gradient even when there was no change in snow depth, which can result in the overestimation of snow depth in regular empirical models. The temperature gradient index (TGI) approach is a dynamic model proposed by [75] which makes use of time series smoothened air temperature and spectral gradient of TB (19H and 37H GHz) from SSM/I to estimate snow depth. TGI represents the cumulative effect of the bulk temperature gradient on the snowpack throughout the season, as given in Equation (4). The TGI model accounts for potential grain size metamorphism using the relationship between air temperature and BTD, and thereby estimates snow depth.
TGI = 1 C ∫ 0 t T g − T air SD t dt
(4)
where Tg = Temperature of soil under snowpack, Tair = air temperature, SD(t) = snow depth at time (t), and C = scaling constant (20 °C/m).
TGI is related to brightness temperature difference, which then is used for formulating snow depth model as given below.
BTD 19 , 37 H = ∝ TGI + β
(5)
where BTD19,37H = brightness temperature difference between 19 and 37 GHz, and (α, β) are model coefficients. Substitution of Equation (4) in Equation (5) allows snow depth to be obtained.
SD t = α T g − T air C dBTD dt
(6)
However, the TGI model is valid only for conditions where air temperature is below 0 °C (typically, winters), and ground temperature is higher than air temperature. Further, the model cannot be used if BTD is not varying temporally, as the temporal derivative of BTD is present in the denominator of Equation (6). The TGI model is extended by combination with a static model developed by Grippa and others [100]. In [100] the daily SSM/I TB data is averaged over pentads (5-day period), which then is used to calculate the daily BTD over the Northern Greater Plains of the United States. Until the BTD reaches 1 K/pentad, the model given in Equation (6) is used to estimate snow depth for a given pixel. At the time of transition, i.e., when BTD rate becomes less than 1 K/pentad, instead of the TGI model (in Equation (6)), a static model (in Equation (2)) is used for extending the snow depth estimation temporally. In the static snow depth model, a coefficient of 1.59 is used while determining snow depth for all pixels. However, in [100] for each pixel, a coefficient value is calculated using the TBD, and SD observed at the time of transition (i.e., when the BTD < 1 K/pentad) using Equation (7). This coefficient is used in static snow depth model (in Equation (2)) instead of 1.59 for estimating snow depth.
a = SD t TBD 19 , 37 H
(7)
Kelly and Chang [76] have used a dynamic approach which again was built upon the static empirical model [22] for estimating snow depth at a global level. Their study used regression coefficients of several independent stations with a semi-variogram to obtain model coefficients for other regions. The dynamic model by Kelly and Chang [76] also considers the bias generated due to forest-cover fraction to improve the snow depth estimates. Another dynamic model was developed by Kelly [24], one which uses multifrequency PMW observations for detecting snow, and then distinguishing shallow and deep snow for estimating snow depth. Dynamic coefficients are used for accounting seasonal grain size variation, which can lead to overestimation, particularly in shallow snow depth regions. Then, snow depth is estimated using a weighted sum of forest and non-forest regions, as given in Equation (8).
SD = ff × p 1 × ( TB 18 V − TB 36 V ) 1 − 0.6 × fd + 1 − ff × p 1 × ( TB 10 V − TB 36 V + p 2 × ( TB 10 V − TB 18 V ) ]
(8)
where ff = forest cover fraction; fd = forest density; p1, p2 = dynamic coefficients; and TB10v, TB18v, TB36v = vertically polarized PMW brightness temperatures at 10, 18, and 36 GHz, respectively.
3.2.2. Dynamic Models Based on Semi-Empirical, and Physical Models
Many statistical dynamic approaches require in-situ data for development of snow depth model. However, this can be a constraint in data-scarce regions. Further, the seasonal snowpack evolution affects the interlayer scattering of microwaves at different frequencies leading to inconsistency in the accuracy of temporal snow depth estimations. These limitations can be addressed to certain extent by implementing statistical and other approaches developed with help of physically-based snowpack emission models, and land surface modelling schemes using the radiative transfer theory, etc. Depending on the snow emission model, the configuration of the snowpack can be treated as a single layer [78,79] or multiple layers [64,80,101]. Snowpack emission models are capable of generating PMW response of a snowpack by considering the volumetric scattering, and the scattering at snow-ground and snow-air interfaces. Each emission model is comprised of its own snow microstructure parameterization, a scheme for solving radiative transfer equation, and a scheme for representing microwave scattering, emission, and attenuation within the snowpack.
Various snow emission models, such as the Helsinki University of Technology Model (HUT) [78], the Microwave Emission Model for Layered Snowpacks (MEMLS) [64], and the Dense Media Radiative Transfer Model (DMRT) [79,80], etc., were developed to forward modelling of snow emission for different snow conditions. These models are semi-empirical (e.g., HUT and MEMLS) or completely physically based (e.g., DMRT) in nature and consider contributions from snow, underlying soil, vegetation, and atmosphere for simulating the brightness temperature of snowpacks. Further, these models have allowed for the representation of snow as a multi-layered medium with diverse characteristics in each layer ([64,101], unlike the empirical snow depth models where snow was considered as a single homogeneous layer. Distinct schemes such as six-flux theory [64], two-flux approximation [78], etc., were employed within the models for solving the radiative transfer equation following the theoretical basis to simulate the microwave response for different snowpack conditions.
Multiple studies have been carried out by integrating existing snow information as forcing data to drive various snow emission models such as HUT and MEMLS for developing dynamic models [27,71,102,103]. A dynamic snow depth inversion algorithm was proposed by Wei and others [74], one developed over northeast China using AMSR-2 data and the MEMLS model. Snow characteristics collected from the field observations are used as inputs for MEMLS model to simulate TB of 18 and 36 GHz of both polarizations, which are used for calculating dynamic coefficient (in Equation (9)).
C M = BTD 18 , 36 H SD
(9)
where CM = dynamic coefficient for a given snow depth (SD) observation, and BTD 18,36H = the difference between horizontally polarized TB of 18 and 36 GHz.
The dynamic coefficients thus retrieved (using Equation (9)) and vertically polarized brightness temperatures are then used to formulate the empirical dynamic coefficient and snow depth models as given in Equations (10) and (11), respectively. The dynamic coefficient accounts for variations in snow particle size and density. In case of vegetation-covered pixels, the BTD was weighed with forest cover fractions to improve snow depth approvals from this approach [74]. The dynamic approach by Wei and others [74] has given improved snow depth estimates with RMSE of ~10 cm vs. ~31 cm of operational AMSR-2 SD product over China.
BTD 18 , 36 V = 10 C M
(10)
By combining Equations (9) and (10), snow depth can be estimated as:
SD = BTD 18 , 36 H log 10 BTD 18 , 36 V
(11)
In few studies, the MEMLS model was used to establish lookup tables for inversion of snow depth [77,102,104]. In lookup table approaches, the observed PMW brightness temperature data are compared for a match with the model simulated brightness temperatures to identify the snow depth. Dai and others [77] proposed to use the lookup tables generated on daily basis from MEMLS using the priori characteristics (i.e., snow stratigraphy, density, and grain size from meteorological stations) for snow depth estimation over Xinjiang, China. Ref. [104] have used snow survey data collected over northeast China from December 2017 to January 2018 to obtain the average estimates of snow grain size, density, snow temperature, etc. This data was used in the MEMLS model for creating lookup tables for accumulation, stabilization, and ablation phases of snow in order to estimate snow depth. These approaches [77,104] have shown lesser RMSE, MAE errors compared to Chang model, and AMSR-2 snow depth product over China.
The HUT model has been used in various assimilation schemes and dynamic models for improving the snow depth estimates. A localized HUT model, and Fengyun-3 microwave radiation imager (MWRI) data are used to invert snow depth over China using a genetic algorithm approach [103]. The extinction coefficient of HUT was modified using an empirical equation to suit the local region. Results from the study indicate that the localized model has shown better performance in simulating snowpack response than the default HUT model. DMRT model is adopted in inversion of snow depth and SWE in various studies [76,105,106,107,108].
A prototype global snow depth algorithm for AMSR-E was proposed by Kelly using a DMRT model and SSM/I data [76]. In their study, average snow grain radius and density were determined with empirical models using kinetic temperature information. The observed ranges of variation in grain size and density are considered while giving inputs to a DMRT model for simulating brightness temperatures at 19 and 37 GHz. A polynomial model (given in Equation (12)) using the brightness temperature difference of 19 and 37 GHz was developed from the TB simulations, where the coefficients are dependent on grain size and snow density. Their results [76] indicate that the average bias in the estimations~(−2 to −6 cm) is reduced compared to Chang’s static snow depth model~(−6 to −11 cm) [22]; however, the large errors are more, which resulted in a higher RMSE error of ~(20–23 cm) compared to Chang’s model~(16 to 18 cm).
SD = b ( Δ TB ) 2 + c Δ TB cm
(12)
where b and c are empirical coefficients which varies based on grain size and snow volume fraction.
The above dynamic approach [76] is improved [105], where instead of polynomial fit a lookup table derived from DMRT is adopted. The method used a difference optimization scheme in which five-day Gaussian moving averages of AMSR-2 TB, and DMRT model TB are used as inputs for inversion of snow depth [105]. The results from their study [105] indicate that the DMRT-based model has provided improved snow depth estimates, with an RMSE of ~21 cm, more accurate than an AMSR-2 product’s ~30 cm, when compared with Canadian Meteorological Centre’s (CMC) daily snow depth dataset.
Overall, these studies have demonstrated that the integration of fully physical or semi-empirical models such as DMRT, MEMLS, and HUT in snow depth modelling approaches can result in improved performance. These approaches, despite their complexity, are more capable of accurately representing the microwave response of a snowpack. However, the limitation in snow depth estimation due to the saturation of PMW radiation with increasing snow depth, grain size, and wetness cannot be alleviated. Further, many of the approaches have considered the snowpack as a single layer with snow depth, density, and grain size as the variables, while keeping the other snowpack characteristics constant due to insufficient data, limiting their full potential. Thus, these approaches also have limitations in retrieving accurate snow depth estimates.
3.3. Models Based on Data Assimilation
The snow depth retrievals from many PMW approaches have significant uncertainty because of the approximations that are made in their retrieval schemes. Different models employ different approaches to reduce the uncertainty and gap between actual and estimated snow information. Different types of information, such as vegetation, meteorological station information, terrain information, etc., were added with remote sensing data in a number of models to enhance the accuracy of snow depth estimates. Land Surface Models (LSM) make use of energy balance approaches to simulate snowpack accumulation and melt, and therefore can provide valuable information related to snow depth [86,89,109,110]. However, inaccuracies can prevail in the snow depth estimates resulting from the uncertainties present in input datasets, models’ inherent structural error, improper parameterization (for example, in MEMLS, HUT, and DMRT models). Data assimilation techniques provide a framework for the effective utilization of available PMW data, auxiliary snow and topographical information for reducing uncertainty in different snow depth estimation models, thereby improving estimates. Assimilation approaches enable the models to take advantage of statistical and physical based techniques by combining various in-situ, or remote sensing observations and improve the output by a balanced combination of model states and observations as a function of their uncertainties. The data assimilation approach alleviates the models’ uncertainty by optimally ingesting the PMW data and other auxiliary information before estimating the model fluxes i.e., snow [89,111,112,113] in the present context.
Different assimilation approaches used in the snow modelling studies can be classified for the most part into two categories, i.e., variational and sequential approaches [114]. In the sequential approach, observations are assimilated into the model sequentially at each time step, i.e., as and when they become available. Whereas, in the variational approach, a time window is fixed and all the observations lying within this time window are assimilated together to adjust the model’s initial condition, boundary condition and parameters. By doing so, the overall model trajectory will move closer to the observations (in essence, the true state). Direct insertion [115,116,117], optimal interpolation [118], Kalman Filter (KF) and its extensions [89,90,112,116,119,120], particle filter (PF) and its extensions [110,121,122], etc., are some of the widely used data assimilation approaches in improving snow depth estimations. In a study by Revuelto and others [117], snow depth maps derived using terrestrial laser scanner are directly inserted to improve snow depth estimations, and snow melt timing over a Spanish catchment. However, a direct insertion method considers the assimilated variables as being perfect without analysing the observation and model errors and their mutual relationship. Hence, other sophisticated assimilation schemes such as Extended Kalman Filter (EKF), Ensemble Kalman Filter (EnKF), and PF are explored to improve snow depth and SWE in various snow studies [90,110,116,121,123]. The sophisticated approaches, i.e., EKF, EnKF, PF, etc., consider the uncertainty in observation and model values.
Many assimilation studies were carried out globally using PMW datasets, and LSMs such as the Biosphere–Atmosphere Transfer Scheme (BATS), Simple Biosphere (SiB),Noah model, etc., for snow depth estimation at various scales [89,90,109]. Space-borne remote sensing observations such as PMW TB data, surface reflectance, snow cover data, etc., snow emission model observations, and in-situ observations such as snow depth, grain size, land cover fractions, etc., are widely used for assimilation in different studies to improve snow depth [55,74,87,90]. Different objectives of data assimilation in PMW snow depth research are: (i) enhancing the accuracy of snow depth estimates and (ii) improving the resolution of PMW snow depth.
Assimilation of ancillary information about the snowpack can improve PMW snow depth models estimates, as reported in several studies [86,87,89,124]. Depending on the nature of inputs, additional tools/models, and the number of calculations required assimilation schemes can be simple or very complicated. Regression approaches offer relatively simple schemes for combining various ancillary information into the model for snow depth estimation [87]. Tedesco and others [87] presented three different approaches for assimilation of meteorological snow depth data with SSM/I PMW observations. Two approaches use dynamic regression models, while the third model uses the outputs of the NASA catchment land surface model (CLSM) and HUT simulations with PMW data. The regression coefficient in the first dynamic model was adjusted once-weekly by relating snow depth observations with PMW observations. In the second model, the seasonal average of regression coefficient was computed and used for snow depth estimation. In the third approach, the daily estimates (i.e., snow density, snow temperature) from the LSM were used as an input to the HUT model for simulating TB. The snow grain size used in the HUT model was updated periodically by minimizing the difference between the modelled and observed TB data. Between the update periods, snow depth was estimated by minimizing the difference between simulated and observed TB. The evaluation results indicated that regression models have better performance as compared to the emission model-based approach [87].
Ref. [125] presented an assimilation approach for snow depth and SWE estimation over boreal and arctic zones of Eurasia and Finland. Brightness temperature data obtained from forward modelling of the snowpack using HUT were related with observed spaceborne TB data in an iterative error minimization scheme to retrieve the snow grain size. The study [125] adopted a Bayesian optimization scheme for assimilation of SSM/I and AMSR-E TB data, interpolated reference snow depth information obtained from observation stations, and snow grain radius from the HUT model. The results indicate a considerable improvement in assimilation model estimates compared to interpolation estimates in over 60% of the investigated 3300 cases in northern Eurasia.
Radiance assimilation approaches are implemented in different studies, where microwave snow emission models and snowpack evolution models are combined using a probabilistic framework to derive improved snowpack estimates [89,90,91,125]. Space borne PMW TB observations are assimilated into snow evolution models and snow modules of land surface models (LSM) in radiance assimilation. Assimilation of radiance data in a land surface model can improve snow depth estimates depending on snow parameterization used for retrieving snowpack variables [89,109,123,126]. Snow-state vectors i.e., snow depth, density, grain size, temperature obtained from LSM were used as inputs to snow emission models to predict the PMW radiance in a forward modelling scheme. Further, techniques such as ensemble Kalman Filter (EnKF) and Bayesian optimization were used to minimize the difference between observed and predicted PMW radiance from models (ex: MEMLS, HUT, DMRT) and update the LSM models in different studies to improve the predictions of snow states which includes snow depth [89,90,91]. A decrease in the accuracy of retrieved snow depth in the ablation period was reported by [89]. Further, continental and global scale assimilation studies [90,127] indicate large uncertainties in estimates particularly in data sparse regions leaving the scope for further improvement.
Though data assimilation approaches provide a robust framework for improving snow depth estimates, significant problems still persist and require enhancement [128]. The temporal inconsistency and scale mismatch between a sparse network of assimilated in-situ point observations, and modelled snow depth is one such problem, particularly in case of mixed land-cover grids and complex mountain terrains. Assimilation techniques comprising LSM, PMW data, and ancillary information in a machine learning framework have recently been reported in the literature [92,93]. Machine learning schemes such as Artificial Neural Network (ANN), Support Vector Machine (SVM), and Random Forest (RF) were used for combining optical, PMW remote sensing datasets and ancillary information for obtaining snow depth estimates in various studies [27,81,83,129]. Additional case studies and observations related to machine learning are presented in Section 3.4.
3.4. Non-Linear Models Based on Machine Learning
The advancement of machine learning has given rise to a new direction in the research of various fields of earth sciences, and the early results of such studies seem highly promising. With the availability of large amounts of data, artificial intelligence and machine learning based techniques have become very important drivers in various environmental and climate related remote sensing applications, along with the cryosphere. Machine learning methods do not require knowledge about the physical process which is being modelled and accomplish their results by learning and generalizing the knowledge formed from the training data of respective problems.
In the current review, we have reported various studies demonstrating the utility of three widely used machine learning techniques, ANN, SVM, and RF in snow depth estimation. The merits and limitations of these methods over different static and dynamic algorithms are also presented.
3.4.1. ANN-Based Snow Depth Estimation
ANN is a machine learning technique that has the potential to identify the non-linear pattern existing in the data. ANN is composed of one or multiple layers of nodes (i.e., neurons) depending on the model architecture. These nodes are connected through weighted links, the weights of which keep updated as data from input nodes traverse to the output node during the training phase. The trained ANN model is used for predicting the outputs. Many studies have explored ANN of different configurations for the estimation of snow depth and related products at various regional and continental scales [81,130,131,132,133]. Some early studies have demonstrated the usefulness of ANN in snow science in inverting snow attributes such as snow grain size, snow depth, and snow density from PMW data using an ANN model trained from various input and output combinations of the DMRT model [134,135]. Tedesco and others [132]., have reported a study where the ANN model was trained with values from an HUT model for estimation of snow depth. The ANN method has delivered improved estimates compared to linear algorithms i.e., Chang’s model [22] and the Spectral polarization difference (SPD) model [132]. ANN was used in snow grain estimation for the development of AMSR-2 SWE product [81]. Cao and others [130] have reported improvement in snow depth estimates by integrating Bayesian optimization in an ANN scheme comprised of AMSR-E TB data and in-situ data. PMW TB observed from a sensor are sensitive to various snow characteristics [136]; hence, training an ANN model with TB alone may not provide reliable results. Further, it is important to validate the performance of ANN model to the sensitivity of different snow parameters, as the model’s ability to generalize outside (heterogeneous conditions) the training data is not reliable [137]. The limitation of ANN is it doesn’t consider the physics behind the input and output variables and works as a black-box model from outside. Though the ANN technique has the potential to improve snow depth estimates, the type of ANN network and training scheme (i.e., input data, hyperparameters, etc.) adopted in the methodology can have a significant impact on snow depth estimation [131,133]. Depending on how the training is conducted to the model, ANN can get stuck in local optima, or sometimes overfit the training data, making model predictions unreliable outside the training sample.
3.4.2. SVM-Based Snow Depth Estimation
SVM is a supervised machine learning technique that can be used for solving both classification and regression problems in various fields. SVM regression (hereafter referred to as SVM) uses the concept of hyperplane for fitting a model to the data represented in an n-dimensional plane. SVM is widely used in estimating snow depth across various studies [26,83,84]. Visible and near-infrared radiation is sensitive to snow grain size. Improvement in snow depth retrievals was reported when TB data was integrated with surface reflectance data in an SVM framework [83]. Ref. [26] implemented the SVM approach for retrieving snow depth at a larger scale (over Eurasia). The study [26] used SSM/I and SSMIS TB data (19, 37, and 87 GHz) of both polarizations, in-situ snow depth observations, MODIS land-cover data, elevation data, and various auxiliary information as inputs for constructing 24 different SVM models based on different snow phases (i.e., accumulation, stabilization, and ablation) and land-cover. The results of different studies indicate that both SVM and ANN have outperformed other linear models such as Chang model, SPD model, and linear regression in retrieving snow depth with better sensitivity to deeper snow; however, SVM has performed better than ANN [26,83]. Further, the potential of SVM was also investigated in snow depth downscaling and assimilation studies [85,92,129,138,139]. Though SVM has improved performance over ANN in few studies, the random nature of data sets and the type of training adopted can greatly impact the performance of the methods, and the results can vary from one region to another. The SVM model performs poorly with imbalanced data and is sensitive to the outliers, hence exploratory data analysis, and feature engineering are essential for developing the ML model.
3.4.3. Random Forest-Based Snow Depth Estimation
RF is a machine learning approach where predictions from multiple decision trees are aggregated into a single prediction in a systematic framework defined by the rules of the algorithm. Due to the simplicity, many studies have explored the potential of RF in various applications including SD estimation [27,85,140,141,142]. Using several input variables which have correlation with snow depth, machine learning techniques to a certain extent can account for the heterogeneity associated with the snowpack of a given depth. Yang and others have conducted few studies over China [27,142] which have demonstrated the ability of RF algorithms in snow depth estimation. Ref. [142] used SSM/I data, land cover, elevation, and other information for training different RF models over China for retrieving snow depth. The RF model has shown improved correlation with in-situ data but has a larger bias at few regions compared to the WESTDC SD dataset which was derived using linear methods. The drawback of the study [142] is that the quality of the results declined outside the training region of the model. This can be due to the dynamic spatiotemporal variation of snow properties and their interrelationship.
As machine learning models do not natively consider physical relation existing among the snow variables, it is necessary to adopt relevant input variables and training schemes for improving the performance. Ref. [55] used effective interpolated snow grain size from HUT simulation, in-situ snow depth in a Bayesian optimization scheme with SSM/I data for developing GlobSnow product. In a similar approach, RF was used instead of Bayesian optimization for retrieving snow depth from AMSR-2 PMW data [27]. The study revealed that RF estimates were more correlated to in-situ observations compared to globsnow-2 and AMSR-2 snow depth products. RF models cannot extrapolate outside the training range, hence transferability of the RF model to other areas is a concern. However, the studies conducted demonstrate RF has good potential in regional studies. Different machine learning models were compared to estimate SD to develop a new pixel- based algorithm over China [143]. In [143], the pixel-based algorithm is developed using a static approach with help of TB observations (at 10, 18 and 36 GHz) and RF-derived snow depth as reference data. For each pixel, regression model coefficients are derived using TB data, and an RF snow depth product. The results from [143] demonstrate outperformance of the pixel-based model developed with help of RF model, compared to other SD products i.e., GlobSnow [144], and AMSR2 [81].
Snow depth derived using sentinel-1 has shown encouraging results in mountainous regions [37]. However, the sentinel-1 SD product is available only for 2016–2020 [37]. Therefore, to extend the spatial and temporal coverage, a new approach making use of PMW TB observations, topographic parameters, with sentinel-1 SD as target is proposed by Xiong and others [145] over Colorado, and Mexico of the United States. The approach [145] has shown promising results with SD retrievals above 1 m, when tested over independent regions (i.e., Idaho, Montana, and Wyoming) which are outside the study region used for model development.
Though machine learning techniques have shown good potential, the ill-posed problem nature of snow depth estimation with PMW remote sensing can cause uncertainties in the retrieval algorithms. Microwave brightness temperatures are highly sensitive to snow grain size, wetness, and density as well. Different snow physical parameter combinations can result in similar or exact brightness temperatures at different snow depths. Hence, retrieval methods based on observed brightness temperatures and snow depth may not yield accurate results and include some uncertainty. To improve the reliability of existing machine learning and empirical model-based estimations, it is very much necessary to assess their performance over different regions at different time periods. Further, it is also important to incorporate additional parameters such as snow grain size, snow density, or other proxy parameters which can account for the ill-posed nature. Multiple algorithms catering to different sub-regions of a large region can also be considered, as snow physical parameters can change greatly from one region to another region. Another approach is to implement physics informed machine learning models for snow depth estimation.
3.5. Downscaling Snow Depth from PMW Observations
PMW remote sensing has been highly useful in providing various information for retrieving snow depth. However, the coarse resolution of snow depth obtained from stand-alone PMW approaches can impede the efficiency and performance of various applications. The low resolution of PMW datasets accommodates heterogenous land-cover features, and snow types (such as dry and wet, shallow and deep, etc.) with in a single pixel, thereby making the retrievals unreliable at smaller scale. Particularly in complex terrain regions such as Himalayas, the coarse resolution of 10–25 km is not sufficient to represent the high variability of snow information. Many of the downscaling techniques (i.e., machine learning schemes, assimilation approaches, various linear and non-linear models) have combined resampled multifrequency PMW TB data of different polarizations with in-situ data and other good spatial resolution datasets which have a correlation with snow characteristics to improve snow depth resolution. Combining optical remote sensing data sensitive to snow cover with PMW data is an important step in many downscaling models [73,99,146]. Ground emissivity observed at different PMW frequencies (e.g., 18 and 36 GHz) varies spatially and temporally and its variation can lead to variation in BTD difference of respective frequencies [77,147]. Ref. [77] developed a lookup table for retrieval coefficients used in the Chang model [22], using the TB simulations from a forward radiation model (MEMLS) with varying ground emissivity. The emissivity values calculated from remote sensing data were used to retrieve snow depth at enhanced resolution over the Tibetan plateau. Though the reported technique has shown better performance for moderate snow depth (i.e., less than 30 cm), the higher snow depth values are not estimated with good accuracy [77].
The correlation present between snow depth and various other information (PMW data, elevation, land-cover fraction, latitude, longitude, etc.) can be used for developing linear/Non-linear regression models. Multifactor regression models comprising of PMW data and high-resolution auxiliary information were used to downscale snow depth and improve shallow and deep snow depth retrievals in few studies [73,74,99]. In several studies [74,99,148] carried out over different regions, MODIS snow cover fraction (SCF) data was used alongside PMW datasets to downscale the snow depth. Yan and others [146] used spatial snow cover probability (SCP) information calculated from MODIS data and temporal snow depth information from PMW data (from SMMR, SSM/I, SSMI/S sensors) during an -day period to enhance the resolution of snow depth product to 0.05⁰. The downscaled data has shown better accuracy compared to the coarse resolution PMW snow depth product [146]. Further, Wei and others [149] have used snow cover duration, and topographical factors such as elevation, slope, land-cover, etc., in a machine learning approach to downscale AMSR-2 snow depth product. The potential of deep learning techniques in downscaling PMW snow depth downscaling was demonstrated in a recent study [129]. However, their operational utility is yet to be examined. Though many methods have considered downscaling snow depth, the approaches were simply based on blending different satellite and auxiliary information with the datasets. The physical processes underlying various snowpack characteristics were not utilized natively in the approaches leaving the scope for further improvement.
4. PMW Global Snow Depth Products
PMW remote sensing observations are extensively used for generating several snow depth products at both the regional and hemispheric scales. In this section, few popular global PMW snow depth products are discussed.
4.1. GlobSnow Product
Global Snow Monitoring for Climate Research (GlobSnow) products were developed from European Space Agency (ESA) funded missions with the objective of developing long-term snow information (Snow extent and SWE) at a global scale. GlobSnow products were developed using PMW data from the Scanning Multichannel Microwave Radiometer (SMMR, 1980–1987), Special Sensor Microwave Imager (SSM/I), and the Special Sensor Microwave Imager/Sounder (SSMI/S) (1988–till). GlobSnow SWE product is the first satellite-based daily product for the northern hemisphere which extends over four decades. GlobSnow-1 and GlobSnow-2 projects are part of the GlobSnow mission, with the latest being GlobSnow-3. In contrast to the AMSR family of snow depth and SWE products [24] which relied totally on PMW data, GlobSnow products are developed using a novel data assimilation scheme which makes use of existing snow depth information, PMW data from satellites, and inputs from HUT snow emission model [55,144]. The snow depth estimation in GlobSnow-3 is comprised of three critical steps: (1) estimation of snow grain size for pixels snow information using HUT model; (2) generation of background snow depth and snow grain size using Kriging; and (3) estimation of snow depth using a Bayesian assimilation scheme. The snow depth estimates are converted into SWE using a density value of 0.24 g/cm3 [144]. Hence, though only GlobSnow SWE products are distributed they can be easily transformed snow depth. The SWE daily products are corrected using monthly bias estimates and are made available through a data portal (https://www.globsnow.info, accessed on 1 November 2022).
4.2. AMSR-E Product
AMSR-E is a PMW scanning radiometer mounted on NASA’s Aqua platform, which was active from 2002 until 2011. The theoretical basis for developing snow depth products was discussed in detail in [24]. The methodology for estimating snow depth consists of two major steps: (1) detecting the presence of snow cover, and (2) estimation of the snow’s thickness. Snow presence is detected using the various conditions and filters formed with brightness temperatures. MODIS land cover data was used for detecting forest cover, forest density, land type, and snow depth was estimated from the area-based weighted sum of snow depth in forest and non-forest fractions of the PMW pixel. The calculated snow depth from AMSR-E was converted into SWE using a global snow density map derived from existing snow density data and climatology information [150,151]. The drawback of the dynamic method adopted in [81] is that the retrieval coefficient used for developing AMSR-E product was obtained from a polarization factor, which is a weak representation of snow grain size.
4.3. AMSR-2 Product
AMSR-2 is a successor to AMSR-E and it is onboard the Global Change Observation Mission–Water (GCOM-W1) satellite launched by JAXA. The utility and limitations of AMSR-E snow depth have been highlighted in several studies [25,124]. AMSR-2 snow depth product development involves an artificial neural network, snow emission modelling, and climatological snow depth data for the estimation of snow depth [81]. In AMSR-2 products, an electromagnetic snow emission model, HUT [78] was used for simulation of TB for various snowpack configurations. Various input and output combinations used in the HUT model were trained in an ANN model for establishing the snow grain model. Then, snow depth was estimated using the area-weighted sum of snow depth from the forest and non-forest components. Unlike the AMSR-E, in AMSR-2 products, snow density is dynamically computed by making use of improved snow density climatology [56].
AMSR-E, AMSR-2, and GlobSnow snow depth products provide immense value to the scientific community in various fields of applications and are widely adopted in different studies [37,152,153]. Recent studies have used machine learning-based approaches for developing snow depth products at regional and continental scales [85,142], and these products have yet to be analysed by the global scientific community, and hence, are not elaborated here.
5. Causes of Uncertainties in Estimated Snow Depths from PMW
Though PMW remote sensing has provided snow depth information for over four decades in many studies, there are many factors that can lead to uncertainties in the retrieved snow information. The uncertainty in PMW snow depth retrievals can originate from sensors, model data characteristics, and constraints in retrieval approaches. The important sources of error are as follows: (1) spatio-temporal variation of snowpack characteristics; (2) underlying ground, and land-cover; and (3) environmental factors. Uncertainties triggered by various factors from these sources can impede the reliability of snow depth retrievals. Some of the important factors that are responsible for the uncertainties in PMW snow depth estimates are discussed below.
5.1. Effect of Vegetation
Numerous studies have demonstrated the uncertainty associated with forest cover in snow depth and SWE estimation using PMW [23,65,139]. The standing vegetation over snow cover intercepts falling snow and PMW emission from underlying snow cover by absorption [154]. Further, upwelling PMW radiation from stems and leaves of vegetation overwhelms the snow radiation at 37 GHz. Increased sensitivity of TB to changes in canopy temperature was reported in various studies [155] resulting in the underestimation of snow depth. Depending on the amount of forest fraction and its density the underestimation can be as high as 50% [62]. The study by Vuyovich and others [156] indicates a decrease in correlation between PMW (i.e., AMSR-E, SSM/I) SWE and simulated SWE when the forest cover fraction exceeds 20%. Though many algorithms have integrated forest cover fraction into snow depth [23,73,157], studies considering the type of vegetation and their height are not very extensive. Few studies have used land-cover products developed from remote sensing data, however, dynamic changes in vegetation cover cannot be captured by making use of land-cover products which are updated periodically. In a coarse resolution PMW pixel, discriminating the responses of snow cover and forest cover is a complex task resulting in uncertainty in snow estimates.
5.2. Effect of Snow Grain Dimension and Snow Density
The microwave response from a snowpack can vary significantly depending on snow grain size. Ref. [22] have used an average snow grain of 0.3 mm for developing the relationship between PMW TB and snow depth. However, the radius of snow grain varies both spatially and temporally, potentially leading to significant bias in estimates. Unfortunately, in many instances, the knowledge of snow grain size is available at a very limited scale. An increase in grain size provides more area for scattering, resulting in a lesser TB value. A large temperature gradient within the snowpack results in the formation of depth hoar (large, faceted ice crystals), which skews the relationship between snow depth and PMW TB. An increase in grain size can cause an overestimation of snow depth particularly in the late winter [158]. Other than snow grain radius, snow density has a considerable effect on TB observations at various frequencies. Similar to snow grain size, snow density also changes both spatially and temporally, but has lesser spatial variability when compared with snow depth [159]. However, lack of priori information forced many algorithms to adopt a static value: snow density climatology values [22,56] for density. Further, it is very challenging to model the evolution of snow density considering various factors that can affect the density. Varying grain size, and snow density in a study region can make a PMW model ineffective in distinguishing between shallow and deep snow depths. TB data from additional frequencies, auxiliary parameters (i.e., terrain, location, etc.), and effective grainsize, snow climatological information (i.e., snow class, snow cover duration, etc.) are used in different models to account for this limitation [55].
5.3. Saturation of PMW Signals
TB data of 19 GHz and 37 GHz PMW frequencies are widely adopted for estimating snow depth in various studies, while it is not uncommon to see the usage of data from other frequencies. In deep snow conditions, the PMW signal at 37 GHz saturates after a threshold depth depending on snow conditions [95,97]. Studies [97,160] have shown the reversal of the relationship between TB and SWE after approximately 120 mm (60 cm snow depth at 0.2 g/cm3 density). Deep snow and snow with depth hoar, can even scatter 19 GHz PMW signals [96] leading to early saturation. Few studies have suggested the use of TB data of 10 GHz and 87 GHz for improving the deep snow and shallow snow estimates respectively. Thus, snow thickness, particularly deep snow can have a profound effect on PMW response from a snowpack. Due to these inherent uncertainties, GlobSnow product has filtered out few mountainous regions (i.e., Western Himalaya) and regions with high snow thickness [144].
5.4. Effect of Wet Snow
The presence of wet snow can cause great uncertainties in the estimation of snow depth. Microwave emissions from a snowpack are highly susceptible to the liquid water content (LWC) present in the snow [161,162]. The water content present in the snow affects the dielectric constant, resulting in increased emissivity significantly and higher TB observations from a snowpack [163,164,165]. Ref. [108] conducted a study to understand the impact of melt-freeze events on TB of snow. The study reports that the presence of a mere 0.5% LWC in the upper layer of the snowpack can trigger the TB changes, particularly at higher MW frequencies. However, the increase in TB is mainly due to water content, and the increment saturates when LWC reaches near 1%. The LWC in the upper layer of snow absorbs the PMW scattering from snow and contributes to PMW signature mainly through emission. Thereby, rendering PMW is not useful for snow depth in case of wet snow conditions. To avoid the uncertainty associated with wet snow, many studies have removed wet snow pixels using various techniques [124,166] and used the data acquired during night time passes i.e., for retrieving snow depth [102,142].
5.5. Effect of Water Bodies
The TB observation from a coarse pixel of PMW is the result of the combined responses from heterogeneous land cover types with varied characteristics. The presence of water bodies such as lakes within and near a pixel can greatly affect the PMW response of a pixel [65,88,167]. The PMW radiation at lower frequencies (10 and 19 GHz) has strong interaction with waterbodies [168]. A drop in TB at 19 GHz was reported over lake ice cover regions resulting in incorrect estimates of snow depth [169]. Thus, the amount of uncertainty in estimated snow depth will vary depending on the fraction of the area covered with water bodies. Further, state of the water body, i.e., fully/partially frozen, its size and depth, salinity, and the vicinity to pixel under observation can add to the complexity in accurately retrieving PMW response within a pixel leading to uncertainties [168,169].
5.6. Effect of the Atmosphere
The PMW signal coming from a snowpack is subjected to both absorption and emission by the atmospheric constituents (water vapor, clouds, etc.) before it gets recorded by the sensor [98]. Though the magnitude of atmospheric effect on widely used PMW TB (19 and 37 GHz) for snow depth is not very high, it still leads to quantifiable bias in the estimates of snow depth [28,170,171].
5.7. Other Factors
Many algorithms consider PMW pixel as complete snow for retrieval of snow depth. However, the coarse PMW pixel can include various land-cover (e.g., vegetation, barren land, body of water), and snow categories (dry and wet, or deep and shallow). This can result in poor reliability of snow depth estimates at finer scale. Though techniques such as spectral decomposition [172,173,174] have attempted to solve the mixed pixel problem, significant improvement is still needed. In addition to vegetation, deep snow saturation, snow grain size, wet snow, and presence of water bodies there are many other factors that can lead to uncertainties in the TB and thereby in the. .//snow depth estimates. Dong and others [175] have reported several observations regarding the uncertainties in PMW estimates of SWE due to snow mass, waterbodies, diurnal temperature, surface roughness, and aspect, etc. These uncertainties [175] are applicable to snow depth estimation as well. Snow is naturally present in the form of multiple layers with varied characteristics in each layer such as grain size, temperature, density, etc. However, single-layer snow scheme was considered in many studies [55,73,76,176]. However, this assumption of simplified stratigraphy can result in uncertainty in the PMW snow depth estimates due to non-representation of true snowpack structure [177]. The relief of terrain has a considerable effect on PMW emissivity, particularly on PMW observations of vertical polarization compared to horizontal polarization [178,179]. The effect of terrain relief and elevation in retrieving snow estimates were reported by [180].
In mountainous terrain conditions, the leeward side of topography gets masked depending on the viewing geometry of the satellite sensor. This can result in aspect-related errors which were generally not considered in many PMW snow depth algorithms. The emissivity of ground covered by snow varies with frequency and depends mainly on the condition of the ground (i.e., dry frozen or unfrozen wet), soil texture, and amount of ice [22,181]. However, the condition of ground was not treated accordingly or ignored by many algorithms. Usage of point scale observations for comparing and validating the model can also cause uncertainty. Many retrieval algorithms are also not efficient when snowpack is very thin (less than 5 cm) as the PMW spectral gradient is significantly less. Few other factors that can lead to uncertainty in snow depth retrievals consist of assumptions made in the various modelling approaches, interpolation of snow characteristics, and simplification of physically based models to reduce complexity, etc. In addition to multifaceted dynamics that are present between various snow characteristics, the heterogeneous elements present within the coarse pixel of PMW add to the confounding complexity in modelling the accurate snow depth estimates.
6. Summary, Conclusions and Future Directions
Over the past four decades (1980–2021), significant progress has been made in the study of snow depth along with other snowpack characteristics using PMW remote sensing. Despite the progress, still there exist significant uncertainty in the snow depth estimates particularly at the hemispheric scale. Depending on the available data, scientific knowledge, and operating constraints several approaches ranging from simple static relations to fully physically based models were developed by the scientific community. Stand-alone PMW approaches which provides snow depth at coarse resolution are limited by their inability to address the spatial variability of topographical and land-cover present within the pixel. This is predominant in mountain regions with vegetation, deep and wet snow conditions. Simple static approaches and heritage models which relied only on the relationship between PMW TB, and snow depth were applicable only to specific regional boundaries and failed to produce accurate estimates at hemispheric and global levels with errors close to 100% at some locations [182]. Hence, many global PMW snow depth products (ex: GlobSnow) have masked out or provided less no of observations in the mountain regions such as Himalaya.
Knowledge of snowpack characteristics such as density, snow grain dimension, stratigraphy, and their effect on PMW emission is essential in improving the model performance. This information generally is collected from ground observations, remote sensing data, model estimates, and reanalysis products. These snow parameters change significantly over spatial and temporal scales and have a dynamic relationship with the PMW response of snowpack complicating the accurate development of the model. To account for these errors, various dynamic, semi-empirical, and assimilation models were developed by considering additional snow parameters from various data sources. These models were able to produce improved results compared to static empirical algorithms, however, a lot of systematic and random bias was noticed in many investigations. Despite the usage of additional parameters, the data constraints and assumptions made to simplify the models, and limitations in accurately modelling the physical relation between the parameters have led to uncertainty in snow depth model retrievals.
Forward radiance models which are semi-empirical or fully physical were used by researchers to simulate PMW radiance for various snowpack characteristics, which was inverted to obtain snow depth or other snow variables. These techniques have shown significant improvement compared to many linear and dynamic approaches. Further, several radiance assimilation schemes, which mainly rely on the physical relation between the input data parameters, were proposed. Many radiance assimilation techniques used simulated or inverted data from snow emission models to generate the snow states inherently in the approach. The radiance assimilation schemes based on observed PMW data and simulated PMW radiance data from snow emission models, used optimization techniques such as Bayesian optimization, Kalman filters, etc., for updating and improving the snow depth estimates. While these models are efficient in representing the physical relationship between the parameters, the input data used in such models is not available readily and was obtained from different approaches. With the availability of more data, non-linear and data-driven approaches were also increasingly used by the researchers to discern the patterns which otherwise are very difficult to assess. These data-driven approaches have shown promising results in several studies.
While there are a multitude of snowpack characteristics that can lead to the randomness and uncertainty in the estimated snow depth from the models, it is also important to note the inherent limitation due to PMW interaction with snowpack. PMW emission saturation with deep snowpack and the presence of wetness can significantly limit the quality of estimates and its usage in many regions globally. The heterogeneous land features present within the coarse pixel also add to the difficulty in accurately modelling the snow depth from PMW. Other than these, topographic characteristics and environmental characteristics also affect the PMW response of a snowpack before being recorded by a spaceborne sensor.
To conclude, despite the limitations and uncertainties present, significant progress has been made in the past four decades with respect to the retrieval of snow depth and other characteristics. PMW TB data, and PMW snow depth products provide valuable information on snow depth along with other snow characteristics which are highly useful to the scientific and global community in various fields of applications. Further, PMW provides nearly four decades of valuable data archive which can be highly useful to understand the dynamics of various land and climate phenomena. A good spatial coverage and temporal resolution can overweigh the limitation of coarse pixel resolution, which is a technical difficulty to be pondered on. The results and observations from the research progress illustrate the implementation of complete physically based models driven by assimilation schemes, data-driven models and optimization schemes can potentially improve the snow depth estimates.
Scope for Future Directions
Though data from various PMW missions has provided lot of useful information for retrieving snow depth information, many uncertainties persist because of various limitations, as discussed in Section 5. There exist gaps in incorporating physics of snowpack into modelling approaches due to limited knowledge of various snowpack characteristics, and complexity of modelling approaches. New approaches should focus on bridging the gap between physical models and simplified models. To bridge the gap, further research should be carried out in improving the knowledge of various factors that affect the quality of PMW snow depth estimations. The coarse resolution makes it very unreliable particularly in mountain regions, where snow depth changes very dynamically with time and place [144]; hence, other approaches are used in such regions for retrieving snow depth [37,183,184]. The next research efforts can be towards assimilating diverse high resolution optical, infrared, microwave remote sensing products with PMW datasets for reducing the uncertainty and improving the resolution and accuracy. Use of airborne PMW datasets for assimilation is another research direction which can help in effective utilization of data from existing and forthcoming PMW missions. Different studies carried out about the sub-pixel snow depth variation [17,185] suggest that the use of point-based observations for representing and validating snow depth over a large region is not very reliable approach. The current validation of PMW snow depth approaches is mainly based on point-based observations, hence represent a higher bias [186]. To improve the validation of PMW snow depth, there is a need of high-resolution snow depth estimation studies using techniques such as UAV, satellite altimetry, and snow studies with field observation, particularly in regions where complex conditions are present. Apart from UAV, satellite altimetry, there is a need for the development of new techniques, such as point-to-surface upscaling [186], which does not require new data acquisition using novel techniques, but makes use of existing ground snow depth observations to upscale the snow depth information. Further, the current monitoring network density for snow observations is sparse across the world. This highlights the need for extending the current monitoring network of snow observations. Current PMW snow depth products and approaches are not reliable when snow depth is over 1 m. Further, mountain regions are masked out in products such as GlobSnow [144]. The implementation of lower frequency bands into modelling schemes shall be considered to improve estimation of deeper snowpack, as these have shown promising results in AMW studies. The dynamic models, non-linear and machine learning approaches adopted at regional scales have shown promising results. Hence, approaches implementing the dynamic and non-linear schemes should be evaluated. The current global snow depth products use simplified schemes for estimating the snow depth, hence showing different accuracy over different regions. Incorporating numerous regional specific algorithms into a global algorithm could improve the results of such products. Further, the potential of physics-informed machine learning/deep learning models is another approach that needs more attention for development of global snow depth products. The way forward is with the advances in computing and modelling techniques and upcoming missions; the improvements are expected to continue further.
Author Contributions
Conceptualization, S.T. and R.R.; methodology, S.T. and R.R.; formal analysis, S.T. and R.R.; investigation, S.T.; resources, S.T.; data curation, S.T.; writing—original draft preparation, S.T.; writing—review and editing, S.T. and R.R.; visualization, S.T.; supervision, R.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
We are very grateful to the three anonymous reviewers for their careful reading and comments that improved the flow and presentation of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| AMSR-E | Advanced Microwave Scanning Radiometer for Earth observation |
|---|---|
| AMW | Active Microwave |
| ANN | Artificial Neural Network |
| BTD | Brightness Temperature Difference |
| CLSM | Catchment Land Surface Model |
| DEM | Digital Elevation Model |
| DMRT | Dense Media Radiative Transfer |
| DMSP | Defense Meteorological Satellite Program |
| EnKF | Ensemble Kalman Filter |
| ESA | European Space Agency |
| ESMR | Electronically Scanning Microwave Radiometer |
| GCOM-W | Global Change Observation Mission for Water |
| HUT | Helsinki University of Technology |
| LSM | Land Surface Model |
| LWC | Liquid Water Content |
| MEMLS | Microwave Emission Model for Layered Snowpacks |
| MWRI | Microwave Radiation Imager |
| NSIDC | National Snow and Ice Data Center |
| PMW | Passive Microwave |
| RF | Random Forest |
| SAST | Snow Atmosphere Soil Transfer |
| SCP | Snow Cover Probability |
| SMMR | Scanning Multichannel Microwave Radiometer |
| SPD | Spectral Polarization Difference |
| SSiB | Simplified Simple Biosphere |
| SSM/I | Special Sensor Microwave/Imager |
| SSMI/S | Special Sensor Microwave Imager/Sounder |
| SVM | Support Vector Machine |
| SWE | Snow Water Equivalent |
| TB | Brightness temperature |
| TGI | Temperature Gradient Index |
| UAV | Unmanned Aerial Vehicle |
Appendix A
Table A1. Characteristics of different PMW sensors from selected satellite missions.
Table A1. Characteristics of different PMW sensors from selected satellite missions.
| Platform | Operational Period | Sensor | Frequency (GHz) | Polarization | Foot Print (km × km) | Swath Width (km) | Incidence Angle |
|---|---|---|---|---|---|---|---|
| Nimbus-7 | (1978–1987) | SMMR | 6.6 | H and V | 95 × 148 | 780 | 50.2 |
| 10.69 | 70 × 109 | ||||||
| 18 | 43 × 68 | ||||||
| 21 | 36 × 56 | ||||||
| 37 | 18 × 27 | ||||||
| DMSP F8–F15 | (1987–ongoing) | SSM/I | 19.35 | H and V | 45 × 68 | 1400 | 53.1 |
| 22.235 * | 40 × 60 | ||||||
| 37 | 24 × 36 | ||||||
| 85.5 | 11 × 16 | ||||||
| AQUA | (2002–2011) | AMSR-E | 6.925 | H and V | 43 × 74 | 1450 | 55 |
| 10.65 | 30 × 51 | ||||||
| 18.7 | 16 × 27 | ||||||
| 23.8 | 18 × 31 | ||||||
| 36.5 | 9 × 14 | ||||||
| 89 | 4 × 6 | ||||||
| DMSP F16–F20 | (2003–ongoing) | SSMIS | 21 frequencies including below | H and V | 1700 | 53.1 | |
| 19.35 | 42.4 × 70.1 | ||||||
| 22.235 | 42.4 × 70.1 | ||||||
| 37 | 27.5 × 4 4.2 | ||||||
| 91.655 | 13.1 × 14.4 | ||||||
| FY3-B/C | (2010–ongoing) | MWRI | 10.65 | H and V | 51 × 85 | 1400 | 53.1 |
| 18.7 | 30 × 50 | ||||||
| 23.8 | 27 × 45 | ||||||
| 36.5 | 18 × 30 | ||||||
| 89 | 9 × 15 | ||||||
| GCOM-W1 | (2012–ongoing) | AMSR-2 | 6.925 | H and V | 35 × 62 | 1450 | 55 |
| 7.3 | 34 × 58 | ||||||
| 10.65 | 24 × 42 | ||||||
| 18.7 | 14 × 22 | ||||||
| 23.8 | 15 × 26 | ||||||
| 36.5 | 7 × 12 | ||||||
| 89 | 3 × 5 | ||||||
| GOSAT-GW | Planned (2023) | AMSR-3 | 12 frequencies including below | H and V | 1450 | 55 | |
| 10.65 | 22 × 69 | ||||||
| 18.7 | 12 × 21 | ||||||
| 23.8 | 14 × 24 | ||||||
| 36.5 | 7 × 11 | ||||||
| 89 | 3 × 5 |
Figure A1. PMW Satellite missions.
Figure A1. PMW Satellite missions.

References
- Aguirre, F.; Carrasco, J.; Sauter, T.; Schneider, C.; Gaete, K.; Garín, E.; Adaros, R.; Butorovic, N.; Jaña, R.; Casassa, G. Snow Cover Change as a Climate Indicator in Brunswick Peninsula, Patagonia. Front. Earth Sci. 2018, 6, 130. [Google Scholar] [CrossRef]
- Bender, E.; Lehning, M.; Fiddes, J. Changes in Climatology, Snow Cover, and Ground Temperatures at High Alpine Locations. Front. Earth Sci. 2020, 8, 100. [Google Scholar] [CrossRef]
- ul Shafiq, M.; Ahmed, P.; ul Islam, Z.; Joshi, P.K.; Bhat, W.A. Snow Cover Area Change and Its Relations with Climatic Variability in Kashmir Himalayas, India. Geocarto Int. 2019, 34, 688–702. [Google Scholar] [CrossRef]
- Estilow, T.W.; Young, A.H.; Robinson, D.A. A Long-Term Northern Hemisphere Snow Cover Extent Data Record for Climate Studies and Monitoring. Earth Syst. Sci. Data 2015, 7, 137–142. [Google Scholar] [CrossRef] [Green Version]
- Lemke, P.; Ren, J.; Alley, R.B.; Allison, I.; Carrasco, J.; Flato, G.; Fujii, Y.; Kaser, G.; Mote, P.; Thomas, R.H.; et al. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; ISBN 978-0521705967. [Google Scholar]
- Yang, F.; Kumar, A.; Wang, W.; Juang, H.M.H.; Kanamitsu, M. Snow-Albedo Feedback and Seasonal Climate Variability over North America. J. Clim. 2001, 14, 4245–4248. [Google Scholar] [CrossRef]
- Liu, X.; Chen, R.; Liu, J.; Wang, X.; Zhang, B.; Han, C.; Liu, G.; Guo, S.; Liu, Z.; Song, Y.; et al. Effects of Snow-Depth Change on Spring Runoff in Cryosphere Areas of China. Hydrol. Sci. J. 2019, 64, 789–797. [Google Scholar] [CrossRef]
- Stigter, E.M.; Wanders, N.; Saloranta, T.M.; Shea, J.M.; Bierkens, M.F.P.; Immerzeel, W.W. Assimilation of Snow Cover and Snow Depth into a Snow Model to Estimate Snow Water Equivalent and Snowmelt Runoff in a Himalayan Catchment. Cryosphere 2017, 11, 1647–1664. [Google Scholar] [CrossRef] [Green Version]
- Schweizer, J.; Jamieson, J.B.; Schneebeli, M. Snow Avalanche Formation. Rev. Geophys. 2003, 41, 1016. [Google Scholar] [CrossRef] [Green Version]
- Beniston, M. Variations of Snow Depth and Duration in the Swiss Alps Over the Last 50 Years: Links to Changes in Large-Scale Climatic Forcings. In Climatic Change at High Elevation Sites; Springer: Dordrecht, The Netherlands, 1997; pp. 49–68. [Google Scholar] [CrossRef]
- Lutz, A.F.; Immerzeel, W.W.; Shrestha, A.B.; Bierkens, M.F.P. Consistent Increase in High Asia’s Runoff Due to Increasing Glacier Melt and Precipitation. Nat. Clim. Change 2014, 4, 587–592. [Google Scholar] [CrossRef]
- Kirkham, J.D.; Koch, I.; Saloranta, T.M.; Litt, M.; Stigter, E.E.; Møen, K.; Thapa, A.; Melvold, K.; Immerzeel, W.W. Near Real-Time Measurement of Snow Water Equivalent in the Nepal Himalayas. Front. Earth Sci. 2019, 7, 177. [Google Scholar] [CrossRef] [Green Version]
- Kinar, N.J.; Pomeroy, J.W. Measurement of the Physical Properties of the Snowpack. Rev. Geophys. 2015, 53, 481–544. [Google Scholar] [CrossRef]
- Singh, K.K.; Kumar, A.; Kulkarni, A.V.; Datt, P.; Dewali, S.K.; Kumar, V.; Chauhan, R. Snow Depth Estimation in the Indian Himalaya Using Multi-Channel Passive Microwave Radiometer. Curr. Sci. 2015, 108, 942–953. [Google Scholar] [CrossRef]
- Dong, C. Remote Sensing, Hydrological Modeling and in Situ Observations in Snow Cover Research: A Review. J. Hydrol. 2018, 561, 573–583. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Fassnacht, S.R.; Beguería, S.; Latron, J.B.P. Variability of Snow Depth at the Plot Scale: Implications for Mean Depth Estimation and Sampling Strategies. Cryosphere 2011, 5, 617–629. [Google Scholar] [CrossRef] [Green Version]
- Meromy, L.; Molotch, N.P.; Link, T.E.; Fassnacht, S.R.; Rice, R. Subgrid Variability of Snow Water Equivalent at Operational Snow Stations in the Western USA. Hydrol. Process. 2013, 27, 2383–2400. [Google Scholar] [CrossRef]
- Kongoli, C.; Key, J.; Smith, T.M. Mapping of Snow Depth by Blending Satellite and In-Situ Data Using Two-Dimensional Optimal Interpolation-Application to AMSR2. Remote Sens. 2019, 11, 3049. [Google Scholar] [CrossRef] [Green Version]
- Woody, J.; Lu, Q.Q.; Livsey, J. Statistical Methods for Forecasting Daily Snow Depths and Assessing Trends in Inter-Annual Snow Depth Dynamics. Environ. Ecol. Stat. 2020, 27, 609–628. [Google Scholar] [CrossRef]
- Buhler, Y.; Adams, M.S.; Bosch, R.; Stoffel, A. Mapping Snow Depth in Alpine Terrain with Unmanned Aerial Systems (UASs): Potential and Limitations. Cryosphere 2016, 10, 1075–1088. [Google Scholar] [CrossRef] [Green Version]
- Maier, K.; Nascetti, A.; van Pelt, W.; Rosqvist, G. Direct Photogrammetry with Multispectral Imagery for UAV-Based Snow Depth Estimation. ISPRS J. Photogramm. Remote Sens. 2022, 186, 1–18. [Google Scholar] [CrossRef]
- Chang, A.T.C.; Foster, J.L.; Hall, D.K. Nimbus-7 SMMR Derived Global Snow Cover Parameters. Ann. Glaciol. 1987, 9, 39–44. [Google Scholar] [CrossRef] [Green Version]
- Foster, J.L.; Chang, A.T.C.; Hall, D.K. Comparison of Snow Mass Estimates from a Prototype Passive Microwave Snow Algorithm, a Revised Algorithm and a Snow Depth Climatology. Remote Sens. Environ. 1997, 62, 132–142. [Google Scholar] [CrossRef]
- Kelly, R. The AMSR-E Snow Depth Algorithm: Description and Initial Results. J. Remote Sens. Soc. Jpn. 2009, 29, 307–317. [Google Scholar] [CrossRef]
- Lee, J.-E.; Lee, G.W.; Earle, M.; Nitu, R. Uncertainty Analysis for Evaluating the Accuracy of Snow Depth Measurements. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 4157–4190. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, T.; Zhong, X.; Shao, W.; Li, X. Support Vector Regression Snow-Depth Retrieval Algorithm Using Passive Microwave Remote Sensing Data. Remote Sens. Environ. 2018, 210, 48–64. [Google Scholar] [CrossRef]
- Yang, J.W.; Jiang, L.M.; Lemmetyinen, J.; Pan, J.M.; Luojus, K.; Takala, M. Improving Snow Depth Estimation by Coupling HUT-Optimized Effective Snow Grain Size Parameters with the Random Forest Approach. Remote Sens. Environ. 2021, 264, 112630. [Google Scholar] [CrossRef]
- Shi, L.; Qiu, Y.; Lemmetyinen, J.; Shi, J. Atmospheric Correction of Passive Microwave Brightness Temperature on the Estimation of Snow Depth. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; pp. 3982–3985. [Google Scholar] [CrossRef]
- Bühler, Y.; Marty, M.; Egli, L.; Veitinger, J.; Jonas, T.; Thee, P.; Ginzler, C. Snow Depth Mapping in High-Alpine Catchments Using Digital Photogrammetry. Cryosphere 2015, 9, 229–243. [Google Scholar] [CrossRef] [Green Version]
- Hall, D.K.; Kelly, R.E.; Foster, J.L.; Chang, A.T. Encyclopedia of Hydrological Sciences; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; Chapter 55; pp. 812–830. ISBN 9780471491033. [Google Scholar]
- Nolin, A.W. Recent Advances in Remote Sensing of Seasonal Snow. J. Glaciol. 2010, 56, 1141–1150. [Google Scholar] [CrossRef] [Green Version]
- Prokop, A. Assessing the Applicability of Terrestrial Laser Scanning for Spatial Snow Depth Measurements. Cold Reg. Sci. Technol. 2008, 54, 155–163. [Google Scholar] [CrossRef]
- Bernier, P.Y. Microwave Remote Sensing of Snowpack Properties: Potential and Limitations. Hydrol. Res. 1987, 18, 1–20. [Google Scholar] [CrossRef]
- Hallikainen, M.; Lemmetyinen, J.; Jiang, L. Snow Properties from Passive Microwave. Compr. Remote Sens. 2018, 4, 224–236. [Google Scholar] [CrossRef]
- Leinss, S.; Parrella, G.; Hajnsek, I. Snow Height Determination by Polarimetric Phase Differences in X-Band SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3794–3810. [Google Scholar] [CrossRef]
- Li, H.; Wang, Z.; He, G.; Man, W. Estimating Snow Depth and Snow Water Equivalence Using Repeat-Pass Interferometric SAR in the Northern Piedmont Region of the Tianshan Mountains. J. Sens. 2017, 2017, 8739598. [Google Scholar] [CrossRef] [Green Version]
- Lievens, H.; Demuzere, M.; Marshall, H.P.; Reichle, R.H.; Brucker, L.; Brangers, I.; de Rosnay, P.; Dumont, M.; Girotto, M.; Immerzeel, W.W.; et al. Snow Depth Variability in the Northern Hemisphere Mountains Observed from Space. Nat. Commun. 2019, 10, 4629. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mahmoodzada, A.B.; Varade, D.; Shimada, S. Estimation of Snow Depth in the Hindu Kush Himalayas of Afghanistan during Peakwinter and Early Melt Season. Remote Sens. 2020, 12, 2788. [Google Scholar] [CrossRef]
- Patil, A.; Singh, G.; Rüdiger, C. Retrieval of Snow Depth and Snow Water Equivalent Using Dual Polarization SAR Data. Remote Sens. 2020, 12, 1183. [Google Scholar] [CrossRef] [Green Version]
- Patil, A.; Mohanty, S.; Singh, G. Snow Depth and Snow Water Equivalent Retrieval Using X-Band PolInSAR Data. Remote Sens. Lett. 2020, 11, 817–826. [Google Scholar] [CrossRef]
- Maass, N.; Kaleschke, L.; Tian-Kunze, X.; Tonboe, R.T. Snow Thickness Retrieval from L-Band Brightness Temperatures: A Model Comparison. Ann. Glaciol. 2015, 56, 9–17. [Google Scholar] [CrossRef] [Green Version]
- Rignot, E.; Echelmeyer, K.; Krabill, W. Penetration Depth of Interferometric Synthetic-Aperture Radar Signals in Snow and Ice. Geophys. Res. Lett. 2001, 28, 3501–3504. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Stiles, W.H. Microwave response of snow. Adv. Space Res 1981, 1, 131–149. [Google Scholar] [CrossRef]
- Tsai, Y.L.S.; Dietz, A.; Oppelt, N.; Kuenzer, C. Remote Sensing of Snow Cover Using Spaceborne SAR: A Review. Remote Sens. 2019, 11, 1456. [Google Scholar] [CrossRef] [Green Version]
- Amlien, J. Remote Sensing of Snow with Passive Microwave Radiometers. A Review of Current Algorithms; Report no 1019, Norsk Regnesentral, 2008. ISBN 978-82-539-0529-7. Available online: https://vdocuments.mx/remote-sensing-of-snow-with-passive-microwave-radiometers-6-remote-sensing-of-snow.html?page=1 (accessed on 1 November 2022).
- Awasthi, S.; Varade, D. Recent Advances in the Remote Sensing of Alpine Snow: A Review. GIScience Remote Sens. 2021, 58, 852–888. [Google Scholar] [CrossRef]
- Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote Sensing of Snow—A Review of Available Methods. Int. J. Remote Sens. 2011, 33, 4094–4134. [Google Scholar] [CrossRef]
- Saberi, N.; Kelly, R.; Flemming, M.; Li, Q. Review of Snow Water Equivalent Retrieval Methods Using Spaceborne Passive Microwave Radiometry. Int. J. Remote Sens. 2019, 41, 996–1018. [Google Scholar] [CrossRef]
- Cho, E.; Tuttle, S.; Jacobs, J. Evaluating Consistency of Snow Water Equivalent Retrievals from Passive Microwave Sensors over the North Central U.S.: SSM/I vs. SSMIS and AMSR-E vs. AMSR2. Remote Sens. 2017, 9, 465. [Google Scholar] [CrossRef] [Green Version]
- Lemmetyinen, J.; Derksen, C.; Rott, H.; Macelloni, G.; King, J.; Schneebeli, M.; Wiesmann, A.; Leppänen, L.; Kontu, A.; Pulliainen, J. Retrieval of Effective Correlation Length and Snow Water Equivalent from Radar and Passive Microwave Measurements. Remote Sens. 2018, 10, 170. [Google Scholar] [CrossRef] [Green Version]
- Clifford, D. Global Estimates of Snow Water Equivalent from Passive Microwave Instruments: History, Challenges and Future Developments. Int. J. Remote Sens. 2010, 31, 3707–3726. [Google Scholar] [CrossRef]
- Vuyovich, C.; Jacobs, J.M. Snowpack and Runoff Generation Using AMSR-E Passive Microwave Observations in the Upper Helmand Watershed, Afghanistan. Remote Sens. Environ. 2011, 115, 3313–3321. [Google Scholar] [CrossRef]
- Merkouriadi, I.; Lemmetyinen, J.; Liston, G.E.; Pulliainen, J. Solving Challenges of Assimilating Microwave Remote Sensing Signatures with a Physical Model to Estimate Snow Water Equivalent. Water Resour. Res. 2021, 57, e2021WR030119. [Google Scholar] [CrossRef]
- Jiang, L.; Yang, J.; Zhang, C.; Wu, S.; Li, Z.; Dai, L.; Li, X.; Qiu, Y. Daily Snow Water Equivalent Product with SMMR, SSM/I and SSMIS from 1980 to 2020 over China. Big Earth Data 2022, 6, 420–434. [Google Scholar] [CrossRef]
- Takala, M.; Luojus, K.; Pulliainen, J.; Derksen, C.; Lemmetyinen, J.; Kärnä, J.P.; Koskinen, J.; Bojkov, B. Estimating Northern Hemisphere Snow Water Equivalent for Climate Research through Assimilation of Space-Borne Radiometer Data and Ground-Based Measurements. Remote Sens. Environ. 2011, 115, 3517–3529. [Google Scholar] [CrossRef]
- Sturm, M.; Taras, B.; Liston, G.E.; Derksen, C.; Jonas, T.; Lea, J. Estimating Snow Water Equivalent Using Snow Depth Data and Climate Classes. J. Hydrometeorol. 2010, 11, 1380–1394. [Google Scholar] [CrossRef]
- Denoth, A. Snow Dielectric Measurements. Adv. Space Res. 1989, 9, 233–243. [Google Scholar] [CrossRef]
- Mätzler, C.; Wegmüller, U. Dielectric Properties of Fresh-Water Ice at Microwave Frequencies. J. Phys. D Appl. Phys. 1988, 21, 1660. [Google Scholar] [CrossRef]
- Chang, T.C.; Gloersen, P.; Schmugge, T.; Wilheit, T.T.; Zwally, H.J. Microwave Emission from Snow and Glacier Ice. J. Glaciol. 1976, 16, 23–39. [Google Scholar] [CrossRef] [Green Version]
- Lakhankar, T.; Azar, A.E.; Shahroudi, N.; Powell, A.; Khanbilvardi, R. Analysis of the Effects of Snowpack Properties on Satellite Microwave Brightness Temperature and Emissivity Data. J. Remote Sens. GIS 2012, 1, 1–6. [Google Scholar] [CrossRef]
- Saraf, A.K.; Tarafdar, S.; Foster, J.L.; Singh, P. Passive Microwave Data for Snow-Depth and Snow-Extent Estimations in the Himalayan Mountains. Int. J. Remote Sens. 1999, 20, 83–95. [Google Scholar] [CrossRef]
- Chang, A.T.C.; Hall, D.K.; Foster, J.L.; Rango, A.; Schmugge, T.J. Studies of Snowpack Properties by Passive Microwave Radiometry. 1979. Available online: https://ntrs.nasa.gov/citations/19790008308 (accessed on 15 November 2022).
- Matzler, C. Microwave Properties of Ice and Snow. In Solar System Ices. Astrophysics and Space Science Library; Schmitt, B., De Bergh, C., Festou, M., Eds.; Springer: Dordrecht, The Netherlands, 1998; Volume 227, pp. 241–257. [Google Scholar] [CrossRef]
- Wiesmann, A.; Mätzler, C. Microwave Emission Model of Layered Snowpacks. Remote Sens. Environ. 1999, 70, 307–316. [Google Scholar] [CrossRef]
- Foster, J.L.; Sun, C.; Walker, J.P.; Kelly, R.; Chang, A.; Dong, J.; Powell, H. Quantifying the Uncertainty in Passive Microwave Snow Water Equivalent Observations. Remote Sens. Environ. 2005, 94, 187–203. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Jin, R.; Armstrong, R.; Zhang, T. Snow Depth Derived from Passive Microwave Remote-Sensing Data in China. Ann. Glaciol. 2008, 49, 145–154. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Kutuza, B.G. Cosmos-243 as the Starting Point for the Development of Microwave Radiometry Methods of the Earth’s Atmosphere and Surface. Izv. Atmos. Ocean. Phys. 2018, 54, 275–281. [Google Scholar] [CrossRef]
- Kunzi, K.F.; Rott, H.; Patil, S. Snow-Cover Parameters Retrieved from Nimbus-7 Scanning Multichannel Microwave Radiometer (SMMR) Data. IEEE Trans. Geosci. Remote Sens. 1982, GE-20, 452–467. [Google Scholar] [CrossRef]
- Chang, A.T.C.; Foster, J.L.; Hall, D.K.; Rango, A.; Hartline, B.K. Snow Water Equivalent Estimation by Microwave Radiometry. Cold Reg. Sci. Technol. 1982, 5, 259–267. [Google Scholar] [CrossRef]
- Jiang, L.M.; Wang, P.; Zhang, L.X.; Yang, H.; Yang, J.T. Improvement of Snow Depth Retrieval for FY3B-MWRI in China. Sci. China Earth Sci. 2014, 57, 1278–1292. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Yu, H. Snow Depth Estimation Using a Lookup Table Method Based on MEMLS. Gaojishu Tongxin/Chin. High Technol. Lett. 2014, 24, 915–921. [Google Scholar] [CrossRef]
- Chang, A.T.C.; Foster, J.L.; Hall, D.K.; Goodison, B.E.; Walker, A.E.; Metcalfe, J.R.; Harby, A. Snow Parameters Derived from Microwave Measurements during the BOREAS Winter Field Campaign. J. Geophys. Res. Atmos. 1997, 102, 29663–29671. [Google Scholar] [CrossRef]
- Wang, J.; Huang, X.; Wang, Y.; Liang, T. Retrieving Snow Depth Information from AMSR2 Data for Qinghai-Tibet Plateau. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 752–768. [Google Scholar] [CrossRef]
- Wei, P.; Zhang, T.; Zhou, X.; Yi, G.; Li, J.; Wang, N.; Wen, B. Reconstruction of Snow Depth Data at Moderate Spatial Resolution (1 km) from Remotely Sensed Snow Data and Multiple Optimized Environmental Factors: A Case Study over the Qinghai-Tibetan Plateau. Remote Sens. 2021, 13, 657. [Google Scholar] [CrossRef]
- Josberger, E.G.; Mognard, N.M. A Passive Microwave Snow Depth Algorithm with a Proxy for Snow Metamorphism. Hydrol. Process. 2002, 16, 1557–1568. [Google Scholar] [CrossRef]
- Kelly, R.E.J.; Chang, A.T.C. Development of a Passive Microwave Global Snow Depth Retrieval Algorithm for Special Sensor Microwave Imager (SSM/I) and Advanced Microwave Scanning Radiometer-EOS (AMSR-E) Data. Radio Sci. 2003, 38, 8076. [Google Scholar] [CrossRef]
- Dai, L.; Che, T.; Xie, H.; Wu, X. Estimation of Snow Depth over the Qinghai-Tibetan Plateau Based on AMSR-E and MODIS Data. Remote Sens. 2018, 10, 1989. [Google Scholar] [CrossRef] [Green Version]
- Pulliainen, J.T.; Grandeil, J. HUT Snow Emission Model and Its Applicability to Snow Water Equivalent Retrieval. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1378–1390. [Google Scholar] [CrossRef]
- Tsang, L.; Chen, C.-T.; Chang, A.T.C.; Guo, J.; Ding, K.H. Dense Media Radiative Transfer Theory Based on Quasicrystalline Approximation with Applications to Passive Microwave Remote Sensing of Snow. Radio Sci. 2000, 35, 731–749. [Google Scholar] [CrossRef]
- Picard, G.; Brucker, L.; Roy, A.; Dupont, F.; Fily, M.; Royer, A.; Harlow, C. Simulation of the Microwave Emission of Multi-Layered Snowpacks Using the Dense Media Radiative Transfer Theory: The DMRT-ML Model. Geosci. Model Dev. 2013, 6, 1061–1078. [Google Scholar] [CrossRef] [Green Version]
- Tedesco, M.; Jeyaratnam, J. A New Operational Snow Retrieval Algorithm Applied to Historical AMSR-E Brightness Temperatures. Remote Sens. 2016, 8, 1037. [Google Scholar] [CrossRef] [Green Version]
- Xue, Y.; Forman, B.A. Comparison of Passive Microwave Brightness Temperature Prediction Sensitivities over Snow-Covered Land in North America Using Machine Learning Algorithms and the Advanced Microwave Scanning Radiometer. Remote Sens. Environ. 2015, 170, 153–165. [Google Scholar] [CrossRef]
- Liang, J.; Liu, X.; Huang, K.; Li, X.; Shi, X.; Chen, Y.; Li, J. Improved Snow Depth Retrieval by Integrating Microwave Brightness Temperature and Visible/Infrared Reflectance. Remote Sens. Environ. 2015, 156, 500–509. [Google Scholar] [CrossRef]
- Nikraftar, Z.; Hasanlou, M.; Esmaeilzadeh, M. Novel Snow Depth Retrieval Method Using Time Series SSMI Passive Microwave Imagery. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences—ISPRS Archives, Prague, Czech Republic, 12–19 July 2016; Volume 41. [Google Scholar]
- Hu, Y.; Che, T.; Dai, L.; Xiao, L. Snow Depth Fusion Based on Machine Learning Methods for the Northern Hemisphere. Remote Sens. 2021, 13, 1250. [Google Scholar] [CrossRef]
- Durand, M.; Margulis, S.A. Feasibility Test of Multifrequency Radiometric Data Assimilation to Estimate Snow Water Equivalent. J. Hydrometeorol. 2006, 7, 443–457. [Google Scholar] [CrossRef]
- Tedesco, M.; Reichle, R.; Löw, A.; Markus, T.; Foster, J.L. Dynamic Approaches for Snow Depth Retrieval from Spaceborne Microwave Brightness Temperature. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1955–1967. [Google Scholar] [CrossRef]
- Lemmetyinen, J.; Kontu, A.; Kärnä, J.P.; Vehviläinen, J.; Takala, M.; Pulliainen, J. Correcting for the Influence of Frozen Lakes in Satellite Microwave Radiometer Observations through Application of a Microwave Emission Model. Remote Sens. Environ. 2011, 115, 3695–3706. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Jin, R.; Huang, C. Assimilating Passive Microwave Remote Sensing Data into a Land Surface Model to Improve the Estimation of Snow Depth. Remote Sens. Environ. 2014, 143, 54–63. [Google Scholar] [CrossRef]
- Kwon, Y.; Yang, Z.L.; Hoar, T.J.; Toure, A.M. Improving the Radiance Assimilation Performance in Estimating Snow Water Storage across Snow and Land-Cover Types in North America. J. Hydrometeorol. 2017, 18, 651–668. [Google Scholar] [CrossRef]
- Wainwright, H.M.; Liljedahl, A.K.; Dafflon, B.; Ulrich, C.; Peterson, J.E.; Gusmeroli, A.; Hubbard, S.S. Mapping Snow Depth within a Tundra Ecosystem Using Multiscale Observations and Bayesian Methods. Cryosphere 2017, 11, 857–875. [Google Scholar] [CrossRef] [Green Version]
- Kwon, Y.; Forman, B.A.; Ahmad, J.A.; Kumar, S.V.; Yoon, Y. Exploring the Utility of Machine Learning-Based Passive Microwave Brightness Temperature Data Assimilation over Terrestrial Snow in High Mountain Asia. Remote Sens. 2019, 11, 2265. [Google Scholar] [CrossRef] [Green Version]
- Hou, J.; Huang, C.; Chen, W.; Zhang, Y. Improving Snow Estimates Through Assimilation of MODIS Fractional Snow Cover Data Using Machine Learning Algorithms and the Common Land Model. Water Resour. Res. 2021, 57, e2020WR029010. [Google Scholar] [CrossRef]
- Das, I.; Sarwade, R.N. Snow Depth Estimation over North-Western Indian Himalaya Using AMSR-E. Int. J. Remote Sens. 2008, 29, 4237–4248. [Google Scholar] [CrossRef]
- de Sève, D.; Bernier, M.; Fortin, J.P.; Walker, A. Preliminary Analysis of Snow Microwave Radiometry Using the SSM/I Passive-Microwave Data: The Case of La Grande River Watershed (Quebec). Ann. Glaciol. 1997, 25, 353–361. [Google Scholar] [CrossRef]
- Derksen, C. The Contribution of AMSR-E 18.7 and 10.7 GHz Measurements to Improved Boreal Forest Snow Water Equivalent Retrievals. Remote Sens. Environ. 2008, 112, 2701–2710. [Google Scholar] [CrossRef]
- Schanda, E.; Kunzi, C.M. & K. Microwave Remote Sensing of Snow Cover. Int. J. Remote Sens. 1983, 4, 149–158. [Google Scholar] [CrossRef]
- Aschbacher, J.; Rott, H. Microwave Emission of Snow-Covered and Snow-Free Terrain from Satellite Measurements. Adv. Space Res. 1989, 9, 289–295. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, X.; Wang, J.; Zhou, M.; Liang, T. AMSR2 Snow Depth Downscaling Algorithm Based on a Multifactor Approach over the Tibetan Plateau, China. Remote Sens. Environ. 2019, 231, 111268. [Google Scholar] [CrossRef]
- Grippa, M.; Mognard, N.; le Toan, T.; Josberger, E.G. Siberia Snow Depth Climatology Derived from SSM/I Data Using a Combined Dynamic and Static Algorithm. Remote Sens. Environ. 2004, 93, 30–41. [Google Scholar] [CrossRef]
- Lemmetyinen, J.; Pulliainen, J.; Rees, A.; Kontu, A.; Qiu, Y.; Derksen, C. Multiple-Layer Adaptation of HUT Snow Emission Model: Comparison with Experimental Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2781–2794. [Google Scholar] [CrossRef]
- Dai, L.; Che, T.; Wang, J.; Zhang, P. Snow Depth and Snow Water Equivalent Estimation from AMSR-E Data Based on a Priori Snow Characteristics in Xinjiang, China. Remote Sens. Environ. 2012, 127, 14–29. [Google Scholar] [CrossRef]
- Wu, L.; Li, X.; Zhao, K.; Zheng, X. Snow Depth Inversion Using the Localized HUT Model Based on FY-3B MWRI Data in the Farmland of Heilongjiang Province, China. J. Indian Soc. Remote Sens. 2017, 45, 89–100. [Google Scholar] [CrossRef]
- Gu, L.; Fan, X.; Li, X.; Wei, Y. Snow Depth Retrieval in Farmland Based on a Statistical Lookup Table from Passive Microwave Data in Northeast China. Remote Sens. 2019, 11, 3037. [Google Scholar] [CrossRef] [Green Version]
- Kelly, R.; Li, Q.; Saberi, N. ’The AMSR2 Satellite-Based Microwave Snow Algorithm (SMSA): A New Algorithm for Estimating Global Snow Accumulation. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; pp. 5606–5609. [Google Scholar] [CrossRef]
- Saberi, N.; Kelly, R.; Pan, J.; Durand, M.; Goh, J.; Scott, K.A. The Use of a Monte Carlo Markov Chain Method for Snow-Depth Retrievals: A Case Study Based on Airborne Microwave Observations and Emission Modeling Experiments of Tundra Snow. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1876–1889. [Google Scholar] [CrossRef]
- Saberi, N.; Kelly, R. An Evaluation of DMRT-ML for AMSR2 Estimates of Snow Depth. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 1943–1946. [Google Scholar] [CrossRef]
- Tedesco, M.; Kim, E.J. Retrieval of Dry-Snow Parameters from Microwave Radiometric Data Using a Dense-Medium Model and Genetic Algorithms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2143–2151. [Google Scholar] [CrossRef]
- Durand, M.; Kim, E.J.; Margulis, S.A. Radiance Assimilation Shows Promise for Snowpack Characterization. Geophys. Res. Lett. 2009, 36, 2503. [Google Scholar] [CrossRef]
- Piazzi, G.; Thirel, G.; Campo, L.; Gabellani, S. A Particle Filter Scheme for Multivariate Data Assimilation into a Point-Scale Snowpack Model in an Alpine Environment. Cryosphere 2018, 12, 2287–2306. [Google Scholar] [CrossRef] [Green Version]
- Andreadis, K.M.; Lettenmaier, D.P. Assimilating Remotely Sensed Snow Observations into a Macroscale Hydrology Model. Adv. Water Resour. 2006, 29, 872–886. [Google Scholar] [CrossRef]
- Graf, T.; Koike, T.; Li, X.; Hirai, M.; Tsutsui, H. Assimilating Passive Microwave Brightness Temperature Data into a Land Surface Model to Improve the Snow Depth Predictability. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Denver, CO, USA, 31 July–4 August 2006; pp. 710–713. [Google Scholar] [CrossRef]
- Liu, Y.; Peters-Lidard, C.D.; Kumar, S.; Foster, J.L.; Shaw, M.; Tian, Y.; Fall, G.M. Assimilating Satellite-Based Snow Depth and Snow Cover Products for Improving Snow Predictions in Alaska. Adv. Water Resour. 2013, 54, 208–227. [Google Scholar] [CrossRef]
- Helmert, J.; Şorman, A.Ş.; Montero, R.A.; de Michele, C.; de Rosnay, P.; Dumont, M.; Finger, D.C.; Lange, M.; Picard, G.; Potopová, V.; et al. Review of Snow Data Assimilation Methods for Hydrological, Land Surface, Meteorological and Climate Models: Results from a COST Harmosnow Survey. Geosciences 2018, 8, 489. [Google Scholar] [CrossRef] [Green Version]
- Hedrick, A.R.; Marks, D.; Havens, S.; Robertson, M.; Johnson, M.; Sandusky, M.; Marshall, H.; Kormos, P.R.; Bormann, K.J.; Painter, T.H. Direct Insertion of NASA Airborne Snow Observatory-Derived Snow Depth Time Series Into the ISnobal Energy Balance Snow Model. Water Resour. Res. 2018, 54, 8045–8063. [Google Scholar] [CrossRef]
- Xu, J.; Shu, H. Assimilating MODIS-Based Albedo and Snow Cover Fraction into the Common Land Model to Improve Snow Depth Simulation with Direct Insertion and Deterministic Ensemble Kalman Filter Methods. J. Geophys. Res. Atmos. 2014, 119, 10684–10701. [Google Scholar] [CrossRef]
- Revuelto, J.; Vionnet, V.; López-Moreno, J.I.; Lafaysse, M.; Morin, S. Combining Snowpack Modeling and Terrestrial Laser Scanner Observations Improves the Simulation of Small Scale Snow Dynamics. J. Hydrol. 2016, 533, 291–307. [Google Scholar] [CrossRef]
- Liston, G.E.; Hiemstra, C.A. A Simple Data Assimilation System for Complex Snow Distributions (SnowAssim). J. Hydrometeorol. 2008, 9, 989–1004. [Google Scholar] [CrossRef]
- Avanzi, F.; Zheng, Z.; Coogan, A.; Rice, R.; Akella, R.; Conklin, M.H. Gap-Filling Snow-Depth Time-Series with Kalman Filtering-Smoothing and Expectation Maximization: Proof of Concept Using Spatially Dense Wireless-Sensor-Network Data. Cold Reg. Sci. Technol. 2020, 175, 103066. [Google Scholar] [CrossRef]
- Yang, J.; Li, C. Assimilation of D-InSAR Snow Depth Data by an Ensemble Kalman Filter. Arab. J. Geosci. 2021, 14, 505. [Google Scholar] [CrossRef]
- Magnusson, J.; Winstral, A.; Stordal, A.S.; Essery, R.; Jonas, T. Improving Physically Based Snow Simulations by Assimilating Snow Depths Using the Particle Filter. Water Resour. Res. 2017, 53, 1125–1143. [Google Scholar] [CrossRef] [Green Version]
- Smyth, E.J.; Raleigh, M.S.; Small, E.E. Particle Filter Data Assimilation of Monthly Snow Depth Observations Improves Estimation of Snow Density and SWE. Water Resour. Res. 2019, 55, 1296–1311. [Google Scholar] [CrossRef]
- Kim, R.S.; Durand, M.; Li, D.; Baldo, E.; Margulis, S.A.; Dumont, M.; Morin, S. Estimating Alpine Snow Depth by Combining Multifrequency Passive Radiance Observations with Ensemble Snowpack Modeling. Remote Sens. Environ. 2019, 226, 1–15. [Google Scholar] [CrossRef]
- Tedesco, M.; Narvekar, P.S. Assessment of the NASA AMSR-E SWE Product. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 141–159. [Google Scholar] [CrossRef]
- Pulliainen, J. Mapping of Snow Water Equivalent and Snow Depth in Boreal and Sub-Arctic Zones by Assimilating Space-Borne Microwave Radiometer Data and Ground-Based Observations. Remote Sens. Environ. 2006, 101, 257–269. [Google Scholar] [CrossRef]
- Kumar, S.V.; Peters-Lidard, C.D.; Arsenault, K.R.; Getirana, A.; Mocko, D.; Liu, Y. Quantifying the Added Value of Snow Cover Area Observations in Passive Microwave Snow Depth Data Assimilation. J. Hydrometeorol. 2015, 16, 1736–1741. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Hoar, T.J.; Yang, Z.L.; Anderson, J.L.; Toure, A.M.; Rodell, M. Assimilation of MODIS Snow Cover through the Data Assimilation Research Testbed and the Community Land Model Version 4. J. Geophys. Res. Atmos. 2014, 119, 7091–7103. [Google Scholar] [CrossRef]
- Kumar, S.V.; Dong, J.; Peters-Lidard, C.D.; Mocko, D.; Gómez, B. Role of Forcing Uncertainty and Background Model Error Characterization in Snow Data Assimilation. Hydrol. Earth Syst. Sci. 2017, 21, 2637–2647. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.; Zhang, Y.; Wang, J.; Tian, W.; Liu, Q.; Ma, G.; Kan, X.; Chu, Y. Downscaling Snow Depth Mapping by Fusion of Microwave and Optical Remote-Sensing Data Based on Deep Learning. Remote Sens. 2021, 13, 584. [Google Scholar] [CrossRef]
- Cao, Y.; Yang, X.; Zhu, X. Retrieval Snow Depth by Artificial Neural Network Methodology from Integrated AMSR-E and in-Situ Data—A Case Study in Qinghai-Tibet Plateau. Chin. Geogr. Sci. 2008, 18, 356–360. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S.; Abyaneh, H.Z.; Sharifi, M.R. Comparison of Artificial Neural Network and Combined Models in Estimating Spatial Distribution of Snow Depth and Snow Water Equivalent in Samsami Basin of Iran. Neural. Comput. Appl. 2010, 19, 625–635. [Google Scholar] [CrossRef]
- Tedesco, M.; Pulliainen, J.; Takala, M.; Hallikainen, M.; Pampaloni, P. Artificial Neural Network-Based Techniques for the Retrieval of SWE and Snow Depth from SSM/I Data. Remote Sens. Environ. 2004, 90, 76–85. [Google Scholar] [CrossRef]
- Zaerpour, A.; Adib, A.; Motamedi, A. Snow Depth Retrieval from Passive Microwave Imagery Using Different Artificial Neural Networks. Arab. J. Geosci. 2020, 13, 696. [Google Scholar] [CrossRef]
- Davis, D.T.; Chen, Z.; Tsang, L.; Hwang, J.N.; Chang, A.T.C. Retrieval of Snow Parameters by Iterative Inversion of a Neural Network. IEEE Trans. Geosci. Remote Sens. 1993, 31, 842–852. [Google Scholar] [CrossRef]
- Tsang, L.; Chen, Z.; Oh, S.; Marks, R.J.; Chang, A.T.C. Inversion of Snow Parameters from Passive Microwave Remote Sensing Measurements by a Neural Network Trained with a Multiple Scattering Model. IEEE Trans. Geosci. Remote Sens. 1992, 30, 1015–1024. [Google Scholar] [CrossRef]
- Kang, D.H.; Tan, S.; Kim, E.J. Evaluation of Brightness Temperature Sensitivity to Snowpack Physical Properties Using Coupled Snow Physics and Microwave Radiative Transfer Models. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10241–10251. [Google Scholar] [CrossRef]
- Karystinos, G.N.; Pados, D.A. On Overfitting, Generalization, and Randomly Expanded Training Sets. IEEE Trans Neural Netw 2000, 11, 1050–1057. [Google Scholar] [CrossRef]
- Ahmad, J.A.; Forman, B.A.; Kwon, Y. Analyzing Machine Learning Predictions of Passive Microwave Brightness Temperature Spectral Difference Over Snow-Covered Terrain in High Mountain Asia. Front. Earth Sci. 2019, 7, 212. [Google Scholar] [CrossRef] [Green Version]
- Xue, Y.; Forman, B.A. Integration of Satellite-Based Passive Microwave Brightness Temperature Observations and an Ensemble-Based Land Data Assimilation Framework to Improve Snow Estimation in Forested Regions. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 311–314. [Google Scholar] [CrossRef]
- Revuelto, J.; Billecocq, P.; Tuzet, F.; Cluzet, B.; Lamare, M.; Larue, F.; Dumont, M. Random Forests as a Tool to Understand the Snow Depth Distribution and Its Evolution in Mountain Areas. Hydrol. Process. 2020, 34, 5384–5401. [Google Scholar] [CrossRef]
- Zhang, J.; Pohjola, V.A.; Pettersson, R.; Norell, B.; Marchand, W.-D.; Clemenzi, I.; Gustafsson, D. Improving the Snowpack Monitoring in the Mountainous Areas of Sweden from Space: A Machine Learning Approach. Environ. Res. Lett. 2021, 16, 84007. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.; Luojus, K.; Pan, J.; Lemmetyinen, J.; Takala, M.; Wu, S. Snow Depth Estimation and Historical Data Reconstruction over China Based on a Random Forest Machine Learning Approach. Cryosphere 2020, 14, 1763–1778. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.; Pan, J.; Shi, J.; Wu, S.; Wang, J.; Pan, F. Comparison of Machine Learning-Based Snow Depth Estimates and Development of a New Operational Retrieval Algorithm over China. Remote Sens. 2022, 14, 2800. [Google Scholar] [CrossRef]
- Luojus, K.; Pulliainen, J.; Takala, M.; Lemmetyinen, J.; Mortimer, C.; Derksen, C.; Mudryk, L.; Moisander, M.; Hiltunen, M.; Smolander, T.; et al. GlobSnow v3.0 Northern Hemisphere Snow Water Equivalent Dataset. Sci. Data 2021, 8, 163. [Google Scholar] [CrossRef] [PubMed]
- Xiong, C.; Yang, J.; Pan, J.; Lei, Y.; Shi, J. Mountain Snow Depth Retrieval from Optical and Passive Microwave Remote Sensing Using Machine Learning. IEEE Geosci. Remote Sens. Lett. 2022, 19, 2001705. [Google Scholar] [CrossRef]
- Yan, D.; Ma, N.; Zhang, Y. Development of a Fine-Resolution Snow Depth Product Based on the Snow Cover Probability for the Tibetan Plateau: Validation and Spatial–Temporal Analyses. J. Hydrol. 2021, 604, 127027. [Google Scholar] [CrossRef]
- Dai, L.; Che, T.; DIng, Y.; Hao, X. Evaluation of Snow Cover and Snow Depth on the Qinghai-Tibetan Plateau Derived from Passive Microwave Remote Sensing. Cryosphere 2017, 11, 1933–1948. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Zhang, X.; Liang, T.; Xie, H.; Wang, X.; Feng, Q.; Chen, Q. A New Approach of Dynamic Monitoring of 5-Day Snow Cover Extent and Snow Depth Based on MODIS and AMSR-E Data from Northern Xinjiang Region. Hydrol. Process. 2012, 26, 3052–3061. [Google Scholar] [CrossRef]
- Wei, Y.; Li, X.; Li, L.; Gu, L.; Zheng, X.; Jiang, T.; Li, X. An Approach to Improve the Spatial Resolution and Accuracy of AMSR2 Passive Microwave Snow Depth Product Using Machine Learning in Northeast China. Remote Sens. 2022, 14, 1480. [Google Scholar] [CrossRef]
- Brown, R.D.; Braaten, R.O. Spatial and Temporal Variability of Canadian Monthly Snow Depths, 1946–1995. Atmos. -Ocean 2010, 36, 37–54. [Google Scholar] [CrossRef]
- Sturm, M.; Holmgren, J.; Liston, G.E. A Seasonal Snow Cover Classification System for Local to Global Applications. J. Clim. 1995, 8, 1261–1283. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, T.; Zhong, X.; Li, X. Spatiotemporal Variation of Snow Depth in the Northern Hemisphere from 1992 to 2016. Remote Sens. 2020, 12, 2728. [Google Scholar] [CrossRef]
- Girotto, M.; Musselman, K.N.; Essery, R.L.H. Data Assimilation Improves Estimates of Climate-Sensitive Seasonal Snow. Curr. Clim. Change Rep. 2020, 6, 81–94. [Google Scholar] [CrossRef]
- Hedstrom, N.R.; Pomeroy, J.W. Measurements and Modelling of Snow Interception in the Boreal Forest. Hydrol. Process. 1998, 12, 1611–1625. [Google Scholar] [CrossRef]
- Kurvonen, L.; Hallikainen, M. Influence of Land-Cover Category on Brightness Temperature of Snow. IEEE Trans. Geosci. Remote Sens. 1997, 35, 367–377. [Google Scholar] [CrossRef]
- Vuyovich, C.M.; Jacobs, J.M.; Daly, S.F. Comparison of Passive Microwave and Modeled Estimates of Total Watershed SWE in the Continental United States. Water Resour. Res. 2014, 50, 9088–9102. [Google Scholar] [CrossRef] [Green Version]
- Che, T.; Dai, L.; Zheng, X.; Li, X.; Zhao, K. Estimation of Snow Depth from Passive Microwave Brightness Temperature Data in Forest Regions of Northeast China. Remote Sens. Environ. 2016, 183, 334–349. [Google Scholar] [CrossRef]
- Markus, T.; Powell, D.C.; Wang, J.R. Sensitivity of Passive Microwave Snow Depth Retrievals to Weather Effects and Snow Evolution. IEEE Trans. Geosci. Remote Sens. 2006, 44, 68–77. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Fassnacht, S.R.; Heath, J.T.; Musselman, K.N.; Revuelto, J.; Latron, J.; Morán-Tejeda, E.; Jonas, T. Small Scale Spatial Variability of Snow Density and Depth over Complex Alpine Terrain: Implications for Estimating Snow Water Equivalent. Adv. Water Resour. 2013, 55, 40–52. [Google Scholar] [CrossRef] [Green Version]
- Good, W.; Schanda, E. Towards the Definition of Optimum Sensor Specifications for Microwave Remote Sensing of Snow. IEEE Trans. Geosci. Remote Sens. 1982, 20, 57–66. [Google Scholar] [CrossRef]
- Kang, D.H.; Barros, A.P.; Déry, S.J. Evaluating Passive Microwave Radiometry for the Dynamical Transition from Dry to Wet Snowpacks. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3–15. [Google Scholar] [CrossRef]
- Vuyovich, C.M.; Jacobs, J.M.; Hiemstra, C.A.; Deeb, E.J. Effect of Spatial Variability of Wet Snow on Modeled and Observed Microwave Emissions. Remote Sens. Environ. 2017, 198, 310–320. [Google Scholar] [CrossRef]
- Stiles, W.H.; Ulaby, F.T. The Active and Passive Microwave Response to Snow Parameters: 1. Wetness. J. Geophys. Res. Ocean. 1980, 85, 1037–1044. [Google Scholar] [CrossRef]
- Hallikainen, M.T.; Ulaby, F.T.; Abdelrazik, M. Dielectric Properties of Snow In the 3 to 37 GHz Range. IEEE Trans. Antennas Propag. 1986, AP-34, 1329–1340. [Google Scholar] [CrossRef]
- Walker, A.E.; Goodison, B.E. Discrimination of a Wet Snow Cover Using Passive Microwave Satellite Data. Ann. Glaciol. 1993, 17, 307–311. [Google Scholar] [CrossRef]
- Grody, N.C.; Basist, A.N. Global Identification of Snowcover Using Ssm/i Measurements. IEEE Trans. Geosci. Remote Sens. 1996, 34, 237–249. [Google Scholar] [CrossRef]
- Rees, A.; Derksen, C.; English, M.; Walker, A.; Duguay, C. Uncertainty in Snow Mass Retrievals from Satellite Passive Microwave Data in Lake-Rich High-Latitude Environments. Hydrol. Process. 2006, 20, 1019–1022. [Google Scholar] [CrossRef]
- Gunn, G.E.; Duguay, C.R.; Derksen, C.; Lemmetyinen, J.; Toose, P. Evaluation of the HUT Modified Snow Emission Model over Lake Ice Using Airborne Passive Microwave Measurements. Remote Sens. Environ. 2011, 115, 233–244. [Google Scholar] [CrossRef]
- Duguay, C.; English, M.C.; Profile, S.; Rees, A. Preliminary Assessment of the Impact of Lakes on Passive Microwave Snow Retrieval Algorithms in the Arctic. In Proceedings of the 62nd Eastern Snow Conference Proceedings, Waterloo, ON, Canada, 7–10 June 2005; pp. 223–228. [Google Scholar]
- Tedesco, M.; Wang, J.R. Atmospheric Correction of AMSR-E Brightness Temperatures for Dry Snow Cover Mapping. IEEE Geosci. Remote Sens. Lett. 2006, 3, 320–324. [Google Scholar] [CrossRef]
- Wang, J.R.; Tedesco, M. Identification of Atmospheric Influences on the Estimation of Snow Water Equivalent from AMSR-E Measurements. Remote Sens. Environ. 2007, 111, 398–408. [Google Scholar] [CrossRef]
- Gu, L.; Ren, R.; Li, X. Snow Depth Retrieval Based on a Multifrequency Dual-Polarized Passive Microwave Unmixing Method from Mixed Forest Observations. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7279–7291. [Google Scholar] [CrossRef]
- Gu, L.; Ren, R.; Li, X.; Zhao, K. Snow Depth Retrieval Based on a Multifrequency Passive Microwave Unmixing Method for Saline-Alkaline Land in the Western Jilin Province of China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2210–2222. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, L.; Wang, G.; Hao, S.; Chen, Z. Using a Linear Unmixing Method to Improve Passive Microwave Snow Depth Retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4414–4429. [Google Scholar] [CrossRef]
- Dong, J.; Walker, J.P.; Houser, P.R. Factors Affecting Remotely Sensed Snow Water Equivalent Uncertainty. Remote Sens. Environ. 2005, 97, 68–82. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.; Dai, L.; Pan, J.; Wu, S.; Wang, G. The Consistency of SSM/I vs. SSMIS and the Influence on Snow Cover Detection and Snow Depth Estimation over China. Remote Sens. 2019, 11, 1879. [Google Scholar] [CrossRef]
- Durand, M.; Kim, E.J.; Margulis, S.A.; Molotch, N.P. A First-Order Characterization of Errors from Neglecting Stratigraphy in Forward and Inverse Passive Microwave Modeling of Snow. IEEE Geosci. Remote Sens. Lett. 2011, 8, 730–734. [Google Scholar] [CrossRef]
- Guo, Y.; Shi, J.; Du, J.; Fu, X. Evaluation of Terrain Effect on Microwave Radiometer Measurement and Its Correction. Int. J. Remote Sens. 2011, 32, 8899–8913. [Google Scholar] [CrossRef]
- Mätzler, C.; Standley, A.; Ma¨tzler, C.; Ma¨tzler, M. Technical Note: Relief Effects for Passive Microwave Remote Sensing Technical Note Relief EOE Ects for Passive Microwave Remote Sensing. Int. J. Remote Sens. 2000, 21, 2403–2412. [Google Scholar] [CrossRef]
- Wang, P.; Jiang, L.; Zhang, L.; Guo, Y. Impact of Terrain Topography on Retrieval of Snow Water Equivalence Using Passive Microwave Remote Sensing. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 1757–1760. [Google Scholar] [CrossRef]
- Jin, R.; Li, X.; Che, T. A Decision Tree Algorithm for Surface Soil Freeze/Thaw Classification over China Using SSM/I Brightness Temperature. Remote Sens. Environ. 2009, 113, 2651–2660. [Google Scholar] [CrossRef]
- Armstrong, R.L.; Brodzik, M.J. Hemispheric-Scale Comparison and Evaluation of Passive-Microwave Snow Algorithms. Ann. Glaciol. 2002, 34, 38–44. [Google Scholar] [CrossRef] [Green Version]
- Deschamps-Berger, C.; Gascoin, S.; Berthier, E.; Deems, J.; Gutmann, E.; Dehecq, A.; Shean, D.; Dumont, M. Snow Depth Mapping from Stereo Satellite Imagery in Mountainous Terrain: Evaluation Using Airborne Laser-Scanning Data. Cryosphere 2020, 14, 2925–2940. [Google Scholar] [CrossRef]
- Lievens, H.; Brangers, I.; Marshall, H.P.; Jonas, T.; Olefs, M.; de Lannoy, G. Sentinel-1 Snow Depth Retrieval at Sub-Kilometer Resolution over the European Alps. Cryosphere 2022, 16, 159–177. [Google Scholar] [CrossRef]
- He, S.; Ohara, N.; Miller, S.N. Understanding Subgrid Variability of Snow Depth at 1-Km Scale Using Lidar Measurements. Hydrol. Process. 2019, 33, 1525–1537. [Google Scholar] [CrossRef]
- Hou, Y.; Huang, X.; Zhao, L. Point-to-Surface Upscaling Algorithms for Snow Depth Ground Observations. Remote Sens. 2022, 14, 4840. [Google Scholar] [CrossRef]
Figure 1. Brightness temperature variation with snow depth simulated using MEMLS snow emission model.
Figure 1. Brightness temperature variation with snow depth simulated using MEMLS snow emission model.

Figure 2. Horizontally polarized Brightness temperature difference (BTD18,36 GHz) between 18 and 36 GHz variation with snow density and grain size as simulated by MEMLS.
Figure 2. Horizontally polarized Brightness temperature difference (BTD18,36 GHz) between 18 and 36 GHz variation with snow density and grain size as simulated by MEMLS.

Figure 3. Different types of PMW based snow depth estimation models.
Figure 3. Different types of PMW based snow depth estimation models.

| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
|---|
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Tanniru, S.; Ramsankaran, R. Passive Microwave Remote Sensing of Snow Depth: Techniques, Challenges and Future Directions. Remote Sens. 2023, 15, 1052. https://doi.org/10.3390/rs15041052
AMA Style
Tanniru S, Ramsankaran R. Passive Microwave Remote Sensing of Snow Depth: Techniques, Challenges and Future Directions. Remote Sensing. 2023; 15(4):1052. https://doi.org/10.3390/rs15041052
Chicago/Turabian Style
Tanniru, Srinivasarao, and RAAJ Ramsankaran. 2023. "Passive Microwave Remote Sensing of Snow Depth: Techniques, Challenges and Future Directions" Remote Sensing 15, no. 4: 1052. https://doi.org/10.3390/rs15041052
APA Style
Tanniru, S., & Ramsankaran, R. (2023). Passive Microwave Remote Sensing of Snow Depth: Techniques, Challenges and Future Directions. Remote Sensing, 15(4), 1052. https://doi.org/10.3390/rs15041052
Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.
Article Metrics
Article Access Statistics
For more information on the journal statistics, click here.
Multiple requests from the same IP address are counted as one view.
We use cookies on our website to ensure you get the best experience.
Read more about our cookies here.