Water Constituents and Water Depth Retrieval from Sentinel-2A—A First Evaluation in an Oligotrophic Lake (original) (raw)
Author / Affiliation / Email
Article Menu
/ajax/scifeed/subscribe
Font Type:
Arial Georgia Verdana
Open AccessArticle
by
Katja Dörnhöfer
Anna Göritz
2,3,
Peter Gege
Bringfried Pflug
Natascha Oppelt
1
Earth Observation and Modelling, Department of Geography, Christian-Albrechts-Universität zu Kiel, Ludewig-Meyn-Str. 14, Kiel D-24098, Germany
2
German Aerospace Center, Remote Sensing Technology Institute, Münchner Str. 20, Oberpfaffenhofen, Weßling D-82234, Germany
3
Remote Sensing Technology, Technische Universität München, Arcisstr. 21, München D-80333, Germany
4
German Aerospace Center, Remote Sensing Technology Institute, Rutherfordstr. 2, Berlin-Adlershof D-12489, Germany
*
Author to whom correspondence should be addressed.
Submission received: 30 August 2016 /Revised: 17 October 2016 /Accepted: 3 November 2016 /Published: 11 November 2016
Abstract
:
Satellite remote sensing may assist in meeting the needs of lake monitoring. In this study, we aim to evaluate the potential of Sentinel-2 to assess and monitor water constituents and bottom characteristics of lakes at spatio-temporal synoptic scales. In a field campaign at Lake Starnberg, Germany, we collected validation data concurrently to a Sentinel-2A (S2-A) overpass. We compared the results of three different atmospheric corrections, i.e., Sen2Cor, ACOLITE and MIP, with in situ reflectance measurements, whereof MIP performed best (r = 0.987, RMSE = 0.002 sr−1). Using the bio-optical modelling tool WASI-2D, we retrieved absorption by coloured dissolved organic matter (aCDOM(440)), backscattering and concentration of suspended particulate matter (SPM) in optically deep water; water depths, bottom substrates and aCDOM(440) were modelled in optically shallow water. In deep water, SPM and aCDOM(440) showed reasonable spatial patterns. Comparisons with in situ data (mean: 0.43 m−1) showed an underestimation of S2-A derived aCDOM(440) (mean: 0.14 m−1); S2-A backscattering of SPM was slightly higher than backscattering from in situ data (mean: 0.027 m−1 vs. 0.019 m−1). Chlorophyll-a concentrations (~1 mg·m−3) of the lake were too low for a retrieval. In shallow water, retrieved water depths exhibited a high correlation with echo sounding data (r = 0.95, residual standard deviation = 0.12 m) up to 2.5 m (Secchi disk depth: 4.2 m), though water depths were slightly underestimated (RMSE = 0.56 m). In deeper water, Sentinel-2A bands were incapable of allowing a WASI-2D based separation of macrophytes and sediment which led to erroneous water depths. Overall, the results encourage further research on lakes with varying optical properties and trophic states with Sentinel-2A.
Graphical Abstract
1. Introduction
The monitoring of lake water quality is gaining increasing importance due to an increase in stressors such as climate change, eutrophication, contamination of organic and inorganic substances, and anthropogenic influences which threaten ecological functions [1,2]. Humans both benefit from and depend on a variety of ecosystem services provided by lakes, e.g., drinking water, irrigation, energy production, fisheries, and recreation [3]. Therefore, healthy lake ecosystems are of great importance. International and national legislations such as the European Water Framework Directive [4] or the US Clean Water Act [5] include regular monitoring schemes that observe the ecological states of lakes and detect changes which may influence lake ecology and water quality [6]. Most monitoring schemes are based on selective sampling during summer or installation of measurement buoys [7]. Deploying these sampling strategies is labour, time and cost intensive [8]; yet, it may not allow for the detection of changes which occur on varying temporal and spatial scales [9].
To overcome spatio-temporal limitations, remote sensing may assist in situ monitoring since it can extract indicators on water transparency, biota, bathymetry, water surface temperature and ice phenology [10]. Empirical and physical-based algorithms can be used to retrieve water constituents, water depths and bottom substrates. Several publications provide reviews of existing approaches [10,11,12,13,14]. Compared to empirical algorithms, physically-based approaches are broadly applicable and transferable among lakes and sensors. Suitable sensors must deploy bands in the visible and near-infrared (VNIR) wavelengths with high radiometric sensitivity such as ocean colour sensors (e.g., MODIS and MERIS). Owing to their spatial resolution (≥300 m), studies conducted with these sensors focus mainly on large lakes such as Lake Balaton [15], Lake Geneva [16], Lake Taihu [17,18,19], or Great Lakes [20], but rarely on small lakes [21,22]. Studies on smaller lakes refer to less sensitive Landsat data [23] or to high spatial resolutions from commercial sensors such as WorldView [24] or Quickbird [25]. Moreover, airborne hyperspectral data often are used for mapping bottom substrates or water depths (e.g., [26,27,28]). Though designed primarily for land applications, the new generation of multispectral sensors such as Landsat 8 and Sentinel-2 offers unprecedented opportunities for lake remote sensing [10,29]. Additional bands in the VNIR wavelengths, higher radiometric sensitivity, signal-to-noise ratios and, in the case of Sentinel-2—the spatial resolution of up to 10 m, enables detailed lake analyses. Synergetic multi-sensor use may increase temporal coverage and allow for cloud-free data [10]. Landsat 8 has the capabilities for retrieving water constituents [30,31,32,33], water depths [31,34], Secchi disk depth [35] and bottom substrates [34]. Model based sensitivity and field data analyses have revealed a high potential of Sentinel-2 for water constituent retrieval [36,37] and bottom substrate mapping such as coral reefs [38]. A study by Toming et al. ([39], this special issue) focused on transferring empirical algorithms to S2-A for retrieving water quality parameters in optically deep water.
This study was conducted at Lake Starnberg, a clear, deep lake located in the peri-alpine region; its current trophic state is oligotrophic [40]. The shallow waters along the shoreline are partially covered by submerged macrophytes, sand or stony ground. Earlier studies at Lake Starnberg analysed multi-temporal RapidEye data with a depth-invariant index to track the development of submerged native and invasive macrophytes [41,42]. Rößler et al. [43] applied the bio-optical modelling tool BOMBER [44] in order to retrieve water constituents and submerged macrophytes from airborne hyperspectral imagery. Gege [45] also used a physical based bio-optical modelling tool, i.e., WASI-2D [46], and focused on deriving water depths from airborne hyperspectral imagery.
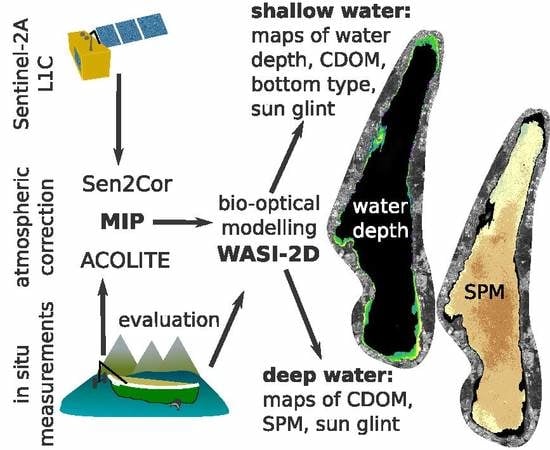
In this study, we assess the suitability of S2-A for retrieving water constituents, water depths and bottom substrates using the physically-based model, WASI-2D. The study is based on the results by Dörnhöfer et al. [47] who demonstrated the potential of S2-A data for retrieving SPM, aCDOM(440) and water depths. We aim (1) to compare the performance of three different atmospheric corrections over water surfaces (2) to evaluate the capability of S2-A to retrieve absorption by coloured dissolved organic matter (aCDOM), backscattering and concentration of suspended particulate matter (SPM) in optically deep water; (3) to derive water depths and bottom substrates in optically shallow waters. For validation, we use in situ data acquired during a measurement campaign concurrently with a S2-A image acquisition from August 2015.
2. Materials and Methods
2.1. Study Area and Field Data
Located in the pre-alpine region, Lake Starnberg (11°19′14′′E, 47°49′34′′N) formed during the last ice age. With an area of 56.4 km², it is the fifth largest lake in Germany reaching a maximum depth of 127.8 m (average depth: 53.2 m) [48]. In comparison to the lake’s total volume (2.999 Mio. m³), the catchment area, made up primarily of forest and cultivated grassland, is relatively small (315 km²). Inflows are slow, and consist of groundwater flows, small creeks and streams. Outflows include the river Würm, located at the northern end of the lake which also has a slow discharge. Low inflow (3.6 m³·s−1 [49]) and low discharge (4.5 m³·s−1 [49]) result in a long residence time of water (21 years) [48]. After showing rising levels of eutrophication, a drainage system was introduced in the 1970s. Since then, the water quality steadily increased and the lake turned into a popular recreation area. Between 2004 and 2014, the average total phosphorous concentration was around 6 ± 2 mg·m−3, nitrogen concentration around 0.3 ± 0.1 g·m−3, average chlorophyll-a (chl-a) concentration in 2 m water depth was 2.3 ± 1.0 mg·m−3; Secchi disk depth was on average 9 ± 2 m during winter and 6 ± 2 m during summer season [50]. Sandy sediments are the predominating substrate, gravel forms the substrate in the very shallow water (<0.5 m water depth). A variety of submerged macrophytes colonise shallow waters; Chara sp. are the predominating macrophyte species with interspersed patches of Potamogeton sp. In the northern and western parts of the lake (Elodea nuttallii, Elodea canadensis) and south-western parts (Najas marina), invasive macrophyte species are present. Recently, the monomictic lake has been classified as oligotrophic—equal to its natural state [40].
To evaluate S2-A ability to retrieve information on lake ecology indicators, such as SPM, aCDOM(440) or bottom substrates [10], we conducted a measurement campaign on 12–13 August 2015. We compiled field data which allow us to assess performance of atmospheric correction procedures, to adapt and regionalise a bio-optical model, and to validate resulting S2-A derived products. We focused on the southern lake area with moderately sloping regions (Figure 1). At the end of the text, a list of all used abbreviations is provided. Figure 2 provides a schematic illustration of the methodological workflow.
Close to the satellite overpass, we measured aerosol optical thickness (AOT) with Microtops sun photometers (AOT = 0.151 at 550 nm, 12:17 UTC + 2). AOT data from a nearby (23 km) Aeronet station “Hohenpeißenberg” (989 m AMSL, AOT = 0.168 at 550 nm, 12:22 UTC + 2) were extrapolated to lake elevation (AOT = 0.179 at 550 nm) [51]. Using an Ibsen FREEDOM VIS FSV-305 spectroradiometer (390–850 nm, 0.5 nm sampling interval) and a Labsphere reflectance standard with ~10% diffuse reflectance [52], we measured radiance reflectance spectra nadir-looking approx. 0.5 m above the water surface R r s − F R E E D O M B O A ( 0 + , λ ) at all seven measurement sites concurrently (−1 to +2 h) to the S2-A overpass on 13 August 2015 (12:16 UTC + 2). The location and number of measurement sites was a trade-off between covering different water depths, bottom substrates, deep and shallow water within a narrow time window. Measurement sites A to E were located in optically shallow water where the ground was visible; F and G were located in optically deep water with a measured mean Secchi disk depth of 4.2 ± 0.3 m. Sediment samples were collected with a Ekman-Birge type bottom sampler at each measurement site and R r s − F R E E D O M B O A ( 0 + , λ ) recorded ex situ using the FREEDOM spectroradiometer. We measured downwelling spectral irradiance E d ( z , λ ) using a TriOS RAMSES ACC-VIS sensor, and upwelling spectral radiance L u ( z , λ ) with a TriOS RAMSES ARC-VIS sensor (320–950 nm, 3.3 nm sampling interval). These radiometers and a Tritech PA500 altimeter were mounted on a custom built frame ensuring that the entrance optics of each instrument were at the same depth (z). This setup allowed for simultaneous measurements of all instruments at varying sensor depths (z) below (z < 0, measurement site A–E, G) and above water (z = 0 + at F and G). The depth of the sensor level was determined using a step counter for measuring the cable length (uncertainty for levelling the sensor: Approx. ± 2 cm at calm conditions ); the distance to the ground was measured in a range from 0 to 10 m at a resolution of 1 mm with the Tritech PA500 altimeter. Radiance reflectance was calculated simultaneously for each recorded pair of measurements as R r s − R A M S E S ( z , λ ) = L u ( z , λ ) / E d ( z , λ ) . To account for the spectral differences of the L u and E d sensors, we resampled the spectra to a uniform 1 nm grid using cubic interpolation.
A second data set was collected on the previous day at the same seven locations. Geolocation uncertainties (5–20 m, at D: 50m) due to boat drift and GPS positional inaccuracies were considered in the validation process as described in Section 2.2. During this campaign, we measured E d ( z , λ ) and L u ( z , λ ) in several depths with a second set of identical RAMSES radiometers [53]. Furthermore, we collected water samples from the top (0.3 m) water layer for further laboratory analysis. The temporal offset between water sampling and S2-A overpass is noticeable. Lakes are dynamic systems requiring sampling temporally close to image acquisition. Water body conditions can change between sampling dates, causing discrepancies and incorrect validation. The weather conditions were stable and did not indicate changing water constituent concentrations between both days [54]. RAMSES data of both campaign dates showed similar reflectances and indicated stable water conditions. Therefore, the water samples taken the day before seem to be comparable. We determined SPM concentration gravimetrically according to Strömbeck and Pierson [55]; a 1 L water sample was filtered through pre-weighed cellulose-acetate filters (pore size: 0.45 µm). The filters were then dried at 105 °C and weighed again. To retrieve concentration of chl-a, we filtered a 1 L water sample through a GF/F filter (pore size: 0.7 µm). Pigments were removed from filter using 99.9% acetone. Pigment concentration was measured using high performance liquid chromatography.
For assessing the accuracy of retrieved water depths, we used echo sounding data (BioSonics MX aquatic habitat echosounder) acquired in June 2012 in the southern part of the lake (near Seeshaupt). Water level measurements on 13 August (584.3 m AMSL, [56]) were close to mean water level measured during June 2012 (584.4 m AMSL, [56]). The data therefore seem to be comparable. We distinguished optically deep and shallow water with the 8 m water depth line in reference to the official bathymetry map (Figure 1, [57]).
2.2. Preprocessing of S2-A Data
S2-A acquired an image over Lake Starnberg on 13 August at 12:16 (UTC+2). We conducted atmospheric correction procedures on reprocessed L1C data (processing baseline: 02.01) using three different algorithms, i.e., Sen2Cor (Version 2.2.1, [58]), ACOLITE (Version 20160520.1, [59,60]) and MIP (Modular Inversion and Processing System, [61,62,63]).
Prior to atmospheric correction, Sen2Cor classifies the scene roughly into cloud and land cover classes. The atmospheric correction is based on 24 look-up table sets modelled with libRadtran [58]. Sen2Cor applied a dense, dark vegetation approach to determine AOT using bands B12 (2190 nm), B04 (665 nm) and B03 (560 nm). For assessing water vapour column height, the bands B8A (865 nm) and B09 (945 nm) were used [58]. We configured Sen2Cor for processing with default settings including correction for adjacency effects with an adjacency range of 1000 m. We used the rural aerosol model, a SRTM-digital elevation model and selected ozone concentration calculation based on the value provided in the metadata. We calculated Sen2Cor products on the 10 m pixel size; bands with a spatially lower resolution were only resampled rather than interpolated. Since Sen2Cor has been developed for land surfaces it lacks a correction of water surface effects and provides the corrected data in units of bottom of atmosphere irradiance reflectance R B O A ( 0 + , λ ) . For analysing the water body, we used bottom of atmosphere radiance reflectance R r s B O A ( 0 + , λ ) as the sum of remote sensing reflectance and water surface reflectance; we therefore converted R B O A ( 0 + , λ ) to R r s B O A ( 0 + , λ ) according to Equation (1) [64]:
R r s B O A ( 0 + , λ ) [ s r − 1 ] = R B O A ( 0 + , λ ) π
(1)
ACOLITE is an atmospheric correction tool specifically developed for water bodies, currently available for Landsat 8 and Sentinel-2 [59,60,65]. ACOLITE amended atmospheric Rayleigh reflectance using a Second Simulation of the Satellite Signal in the Solar Spectrum (6S)-V look-up table which considers sensor and sun geometry as well as sun and sky glint (modelled for a wind speed of 1 m·s−1) [60]. Atmospheric pressure correction was conducted for the site elevation of 595 m AMSL. Pixels having a Rayleigh corrected irradiance reflectance above 0.03 (0.0215 by default) in band B09 (1610 nm) were masked as non-water. Using the ratio between shortwave infrared (SWIR) bands B09 (1610 nm) and B10 (2190 nm) ACOLITE estimated the aerosol type over water pixels. The reflectance in SWIR bands above water bodies was assumed to be zero, observed reflectance was assumed to result solely from aerosol. Aerosol reflectance was then extrapolated exponentially to VNIR wavelengths [60]. We chose the option “estimating aerosol type on a per pixel basis”, but also followed the suggestion by Vanhellemont and Ruddick [59] to conduct the estimation on spatially binned (320 × 320 m²) SWIR bands to reduce noise effects from low signal-to-noise ratio and low reflectances in these bands. The resulting R r s B O A ( 0 + , λ ) dataset was resampled to 10 m pixel size, whereas bands with 20 m and 60 m spatial resolution were replicated.
MIP is a physics-based, sensor-independent, atmospheric correction software developed for coastal and inland waters [61,62,63]. Atmospheric scattering and absorption is calculated based on radiative transfer modelling considering bidirectional properties. Vertical characterisation of atmospheric layers follows MODTRAN, and considers different seasons, aerosol types and AOT. Furthermore, MIP analytically calculates, and subtracts the contribution of adjacent pixels on the reflectance [61]. Currently, MIP does not correct sun glint for sensors such as S2-A. Land and cloud masking is conducted automatically during processing. The resulting R r s B O A ( 0 + , λ ) dataset was interpolated to 10 m pixel size using a regression based filtering approach. Additionally, MIP calculated a quality indicator for each pixel which documents fit performance and sun glint [61]. EOMAP GmbH & Co.KG holds MIP, distributes atmospherically corrected products and conducted data processing.
For evaluating the performance of the three different atmospheric correction algorithms, we resampled the FREEDOM R r s − F R E E D O M B O A ( 0 + , λ ) measurements to the S2-A spectral response curves [66] according to Equation (2):
R r s − F R E E D O M B O A ( 0 + , λ X ) = ∑ i = λ m i n λ m a x r ( λ i ) · R r s − F R E E D O M B O A ( 0 + , λ i ) ∑ i = λ m i n λ m a x r ( λ i )
(2)
where R r s − F R E E D O M B O A ( 0 + , λ X ) is the band equivalent reflectance for band X , λ m i n and λ m a x represent start and end wavelengths of the filter function for band X , r ( λ i ) is the relative response for band X at wavelength λ i , R r s − F R E E D O M B O A ( 0 + , λ i ) is the reflectance measured by the FREEDOM spectroradiometer at band i centred at wavelength λ i .
In cases with more than 1 resp. 2 measurements at a measurement site, we calculated the mean and standard deviation of in situ measured reflectance. In the 10 × 10 m² pixel size S2-A data, we located the pixel corresponding to the GPS location of a measurement site. To address GPS positional inaccuracies, potential boat drifting and water masses, we calculated the mean spectrum and standard deviation of the S2-A R r s − S 2 − A B O A ( 0 + , λ ) spectra based on a 7 × 7 pixel environment for deep water measurement sites (F and G). To reduce the effect of bottom heterogeneity we chose a 3 × 3 pixel environment in shallow water (site A to E). We then compared resampled mean in situ R r s − F R E E D O M B O A ( 0 + , λ ) and mean S2-A R r s − S 2 − A B O A ( 0 + , λ ) spectra, and calculated Pearson’s correlation coefficient (r, Equation (3)) to evaluate the correspondence in shape.
r = ∑ X = 1 n ( R r s − F R E E D O M B O A ( 0 + , λ X ) − R r s − F R E E D O M B O A ( 0 + ) ¯ ) · ( R r s − S 2 − A B O A ( 0 + , λ X ) − R r s − S 2 − A B O A ( 0 + ) ¯ ) ∑ X = 1 n ( R r s − F R E E D O M B O A ( 0 + , λ X ) − R r s − F R E E D O M B O A ¯ ( 0 + ) ) 2 · ∑ i = 1 7 ( R r s − S 2 − A B O A ( 0 + , λ X ) − R r s − S 2 − A B O A ( 0 + ) ¯ ) 2
(3)
with R r s − F R E E D O M B O A ( 0 + , λ X ) and R r s − S 2 − A B O A ( 0 + , λ X ) being the reflectance at band λ X (band B01- B07) of resampled in situ respectively S2-A data; R r s − F R E E D O M B O A ( 0 + ) ¯ respectively R r s − S 2 − A B O A ( 0 + ) ¯ are the mean reflectance values calculated from band B01–B07 (n = 7).
The second calculated performance indicator was Root Mean Square Error (RMSE, Equation (4)) which expressed the absolute difference between both reflectance spectra [67].
R M S E = ∑ X = 1 n ( R r s − F R E E D O M B O A ( 0 + , λ X ) − R r s − S 2 − A B O A ( 0 + , λ X ) ) 2 n
(4)
We further calculated the Chi-square ( X 2 , Equation (5)) which incorporates both shape and intensity of spectra, and the mean absolute percentage error (MAPE, Equation (6)) which usually is easier to comprehend due to the percentage statement.
X 2 = ∑ X = 1 n ( R r s − S 2 − A B O A ( 0 + , λ X ) − R r s − F R E E D O M B O A ( 0 + , λ X ) ) 2 R r s − F R E E D O M B O A ( 0 + , λ X )
(5)
M A P E = 1 n · ∑ X = 1 n | R r s − F R E E D O M B O A ( 0 + , λ X ) − R r s − S 2 − A B O A ( 0 + , λ X ) R r s − F R E E D O M B O A ( 0 + , λ X ) | · 100
(6)
MIP showed best performance (cf. Section 3.1); we therefore used the MIP corrected dataset for further processing and analysis. The MIP R r s B O A ( 0 + , λ ) product with 10 m pixel size was resampled to 20 m and 60 m using nearest neighbour approach. For each data set (10 m, 20 m, and 60 m), we calculated the noise-equivalent remote sensing reflectance difference, NEΔRrsE, as the standard deviation of MIP R r s B O A ( 0 + , λ ) spectra within a relatively homogenous area in optically deep water [68]. It is an indicator for the suitability of the data for analysing water constituents concerning random noise. We chose an area of 320 × 320 m² which corresponds to 32 × 32 pixels in the 10 m product, 9 × 9 in the 20 m, and 3 × 3 in the 60 m product. Apart from the signal-to-noise ratio, the applied atmospheric correction and environmental conditions during image acquisition, such as water surface or downwelling irradiance, influence the NEΔRrsE. For analysing water constituents from remote sensing data, NEΔRrsE < 0.00025 sr−1 is optimal ([27], see black line in Figure 3). Figure 3 shows the resulting band and pixel size dependence of NEΔRrsE. Mean values of bands B01–B07 were 0.00014 sr−1, 0.00014 sr−1 and 0.00012 sr−1 for 10 m, 20 m and 60 m pixel size, respectively. Referring to Figure 3 and mean values, spatial binning from 10 m to 20 m barely improved NEΔRrsE; spatial binning to 60 m reduced NEΔRrsE in bands B01–B04, but slightly increased it in bands B05–B07. Except for band B01 (10 m and 20 m), all bands achieved values <0.00025 sr−1; concerning noise, we therefore considered the MIP corrected scene appropriate for further analyses.
2.3. Inverse Modelling with WASI-2D
WASI-2D is a freely available software tool (http://www.ioccg.org/data/software.html) for analysing atmospherically corrected multispectral and hyperspectral imagery in both optically deep and shallow water [46]. In optically deep water, absorption and scattering by optically active water constituents such as chl-a, SPM, CDOM and water itself, shape water reflectance. In optically shallow water, bottom reflectance and water depth additionally influence reflectance [10,14]. Satellite sensors, such as S2-A, measure top-of-atmosphere spectral radiances; the atmospheric correction algorithm then converts them to bottom-of-atmosphere reflectances. Such algorithms often lack a correction of specular reflectance of sun and sky at the surface, which can be quite significant for water. WASI-2D therefore includes a sky radiance model for correcting sun and sky glint.
To derive information on water constituents, bottom substrate and water depth from R r s B O A ( 0 + , λ ) spectra, WASI-2D includes several analytic models to analyse measured spectra using an optimisation approach. The optimisation procedure inversely models the R r s B O A ( 0 + , λ ) spectrum of each pixel adjusting a number of model parameters, called fit parameters, until the calculated spectrum matches R r s B O A ( 0 + , λ ) as close as possible. Fit parameters vary within a predefined range, depending on the study area’s characteristics. Curve fitting terminates when measured and inversely modelled spectra correspond best (residuum < 1.0 × 10−4, least squares). If the residuum criterion is not met, the fit routine stops after a pre-defined number of iterations. WASI-2D writes the final values of fit parameters for each pixel to file, resulting in a multi-band raster image where each band corresponds to a fit parameter. For modelling R r s B O A ( 0 + , λ ) in optically deep and shallow water, we applied the analytic equation of Albert and Mobley [69]. In the WASI implementation of this model, SPM and water comprise the backscattering properties; water, different classes of phytoplankton, CDOM and detritus can be selected as the absorbing components. In optically shallow water, water depth is additionally included in calculating reflectance of water; WASI-2D further considers contributions of up to six linearly mixed bottom types. To address surface reflectance, we applied the implemented model of sky radiance which is based on the downwelling irradiance model by Gregg and Carder [70]. In our data processing, WASI-2D accounted for reflected solar irradiance (sun glint) during inverse modelling. We omitted considerations to diffuse reflectance (sky glint) as it was included in MIP. A detailed description of the models can be found in Gege [46].
Inverse modelling was conducted using the MIP atmospherically corrected R r s B O A ( 0 + , λ ) dataset and bands B01 (443 nm) to B07 (783 nm). We therefore resampled the WASI-2D spectral database to the S2-A spectral response curves [66] adopting Equation (2). According to a previous study at Lake Starnberg dinoflagellates were chosen as phytoplankton type [45]. Based on results of the water sample analysis, the chl-a concentration was fixed to 1 mg·m−3. The CDOM absorption coefficient was modelled according to Equation (7),
a C D O M ( λ ) = a C D O M ( 440 ) · e − S C D O M · ( λ − 440 )
(7)
where a C D O M ( 440 ) (m−1) was treated as fit parameter while the slope factor S C D O M was set as constant (0.0155 nm−1, mean of in situ S). Backscattering of suspended matter was calculated according to Equation (8),
b b , S P M ( 550 ) = S P M · b b , S P M * ( 550 )
(8)
with SPM (g·m−3) treated as fit parameter in optically deep water, and set constant in shallow water (1.8 g·m−3, mean SPM of deep water result). When considering bottom reflectance in modelling shallow water, WASI-2D requires irradiance reflectance spectra representing the bottom types at the test site. WASI-2D allows for up to six different bottom types. Giardino et al. [34] advised using not more than two bottom types for multispectral imagery. We used a sandy sediment spectrum acquired ex situ with the FREEDOM radiometer on 13 August 2015 (Section 2.1), and a macrophyte spectrum of the predominating species (Chara sp., WASI-2D database) growing at the southern part of Lake Starnberg (Figure 4). The sum of fractional area (fA[sediment] and fA[macrophyte]) was allowed to range between 1.0 and 1.2. Since MIP lacked a correction of sun glint, the fraction of sun glint per pixel area (gdd) was chosen as a fit parameter in both optically shallow and deep water.
2.4. Retrieval of Inherent Optical Properties from In Situ Measurements
The downwelling irradiance in water, E d ( z < 0 , λ ) , can be used for determining the concentration of phytoplankton [71] and CDOM [72] if sensor depth z is large enough to capture the impact of absorption by water constituents on the spectral signature of E d ( z < 0 , λ ) . For lakes with chl-a and CDOM concentrations similar to Lake Starnberg, this critical depth is in the order of 1.0–1.5 m [71,72]. Following this principle, we estimated the CDOM parameters aCDOM(440) and S from RAMSES E d ( z < 0 , λ ) measurements in water.
First, we fitted the above water RAMSES measurements of downwelling irradiance E d ( 0 + , λ ) in WASI-2D using the Gregg and Carder model [70] to derive the atmospheric parameters required as input for modelling the under-water E d ( z < 0 , λ ) spectra. The turbiditiy coefficient and water vapour concentration were treated as fit parameters, the Angström exponent of aerosol scattering (1.32) and the scale height of ozone (0.45 cm) were kept constant. Second, we retrieved aCDOM(440) and S from E d ( z < 0 , λ ) measurements with z < −1 m by inverse modelling. The atmospheric parameters were kept constant at the results of step 1 for the actual site; phytoplankton was kept constant at 1 mg·m−3. The fractions of the direct and diffuse components of Ed(λ) and sensor depth were fitted along with aCDOM(440) and S.
Above water measurements of R r s B O A ( 0 + , λ ) from the RAMSES and FREEDOM sensors were used to estimate the backscattering coefficient of SPM, bb,SPM(550). Using WASI, we inversely modelled R r s − F R E E D O M B O A ( 0 + , λ ) and R r s − R A M S E S B O A ( 0 + , λ ) spectra which were measured at the optically deep sites F and G.
3. Results and Discussion
3.1. Comparison of Atmospheric Correction Approaches
We compared three approaches for atmospheric correction from which two were specifically developed for water surfaces. Figure 5a–g show resampled in situ spectra and atmospherically corrected spectra of the corresponding pixel environment. The common feature of the seven measurement sites is that all approaches retrieved different R r s B O A ( 0 + , λ ) spectra. Table 1 summarises performance indicators for evaluating the results of the three different atmospheric correction algorithms. MIP outperformed Sen2Cor and ACOLITE at most measurement sites (Table 1).
At all measurement sites, Sen2Cor obtained R r s B O A ( 0 + , λ ) values at band B01 (443 nm) and B02 (490 nm) significantly lower than the in situ data. This observation presumably resulted from an erroneous aerosol parameterisation. Sen2Cor obtained an AOT value of 0.185 ± 0.002 (550 nm) for southern Lake Starnberg pixels which was higher compared to measurements with sun photometers (0.151) and at the Aeronet Station (0.179). Thus, Sen2Cor overestimated aerosol reflectance resulting in overcorrected R r s B O A ( 0 + , λ ) spectra. Both, ACOLITE and Sen2Cor calculated R r s B O A ( 0 + , λ ) values in bands B06 (740 nm) and B07 (783 nm) higher than in situ measurements. ACOLITE lacks a correction of adjacency effects, and reflectance from neighbouring land pixels therefore contributes to the signal and accounted for higher reflectance values above 705 nm. Extrapolating aerosol reflectance from the SWIR bands to the shorter wavelengths thus may result in overcorrected spectra. Similar to Sen2Cor, ACOLITE tended to lower reflectance values compared to in situ measurements, though inconsistently. Sen2Cor includes a correction for adjacency effects based on a range-independent reflectance in a large neighbourhood of each pixel, which performs insufficiently for water pixels close to the shoreline. At wavelengths above 700 nm, the impact of adjacency effects is particularly strong since neighbouring land pixels show distinctly higher reflectance [67]. The distance between measurement sites and land varied between 40 m (B) and 600 m (F); consequently, adjacency effects altered all pixel environments (Figure 5). The same applies for all lake pixels due to the lake’s width ranging from 1 km to 4.5 km. Sterckx et al. [73] illustrated that adjacency effects occur even for pixels several hundred metres away from the shoreline. Santer and Schmechting [74] indicated that for similar solar elevation, adjacency effects become negligible (less than 0.1%) only for a distance greater than 5 km from the shoreline. Thus, a correction of adjacency effects appropriate for the water/land environment is essential for reliable spectra. At all measurement sites, MIP retrieved reflectances in bands B06 and B07 slightly above zero, similar to the in situ measurements. MIP calculated zero values for 1.2% of lake pixels in B06 (740 nm) and for 19.0% in B07 (783 nm), which may result from sky glint overcorrection. At A-C, MIP performed well in retrieving both shape and intensity (high r, low RMSE, low X², cf. Table 1); at other sites, MIP obtained comparable shapes, but showed higher intensities compared to in situ measurements and spectra from ACOLITE and Sen2Cor. In the validation area, MIP calculated an AOT of 0.160 (550 nm) which was close to Microtops measurement values; MIP AOT was lower than AOT calculated by Sen2Cor which partly explains the significantly higher spectra compared to Sen2Cor. Different treatment of adjacency effects, sky glint correction and the used aerosol model for calculating atmospheric scattering may further account for differences in spectral shape.
Apart from temporal differences, one has to bear in mind the problem of upscaling while comparing in situ measured reflectance over a small area of water (<1 m) compared to the spatial measurement of S2-A (10 m, 20 m and 60 m). Measurement sites A–E were located in optically shallow water, where varying bottom characteristics (i.e., different macrophytes or sediments), and water depths, influence water reflectance. The satellite sensor records a mixed signal from this variance. Statistical approaches to overcome upscaling problems from point to pixel scale were developed for ocean-colour sensors [75]. Furthermore, in situ measurements also underlie a number of uncertainties such as shading by instrument, boat and changes in incident radiation due to atmospheric variability [76]. Larger error bars (standard deviation) of both in situ and atmospherically corrected spectra in Figure 5b indicate the resulting higher standard deviations.
For case-1 open ocean water algorithms, the required accuracy of water-leaving radiances is 5% to achieve a Chl-a product with ~30% accuracy, for instance [77]. To our knowledge, a comparable accuracy target is not yet defined for atmospheric correction algorithms over inland waters. The evaluated atmospheric corrections showed MAPE values between 61% and 91% on average and underpin that atmospheric correction over inland waters still is an unresolved problem. The large differences of atmospheric corrections are another critical point. Each atmospheric correction model resulted in a different R r s B O A ( 0 + , λ ) spectrum from the same S2-A at-sensor radiance. An EU-FP7 GLaSS project report also compared different atmospheric correction algorithms retrieving highly varying results [78]. Caused by the low reflectance of water, small absolute differences in reflectance rapidly result in large relative differences. These differences may propagate to the subsequent retrieval of lake ecology indicators when using (analytic) approaches that rely on both shape and intensity of spectra. Assessing this issue, however, is beyond the scope of this study and may be expanded to other sensors as well.
3.2. Optically Deep Water
Fit parameters in optically deep water were aCDOM(440) and SPM concentration. Since the R r s B O A ( 0 + , λ ) data used during inverse modelling (bands B01–B07) were not corrected for sun glint, we also selected the fraction of sun glint per pixel area, gdd, as a fit parameter. Table 2 summarises in situ and S2-A derived values at the measurement sites. Variations due to spatial resampling were minor. Absence of processing artefacts, such as stripping, in the resulting parameter maps (Figure 6) shows that processing performed well. Low residuals (mean: 3.96 × 10−4 ± 3.82 × 10−5) between S2-A and inversely modelled spectra underpinned a good modelling performance. The gdd map (Figure 6c) indicates higher sun glint in the northern part of the lake, while the southern region including our measurement sites was only slightly affected. Retrieved aCDOM(440) ranged between 0.10 and 0.74 m−1 (mean: 0.14 ± 0.02 m−1), SPM between 1.1 and 5.1 g·m−3 (mean: 1.8 ± 0.2 g·m−3). These ranges correspond well with concentrations obtained from hyperspectral imagery in other studies at Lake Starnberg [43,45]. Referring to the different spatial resolutions, WASI-2D retrieved similar concentration values (Table 2). Reducing the pixel size of S2-A data must not necessarily result in a significant improvement which might be interesting for analysing small lakes.
Both SPM concentrations and aCDOM(440) showed little variations indicating homogenous and clear lake conditions (Figure 6). SPM in the water column may result from resuspension [79] or from catchment erosion [80]. The lowest SPM concentrations around 1.4 g·m−3 occurred in the northern part of the lake; slightly higher concentrations around 2.0 g·m−3 were retrieved in the southern part. CDOM originates from allochthonous sources from rotting plants in the catchment, or from autochthonous sources such as decomposing phytoplankton or macrophytes [81]. In the S2-A data, aCDOM(440) values were slightly higher in the southern regions compared to the northern part. External input from catchment of both SPM and aCDOM(440) was presumably low since no rainfall occurred the week prior to image acquisition [54]. Furthermore, Lake Starnberg receives mainly groundwater inflows [48], thus, the low values of both SPM concentration and aCDOM(440) are reasonable. Chl-a was considered as a constant parameter during inverse modelling. Water sample analyses also revealed low concentrations of chl-a (~1 mg·m−3) causing water absorption to be predominated by CDOM. Both chl-a and CDOM absorb in the blue wavelength region [13]. Compared to Landsat 8 OLI, S2-A offers an additional band at 705 nm (B06) which may support chl-a assessment [59]. Under low chl-a concentrations, however, other optically active constituents may superimpose the absorption feature. Empirical NIR-red algorithms based on the feature, for instance, perform more reliable at chl-a concentrations >10 mg·m−3 [14,82]. At Lake Starnberg, chl-a concentrations were too low for a retrieval along with aCDOM(440) and SPM.
Spatial patterns of gdd (Figure 6c) revealed high sun glint influence in the northern and western lake regions, whereas the southern and eastern regions were only slightly affected by sun glint. Sun glint occurs on water surfaces where radiation is directly reflected to the sensor as a combination of surface roughness, sun position and sensor viewing angle [83]. The statistical model for predicting sun glint probability by Cox and Munk [84] is widely used in ocean colour remote sensing; it shows that increasing wind speed increases the probability of the water surface being oriented to cause sun glint. Wind direction was from east-southeast (120°, wind speed: 3.0 m·s−1 [54]) close to image acquisition (12:00 UTC+2). Due to a lateral moraine extending from north to south the eastern parts of the lake were less exposed to wind. The southern part was even more sheltered since the ridge becomes broader and is covered by forest. Thus, the smoother water surface resulted in less sun glint in sheltered regions; the probably roughened surface caused higher sun glint in the more wind exposed northern part. Integrating wind maps, if available, into remote sensing analyses of lakes may further help to understand these patterns. The spatial variability of retrieved sun glint underpins the need for considering the spatial variability of these parameters. Kay et al. [83] reviewed existing correction approaches: the statistical model by Cox and Munk performed insufficiently for sensors with spatial resolutions <100 m; furthermore, at inland waters local wind fields can hardly be predicted. Approaches based on zero water reflectance in the NIR often assume spatially constant sun glint and are inapplicable in shallow or turbid waters [83]. The spectral model of sun glint implemented in WASI-2D addresses both spatial variability and spectral dependency. Gege and Groetsch [85] provide a detailed description and analysis of this topic.
To assess the performance of SPM and aCDOM(440) retrieval, we compared WASI-2D values with concentrations and backscattering or absorption coefficients from in situ measurements (Table 2). A common approach is to compare SPM mass concentrations derived from water samples with concentrations derived from remote sensing algorithms [10]. WASI-2D derived SPM concentrations fell within the range of measured concentrations; on average, they were slightly higher than measured SPM. Arriving at an identical match, however, would be credited to mere coincidence rather than a flawless model. We compared two different methods of SPM estimation: in situ data from a gravimetric measurement of a 1 L water sample, and SPM from S2-A radiance values of selected pixels at varying spatial resolutions, i.e., 10–60 m. Gravimetric analyses of SPM contain a variety of uncertainties, such as loss of filter or sample material [86]. Thus, SPM concentrations retrieved from water samples should not be considered absolute. Moreover, the term b*b,SPM(550) (Equation (8)) introduces additional uncertainties while comparing SPM concentrations retrieved from water samples and S2-A data. b*b,SPM(550) is used to convert bb,SPM(λ) to SPM concentrations (Equation (8)). b*b,SPM(550) depends on mineral composition, size, and shape of particles [87,88] and therefore is lake specific, but also temporally and spatially variable within a particular lake. We adapted b*b,SPM(550) to the study area by inverse modelling of in situ measured RAMSES reflectance data considering SPM concentrations from water samples as correct. To further assess the suitability of S2-A for analysing water bodies, we considered an evaluation of a parameter directly retrieved from S2-A R r s B O A ( 0 + , λ ) spectra, i.e., bb,SPM(550). At measurement site F and G, we retrieved bb,SPM(550) from in situ measured R r s − F R E E D O M B O A ( 0 + , λ ) and R r s − R A M S E S B O A ( 0 + , λ ) using FREEDOM and RAMSES (only G) radiometers. Values of bb,SPM(550) from in situ and S2-A data matched well; on the contrary, modelled and in situ SPM concentrations differed notably. SPM concentration is often measured in lake ecology or hydrology and is easier to grasp than bb,SPM(550); retrieval of the latter, however, is more accurate since it is directly assessed from remote sensing data. Thus, bb,SPM(550) represents the parameter most relevant for assessing quality of remote sensing products.
Table 2 compares the S2-A derived aCDOM(440) values with aCDOM(440) obtained from under-water RAMSES E d ( z < 0 , λ ) measurements. The S2-A derived aCDOM(440) values were lower compared to the values retrieved from E d ( z < 0 , λ ) measurements.
Bearing in mind that we only have two measurement sites in optically deep water, our results are a first evaluation. Further assessments are required. Our results show that it was possible to distinguish small differences in water constituents even for low concentrations—at least for SPM and CDOM. The spatially synoptic view of S2-A across the entire lake showed a relatively clear and homogenous water surface of optically deep water during image acquisition.
3.3. Optically Shallow Water
In optically shallow water, we conducted inverse modelling on the datasets with pixel sizes of 10 m and 20 m. In some parts of the lake, the shallow zone has a width of less than 100 m; water depth and bottom substrates may also change, even within 10 m pixels. gdd, aCDOM(440), water depth and the aerial fraction (fA) of two bottom types (macrophyte and sandy sediment) were chosen as fit parameters. SPM was kept constant (SPM = 1.8 g·m−3) to avoid excess fit parameters. Figure 7 illustrates the resulting maps of aCDOM(440) and gdd. Figure 8 presents the retrieved bottom types and Figure 9 the water depth map. Higher reflectances caused slightly higher residuals on average (4.0 × 10−4 ± 2.8 × 10−4) compared to optically deep water. Similar to deep water, no processing artefacts such as striping occurred.
The parameter aCDOM(440) varied between 0.1 and 1.5 m−1 (mean: 0.15 ± 0.11 m−1) in calculated water depths above 1 m. Table 3 summarises modelled and aCDOM(440) values derived from E d ( z < 0 , λ ) and water depths. As in deep water, S2-A derived aCDOM(440) was lower compared to aCDOM(440) values from in situ measurements. The parameter gdd showed a consistent spatial distribution as in deep water: higher values in the northern lake area than in the southern part. The speckled results (zoomed parts in Figure 7b,c) indicate that gdd alleviates sun glint induced irregularities; thus, the other parameters retrieved in optically shallow water appeared less noisy.
Accurate information of bottom substrate and water depths is crucial in optically shallow water. Following the suggestions in Giardino et al. [34], we differentiated only two substrate types, i.e., macrophytes and sandy sediment. The resulting map revealed reasonable spatial patterns with sandy sediment predominating along the south-eastern shoreline close to ”Seeshaup” (Figure 8d). High macrophytes coverage towards deeper water at Seeshaupt, however, appears unreasonable. Unfortunately, no bottom substrate mappings exist for 2015. Nevertheless, to check the plausibility, we compared our results with those of previous studies at Lake Starnberg conducted in 2011. In accordance to Rößler et al. [41], the bottom north of the “Roseninsel” (Figure 8b) was identified as sandy sediment. At “Karpfenwinkel” (Figure 8c), WASI-2D retrieved an oval shaped structure of sediment; dense macrophytes occurred south-east of it. Rößler et al. [43] also described these patterns using airborne hyperspectral data. Nevertheless, bottom characteristics are highly variable at Lake Starnberg; a variety of macrophyte species are present and also bare substrate varies between stony, sandy and dark or light coloured. Neither the in situ measured sandy sediment spectrum nor the spectrum of one single macrophyte species is able to cover the spectral variability of the entire lake’s bottom. Parameterising classification algorithms or bio-optical models with appropriate spectra therefore remains challenging. Currently, several approaches are available such as ex situ measurements ([27,34], this study), image based derivation [45] or seasonal dependent reflectance models based on empiric measurements [89]. Assessing the suitability of S2-A for distinguishing bottom types in detail may therefore be of interest for subsequent studies.
Bottom substrate unmixing is accompanied by fitting water depths. Figure 9a depicts water depths around the entire lake and for regions with extensive shallow water areas. Water depths reasonably increased from the shore line towards the deep water mask, remained, however, in most parts of the lake below 2.0 m. At the northern end of the lake, calculated water depths rarely exceeded 1.5 m which is a clear underestimation of the actual water depths. The shallow water mask was oriented at the 8 m depth line (Figure 1) of the official bathymetry map. A reason could be that bottom type spectra were inappropriate for this area. In situ measurements were conducted at the southern end. At measurement sites, S2-A-derived water depths underestimated measured water depths about 0.5 m (Table 3). At measurement site D, water depths differed more than 2.5 m. This measurement site is located close to a ledge; minor GPS variations and positioning inaccuracy may therefore result in contradicting values; nevertheless, geolocation uncertainties exclusively hardly explain such a strong deviation (next paragraph).
To quantitatively evaluate the capability of S2-A 10 m data for water depth retrieval, we used echo sounding data (Figure 1b, [45]) as a validation source (Figure 10). Echo sounding and S2-A derived water depths are highly correlated (r = 0.95, residual standard deviation = 0.12 m) up to 2.5 m (echo sounding). Nevertheless, the RMSE (0.56 m) and offset from the 1:1 line (Figure 10a) indicate that WASI-2D underestimated water depths. In water depths ranging between 0 and 4 m (measured Secchi disk depth), RMSE was 0.95 m which was higher than RMSE values obtained by Gege [45] (mean (0–4 m) = 0.29 m) using airborne hyperspectral data. In water depths deeper than 2.5 m, WASI-2D modelled water depths at around 1.8 m (Figure 10a). For these pixels, WASI-2D retrieved lower shares of sediment, and consequently higher macrophyte coverages, which is also indicated by a greenish colour in Figure 10a; WASI-2D therefore considered a dark bottom type (low reflectance values due to high macrophytes coverage) accompanied by lower water depths instead of a bottom covered by sediment (high reflectance) and high water depths. Thus, WASI-2D achieved a low residuum between S2-A and modelled spectrum, correct spectral unmixing, however, failed; at water depths deeper than 2.5 m, the spectral signatures of both bottom types were too similar for a correct differentiation. At the points which scattered around the 1:1 line above 4 m, WASI-2D correctly fitted pure macrophyte coverage (dark green colour) and consequently retrieved correct water depths. To check these presumptions, we repeated modelling in shallow water and fixed the bottom type as sediment (fA[Sediment] = 1). Indeed, WASI-2D retrieved higher water depths, though still underestimating absolute values, with a high correlation up to 4 m (r = 0.96, residual standard deviation = 0.15 m) which was slightly below Secchi disk depth measured on 13 August (4.2 m ± 0.3 m). The MIP retrieved R r s B O A ( 0 + , λ ) spectra in shallow water were higher (except B) compared to in situ measured spectra. Assuming the same bottom type, higher reflectance means lower water depth which may partly explain the systematic underestimation of around 0.6 m. Furthermore, sedimentation processes may have altered bottom conditions slightly within the time difference being four years between echo sounding and image acquisition. Using sediment as fixed bottom type, WASI-2D overestimated or reached maximum value for water depths above 4 m (Figure 10b). The previous setting indicated pure macrophyte coverage at these echo sounding points. Modelling with fixed sediment coverage, consequently, caused miscalculations.
Small scale variance, however, may not be captured even with using the 10 m data set. Furthermore, echo sounding data also may include measurement uncertainties, especially at ledges. S2-A geolocation uncertainty, which was 12.36 m for processing baseline 02.01 [90], may also result in misalignments between echo sounding and satellite data.
Overall, the water depths retrieval performed better with fixed bottom coverage. We therefore conclude that S2-A spectral information was insufficient to accurately separate mixed coverages of macrophytes and sediment in water depths deeper than 2.5 m. This conclusion certainly is restricted to the specific lake conditions during image acquisition date, atmospheric correction algorithm (MIP) and bio-optical model applied (WASI-2D). The atmospheric correction algorithm is crucial, in particular for the application of bio-optical models which need high accuracies of both shape and intensity of R r s B O A ( 0 + , λ ) spectra. MIP retrieved the best R r s B O A ( 0 + , λ ) spectra compared to the available in situ spectra; however, they also showed deviations. Furthermore, MIP lacks a sun glint correction for S2-A data. For this reason, we included sun glint assessment in the bio-optical modelling process. Improvements towards sun glint correction during atmospheric correction procedures may therefore also improve bio-optical analyses of lakes.
4. Conclusions
This study used a physically based processing chain to test the suitability of S2-A for retrieving lake ecology indicators, i.e., SPM, aCDOM(440), water depths and bottom substrates. To this end, we conducted a measurement campaign at Lake Starnberg (Germany) concurrently to a S2-A overpass. Analysing the results of three different atmospheric correction algorithms (Sen2Cor [58], ACOLITE [59] and MIP [61]) revealed different spectra for each algorithm. By comparing R r s B O A ( 0 + , λ ) spectra with in situ measured reflectance, MIP performed best and therefore was used for further processing. We then applied the bio-optical modelling software WASI-2D [46]. S2-A band positions and calibration as well as low NEΔRrsE of the scene (mean: 0.00014 sr−1 for the 10 m data set) allowed retrieval of SPM and aCDOM(440), even at low concentrations. Absorption by chl-a, however, was too low for assessment along with the other constituents. Modelled aCDOM(440) was lower than in situ values (in situ: 0.42–0.44 m−1, S2-A: 0.1–0.74 m−1, mean: 0.14 ± 0.02 m−1). Resulting SPM concentrations (in situ: 0.4–1.9 g·m−3, S2-A: 1.1–5.1 g·m−3, mean: 1.8 ± 0.2 g·m−3) were within the range of analysed water samples. A comparison with backscattering coefficients of SPM (in situ: 0.015–0.021 m−1, S2-A: 0.018–0.077 m−1) approved even better performance. Spatial resampling of the S2-A data to 20 m or 60 m showed negligibly different results. In optically shallow water, parameters of interest were bottom substrate and water depths. We obtained reasonable patterns of macrophytes and sandy sediment in most parts of the lake. Modelled water depths also showed reasonable patterns. Quantitative evaluation approved a good correlation, but underestimation occurred between 0 and 2.5 m (RMSE: 0.56 m, r: 0.95). With water deeper than 2.5 m, S2-A spectral information was inadequate to differentiate mixed coverages of macrophytes and sediment. Furthermore, the time difference between echo sounding and image acquisition and the challenging measurement of representative bottom spectra contributes to inaccurate bottom coverage and water depth retrieval.
This study points out that S2-A has great potential to assist lake ecology in retrieving indicators on a spatially synoptic scale. The study was conducted under conditions with low water constituent concentrations and low spatial variability. Studies of lakes with different optical properties and trophic characteristics may further advance knowledge of S2-A’s suitability for lake monitoring. Shape and intensity of spectra strongly depend on the applied atmospheric correction algorithm; further research and improvements in this field are required.
Acknowledgments
This work was conducted within the project LAKESAT (grant No.: 50EE1340) funded by the Federal Ministry for Economic Affairs and Energy, Germany. We acknowledge financial support for publications costs by Land Schleswig-Holstein within the funding programme Open Access Publikationsfonds. A. Göritz would like to thank for support by Deutsche Forschungsgemeinschaft (DFG) through the TUM International Graduate School of Science and Engineering (IGSSE). We further thank ESA for providing Sentinel-2A data. We thank Philip Klinger of EOMAP GmbH & Co. KG for processing Sentinel-2A data with MIP. We are very grateful to Christine Fritz (TUM), Markus Hoffmann (TUM), Sebastian Riedel (CAU Kiel/DLR) and Thomas Schneider (TUM) for assistance in fieldwork and laboratory analyses. We further thank Austin Saly (CAU Kiel) for English language editing. We thank five anonymous reviewers for their effort and helpful comments.
Author Contributions
Katja Dörnhöfer, Peter Gege, Bringfried Pflug, Anna Göritz and Natascha Oppelt conceived and designed the study. Katja Dörnhöfer conducted image data processing and validation, wrote the paper and prepared figures. Bringfried Pflug conducted Sen2Cor processing. Peter Gege and Anna Göritz performed and analysed in situ measurements. All authors contributed equally in reviewing and finalizing the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| aCDOM(440) | absorption of coloured dissolved organic matter at reference wavelength 440 nm |
|---|---|
| AOT | aerosol optical thickness |
| b*b,SPM(550) | mass-specific backscattering coefficient of SPM at reference wavelength 550 nm |
| bb,SPM(λ) | backscattering coefficient of SPM at reference wavelength 550 nm |
| CDOM | coloured dissolved organic matter |
| Chl-a | chlorophyll-a |
| Ed(z,λ) | downwelling spectral irradiance |
| gdd | fraction of sun glint per pixel area |
| Lu(z,λ) | upwelling spectral radiance |
| MAPE | Mean absolute percentage error |
| MIP | Modular Inverse Processing System |
| NEΔRrsE | Noise-equivalent remote sensing reflectance difference |
| S2-A | Sentinel-2A |
| r | Pearson’s correlation coefficient |
| RMSE | Root Mean Square Error |
| R r s B O A (0+, λ) | radiance reflectance above water |
| R r s − F R E E D O M B O A (0+, λ) | radiance reflectance above water derived from FREEDOM measurements |
| R r s − R A M S E S B O A (0+, λ) | radiance reflectance above water derived from RAMSES measurements |
| SPM | suspended particulate matter |
| SWIR | shortwave infrared |
| VNIR | visible near-infrared |
| X² | Chi-Square |
| z | sensor depth |
References
- Adrian, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; van Donk, E.; et al. Lakes as sentinels of climate change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stendera, S.; Adrian, R.; Bonada, N.; Cañedo-Argüelles, M.; Hugueny, B.; Januschke, K.; Pletterbauer, F.; Hering, D. Drivers and stressors of freshwater biodiversity patterns across different ecosystems and scales: A review. Hydrobiologia 2012, 696, 1–28. [Google Scholar] [CrossRef]
- Millennium Ecosystem Assessment. Ecosystems and Human Well-Being: Wetlands and Water Synthesis; World Resources Institute: Washington, DC, USA, 2005; pp. 1–68. [Google Scholar]
- European Commission. The Water Framework Directive (Directive 2000/60/EC of the European Parliament and of the Council of 23 October 2000 Establishing A Framework for Community Action in the Field of Water Policy); Official Journal of the European Communities: Brussels, Belgium, 2000; pp. 1–72. [Google Scholar]
- United States Congress House. Federal Water Pollution Control Act, 33 U.S.C. §1251–1387; Environmental Protection Agency: Washington, DC, USA, 2002; pp. 1–234.
- Hering, D.; Borja, A.; Carstensen, J.; Carvalho, L.; Elliott, M.; Feld, C.K.; Heiskanen, A.S.; Johnson, R.K.; Moe, J.; Pont, D.; et al. The European Water Framework Directive at the age of 10: A critical review of the achievements with recommendations for the future. Sci. Total Environ. 2010, 408, 4007–4019. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Birk, S.; Bonne, W.; Borja, A.; Brucet, S.; Courrat, A.; Poikane, S.; Solimini, A.; van de Bund, W.; Zampoukas, N.; Hering, D. Three hundred ways to assess Europe’s surface waters: An almost complete overview of biological methods to implement the Water Framework Directive. Ecol. Indic. 2012, 18, 31–41. [Google Scholar] [CrossRef]
- Schaeffer, B.A.; Schaeffer, K.G.; Keith, D.J.; Lunetta, R.S.; Conmy, R.; Gould, R.W. Barriers to adopting satellite remote sensing for water quality management. Int. J. Remote Sens. 2013, 34, 7534–7544. [Google Scholar] [CrossRef]
- Reyjol, Y.; Argillier, C.; Bonne, W.; Borja, A.; Buijse, A.D.; Cardoso, A.C.; Daufresne, M.; Kernan, M.; Ferreira, M.T.; Poikane, S.; et al. Assessing the ecological status in the context of the European Water Framework Directive: Where do we go now? Sci. Total Environ. 2014, 497–498, 332–344. [Google Scholar] [CrossRef] [PubMed]
- Dörnhöfer, K.; Oppelt, N. Remote sensing for lake research and monitoring—Recent advances. Ecol. Indic. 2016, 64, 105–122. [Google Scholar] [CrossRef]
- Dekker, A.G.; Phinn, S.R.; Anstee, J.M.; Bissett, W.P.; Brando, V.E.; Casey, B.; Fearns, P.R.; Hedley, J.D.; Klonowski, W.; Lee, Z.P.; et al. Intercomparison of shallow water bathymetry, hydro-optics, and benthos mapping techniques in Australian and Caribbean coastal environments. Limnol. Oceanogr. Methods 2011, 9, 396–425. [Google Scholar] [CrossRef]
- Gao, J. Bathymetric mapping by means of remote sensing: Methods, accuracy and limitations. Prog. Phys. Geogr. 2009, 33, 103–116. [Google Scholar] [CrossRef]
- Matthews, M.W. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef] [Green Version]
- Palmer, S.; Odermatt, D.; Hunter, P.D.; Brockmann, C.; Présing, M.; Balzter, H.; Tóth, V.R. Satellite remote sensing of phytoplankton phenology in Lake Balaton using 10 years of MERIS observations. Remote Sens. Environ. 2015, 158, 441–452. [Google Scholar] [CrossRef] [Green Version]
- Kiefer, I.; Odermatt, D.; Anneville, O.; Wüest, A.; Bouffard, D. Application of remote sensing for the optimization of in-situ sampling for monitoring of phytoplankton abundance in a large lake. Sci. Total Environ. 2015, 527–528, 493–506. [Google Scholar] [CrossRef] [PubMed]
- Jiang, G.; Ma, R.; Loiselle, S.A.; Duan, H.; Su, W.; Cai, W.; Huang, C.; Yang, J.; Yu, W. Remote sensing of particulate organic carbon dynamics in a eutrophic lake (Taihu Lake, China). Sci. Total Environ. 2015, 532, 245–254. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Li, X.; Ma, R.; Li, F.; Duan, H.; Hu, W.; Qin, B.; Huang, W. Applying remote sensing techniques to monitoring seasonal and interannual changes of aquatic vegetation in Taihu Lake, China. Ecol. Indic. 2016, 60, 503–513. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, Y.; Zhu, G.; Liu, X.; Zhou, Y.; Xu, H.; Qin, B.; Liu, G.; Li, Y. Long-term remote monitoring of total suspended matter concentration in Lake Taihu using 250 m MODIS-Aqua data. Remote Sens. Environ. 2015, 164, 43–56. [Google Scholar] [CrossRef]
- Binding, C.E.; Greenberg, T.A.; Watson, S.B.; Rastin, S.; Gould, J. Long term water clarity changes in North America’s Great Lakes from multi-sensor satellite observations. Limnol. Oceanogr. 2015, 60, 1976–1995. [Google Scholar] [CrossRef]
- Matthews, M.W. Eutrophication and cyanobacterial blooms in South African inland waters: 10 years of MERIS observations. Remote Sens. Environ. 2014, 155, 161–177. [Google Scholar] [CrossRef]
- Matthews, M.W.; Bernard, S.; Winter, K. Remote sensing of cyanobacteria-dominant algal blooms and water quality parameters in Zeekoevlei, a small hypertrophic lake, using MERIS. Remote Sens. Environ. 2010, 114, 2070–2087. [Google Scholar] [CrossRef]
- Chao Rodríguez, Y.; el Anjoumi, A.; Domínguez-Gómez, J.A.; Rodríguez Pérez, D.; Rico, E. Using Landsat image time series to study a small water body in Northern Spain. Environ. Monit. Assess. 2014, 186, 3511–3522. [Google Scholar] [CrossRef] [PubMed]
- Yuzugullu, O.; Aksoy, A. Generation of the bathymetry of a eutrophic shallow lake using WorldView-2 imagery. J. Hydroinform. 2014, 16, 50–59. [Google Scholar] [CrossRef]
- Heblinski, J.; Schmieder, K.; Heege, T.; Agyemang, T.K.; Sayadyan, H.; Vardanyan, L. High-resolution satellite remote sensing of littoral vegetation of Lake Sevan (Armenia) as a basis for monitoring and assessment. Hydrobiologia 2011, 661, 97–111. [Google Scholar] [CrossRef]
- Bolpagni, R.; Bresciani, M.; Laini, A.; Pinardi, M.; Matta, E.; Ampe, E.M.; Giardino, C.; Viaroli, P.; Bartoli, M. Remote sensing of phytoplankton-macrophyte coexistence in shallow hypereutrophic fluvial lakes. Hydrobiologia 2014, 737, 67–76. [Google Scholar] [CrossRef]
- Giardino, C.; Bresciani, M.; Valentini, E.; Gasperini, L.; Bolpagni, R.; Brando, V.E. Airborne hyperspectral data to assess suspended particulate matter and aquatic vegetation in a shallow and turbid lake. Remote Sens. Environ. 2015, 157, 48–57. [Google Scholar] [CrossRef]
- Hunter, P.D.; Gilvear, D.J.; Tyler, A.N.; Willby, N.J.; Kelly, A. Mapping macrophytic vegetation in shallow lakes using the Compact Airborne Spectrographic Imager (CASI). Aquat. Conserv. Mar. Freshw. Ecosyst. 2010, 20, 717–727. [Google Scholar] [CrossRef]
- Palmer, S.C.; Kutser, T.; Hunter, P.D. Remote sensing of inland waters: Challenges, progress and future directions. Remote Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef]
- Eder, E.; Dörnhöfer, K.; Gege, P.; Schenk, K.; Klinger, P.; Wenzel, J.; Oppelt, N.; Gruber, N. Analysis of mineral-rich suspended matter in glacial lakes using simulations and satellite data. In Living Planet Symposium; Ouwehand, L., Ed.; ESA Communications: Noordwijk, The Netherlands, 2016; Volume 740. [Google Scholar]
- Giardino, C.; Bresciani, M.; Cazzaniga, I.; Schenk, K.; Rieger, P.; Braga, F.; Matta, E.; Brando, V.E. Evaluation of multi-resolution satellite sensors for assessing water quality and bottom depth of Lake Garda. Sensors 2014, 14, 24116–24131. [Google Scholar] [CrossRef] [PubMed]
- Lobo, F.L.; Costa, M.P.; Novo, E.M. Time-series analysis of Landsat-MSS/TM/OLI images over Amazonian waters impacted by gold mining activities. Remote Sens. Environ. 2015, 157, 170–184. [Google Scholar] [CrossRef]
- Slonecker, E.T.; Jones, D.K.; Pellerin, B.A. The new Landsat 8 potential for remote sensing of colored dissolved organic matter (CDOM). Mar. Pollut. Bull. 2016, 107, 518–527. [Google Scholar] [CrossRef] [PubMed]
- Giardino, C.; Bresciani, M.; Fava, F.; Matta, E.; Brando, V.E.; Colombo, R. Mapping submerged habitats and mangroves of Lampi Island Marine National Park (Myanmar) from in situ and satellite observations. Remote Sens. 2016, 8, 2. [Google Scholar] [CrossRef]
- Lee, Z.P.; Shang, S.; Qi, L.; Yan, J.; Lin, G. A semi-analytical scheme to estimate Secchi-disk depth from Landsat-8 measurements. Remote Sens. Environ. 2016, 177, 101–106. [Google Scholar] [CrossRef]
- Manzo, C.; Bresciani, M.; Giardino, C.; Braga, F.; Bassani, C. Sensitivity analysis of a bio-optical model for Italian lakes focused on Landsat-8, Sentinel-2 and Sentinel-3. Eur. J. Remote Sens. 2015, 48, 17–32. [Google Scholar] [CrossRef]
- Kutser, T.; Paavel, B.; Verpoorter, C.; Ligi, M.; Soomets, T.; Toming, K.; Casal, G. Remote sensing of Black Lakes and using 810 nm reflectance peak for retrieving water quality parameters of optically complex waters. Remote Sens. 2016, 8, 497. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.; Koetz, B.; Phinn, S. Capability of the Sentinel 2 mission for tropical coral reef mapping and coral bleaching detection. Remote Sens. Environ. 2012, 120, 145–155. [Google Scholar] [CrossRef]
- Toming, K.; Kutser, T.; Laas, A.; Sepp, M.; Paavel, B.; Nõges, T. First experiences in mapping lake water quality parameters with Sentinel-2 MSI imagery. Remote Sens. 2016, 8, 640. [Google Scholar] [CrossRef]
- Arle, J.; Blondzik, K.; Claussen, U.; Duffek, A.; Grimm, S.; Hilliges, F.; Hoffmann, A.; Leujak, W.; Mohaupt, V.; Naumann, S.; et al. Wasserwirtschaft in Deutschland. Teil 2. Gewässergüte; Umweltbundesamt (UBA): Bonn, Germany, 2013. [Google Scholar]
- Roessler, S.; Wolf, P.; Schneider, T.; Melzer, A. Multispectral remote sensing of invasive aquatic plants using RapidEye. In Earth Observation of Global Changes (EOGC); Krisp, J.M., Meng, L., Pail, R., Stilla, U., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 109–123. [Google Scholar]
- Rößler, S.; Wolf, P.; Schneider, T.; Melzer, A. Monitoring of invasive aquatic plants using multitemporal RapidEye-data. In Proceedings of the 1st EARSeL Workshop on Temporal Analysis of Satellite Images, Mykonos, Greece, 23–25 May 2012; EARSeL: Mykonos Island, Greece, 2012. [Google Scholar]
- Rößler, S.; Wolf, P.; Schneider, T.; Zimmermann, S.; Melzer, A. Water constituent retrieval and littoral bottom mapping using hyperspectral APEX imagery and submersed artificial surfaces. EARSeL eProc. 2013, 12, 44–57. [Google Scholar]
- Giardino, C.; Candiani, G.; Bresciani, M.; Lee, Z.P.; Gagliano, S.; Pepe, M. BOMBER: A tool for estimating water quality and bottom properties from remote sensing images. Comput. Geosci. 2012, 45, 313–318. [Google Scholar] [CrossRef]
- Gege, P. A case study at Starnberger See for hyperspectral bathymetry mapping using inverse modelling. In Proceedings of the WHISPERS conference, Lausanne, Switzerland, 25–27 June 2014; pp. 1–4.
- Gege, P. WASI-2D: A software tool for regionally optimized analysis of imaging spectrometer data from deep and shallow waters. Comput. Geosci. 2014, 62, 208–215. [Google Scholar] [CrossRef]
- Dörnhöfer, K.; Gege, P.; Pflug, B.; Oppelt, N. Mapping indicators of lake ecology at Lake Starnberg, Germany—First results of Sentinel-2A. In Living Planet Symposium; Ouwehand, L., Ed.; ESA Communications: Noordwijk, The Netherlands, 2016; Volume 740. [Google Scholar]
- Wöbbecke, K.; Klett, G.; Rechenberk, B. Wasserbeschaffenheit der Wichtigsten Seen in der Bundesrepublik Deutschland: Datensammlung 1981–2000; Umweltbundesamt (UBA): Berlin, Germany, 2003. [Google Scholar]
- Melzer, A.; Zimmermann, S.; Schorer, A. Seelitorale in Bayern: Starnberger See, Makrophyten-Kartierungen 1979, 1989 und 2000; Bayerisches Landesamt für Wasserwirtschaft: München, Germany, 2003. [Google Scholar]
- GKD Bayern. Data of Measure Point Lake Starnberg, 2013. Available online: http://www.gkd.bayern.de/seen/chemie/karten/index.php?thema=gkd&rubrik=seen&produkt=chemie&gknr=0 (accessed on 14 April 2016).
- Riedel, S.; Gege, P.; Schneider, M.; Pflug, B.; Oppelt, N. Comparison of atmospheric parameters derived from in-situ and hyperspectral remote sensing data beautiful Bavarian lakes. In Living Planet Symposium; Ouwehand, L., Ed.; ESA Communications: Noordwijk, The Netherlands, 2016; Volume 740. [Google Scholar]
- Labsphere. Spectralon, Diffuse Reflectance Targets. 10% nominal reflectance value. SRT 10-050 Nr. 50 039084 000. Available online: https://www.labsphere.com/site/assets/files/1828/spectralon_targets.pdf (accessed on 8 November 2016).
- TriOS. RAMSES Radiometer, 2015. Available online: http://www.trios.de/en/products/sensors/ramses.html (accessed on 5 July 2016).
- Deutscher Wetterdienst (DWD). Climatological time series of station Starnberg and Attenkam. WebWerdis, 2016. Available online: https://werdis.dwd.de/werdis/start_js_JSP.do (accessed on 5 July 2016).
- Strömbeck, N.; Pierson, D.C. The effects of variability in the inherent optical properties on estimations of chlorophyll a by remote sensing in Swedish freshwaters. Sci. Total Environ. 2001, 268, 123–137. [Google Scholar] [CrossRef]
- Bavarian Environmental Agency (BEA). Download Gauge Starnberg, Starnberger See. Available online: http://www.gkd.bayern.de/fluesse/abfluss/stationen/stammdaten/index.php?thema=gkd&rubrik=seen&produkt=wasserstand&gknr=0&msnr=16663002 (accessed on 5 July 2016).
- Bavarian Environmental Agency (BEA). Digital Elevation Model of Lake Starnberg; BEA: Augsburg, Germany, 2000. [Google Scholar]
- Müller-Wilm, U. S2PAD SEN2COR 2.2.0–Readme, S2PAD-VEGA-SRN-0001; Telespazio VEGA Deutschland GmbH: Darmstadt, Germany, 2016. [Google Scholar]
- Vanhellemont, Q.; Ruddick, K. ACOLITE for Sentinel-2: Aquatic applications of MSI imagery. In Living Planet Symposium; Ouwehand, L., Ed.; ESA Communications: Noordwijk, The Netherlands, 2016; Volume 740. [Google Scholar]
- Vanhellemont, Q.; Ruddick, K. Advantages of high quality SWIR bands for ocean colour processing: Examples from Landsat-8. Remote Sens. Environ. 2015, 161, 89–106. [Google Scholar] [CrossRef]
- Heege, T.; Kiselev, V.; Wettle, M.; Hung, N.N. Operational multi-sensor monitoring of turbidity for the entire Mekong Delta. Int. J. Remote Sens. 2014, 35, 2910–2926. [Google Scholar] [CrossRef]
- Heege, T.; Fischer, J. Mapping of water constituents in Lake Constance using multispectral airborne scanner data and a physically based processing scheme. Can. J. Remote Sens. 2004, 30, 77–86. [Google Scholar] [CrossRef]
- Heege, T. Flugzeuggestützte Fernerkundung von Wasserinhaltsstoffen am Bodensee. Ph.D. Thesis, Freien Universitat Berlin, Berlin, Germany, 2000. [Google Scholar]
- Mobley, C.D.; Boss, E.; Roesler, C. Ocean Optics Web Book, 2015. Available online: http://www.oceanopticsbook.info/ (accessed on 11 October 2016).
- Vanhellemont, Q.; Ruddick, K. Turbid wakes associated with offshore wind turbines observed with Landsat 8. Remote Sens. Environ. 2014, 145, 105–115. [Google Scholar] [CrossRef]
- European Space Agency (ESA). Sentinel-2A Spectral Response Functions (S2A-SRF), 2015. Available online: https://earth.esa.int/web/sentinel/user-guides/document-library/-/asset_publisher/xlslt4309D5h/content/sentinel-2a-spectral-responses;jsessionid=1D8024CC54B3F0A8C66B6C9D562987C4.eodisp-prod4040?redirect=https%3A%2F%2Fearth.esa.int%2Fweb%2Fsentinel%2Fuser-guides%2Fdocument-library%3Bjsessionid%3D1D8024CC54B3F0A8C66B6C9D562987C4.eodisp-prod4040%3Fp_p_id%3D101_INSTANCE_xlslt4309D5h%26p_p_lifecycle%3D0%26p_p_state%3Dnormal%26p_p_mode%3Dview%26p_p_col_id%3Dcolumn-1%26p_p_col_count%3D1 (accessed on 14 April 2016).
- Sterckx, S.; Knaeps, E.; Kratzer, S.; Ruddick, K. SIMilarity Environment Correction (SIMEC) applied to MERIS data over inland and coastal waters. Remote Sens. Environ. 2015, 157, 96–110. [Google Scholar] [CrossRef]
- Brando, V.E.; Dekker, A.G. Satellite hyperspectral remote sensing for estimating estuarine and coastal water quality. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1378–1387. [Google Scholar] [CrossRef]
- Albert, A.; Mobley, C.D. An analytical model for subsurface irradiance and remote sensing reflectance in deep and shallow case-2 waters. Opt. Express 2003, 11, 2873–2890. [Google Scholar] [CrossRef] [PubMed]
- Gregg, W.W.; Carder, K.L. A simple spectral solar irradiance model for cloudless maritime atmospheres. Limnol. Oceanogr. 1990, 35, 1657–1675. [Google Scholar] [CrossRef]
- Gege, P. Estimation of phytoplankton concentration from downwelling irradiance measurements in water. Israel J. Plant Sci. 2012, 60, 193–207. [Google Scholar] [CrossRef] [Green Version]
- Linnemann, K.; Gege, P.; Rößler, S.; Schneider, T.; Melzer, A. CDOM retrieval using measurements of downwelling irradiance. In SPIE Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions 2013; Bostater, C.R., Mertikas, S.P., Neyt, X., Eds.; SPIE: Dresden, Germany, 2013. [Google Scholar]
- Sterckx, S.; Knaeps, E.; Ruddick, K. Detection and correction of adjacency effects in hyperspectral airborne data of coastal and inland waters: The use of the near infrared similarity spectrum. Int. J. Remote Sens. 2011, 32, 6479–6505. [Google Scholar] [CrossRef]
- Santer, R.; Schmechtig, C. Adjacency effects on water surfaces: Primary scattering approximation and sensitivity study. Appl. Opt. 2000, 39, 361–375. [Google Scholar] [CrossRef] [PubMed]
- Salama, M.S.; Su, Z. Resolving the subscale spatial variability of apparent and inherent optical properties in ocean color match-up sites. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2612–2622. [Google Scholar] [CrossRef]
- Mueller, J.L.; Morel, A.; Frouin, R.; Davis, C.O.; Arone, R.; Carder, K.L.; Lee, Z.P.; Steward, R.G.; Hooker, S.; Mobley, C.D.; et al. Ocean Optics Protocols For Satellite Ocean Color Sensor Validation, Revision 4, Volume III: Radiometric Measurements and Data Analysis Protocols, NASA/TM-2003-21621/Rev-Vol III, 2003. Available online: http://oceancolor.gsfc.nasa.gov/DOCS/Protocols_Ver4_VolIII.pdf (accessed on 10 August 2016).
- International Ocean-Colour Coordinating Group (IOCCG). Mission Requirements for Future Ocean-Colour Sensors; McClain, C.R., Meister, G., Eds.; Reports of the International Ocean-Colour Coordinating Group, No. 13; IOCCG: Dartmouth, NS, Canada, 2012. [Google Scholar]
- GLaSS. GLaSS Deliverable 3.2, 2014. Global Lakes Sentinel Services, D3.2: Harmonized Atmospheric Correction Method, EOMAP, WI, BC, CNR, SYKE, TO, VU/VUmc, 2014. Available online: www.glass-project.eu/downloads (accessed on 5 July 2016).
- Madsen, J.D.; Chambers, P.A.; James, W.F.; Koch, E.W.; Westlake, D.F. The interaction between water movement, sediment dynamics and submersed macrophytes. Hydrobiologia 2001, 444, 71–84. [Google Scholar] [CrossRef]
- Lindström, M.; Håkanson, L.; Abrahamsson, O.; Johansson, H. An empirical model for prediction of lake water suspended particulate matter. Ecol. Model. 1999, 121, 185–198. [Google Scholar] [CrossRef]
- Brezonik, P.L.; Olmanson, L.G.; Finlay, J.C.; Bauer, M.E. Factors affecting the measurement of CDOM by remote sensing of optically complex inland waters. Remote Sens. Environ. 2015, 157, 199–215. [Google Scholar] [CrossRef]
- Gitelson, A.; Dall’Olmo, G.; Moses, W.; Rundquist, D.C.; Barrow, T.; Fisher, T.R.; Gurlin, D.; Holz, J. A simple semi-analytical model for remote estimation of chlorophyll-a in turbid waters: Validation. Remote Sens. Environ. 2008, 112, 3582–3593. [Google Scholar] [CrossRef]
- Kay, S.; Hedley, J.D.; Lavender, S. Sun glint correction of high and low spatial resolution images of aquatic scenes: A review of methods for visible and near-infrared wavelengths. Remote Sens. 2009, 1, 697–730. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Measurement of the roughness of the sea surface from photographs of the sun’s glitter. J. Opt. Soc. Am. 1954, 44, 838. [Google Scholar] [CrossRef]
- Gege, P.; Groetsch, P. A spectral model for correcting sun glint and sky glint. In Proceedings of Ocean Optics XXIII, Victoria, BC, Canada, 23–28 October 2016.
- Röttgers, R.; Heymann, K.; Krasemann, H. Suspended matter concentrations in coastal waters: Methodological improvements to quantify individual measurement uncertainty. Estuar. Coast. Mar. Sci. 2014, 151, 148–155. [Google Scholar] [CrossRef]
- Effler, S.W.; Peng, F.; O’Donnell, D.M.; Strait, C. The backscattering coefficient and its components in the Great Lakes: A review and synthesis. J. Great Lakes Res. 2013, 39, 108–122. [Google Scholar] [CrossRef]
- Peng, F.; Effler, S.W. Mass-specific scattering coefficient for natural minerogenic particle populations: Particle size distribution effect and closure analyses. Appl. Opt. 2012, 51, 2236–2249. [Google Scholar] [CrossRef] [PubMed]
- Wolf, P.; Rößler, S.; Schneider, T.; Melzer, A. Collecting in situ remote sensing reflectances of submersed macrophytes to build up a spectral library for lake monitoring. Eur. J. Remote. Sens. 2013, 46, 401–416. [Google Scholar] [CrossRef]
- European Space Agency (ESA). S2 MPC. Data Quality Report. Reference S2-PDGS-MPC-DQR. Issue 02. 4 November 2016. Available online: https://sentinel.esa.int/documents/247904/685211/Sentinel-2+Data+Quality+Report+(DQR)/f42497d3-611f-4165-bcc1-2f81421c646a (accessed on 10 August 2016).
Figure 1. S2-A true-colour composite (R-G-B: 665 nm-560 nm-490 nm, 13 August 2015, 10 m) of Lake Starnberg, Germany (a) and location of measurement sites (b).
Figure 1. S2-A true-colour composite (R-G-B: 665 nm-560 nm-490 nm, 13 August 2015, 10 m) of Lake Starnberg, Germany (a) and location of measurement sites (b).

Figure 2. Simplified methodological workflow of the study.
Figure 2. Simplified methodological workflow of the study.

Figure 3. NEΔRrsE for each band calculated for the MIP atmospherically corrected dataset.
Figure 3. NEΔRrsE for each band calculated for the MIP atmospherically corrected dataset.

Figure 4. S2-A resampled irradiance reflectance spectra of the two considered bottom types. The sediment spectrum is the average of reflectance measurements on 13 August 2015, the macrophyte spectrum originates from the WASI-2D database.
Figure 4. S2-A resampled irradiance reflectance spectra of the two considered bottom types. The sediment spectrum is the average of reflectance measurements on 13 August 2015, the macrophyte spectrum originates from the WASI-2D database.

Figure 5. Comparisons of resampled in situ and mean atmospherically corrected R r s B O A ( 0 + , λ ) spectra. Error bars represent the standard deviation within a 3 × 3 ((a–e) shallow water) and 7 × 7 ((f–g) deep water) pixel environment and standard deviation of in situ spectra. Note different scaling of ordinate axis.
Figure 5. Comparisons of resampled in situ and mean atmospherically corrected R r s B O A ( 0 + , λ ) spectra. Error bars represent the standard deviation within a 3 × 3 ((a–e) shallow water) and 7 × 7 ((f–g) deep water) pixel environment and standard deviation of in situ spectra. Note different scaling of ordinate axis.

Figure 6. Results of deep water inversion using the MIP 20 m pixel size dataset. Background is gray scaled S2-A band B05 (705 nm).
Figure 6. Results of deep water inversion using the MIP 20 m pixel size dataset. Background is gray scaled S2-A band B05 (705 nm).

Figure 7. Results of gdd (a–c) and aCDOM(440) (d–f) of shallow water inversion using the MIP 10 m pixel size dataset. Background is gray scaled S2-A band B05 (705 nm).
Figure 7. Results of gdd (a–c) and aCDOM(440) (d–f) of shallow water inversion using the MIP 10 m pixel size dataset. Background is gray scaled S2-A band B05 (705 nm).

Figure 8. Results of bottom substrate unmixing using the MIP 10 m dataset (a); Zoomed areas are Roseninsel (b); Karpfenwinkel (c) and Seeshaupt (d). Low shares of sediment are illustrated as high macrophyte coverage. Background is gray scaled S2-A band B05 (705 nm).
Figure 8. Results of bottom substrate unmixing using the MIP 10 m dataset (a); Zoomed areas are Roseninsel (b); Karpfenwinkel (c) and Seeshaupt (d). Low shares of sediment are illustrated as high macrophyte coverage. Background is gray scaled S2-A band B05 (705 nm).

Figure 9. Results of water depths retrieval during shallow water inversion using the MIP 10 m pixel size dataset (a); Zoomed areas are Karpfenwinkel (b); validation area Seeshaupt (c) and Roseninsel (d). Background is gray scaled S2-A band B05 (705 nm).
Figure 9. Results of water depths retrieval during shallow water inversion using the MIP 10 m pixel size dataset (a); Zoomed areas are Karpfenwinkel (b); validation area Seeshaupt (c) and Roseninsel (d). Background is gray scaled S2-A band B05 (705 nm).

Figure 10. Scatterplots comparing echo sounding data (acquisition June 2012) and S2-A (WASI-2D) derived water depths (10 m) while unmixing two bottom types; the colour gradient highlights bottom type (a). Scatterplot (b) results from modelling water depths with fixed sediment coverage (fA[Sediment] = 1.0).
Figure 10. Scatterplots comparing echo sounding data (acquisition June 2012) and S2-A (WASI-2D) derived water depths (10 m) while unmixing two bottom types; the colour gradient highlights bottom type (a). Scatterplot (b) results from modelling water depths with fixed sediment coverage (fA[Sediment] = 1.0).

Table 1. Performance indicators of resampled in situ and atmospherically corrected spectra at measurement sites in optically shallow (A–E) and deep (F–G) water. Green colour highlights the atmospheric correction algorithm with the best performance.
Table 1. Performance indicators of resampled in situ and atmospherically corrected spectra at measurement sites in optically shallow (A–E) and deep (F–G) water. Green colour highlights the atmospheric correction algorithm with the best performance.
| | A | B | C | D | E | F | G | Mean | | | ---------------------- | ---------- | ----- | ----- | ----- | ----- | ----- | ----- | ----- | | | Shallow Water | Deep Water | | | | | | | | | Measurement time (UTC) | 11:54 | 11:44 | 11:20 | 11:07 | 12:23 | 10:50 | 09:52 | | | MIP (r) | 0.990 | 0.993 | 0.993 | 0.985 | 0.976 | 0.986 | 0.984 | 0.987 | | RMSE (sr−1) | 0.002 | 0.002 | 0.001 | 0.004 | 0.003 | 0.002 | 0.003 | 0.002 | | MAPE (%) | 46.8 | 17.7 | 45.0 | 98.9 | 83.6 | 60.8 | 72.4 | 60.7 | | X² (sr−1) | 0.005 | 0.001 | 0.004 | 0.021 | 0.016 | 0.007 | 0.010 | 0.009 | | Sen2Cor (r) | 0.953 | 0.953 | 0.940 | 0.846 | 0.757 | 0.795 | 0.838 | 0.869 | | RMSE (sr−1) | 0.002 | 0.005 | 0.003 | 0.002 | 0.002 | 0.003 | 0.002 | 0.003 | | MAPE | 120.1 | 96.5 | 61.6 | 83.9 | 95.4 | 78.6 | 83.8 | 88.6 | | X² (sr−1) | 0.021 | 0.023 | 0.010 | 0.010 | 0.015 | 0.012 | 0.012 | 0.015 | | ACOLITE (r) | 0.979 | 0.980 | 0.978 | 0.960 | 0.853 | 0.953 | 0.953 | 0.951 | | RMSE (sr−1) | 0.003 | 0.006 | 0.003 | 0.001 | 0.002 | 0.002 | 0.002 | 0.003 | | MAPE | 131.4 | 110.2 | 67.4 | 76.4 | 97.4 | 73.8 | 77.3 | 90.6 | | X² (sr−1) | 0.026 | 0.032 | 0.011 | 0.010 | 0.017 | 0.011 | 0.011 | 0.017 |
Table 2. Comparison of in situ and S2-A (WASI-2D) results in optically deep water. Term in parentheses indicates in situ data source. SPM values originate from water samples taken the day before image acquisition. Mean and standard deviation of 5 × 5 respectively 3 × 3 pixel environment were calculated for 10 m and 20 m pixel size, respectively, and reflect spatial variability. The values of the 60 m pixels correspond to GPS coordinates. Errors for in situ (RAMSES) are derived from inversion and reflect variability during a measurements series.
Table 2. Comparison of in situ and S2-A (WASI-2D) results in optically deep water. Term in parentheses indicates in situ data source. SPM values originate from water samples taken the day before image acquisition. Mean and standard deviation of 5 × 5 respectively 3 × 3 pixel environment were calculated for 10 m and 20 m pixel size, respectively, and reflect spatial variability. The values of the 60 m pixels correspond to GPS coordinates. Errors for in situ (RAMSES) are derived from inversion and reflect variability during a measurements series.
| Point | Pixel Size | SPM (g·m−3) | bb,SPM(550) (m−1) | aCDOM(440) (m−1) | ||||
|---|---|---|---|---|---|---|---|---|
| In Situ (Sample) | S2-A_WASI-2D | In Situ (RAMSES) | In Situ (FREEDOM) | S2-A_WASI-2D | In Situ(RAMSES) | S2-A_WASI-2D | ||
| F | 10 | 1.9 | 1.44 ± 0.65 | no measurement | 0.015; 0.020 * | 0.0216 ± 0.0098 | 0.436 ± 0.003 | 0.14 ± 0.06 |
| 20 | 1.72 ± 0.04 | 0.0258 ± 0.0006 | 0.16 ± 0.01 | |||||
| 60 | 1.71 | 0.0257 | 0.16 | |||||
| G | 10 | 0.4 | 1.80 ± 0.04 | 0.021 ± 0.001 | 0.021 * | 0.0270 ± 0.0006 | 0.418 ± 0.003 | 0.17 ± 0.04 |
| 20 | 1.77 ± 0.03 | 0.0266 ± 0.0005 | 0.16 ± 0.01 | |||||
| 60 | 1.76 | 0.0264 | 0.16 |
Table 3. Comparison between in situ measured and S2-A (WASI-2D) results in optically shallow water. Term in parentheses indicates in situ data source. Mean and standard deviation of 5 × 5 respectively 3 × 3 pixel environment were calculated for 10 m respectively 20 m pixel size and reflect spatial variability. Errors for in situ data (RAMSES) are derived from inversion and reflect variability during a measurement series.
Table 3. Comparison between in situ measured and S2-A (WASI-2D) results in optically shallow water. Term in parentheses indicates in situ data source. Mean and standard deviation of 5 × 5 respectively 3 × 3 pixel environment were calculated for 10 m respectively 20 m pixel size and reflect spatial variability. Errors for in situ data (RAMSES) are derived from inversion and reflect variability during a measurement series.
| Point | Pixel Size | aCDOM(440) (m−1)In Situ (RAMSES) | aCDOM(440) (m−1)S2-A_WASI-2D | Water Depth (m)In Situ (Measured) | Water Depth (m)S2-A_WASI-2D |
|---|---|---|---|---|---|
| A | 10 | 0.46 ± 0.06 | 0.28 ± 0.06 | 1.65 | 1.11 ± 0.07 |
| 20 | 0.25 ± 0.07 | 1.11 ± 0.08 | |||
| B | 10 | 0.73 ± 0.18 | 0.17 ± 0.12 | 0.86 | 0.58 ± 0.07 |
| 20 | 0.16 ± 0.11 | 0.65 ± 0.09 | |||
| C | 10 | 0.52 ± 0.09 | 0.19 ± 0.07 | 2.75 | 1.58 ± 0.18 |
| 20 | 0.17 ± 0.07 | 1.50 ± 0.16 | |||
| D | 10 | 0.49 ± 0.06 | 0.15 ± 0.01 | 3.85 | 1.59 ± 0.05 |
| 20 | 0.14 ± 0.02 | 1.59 ± 0.04 | |||
| E | 10 | no measurements | 0.13 ± 0.03 | 1.59 | 0.92 ± 0.05 |
| 20 | 0.14 ± 0.03 | 0.96 ± 0.04 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Dörnhöfer, K.; Göritz, A.; Gege, P.; Pflug, B.; Oppelt, N. Water Constituents and Water Depth Retrieval from Sentinel-2A—A First Evaluation in an Oligotrophic Lake. Remote Sens. 2016, 8, 941. https://doi.org/10.3390/rs8110941
AMA Style
Dörnhöfer K, Göritz A, Gege P, Pflug B, Oppelt N. Water Constituents and Water Depth Retrieval from Sentinel-2A—A First Evaluation in an Oligotrophic Lake. Remote Sensing. 2016; 8(11):941. https://doi.org/10.3390/rs8110941
Chicago/Turabian Style
Dörnhöfer, Katja, Anna Göritz, Peter Gege, Bringfried Pflug, and Natascha Oppelt. 2016. "Water Constituents and Water Depth Retrieval from Sentinel-2A—A First Evaluation in an Oligotrophic Lake" Remote Sensing 8, no. 11: 941. https://doi.org/10.3390/rs8110941
APA Style
Dörnhöfer, K., Göritz, A., Gege, P., Pflug, B., & Oppelt, N. (2016). Water Constituents and Water Depth Retrieval from Sentinel-2A—A First Evaluation in an Oligotrophic Lake. Remote Sensing, 8(11), 941. https://doi.org/10.3390/rs8110941
Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.
Article Metrics
Article Access Statistics
For more information on the journal statistics, click here.
Multiple requests from the same IP address are counted as one view.
We use cookies on our website to ensure you get the best experience.
Read more about our cookies here.