On the Product of the Primes | Canadian Mathematical Bulletin | Cambridge Core (original) (raw)

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In recent years several attempts have been made to obtain estimates for the product of the primes less than or equal to a given integer n. Denote by 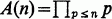the above-mentioned product and define as usual

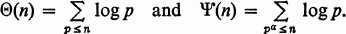
Analysis of binomial and multinomial coefficients has led to results such as A(n)<4n, due to Erdôs and Kalmar (see [2]). A note by Moser [3] gave an inductive proof of A(n)<(3.37)n, and Selfridge (unpublished) proved A(n)<(3.05)n More accurate results are known, in particular those in a paper of Rosser and Schoenfeld [4] in which they prove Θ(n)< 1.01624n; however their methods are considerably deeper and involve the theory of a complex variable as well as heavy computations. Using only elementary methods we will prove the following theorem, which improves the results of [2] and [3] considerably.

Type

Research Article

References

Appel, K. I. and Rosser, J. B., Tables for estimating functions of primes, Comm. Research Div. Technical No. 4, Von Neumann Hall, Princeton, N.J. (Sept. 1961).Google Scholar
Hardy, G. H. and Wright, E. M., The theory of numbers, Oxford Univ. Press, London, Ch. XXII, 4th éd., 1959.Google Scholar
Moser, L., On the product of the primes not exceeding n , Canad. Math. Bull. (2) 2 (1959), 119-121.Google Scholar
Rosser, J. B. and Schoenfeld, L., Approximate formulas for some functions of prime numbers, Illinois J. Math. 6 (1962), 64-94.Google Scholar