The impacts of climate change on river flood risk at the global scale (original) (raw)
1 Introduction
One of the most frequently cited impacts of future climate change is a potential increase in the river flood hazard. There have, however, been very few assessments of changing flood hazard at any scale, and most of these have focused on just one indicator of flood hazard: changes in the frequency of occurrence of specific frequency events (e.g. Bell et al. 2007; Prudhomme et al. 2003; Milly et al. 2002; Lehner et al. 2006; Hirabayashi et al. 2008; Dankers and Feyen [2009](/article/10.1007/s10584-014-1084-5#ref-CR5 "Dankers R, Feyen L (2009) Flood hazard in Europe in an ensemble of regional climate scenarios. J Geophys Res Atmos 114. doi: 10.1029/2008jd011523
"); Dankers et al. [2013](/article/10.1007/s10584-014-1084-5#ref-CR6 "Dankers R et al (2013) A first look at changes in flood hazard in the ISI-MIP ensemble. Proc Natl Acad Sci. doi:
10.1073/pnas.1302078110
")). A key conclusion of such studies is that the projected effects of climate change on the flood hazard may be very substantial, but are very dependent on climate scenario. Very few studies have considered indicators of the human impact of changes in the flood hazard. Kleinen and Petschel-Held ([2007](/article/10.1007/s10584-014-1084-5#ref-CR18 "Kleinen T, Petschel-Held G (2007) Integrated assessment of changes in flooding probabilities due to climate change. Clim Chang 81:283–312")) summed the numbers of people living in river basins where the return period of the current 50-year return period event reduces due to climate change. Hirabayashi and Kanae ([2009](/article/10.1007/s10584-014-1084-5#ref-CR14 "Hirabayashi Y, Kanae S (2009) First estimate of the future global population at risk of flooding. Hydrol Res Lett 3:6–9")) and Hirabayashi et al. ([2013](/article/10.1007/s10584-014-1084-5#ref-CR16 "Hirabayashi Y et al (2013) Global flood risk under climate change. Nat Clim Chang. doi:
10.1038/nclimate1911
")) counted each year the number of people living in 1 × 1° grid cells and flood-prone areas respectively where the simulated flood peak exceeded the current 100-year flood. Feyen et al. ([2009](/article/10.1007/s10584-014-1084-5#ref-CR7 "Feyen L, Barredo JI, Dankers R (2009) Implications of global warming and urban land use change on flooding in Europe. In: Feyen J, Shannon K, Neville M (eds) Water and urban development paradigms—towards an integration of engineering, design and management approaches. CRC Press, London, pp 217–225"), [2012](/article/10.1007/s10584-014-1084-5#ref-CR8 "Feyen L et al (2012) Fluvial flood risk in Europe in present and future climates. Clim Chang 112:47–62")) combined simulated flood frequency curves with flood depth-damage functions to estimate current and future average annual damage.The aims of this paper are (i) to assess the implications of climate change for a number of indicators of flood hazard, across the global domain, and (ii) to assess the effect of climate model uncertainty by using scenarios constructed from a wide range of climate models. The study uses a global-scale hydrological model to simulate river flows (Gosling and Arnell 2011; Arnell and Gosling 2013). Four sets of indicators of flood hazard are used, representing changes in flood frequency, changes in risk, and the numbers of people and area of cropland exposed to changes in hazard. Climate scenarios are derived from the 21 climate models in the Coupled Model Intercomparison Project Phase 3 (CMIP3) data set (Meehl et al. 2007a).
2 Methodology
2.1 Introduction
Four indicators of the flood hazard are considered here (Section 2.5) based on the simulation of the flood frequency curve under current and changed climatic conditions. Impacts are summarised across 20 world regions (Supplementary Table 1).
2.2 Climate scenarios
The effects of climate change are represented by two types of scenario. The first characterise changes in climate under the four IPCC SRES emissions scenarios, corresponding to different rates of future emissions of greenhouse gases. The second characterise changes in climate associated with specific prescribed changes in global mean surface temperature. These scenarios allow an assessment of the relationship between rate of climate forcing and impact response, and a preliminary evaluation of the magnitude of impact at different levels of change in temperature. The CRU TS3.1 data set (Harris et al. [2013](/article/10.1007/s10584-014-1084-5#ref-CR12 "Harris I, Jones PD, Osborn TJ, Lister DH (2013) Updated high-resolution grids of monthly climatic observations: the CRU TS3.10 data set. Int J Climatol. doi: 10.1002/joc.3711
")) is used here to characterise current climate, and the period 1961–1990 is taken as the climate baseline: this is approximately 0.3 °C above pre-industrial.Both sets of scenarios are constructed by pattern-scaling the output from 21 of the climate models in the CMIP3 multi-model dataset (Meehl et al. 2007a, b) (Supplementary Table 2). The 21 climate models do not represent a set of independent models, and are not of course to be interpreted as predictions. For the sake of this analysis are all assumed to be equally plausible representations of possible future climates.
Pattern-scaling assumes that the spatial fields of change per degree change in global mean surface temperature in climate variables extracted from climate model output can be rescaled to match a defined change in global mean surface temperature. Whilst this has been demonstrated to be broadly reasonable for moderate amounts of temperature and precipitation change (Mitchell 2003; Tebaldi and Arblaster [2014](/article/10.1007/s10584-014-1084-5#ref-CR30 "Tebaldi C, Arblaster JM (2014) Pattern-scaling: its strengths and limitations, and an update on the latest model simulations. Clim Chang. doi: 10.1007/s10584-013-1032-9
")), it may not hold for high temperature changes or where forcing stabilises or declines. Pattern-scaled scenarios are used here in preference to scenarios extracted directly from climate model output for two reasons. First, time series of climate model output incorporate not only a gradual climate change trend, but also multi-decadal variability. This complicates comparisons between time periods, emissions scenarios and climate models. Second, climate scenarios can be constructed to represent a wider range of forcings than in the original set of model simulations: not all the CMIP3 models, for example, were run with all SRES emissions scenarios.This study uses the ClimGen software (Osborn 2009) to derive change patterns and apply them to the CRU TS3.1 baseline climatology to produce scenarios for future monthly climate. The patterns define change in mean monthly temperature, vapour pressure and cloud cover, mean monthly precipitation, the inter-annual variance in monthly precipitation, and the mean monthly number of rain-days. A simple interpolation procedure is used to downscale the change fields from the native climate model resolution to the 0.5 × 0.5° resolution of the baseline climatology.
Climate scenarios for the four SRES emissions scenarios were constructed by rescaling the climate model patterns to the change in global mean surface temperature as estimated with SRES emissions by the simple climate model MAGICC (Osborn 2009). Different MAGICC model parameters are used for each climate model in order to represent different sensitivities to climate change, so the change in global mean surface temperature for a given emissions scenario varies between models (for three of the climate models, patterns were scaled by the average global mean surface temperature from the other models). Climate scenarios for specific prescribed changes in global mean surface temperature were constructed simply by scaling to the defined changes.
2.3 Socio-economic scenarios
Gridded population and GDP estimates through the 21st century at a spatial resolution of 0.5 × 0.5° were taken from the IMAGE 2.3 projections for the SRES storylines (van Vuuren et al. 2007). The population projections for A1 and B1 are the same, with a global population total of 8.1 billion in 2050, and the totals for A2 and B2 are 10.4 and 9 billion respectively. Global per capita GDP is highest in the A1 world, and lowest in A2, but there are large regional differences between the four scenarios. The A1 world is, in most regions, the least diverse, and A2 shows the greatest difference between regions.
Estimates of the numbers of people living in flood-prone areas at a spatial resolution of 0.5 × 0.5° were derived by combining 5′ flood-prone areas identified on the UN PREVIEW Global Risk Data Platform (preview.grid.unep.ch; Peduzzi et al. 2009), with the CIESIN GRUMP population data set for the year 2000 (CIESIN [2004](/article/10.1007/s10584-014-1084-5#ref-CR4 "Center for International Earth Science Information Network (CIESIN) CU, (IFPRI); IFPRI, Bank; TW, (CIAT); CIdAT (2004) Global Rural-Urban Mapping Project (GRUMP), alpha version: population grids. Socioeconomic Data and Applications Center (SEDAC), Columbia University. Available at http://sedac.ciesin.columbia.edu/gpw
. (1 April 2011). NY, Palisades")). It is assumed that the proportion of grid cell population living in flood-prone areas does not change over time, and that flood extent does not change. Approximately 623 million people live in flood-prone areas in 2000, rising to 843, 1,083 and 934 million in 2050 under the A1/B1, A2 and B2 population projections respectively (Supplementary Table [3](/article/10.1007/s10584-014-1084-5#MOESM8) shows the regional distribution of flood-prone populations). A similar approach was used by Jongman et al. ([2012](/article/10.1007/s10584-014-1084-5#ref-CR17 "Jongman B, Ward PJ, Aerts JCJH (2012) Global exposure to river and coastal flooding: long term trends and challenges. Glob Environ Chang 22:823–835")) to estimate exposure to river flooding.The extent of cropland within each 0.5 × 0.5° grid cell is taken from Ramankutty et al.’s ([2008](/article/10.1007/s10584-014-1084-5#ref-CR29 "Ramankutty N et al (2008) Farming the planet: 1. Geographic distribution of global agricultural lands in the year 2000. Glob Biogeochem Cycles 22. doi: 10.1029/2007gb002952
")) 5′ data set of crop areas in 2000\. It is assumed here that the crop extent does not change through the 21st century. Flood-prone cropland is estimated by overlaying the PREVIEW flood-prone areas with the cropland extent. Approximately 7 % of global cropland (around 1 million km2) is here identified as flood-prone (see Supplementary Table [3](/article/10.1007/s10584-014-1084-5#MOESM8) for the regional distribution).There are, of course, limitations to these estimates of flood-prone populations and croplands. They are based on the accuracy of the delineated floodplains, and are likely to be underestimates, because only the areas prone to flooding from “major” rivers are identified. Small-scale flooding from small rivers, or indeed flash-flooding, is not included, and neither is flash-flooding within urban areas caused by intense rainfall.
2.4 The hydrological model
River flows are simulated at a spatial resolution of 0.5 × 0.5° using Mac-PDM.09 (Gosling et al. 2010; Gosling and Arnell 2011; Arnell and Gosling 2013), a daily water balance model. The model is driven by monthly input climate data, disaggregated statistically to the daily scale, for a period of 30 years. The flood frequency distribution for a grid cell is estimated by fitting a Generalised Extreme Value (GEV) distribution by the method of L-moments to simulated annual maximum daily flows. The model is run 20 times for each grid cell, with different stochastic disaggregations of the monthly input climate data, and the average hydrological behaviour calculated across the 20 repetitions (Gosling and Arnell 2011). River flows are not routed from one grid cell to another, so the frequency curves just represent floods generated within a 0.5 × 0.5° (approximately 2,500 km2) catchment. Flood frequency curves tend to become less steep (smaller coefficient of variation) as catchment area increases, so the grid scale curves here are probably steeper than the actual frequency curves in cells with large upstream contributions. It is assumed that there is no change in catchment land use with time.
Mac-PDM.09 simulates well the average annual water balance and the distribution of flows through the year (Gosling and Arnell 2011), and produces estimates within the range of other global hydrological models (Haddeland et al. 2011). Validation of simulated flood frequency curves is more challenging because of a lack of observed data. Avisual comparison with Meigh et al’s (1997) regional GEV distributions suggests that the simulated flood frequency curve is close to the “observed” curve in some regions (e.g. South Korea and much of wet south east Asia), is steeper than the observed curve in some regions (e.g. west Africa and south west India), and flatter in other regions (e.g. Zimbabwe and Malawi). There is no clear pattern in the differences between simulated and observed frequency distributions, but no evidence of a consistent bias.
2.5 Indicators of flood hazard
2.5.1 Flood frequency
Changes in flood frequency are indexed by (i) change in the return period of the current 100-year flood and (ii) change in the magnitude of the 100-year flood. The focus on the 100-year event enables a direct comparison with other studies (Lehner et al. 2006; Hirabayashi et al. 2008; Dankers and Feyen [2009](/article/10.1007/s10584-014-1084-5#ref-CR5 "Dankers R, Feyen L (2009) Flood hazard in Europe in an ensemble of regional climate scenarios. J Geophys Res Atmos 114. doi: 10.1029/2008jd011523
")).2.5.2 Population exposed to change in river flood hazard
This indicator represents the numbers of people exposed to a “substantial” change in the frequency of flooding. It is calculated by counting the number of flood-prone people in grid cells within a region in which the return period of the current 20-year flood declines to less than 10 years or increases to more than 40 years (a doubling or halving of frequency). The 20-year flood is used as the basis of the indicator because it is assumed that this approximates the lowest level at which development in unprotected floodplains occurs. It is not appropriate to calculate the regional net effect, because the consequences of an increase and decrease in flood frequency are not equivalent.
This indicator is similar in principle to that used by Kleinen and Petschel-Held (2007), but they calculated flood frequency curves at the outlet of major river basins and assumed that everybody within that basin was affected by a change in flood frequency. The current analysis operates at a far finer spatial resolution.
2.5.3 Cropland exposed to change in hazard
This indicator is constructed in a very similar way to the previous indicator, but this time sums the flood-prone cropland in grid cells exposed to an increase or decrease in the frequency of flooding. Again, the indicator is based on changes in the frequency of the current 20-year flood.
2.5.4 Flood risk
Flood risk is indexed by the average annual flood loss, calculated by combining the probability density function of flood magnitudes with a function relating flood magnitude to flood loss. The calculation of the flood risk indicator in this analysis involves two stages. The first stage estimates grid cell indicative average annual flood loss, by combining the grid cell flood frequency curve with a generalised function relating flood magnitude to notional flood loss (not expressed in monetary terms). The second stage multiplies this grid cell indicative average annual flood loss by grid cell flood-prone population to produce “grid cell flood risk”, and sums across cells to produce watershed, regional or global totals of “regional flood risk”. Scaling by grid cell GDP rather than population would introduce the spatial variability in the value of assets exposed to flooding.
The approach uses generalised non-monetised loss functions which can be applied consistently in each grid cell because it is currently impossible to construct realistic damage functions for each grid cell across the world. The two key issues in the construction of a generalised loss function are (i) the shape of the relationship between flood magnitude and flood loss, and (ii) the return period at which damage begins. The analysis here assumes flood damage starts at the (baseline) 20-year flood level, and focuses on a linear loss function (with loss of 1 corresponding to the flood 50 % larger than the 20-year flood). It is assumed in this study that there is no protection against flooding. Grid cell average annual loss, and grid cell and regional risk, can therefore be interpreted as representing the sum of flood protection costs and residual impacts. Sensitivity analyses (Section 3.5) assess the effects of different assumptions about the starting frequency, the shape of the loss function, and level of protection, and of using GDP rather than population to scale grid cell risk.
Feyen et al. (2009, 2012) calculated a similar index of flood risk for Europe, although in more detail. They estimated flood depths from simulated river flows, using a high-resolution digital elevation model, and used country-specific depth-damage functions to estimate average annual damage at each model grid cell. They also truncated the damage functions at defined return periods to represent the effect of flood protection, with the protection standard assumed to depend on country GDP. Ward et al. ([2013](/article/10.1007/s10584-014-1084-5#ref-CR32 "Ward PJ et al (2013) Assessing flood risk at the global scale: model setup, results and sensitivity. Environ Res Lett 8:044019. doi: 10.1088/1748-9326/8/4/044019
")) use a generic global stage-damage function, which is almost linear between a depth of 0 and 5 m.3 Impacts of climate change on river flood hazard
3.1 Change in flood frequency: a physical overview
River floods are generated differently in different geographic environments. They may be generated by intense rainfall exceeding the infiltration capacity of soil, or by rain falling on saturated ground; in this case, the amount of flooding from a given amount of rainfall depends on the extent of saturation. Floods may be generated by the melting of accumulated snow. The effects of climate change on flood characteristics therefore vary across space, depending on flood generating mechanism. Where floods are largely generated by intense rainfall and antecedent conditions are not relevant, then changes in flood characteristics are strongly influenced by changes in the frequency of intense rainfall. Where the extent of saturation is important, then changes in flood characteristics are influenced not only by changes in intense rainfall, but changes in the occurrence of saturated conditions over time; this will depend on both accumulated rainfall and evaporation. Where snowmelt floods are currently important, future floods may increase if snow accumulation increases, and would occur earlier if snowmelt occurs earlier; if higher temperatures mean more winter precipitation falls as rain, then snow accumulation would reduce and snowmelt peaks reduce. At the extreme, the flood regime may change from one dominated by spring snowmelt floods to one characterised by smaller, more frequent rain-fed floods in winter. The effects of climate change on flood characteristics are therefore dependent on context, and are not necessarily a simple function of change in precipitation.
3.2 Change in flood frequency characteristics
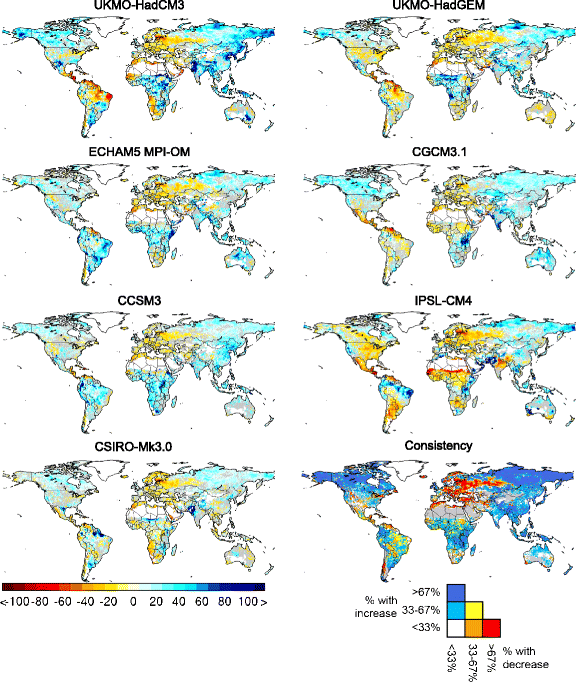
Figure 1 shows the change in the magnitude of the estimated 100-year flood under the SRES A1b emissions scenario for 2050 for the seven illustrative climate models, plus a “consistency map” showing changes with all 21 climate model patterns. Changes across large parts of the world are greater than plus or minus 20 %, and although there are important regional differences between the different climate model patterns, the “consistency map” shows strong agreement on the direction of change across much of the world. There are consistent increases in flood magnitude across humid tropical Africa, south and east Asia, much of South America, and in high latitude Asia and North America. There are consistent decreases in flood magnitude around the Mediterranean, in south west Africa, central America, central Europe and the European parts of Russia. In other parts of the world—including western Europe and much of North America—there is less consistency in change. This is similar to the results of other regional studies (e.g. Lehner et al. (2006), Dankers and Feyen ([2009](/article/10.1007/s10584-014-1084-5#ref-CR5 "Dankers R, Feyen L (2009) Flood hazard in Europe in an ensemble of regional climate scenarios. J Geophys Res Atmos 114. doi: 10.1029/2008jd011523
")) and Hirabayashi et al. ([2008](/article/10.1007/s10584-014-1084-5#ref-CR15 "Hirabayashi Y et al (2008) Global projections of changing risks of floods and droughts in a changing climate. Hydrol Sci J 53:754–772"))) which found differences in impacts between scenarios. Increases in the magnitude of the 100-year flood occur where precipitation increases during at least the flood-generating season(s). Decreases in the magnitude of the 100-year flood occur not only where precipitation decreases (such as around the Mediterranean), but also where precipitation in the future falls as rain rather than snow and the resulting rain-generated peaks are smaller than the current snowmelt-generated peaks. This occurs for example across parts of central Europe and north eastern North America. The percentage change in the magnitude of the 100-year flood is generally larger than the change in the 20-year flood (Supplementary Figure [1](/article/10.1007/s10584-014-1084-5#MOESM1)).Fig. 1
Percentage change in the magnitude of the estimated 100-year flood under SRES A1b emissions in 2050, for seven climate models, plus the consistency (expressed as a percentage of the total number of models) in projected change across 21 climate models. Grid cells where the change is less than the standard deviation due to natural unforced multi-decadal variability (see Arnell and Gosling 2013) are shaded grey. For the consistency plot, grid cells where baseline average annual runoff is less than 10 mm/year are shaded grey
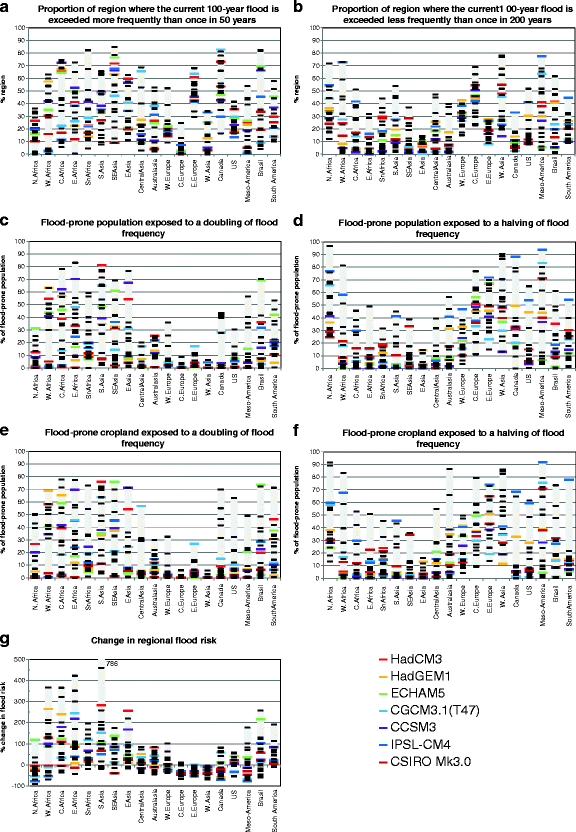
The pattern of change in the return period of the current 100-year flood is similar to the change in the magnitude of the 100-year flood (Supplementary Figure 2). Across large parts of the world the frequency of the current 100-year flood reduces to less than once in 50 years or more than once every 200 years (Fig. 2a and b). For example, with the HadCM3 climate model pattern the current 100-year flood would occur twice as often across 40 % of the world and over 60 % of south east Asia, central Africa, eastern Europe and Canada.
Fig. 2
Regional change in indicators of flood risk under SRES A1b emissions in 2050. a and b proportion of region where the return period of the current 100-year flood changes to less than 50 years or greater than 200 years. c and d flood-prone population exposed to a doubling or halving of flood frequency. e and f flood-prone cropland exposed to a doubling or halving of flood frequency. g change in regional flood risk. All 21 climate models are shown, and seven illustrative models are highlighted. The grey bars represent the range across all models
3.3 Populations exposed to change in flood frequency
Table 1 shows the global totals of people exposed to changes in the frequency of flooding in 2050, under the four emissions and associated socio-economic scenarios. With the HadCM3 climate model pattern, for example, the total population exposed to a doubling of flood frequency ranges from 323 million under B1 emissions and population to 570 million under A2 emissions and population; considerably more people are exposed to an increase in flood frequency than would see a decrease. The variability in impact, however, is greater between climate models than between future emissions and socio-economic scenarios. Under A1b, for example, the population exposed to a doubling of flood frequency ranges from 31 to 449 million across all 21 models. The difference in absolute impact between A1b and A2 is largely due to the higher population in A2 (the temperature change in 2050 is similar between the two), whilst the difference in absolute impact between A1b and B1 is entirely due to the difference in emissions/temperature (because the populations are the same). B2 has a smaller climate change than A1b but a higher population, so has only a slightly smaller absolute impact than A1b. The numbers exposed to an increase in frequency are greater than those who would see a reduction in frequency in most models, but in some more people see a reduction in flood frequency.
Table 1 Global population and cropland exposed to an increase or decrease in flood frequency; 2050
The reasons for the variability in global impact between climate models are primarily due to regional differences in the projected precipitation, and hence flood frequency, particularly in the areas of south and east Asia where most flood-prone people live. This is illustrated further in Fig. 2c and d, which shows the regional proportions of people exposed to substantial changes in the frequency of flooding in 2050, under the A1b emissions and socio-economic scenario.
Figure 3a and b show the relationship between change in global mean surface temperature (relative to 1961–1990) and the global proportion of flood-prone people in 2050 exposed to a doubling or halving in the frequency of flooding. In general, a greater proportion of global flood-prone population is exposed to an increase in flood frequency than a decrease, and the range between the climate model patterns is large. For all but two of the models there is little impact until temperatures reach 0.5 °C above the 1961–1990 mean, and for most the rate of change in impact slows as temperature increases. This is because the indicator is based on the exceedance of a threshold..
Fig. 3
Relationship between global temperature increase (relative to 1961–1990 mean) and the global-scale impacts of flooding in 2050; a and b population exposed to change in flood frequency, c and d cropland exposed to change in flood frequency and e global flood risk. All 21 climate models are shown, and seven illustrative models are highlighted. The SRES A1b 2050 population is assumed
The population exposed to a doubling of flood frequency is sensitive to the selection of return period (Supplementary Figure 3). A greater proportion of regional population is exposed to a doubling in frequency of the 100-year flood than to a doubling in frequency of the 20-year flood (62 % of global flood-prone population under HadCM3 compared with 53 %). The proportion exposed to a halving of flood frequency is less sensitive.
3.4 Cropland exposed to change in flood frequency
The global flood-prone cropland extent exposed to changes in the frequency of flooding in 2050 is shown in Table 1, under the four emissions scenarios (the cropland area is the same under each scenario, so the differences are entirely due to different changes in temperature). Under the HadCM3 climate model pattern, for example, the area of cropland exposed to an increase in flood frequency ranges from 315 to 428 thousand km2. As with the population exposed to change in frequency, the difference between climate model patterns is greater than the difference between emissions scenarios, and with most models a greater proportion of flood-prone cropland sees an increase in flood frequency than sees a decrease. Again, IPSL and CSIRO-MK3.0 show a greater proportion of cropland with a decrease in flood frequency; HadGEM also shows more cropland with a decrease in flood frequency than an increase, in contrast to projected changes in exposed populations.
As with populations exposed to changing flood frequency, the differences in global totals between models are due to differences in projected regional climates and hence flood frequencies (Fig. 2). The differences between impacts on flood-prone people and flood-prone cropland reflect the different distribution of the two exposed sectors. The cropland exposed to a doubling of flood frequency is sensitive to the selection of return period (Supplementary Figure 3).
The relationship between change in global mean surface temperature and the global proportion of flood-prone cropland exposed to a change in the frequency of flooding is shown in Fig. 3c and d. The shapes of the functions are similar to those for flood-prone population exposed to changes in flood frequency.
3.5 Change in flood risk
The percentage change in global flood risk is shown in Table 1. As with the other indicators, the variation between climate models is greater than the difference between emissions and socio-economic scenarios. With the HadCM3 climate model pattern, for example, global flood risk increases by 122 % under B1 and 187 % under A1b, but the range across all 21 climate models under A1b is from a decrease in risk of 9 % to an increase of 376 %. Only three of the 21 models show a decrease (and, incidentally, all are models with another variant amongst the 21 which show an increase in risk).
Regional change in flood risk in 2050 (under the A1b scenario) is summarised in Fig. 2g, for the seven illustrative climate models. The global total is strongly influenced by changes in south and east Asia, which varies between climate models. In all models, flood risk decreases in some regions. All seven of the models here show a reduction in regional flood risk across western, central and eastern Europe, although in each case there are strong sub-regional variations. In most cases, flood risk in the UK, France and Ireland increases, but is offset by larger decreases in risk in Germany. Change in risk at the cell-level is strongly related to change in the frequency with which flooding begins (Supplementary Figure 4).
The relationship between change in global mean surface temperature and global flood risk in 2050 is shown in Fig. 3e. The wide range between climate model patterns is clear, but two other points are of interest. First, the rate of change in risk does not decrease with increasing temperature, unlike with the other indicators, and for some model patterns accelerates. This is because the indicator is not based on the exceedance of a threshold. Second, for four models global risk decreases with small increases in temperature, but increases thereafter. This is partly because in some populous flood-prone areas the effects of higher temperatures and hence evaporation initially lead to reductions in flooding before being offset by increases in precipitation, and partly because in some regions the proportion of precipitation falling as snow and hence snowmelt floods falls as temperatures rise.
Table 1 and Figs. 2g and 3e show change in flood risk assuming a linear damage function, with damage starting at the baseline 20-year flood level, and weighting each cell by flood-prone population. The estimated change in regional risk varies in detail with the assumed shape of the damage function and starting threshold (Supplementary Figure 5a), but the broad patterns are similar and the differences between assumptions are small compared with the differences between the climate models. Similarly, there is generally little difference in regional risk when grid-cell risk is scaled by GDP rather than population (Supplementary Figure 5b). Change in risk is also slightly sensitive to the assumed level of protection (Supplementary Figure 5c: the percentage change is higher when it is assumed that there is some protection to the baseline 50-year flood), but the difference is again small compared with the difference between climate model patterns. The estimated change in risk is also relatively insensitive to whether risk is aggregated over just flood-prone areas or over all populated grid cells (Supplementary Figure 5d).
4 Caveats
There are a number of important caveats with this analysis, primarily relating to the climate scenarios as they are applied, the hydrological model used to construct grid cell frequency curves, and the indicators of flood risk. To some extent, they are attributable to the global-scale of analysis, which requires generalisation across large spatial domains; all require further investigation.
The climate scenarios define changes in mean monthly precipitation and the year-to-year variability in precipitation. However, they do not include changes in the intensity of large daily precipitation events (an increasing proportion of precipitation falling in larger events is a robust response to climate change: Held and Soden (2006)), and they do not characterise changes in the frequency or spacing of flood-producing precipitation events. They therefore potentially underestimate the effect of climate change on flooding.
The hydrological model assumes globally-consistent within-cell routing parameters, so reproduces daily flow regimes of “typical” catchments, rather than catchments with either very rapid or very slow flood responses. It does not route flood flows from one grid cell to another, so assumes that the grid cell frequency curve adequately characterises the flood hazard in a cell even where in practice flooding in the cell is caused by floods generated upstream. This would probably tend to overestimate the slope of the frequency curve in areas prone to flooding generated from considerable distances upstream, because flood frequency curves tend to flatten as catchment area increases. Also, the flood-prone area is likely to be underestimated, and new data bases (e.g. Pappenberger et al. 2012) may give different indications of regional exposure to flood risk. Dankers et al. ([2013](/article/10.1007/s10584-014-1084-5#ref-CR6 "Dankers R et al (2013) A first look at changes in flood hazard in the ISI-MIP ensemble. Proc Natl Acad Sci. doi: 10.1073/pnas.1302078110
")) show how projected changes in flood magnitudes can vary considerably between different global hydrological models, largely due to their different representation of evaporation and snowmelt processes. New attempts to estimate current global flood risk (e.g. Ward et al. [2013](/article/10.1007/s10584-014-1084-5#ref-CR32 "Ward PJ et al (2013) Assessing flood risk at the global scale: model setup, results and sensitivity. Environ Res Lett 8:044019. doi:
10.1088/1748-9326/8/4/044019
")) use hydrological models at a much finer resolution (of the order of 1x1km2), but these have not yet been applied to estimate future risk.The indicators of changing exposure to flood hazard are based on simple measures of change (a doubling or halving of flood frequency) applied consistently across the globe. Similarly, the grid-cell risk estimates assume that the relationship between flood magnitude and flood loss follows a generic loss function, and that the return period at which flood loss begins is consistent across the globe. Finally, the indicators do not incorporate the effects of existing or future adaptation; they are to be interpreted as measures of exposure to hazard, rather than actual impact. The change in risk indicator can be interpreted as incorporating both the damages caused by flooding and the costs of investment in protection against loss. Other studies (e.g. Hirabayashi et al. [2013](/article/10.1007/s10584-014-1084-5#ref-CR16 "Hirabayashi Y et al (2013) Global flood risk under climate change. Nat Clim Chang. doi: 10.1038/nclimate1911
")) have used different indicators.The impacts presented here are based on CMIP3 climate models. Climate scenarios from the later generation CMIP5 models are now available, although have been run with different forcings. Arnell and Lloyd-Hughes (2014) estimated populations exposed to changes in flooding using the same approach as in this study, with CMIP5 models and different socio-economic assumptions. The most direct comparison is between the A2 scenario here which produces a range across models of 37–588 million for the population exposed to increased flooding (Table 1), and the combination of RCP8.5 and SSP3 in Arnell and Lloyd-Hughes (2014) which has a range of 118–567 million. The CMIP5 models do not therefore produce substantially different indications of the range in potential impacts.
5 Conclusions
The key conclusion of this paper is that climate change has the potential to substantially change human exposure to the flood hazard, but that there is considerable uncertainty in the magnitude of this impact between different projections of regional change in climate (particularly precipitation). For example, under one climate model pattern (HadCM3) and future scenario (A1b), in 2050 approximately 450 million flood-prone people would be exposed to a doubling of flood frequency, as would around 430 thousand km2 of flood-prone cropland. The total global flood risk would increase by 187 %, compared to the situation in the absence of climate change. At the same time, flood frequency would be reduced for around 75 million people and 180 thousand km2 of flood-prone cropland. With the HadCM3 climate model pattern, most of these impacts would arise in south and east Asia, where precipitation is projected to increase across flood-prone areas. Other climate models project different changes in precipitation in these populous areas (some more, most less), and this is the primary reason why estimates of impact vary between climate models. The ranges in 2050 (with the A1b scenario) in estimated numbers of people and cropland exposed to a doubling of flood frequency, and change in risk are 31–449 million, 59–428 thousand and −9 % to 376 % respectively across 21 climate models. The range between climate models is considerably larger than the range (for a given climate model) between emissions and socio-economic scenarios, and is largely driven by changes in projected flood characteristics in Asia.
References
- Arnell NW, Gosling SN (2013) The impacts of climate change on hydrological regimes at the global scale. J Hydrol 486:351–364
Article Google Scholar - Arnell NW, Lloyd-Hughes B (2014) The global-scale impacts of climate change on water resources and flooding under new climate and socio-economic scenarios. Clim Chang 122:127–140
Article Google Scholar - Bell VA et al (2007) Use of a grid-based hydrological model and regional climate model outputs to assess changing flood risk. Int J Climatol 27:1657–1671
Article Google Scholar - Center for International Earth Science Information Network (CIESIN) CU, (IFPRI); IFPRI, Bank; TW, (CIAT); CIdAT (2004) Global Rural-Urban Mapping Project (GRUMP), alpha version: population grids. Socioeconomic Data and Applications Center (SEDAC), Columbia University. Available at http://sedac.ciesin.columbia.edu/gpw. (1 April 2011). NY, Palisades
- Dankers R, Feyen L (2009) Flood hazard in Europe in an ensemble of regional climate scenarios. J Geophys Res Atmos 114. doi:10.1029/2008jd011523
- Dankers R et al (2013) A first look at changes in flood hazard in the ISI-MIP ensemble. Proc Natl Acad Sci. doi:10.1073/pnas.1302078110
Google Scholar - Feyen L, Barredo JI, Dankers R (2009) Implications of global warming and urban land use change on flooding in Europe. In: Feyen J, Shannon K, Neville M (eds) Water and urban development paradigms—towards an integration of engineering, design and management approaches. CRC Press, London, pp 217–225
- Feyen L et al (2012) Fluvial flood risk in Europe in present and future climates. Clim Chang 112:47–62
Article Google Scholar - Gosling SN, Arnell NW (2011) Simulating current global river runoff with a global hydrological model: model revisions, validation, and sensitivity analysis. Hydrol Process 25:1129–1145
Article Google Scholar - Gosling SN et al (2010) Global hydrology modelling and uncertainty: running multiple ensembles with a campus grid. Philos Trans R Soc A Math Phys Eng Sci 368:4005–4021
Article Google Scholar - Haddeland I et al (2011) Multimodel estimate of the global terrestrial water balance: setup and first results. J Hydrometeorol 12:869–884
Article Google Scholar - Harris I, Jones PD, Osborn TJ, Lister DH (2013) Updated high-resolution grids of monthly climatic observations: the CRU TS3.10 data set. Int J Climatol. doi:10.1002/joc.3711
Google Scholar - Held I, Soden BJ (2006) Robust responses of the hydrological cycle to global warming. J Clim 19:5686–5699
Article Google Scholar - Hirabayashi Y, Kanae S (2009) First estimate of the future global population at risk of flooding. Hydrol Res Lett 3:6–9
Article Google Scholar - Hirabayashi Y et al (2008) Global projections of changing risks of floods and droughts in a changing climate. Hydrol Sci J 53:754–772
Article Google Scholar - Hirabayashi Y et al (2013) Global flood risk under climate change. Nat Clim Chang. doi:10.1038/nclimate1911
Google Scholar - Jongman B, Ward PJ, Aerts JCJH (2012) Global exposure to river and coastal flooding: long term trends and challenges. Glob Environ Chang 22:823–835
Article Google Scholar - Kleinen T, Petschel-Held G (2007) Integrated assessment of changes in flooding probabilities due to climate change. Clim Chang 81:283–312
Article Google Scholar - Lehner B et al (2006) Estimating the impact of global change on flood and drought risks in Europe: a continental, integrated analysis. Clim Chang 75:273–299
Article Google Scholar - Meehl GA et al (2007a) The WCRP CMIP3 multimodel dataset—a new era in climate change research. Bull Am Meteorol Soc 88:1383
Article Google Scholar - Meehl GA et al (2007b) Global climate projections. In: Solomon S (ed) Climate change 2007: the physical science basis. Contribution of working group 1 to the fourth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Google Scholar - Meigh JR, Farquharson FAK, Sutcliffe JV (1997) A worldwide comparison of regional flood estimation methods and climate. Hydrol Sci J 42:225–244
Article Google Scholar - Milly PCD et al (2002) Increasing risk of great floods in a changing climate. Nature 415:514–517
Article Google Scholar - Mitchell TD (2003) Pattern scaling—an examination of the accuracy of the technique for describing future climates. Clim Chang 60:217–242
Article Google Scholar - Osborn TJ (2009) A user guide for ClimGen: a flexible tool for generating monthly climate data sets and scenarios. Climatic Research Unit, University of East Anglia, Norwich, 17pp
Google Scholar - Pappenberger F et al (2012) Deriving global flood hazard maps of fluvial floods through a physical model cascade. Hydrol Earth Syst Sci 16:4143–4156
Article Google Scholar - Peduzzi P et al (2009) Assessing global exposure and vulnerability towards natural hazards: the disaster risk index. Nat Hazards Earth Syst Sci 9:1149–1159
Article Google Scholar - Prudhomme C, Jakob D, Svensson C (2003) Uncertainty and climate change impact on the flood regime of small UK catchments. J Hydrol 277:1–23
Article Google Scholar - Ramankutty N et al (2008) Farming the planet: 1. Geographic distribution of global agricultural lands in the year 2000. Glob Biogeochem Cycles 22. doi:10.1029/2007gb002952
- Tebaldi C, Arblaster JM (2014) Pattern-scaling: its strengths and limitations, and an update on the latest model simulations. Clim Chang. doi:10.1007/s10584-013-1032-9
Google Scholar - van Vuuren DP et al (2007) Stabilizing greenhouse gas concentrations at low levels: an assessment of reduction strategies and costs. Clim Chang 81:119–159
Article Google Scholar - Ward PJ et al (2013) Assessing flood risk at the global scale: model setup, results and sensitivity. Environ Res Lett 8:044019. doi:10.1088/1748-9326/8/4/044019
Article Google Scholar