Permutation notation - Wikiversity (original) (raw)
This article examines different notations for the composition of permutations with each other and with vectors.
Permutations are bijections from a set to itself, and the set does not need to have an order.
They can also be described as operations that move things from one set of places to another set of places — which is the natural mental image when the permutation is, e.g., a rotation of a cube.
In the end it does not matter what kind of mental image is used to understand what a permutation is or does, as long as there is no ambiguity about what result a formula will yield.
When a permutation π {\displaystyle \pi } 
Visualisations of P {\displaystyle P} 
The usual way is as an active permutation or map or substitution:
π {\displaystyle \pi } 


In this case, the result of applying π {\displaystyle \pi } 


π {\displaystyle \pi } 
π {\displaystyle \pi } 


In this case the result of applying π {\displaystyle \pi } 


Confusing these two interpretations will lead to confusing permutations with their inverses.
Active and passive transformations seem to be a related concept.
Composition of permutations is associative, but not commutative.
With prefix notation or left action, π σ ( x ) = π ( σ ( x ) ) {\displaystyle \pi \sigma (x)=\pi {\bigl (}\sigma (x){\bigr )}} 
π σ {\displaystyle \pi \sigma } 


This notation corresponds to the usual way of writing function compositions.
With postfix notation or right action, π σ ( x ) = x π σ = σ ( π ( x ) ) {\displaystyle \pi \sigma (x)=x\pi \sigma =\sigma {\bigl (}\pi (x){\bigr )}} 
π σ {\displaystyle \pi \sigma } 



This notation is common in group theory.
(In the Python examples in this article (P*Q)(2) = 2^P^Q = Q(P(2)). The result is R(2) = 4).
In its graphics this article shows all possible interpretations, including the passive ones.
To avoid confusion, however, the accompanying calculations use only active right notation, which is the notation used by SymPy and Wolfram.
α = ( 1 2 3 3 1 2 ) , β = ( 1 2 3 2 1 3 ) , v = ( v 1 , v 2 , v 3 ) , α − 1 = ( 1 2 3 2 3 1 ) {\displaystyle \alpha ={\begin{pmatrix}1&2&3\\3&1&2\end{pmatrix}},~\beta ={\begin{pmatrix}1&2&3\\2&1&3\end{pmatrix}},~v=(v_{1},v_{2},v_{3}),~~~~~~~~~~~\alpha ^{-1}={\begin{pmatrix}1&2&3\\2&3&1\end{pmatrix}}} 
If permuting v {\displaystyle v} 


| AL |
|---|
If α β = ( 2 1 3 1 3 2 ) ( 1 2 3 2 1 3 ) = ( 1 2 3 1 3 2 ) {\displaystyle \alpha \beta ={\begin{pmatrix}2&1&3\\1&3&2\end{pmatrix}}{\begin{pmatrix}1&2&3\\2&1&3\end{pmatrix}}={\begin{pmatrix}1&2&3\\1&3&2\end{pmatrix}}}  the notation should be seen as active left. * α β {\displaystyle \alpha \beta } the notation should be seen as active left. * α β {\displaystyle \alpha \beta }  means α a f t e r β {\displaystyle \alpha ~{\scriptstyle after}~\beta } means α a f t e r β {\displaystyle \alpha ~{\scriptstyle after}~\beta }  and can be written α ( β ) {\displaystyle \alpha (\beta )} and can be written α ( β ) {\displaystyle \alpha (\beta )}  . α ( 1 ) {\displaystyle \alpha (1)} . α ( 1 ) {\displaystyle \alpha (1)}  can be written α 1 {\displaystyle \alpha 1} can be written α 1 {\displaystyle \alpha 1}  .Permuting v {\displaystyle v} .Permuting v {\displaystyle v}  by α {\displaystyle \alpha } by α {\displaystyle \alpha }  may be written in different ways: v α − 1 = v ( α − 1 ) = α . v = v α − 1 {\displaystyle ~~v_{\alpha ^{-1}}~~=~~v(\alpha ^{-1})~~=~~\alpha .v~~=~~v\alpha ^{-1}} may be written in different ways: v α − 1 = v ( α − 1 ) = α . v = v α − 1 {\displaystyle ~~v_{\alpha ^{-1}}~~=~~v(\alpha ^{-1})~~=~~\alpha .v~~=~~v\alpha ^{-1}}  The notation with the dot is just an abbreviation one may define. With two permutations it means: α . β = ( α β − 1 ) − 1 = β α − 1 {\displaystyle \alpha .\beta ~~=~~(\alpha \beta ^{-1})^{-1}~~=~~\beta \alpha ^{-1}} The notation with the dot is just an abbreviation one may define. With two permutations it means: α . β = ( α β − 1 ) − 1 = β α − 1 {\displaystyle \alpha .\beta ~~=~~(\alpha \beta ^{-1})^{-1}~~=~~\beta \alpha ^{-1}}  |
| AR |
|---|
If α β = ( 1 2 3 3 1 2 ) ( 3 1 2 3 2 1 ) = ( 1 2 3 3 2 1 ) {\displaystyle \alpha \beta ={\begin{pmatrix}1&2&3\\3&1&2\end{pmatrix}}{\begin{pmatrix}3&1&2\\3&2&1\end{pmatrix}}={\begin{pmatrix}1&2&3\\3&2&1\end{pmatrix}}}  the notation should be seen as active right. * α β {\displaystyle \alpha \beta } the notation should be seen as active right. * α β {\displaystyle \alpha \beta }  means α b e f o r e β {\displaystyle \alpha ~{\scriptstyle before}~\beta } means α b e f o r e β {\displaystyle \alpha ~{\scriptstyle before}~\beta }  and can be written β ( α ) {\displaystyle \beta (\alpha )} and can be written β ( α ) {\displaystyle \beta (\alpha )}  . α ( 1 ) {\displaystyle \alpha (1)} . α ( 1 ) {\displaystyle \alpha (1)}  can be written 1 α {\displaystyle 1\alpha } can be written 1 α {\displaystyle 1\alpha }  .Permuting v {\displaystyle v} .Permuting v {\displaystyle v}  by α {\displaystyle \alpha } by α {\displaystyle \alpha }  may be written in different ways: v α − 1 = v ( α − 1 ) = v . α = α − 1 v {\displaystyle ~~v_{\alpha ^{-1}}~~=~~v(\alpha ^{-1})~~=~~v.\alpha ~~=~~\alpha ^{-1}v} may be written in different ways: v α − 1 = v ( α − 1 ) = v . α = α − 1 v {\displaystyle ~~v_{\alpha ^{-1}}~~=~~v(\alpha ^{-1})~~=~~v.\alpha ~~=~~\alpha ^{-1}v}  (Compare box 12a.) The abbreviation with the dot corresponds to the function permute in Wolfram. With two permutations it means: α . β = ( α − 1 β ) − 1 = β − 1 α {\displaystyle \alpha .\beta ~~=~~(\alpha ^{-1}\beta )^{-1}~~=~~\beta ^{-1}\alpha } (Compare box 12a.) The abbreviation with the dot corresponds to the function permute in Wolfram. With two permutations it means: α . β = ( α − 1 β ) − 1 = β − 1 α {\displaystyle \alpha .\beta ~~=~~(\alpha ^{-1}\beta )^{-1}~~=~~\beta ^{-1}\alpha }  |
If permuting v {\displaystyle v} 


Passive left should be seen as a misunderstanding of active right, and passive right should be seen as a misunderstanding of active left. *
* (Unless permuting a vector proofs otherwise.)
Permutations can be combined with
- other permutations (boxes 1 to 11)
- vectors of the same length with arbitrary elements (green boxes 12 and 16)
- vectors of arbitrary length with elements from the same range,
i.e., maps with the same codomain as the permutation, but bijectivity is not required (blue boxes 14 and 15) - scalars from the same range (red boxes 13 and 17, compare blue box 14)
The variables used in the main examples are
- the permutations P = ( 0 1 2 3 4 1 3 0 2 4 ) = ( 0132 ) {\displaystyle P={\begin{pmatrix}0&1&2&3&4\\1&3&0&2&4\end{pmatrix}}=(0132)}
and Q = ( 0 1 2 3 4 4 3 2 1 0 ) = ( 04 ) ( 13 ) {\displaystyle Q={\begin{pmatrix}0&1&2&3&4\\4&3&2&1&0\end{pmatrix}}=(04)(13)}
- the vector V = ( V 0 , … , V 4 ) {\displaystyle V=(V_{0},\dots ,V_{4})}
(in the graphics simply 0 … 4 {\displaystyle 0\dots 4}
)
- the vector E = ( 0 , 0 , 4 , 2 , 3 , 2 ) {\displaystyle E=(0,0,4,2,3,2)}
In the Wolfram calculations, the 1-based equivalents are used.
Permutations of four elements are identified by their index numbers in RevCoLex order, i.e., as the n {\displaystyle n} 
P = ( 0132 ) {\displaystyle P=(0132)} 

(Equivalents for the permutations of five elements would be Q = 119 {\displaystyle Q={\mathit {119}}} 


| Box 0 Initialisation for the computations |
|---|
**Python:**Permutations in SymPy should be interpreted as AR (the documentation states that "p*q means first apply p, then q").But the results do not discourage the interpretation as PL.The simple function before gives the same results.The result of using it on the non-bijective map E {\displaystyle E}  suggests the interpretation as AR,but that of permuting the vector V {\displaystyle V} suggests the interpretation as AR,but that of permuting the vector V {\displaystyle V}  suggests the interpretation as PL. from sympy.combinatorics import Permutation def before(positions, sequence): return [sequence[i] for i in positions] def inv(perm): length = len(perm) if sorted(perm) != list(range(length)): print('Inverse not possible!') else: inverse = [0] * length for key, val in enumerate(perm): inverse[val] = key return inverse p = [1, 3, 0, 2, 4] q = [4, 3, 2, 1, 0] r = before(p, q) P = Permutation(p) Q = Permutation(q) R = P * Q v = ['0', '1', '2', '3', '4'] e = [0, 0, 4, 2, 3, 2] **Wolfram:**Permutations in Mathematica are 1-based: p = {2,4,1,3,5} q = {5,4,3,2,1} v = {v1,v2,v3,v4,v5} e = {1,1,5,3,4,3} suggests the interpretation as PL. from sympy.combinatorics import Permutation def before(positions, sequence): return [sequence[i] for i in positions] def inv(perm): length = len(perm) if sorted(perm) != list(range(length)): print('Inverse not possible!') else: inverse = [0] * length for key, val in enumerate(perm): inverse[val] = key return inverse p = [1, 3, 0, 2, 4] q = [4, 3, 2, 1, 0] r = before(p, q) P = Permutation(p) Q = Permutation(q) R = P * Q v = ['0', '1', '2', '3', '4'] e = [0, 0, 4, 2, 3, 2] **Wolfram:**Permutations in Mathematica are 1-based: p = {2,4,1,3,5} q = {5,4,3,2,1} v = {v1,v2,v3,v4,v5} e = {1,1,5,3,4,3} |
A simple rule to avoid passive permutations: If the rows of a permutation matrix are labelled, the cycles must go clockwise (AR). If the columns are labelled, the cycles must go anticlockwise (AL).
Box 1 Ambiguity of P ⋅ Q = R {\displaystyle P\cdot Q=R}  |
|||
|---|---|---|---|
Passive (PL): P a f t e r Q = R {\displaystyle P~{\scriptstyle after}~Q~=~R}  |
Active (AR): P b e f o r e Q = R {\displaystyle P~{\scriptstyle before}~Q~=~R}  |
||
 |
 |
 |
 |
If it is only required, that P ⋅ Q = R {\displaystyle P\cdot Q=R}  , and no one intends to permute vectors, there is no need to choose an interpretation.In other terms: It only matters that the 1s in the permutation matrices are at ( i , π ( i ) ) {\displaystyle {\bigl (}i,\pi (i){\bigr )}} , and no one intends to permute vectors, there is no need to choose an interpretation.In other terms: It only matters that the 1s in the permutation matrices are at ( i , π ( i ) ) {\displaystyle {\bigl (}i,\pi (i){\bigr )}}  , and the question if the arrows go clockwise (AR) or anticlockwise (PL) is irrelevant.If on the other hand it is only required that a permutation permutes the vector V {\displaystyle V} , and the question if the arrows go clockwise (AR) or anticlockwise (PL) is irrelevant.If on the other hand it is only required that a permutation permutes the vector V {\displaystyle V}  into Y {\displaystyle Y} into Y {\displaystyle Y}  , it does dot matter if it is labelled R {\displaystyle R} , it does dot matter if it is labelled R {\displaystyle R}  or R − 1 {\displaystyle R^{-1}} or R − 1 {\displaystyle R^{-1}}  .In other terms: As long as the arrow goes from 0 to 3, it does not matter if it is labelled 3 (AR) or 0 (PR).While the permutations on the left and right have the same labels and do different things, the permutations below do exactly the same as those above them, but are labelled differently. (Compare box 19, showing the same for 4-element permutations.) Box 1a Ambiguity of P − 1 ⋅ Q − 1 = R − 1 {\displaystyle P^{-1}\cdot Q^{-1}=R^{-1}} .In other terms: As long as the arrow goes from 0 to 3, it does not matter if it is labelled 3 (AR) or 0 (PR).While the permutations on the left and right have the same labels and do different things, the permutations below do exactly the same as those above them, but are labelled differently. (Compare box 19, showing the same for 4-element permutations.) Box 1a Ambiguity of P − 1 ⋅ Q − 1 = R − 1 {\displaystyle P^{-1}\cdot Q^{-1}=R^{-1}}  Active (AL): P − 1 a f t e r Q − 1 = R − 1 {\displaystyle P^{-1}~{\scriptstyle after}~Q^{-1}~=~R^{-1}} Active (AL): P − 1 a f t e r Q − 1 = R − 1 {\displaystyle P^{-1}~{\scriptstyle after}~Q^{-1}~=~R^{-1}}  Passive (PR): P − 1 b e f o r e Q − 1 = R − 1 {\displaystyle P^{-1}~{\scriptstyle before}~Q^{-1}~=~R^{-1}} Passive (PR): P − 1 b e f o r e Q − 1 = R − 1 {\displaystyle P^{-1}~{\scriptstyle before}~Q^{-1}~=~R^{-1}}      In these matrices the 1s are in the positions ( π ( i ) , i ) {\displaystyle {\bigl (}\pi (i),i{\bigr )}} In these matrices the 1s are in the positions ( π ( i ) , i ) {\displaystyle {\bigl (}\pi (i),i{\bigr )}}  . They are exactly as those above, except that rows instead of columns are labelled. . They are exactly as those above, except that rows instead of columns are labelled. |
The following examples show with arrow diagrams what the composed permutations actually do, and how this can be interpreted as a product in two different ways, corresponding to two different matrix multiplications.
The two arrangements of matrices are symmetric to each other, including the direction of the arrows in the matrices.
In other terms: The matrix image on the left and on the right show exactly the same thing in a different way.
The arrows in both arrangements of matrices are the same as in the arrow diagram to their left.
In prefix notation (left action) α ⋅ β {\displaystyle \alpha \cdot \beta } 



Obviously α a f t e r β {\displaystyle \alpha ~{\scriptstyle after}~\beta } 

Box 4 Formulas for R {\displaystyle R}  and S {\displaystyle S} and S {\displaystyle S}  in two-line and cycle notation in two-line and cycle notation |
|
|---|---|
AL: α β = α a f t e r β {\displaystyle \alpha \beta =\alpha ~{\scriptstyle after}~\beta }  |
AR: β α = β b e f o r e α {\displaystyle \beta \alpha =\beta ~{\scriptstyle before}~\alpha }  |
Q P = ( 0 1 2 3 4 4 3 2 1 0 ) ( 0 1 2 3 4 1 3 0 2 4 ) = ( 1 3 0 2 4 3 1 4 2 0 ) ( 0 1 2 3 4 1 3 0 2 4 ) = ( 0 1 2 3 4 3 1 4 2 0 ) = R {\displaystyle {\begin{aligned}QP&~~=~~{\begin{pmatrix}0&1&2&3&4\\4&3&2&1&0\end{pmatrix}}{\begin{pmatrix}0&1&2&3&4\\1&3&0&2&4\end{pmatrix}}\\&~~=~~{\begin{pmatrix}1&3&0&2&4\\3&1&4&2&0\end{pmatrix}}{\begin{pmatrix}0&1&2&3&4\\1&3&0&2&4\end{pmatrix}}\\&~~=~~{\begin{pmatrix}0&1&2&3&4\\3&1&4&2&0\end{pmatrix}}~~=~~R\end{aligned}}}  |
P Q = ( 0 1 2 3 4 1 3 0 2 4 ) ( 0 1 2 3 4 4 3 2 1 0 ) = ( 0 1 2 3 4 1 3 0 2 4 ) ( 1 3 0 2 4 3 1 4 2 0 ) = ( 0 1 2 3 4 3 1 4 2 0 ) = R {\displaystyle {\begin{aligned}PQ&~~=~~{\begin{pmatrix}0&1&2&3&4\\1&3&0&2&4\end{pmatrix}}{\begin{pmatrix}0&1&2&3&4\\4&3&2&1&0\end{pmatrix}}\\&~~=~~{\begin{pmatrix}0&1&2&3&4\\1&3&0&2&4\end{pmatrix}}{\begin{pmatrix}1&3&0&2&4\\3&1&4&2&0\end{pmatrix}}\\&~~=~~{\begin{pmatrix}0&1&2&3&4\\3&1&4&2&0\end{pmatrix}}~~=~~R\end{aligned}}}  |
P Q = ( 0 1 2 3 4 1 3 0 2 4 ) ( 0 1 2 3 4 4 3 2 1 0 ) = ( 4 3 2 1 0 4 2 0 3 1 ) ( 0 1 2 3 4 4 3 2 1 0 ) = ( 0 1 2 3 4 4 2 0 3 1 ) = S {\displaystyle {\begin{aligned}PQ&~~=~~{\begin{pmatrix}0&1&2&3&4\\1&3&0&2&4\end{pmatrix}}{\begin{pmatrix}0&1&2&3&4\\4&3&2&1&0\end{pmatrix}}\\&~~=~~{\begin{pmatrix}4&3&2&1&0\\4&2&0&3&1\end{pmatrix}}{\begin{pmatrix}0&1&2&3&4\\4&3&2&1&0\end{pmatrix}}\\&~~=~~{\begin{pmatrix}0&1&2&3&4\\4&2&0&3&1\end{pmatrix}}~~=~~S\end{aligned}}}  |
Q P = ( 0 1 2 3 4 4 3 2 1 0 ) ( 0 1 2 3 4 1 3 0 2 4 ) = ( 0 1 2 3 4 4 3 2 1 0 ) ( 4 3 2 1 0 4 2 0 3 1 ) = ( 0 1 2 3 4 4 2 0 3 1 ) = S {\displaystyle {\begin{aligned}QP&~~=~~{\begin{pmatrix}0&1&2&3&4\\4&3&2&1&0\end{pmatrix}}{\begin{pmatrix}0&1&2&3&4\\1&3&0&2&4\end{pmatrix}}\\&~~=~~{\begin{pmatrix}0&1&2&3&4\\4&3&2&1&0\end{pmatrix}}{\begin{pmatrix}4&3&2&1&0\\4&2&0&3&1\end{pmatrix}}\\&~~=~~{\begin{pmatrix}0&1&2&3&4\\4&2&0&3&1\end{pmatrix}}~~=~~S\end{aligned}}}  |
| The top left row is reordered like the bottom right, so the bottom left row becomes the result. | The top right row is reordered like the bottom left, so the bottom right row becomes the result. |
Q P = ( 04 ) ( 13 ) ⋅ ( 0132 ) = ( 0324 ) = R {\displaystyle QP~=~(04)(13)\cdot (0132)~=~(0324)~=~R}  |
P Q = ( 0132 ) ⋅ ( 04 ) ( 13 ) = ( 0324 ) = R {\displaystyle PQ~=~(0132)\cdot (04)(13)~=~(0324)~=~R}  |
P Q = ( 0132 ) ⋅ ( 04 ) ( 13 ) = ( 0412 ) = S {\displaystyle PQ~=~(0132)\cdot (04)(13)~=~(0412)~=~S}  |
Q P = ( 04 ) ( 13 ) ⋅ ( 0132 ) = ( 0412 ) = S {\displaystyle QP~=~(04)(13)\cdot (0132)~=~(0412)~=~S}  |
| Box 5 Computation (AR only) |
|---|
| Box 5a Python >>> Permutation.print_cyclic = True >>> P Permutation(4)(0, 1, 3, 2) >>> Q Permutation(0, 4)(1, 3) >>> ~P Permutation(4)(0, 2, 3, 1) >>> ~Q Permutation(0, 4)(1, 3) >>> ~Q * ~P Permutation(0, 4, 2, 3) >>> P * Q Permutation(0, 3, 2, 4) >>> Q * P Permutation(0, 4, 1, 2) >>> Permutation.print_cyclic = False >>> P Permutation[1, 3, 0, 2, 4] >>> Q Permutation[4, 3, 2, 1, 0] >>> ~P Permutation[2, 0, 3, 1, 4] >>> ~Q Permutation[4, 3, 2, 1, 0] >>> ~Q * ~P Permutation[4, 1, 3, 0, 2] >>> P * Q Permutation[3, 1, 4, 2, 0] >>> Q * P Permutation[4, 2, 0, 3, 1] >>> p [1, 3, 0, 2, 4] >>> q [4, 3, 2, 1, 0] >>> inv(p) [2, 0, 3, 1, 4] >>> inv(q) [4, 3, 2, 1, 0] >>> before(inv(q), inv(p)) [4, 1, 3, 0, 2] >>> before(p, q) [3, 1, 4, 2, 0] >>> before(q, p) [4, 2, 0, 3, 1] Box 5b Wolfram I: p O: {2,4,1,3,5} I: q O: {5,4,3,2,1} I: PermutationCycles[p] O: Cycles[{{1,2,4,3}}] I: PermutationCycles[q] O: Cycles[{{1,5},{2,4}}] I: PermutationProduct[InversePermutation[q], InversePermutation[p]] (* R^-1 *) O: {5,2,4,1,3} I: PermutationProduct[p, q] (* R *) O: {4,2,5,3,1} I: PermutationProduct[q, p] (* S *) O: {5,3,1,4,2} |
| Box 14 Concatenation with a scalar as concatenation with a constant |
|---|
       |
The dihedral group Dih4 is the group of symmetries of the square. It has 8 elements and is not abelian - therefore order of operation matters.
In Cayley graphs postfix notation is common. One may find it more natural here, because this way the product read from left to right corresponds to the path from the identity vertex to the vertex of the permutation. (E.g. the path from e {\displaystyle e} 



This section uses prefix notation, because here the permutations are connected to 2×2 signed permutation matrices describing linear maps. E.g. the matrices of 10 {\displaystyle {\mathit {10}}} 


| permutations as linear maps | |||||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
| Cayley tables | ||
|---|---|---|
| The rotations of the square form the cyclic group C4. The 2×2 matrices of the linear maps are a subgroup of SL(2,3), and within that of the quaternion group. | ||
 Cayley table (AL) Cayley table (AL) |
Cayley table of the cyclic subgroup  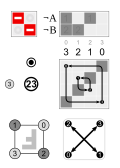               |
 corresponding subgroup of the quaternion group corresponding subgroup of the quaternion group |
Box 19 Ambiguity of 10 ⋅ 2 = 16 {\displaystyle {\mathit {10}}\cdot {\mathit {2}}={\mathit {16}}}  |
|
|---|---|
Passive (PL): 10 a f t e r 2 = 16 {\displaystyle {\mathit {10}}~{\scriptstyle after}~{\mathit {2}}={\mathit {16}}}  |
Active (AR): 10 b e f o r e 2 = 16 {\displaystyle {\mathit {10}}~{\scriptstyle before}~{\mathit {2}}={\mathit {16}}}  |
 |
 |
The inverse of 10 {\displaystyle {\mathit {10}}}  is 13 {\displaystyle {\mathit {13}}} is 13 {\displaystyle {\mathit {13}}}  , while 2 {\displaystyle {\mathit {2}}} , while 2 {\displaystyle {\mathit {2}}}  and 16 {\displaystyle {\mathit {16}}} and 16 {\displaystyle {\mathit {16}}}  are self-conjugate.The Cayley table above contains 10 ⋅ 2 = 16 {\displaystyle {\mathit {10}}\cdot {\mathit {2}}={\mathit {16}}} are self-conjugate.The Cayley table above contains 10 ⋅ 2 = 16 {\displaystyle {\mathit {10}}\cdot {\mathit {2}}={\mathit {16}}}  , so it fits the row above, and it contains 2 ⋅ 13 = 16 {\displaystyle {\mathit {2}}\cdot {\mathit {13}}={\mathit {16}}} , so it fits the row above, and it contains 2 ⋅ 13 = 16 {\displaystyle {\mathit {2}}\cdot {\mathit {13}}={\mathit {16}}}  , so its transpose would fit the row below.As above (box 1) the permutations on the left and right have the same labels and do different things, while the permutations below do exactly the same as those above them, but are labelled differently. Box 19a Ambiguity of 10 − 1 ⋅ 2 − 1 = 16 − 1 {\displaystyle {\mathit {10}}^{-1}\cdot {\mathit {2}}^{-1}={\mathit {16}}^{-1}} , so its transpose would fit the row below.As above (box 1) the permutations on the left and right have the same labels and do different things, while the permutations below do exactly the same as those above them, but are labelled differently. Box 19a Ambiguity of 10 − 1 ⋅ 2 − 1 = 16 − 1 {\displaystyle {\mathit {10}}^{-1}\cdot {\mathit {2}}^{-1}={\mathit {16}}^{-1}}  which is 13 ⋅ 2 = 16 {\displaystyle {\mathit {13}}\cdot {\mathit {2}}={\mathit {16}}} which is 13 ⋅ 2 = 16 {\displaystyle {\mathit {13}}\cdot {\mathit {2}}={\mathit {16}}}  Active (AL): 13 a f t e r 2 = 16 {\displaystyle {\mathit {13}}~{\scriptstyle after}~{\mathit {2}}={\mathit {16}}} Active (AL): 13 a f t e r 2 = 16 {\displaystyle {\mathit {13}}~{\scriptstyle after}~{\mathit {2}}={\mathit {16}}}  Passive (PR): 13 b e f o r e 2 = 16 {\displaystyle {\mathit {13}}~{\scriptstyle before}~{\mathit {2}}={\mathit {16}}} Passive (PR): 13 b e f o r e 2 = 16 {\displaystyle {\mathit {13}}~{\scriptstyle before}~{\mathit {2}}={\mathit {16}}}    |
| Cayley tables | |
|---|---|
 AL (or PR) AL (or PR) |
 AR (or PL) AR (or PL) |
P {\displaystyle P} 
Wolfram Alpha displays permutations in a way that resembles PL representation in this article,
which – if only permutation concatenation is concerned – is the same as AR. (See boxes 1 and 19.)
P {\displaystyle P} 

Wolfram does not accept the element 0, so the examples are converted to 1-based permutations:
P = (1243)(5) = 2 4 1 3 5 http://www.wolframalpha.com/input/?i=permutation+(1+2+4+3)(5) Q = (15)(24)(3) = 5 4 3 2 1 http://www.wolframalpha.com/input/?i=permutation+(1+5)(2+4)(3) R = (1435)(2) = 4 2 5 3 1 http://www.wolframalpha.com/input/?i=permutation+(1+4+3+5)(2) S = (1523)(4) = 5 3 1 4 2 http://www.wolframalpha.com/input/?i=permutation+(1+5+2+3)(4)
A blogpost from 2011 shows that back then the list notation with curly braces was the inverse of the one-line notation.
But in the calculations shown in this article (done in Mathematica Online in December 2016) the permutation p = {2,4,1,3,5} corresponds to Cycles[{{1,2,4,3}}].
Apparently in the meantime a notation people found confusing was dropped in favour of a more mainstream one.
This article uses three binary Wolfram functions:
PermutationProduct[a, b, _c_] gives the product of permutations a, b, c. (box 5b)
PermutationReplace[expr, _perm_] replaces each part in expr by its image under the permutation perm. (boxes 13a, 15a, 17a)
Permute[l, _p_] permutes list l according to permutation p. (boxes 12a, 16a)
http://docs.sympy.org/dev/modules/combinatorics/permutations.html
The composite of two permutations p*q means first apply p, then q, so i^(p*q) = (i^p)^q which is i^p^q according to Python precedence rules.
SymPy has two operators for permutations: Multiplication (*) and what could be called exponentiation (^). The latter seems to be intended only to access elements of a permutation, but can be used to combine two combinations. The result of a^b is the same as ~b*a*b (see Python script), which is a permutation in the same conjugacy class.
| Negative results for ~p(i) |
|---|
Inverse permutations behave strangely when accessed from the right. 15 − 1 {\displaystyle {\mathit {15}}^{-1}}  should behave exactly like 20 {\displaystyle {\mathit {20}}} should behave exactly like 20 {\displaystyle {\mathit {20}}}  . While i^~p15 behaves as expected, ~p15(i) gives negative results: p15 = Permutation([3, 0, 2, 1]), p20 = Permutation([1, 3, 2, 0])The two permutations are inverses: p20 == ~p15 = True [i^~p15 for i in range(4)] = [1, 3, 2, 0] [~p15(i) for i in range(4)] = [-4, -1, -3, -2] These numbers would work to access the values of a list with four elements in Python - e.g. a[-1] = a[3] is the last element of a. [-4, -1, -3, -2] converted accordingly is [0, 3, 1, 2], which is permutation 8 {\displaystyle {\mathit {8}}} . While i^~p15 behaves as expected, ~p15(i) gives negative results: p15 = Permutation([3, 0, 2, 1]), p20 = Permutation([1, 3, 2, 0])The two permutations are inverses: p20 == ~p15 = True [i^~p15 for i in range(4)] = [1, 3, 2, 0] [~p15(i) for i in range(4)] = [-4, -1, -3, -2] These numbers would work to access the values of a list with four elements in Python - e.g. a[-1] = a[3] is the last element of a. [-4, -1, -3, -2] converted accordingly is [0, 3, 1, 2], which is permutation 8 {\displaystyle {\mathit {8}}}  .Doing the same for all permutations of four elements (see Python script) shows the following result:Where the expected permutation is a {\displaystyle a} .Doing the same for all permutations of four elements (see Python script) shows the following result:Where the expected permutation is a {\displaystyle a}  , the converted permutation is b {\displaystyle b} , the converted permutation is b {\displaystyle b}  with a ⋅ b = 23 {\displaystyle a\cdot b={\mathit {23}}} with a ⋅ b = 23 {\displaystyle a\cdot b={\mathit {23}}}  .Here the expected permutations is 20 {\displaystyle {\mathit {20}}} .Here the expected permutations is 20 {\displaystyle {\mathit {20}}}  , and the converted permutation is 8 {\displaystyle {\mathit {8}}} , and the converted permutation is 8 {\displaystyle {\mathit {8}}}  , because 20 ⋅ 8 = 23 {\displaystyle {\mathit {20}}\cdot {\mathit {8}}={\mathit {23}}} , because 20 ⋅ 8 = 23 {\displaystyle {\mathit {20}}\cdot {\mathit {8}}={\mathit {23}}}  . . |
There appear to be no sources that actually use the passive interpretation of permutations, so the sources below are active left and active right.
We read a product always from right to left, thus for
σ = ( 1 2 3 4 5 6 2 3 4 1 6 5 ) {\displaystyle \sigma ={\begin{pmatrix}1&2&3&4&5&6\\2&3&4&1&6&5\end{pmatrix}}}
, τ = ( 1 2 3 4 5 6 1 3 4 5 2 6 ) {\displaystyle \tau ={\begin{pmatrix}1&2&3&4&5&6\\1&3&4&5&2&6\end{pmatrix}}}
,
we have
τ σ = ( 1 2 3 4 5 6 3 4 5 1 6 2 ) {\displaystyle \tau \sigma ={\begin{pmatrix}1&2&3&4&5&6\\3&4&5&1&6&2\end{pmatrix}}}
and σ τ = ( 1 2 3 4 5 6 2 4 1 6 3 5 ) {\displaystyle \sigma \tau ={\begin{pmatrix}1&2&3&4&5&6\\2&4&1&6&3&5\end{pmatrix}}}
.
We call σ = σ ( 1 ) σ ( 2 ) … σ ( n ) {\displaystyle \sigma =\sigma (1)\sigma (2)\dots \sigma (n)}
the word representation of σ {\displaystyle \sigma }
.
Aigner, Martin (2007). A course in enumeration. Berlin New York: Springer. ISBN 3642072534. — Word Representation (p. 27 ff)
In TAoCP Knuth states that in his book permutations are always multiplied from left to right, and gives the following example:
α β = ( 0 1 2 3 4 5 2 5 0 1 4 3 ) ( 0 1 2 3 4 5 5 4 3 2 1 0 ) = ( 0 1 2 3 4 5 2 5 0 1 4 3 ) ( 2 5 0 1 4 3 3 0 5 4 1 2 ) = ( 0 1 2 3 4 5 3 0 5 4 1 2 ) {\displaystyle \alpha \beta ={\begin{pmatrix}0&1&2&3&4&5\\2&5&0&1&4&3\end{pmatrix}}{\begin{pmatrix}0&1&2&3&4&5\\5&4&3&2&1&0\end{pmatrix}}={\begin{pmatrix}0&1&2&3&4&5\\2&5&0&1&4&3\end{pmatrix}}{\begin{pmatrix}2&5&0&1&4&3\\3&0&5&4&1&2\end{pmatrix}}={\begin{pmatrix}0&1&2&3&4&5\\3&0&5&4&1&2\end{pmatrix}}}

α β = ( 02 ) ( 153 ) ⋅ ( 05 ) ( 14 ) ( 23 ) = ( 0341 ) ( 25 ) {\displaystyle \alpha \beta =(02)(153)\cdot (05)(14)(23)=(0341)(25)}

| SymPy |
|---|
| >>> from sympy.combinatorics import Permutation >>> a = Permutation(0, 2)(1, 5, 3) >>> b = Permutation(0, 5)(1, 4)(2, 3) >>> a * b Permutation(0, 3, 4, 1)(2, 5) >>> b * a Permutation(0, 3)(1, 4, 5, 2) >>> Permutation.print_cyclic = False >>> a Permutation[2, 5, 0, 1, 4, 3] >>> b Permutation[5, 4, 3, 2, 1, 0] >>> a * b Permutation[3, 0, 5, 4, 1, 2] >>> b * a Permutation[3, 4, 1, 0, 5, 2] |
The left permutation sees the argument first:
Notice that the image of 1 under α β {\displaystyle \alpha \beta }
is 1 ( α β ) = ( 1 α ) β = 5 β = 0 {\displaystyle 1(\alpha \beta )=(1\alpha )\beta =5\beta =0}
, etc.
SymPy: (1^a)^b = 5^b = 0
This is not to be confused with right to left multiplication of permutations, i.e. the way functions are composed:
[...] traditional functional notation, in which one writes α ( 1 ) = 5 {\displaystyle \alpha (1)=5}
, makes it natural to think that α β ( 1 ) {\displaystyle \alpha \beta (1)}
should mean α ( β ( 1 ) ) = α ( 4 ) = 4 {\displaystyle \alpha (\beta (1))=\alpha (4)=4}
.
SymPy: a(b(1)) = a(4) = 4
Knuth, Donald (1973). The art of computer programming. Reading, Mass: Addison-Wesley Pub. Co. ISBN 0201896850. — Chapter 7.2.1.2. Generating all permutations
Cameron decribes the active form of a permutation as a one-to-one mapping from X = { x 1 , … , x n } {\displaystyle X=\{x_{1},\dots ,x_{n}\}} 

I wrote π ( x ) {\displaystyle \pi (x)}
for the result of applying the function π {\displaystyle \pi }
to the element x {\displaystyle x}
.
[...] In order that the result of applying first π 1 {\displaystyle \pi _{1}}and then π 2 {\displaystyle \pi _{2}}
can be called π 1 π 2 {\displaystyle \pi _{1}\pi _{2}}
, it is more natural to denote the image of x {\displaystyle x}
under π {\displaystyle \pi }
as x π {\displaystyle x\pi }
.
[Footnote:] We say that permutations act on the right if they compose according to this rule.
What Cameron calls the passive permutation is simply the one-line or word representation of an (active) permutation, not a passive permutation in the sense of this article.
Cameron, Peter J. (1994), Combinatorics: Topics, Techniques, Algorithms, Cambridge University Press, ISBN 0-521-45761-0— Chapter 3.5 Permutations (p. 29)
Illustrations of π 1 {\displaystyle \pi _{1}} 


Grimaldi defines π 1 = ( 1 2 3 3 1 2 ) {\displaystyle \pi _{1}={\begin{pmatrix}1&2&3\\3&1&2\end{pmatrix}}} 

Their product π 1 r 1 = ( 1 2 3 3 2 1 ) = r 3 {\displaystyle \pi _{1}r_{1}={\begin{pmatrix}1&2&3\\3&2&1\end{pmatrix}}=r_{3}} 
Grimaldi, Ralph (2004). Discrete and combinatorial mathematics : an applied introduction. Reading, Mass: Addison-Wesley Longman. ISBN 0321211030. — Example 16.7 (p.749)
- ↑ Some authors – see Cameron (1994) – call a permutations one-line notation the passive form. But this article calls a permutation passive when its one-line notation denotes where the arrows in its arrow diagram come from — as opposed to where they go. In the 19th century passive permutations were called permutations, while permutations in the modern sense were called substitutions.
- ↑ Compare this list of the first 40320 finite permutations: https://oeis.org/A198380/a198380_1.txt (1-based)










 with active permutations
with active permutations





 and then doing P − 1 {\displaystyle P^{-1}}
and then doing P − 1 {\displaystyle P^{-1}}  is the same as doing R − 1 {\displaystyle R^{-1}}
is the same as doing R − 1 {\displaystyle R^{-1}} 

 is the same as doing R {\displaystyle R}
is the same as doing R {\displaystyle R} 















 Python: >>> x = before(inv(p), v) >>> x ['2', '0', '3', '1', '4'] >>> before(inv(q), x) # Y ['4', '1', '3', '0', '2'] >>> before(inv(r), v) # Y ['4', '1', '3', '0', '2'] Wolfram: I: x = Permute[v, p] O: {v3,v1,v4,v2,v5} I: Permute[x, q] (* Y *) O: {v5,v2,v4,v1,v3} I: Permute[v, r] (* Y *) O: {v5,v2,v4,v1,v3}
Python: >>> x = before(inv(p), v) >>> x ['2', '0', '3', '1', '4'] >>> before(inv(q), x) # Y ['4', '1', '3', '0', '2'] >>> before(inv(r), v) # Y ['4', '1', '3', '0', '2'] Wolfram: I: x = Permute[v, p] O: {v3,v1,v4,v2,v5} I: Permute[x, q] (* Y *) O: {v5,v2,v4,v1,v3} I: Permute[v, r] (* Y *) O: {v5,v2,v4,v1,v3}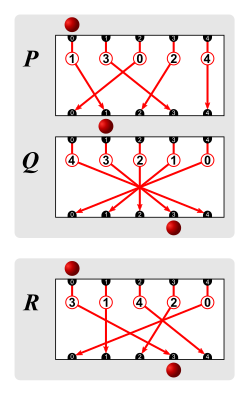













 E R = ( 0 E R , … , 5 E R ) = ( 0 R , 0 R , 4 R , 2 R , 3 R , 2 R ) = ( 3 , 3 , 0 , 4 , 2 , 4 ) = G {\displaystyle {\begin{aligned}ER&~~=~~(0ER,\dots ,5ER)\\&~~=~~(0R,0R,4R,2R,3R,2R)\\&~~=~~(3,3,0,4,2,4)~~=~~G\end{aligned}}}
E R = ( 0 E R , … , 5 E R ) = ( 0 R , 0 R , 4 R , 2 R , 3 R , 2 R ) = ( 3 , 3 , 0 , 4 , 2 , 4 ) = G {\displaystyle {\begin{aligned}ER&~~=~~(0ER,\dots ,5ER)\\&~~=~~(0R,0R,4R,2R,3R,2R)\\&~~=~~(3,3,0,4,2,4)~~=~~G\end{aligned}}}  Box 15a Computation Python: >>> f = before(e, p) >>> f [1, 1, 4, 0, 2, 0] >>> before(f, q) # G [3, 3, 0, 4, 2, 4] >>> before(e, r) # G [3, 3, 0, 4, 2, 4] Wolfram: I: f = PermutationReplace[e, p] O: {2,2,5,1,3,1} I: PermutationReplace[f, q] (* G *) O: {4,4,1,5,3,5} I: PermutationReplace[e, r] (* G *) O: {4,4,1,5,3,5}
Box 15a Computation Python: >>> f = before(e, p) >>> f [1, 1, 4, 0, 2, 0] >>> before(f, q) # G [3, 3, 0, 4, 2, 4] >>> before(e, r) # G [3, 3, 0, 4, 2, 4] Wolfram: I: f = PermutationReplace[e, p] O: {2,2,5,1,3,1} I: PermutationReplace[f, q] (* G *) O: {4,4,1,5,3,5} I: PermutationReplace[e, r] (* G *) O: {4,4,1,5,3,5}





 Python: >>> a = before(q, v) >>> a ['4', '3', '2', '1', '0'] >>> before(p, a) # B ['3', '1', '4', '2', '0'] >>> before(r, v) # B ['3', '1', '4', '2', '0'] Wolfram: I: a = Permute[v, InversePermutation[q]] O: {v5,v4,v3,v2,v1} I: Permute[a, InversePermutation[p]] (* B *) O: {v4,v2,v5,v3,v1} I: Permute[v, InversePermutation[r]] (* B *) O: {v4,v2,v5,v3,v1}
Python: >>> a = before(q, v) >>> a ['4', '3', '2', '1', '0'] >>> before(p, a) # B ['3', '1', '4', '2', '0'] >>> before(r, v) # B ['3', '1', '4', '2', '0'] Wolfram: I: a = Permute[v, InversePermutation[q]] O: {v5,v4,v3,v2,v1} I: Permute[a, InversePermutation[p]] (* B *) O: {v4,v2,v5,v3,v1} I: Permute[v, InversePermutation[r]] (* B *) O: {v4,v2,v5,v3,v1}










 goes from α {\displaystyle \alpha }
goes from α {\displaystyle \alpha }  (orange arrow), t = 2 {\displaystyle t={\mathit {2}}}
(orange arrow), t = 2 {\displaystyle t={\mathit {2}}}  (green edge)
(green edge) (red arrow), b = 7 {\displaystyle b={\mathit {7}}}
(red arrow), b = 7 {\displaystyle b={\mathit {7}}}  (blue edge)
(blue edge) (pink edge)
(pink edge)








 to 16 {\displaystyle {\mathit {16}}}
to 16 {\displaystyle {\mathit {16}}}  green edge between 21 {\displaystyle {\mathit {21}}}
green edge between 21 {\displaystyle {\mathit {21}}}  and 23 ⋅ t = 23 ⋅ 2 = 21 {\displaystyle {\mathit {23}}\cdot t={\mathit {23}}\cdot {\mathit {2}}={\mathit {21}}}
and 23 ⋅ t = 23 ⋅ 2 = 21 {\displaystyle {\mathit {23}}\cdot t={\mathit {23}}\cdot {\mathit {2}}={\mathit {21}}} 
 blue edge between 2 {\displaystyle {\mathit {2}}}
blue edge between 2 {\displaystyle {\mathit {2}}}  and 10 ⋅ b = 10 ⋅ 7 = 2 {\displaystyle {\mathit {10}}\cdot b={\mathit {10}}\cdot {\mathit {7}}={\mathit {2}}}
and 10 ⋅ b = 10 ⋅ 7 = 2 {\displaystyle {\mathit {10}}\cdot b={\mathit {10}}\cdot {\mathit {7}}={\mathit {2}}} 
 and 23 ⋅ c = 23 ⋅ 21 = 2 {\displaystyle {\mathit {23}}\cdot c={\mathit {23}}\cdot {\mathit {21}}={\mathit {2}}}
and 23 ⋅ c = 23 ⋅ 21 = 2 {\displaystyle {\mathit {23}}\cdot c={\mathit {23}}\cdot {\mathit {21}}={\mathit {2}}} 

















