A structural model for unfolded proteins from residual dipolar couplings and small-angle x-ray scattering (original) (raw)

Abstract

Natively unfolded proteins play key roles in normal and pathological biochemical processes. Despite their importance for function, this category of proteins remains beyond the reach of classical structural biology because of their inherent conformational heterogeneity. We present a description of the intrinsic conformational sampling of unfolded proteins based on residue-specific φ/Ψ propensities from loop regions of a folded protein database and simple volume exclusion. This approach is used to propose a structural model of the 57-aa, natively disordered region of the nucleocapsid-binding domain of Sendai virus phosphoprotein. Structural ensembles obeying these simple rules of conformational sampling are used to simulate averaged residual dipolar couplings (RDCs) and small-angle x-ray scattering data. This protein is particularly informative because RDC data from the equally sized folded and unfolded domains both report on the unstructured region, allowing a quantitative analysis of the degree of order present in this part of the protein. Close agreement between experimental and simulated RDC and small-angle x-ray scattering data validates this simple model of conformational sampling, providing a precise description of local structure and dynamics and average dimensions of the ensemble of sampled structures. RDC data from two urea-unfolded systems are also closely reproduced. The demonstration that conformational behavior of unfolded proteins can be accurately predicted from the primary sequence by using a simple set of rules has important consequences for our understanding of the structure and dynamics of the unstructured state.

Keywords: NMR, random coil, protein folding, protein dynamics, conformational sampling

Natively unfolded regions are now predicted to be common in functional proteins, with estimations that contiguous regions longer than 50 aa may be present in up to 50% of proteins encoded in eukaryotic genomes (1, 2). Such inherently unstructured proteins have been shown to play key roles in processes as diverse as regulation of transcription and translation, molecular recognition, signal transduction, and protein phosphorylation and multiprotein complex assembly (3). A number of neurodegenerative diseases also involve the deposition of intrinsically unfolded or misfolded proteins in pathogenic aggregates. Characterization of the conformational behavior of unfolded proteins is crucial to understanding their function for a number of reasons. Inherently unstructured proteins often undergo structural transitions to folded forms on binding to physiological partners (4, 5). Increased conformational freedom is also thought to facilitate the formation of intermolecular complexes with biological partners creating conditions necessary for high binding specificity combined with low affinity.

NMR is well adapted to the study of unstructured proteins in solution, because even for highly disordered states, resonance assignment of isotopically labeled protein is still feasible, allowing site-specific characterization of average properties over the ensemble of conformers (6). In particular, amide proton exchange rates (7), chemical shifts (8), scalar couplings (9), and spin relaxation (10, 11) report on diverse aspects of the behavior of unfolded proteins. Although long-range order is only rarely identified from nuclear Overhauser effect (12), paramagnetic relaxation enhancement has allowed successful detection of ensemble-averaged, transient contacts (13-15) and pulsed field gradient NMR reports on the overall molecular dimensions (16). The introduction of partial molecular alignment (17) has increased still further the impact of NMR on this field, allowing the detection of small degrees of conformational order that would be undetectable under normal conditions (18-20). Residual dipolar couplings (RDCs) measured in partially aligned proteins report on all orientations of internuclear vectors that are sampled in the conformational ensemble up to tens of milliseconds, providing crucial information on both the structure and dynamics of unfolded peptide chains.

NMR data measured in disordered proteins have been used as constraints in restrained molecular dynamics or Monte Carlo simulations to direct conformational sampling so that the ensemble is in agreement with experiment (21, 22). Alternative approaches have been to filter extensive sampling of unfolded states by proposing weighted populations of conformers to match NMR data (23) or compare averaged experimental data with expected distributions in dihedral angle (φ/Ψ) space (24, 25). Here, we propose an approach combining different aspects of these techniques. Structural ensembles describing the behavior of the natively unfolded peptide chain are assembled following specific rules of conformational sampling. Experimental RDCs are then compared with values averaged over the ensembles to test the validity of the models.

Small-angle scattering experiments, reporting on the overall size and shape of the molecular system, have been used to characterize the averaged dimensions of unfolded polymers in solution (26-28). Analysis of the scattering properties of polydisperse solutions provides complementary information to the characterization available from NMR, and in combination these techniques represent a potentially very powerful tool for studying natively unfolded proteins. Despite this complementarity, experimental data from the different techniques have presented contradictory evidence for the extent of transient secondary and tertiary structure in these systems (27). In this study, we reconcile these contradictions by proposing a self-consistent conformational model of the unfolded state that is in agreement with both NMR and small-angle x-ray scattering (SAXS) data.

We have applied this approach to describe the structure and dynamics of the natively disordered region of protein X (PX), the nucleocapsid-binding domain of Sendai virus (SeV) phosphoprotein (P). Protein P from SeV plays a pivotal role in the highly dynamic process of replication and transcription of the negative strand RNA genome. The C-terminal domain contains a coiled coil and is terminated by PX, through which the interaction with nucleoprotein N is mediated. PX comprises a disordered N-terminal domain (residues 474-515) and a C-terminal domain (residues 516-568), forming a three-helix bundle (29). The N-terminal domain of PX is not structured, on the basis of primary sequence analysis, chemical shift information, and interproton nuclear Overhauser effect. Both 15N relaxation and RDCs also suggest differential behavior of this domain compared with the C-terminal domain. Although PX is expressed as an individual domain, the disorder present in its N domain is expected to be present in the entire phosphoprotein and may be of biological importance, as the role of this disordered region is to position the C-terminal domain of PX before binding of protein P to RNA-bound nucleoprotein (30, 31). The advantage of this system for the study of unfolded proteins resides in the presence of approximately equally sized structured and unstructured domains, allowing a quantitative analysis of the nature and extent of conformational disorder present in this protein.

A number of models have been developed to describe the behavior of unfolded peptide chains in terms of the influence of local and long-range interactions on the effective conformational sampling experienced by each individual amino acid (32, 33). The goal of the present study is to identify a set of rules governing conformational sampling in disordered proteins, with the final aim of developing a structural description of the unfolded state directly from the primary sequence. The general nature of the approach that is developed here is illustrated with application to a natively unfolded and two urea-denatured proteins.

Methods

NMR. Experimental conditions used to measure RDC have been described (29).

SAXS Experiments. SAXS experiments were performed on the high brilliance beamline ID2 at the European Radiation Synchrotron Facility (Grenoble, France), at 20°C with a 0.8 mM PX sample in 50 mM phosphate buffer at pH 6, 500 mM salt, and 10 mM DTT. Data were collected by using a two-dimensional detector (x-ray image intensifier coupled to an European Radiation Synchrotron Facility-developed FreLoN charge-coupled device camera) placed at 3 m, yielding a useful Q range of 0.0276 < Q < 0.515 Å-1, where Q = 4πsinθ/λ, and 2θ is the scattering angle. The two-dimensional data reduction consists of (i) normalization to the detector response, exposure time, and sample transmission, (ii) absolute intensity calibration, (iii) masking of the beamstop and the border regions, (iv) azimuthal integration and averaging, and (v) background subtraction and sample concentration normalization. Several successive frames (10 for PX and 20 for the buffer) of 300 ms each were recorded for both the sample and the buffer. Each frame was inspected to check for the possible presence of protein damage before calculating average intensities.

The effective radius of gyration, _R_gyr, of PX was evaluated by using the Debye equation (34)

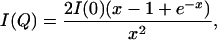graphic file with name M1.gif [1]

where x = (_QR_gyr)2. It has been shown that for unfolded systems the Debye approach remains true over a wider range of Q values (≤ 1.4/_R_gyr) than the commonly used Guinier approximation (35). A range of Q < 0.056 Å has been used for the fitting of the curves to obtain _R_gyr and I(0). In all cases, the derived I(0) was used to normalize the scattering curves.

Generation of the Conformational Ensemble. An algorithm, flexible-meccano, was developed to sample conformational space efficiently. This algorithm uses conformational sampling based on amino acid propensity and side-chain volume. Consecutive peptide planes and tetrahedral junctions are constructed (36) in the inverse direction to the primary sequence, starting from the N terminus of the folded domain to the N terminus of the flexible domain for PX and from the C-terminal residue to the N terminus for apo-myoglobin and staphyloccal nuclease Δ131Δ. The position of peptide plane (i) is defined from the Cα and C′ atoms of plane (i + 1), the selected φ/Ψ combination and the tetrahedral angle. Amino acid-specific φ/Ψ combinations are randomly extracted from a database of loop structures, built from 500 high-resolution x-ray structures (resolutions < 1.8 Å and B factors < 30 Å2) (37) from which all residues in α-helices and β-sheets were removed. Residues preceding prolines were considered as an additional amino acid type because of restricted sampling (38). A second conformational model where φ and Ψ has any value from -180° to 180° was also tested. Residue-specific exclusion volume was used to avoid clash between different amino acids of the same conformer. Amino acid-specific volumes were represented by spheres placed at Cβ (or Cα for Gly) (39). In the case of steric clash with another amino acid of the chain, or with the invariant folded fragment, the φ/Ψ pair is rejected and another set of φ/Ψ dihedral angles is selected, until no overlap was found. All ensembles comprise 100,000 conformers, and simulated properties are averaged over all members.

Prediction of RDCs from the Conformational Ensemble. Alignment properties of molecules dissolved in neutral alignment media can be reasonably reproduced by using a steric exclusion model (40). The alignment tensor for each member of the ensemble was calculated by using a model exploiting the similarity between the alignment and the radius of gyration tensors (41). RDCs were calculated from throughout the molecule, both folded and unfolded, with respect to this tensor by using the relationship:

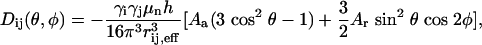graphic file with name M2.gif [2]

where _A_a and _A_r are the axial and rhombic components, respectively, of the alignment tensor, and θ and φ are the polar angles of the vector with respect to these axes. High correlation (R = 0.97) between RDCs calculated in this way and values predicted on the basis of the shape of the molecule with pales (40) indicates that this computationally faster method is a reasonable approximation even for molecules with an anisotropic mass distribution. Effective RDCs were averaged over all values by using Eq. 2 from the 100,000 conformers. Determination of the simulated and experimental alignment tensors for the folded domain was performed with module (42).

Prediction of SAXS Data from the Conformational Ensemble. Side chains were added in the unfolded domain by using the sccomp program (43), and SAXS intensity curves were predicted by using the program crysol (44). Individual intensities from each of the conformers were averaged and treated in an equivalent way to experimental data. In this case 2,000 conformers were sufficient to achieve convergence of the relevant scattering properties simulated from the ensemble.

Optimization of the Relative Orientation of the Domains. The orientation of the peptide units at the beginning of the unfolded domain is arbitrary, resulting in potentially ill-defined relative orientation of the ensemble of conformers and the folded domain. The entire process outlined above was therefore repeated with the first residue of the unfolded domain rotated such that the effective alignment tensor frames of the folded and unfolded domains resulting from the initial calculation were aligned. This corrected structure was used to calculate a new ensemble and associated averaged RDCs. This process is repeated until convergence of the simulated alignment tensors was observed (in practice this required one slight adjustment).

Results and Discussion

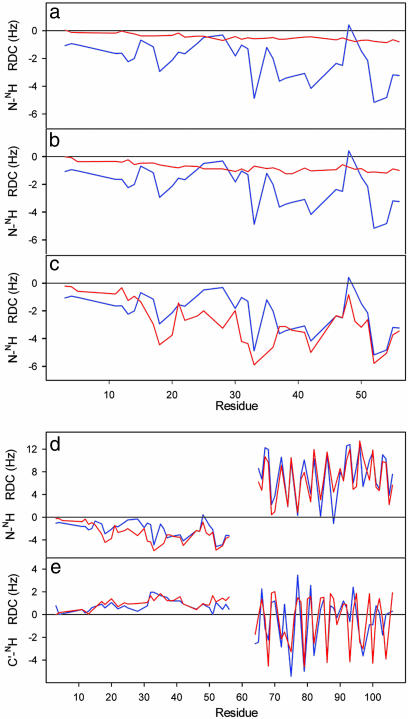
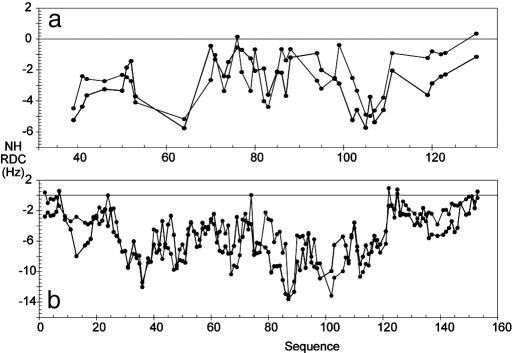
In this study, experimental RDCs and SAXS data are combined with a conformational sampling algorithm to develop a structural model of the 57-aa unfolded domain of PX. Although they cover a smaller range than the RDCs measured in the folded domain, the N-NH and C′-NH RDC measured for PX aligned in 5% of C12E6/hexanol nevertheless present identifiable fine structure and values that are non-negligible compared with the folded domain. The observation of finite RDCs in a natively unfolded strand agrees with the theoretical prediction that vectors present on any random flight chain experience incomplete sampling of orientational space. In the case of a simple linear polymer, RDCs would follow a bell-shaped curve with a maximum at the center of the sequence, whose amplitude depends on the length of the strand (19). The fine structure and range of the measured couplings present in PX (Fig. 1) suggest more complex conformational sampling behavior for this sequence.

Fig. 1.

Fig. 1.

Comparison of simulated (red) and experimental (blue) RDCs from PX. For ease of presentation, PX is numbered from 1 to 109 and contains the 14-residue His tag, such that residues 15-109 correspond to the region 474-568 in the intact C-terminal domain protein. (a) Experimental N-NH RDCs compared with RDCs simulated in the unfolded domain of PX using random sampling of backbone dihedral angle (φ/Ψ) space. In this model (I) no nonbonded interactions were taken into account except for avoiding overlap between the folded and unfolded domains. This model is essentially a random flight chain model of the polymer and reproduces the expected bell-shaped distribution along the chain. (b) Experimental N-NH RDCs compared with RDCs simulated in the unfolded domain of PX by using random sampling of backbone dihedral angle (φ/Ψ) space. In this model (II) nonbonded interactions between residues in the unfolded domain were taken into account by using a simple steric repulsion model. Overlap between the folded and unfolded domains was also avoided. (c) Experimental N-NH RDCs compared with RDCs simulated in the unfolded domain of PX by using random sampling residue-specific (φ/Ψ) propensities found in loop regions of a database of folded proteins combined with the simple volume exclusion model (model III). (d) Simulated and experimental N-NH RDCs from the entire protein by using model III. (e) Simulated and experimental C′-NH RDCs from the entire protein by using model III.

We have used the experimental RDCs as indicators of the relevance of increasingly complex models of conformational sampling. The results are presented in Fig. 1 where simulated and experimental RDCs from three basic models are compared. RDCs from each ensemble were weighted by using a single scaling factor to equalize maximum simulated and experimental N-NH RDCs in the folded domain.

The first model presented (model I) essentially reiterates the random flight chain, with the essential difference that in our case the folded domain is present and overlap with this volume is excluded. The resulting N-NH RDC profile, shown in Fig. 1_a_, reproduces the expected bell-shaped distribution along the unfolded sequence (19) and provides neither the fine structure with respect to the primary sequence nor the range of the experimental values. Introduction of a simple exclusion volume term to avoid steric clash within the N-terminal domain (model II) increases the amplitude of the bell-shaped curve, but again induces no significant fine structure (Fig. 1_b_). Excellent agreement is, however, found when a simple model (model III) is used to define the sampling properties of the ensemble, combining side-chain volume exclusion with amino acid-specific backbone dihedral angle (φ/Ψ) propensities defined by loop conformations found in a high-resolution structural database of folded proteins (Fig. 1_c_) and (Fig. 6, which is published as supporting information on the PNAS web site). Both the range and sequence-specific features of the experimental RDCs are reproduced in the unfolded domain (Pearson's correlation coefficient, R = 0.88). This model also reproduces the profile of the two-bond C′-NH RDCs from the unfolded domain in terms of fine structure, coupling sign, and relative magnitude. The reproduction of the experimental data are significantly worse if all conformations, including those present in secondary structural elements, are retained in the residue-specific dihedral angle database (data not shown). We conclude that the coil database used here is more appropriate to unfolded states. Similar observations have been made from J-couplings measured in peptides (24).

RDCs measured in the folded domain also report on the sampling behavior of the flexible strand, and their distribution can therefore be usefully compared with the couplings simulated from the ensemble to give a quantitative analysis of the extent and nature of conformational sampling in the unfolded domain. Comparison of calculated and experimental N-NH and C′-NH RDCs for the folded and unfolded domains are shown in Figs. 1 d and e and 6. The relative amplitude of the RDC values in the two domains closely reproduces the experimental data (Pearson's correlation coefficient, R = 0.92). This correspondence is by no means evident a priori, as each individual conformation tends to have very much larger RDCs in the unfolded domain, because of the more extended nature of the strand compared with the helical folded domain and very different alignment tensors (Fig. 7, which is published as supporting information on the PNAS web site). For the random flight chain model these large values average very efficiently to a low-valued, smooth distribution throughout the unfolded chain, whereas with model III the averaging closely follows the experimental characteristics. The enhanced fast local dynamics present in the unstructured domain, revealed by the lower 1H-15N nuclear Overhauser effect compared with the folded part (29), may explain the slightly lower experimental RDCs compared with the simulated values, implying that additional, small amplitude fast (ps-ns) dynamics may exist that are not accounted for by the conformational sampling algorithm.

The fine structure and relative amplitude of the RDC values also reproduce the experimental data very closely within the folded domain, which results in good agreement between the effective rhombicity and orientation of the alignment tensor predicted from the conformational ensemble and the experimentally determined tensor (Fig. 2). We note that one-step iteration is required to align the first peptide in the unfolded domain correctly such that the effective alignment tensor of the ensemble is oriented as determined from the experimentally measured couplings from the folded domain. When this slight reorientation is applied and the entire procedure is repeated the effective alignment tensors compare very closely, demonstrating the convergence of this procedure. Although the number of conformers calculated may appear large, convergence characteristics of the simulated RDCs show that up to 50,000 conformers may be required before ensemble-averaged RDCs converge (Fig. 8, which is published as supporting information on the PNAS web site).

Fig. 2.

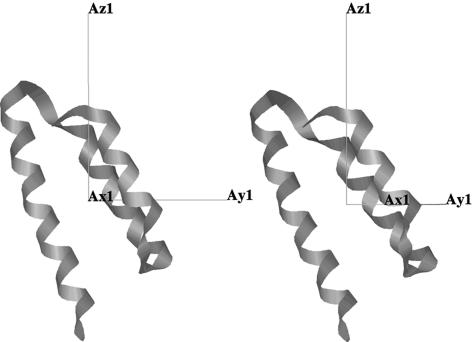
Fig. 2.

Comparison of calculated and experimental alignment tensors. Effective alignment tensor determined from the simulated N-NH and C′-NH RDCs averaged over the ensemble (Right) (model III) and the alignment tensor determined from experimental data (Left). Orientation and rhombicity are relatively well reproduced between the simulated and experimental data sets: R, α, β, γ = 0.30, -104.8°, 62.0°, 43.7° for the simulated ensemble and R, α, β, γ = 0.32, -56.2°, 55.6°, 40.6° for the experimental ensemble.

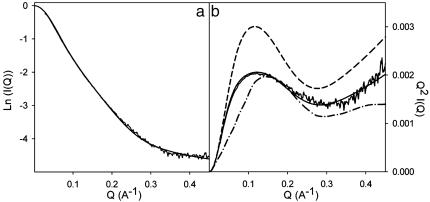
Size and Shape of the Ensemble from SAXS. Small-angle scattering data also report on the size and shape of experimentally averaged parameters from the ensemble of conformers. Initial analysis, extracting the effective radius of gyration (_R_gyr) from the averaged scattering curves calculated from the ensemble, results in a simulated value of 28.7 Å compared with an experimental value of 29.7 Å. Ensembles simulated with a polyglycine sequence for the unfolded domain, or only (φ/Ψ) pairs extracted from the extended region of the Ramachandran plot, give calculated _R_gyr of 22.4 and 67.7 Å, respectively. The similarity of calculated and experimental scattering curves, and Kratky plots, a form of data presentation that is particularly sensitive to the effective shape of the scattering object and in this case to the relative dimensions of the folded and unfolded domains, are also very closely reproduced (Fig. 3). Clear differentiation is found between reproduction of the experimental scattering curve by using model III and selected sampling models. We therefore conclude that the size and shape of the ensemble convincingly reproduce both RDC and SAXS data and that the structural model for the unfolded domain of PX appears to be credible on the basis of the available experimental data.

Fig. 3.

Fig. 3.

SAXS of PX: defining the size and shape of the ensemble. (a) Comparison of background corrected experimental SAXS data [intensity I(Q) versus scattering vector Q (Å-1)] with the simulated scattering curves averaged over the ensemble. The curves were normalized by dividing all intensities by the value of I(0) extracted from fitting to the Debye relationship. (b) Comparison of Kratky plots, where Q_2_I(Q)/I(0) is plotted against the scattering vector Q. This representation of the data is sensitive to the overall shape of the scattering object and in this case to the relative dimensions of the folded and unfolded domains. Experimental data (gray) are shown in comparison to ensembles calculated by using model III with the native sequence (solid line), a polyglycine sequence (dashed line), and a sequence where the φ/Ψ distributions are located in the extended region of the Ramachandran plot (dashed-point line).

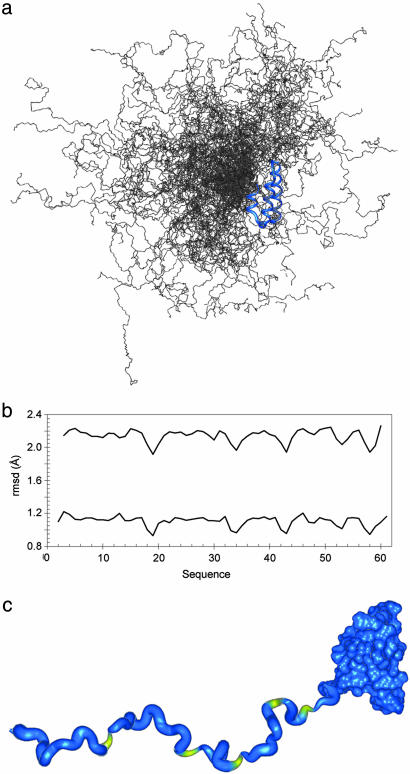
Conformational Sampling in the Unfolded Domain of PX. We now consider the conformational characteristics of this ensemble in more detail. Despite the relatively high RDC values measured in the unfolded domain, the structural ensemble is highly heterogeneous, as shown in Fig. 4_a_. To analyze this heterogeneity in more detail, a sliding window, comparing the local average rms deviation among all pairs of conformers was used (Fig. 4). This analysis reveals a detectable degree of enhanced structuring in the vicinity of the five proline residues in the unfolded domain, in agreement with previous prediction (45), and with experimental observations in chemically unfolded apo-myoglobin (20) and foldon (46), reflecting the reduced Ramachandran space available to residues preceding prolines.

Fig. 4.

Fig. 4.

Long-range and local disorder in the unfolded domain of PX. (a) Representation of the disperse nature of the ensemble of structures calculated by using model III for the unfolded domain. Two hundred structures are shown here for the sake of clarity. (b) Plot of local disorder present in the unfolded domain of PX. A sliding window of 3- and 5-aa length was used to calculate the pairwise rms deviation (rmsd) over an ensemble of 500 structures. These are plotted [5-aa window (Upper) and 3-aa window (Lower)] with respect to the primary sequence. Five regions of increased order can be detected by using this approach that are related to the positions of the prolines in the sequence. (c) Ribbon representation of the information shown in a. The width of the ribbon is proportional to the average pairwise rmsd along the unfolded domain. The ribbon is colored yellow to identify the position of the prolines.

How General Is This Sampling Model? The observations made here for PX may have more widespread consequences. In this study, we have demonstrated that the conformational behavior of a natively unfolded domain can be described by using a very simple description of the conformational behavior of the peptide chain. It is, of course, of interest to determine the extent of the validity of this observation, to assess whether the properties of disordered chains can in general be predicted on the basis of amino acid sequence. For this reason we have used the method described here to simulate dipolar couplings measured in urea-denatured mutant of staphylococcal nuclease (Δ131Δ) (18) and urea-denatured apo-myoglobin (20). For the purposes of comparison all simulated data were multiplied by a single scaling factor that best reproduces the experimental profile. The results demonstrate that the data from both proteins are reasonably well reproduced with this model (Fig. 5), clearly substantiating the dependence of experimental RDC profiles on local conformational sampling observed in PX. Similar results have been found for other natively disordered proteins, suggesting that this model is actually relevant for a number of systems and potentially very general. We note that this kind of analysis cannot exclude the presence of transient long-range contacts that, if present, may only induce small corrections in the simulated profiles.

Fig. 5.

Fig. 5.

Prediction of RDCs from urea-unfolded proteins. (a) Comparison of RDCs calculated by using model III with experimental RDCs measured from 8 M urea-denatured Δ131Δ form of Staphylococcal nuclease (18). (b) Comparison of RDCs calculated by using model III with experimental RDCs measured from 8 M urea-denatured apo-myoglobin (20). In both cases, simulated data were scaled to reproduce the total range of the experimentally measured couplings (gray).

During the revision of this article we became aware of a study (47) where analogous logic is used to develop a statistical coil model of the unfolded state that is again validated on the basis of prediction of experimental RDCs. Jha et al. demonstrate that conformers built by using a similarly constructed coil library reproduce the fine structure of experimental RDCs and the averaged overall molecular size. These observations clearly substantiate our conclusions, although there are some apparent differences between the two approaches that should be discussed. In particular, in the study by Jha et al., RDCs are only well reproduced when an additional term is included in the local conformational sampling potentials, accounting for the identity and conformation of neighboring residues. In contrast, no such term is explicitly present in our conformational sampling procedure, with the exception of the specific conformational properties of amino acids preceding prolines. We note, however, that all conformers are filtered with respect to nonbond contacts with the preceding residues in the sequence, such that the conformation is rejected if overlap is found, and that this procedure implicitly incorporates the properties of all neighbors into the protocol. Differences in results simulated by using the two approaches may also arise from subtle distinction in the procedure for calculating dipolar couplings. Jha et al. simulate RDCs by calculating the orientation of the internuclear vector with respect to the main axis of the inertia tensor of the individual conformations, assuming that this direction alone represents the static magnetic field. This approach ignores asymmetry in the shape of each conformer that is explicitly taken into account in our study by calculating the RDC with respect to all three axes of the gyration tensor. Jha et al. also assume that the extent of alignment of each molecule is identical, thereby assuming that the prefactor, or “amplitude” of the alignment tensor is the same in each case. In our study, we explicitly predict the relative extent of the alignment of each conformer, such that bond vectors in extended conformers give larger RDCs than similarly oriented vectors in more compact structures. A combination of these differences in calculation approaches may account for slight differences in resulting RDC profiles, for example, in the case of Δ131Δ staphylococcal nuclease. These differences are apparently minor and do not detract from the main conclusions of either study.

Conclusions

In summary, we propose a model for the structure and dynamics of a natively unfolded protein, based on residue-specific φ/Ψ propensities from loop regions found in a folded protein structural database and simple volume exclusion. This model is validated by experimental RDCs and SAXS data measured from PX from Sendai virus, a molecule containing folded and unfolded domains, confirming both local conformational sampling and the average size and shape of the ensemble. Despite the highly disperse ensemble, regions of preferential structuring along the flexible chain of PX are detected. These results support recent predictions that finite RDCs will be expected even from linear chains experiencing random sampling of Ramachandran space, but importantly, go one step further, demonstrating that the fine structure of RDCs measured along the primary sequence represents an interpretable structural signature of the unfolded state.

It has been noted that the observation of detectable levels of local structure, derived mainly from NMR spectroscopic data, contradict scattering studies, where overall dimensions rather suggest random coil behavior in unfolded proteins (27). In this study, we appear to have reconciled this inconsistency by demonstrating that the significant RDCs found in the unfolded domain of the protein are entirely consistent with a random coil-like behavior of the chain that satisfies the overall dimensions of the protein as derived from SAXS. This observation concurs with those made by Jha et al. (47). The demonstration that conformational behavior of both natively and chemically unfolded proteins can be accurately predicted from the primary sequence alone holds great promise for our understanding of the structure and dynamics of the unstructured state.

Supplementary Material

Supporting Information

Acknowledgments

We thank Stephanie Finet for SAXS measurement and expertise in data analysis, Peter Wright for data from apo-myoglobin, and Stephan Grzesiek for interesting discussion. This work was supported by the Commisariat `a l'Energie Atomique, Centre National de la Recherche Scientifique, and Université Joseph Fourier. P.B. was supported by a long-term fellowship from the European Molecular Biology Organization.

Author contributions: R.W.H.R. and M.B. designed research; P.B., L.B., P.T., and D.M. performed research; P.B. and M.B. analyzed data; and M.B. wrote the paper.

Conflict of interest statement: No conflicts declared.

This paper was submitted directly (Track II) to the PNAS office.

Abbreviations: RDC, residual dipolar coupling; SAXS, small-angle x-ray scattering; PX, protein X.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information