Physical constraints and functional characteristics of transcription factor–DNA interaction (original) (raw)
Abstract
We study theoretical “design principles” for transcription factor (TF)–DNA interaction in bacteria, focusing particularly on the statistical interaction of the TFs with the genomic background (i.e., the genome without the target sites). We introduce and motivate the concept of programmability, i.e., the ability to set the threshold concentration for TF binding over a wide range merely by mutating the binding sequence of a target site. This functional demand, together with physical constraints arising from the thermodynamics and kinetics of TF–DNA interaction, leads us to a narrow range of “optimal” interaction parameters. We find that this parameter set agrees well with experimental data for the interaction parameters of a few exemplary prokaryotic TFs, which indicates that TF–DNA interaction is indeed programmable. We suggest further experiments to test whether this is a general feature for a large class of TFs.
With rapid advances in the sequencing and annotation of entire genomes, the task of understanding the associated regulatory networks becomes increasingly prominent. Currently, many experimental and computational efforts are devoted to deciphering the genetic wiring diagram of a cell (1–3). Most of these efforts are focused on locating the functional DNA-binding sites of transcription factors (TFs). This knowledge, together with the genomic sequences, will provide a qualitative picture of which gene products may directly affect the expression of which genes. While obtaining such wiring diagrams is tremendously important for the eventual understanding of gene regulation at the system level, this knowledge in itself is not sufficient for the quantitative understanding of system-level effects. This has been shown dramatically in a detailed experimental study of the regulation of the endo16 gene in sea urchin development (4), which revealed an intricate regulatory function where a dozen or so TFs control the expression of a single gene. It would have been impossible to infer even the gross qualitative features of the transcriptional control from the knowledge of the binding sites alone.
A major obstacle to progress is the lack of a quantitative understanding of the physical interaction between the TFs. However, even the simpler interaction between TFs and DNA sequences is not so well understood quantitatively: It is common to classify a potential TF-binding DNA sequence in a “digital” manner—either the sequence is designated for TF binding, or it is not. In this view of TF–DNA interaction, differences between the TF-binding sequences are only nuisances that impede straightforward bioinformatic methods of target-sequence discovery. On the other hand, there are plenty of examples where differences between target sequences are known to be functionally important (5). In many cases, the binding of a TF to one site occurs only in the presence of some other TF, while the binding of the same TF to a different site does not require other TFs. This flexibility in function often is accomplished by differences in the binding sequences and is believed to be the basis for combinatorial control and signal integration in gene regulation (6). Also, different binding sites of the same TF can be “tuned” to bind at different TF concentrations, as suggested by a recent study of the Escherichia coli flagella assembly system (7). If further experimental studies confirm that tuning of binding thresholds indeed is used genome-wide to establish desired gene-regulatory functions, then TF–DNA binding should be regarded more in an analog instead of a digital manner.
In this work, we report our theoretical study on the “design” of TF–DNA interaction, assuming the analog scheme of operation. Specifically, we impose the functional requirement that the threshold concentration for TF binding to a site can be controlled over a wide range by the choice of the sequence alone; we refer to this as the “programmability” of TF–DNA binding. Taken together with thermodynamic and kinetic constraints, this functional requirement leads to a narrow range of “optimal” TF–DNA interaction parameters. We then compare our result to experimentally known parameters for exemplary TFs to determine whether the design of these TFs indeed would allow the analog scheme of operation.
To focus our discussion, we limit ourselves exclusively to the case of bacterial TFs, which are the best characterized experimentally. We study both the equilibrium occupancy of a target sequence and the dynamics of locating the target. Von Hippel, Berg, and Winter have already discussed many aspects of these issues in a series of seminal articles (8–12). Our study is built firmly on their work but includes a number of additional issues: (i) the effect of sequence-specific binding to the genomic background (nontarget sequences) on the equilibrium occupation of a target sequence, (ii) kinetic traps arising statistically from the genomic background, and (iii) the desired programmability of TF–DNA binding. We adopt the model developed by von Hippel and Berg (11) and allow both the sequence-specific and nonspecific modes of TF–DNA binding. Sequence-specific binding occurs if the binding sequence is sufficiently close to the best binding sequence and is governed quantitatively by a specificity parameter. For typical bacterial TFs with binding sequences that are no more than 15 bases long, we find that our physical and functional requirements are best satisfied within a narrow regime of intermediate specificity, amounting to the loss of ≈2 k_B_T for each additional base mismatch from the best binding sequence. Furthermore, the kinetic constraint favors a low threshold to nonspecific binding, while the programmability requirement pushes the threshold to larger values. The optimal tradeoff value only depends on the genome size and lies ≈16 k_B_T above the energy of the best binding sequence for a genome of 107 bases. These values correspond well with the interaction parameters of a number of well characterized TFs, which suggests that programmability of TF–DNA binding is compatible with the reality of protein–DNA interaction and may be used by the organism to accomplish biological functions. We hope to stimulate further experiments determining the interaction parameters for a wider range of TFs (see Discussion). These experiments could either strengthen or falsify the programmability concept depending on whether the interaction parameters are generally in agreement with our prediction.
Model of TF–DNA Interaction
Much of our knowledge on the details of TF–DNA interaction is derived from extensive biochemical experiments on a few exemplary systems dating back to pioneering work in the late 1970s (8–10, 13–15) and continuing through recent years (16–20). Furthermore, detailed structural information is available for many TFs from various structural families (21). Based on this knowledge, quantitative models of TF–DNA interaction have been established (8, 11, 12, 17). Together with the recent availability of genomic sequences, these models can be used to characterize the thermodynamics as well as the dynamics of TFs with genomic DNA in a cell. We briefly review the primary model of TF–DNA interaction in this section, which serves to introduce our notation and formulate the problem.
Biochemical and structural experiments, e.g., using lac repressor (9, 14, 20), have established firmly that (i) TFs bind closely to the DNA with a free energy Δ_G_ns (with respect to the cytoplasm) regardless of its sequence due to electrostatic interaction alone, and (ii) additional sequence-specific binding energy can be gained (via hydrogen bonds) if the binding sequence is close to the recognition sequence of the TF. Let the total binding (free) energy of a TF to a sequence s→ = {_s_1, _s_2, …, _s_L} of L nucleotides si ∈ {A,C,G,T} be Δ_G_[_s→_] (with respect to the cytoplasm), and let s→* be the best binding sequence. Δ_G_[_s→_] becomes sequence-independent, Δ_G_[_s→_] ≡ Δ_G_ns, if s→ is far from s→*. This is believed to occur via a change in the conformation of the TF from one that allows more hydrogen-bond formation to another that brings the positive charges of the TF closer to the negatively charged DNA backbone (10).
For this study, it will be convenient to measure all energies with respect to that of the best binder, Δ_G_[s→*]. Let us define _E_[_s→_] ≡ Δ_G_[_s→_] − Δ_G_[s→*]. Furthermore, we will introduce the threshold energy _E_ns ≡ Δ_G_ns − _ΔG_[s→*], where TF–DNA binding switches from the specific to the nonspecific mode (for lac repressor, _E_ns ≈ 10 kcal/mol). Then given the above model of TF–DNA interaction and assuming that the TF is bound to the DNA essentially all the time,¶ all thermodynamic quantities regarding this TF can be computed from the partition function∥
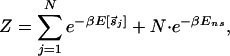
where β−1 = k_B_T ≈ 0.6 kcal/mol and s→j denotes the subsequence of the genomic sequence {_s_1, _s_2, … , sN} from position j to j + L − 1. The binding length of a typical bacterial TF is L = 10 ∼ 20 bp. The length of the genomic sequence, N, is typically several million bp.
The form of the binding energy _E_[_s→_] has been studied experimentally for several TFs (16–19). In particular, recent experiments on the TF Mnt from bacteriophage P22 (16) support the earlier model (11) that the contribution of each nucleotide in the binding sequence to the total binding energy is approximately independent and additive, i.e.,
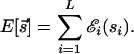
For the TFs Mnt, Cro, and λ repressor, the parameters of the “energy matrix” ℰ_i_(si) have actually been determined experimentally by in vitro measurements of the equilibrium binding constants _K_[_s→_] ∝ e_−β_E_[s→_] for every single-nucleotide mutant of the best binding sequence s→* (16, 18, 19). Due to our definition of the energy scale, ℰ_i(si) = 0 for si = 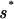 i and ℰ_i(si) > 0 for si ≠
i and ℰ_i(si) > 0 for si ≠ 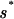 i; the latter will be referred to as “mismatch energies.” While the simple form of the binding energy (Eq. 2) certainly will not hold for all TFs, and di-, trinucleotide correlation effects are likely to be important in many cases [e.g., to some extent for _lac_ repressor (20)], the key results of our study are not sensitive to such correlations as long as there is a wide range of binding energies for different binding sequences. Thus we will adopt the simple form (Eq. 2) for this study. For the three well studied TFs, the mismatch energies are typically in the range of 1 ∼ 3 k_B_T. While the threshold energies _E_ns have not been measured carefully for these TFs, it is believed that nonspecific binding does not occur until the binding sequences are at least 4–5 mismatches away from s→* (G. Stormo, private communication).
i; the latter will be referred to as “mismatch energies.” While the simple form of the binding energy (Eq. 2) certainly will not hold for all TFs, and di-, trinucleotide correlation effects are likely to be important in many cases [e.g., to some extent for _lac_ repressor (20)], the key results of our study are not sensitive to such correlations as long as there is a wide range of binding energies for different binding sequences. Thus we will adopt the simple form (Eq. 2) for this study. For the three well studied TFs, the mismatch energies are typically in the range of 1 ∼ 3 k_B_T. While the threshold energies _E_ns have not been measured carefully for these TFs, it is believed that nonspecific binding does not occur until the binding sequences are at least 4–5 mismatches away from s→* (G. Stormo, private communication).
Genomic Background and Target Recognition
Thermodynamics.
Let us first consider the binding of a single TF to its target sequence, denoted by s→t. We will assume that thermal equilibrium can be reached within the relevant cellular time scale and discuss the important kinetics issue afterward. The effectiveness of the binding of the TF to its target is then described by the equilibrium binding probability Pt, which depends not only on the binding energy Et ≡ _E_[_s→t_] but also on the interaction with the rest of the genomic sequence. Let the contribution of this genomic background to the partition function be Zb, then the binding probability to the target is given by
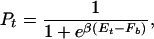
where F_b = −_k_B_T ln _Z_b is the effective binding energy (or free energy) of the entire genomic background. Eq. 3 is a sigmoidal function of Et with a (soft) threshold at _F_b, i.e., a TF binds (with probability Pt > 0.5) if Et < _F_b. Since Et ≥ 0 by definition, we must have
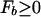
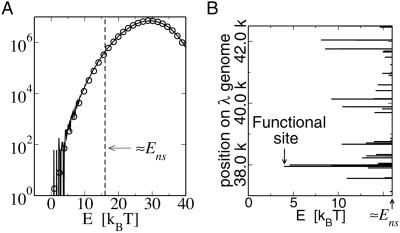
in order for a target sequence to be recognized by a single TF (we consider multiple TFs below). The background contribution can be computed for any given TF and genome according to Eq. 1 if the binding-energy matrix, the threshold energy E_ns, and the genomic sequence is known. We will instead seek a description that is independent of the specifics of the genomic sequences and energy matrices. To accomplish this, we observe first that for the few well studied TFs, the interaction of the TF with the genomic background can be well approximated by the interaction of the TF with random nucleotide sequences of the same length and single-nucleotide frequencies p(s). This is illustrated in Fig. 1A, where the histogram of binding energies obtained by using the binding-energy matrix ℰ_i(s) for the TF Cro on the E. coli genome (solid line) coincides well with the histogram of the same energy matrix applied to random nucleotide sequences (circles). Moreover, there appears to be hardly any positional correlation in the binding energies along the genome, as shown by the “energy landscape” in Fig. 1B (see legend for details). In the following, we will therefore describe the effect of the genomic background by treating it as a random nucleotide sequence for a generic TF. In particular, we will describe the genomic background partition function by _Z_b = _Z_sp + _N_⋅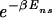 , where the contribution due to sequence-specific binding is
, where the contribution due to sequence-specific binding is
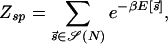
with S(N) denoting a given collection of N random nucleotide sequences of length L drawn according to the frequency p(s) for each nucleotide s.
Fig 1.
For the purpose of TF binding, the genome may be treated as random DNA plus functional target site(s). (A) Histogram of the specific binding energies for Cro [solid line] on the E. coli genome together with the average histogram (circles) for Cro on random nucleotide sequences (synthesized with the same length and single-nucleotide frequencies as the E. coli genome; normalization for both histograms such that maximum is at N). Except for statistical fluctuations at the low-energy end, the histograms are indistinguishable from each other. The approximate position of the threshold energy for nonspecific binding _E_ns is indicated as the thin dashed line. (B) Energy landscape for Cro on the bacteriophage λ DNA. The landscape appears to be random, e.g., no “funnel” guides the TF to the target site. The spatial correlation function of the landscape (not shown) decays quickly to zero beyond the scale of L = 17 for this case. Random-energy landscapes are found also for the other two TFs with known energy matrices (not shown).
Even with the random sequence approximation (Eq. 5), computation of the background energy F_b = −_k_B_T ln _Z_b is nontrivial in principle: From its definition, it is clear that F_b is a random variable, and its precise value will depend on the actual collection of sequences S(N). We are interested in the typical value of F_b, a reasonable approximation of which is its statistical average, 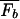 ≡ −_k_B_T
≡ −_k_B_T 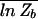 . [We use an overbar to denote averages over an ensemble of different sequence collections S(N).] Computing the average
. [We use an overbar to denote averages over an ensemble of different sequence collections S(N).] Computing the average 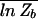 , however, is difficult to do for an arbitrary energy matrix ℰ_i(s) short of performing numerical simulations. An alternative is to compute the ensemble average of _Z_b, i.e.,
, however, is difficult to do for an arbitrary energy matrix ℰ_i(s) short of performing numerical simulations. An alternative is to compute the ensemble average of _Z_b, i.e., 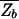 =
= 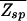 + N
+ N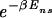 where
where
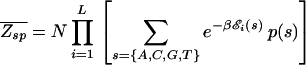
with the single-nucleotide frequencies p(s), and assume that
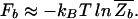
This is, for example, the approach taken by Stormo and Fields (17) in their analysis of the TF Mnt.** We note in passing that 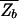 can be written more compactly in terms of the density of states Ωsp(E) for specific binding (the normalized version of the histogram in Fig. 1A), i.e.,
can be written more compactly in terms of the density of states Ωsp(E) for specific binding (the normalized version of the histogram in Fig. 1A), i.e.,
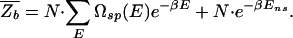
Eq. 7 is based on the so-called annealed approximation 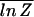 ≈ ln
≈ ln 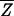 , which is valid for the genomic sequence length N → ∞ but not always appropriate for finite N, e.g., if the partition function is dominated by a few low-energy terms. Much is known from statistical physics about systems of the type defined by the partition function _Z_sp in Eq. 5, generically known as the random-energy model or REM,†† introduced by Derrida (22). It turns out that the annealed approximation is valid as long as the system's entropy is significantly larger than zero, reflecting the contribution of many terms in the partition sum. We will see further below that proper function of the TFs requires the system to be in a regime where the annealed approximation is safely applicable. We thus will take the validity of Eq. 7 for granted. In this case, the condition in Eq. 4 for the recognition of the target sequence by a single TF becomes
, which is valid for the genomic sequence length N → ∞ but not always appropriate for finite N, e.g., if the partition function is dominated by a few low-energy terms. Much is known from statistical physics about systems of the type defined by the partition function _Z_sp in Eq. 5, generically known as the random-energy model or REM,†† introduced by Derrida (22). It turns out that the annealed approximation is valid as long as the system's entropy is significantly larger than zero, reflecting the contribution of many terms in the partition sum. We will see further below that proper function of the TFs requires the system to be in a regime where the annealed approximation is safely applicable. We thus will take the validity of Eq. 7 for granted. In this case, the condition in Eq. 4 for the recognition of the target sequence by a single TF becomes
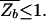
Search Dynamics.
To carry out their function properly, TFs not only need to have a high equilibrium binding probability to their targets but also must be able to locate them in a reasonably short time (e.g., less than a few minutes) after they have been activated by an inducer or freshly produced by a ribosome. This constitutes a constraint on the “search dynamics” of TFs.
In their nonspecific binding mode, TFs are still strongly associated with the DNA but are able to diffuse (i.e., slide) randomly along the genome (8–10). However, pure 1D diffusion would be an inefficient search process, because it is very redundant (e.g., a 1D random walker always returns back to the start.) For instance, assuming generously a 1D diffusion constant of _D_1 ≈ 1 μm2/sec (10), one finds a time _T_1D ∼ _N_2/_D_1 ∼ 106 sec for a single TF to diffuse around a bacterial genome of length N ≈ 5 × 106 bp (≈1 mm). Thus, to find a target within a few minutes via 1D diffusion, one would need at least 100 TFs per cell to search in parallel (so that the search length N is reduced by a factor of 100). On the other hand, there are well documented examples where regulation is accomplished effectively by only a few TFs in a cell (e.g., ≈10 for lac repressor in E. coli; ref. 24).
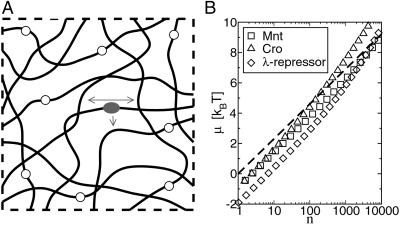
As studied in detail by Winter, Berg, and von Hippel (8–10), the search dynamics of TFs involves instead a combination of sliding along the DNA at short length scales and hopping between different segments of DNA (either over the dissociation barrier through the cytoplasm or by direct intersegment transfer; see Fig. 2A). This search mode is much faster (given the high DNA concentration inside the cell), because the dynamics is essentially 3D diffusion beyond the hopping scale, and 3D diffusion is much less redundant than 1D diffusion. For example, if the TFs were not bound to the DNA at all, a single TF of a few nanometers in linear dimension ℓ would locate its target in a cell volume _V_cell of several μm3 in the average first passage time of T_3_D = _V_cell/(4πℓ_D_3) ∼ 10 sec, given a 3D diffusion constant on the order of D_3 ∼ 10 μm2/sec (25). The search time T_3_D/1_D for the combined 1D/3D diffusion under in vivo conditions can be estimated to be comparable to T_3_D (10). Hence, the search time is short enough to comfortably allow even a single TF to locate its target within the physiological time scale.
Fig 2.
(A) Schematic illustration of the search dynamics: a TF (represented by a solid ellipse) moves among genomic DNA (lines) via a combination of 1D (along the genome) and 3D (hopping between nearby segments) diffusion as illustrated by the arrows. The open circles indicate the potential kinetic traps, which are sites that are preferred by the TF in a random background. (B) Dependence of the chemical potential μ on the number n of TFs in a cell for Mnt, Cro, and λ repressor obtained by directly solving and inverting the defining equation (Eq. 13). The comparison with the dashed line μ = k_B_T ln n shows that μ(n) is sufficiently well described by the simple expression (Eq. 13) over the regime 1 < n < 1,000.
In the study of the search dynamics reviewed above, binding of the TF to the genomic background was assumed to occur at a single energy value, namely, the nonspecific energy Δ_G_ns (8). On the other hand, the energy landscape of Fig. 1B clearly shows that the random genomic background contains many isolated sites with binding energies far below Δ_G_ns. These sites constitute kinetic traps that, in principle, can impede the local search process drastically if the energy difference to their surroundings is sufficiently large.‡‡ Thus to understand the search dynamics fully, we need to characterize the effect of kinetic traps in the genomic background: What is the constraint on the design of TF–DNA interaction imposed by requiring that the effect of kinetic traps be negligible?
At each binding sequence s→j with energy Ej ≡ _E_[_s→j_] < E_ns, the TF typically spends a time τ_j = τ0⋅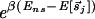 , where τ0 is the average “waiting time” of the TF at a nonspecific binding site. Along the search path of the TF, the average waiting time τ̄ per binding site then is given simply by
, where τ0 is the average “waiting time” of the TF at a nonspecific binding site. Along the search path of the TF, the average waiting time τ̄ per binding site then is given simply by
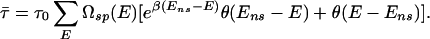
Here we assumed as before that the genomic sequence is random such that the sequence-specific binding energy E can be treated as a random variable drawn from the distribution Ωsp(E). The second term, with the help of the unit step function θ(x), is used to express the fact that there is no kinetic trap for the (majority of) sites with E > _E_ns.
A comparison of Eqs. 10 and 8 for the average partition function 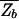 immediately yields the important relation§§
immediately yields the important relation§§
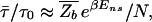
since in Eq. 8, the second term dominates for E > _E_ns. As expected, the kinetic trap factor τ̄/τ0 grows exponentially with E_ns, the threshold to nonspecific binding. On the other hand, we note from 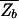 =
= 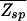 + N
+ N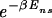 (see Thermodynamics) that the trap factor can be made to be of order 1 such that the dynamical analysis of refs. 8–10 remains qualitatively valid if
(see Thermodynamics) that the trap factor can be made to be of order 1 such that the dynamical analysis of refs. 8–10 remains qualitatively valid if 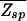 ≤ N
≤ N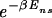 . The physical meaning of this condition is that the average effect of the kinetic traps can be rendered small if the sum of the waiting times does not exceed the order of the plain diffusion time. As we will see, this can be accomplished by choosing the binding-energy matrix ℰ_i(s) and _E_ns appropriately. Combining this kinetic constraint with Eq. 9, we obtain the condition
. The physical meaning of this condition is that the average effect of the kinetic traps can be rendered small if the sum of the waiting times does not exceed the order of the plain diffusion time. As we will see, this can be accomplished by choosing the binding-energy matrix ℰ_i(s) and _E_ns appropriately. Combining this kinetic constraint with Eq. 9, we obtain the condition
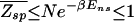
for the rapid recognition of a target sequence by a single TF.
Programmability of Binding Threshold
Multiple TFs.
There are of course typically multiple copies of the same TF in the cell, and the regulatory function is accomplished if anyone of these TFs binds to the target sequence. If the cell contains n copies of a given TF, then the occupation probability for the target sequence, Eq. 3, is replaced by the Fermi distribution (or “Arrhenius function”) Pt = 1/[1 + 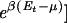 , since each binding sequence can be occupied at most by one TF. The chemical potential μ(n) is determined implicitly from the condition¶¶
, since each binding sequence can be occupied at most by one TF. The chemical potential μ(n) is determined implicitly from the condition¶¶
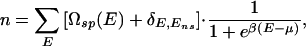
where the quantity in brackets represents the total density of states. In the simplest scenario, where steric exclusion between TFs bound to the nontarget sequences is negligible, one has (11)
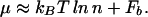
This is empirically found to be a good approximation for those TFs with known binding-energy matrices as shown in Fig. 2B. We will adopt the form of Eq. 14 for the chemical potential of a generic TF in this study; a general argument will be given later to justify this choice even for the case where multiple target sequences are present in the same genome.
Using Eq. 14, the occupation probability can be written more succinctly, Pt = 1/[1 + _ñt/n_], where
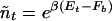
denotes the (soft) threshold concentration of the TF for occupation of the target sequence.
Programmability.
The allowed values of the background free energy _F_b for the binding of the target sequence obviously depend on the TF concentration n. For example, we have the condition in Eq. 4 for n = 1, while smaller values are allowed for n > 1. It thus appears that the allowed _F_b values are different for the different TFs, because they would typically be present in the cell with different concentrations. On the other hand, even for a given TF species, the desired binding threshold may not be at a single concentration for different target sites but can vary depending on functional demands. For example, it can be desirable to turn on different genes/operons at different TF concentrations to maintain a temporal order in the expression of different operons as the concentration of the controlling TF gradually changes over time. This effect was observed recently for the E. coli flagella assembly (7) and SOS response systems (U. Alon, private communication).
As another example, consider the case where a particular TF A is involved in the regulation of two operons, X and Y. Suppose it is desired that A activates the transcription of operon X on its own at a concentration nA, while operon Y should be activated only if A is present (at the same concentration nA) together with another TF B that can bind cooperatively with A. It is desirable then to have a strong binding site for A in the regulatory region of operon X such that its threshold ñ A,X < _nA_, and a weak binding site in the regulatory region of operon _Y_, with a threshold _ñ_ _A_,_Y_ > nA. The latter insures that the operon Y will not be activated accidentally by fluctuations in nA alone, and only when the TF B is present would the attractive interaction between A and B induce the two to bind to their targets.
The above examples show that it is functionally desirable to have the ability to set the binding threshold ñt of a given TF to each of its target-sequence s→t individually. As is clear from the defining expression (Eq. 15), this can be done only through the choice of the target-sequence s→t which affects Et, because the other variable, F_b, is fixed for a given TF. We refer to the ability to control the binding threshold ñt through the choice of the target-sequence s→t alone as programmability of the binding threshold. Assuming that programmability is a desirable feature of TF–DNA interaction (since sequence changes can be accomplished easily by point mutation if the functional need arises), we seek to determine the specifics of the TF–DNA interaction, e.g., the binding matrix ℰ_i(s), the length of the binding sequence L, and the threshold energy _E_ns, which allow the targets to be maximally programmable.
Two-State Model and Parameter Selection.
Specifically, let us require programmability of the binding threshold over the entire range ñ = 1 … 103, since typical cellular TF concentrations range from a few to a few hundred per cell. The lower bound ñ ≈ 1 immediately imposes the condition in Eq. 4 on F_b, or, taking also the kinetic constraint into account, the condition in Eq. 12. Furthermore, to tune ñ throughout the desired range with a reasonable resolution, it is necessary to have the ability to change Et from 0 to k_B_T ln 103 ≈ 7_k_B_T in small increments. This requires the nonzero entries of the binding-energy matrix ℰ_i_(s) to take on small values. Which choices for the TF–DNA interaction parameters [ℰ_i_(s), L, _E_ns] can simultaneously satisfy the latter requirement and condition (Eq. 12)?
The combined effect of these physical constraints and functional demands is understood best by simplifying the energy matrix ℰ such that we retain the essential and generic aspect of sequence-specific binding while eliminating all TF-specific details. Toward this end, we adopt the two-state model originally introduced by von Hippel and Berg (11), characterizing all of the nonzero entries of the significant positions∥∥ in the energy matrix by a single value, i.e.,
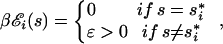
where ɛ is a dimensionless “discrimination energy” (in units of k_B_T). It describes the energetic preference of the TF for the optimal binding sequence s→* and is a crucial parameter controlling the specificity of the TF. Within the two-state model, the binding energy to the target s→t is simply ɛ times the total number of mismatches between the target and the best binder s→*, i.e., _E_[_s→t_] = ɛ⋅|s→t − s→*|, where | … | denotes the Hamming distance between two sequences. Clearly, programmability is best satisfied with a small ɛ, which enhances the resolution of the programmable binding threshold.
The two-state model (Eq. 16) also allows an explicit evaluation of the condition in Eq. 12 via the formula Eq. 6 for 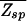 . Assuming for simplicity equal single-nucleotide frequencies in the background (i.e., p(s) = 1/4), the quantity in the bracket of Eq. 6 is evaluated easily. We have
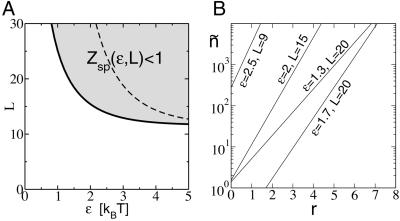
. Assuming for simplicity equal single-nucleotide frequencies in the background (i.e., p(s) = 1/4), the quantity in the bracket of Eq. 6 is evaluated easily. We have 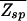 (ɛ, L) = N⋅ζ_L_(ɛ), where ζ ≡ Σ_s_ _e_−βɛ(s)p(s) = (1 + 3_e_−ɛ)/4. Note that ζ−1 is in the range between 1 and 4 and can be regarded as the effective size of the nucleotide “alphabet” as “seen” by the TF in the specific binding mode. The maximum value ζ−1 = 4 is attained if the energy matrix has infinite discrimination, ɛ → ∞, while no discrimination can be achieved at ɛ = 0 where ζ−1 = 1. In Fig. 3A, we indicate the allowed region
(ɛ, L) = N⋅ζ_L_(ɛ), where ζ ≡ Σ_s_ _e_−βɛ(s)p(s) = (1 + 3_e_−ɛ)/4. Note that ζ−1 is in the range between 1 and 4 and can be regarded as the effective size of the nucleotide “alphabet” as “seen” by the TF in the specific binding mode. The maximum value ζ−1 = 4 is attained if the energy matrix has infinite discrimination, ɛ → ∞, while no discrimination can be achieved at ɛ = 0 where ζ−1 = 1. In Fig. 3A, we indicate the allowed region 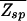 (ɛ, L) ≤ 1 in the parameter space of (ɛ, L) with the boundary L*(ɛ) = ln N/ln ζ−1(ɛ) defined by
(ɛ, L) ≤ 1 in the parameter space of (ɛ, L) with the boundary L*(ɛ) = ln N/ln ζ−1(ɛ) defined by 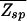 (L*, ɛ) = 1. From Fig. 3, it is clear that the desire for small ɛ pushes the system to the boundary at
(L*, ɛ) = 1. From Fig. 3, it is clear that the desire for small ɛ pushes the system to the boundary at 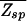 = 1. Along the boundary, the smallest ɛ is given by the largest allowable binding length L. For typical bacterial TFs with binding sequences that are no longer than ≈15 bp (usually dimers), we find ɛ ≈ 2.
= 1. Along the boundary, the smallest ɛ is given by the largest allowable binding length L. For typical bacterial TFs with binding sequences that are no longer than ≈15 bp (usually dimers), we find ɛ ≈ 2.
Fig 3.
(A) Plot of the region where 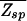 (ɛ,L) ≤ 1. The boundary L*(ɛ) for N = 107 is indicated by the solid line (see text). The dashed line ln(N)/[ln ζ−1(ɛ) − ɛ/(1 + _e_ɛ/3)] indicates the onset of the glass transition in the random-energy model where the annealed approximation breaks down. As argued in the text, the desired parameter regime is close to
(ɛ,L) ≤ 1. The boundary L*(ɛ) for N = 107 is indicated by the solid line (see text). The dashed line ln(N)/[ln ζ−1(ɛ) − ɛ/(1 + _e_ɛ/3)] indicates the onset of the glass transition in the random-energy model where the annealed approximation breaks down. As argued in the text, the desired parameter regime is close to 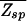 = 1 such that the annealed approximation is justified. (B) The binding threshold ñ as a function of the total number of mismatches r of the target-sequence s→t from the best binder s→* at different parameter combinations (ɛ,L).
= 1 such that the annealed approximation is justified. (B) The binding threshold ñ as a function of the total number of mismatches r of the target-sequence s→t from the best binder s→* at different parameter combinations (ɛ,L).
Although the result on ɛ is somewhat specific to the two-state model, the need for 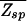 → 1 imposed by the programmability consideration forces the threshold energy to take on the value
→ 1 imposed by the programmability consideration forces the threshold energy to take on the value
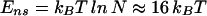
(for N ∼ 107) according to the condition in Eq. 12 independent of the specifics of the binding-energy matrix ɛ. It also follows that
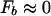
such that the binding threshold is simply given by
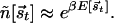
The dependences of the ñ on the number of mismatches for the two-state model are shown in Fig. 3B. We see that at the optimal parameter choice of (ɛ = 2, L = 15), each mismatch increases the binding threshold ñ by nearly 10-fold. In principle, further fine-tuning can be accomplished by using small variations in the mismatch energies.
Discussion
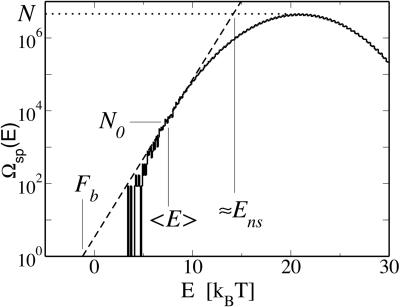
The key results of this study, that maximal programmability of the binding threshold ñ requires the TF–DNA interaction to satisfy the conditions in Eqs. 17 and 18, can be conveniently summarized graphically using the density of states Ωsp(E). In Fig. 4, the density of states is plotted with the normalization that max_E_ Ωsp(E) = N, as indicated by the horizontal dotted line. The background free energy _F_b can be obtained using the Legendre construction: One draws the line 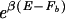 (the dashed line in the semilog plot of Fig. 4) such that it just touches Ωsp(E). _F_b then can be read off as the intercept of the dashed line on the E axis, which should be in the vicinity of the origin according to Eq. 18. Similarly, _E_ns (as given by Eq. 17) can be read off as the E coordinate where the dashed line intersects the horizontal dotted line.
(the dashed line in the semilog plot of Fig. 4) such that it just touches Ωsp(E). _F_b then can be read off as the intercept of the dashed line on the E axis, which should be in the vicinity of the origin according to Eq. 18. Similarly, _E_ns (as given by Eq. 17) can be read off as the E coordinate where the dashed line intersects the horizontal dotted line.
Fig 4.
Graphical construction of the background free energy _F_b and other quantities used in the text.
The point where the dashed line tangents Ωsp(E) also is physically meaningful: The E coordinate of the tangent point gives the ensemble-averaged binding energy E_0 ≡ Σ_E _E_Ωsp(E)e_−β_E/_Z_sp. The vertical coordinate _N_0 of the tangent point is given by the relation _F_b = _E_0 − k_B_T ln _N_0, which expresses the fact that the dominant contribution to the background free energy stems from the _N_0 sequences of energy ≈_E_0 in the collection of N random sequences: The Boltzmann weight of those sequences with E > _E_0 is too small to contribute to the partition sum, while for E < _E_0, there are too few sequences.
The value of _N_0 is an important characteristics of the system. S = ln _N_0 is known as the “entropy” of this system, and H = ln(N/_N_0) is known as the “relative entropy”; the latter has been used to characterize the specificity of the TF–DNA interaction (17). As mentioned before, the annealed approximation is valid only if many terms contribute to the partition sum, i.e., if _N_0 ≫ 1. For the two-state model (Eq. 16), the values of ɛ and L corresponding to the line _N_0 = 1 are far from the line L*(ɛ) selected by the maximal programmability criterion; this justifies the use of the annealed approximation. At the optimal parameter of ɛ = 2 and L = 15, we have _N_0 ≈ 103 ≫ 1. The corresponding relative entropy is H ≈ 7 (≈10 bits).
The large value of _N_0 also provides us with an intuitive understanding of the simple dependence (Eq. 14) of the chemical potential μ on the cellular TF concentration n (see Fig. 2B). As mentioned already, the expression (Eq. 14) is obtained if multiple occupancy of the background sequences is negligible at the TF concentration n. Since there is a large number (i.e., _N_0) binding sequences that contribute significantly to the net effect of background binding, multiple occupancy of these sequences is indeed not likely if n < _N_0. Thus for _N_0 ∼ _O_(103), the expression (Eq. 14) can be taken as a good approximation of the chemical potential over the typical range of cellular TF concentration _n_ = 1 … 103, as shown in Fig. 2_B_ for the three known TFs. We expect this result to hold even if there are multiple target sequences, say _mt_, the binding energy _Et_ of which is much lower than _E_0 as long as _Et_ > k_B_T ln mt such that _F_b is not affected by the addition of these target sequences to the density of states. Having μ(n) independent of the number of targets is a desirable functional robustness property from a system perspective, because one wouldn't want to perturb the recognition of the TFs and the existing targets by the addition of a few new targets. It will be interesting to see to what extent this feature is preserved by studying the energetics of TFs with a large number of target sites, e.g., the catabolic repressor protein CRP in E. coli (5).
Finally, we compare the values of the optimal interaction parameters according to our theory to those of the well studied TFs. From the values listed in Table 1, we see that all the available data are in the neighborhood of the expectation based on the maximal programmability criterion. We do not suggest here that programmability was necessarily the selective driving force that constrained the TF–DNA interaction to its observed form (there could be other reasons, e.g., biochemical restrictions, for the interaction to be of this form). However, the rough correspondence between theory and observation does indicate that it is possible (and perhaps even very likely) that TFs generally have the required energetics for their binding threshold to be programmable over a wide range.
Table 1.
Comparison of the expected values of the background free energy _F_b, relative entropy H, and the threshold to nonspecific binding _E_ns to the known values of these parameters for Mnt, Cro, the λ repressor cI, and the lac repressor LacR
| Theory | Mnt | Cro | cI | LacR | |
|---|---|---|---|---|---|
| _F_b, (k_B_T) | 0 | −1.2 | −1.6 | −0.8 | — |
| H, (bits) | ≈10 | 8.9 | 13.5 | 12.7 | — |
| _E_ns, (k_B_T) | 16 | 17 | — | — | ≈16 |
One obvious short-coming of the above comparison is that the three TFs for which the interaction parameters are known are all from bacteriophages and may not represent typical prokaryotic TFs. It therefore will be very important to experimentally determine the interaction parameters for a variety of different TFs. The results of a sufficient number of such studies will inform us whether programmability is a generic feature of TF–DNA interaction. Knowledge of this kind can be very helpful in developing appropriate coarse-grained models of gene regulation at the system level. In particular, quantitative relations of the type suggested by Eq. 19 will be necessary for an eventual quantitative description of gene-regulatory networks. Also, this knowledge would have important implications for the evolution of gene regulation (26, 27).
Acknowledgments
We acknowledge useful discussions with G. Stormo, P. von Hippel, and K. Sneppen on many aspects of TF–DNA interaction. We are also grateful to the hospitality of the Institute for Theoretical Physics in Santa Barbara, where some of the work was carried out. This research is supported in part by National Science Foundation Grant DMR-9971456. U.G. was supported in part by a German fellowship from the Deutscher Akademischer Austauschdienst, and T.H. was supported in part by a Burroughs Wellcome functional genomics award.
Abbreviations
- TF, transcription factor
This paper was submitted directly (Track II) to the PNAS office.
¶
In vivo measurements for the case of lac repressor found less than 10% of the TFs were unbound (15). This agrees well with an estimate based on a typical prokaryotic cell volume of 3 μm3, a genome length of 5 × 106 bases, and a nonspecific binding constant on the order of 104 M−1 under physiological conditions (13), which yields a fraction of unbound TFs at a few-percent level.
∥
One also should include the reverse complement of the genomic sequence in the evaluation of the partition function Z. In order not to make the notation too complicated, we extend the definition of “genomic sequence” to include its complement.
**
In ref. 17, the nonspecific binding was not included so that 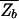 =
= 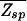 and the energy scale was shifted such that _Z_b = N.
and the energy scale was shifted such that _Z_b = N.
††
In many applications, including protein folding (23), the REM was introduced to approximate the random background interaction. The TF–DNA interaction as defined by Eq. 5 represents one of the few systems for which the REM description is directly applicable.
‡‡
Note that the additional sequence-specific binding energy to a “spurious site” in the background equally increases the kinetic barrier for sliding to a neighboring site as well as for dissociation into the cytoplasm.
§§
Note that this relation is actually independent of the additive form of the binding energy (Eq. 2).
¶¶
Here, the exclusion between overlapping binding sites can be neglected, because n ≪ N. Also, we have not included the (unimportant) exclusion between the specific and unspecific binding mode at a given site.
∥∥
Note that the energy matrices for most TFs contain a number of (fixed) positions that have no strong preference for any of the nucleotides. We will not consider these positions in the ensuing discussion of the two-state model and will use L to refer to the total number of significant positions.
References
- 1.Davidson E. H., Rast, J. P., Oliveri, P., Ransick, A., Calestani, C., Yuh, C.-H., Minokawa, T., Amore, G., Hinman, V., Arenas-Mena, C., et al. (2002) Science 295**,** 1669-1677. [DOI] [PubMed] [Google Scholar]
- 2.Berman B. P., Nibu, Y., Pfeiffer, B. D., Tomancak, P., Celniker, S. E., Levine, M., Rubin, G. M. & Eisen, M. B. (2002) Proc. Natl. Acad. Sci. USA 99**,** 757-762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bussemaker H. J., Li, H. & Siggia, E. D. (2001) Nat. Genet. 27**,** 167-171. [DOI] [PubMed] [Google Scholar]
- 4.Yuh C., Bolouri, H. & Davidson, E. H. (2001) Development (Cambridge, U.K.) 128**,** 617-629. [DOI] [PubMed] [Google Scholar]
- 5.Neidhardt F. C., (1996) Escherichia coli and Salmonella: Cellular and Molecular Biology (Am. Soc. Microbiol., Washington, DC).
- 6.Ptashne M. & Gann, A., (2002) Genes & Signals (Cold Spring Harbor Lab. Press, Plainview, NY).
- 7.Kalir S., McClure, J., Pabbaraju, K., Southward, C., Ronen, M., Leibler, S., Surette, M. G. & Alon, U. (2001) Science 292**,** 2080-2083. [DOI] [PubMed] [Google Scholar]
- 8.Berg O. G., Winter, R. B. & von Hippel, P. H. (1981) Biochemistry 20**,** 6929-6948. [DOI] [PubMed] [Google Scholar]
- 9.Winter R. B. & von Hippel, P. H. (1981) Biochemistry 20**,** 6948-6960. [DOI] [PubMed] [Google Scholar]
- 10.Winter R. B., Berg, O. G. & von Hippel, P. H. (1981) Biochemistry 20**,** 6961-6977. [DOI] [PubMed] [Google Scholar]
- 11.von Hippel P. H. & Berg, O. G. (1986) Proc. Natl. Acad. Sci. USA 83**,** 1608-1612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Berg O. G. & von Hippel, P. H. (1987) J. Mol. Biol. 193**,** 723-750. [DOI] [PubMed] [Google Scholar]
- 13.deHaseth P. L., Gross, C. A., Burgess, R. R. & Record, M. T., Jr. (1977) Biochemistry 16**,** 4777-4783. [DOI] [PubMed] [Google Scholar]
- 14.Record M. T., deHaseth, P. L. & Lohman, T. M. (1977) Biochemistry 16**,** 4791-4796. [DOI] [PubMed] [Google Scholar]
- 15.Kao-Huang Y., Revzin, A., Butler, A. P., O'Conner, P., Noble, D. W. & von Hippel, P. H. (1977) Proc. Natl. Acad. Sci. USA 74**,** 4228-4232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fields D. S., He, Y., Al-Uzri, A. Y. & Stormo, G. D. (1997) J. Mol. Biol. 271**,** 178-194. [DOI] [PubMed] [Google Scholar]
- 17.Stormo G. D. & Fields, D. S. (1998) Trends Biochem. Sci. 23**,** 109-113. [DOI] [PubMed] [Google Scholar]
- 18.Sarai A. & Takeda, Y. (1989) Proc. Natl. Acad. Sci. USA 86**,** 6513-6517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Takeda Y., Sarai, A. & Rivera, V. M. (1989) Proc. Natl. Acad. Sci. USA 86**,** 439-443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Frank D. E., Saecker, R. M., Bond, J. P., Capp, M. W., Tsodikov, O. V., Melcher, S. E., Levandoski, M. M. & Record, M. T., Jr. (1997) J. Mol. Biol. 267**,** 1186-1206. [DOI] [PubMed] [Google Scholar]
- 21.Pabo C. O. & Sauer, R. T. (1992) Annu. Rev. Biochem. 61**,** 1053-1095. [DOI] [PubMed] [Google Scholar]
- 22.Derrida B. (1981) Phys. Rev. B Condens. Matter 24**,** 2613-2626. [Google Scholar]
- 23.Bryngelson J. D. & Wolynes, P. G. (1987) Proc. Natl. Acad. Sci. USA 84**,** 7524-7528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Droge P. & Muller-Hill, B. (2001) BioEssays 23**,** 179-183. [DOI] [PubMed] [Google Scholar]
- 25.Elowitz M. B., Surette, G. S., Wolf, P.-E., Stock, J. B. & Leibler, S. (1999) J. Bacteriol. 181**,** 197-203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sengupta A. M., Djordjevic, M. & Shraiman, B. I. (2002) Proc. Natl. Acad. Sci. USA 99**,** 2072-2077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gerland U. & Hwa, T. (2002) J. Mol. Evol. 55**,** 386-400. [DOI] [PubMed] [Google Scholar]
- 28.Raumann B. E., Knight, K. L. & Sauer, R. T. (1995) Nat. Struct. Biol. 2**,** 1115-1122. [DOI] [PubMed] [Google Scholar]