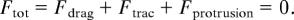Migration of tumor cells in 3D matrices is governed by matrix stiffness along with cell-matrix adhesion and proteolysis (original) (raw)

Abstract

Cell migration on 2D surfaces is governed by a balance between counteracting tractile and adhesion forces. Although biochemical factors such as adhesion receptor and ligand concentration and binding, signaling through cell adhesion complexes, and cytoskeletal structure assembly/disassembly have been studied in detail in a 2D context, the critical biochemical and biophysical parameters that affect cell migration in 3D matrices have not been quantitatively investigated. We demonstrate that, in addition to adhesion and tractile forces, matrix stiffness is a key factor that influences cell movement in 3D. Cell migration assays in which Matrigel density, fibronectin concentration, and β1 integrin binding are systematically varied show that at a specific Matrigel density the migration speed of DU-145 human prostate carcinoma cells is a balance between tractile and adhesion forces. However, when biochemical parameters such as matrix ligand and cell integrin receptor levels are held constant, maximal cell movement shifts to matrices exhibiting lesser stiffness. This behavior contradicts current 2D models but is predicted by a recent force-based computational model of cell movement in a 3D matrix. As expected, this 3D motility through an extracellular environment of pore size much smaller than cellular dimensions does depend on proteolytic activity as broad-spectrum matrix metalloproteinase (MMP) inhibitors limit the migration of DU-145 cells and also HT-1080 fibrosarcoma cells. Our experimental findings here represent, to our knowledge, discovery of a previously undescribed set of balances of cell and matrix properties that govern the ability of tumor cells to migration in 3D environments.

Keywords: cell motility, EGF receptor, extracellular matrix, matrix metalloproteinase

Cell movement is a product of a net force generated by the actin-based machinery within a cell and transmitted through membrane adhesions to the extracellular matrix. Studies of movement on 2D surfaces have led to a conceptual (1–3) and computational (4–7) understanding of how signaling from the cytoskeleton and the cell adhesion complexes is coordinated. A significant feature of cell migration on 2D surfaces is a biphasic relationship between cell speed and cellular adhesive forces (7). Movement slows from a maximum at intermediate adhesion strengths as traction forces decrease (low adhesion force) or when cell detachment becomes inhibited (high adhesion force).

However, cells usually migrate in a 3D extracellular matrix of fibers and glycosaminoglycans during embryonic development, pathogen surveillance, and other physiological processes. In contrast to the 2D case, the traction forces generated by a cell moving in a 3D gel are transmitted through cell/matrix attachments over all surfaces of a cell in contact with the surrounding matrix. Consequently, cells take on a spindle or amoeboid shape as they move through the pores of varying sizes and as adhesions through integrin receptors are modulated (8–12). Unfortunately, the conceptual and computational models developed for migration on 2D surfaces do not account for the full complexity of migration through a 3D gel such as the roles of biochemical factors (e.g., the distribution of cell/matrix attachments over the entire cell), steric factors such as hindrance by fibers of the matrix, and mechanical factors such as stiffness of the matrix fibers (e.g., ref. 13). A recent computational model (14) has predicted that these factors are interlinked and affect migration at multiple levels, for example modulation of ligand density affects pore size, matrix stiffness, and forces generated at the cell–matrix interface.

To understand how these factors are convolved, we investigate here the migration of DU-145 human prostate carcinoma cells (15), both parental and EGF receptor (EGFR)-overexpressors, through 3D fibronectin-constituted Matrigel environments (16, 17). We observe seemingly paradoxical effects of blocking integrin/matrix adhesion using anti-integrin antibodies as the Matrigel density and concentration of added fibronectin are varied, contrasting with expectations from previous understanding for 2D systems. However, our previously undescribed observations can be accounted for in terms of a force-based computational model for cell migration in 3D matrices (14).

Results and Discussion

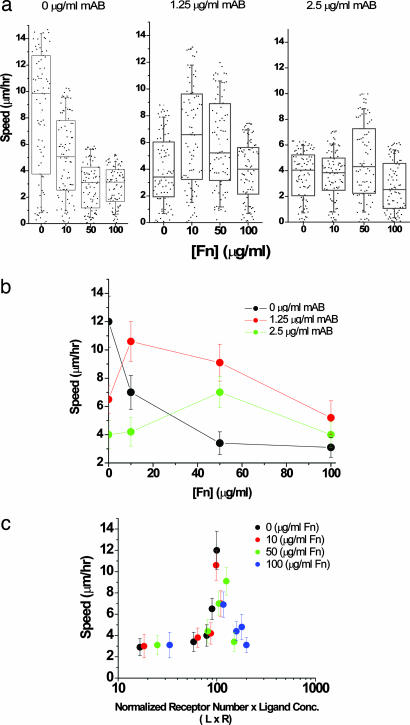
Because cell/substratum adhesion is a governing parameter of cell migration on 2D surfaces (18) and a predicted parameter of cell migration in 3D (14), we first investigated how modulating matrix ligand and adhesion receptor density affected the migration speed through Matrigel. In 67% Matrigel DU-145 parental cells locomoted at a maximum of 12 μm/h in the absence of fibronectin, and their speed diminished as additional fibronectin was presented in the 3D matrix (Fig. 1a and b). The behavior of EGFR-overexpressing DU-145 cells was qualitatively similar but exhibited faster migration speed by ≈2-fold under all conditions (data not shown). When cell/matrix adhesiveness was reduced by use of an β1 integrin-blocking antibody, migration of the parental and EGFR-expressing cells (data not shown) displayed a biphasic character in which the maximum in cell speed shifted to higher fibronectin concentrations as binding to integrin was progressively inhibited (Fig. 1c). This behavior is consistent with previous studies of the effects of integrin/substratum binding inhibition in 2D using an integrin-blocking peptide (19). Because these observations suggested that movements on 2D surfaces and in 3D gels displayed a similar balance between low and high adhesive forces, we replotted cell speed as a function of an “adhesiveness” parameter, ([_L_] × [_R_]), that incorporates the changes in functional ligand and receptor density (Fig. 1c). At a given Matrigel concentration, the variations in fibronectin levels and integrin-binding activity collapse onto a single curve exhibiting an optimum in cell speed at intermediate adhesiveness levels, consistent with analogous previous 2D plots (18, 19). Thus, at first glance we conclude that similar counterbalancing adhesive forces affect cell migration on 2D surfaces and in 3D matrices, implicating a common force-sensing control of the cell migration machinery.

Fig. 1.

Fig. 1.

Maximum cell speed is an optimum between oppositely acting adhesive forces. The adhesivity of DU-145 parental cells to the matrix was modulated by either adding fibronectin to the matrix or inhibiting binding to integrin with 4B4 antibody. (a) Box-and-whiskers plot with all of the raw data overlaid for DU-145 cell migration under specified conditions. The boxes represent 25th and 75th percentile with the median shown by the line bisecting the box. The mean is shown by a black dot inside the box. The whiskers represent 10th and 90th percentiles of the data. Cell speed values of <3 μm/h come from “oscillating” cells or simply active shape changes rather than actively motile cells. These cells are ignored from the cell speed analysis shown in b. (b) In 67% Matrigel concentration, cell speed decreases from 12 μm/h as fibronectin is included in the matrix. As integrin binding is blocked with 4B4 antibody, cell speed displays a biphasic character in which the maximum in cell speed shifts to higher fibronectin concentrations. (c) Cell speed of “motile cells” (see Materials and Methods) over the range of fibronectin concentrations displays a biphasic relationship with an adhesiveness factor, L × R. As the number of available receptors decreases, the loss in integrin activity is compensated by increase in ligand concentration, resulting in a constant relationship between speed and substrate adhesivity. The error bars represent SEM in results from five independent experiments where ≈15–20 cells were tracked per experiment.

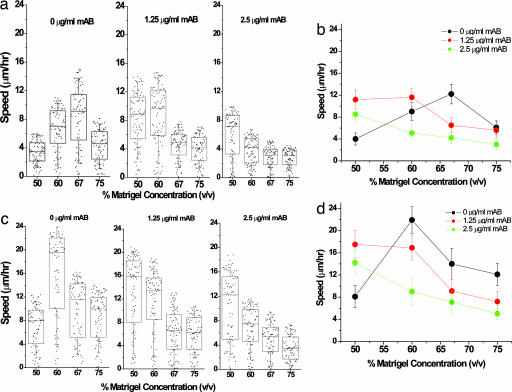
With this initial foundation, our main goal was to investigate the influence of effects likely present in 3D but generally not in 2D, such as steric (e.g., porosity and/or fiber size) and mechanical (i.e., stiffness or compliance) properties of a gel (20) that are typically convoluted in a single term such as matrix density. Lastly, we determined whether proteolysis was required for migration through steric barriers posed by an extracellular matrix in which the pore size is significantly smaller than cellular dimensions. We experimentally separated the biochemical factors from the steric and biomechanical factors. When DU-145 cells were tracked in matrix of different densities, migration of both the parental and EGFR-overexpressing cells showed a biphasic dependence on Matrigel concentration (Fig. 2), with the EGFR-overexpressing cells again moving at approximately twice the speed of the parental cells under all conditions. This biphasic behavior can again be interpreted in terms of a balance between forward and rearward traction forces as the density of ligand is varied. Our 3D results showing an increase in speed with EGFR overexpression agree with migration experiments in 2D, which have shown an increase in speed with EGFR overexpression in DU-145 cells (17).

Fig. 2.

Fig. 2.

Integrin inhibition shifts the maximum cell speed to lower Matrigel concentrations. DU-145 parental (a and b) and EGFR-overexpressing (c and d) cells were mixed with different concentrations of Matrigel and 4B4 antibody, and the cell speed was measured for 75–100 cells at each Matrigel and antibody data point. a and c show box-and-whiskers plot of cell speed distribution with raw data overlaid as described in Fig. 1. The number of motile cells varies with both integrin inhibition and matrix concentration. The average number of motile cells decreases with increase in concentration of anti-integrin blocking antibody, while average speed shows somewhat of a bimodal behavior with variations in gel density, reaching a maximum with intermediate gel concentration. In the absence of 4B4 antibody, the optimal cell speed of the parental cells was 12 μm/h at 67% Matrigel and for the EGFR-overexpressing cells was 24 μm/h at 60% Matrigel. The presence of 4B4 antibody slowed cell speed and shifted the maximum to lower Matrigel concentrations. In excess 4B4 antibody, cell speed reached a negligible value (3 μm/h) in both DU-145 parental and EGFR-overexpressing cells. The error bars represent SEM in results from five experiments where ≈15–20 cells were tracked per experiment.

In 2D systems, a decrease in traction force by reducing integrin expression (18) or employing an anti-integrin blocking peptide (19) is balanced by shifting the maximum in cell speed to higher matrix (ligand) densities, i.e., a “right shift.” To test whether ligand and receptor levels display a similar relationship in a 3D context, we challenged DU-145 cell migration with various levels of mAb 4B4, a β1 integrin-blocking antibody. In striking contrast to the well established results for 2D substrates, the biphasic curve in 3D for both DU-145 parental and EGFR overexpressing cells showed a “left shift” toward lower Matrigel concentrations as binding through β1 integrin is inhibited (Fig. 2). In the limit of excess of blocking antibody (10 μg/ml or more), cell speed is reduced to 3 μm/h (data not shown). These data therefore indicate that migration in 2D and 3D can exhibit diametrically opposite behaviors upon integrin blocking. Instead of compensating for a decrease in the number of receptors by binding at higher ligand concentrations, cells in a 3D gel paradoxically appear to shift their maximum speed to lower traction forces.

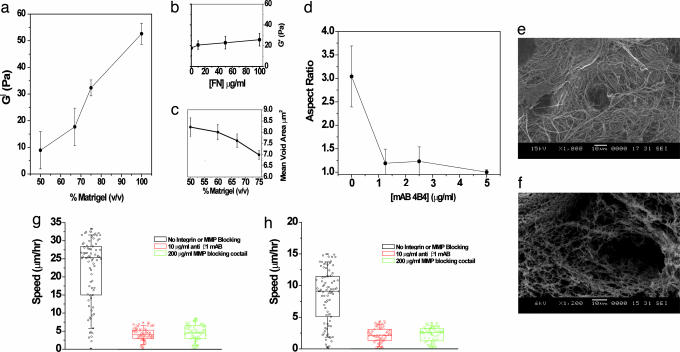
Along with the effects of cell/matrix adhesiveness, our recently published computational model for 3D migration predicts that matrix stiffness also may modulate cell speed (14). To quantify these convoluting factors, we measured the viscoelastic properties of gels assembled at different Matrigel concentrations (Fig. 3a). Over a range of 50–100% Matrigel, the stiffness of the gel changes linearly 5-fold and is consistent with transmission electron microscopy (TEM) images that show a corresponding increase in network density (Fig. 3c and Fig. 5, which is published as supporting information on the PNAS web site). In contrast to the 5-fold change in stiffness, the ligand concentration can be reasonably assumed to change by 2-fold over the same range of Matrigel concentrations because no other ligands were added. The pore size also varies with change in Matrigel concentration; however, even at 50% gel concentration the average pore size is much smaller than the cellular dimensions (average pore size ≈ 2 μm at 50% Matrigel; see Fig. 5).

Fig. 3.

Fig. 3.

Matrigel stiffness and steric properties influence migration. (a and b) The stiffness, _G_′, of Matrigel was measured for different concentrations of matrix (a) and for different amounts of exogenously added fibronectin at 67% Matrigel (b). Between 50% and 100% Matrigel, the storage modulus increases 5-fold. (c) The mean void area decreases as the Matrigel concentration is increased. (d) Aspect ratio (length of major axis/minor axis) of DU-145 parental cells as a function of mAb 4B4 concentration. The error bars show SEM for 10 different cells. The results for EGFR-overexpressed DU-145 are similar (data not shown). (e) Scanning electron microscopy images of Matrigel and collagen show starkly different matrix structures at the same resolution. Matrigel stock concentration is ≈10–12 mg/ml, and collagen I is typically used at a concentration of 1–2 mg/ml. (f) Collagen I structure at a concentration of 2.8 mg/ml. (g) Although HT-1080 cells show plasticity in migration in collagen matrices (10), they are unable to migrate when they are unable to either adhere or proteolyse the matrix (see Movies 1–6). (h) Similar to HT-1080 cells, DU-145 parental cells (EGFR cells show qualitatively similar behavior) show negligible motility in the presence of anti-integrin antibody or matrix metalloproteinase (MMP)-inhibiting mixture (see Movies 1–6).

In contrast, when fibronectin (at 0–100 μg/ml) was incorporated within the matrix, the added ligand had a relatively small effect on gel stiffness (Fig. 3b). Although the effect was small, the gel still showed a minor increase in stiffness upon fibronectin addition, suggesting that fibronectin was in fact getting incorporated in the matrix rather than simply being trapped in the holes and crevices of the gel. The changes in Matrigel density here affect the mechanical compliance of this matrix more significantly than they do ligand-mediated adhesiveness. We conclude from these measurements of matrix mechanical stiffness that, in addition to contractile force and the cell/matrix adhesiveness translating contractile force into traction, matrix stiffness is another critical factor in modulating cell migration. Because maximal migration speed occurs when the contractile force and adhesiveness are in a balance permitting most effective asymmetry in traction from the front of the cell to the rear of the cell (7, 14), a decrease in adhesiveness caused by integrin-blocking will shift the location of this optimal balance to a matrix stiffness yielding commensurate decrease in effective traction force. Thus, this “third factor” consideration is able to account for the otherwise-surprising left shift observed in Fig. 2.

In addition to the “mechanics” factor, steric hindrance, proteolysis, and cell morphology further contribute to the observed left shift in the biphasic migration behavior. Upon addition of mAb 4B4 to block β1 integrins, we observe a change in cell morphology from a more elongated and mesenchymal state to a more rounded, amoeboid-like state (Fig. 3d; see also Figs. 6 and 7, which is published as supporting information on the PNAS web site). This change in shape arises from the decrease of cell/matrix adhesion and suggests that along with loss of traction the amoeboid-like cells may have greater difficulty locomoting in sterically hindered environments. Thus, in conditions where cells have a weaker adhesion machinery because of integrin blocking, cell migration could be enhanced in matrix environments possessing larger pores, reinforcing the left shift resulting from blocking integrin–matrix interactions. This observation may seem contradictory to published results of HT-1080 cells migrating in 3D collagen gels, where Friedl and coworkers (10) carried out extensive experiments and careful analyses and showed the presence of a compensating ameoboid motility in HT-1080 cells with little or no loss of overall speed. Further experiments with both HT-1080 and DU-145 cells and a close analysis of our results suggest that our experiments are in agreement and provide an additional explanation of the observed phenomenon in Matrigel. Typical collagen experiments are performed at a collagen density (1–2 mg/ml) that is 10-fold lower than Matrigel. Scanning electron microscopy shows that Matrigel presents a much denser and sterically constrained matrix than collagen I (Fig. 3 e and f). Although cells are able to switch the motility mechanism from mesenchymal to amoeboid, upon integrin inhibition or lack of proteolytic activity in collagen matrices, they are unable to move appreciably in Matrigel matrices in the absence of proteolysis or integrin expression because of steric hindrances. We also note that simply by virtue of becoming more spherical, cells are not inhibited from locomoting (because they are able to do so under partial integrin inhibition), but rather it is the lack of adhesive machinery or proteolytic activity that impairs their ability to move in 3D Matrigel matrices (Fig. 3 g and h; see also Fig. 8 and Movies 1–6, which are published as supporting information on the PNAS web site). Analysis of our experimental data failed to show any cells necking down to micrometer or submicrometer dimensions, suggesting that the cells had to use their proteolysis machinery and were not able to “squeeze” through the existing pores. Alternatively, cells might move through pores of these dimensions by deforming the matrix and creating open spaces to migrate through. This option is conceivable given the relatively low storage modulus (_G_′) of Matrigel and has been observed in experiments with endothelial cells forming 3D networks in synthetic peptide gels of similar shear moduli (A.S., C. E. Semino, and R.D.K., unpublished data). However, this motility mechanism through submicrometer pores is also a matter of gel stiffness rather than pore size. Thus, our assessment is that under our experimental conditions, where Matrigel pore sizes are much smaller than cellular dimensions, pore size exerts less of an influence on migration than mechanical stiffness, proteolysis, and integrin expression. Our experimental results demonstrate that movement in 3D requires multiple balances between integrin activity, adhesion ligand density, and matrix stiffness, as well as proteolysis and steric hindrance. At a minimum, as shown here, these include a balance between the following: (i) cell/matrix adhesiveness and cell-generated force; (ii) cell/matrix adhesiveness and matrix stiffness; and (iii) traction force and matrix sterics.

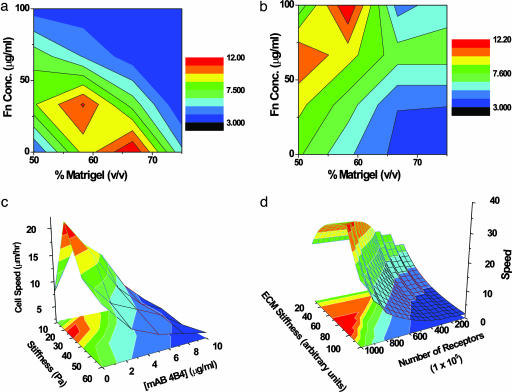
A multidimensional landscape plot (Fig. 4) of our experimental data, illustrates that migration speed is a joint function of two key system variables: Matrigel density (representing matrix stiffness and sterics) and fibronectin level (mainly representing ligand density). In the absence of integrin-blocking antibody (Fig. 4a), a maximum in motility lies at an intermediate matrix stiffness. At a constant stiffness, cell speed displays the same biphasic dependence on adhesion as demonstrated for cell migration on 2D surfaces. A decrease in adhesiveness caused by blocking integrin receptors (Fig. 4b) is accompanied by a shift in the maximum to higher ligand concentration and lower matrix stiffness, thus accounting for both the right shift found in Fig. 1 and the left shift found in Fig. 2. The dominating influence of stiffness on cell speed found experimentally (Fig. 4c) is predicted by the computational model (Fig. 4d) for cell movement in 3D matrices (14). At any integrin density, cell speed increases as matrix stiffness decreases, and an optimal speed is predicted at high receptor density. Likewise, the left shift in maximal cell speed to lower matrix stiffness when receptor density decreases is also seen in the direction of the contour lines predicted by the model.

Fig. 4.

Fig. 4.

The 3D migration landscape. (a and b) A contour plot of experimentally measured DU-145 parental cell speed as a function of fibronectin and Matrigel concentrations in the absence (a) and presence (b) of 2.5 μg/ml 4B4 antibody. The region of highest speed (red zone) lies at intermediate stiffness and low adhesion (bottom center) and shifts to the region of high adhesion and low stiffness (top left) when integrin binding is blocked. The rest of the landscape shifts and accommodates the changes due to this decrease in the effective number of available β1 integrins. (c) Experimentally measured speed of DU-145 parental cells as a function of receptor number and Matrigel stiffness. (d) Model-predicted dependence of cell speed on matrix stiffness and adhesiveness from the computational model of Zaman et al. (14). The quantitative differences between computation and experiment are due to assumptions of the model regarding the approximate number of receptors, the order of magnitude estimate of protrusion and drag forces, and limitations of the model in capturing the change in cell shape as a function of integrin inhibition.

Cell migration for 2D systems is influenced by substrate compliance. Pelham and Wang (21) found that 3T3 fibroblast migration speed on acrylamide substrata was monotonically greater on surfaces of decreasing stiffness; this finding could be consistent with the right-hand side of the biphasic curves we show in Fig. 2. Peyton and Putnam (22) reported that maximal migration speed of smooth muscle cells on fibronectin-coated acrylamide substrata occurred on a less stiff surface for a higher fibronectin level, which appears to contrast with our results. However, the differences in migration speed they observed across their various conditions were relatively small, <2-fold, so possibly smooth muscle cells operate on a much milder parametric landscape, enabling other cell or substratum properties to play a relatively more significant role.

Although we have probed cell migration as a function of bulk matrix stiffness, we realize that matrix heterogeneity and changes in local stiffness of the gel also may play an important role in determining the overall landscape of migration. Recent advances in multiple particle-tracking rheology (23, 24) as well as the use of nested collagen matrices (25, 26) to probe tension in the proximity of cells have shown great promise in improving our understanding of cell–matrix interactions at these length scales.

Finally, an unexplained observation of our experiments is the 2-fold difference in speed between parental and EGFR-overexpressing cells that display the same amount of integrin at their cell surface. Many laboratories are attempting to determine how motility-related signals might be connected (often in two-way fashion) to the proximally governing biophysical mechanisms (22, 27, 28). Because of the great complexity of biochemical signaling networks and of their connections to biophysical mechanisms by which cell functional responses such as motility are conducted (29), we are convinced that construction of cell signal–response models will require multivariate computational analysis (30, 31).

Materials and Methods

Reagents and Materials.

3D matrices were reconstituted from Matrigel (BD Biosciences, San Jose, CA). Matrix binding to integrin β1 was blocked with a mouse mAb 4B4 (Beckman Coulter). Integrin β1 expression on the cell surface was quantified by FACS analysis with a 4B4–FITC conjugate (Beckman Coulter). Matrix ligand was modulated with fibronectin (BD Biosciences). Matrix metalloproteinase (MMP) inhibition experiments were carried out by using 100 μg/ml each of actinonin and GM 6001 (Biomol, Plymouth Meeting, PA).

Cell Culture.

Cell migration was measured for a prostate cancer cell line, DU-145 (32). Enhanced motility was studied with a DU-145 line that expresses exogenously encoded EGFR (15). Both parental and EGFR-overexpressing cell lines were maintained in DMEM (Mediatech, Herndon, VA), supplemented with 10% FBS and 5% penicillin/streptomycin. HT-1080 (fibrosarcoma) cells were maintained in DMEM (Mediatech) supplemented with 10% FBS and 5% penicillin/streptomycin.

3D Cell Migration Assay.

Flasks of cells were stained with a live cell membrane dye CMFDA (Molecular Probes), washed 2× with calcium- and magnesium-free Dulbecco’s PBS, and resuspended in 1 ml of phenol red-free DMEM. The cell suspension (50 μl) was combined with serum-free DMEM, 4B4 antibody (0, 1.25, 2.5, 5, and 10 μg/ml), and Matrigel (final concentration of 50%, 60%, 67%, and 75%) to 200 μl final volume. The matrix also contained ≈1 million 1-μm sulfate Fluo-Spheres (Molecular Probes), detectable at 580/605 nm, as fiduciary markers to assess movement of the matrix. After 1 h, the matrices were covered with 2 ml of phenol red-free DMEM and incubated for another 5 h. Cells were imaged at 25× magnification with a PerkinElmer RS-3 confocal microscope (488 nm). A time-lapse series of images was collected at 15-min intervals for 6 h. Each image consisted of a 100-μm _z_-stack at 0.5-μm intervals.

Cell Tracking.

The overall average speed of cell migration on 2D and in 3D matrices was computed by tracking cell position vs. time with imaris (Bitplane, St. Paul, MN), using the built-in spots and isosurface tracking routines (33). In the 2D assays, cell speed for each condition was calculated from ≈600 cells (80–100 cells per well, 8 wells per condition). In the 3D assays ≈20 cells were tracked per experiment. Cells for speed calculation were selected if the cell centroid moved more than one cell diameter over the period of 6 h. Cell speed was calculated as average speed of all selected cells in at least five different experiments. Cells undergoing division or cell blebbing were ignored from the calculation. Normally the number of cells dividing or blebbing was <20% of the total cell population in the gel. The average speed of the fluorescent beads in the matrix was calculated and subtracted from the average cell speed. To avoid the typical problems of automated cell tracking, where oscillations or ordinary shape changes would be considered “movement” by the software, we used the following strategy:

  1. Cells were screened visually before selection and “obvious” nonmoving cells were not selected for analysis.
  2. The spots routine in imaris allows for variations in size of spots, and hence generation of very small spots captures the oscillations in the centroid, whereas larger spots are blind to small oscillations and shape change. We analyzed our data by systematically varying the spot size from 1/10 of cell diameter (≈1–2 μm) to1/2 of cell diameter. Only results that were consistent among all spot sizes were included in the data analysis.
  3. Every experiment, at 25× and 40×, was performed in gels with embedded fluorescent beads to correct for any microscopic or thermal drift. The final cell speed was subtracted from the bead movement to correct for any movement due to contraction, drift, or shape change.
  4. All cells were tracked in _z_-planes in the central part of the gel (typically three to four cell lengths) away from the top and the bottom to avoid edge effects.

Rheological Measurements.

Stainless steel washer molds (8.5-mm inner diameter, 0.9-mm high) on squares of wetted parchment paper (2 × 2 cm) were slightly overfilled with 85 μl of cold, liquid Matrigel mixed with fibronectin (0, 100 μg/ml). Matrigel solutions were allowed to gel for 30 min at 37°C. Gels were cut to the height of the washer with a scalpel blade, and the washer was gently removed. Cylindrical gels were transferred to the plate of an AR1000 rheometer (TA Instruments, New Castle, DE) on the parchment paper, and an 8-mm plate was lowered to the gel surface. Storage moduli (_G_′) of gels were obtained over a range of frequencies from 0.1 to 1 rad/s at 0.1 μN·m oscillatory torque.

Estimation of Effective Receptor Numbers and Ligand Density.

The normalized receptor number was calculated from FACS experiments. FITC-labeled mAb 4B4 was used to label β1 integrins. The total number of available β1 integrins was maximum at 0 μg/ml and lowest at 10 μg/ml. Increasing the mAb concentration to 20 μg/ml increased the percent fluorescence signal by ≈3%. Further increase of mAb concentration to 30 μg/ml resulted in no net increase in fluorescence. We calculated the normalized receptor number at each mAb concentration by assuming that the fluorescence signal at 20 μg/ml corresponded to <1% available β1 integrin receptors (>99% blocking as further increase in mAb resulted in no net increase in fluorescence signal) and that the background fluorescence value at 0 μg/ml mAb corresponded to 100% available β1 integrin receptors. Thus, at each mAb concentration the normalized receptor number is equal to

graphic file with name zpq02906-2814-m01.jpg

The above formula ensures that at 0 μg/ml the normalized receptor number has a maximum value of 1, and at 20 μg/ml the normalized receptor number value is at a minimum.

The concentration of available ligands was calculated by assuming a similar binding constant between integrins and fibronectin as the binding constant between integrins and all of the other integrin binding proteins in Matrigel (laminin, collagen, etc). Thus, the total available ligands was equal to the amount of fibronectin added plus the concentration of Matrigel (≈500 μg/ml at 67% Matrigel).

Mean Void Area Calculation.

Matrigel at varying concentrations was imaged by using quick-freeze deep etch (QFDE). The digital images were binarized by using imagej (http://rsb.info.nih.gov/ij). The digitized binary images were then skeletonized, and the surface area covered by the fibers (dark pixels) was calculated. The mean void area was calculated by taking the reciprocal of the mean covered area in five independently measured gel samples.

Calculation of Aspect Ratio.

The aspect ratio of cells in 3D Matrigel environment with varying levels of mAb 4B4 was calculated by collapsing the 3D image onto 2D and approximating the cell shape as an ellipse. The aspect ratio is the ratio of the length of the major axis to the minor axis for this ellipse. For an amoeboid cell (spherical morphology), the aspect ratio → 1, whereas for mesenchymal cells (elongated morphology) the aspect ratio is >1.

Computational Model.

The details of the model are given elsewhere (14). Briefly, the computational model predicts the speed and persistence of cell migration by calculating the total force, represented as a vector, acting on the cell centroid at each time step (Δ_t_ = 600 s). Total force is divided into adhesive forces (_F_trac) acting at the front and the rear of the cell, protrusive forces (_F_protrusion) from the cell in a 3D matrix, and resistive forces (_F_drag), viscous drag experienced by the cell due to the viscoelastic nature of the extracellular matrix

graphic file with name zpq02906-2814-m02.jpg

The model calculates the velocity and position of the cell by using Newton’s equations of motion and addresses the relationship between steric resistance and adhesivity for a migrating cell. Our approach assumes that ligand density is proportional to steric hindrance and that at very high ligand concentration, the matrix is too dense for the cells to migrate. Computations were performed in mathematica 4.1 (Wolfram Research, Champaign, IL). A total of 10,000 simulations of 300 time steps each (to simulate ≈48 h of migration) were computed on a PIV cluster (Intel, Santa Clara, CA) . The initial location of the cell in the extracellular matrix and the protrusion vectors were determined by using a random number generator.

Supplementary Material

Supporting Information

Acknowledgments

We thank Prof. Fred Grinnell (University of Texas Southwestern Medical Center, Dallas, TX) for careful reading of the manuscript and members of our laboratories for numerous enlightening discussions. This work was supported by National Institutes of Health Grants R01-GM 57418 (to P.M.) and P01-HL064858 (to R.D.K.); National Science Foundation Grant NIRT 0304128 (to P.M.); the National Institute of General Medical Sciences (NIGMS) Cell Migration Consortium (to D.A.L.); the National Cancer Institute Integrative Cancer Biology Program (to D.A.L.); and NIGMS Grants 1-R01-GM-076689 (to R.D.K.) and GM069668 (to A.W.). M.H.Z. was supported by a Sokol Foundation Fellowship.

Abbreviation

EGFR

EGF receptor.

Footnotes

Conflict of interest statement: No conflicts declared.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information