Automated extraction of backbone deuteration levels from amide H/2H mass spectrometry experiments (original) (raw)
Abstract
A Fourier deconvolution method has been developed to explicitly determine the amount of backbone amide deuterium incorporated into protein regions or segments by hydrogen/deuterium (H/D) exchange with high-resolution mass spectrometry. Determination and analysis of the level and number of backbone amide exchanging in solution provide more information about the solvent accessibility of the protein than do previous centroid methods, which only calculate the average deuterons exchanged. After exchange, a protein is digested into peptides as a way of determining the exchange within a local area of the protein. The mass of a peptide upon deuteration is a sum of the natural isotope abundance, fast exchanging side-chain hydrogens (present in MALDI-TOF H/2H data) and backbone amide exchange. Removal of the components of the isotopic distribution due to the natural isotope abundances and the fast exchanging side-chains allows for a precise quantification of the levels of backbone amide exchange, as is shown by an example from protein kinase A. The deconvoluted results are affected by overlapping peptides or inconsistent mass envelopes, and evaluation procedures for these cases are discussed. Finally, a method for determining the back exchange corrected populations is presented, and its effect on the data is discussed under various circumstances.
Keywords: amide H/2H exchange, MALDI-TOF, deconvolution, back exchange correction
Protein backbone amide hydrogens can exchange with deuterons from solution, providing a probe along a protein backbone to monitor solvent accessibility in solution (Hvidt and Linderstrøm-Lang 1954; Englander and Kallenbach 1983; Englander 1993; Zhang and Smith 1993). Hydrogen/deuterium (H/D) exchange experiments coupled to mass spectrometry (MS) have shown great promise for their ability to probe backbone solvent accessibility of a protein without requiring special modifications to the protein structure (Zhang and Smith 1993; Mandell et al. 1998a). NMR methods allow measurement of the rates of exchange of individual amides in proteins (Jeng and Dyson 1995; Dempsey 2001). Some amides exchange too rapidly to be measured with standard NMR techniques, making the study of most protein–protein interactions difficult by NMR (Paterson et al. 1990). H/D exchange with MALDI-TOF MS has emerged as a suitable method for mapping protein–protein and protein–ligand interactions (Mandell et al 1998b, 2001). The protein interactions within viral coat proteins have been mapped by several investigators by using H/D exchange coupled to ESI-FTICR and MALDI-TOF methods (Tuma et al. 2001; Lanman et al. 2003; Wang and Smith 2005). Intermolecular and intramolecular protein–protein and protein–ligand interactions in kinases have also been studied (Mandell et al. 1998a; Gmeiner et al. 2001; Nazabal et al. 2003; Lee et al. 2004).
In H/D exchange with MALDI-TOF, all the pepsin digest fragments of a protein are detected by MS over a range generally between 500 and 3000 daltons. By comparing how much the mass of each peptide has shifted by the addition of deuterons, qualitative and basic quantitative conclusions can be drawn about the number of exchangeable sites incorporated into each section of the protein (Mandell et al. 1998b). H/D exchange coupled to MALDI-TOF MS has been successful in determining the solvent accessibility of different regions of a protein in solution and allows mapping of the interaction surface upon complexation between binding partners (Hughes et al 2001; Mandell et al. 2001; Anand et al. 2002, 2003), but it has not been fully explored beyond measuring the average number of deuterons exchanged. The most common method of H/D analysis consists of centroid comparison, which is the weighted mean of all points between a user-defined upper and lower bound for each mass envelope. Taking the centroid of this entire mass envelope loses information contained within the isotopic distribution, particularly that of the number of sites exchanging. Other methods have been previously utilized to extract additional information from the isotope envelope using other MS instruments, including modeling natural isotope abundance to find incorporated deuterium, but the information obtained was of a lower resolution and required extracting deuteration rates from centroid values (Zhang et al. 1996). When H/D exchange is measured by MALDI-TOF MS or with the new higher resolution ESI-qTOF instruments, each peptide is present in the mass spectrum as an envelope of peaks differing mainly by 13C content and 2H (D) when present. The new approach presented here allows extraction of this additional information from higher resolution peptide mass envelopes without first extracting deuteration rates from centroids; instead it determines the explicit deuteration levels directly from the MS data. One group has applied a maximum entropy method (MEM) to explicitly determine the backbone deuteration levels (Zhang et al. 1997). The MEM method has some similarities to the method described in this article, and the advantages of each method will be discussed.
An improved, high-throughput method of extracting additional information from MS data is presented here, including the determination of the amount of deuterium present in each fragment, the relative amount of side-chain deuteration (present in MALDI-TOF H/D MS data), and, finally, determination of the number and level of backbone amide deuteration. This method is demonstrated on actual experimental data previously analyzed by centroid methods for the C-subunit of PKA (Anand et al. 2003). After determining the level of observed backbone amide exchange by the new method, the populations must be corrected for the back exchange that occurs during the quench phase. An introduction and application of the proper back exchange correction method is also presented here by using simulated backbone amide exchange levels for illustrative purposes. This new method extracts more information from the data, and proper interpretation enables one to obtain a greater understanding about the H/D exchange process. A thorough explanation of each component comprising the final observed deuterated peptide mass envelope is presented here, including how variation of the data can impact the calculation of the final backbone amide deuteration.
The new method is based on the separation of the unchanging natural abundance and fast exchanging profiles of a peptide from the amount of backbone deuteration that is incorporated into that peptide during the experiment. Extraction of explicit backbone amide exchange is determined by the best fit of the data to binomial exchange models. This is done by a fast Fourier transform (FFT) of the MS data in conjunction with the natural abundance and fast exchanging profiles in a deconvolution process that reveals the level of backbone deuteration. The backbone amide exchange is finally corrected for the back exchange during the quench phase by solving the binomial expressions given by the back exchange correction factor, resulting in the explicit levels of backbone amide exchange during the experiment. The new software package called DEX (deconvolution of exchange data) is able to extract any high-resolution MS data and calculate the amount of deuteration automatically for many experiments at once, providing the user with all the information needed for detailed analysis and interpretation in a matter of seconds. Previous H/D exchange experiments with protein kinase A RIα-C(94–244) subunits are used as data for proof of principle calculations. Simulated mass envelopes illustrate the results of deconvolution on cases in which the mass envelopes are not ideal. Finally, the calculation of back exchange, and its effect on the ability of distinguishing between different backbone amide states, is discussed.
Theory
Natural isotope profiles
Given a particular empirical formula, for example, C57H94N15O17, the probability that one molecule will have the mass of 1260.70 is related to the natural abundance of isotopes for each element. For example, the naturally occurring abundance of carbon isotopes is 98.90% 12C, 1.10% 13C, and <0.01% 14C (Lide 1995). For many molecules with the same empirical formula, there will be a distribution of species, or populations, due to the probability of each molecule containing a higher isotope for a particular atom. Each molecule will vary by an offset of ~1.00 mass unit increments, since each isotope varies by one or more neutrons. Although 13C weighs 1.003354826 more than 12C and 2H weighs 1.006276744 more than 1H, the values are close to a difference of one mass unit, and the value will be treated as one for the present purposes (Lide 1995). For masses close to the monoisotopic value, the difference between one and the real mass is negligible, but for highly deuterated species, the nonunitary difference must be taken into account in the interval used for deconvolution. The minimum mass, called the monoisotopic mass, is the sum of atomic weights when all atoms are present only as their lowest isotope (12C, 1H, 14N, 16O, and 32S). The probability of one molecule having the monoisotopic mass (M(0)) can be found by finding the binomial distribution of each atom in the lowest isotope and multiplying the probabilities together to create a total probability. For the formula C57H94N15O17, the probability is 47.49%, assuming the standard natural abundances for each isotope (Yergey 1983; Clauser et al. 1999). Other methods for calculating the isotopic distribution exist, including an FFT method (Rockwood et al. 2003), and all methods should report equivalent answers. The probability of the molecule having the monoisotopic weight plus one mass unit (M(1)) is calculated by the same method, except only one atom can have a higher alternate isotope and is 33.89% for this case. When a very large number of molecules with the same chemical formula are measured, as is the case with MS data, the result will be a distribution that closely follows the natural abundances calculated for each mass. This distribution is called the natural isotope profile, and it is constant for given natural isotopic abundances.
Deconvolution of MS data
The profile of a peptide undergoing H/D exchange will be different from the natural isotopic profile. The populations, or peaks, above the monoisotopic species of a deuterated peptide are a combination of the naturally occurring isotopes and exchange of 2H isotopes from the artificially enriched solution. For example, if there were 100% deuteration at one site and no other artificial deuteration for a particular population of a peptide, the masses of each peptide fragment would be approximately one mass unit higher than their comparative natural abundances. In general, for a deuterated peptide, the natural isotope profile is successively shifted higher by one mass unit for each deuteron that is added to the peptide.
If we let p(r) be the natural isotope profile for r mass units above the monoisotopic mass and w(x) be the weights for x deuterons exchanging, then the ideal H/D exchange spectrum in the discrete form is
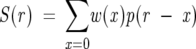 |
(1) |
|---|
where S(r) represents the ideal spectrum for r mass units above M(0). For a real observed spectrum, there is an additional component of random noise. Adding this becomes
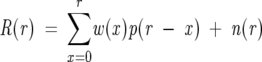 |
(2) |
|---|
where R(r) represents the real spectrum for r mass units above M(0), and n(r) represents the random noise component of the spectra.
Equation 2 is mathematically described as a convolution (Hirschman and Widder 1955; Weisstein 1999). The convolution theorem states that the Fourier transform of the convolution product of two functions is the point by point product of the Fourier transforms of the two functions. Denoting the Fourier transform of a sequence (and the index) by the “hat” symbol, we have
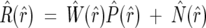 |
(3) |
|---|
where R̂ (r̂), Ŵ (r̂), P̂ (r̂), and N̂ (r̂) represent the one-dimensional FTs of R(r), w(r), p(r), and n(r), indexed respectively by r̂ and r. When the natural abundance profile is removed from the observed H/D MS spectrum, the only remaining peaks are due to the deuteration from the solution. This removal is done by a deconvolution process, which is an inversion of a convolution. Rearranging Equation 3 becomes
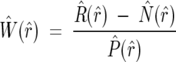 |
(4) |
|---|
By calculating a reverse FT of Equation 4, we can extract values of function w(r):
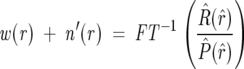 |
(5) |
|---|
which are the weights of deuterated species for each r deuteron exchanging shown in Equation 5. This reveals the deuteration levels at each point in the spectrum. The modified noise n_′(r)_ is the deconvolution of a random variable with a set of positive point weights and is thus still a random variable. The calculation of the weights by a FT deconvolution process also results in somewhat cleaner data because the noise is subjected to a local averaging process.
When implemented in practice, a separate one-dimensional FT of the MS data and the natural abundance profile scalar values are each determined over the range of data. Then the observed MS FT (R̂ (r̂)) is divided by the theoretical profile FT (P̂ (r̂)) and checked for unrealistic values caused by nonconforming data (as described in Materials and Methods).
A mathematically equivalent method of determining the weights to take Equation 2 at each value of r as a set of linear equations and solve for w(x) by least squares (Zhang et al. 1997). In this manner, the real spectrum R(r) for each peak is equal to the combination of offsets of w(x), p(r), and n(r) as follows:
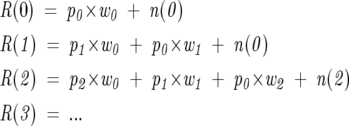 |
(6) |
|---|
This method is slower than the Fourier method, unless the peaks are integrated into line spectra, and is not as numerically stable. In contrast, the deconvolution determination can analyze the data without peak integration. Peak integration can provide smoothing but can also hide errors due to contaminants or other forms of systemic bias. The Fourier method provides a stringent test for the presence of such artifacts in the observation. Solving the set of linear equations is a valid method for this problem and may be utilized with success under certain circumstances.
Back exchange correction for backbone amide exchange
Back exchange occurs because of the slow backbone amide exchange with the solvent protons (t1/2 ~30 min) during the quench, digestion, and analysis of the peptide fragments. Because it is considered to occur after the quench step and during digestion, the peptides are assumed to be disordered, and thus all the backbone amides are completely exposed to the solvent and exchange at similar rates. Thus the loss of deuterons from the backbone is random on each peptide, but the total level of back exchange is known from control experiments (Hughes et al. 2001). The amount lost is called the back exchange, and generally ranges from 15%–50% for most systems. Because the loss is assumed to be random, it is possible to determine the exact level of deuteration for each population after the backbone deuteration profile is calculated from the deconvolution, provided that the back exchange percentage is known. With centroids, the back exchange correction is simply a multiplicative factor, but the calculation is more complex when explicitly determining the values for each population ensemble, and it is described here.
Assuming a back exchange factor of F, each deuteron that on-exchanged under the experimental conditions in a peptide will back exchange, on average, F% of the time. Because the back exchange is random and all sites are equivalent under quench conditions, the distribution will follow a binomial model. If we assume each peptide sequence has added x number of backbone deuterons during the experimental conditions and we let n be the number of deuterons lost for each peptide, then the weights after back exchange for a population of peptide molecules are calculated by Equation 7:
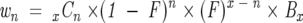 |
(7) |
|---|
where n ranges from 0 to x, w n is the observed back exchange corrected weight for the _n_th population above M(0), x C n is the number of combinations from retaining n deuterons out of x possibilities during the back exchange, and B x is the value of the _x_th weight before the back exchange occurred (the deuteration weights at the end of the experimental conditions). Normally, w n is the observed weight after the deconvolution and therefore a known value, while B x is an unknown value. Equation 7 can be solved for B x if one knows w n. If the ensemble of peptides has several different deuteration populations (various levels of deuteration), the population (B x) that exhibits the most deuteration evident after back exchange can be calculated by using Equation 7 with n = x. The calculation for each population with n starting at n = x − 1 and moving to n = 0 (in descending order) is shown in Equation 8:
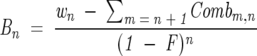 |
(8) |
|---|
where B n is the value of the _n_th weight before back exchange, w n is the observed _n_th weight after back exchange, and F is the back exchange factor. Comb m,n is calculated as:
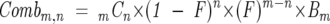 |
(10) |
|---|
which is similar to Equation 7 with x = m. Note that B n + 1 must be calculated before B n can be determined, so n must descend from the population with the most deuterons to the undeuterated species. This is because the highest pre-back exchange deuterated population contributed, after the back exchange, to the measured lower population states. To remove this overpopulation of the lower weights (for they contain the back exchanged higher weights as well as the pre-back exchanged lower weights), we must subtract the weight we know is due to the back exchange of the higher weights. This method also assumes that the highest population measured is meaningful, and can be separated from noise. See the Results and Discussion section for back exchange calculation examples for both one and multipopulation ensembles (Equation 9).
Results and Discussion
Resampling and deconvoluting the natural abundance profile
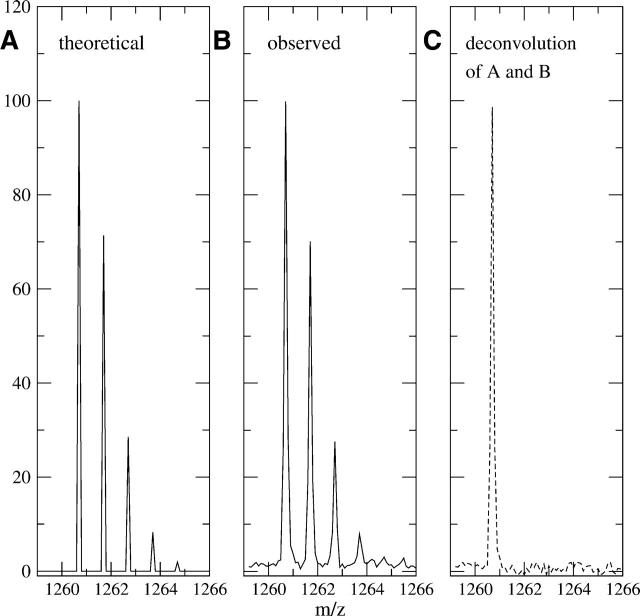
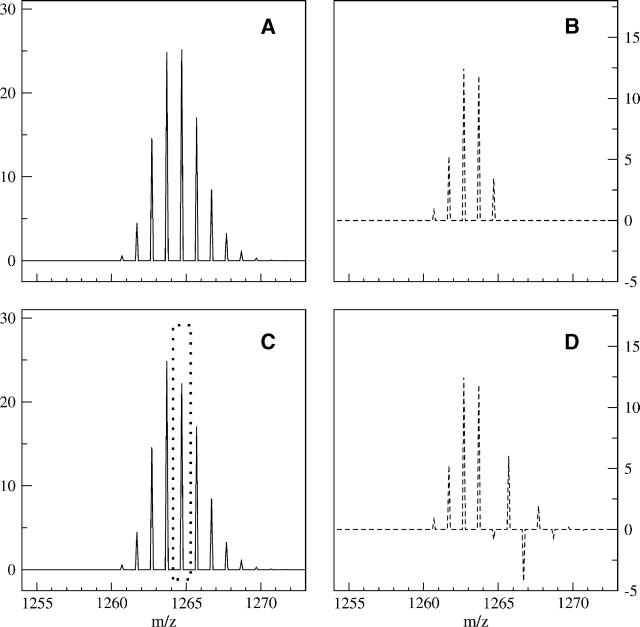
The deconvolution routine is very fast and can be completed in seconds on a standard LINUX PC system. The results are stored on the same m/z scale as the observed data, allowing for easy graphical comparison between the observed and deconvoluted results (for program specifics, see Materials and Methods). The Fourier transform requires both the observed data and natural abundance profile data to be discrete data and have the same evenly spaced intervals between data points. Most mass spectrometers do not record data in evenly spaced intervals, and thus the first step in the deconvolution process is to resample the data into evenly spaced intervals. Figure 1A shows a visual representation of the theoretical profile for the peptide sequence IYRDLKPENL (residues 163–172, of the C-subunit of PKA) (molecular formula C57H94N15O17), given the standard natural abundance of each element. Figure 1B shows the observed (nondeuterated) spectrum for the same peptide, while Figure 1C shows the result of the deconvolution on the observed data. All three parts have the same sample spacing of 0.100 mass units. Notice the only peak of significance in the deconvoluted spectra is the M(0) peak, indicating that there is no deuteration of this peptide. This result confirms the expected level of deuteration (none) and serves as a validation of the natural abundance model.
Figure 1.
(A) A theoretical natural isotope profile for the peptide with sequence IYRDLKPENL (residues 163–172) of C-subunit of PKA, using the standard natural abundances of each elements’ isotopes (sample spacing was 0.100 mass units). (B) An observed nondeuterated MALDI-TOF mass envelope for sequence IYRDLKPENL (residues 163–172). (C) The dashed line represents the result of profile B after deconvolution with A and reveals the only significant peak is at the monoisotopic weight of m/z = 1260.70 (using a 0.100 mass unit sample interval). This indicates the observed mass spectrum corresponds closely with the theoretical natural isotope and no extra deuteration exists.
Correction of residual side-chain deuteration
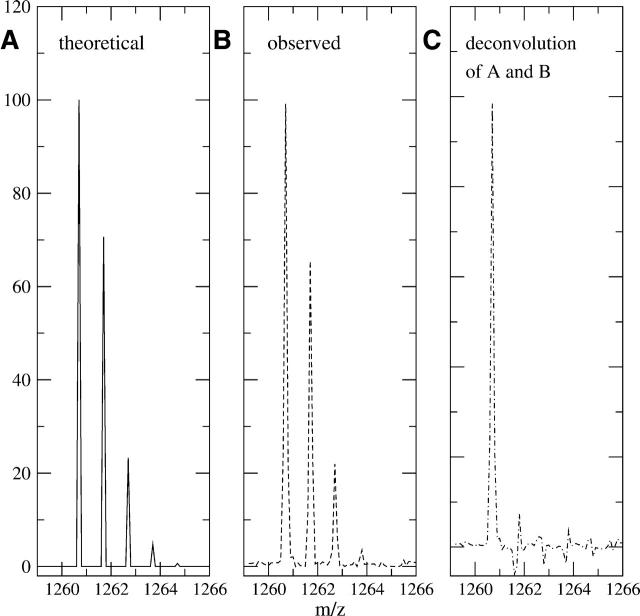
In H/D exchange with MALDI-TOF detection, a residual amount of HOD is present in the sample, resulting in a small percentage of exchange of side-chain OH and NH and terminus protons (Smith et al. 1997). In ESI MS, no residual HOD is present. For MALDI-TOF MS, the side-chain OH and NH and terminus protons exchange rapidly to the extent that residual HOD is present (Hughes et al. 2001). Backbone amide exchange is not as rapid and is only slightly reversible under quench conditions. The number of backbone amides exchanging, and their percentage of exchange, is the deuteration of biological interest and can be explicitly determined by removing the amount of deuteration due to the rapidly exchanging side-chain OH and NH and terminus protons from the deconvoluted deuteration profile. This step is not necessary for ESI MS, as there is no residual HOD present to exchange with side-chains and complicate the mass envelope.
The determination of the fast exchanging hydrogen profile is possible by additional binomial modeling of the side-chain deuteration. The number of fast exchanging side-chain hydrogens for each amino acid is shown in Table 1. For the previous sequence IYRDLKPENL, the total number of fast exchanging hydrogens is 15. Because all 15 of these hydrogens exchange rapidly during the quench conditions, the final measured proportion of deuterated sites is equal to the final concentration of 2H2O in the quenched sample. It does not depend on the time the sample is deuterated. In this example, the final concentration of deuterons in solution based on the various dilutions was determined to be 4.5%, and thus all 15 sites had a 4.5% chance of containing a deuteron instead of a proton. When modeled with a binomial distribution, the theoretical distribution for side-chain deuteration for this peptide showed significant percentages with zero, one, and two deuterons added, as well as a small number with three added as shown in Figure 2A. Although this profile is similar in this specific case to the one in Figure 1A, this is a coincidence and other peptides have more differences between the two profiles. Figure 2B shows the deconvoluted data of peptide IYRDLK PENL, where the natural isotopic profile has already been removed, leaving only the deuteration profile. This spectrum was of a sample that was only deuterated under quench conditions, thus only the fast exchanging hydrogens should exchange. As shown, the actual deuteration profile (Fig. 2B) closely mirrors the theoretical profile (Fig. 2A). After extracting the fast exchanging hydrogens from the deuterated spectrum by a second deconvolution, the result is shown in Figure 2C. The large M(0) peak here now refers not to the amount of deuteration in the peptide (as in Fig. 1C) but rather to the amount of deuteration for the backbone amides. In this case, there is essentially no backbone deuteration, which confirms our assumption that the quench conditions prevent nearly all backbone amide on-exchange, but not side-chain exchange. The small M(1) and M(2) peaks are <1% of the size of the M(0) peak and are interpreted as normal variance within the sample.
Table 1.
The number of fast-exchanging hydrogens for each residue type, by single letter designation, for MS with m/z = +1 and PH=2.5
| Fast exchanging hydrogens for each amino acid type | ||||
|---|---|---|---|---|
| A =0 | C =1 | D =1 | E =1 | F =0 |
| G =0 | H =1 | I =0 | K =2 | L =0 |
| M=0 | N =2 | P =0 | Q =2 | R =4 |
| S =1 | T =1 | V =0 | W=1 | Y =1 |
Figure 2.
(A) The theoretical distribution of fast exchanging side-chain and termini hydrogens for sequence IYRDLKPENL (residues 163–172). According to Table 1, there are 15 fast exchanging hydrogens for this sequence, and the final deuterium in solution was 4.5%. (B) The observed deuteration profile of the same peptide in the quench conditions only. The natural isotopic profile has already been removed by deconvolution, revealing the total level of deuteration present in this spectrum. (C) The deconvolution of B with A reveals the deuteration due solely to backbone amide exchange. In this case, there is no backbone amide on-exchange, which is consistent with quench conditions.
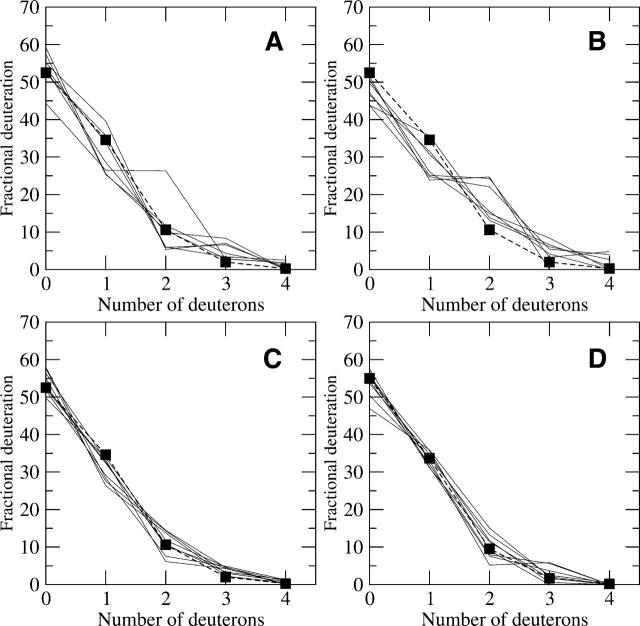
The fast exchanging side-chain model was tested on samples that were quenched and deuterated simultaneously and thus should only have residual deuteration at the rapidly exchanging positions. The peptide mass envelopes were deconvoluted once to remove the natural abundance, leaving the residual level of deuteration attributed to the rapidly exchanging positions. In general, the theoretical models reflected the data with a high degree of consistency. Data from four different protein kinase A peptides with different signal-to-noise values were tested (Anand et al. 2002) and shown in Figure 3. When the signal-to-noise decreased, the variation between the peaks in a peptide mass envelope increased, and this is reflected in poorer agreement with the model (Fig. 3A,B). This relationship illustrates the sensitivity of the deconvolution to very accurate intraprofile signal levels. The three trials with significantly higher populations of peptides with two deuterons and lower populations of one deuteron in Figure 3B may be due to deamination. Nonetheless, the four peptides in Figure 3 indicate that the fast exchanging hydrogen model, proposed by Hughes et al. (2001) and calculated by using Table 1, appears to correctly predict the level of deuteration during the quench phase.
Figure 3.
(A–D) Trials of four different peptides deuterated in only the quench solution from the C-subunit of PKA and their comparison with the theoretical fast exchanging profiles (dashed lines and square symbols). The sequences are as follows: (A) KRILQAVNF (m/z(0) = 1088.658), residues 92–100; (B) SKGYNKAVDW (m/z(0) = 1167.580), residues 212–221; (C) DRIKTLGTGSF (m/z(0) = 1194.648), residues 44–54; and (D) IYRDLKPENL (m/z(0) = 1260.695), residues 163–172, respectively. The signal-to-noise ratios for A–D are 77, 48, 191, and 150, respectively. The higher signal-to-noise ratios had higher correlation with the theoretical profile, but all sequences showed general agreement. The three outlying trials in B may be due to deamination of asparagines.
Extracting backbone deuteration amounts
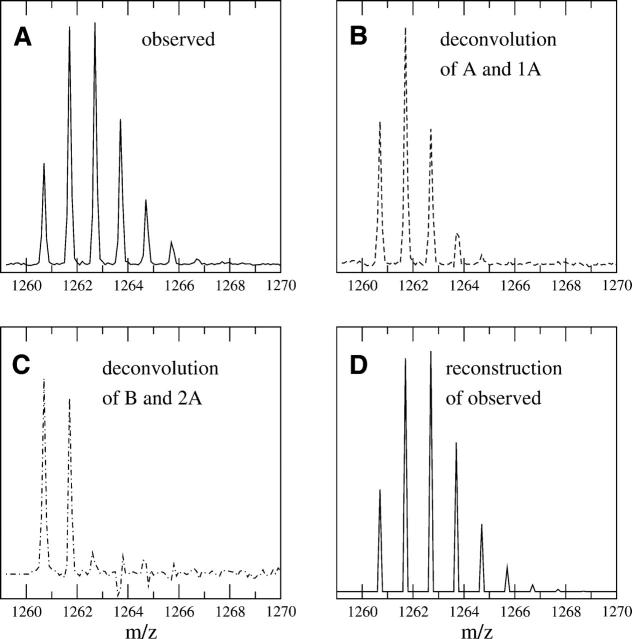
Once the contribution from the natural isotope distribution and from the rapidly exchanging protons is calculated and extracted from the original MS data, we are left with the amount of backbone deuteration. Figure 4A–D shows how this deconvolution based extraction process is used to reveal the backbone deuteration profile for a mass envelope of sequence IYRDLKPENL deuterated for 120 sec. First, the original mass spectrum is resampled to 0.1 mass unit intervals (Fig. 4A). Next, the resampled spectrum is deconvoluted with the theoretical natural isotopic profile shown in Figure 1A (Fig. 4B). The resulting distribution represents the deuteration weights for both the fast exchanging side-chain hydrogens and the backbone amide hydrogens. Deconvolution of the distribution shown in Figure 4B with the theoretical fast exchanging profile from Figure 2A gives the deuterium incorporation due solely to backbone exchange (Fig. 4C). The most significant peaks are the M(0) and M(1) states, indicating that only one backbone amide hydrogen is exposed in this peptide over 120 sec. When the normalized weights are calculated for this spectrum, the result is that 58% of the peptides contain no backbone deuteration, 42% contain one backbone amide deuteron, and a small percentage contain two backbone deuterons. The M(2) peak might indicate a small fraction of the time a second backbone amide exchanges, although it is difficult to distinguish this value from the noise at this time point. Analysis of data from experiments with longer deuteration times can help ascertain whether a second deuteron may be present. It is conclusively shown, however, that there are not two equally exchanging backbone amide sites, a fact that could not be determined purely from centroid analysis. Finally, Figure 4D is the reconstructed spectrum after reconvoluting the three models, the theoretical natural isotope (Fig. 1A), 15 rapidly exchanging side-chains at 4.5% (Fig. 2A) and one backbone amide hydrogen exchanging 42% (Fig. 4C). When compared with Figure 4A, the areas are nearly identical, and the average absolute percentage deviation for each peak is 0.19% between the observed and reconstructed spectra and a correlation coefficient of 0.9953. Thus, we are confident the model accounts for all portions of the deuterated peptide mass envelope.
Figure 4.
(A) An observed MALDI-TOF mass envelope for sequence IYRDLKPENL, deuterated for 120 sec under experimental conditions. (B) The deconvoluted result of the theoretical natural isotopic profile (Fig. 1A) with the spectrum in A. The signal corresponds to the weights of deuterium incorporation, which is a combination of fast exchanging side-chain hydrogen exchange and backbone amide hydrogen exchange. (C) Deconvoluting the total deuteration profile (B) with the theoretical fast exchange profile (Fig. 2A) results in the deuteration due solely to the backbone amide exchange. This figure clearly shows significant populations of peptides with zero and one backbone amides exchanging, while the small M(2) peak is inconclusive. Nonetheless, it is shown that there are not two equally exchanging backbone amide sites at this time point. (D) A theoretical mass envelope reconstructed by using only the following information: one backbone amide exchanging at 49%, 15 fast exchanging side-chains at 4.5%, and the natural isotope profile for sequence IYRDLKPENL. A comparison of D with A illustrates how well the three parts of the model explain the entire observed mass envelope. The high correlation coefficient of 0.9953 between the two values’ mass envelopes indicates complete extraction of the important components of the original mass envelope.
Since the observed spectrum has lost some of the deuteration as a result of back exchange during the quench phase, it is still necessary to determine the back exchange corrected backbone amide exchange values. This is described later under the back exchange correction procedure. However, even without the back correction factor, the new procedure gives added information, specifically about the ensemble of species that makes up the deuterated peptide mass envelope. With this information, one can then interpret the backbone amide exchange within the biochemical context with far more specificity than was previously possible.
Computing the centroid of the mass envelope
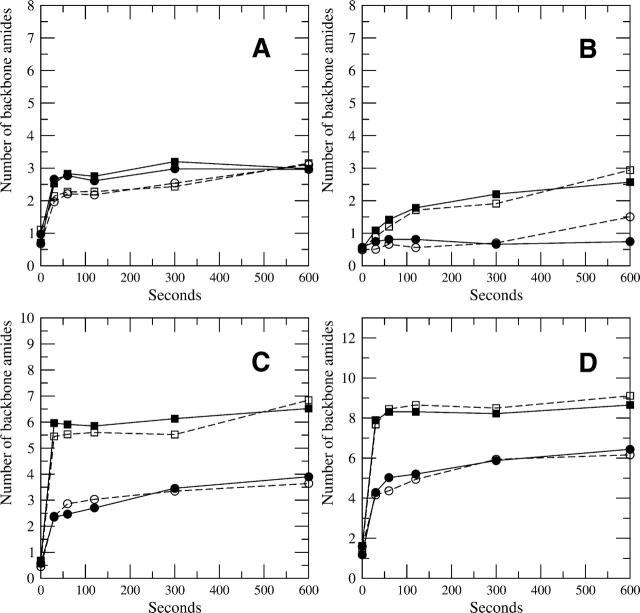
It is important to note that the deconvolution of the natural isotopic and fast exchanging profiles does not change the centroid value for the amount of deuterium incorporated into samples. The deconvolution calculation provides a direct determination of the centroid of the mass envelope because it can be computed directly from the backbone deuterium population distribution. The results of such direct calculations are consistent with published centroid results computed by subtraction regardless of the signal-to-noise of the particular mass envelope. Figure 5A–D, shows the centroid comparison between four different peptides from the C-subunit of PKA (original data from Anand et al. 2003). For all four parts of Figure 5, the open squares and circles represent the backbone deuteration centroids for peptide from the free C-subunit and from the complex with the RIα subunit, calculated from the centroids of the mass envelopes. The filled squares and circles represent the centroid of the backbone amides weights calculated from deconvoluted spectra for the same data. The close agreement between all cases illustrates the consistency between the two methods. Where there are notable differences, such as the last time point in Figure 5B for both the free and complex state, the centroids derived from the deconvolution are more accurate, because they were calculated with a background correction, whereas the originally published centroids had some systematic bias at longer time points. The program developed here thus slightly improves on the method for determining the centroids compared with other commonly used methods.
Figure 5.
(A–D) A centroid comparison of backbone deuteration by two methods using four peptides for the C-subunit of PKA. One method calculates the centroids from the mass envelope and subtracts the control centroid to reveal the level of backbone deuteration (open squares and circles represent the free and complex backbone deuteration levels, respectively). The other method calculates the centroids by using the backbone deuteration peaks after deconvolution (filled squares and circles for the free and complex backbone deuteration levels, respectively). The sequences are as follows: (A) KRILQAVNF (m/z(0)= 1088.658), residues 92–100; (B) IYRDLKPENL (m/z(0)= 1260.695), residues 163–172; (C) DRIKTLGTGSF (m/z(0) = 1194.648), residues 44–54; and (D) DQFDRIKTLGTGSF (m/z(0) = 1584.802), residues 41–54, respectively. The general agreement among all peptides shows the consistency between the two methods.
Deconvolution reveals inconsistencies in the data
If either the natural isotope or the fast exchanging model is inconsistent with the data, the deconvoluted results will clearly indicate this, which is a major advantage of this method. The fast exchanging model applies to all of the peptide mass envelopes in the spectrum, so an error in the dilution factors or in the counting of the side-chains should be reflected in poor fits for all of the data. Errors in identification of the peptides resulting in wrong sequences would be reflected in poor fits of the natural isotope model. A special case of this has to do with the deamination of asparagines and/or glutamines. In this case, a peptide with a mass one greater than the peptide sequence is convoluted with it and the natural isotope model does not fit. This can be readily seen in the high-resolution raw data before deuteration. In general, the profiles with the highest signal to noise are best reflective of the models.
One problem in the observed data is the slight shifting of one signal peak compared with its neighbors. Because the FFT deconvolution method requires that each spectrum have the same uniform sampling interval, any shifting will result in up–down positive–negative population weights after the deconvolution, as evidenced slightly in the M(1) peak in Figure 2C. This problem also occurs when the peaks broaden, as they often do at the high m/z ratios, where the instrument’s results have a wider interval than at lower m/z ratios. The deconvolution method is quite sensitive to any abnormally shaped peaks, and in these cases, the peaks can be integrated or the shapes can be normalized before deconvolution. Integrating the peaks will not change the overall areas though, and the resulting backbone amide exchange profile will not change as a result if the total peak areas are compared between integrated peaks and nonintegrated peaks.
A common issue with MS data is a systematic mass shift due to instrumental drift or miscalibration. This causes all the peaks to move in the same direction compared with their theoretical values. Mass shift does not present a problem with this deconvolution method, as long as the interval between the peaks does not change. The deconvolution is relative to the position of the M(0) peak, not to the absolute position of a shifted peak.
Deconvolution of low signal-to-noise data
The deconvolution, when properly executed, is able to increase the signal to noise of the data by reducing the inherent noise in the data. The noise reduction occurs because a data point is considered noise when there is no repeating set of peaks offset by multiples of the mass of the deuteron. The noise reduction occurs during the deconvolution step, due to averaging the noise by Fourier transforms (for more information, see Materials and Methods). This has been very helpful for some fragments that are not resolved with the same consistency across the trials, such as peptide m/z = 1347.75 (residues 278–289) of the C-subunit (Anand et al. 2003; Law et al. 2005).
With a low signal-to-noise profile, the peaks are not sufficiently discriminated beyond the background level to determine the correct weights. Since the method relies on accurate measurement of the monoisotopic peak, as well as all the less intense offsets, application of the deconvolution method to low signal-to-noise data will not result in clear weights for deuteration. In these cases, the noise is such an integral part of the spectrum, the peaks are hardly distinguishable and the weights are thus not extracted with any reliability. The best solution is to gather better data, but if that is not feasible, a less sensitive comparison such as a centroid or use of MEM may be appropriate. It must be understood, however, that in such cases the centroid values will have more uncertainty compared with high signal-to-noise spectra because the accuracy of the underlying model cannot be demonstrated. When any backbone amide profile peak is lower (negative) than the low range of the average background level (noise) deviation, or the peak pattern is not explainable (due to missing or misshapen profiles), the interpretation of these data should be treated with caution.
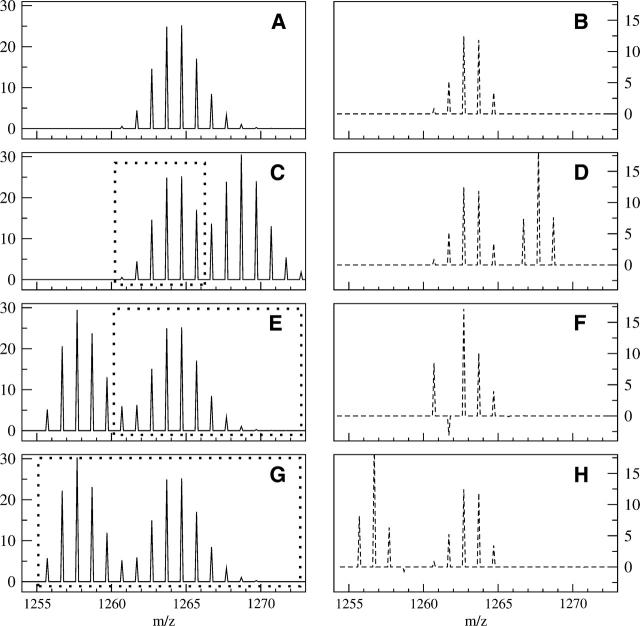
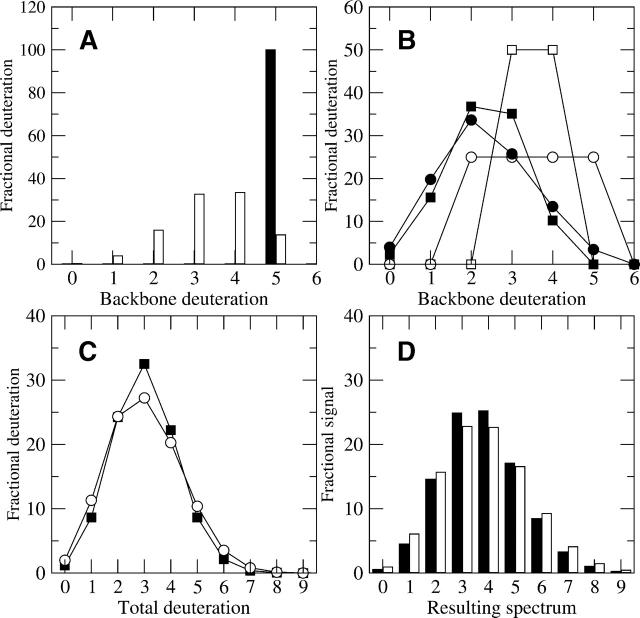
An example of a low signal-to-noise profile is shown in Figure 6, where it is compared to a simulated ideal spectrum for clarity. In Figure 6A, a simulated, ideal mass envelope was generated that has up to four backbone amides exchanging, created from the sequence IYRDLKPENL with 4.5% residual solvent HOD during quench. The result of the deconvolution (over the range 1260.70–1273.70) of Figure 6A with both the natural isotopic profile (Fig. 1A) and rapidly exchanging profile (Fig. 2A) reveals the backbone amide level of exchange (Fig. 6B). Five backbone amide peaks are evident, with the most deuterated species at M(4). The centroid of the entire mass envelope in Figure 6A is 3.79 mass units above the M(0) (before subtracting the standard control of 1.46). Subtracting the control from the value of 3.79 reveals the backbone deuteration level, which is 2.33 D. The amount of backbone amide deuteration calculated from the centroid of Figure 6B is 2.33 D, which is equivalent to the corrected value from 6A.
Figure 6.
(A) An ideal, simulated mass envelope for sequence IYRDLKPENL using 4.5% HOD. (B) The result of deconvolution of A with both the natural isotopic and fast exchanging profiles reveals the backbone amide deuteration profile, which has up to four backbone amides exchanging. (C) Inconsistent intraprofile signals (shown by the dashed box in C) in mass envelopes also cause problems for deconvolution methods. The mass envelope has an M(4) signal that is only 22% of the total signal (C), compared with the original level of 25% (A). (D) The effects of the inconsistent signals are replicated downstream due to a mismatch between the model and the mass envelope, causing difficulty in analyzing the backbone amide populations explicitly, but the centroid calculation is fairly robust in this situation, even when applied to the deconvoluted profiles.
Often in low signal-to-noise mass envelopes, the intra-profile weights are inconsistent across trials. This is represented in Figure 6C by a mass envelope where the M(4) signal was not detected robustly, resulting in a smaller value compared with the ideal. The signal was reduced from 25.2% for the M(4) peak of the ideal simulation to 22.2% in Figure 6C, a seemingly small change (shown by the dashed box in Fig. 6C). The centroid for Figure 6C is 3.67, only 3.2% less than the ideal mass envelope in Figure 6A (before correction). Although this difference is small, the user would have no indication that the centroid was obtained from a problematic mass envelope, because it otherwise looks normal. Because the deconvolution procedure expects to see offsets at the higher masses based on the isotopic and fast exchanging conditions, an inconsistent drop in one peak will result in an unrealistic result after deconvoluting the spectrum. This is shown by deconvoluting the mass envelope in Figure 6C to produce the backbone amide result in Figure 6D. While the M(0) to M(3) peaks in Figure 6D are the same as the ideal result in Figure 6B, the M(4) peak of Figure 6D is slightly negative, followed by a positive–negative oscillation that fades to zero by the M(9) peak. Although determination of the most deuterated population is not possible from a result such as this, the backbone deuteration centroid of 6B is 2.35 D above the M(0), while the centroid in 6D is 2.34 D. Thus the centroid of the profile is robust even when the populations vary widely due to inconsistent data. For spectra of lower quality, results such as the result in Figure 6D are not uncommon, but by averaging the peaks of several replicate trials together it is possible to obtain more realistic results after deconvolution. Otherwise, centroid or MEM calculations may be the best and most robust alternatives.
Deconvolution of overlapped peptide mass envelopes
Some major difficulties in analyzing H/D MS data occur when the peptide mass envelope of interest overlaps with another. A front overlap occurs when a foreign peptide has signal at the M(0) end of the peptide mass envelope, while an end overlap occurs at the higher mass tail of the peptide mass envelope. Examples of front and end overlaps, as well as a comparison to the ideal simulated spectrum are shown in Figure 7. The simulated, ideal mass envelope in Figure 7A and its deconvoluted result in Figure 7B are the same as in Figure 6, A and B. In Figure 7C, the same ideal, simulated MS mass envelope from Figure 7A is shown overlapping with another mass envelope, which has a monoisotopic mass of 1266.70, or six mass units heavier than our original spectrum. Since the range from 1260.70–1266.60 is uncontaminated by the heavier peptide (as shown by the dashed box), one can attempt a partial centroid over this range. The partial centroid value is 2.95 above the monoisotopic envelope in Figure 7C, which is 78% of the original centroid of the uncontaminated spectra in Figure 7A. Thus the partial centroid is underreporting the true amount of deuteration by 22%. If the same deconvolution upper and lower limits from Figure 7A (the range from 1260.70–1273.70) are used for the theoretical spectrum in Figure 7C, one obtains the deconvolution result shown in Figure 7D. It is clear that after deconvolution, the deconvoluted result for the peptide mass envelope with the monoisotopic envelope of 1260.70 is the same between panels B and D of Figure 7. The centroid for the backbone amide deuteration calculated over the range of 1260.70–1266.60 in Figure 7D is 2.33 D, which is the same as the uncontaminated centroid from Figure 7B. Thus none of the deuteration level is lost. Even though only 78% of the original profile was present within the limits of 1260.70 and 1266.60 in Figure 7C, the small peaks from the first mass envelope at 1266.70–1268.70 are due only to the natural isotope abundances and side-chain deuteration. Thus removing the peaks due to both of these stable profiles removes the overlap.
Figure 7.
Examples of separating a desired mass envelope from two overlapping spectra. (A, B) The same ideal, simulated mass spectrum and deconvoluted result as in Figure 6, A and B. (C) A theoretical mass spectrum in which a peptide with a monoisotopic mass of 1266.70 overlaps the original peptide shown in A, causing an end overlap. The dashed box in C represents the portion of the original spectrum that is uncontaminated signal from sequence IYRDLKPENL. (D) The resulting backbone deuteration distribution after deconvolution of the natural abundance and side-chain profiles present in spectrum B. A comparison between D and B shows the complete extraction of the first mass envelope’s backbone amide deuteration profile. (E) Another theoretical spectrum in which a peptide with a monoisotopic mass of 1255.70 overlaps the original peptide, causing a front overlap for the desired mass envelope. (F) Attempting to deconvolute the mass envelope with the original range of 1260.70 to 1272.70 (dashed box in E) causes problems. The extra signal in the M(0), M(1) portion of the mass envelope is contained in the model spectrum, resulting in negative weights that are physically unrealistic. (G) The same spectrum as in E, but the theoretical profile (dashed box) has been shifted to start at the front of the first overlapping envelope. (H) The result of deconvolution of the mass envelope in G over the larger interval. The change in the deconvolution starting point allowed the calculation to separate the signal due to the other peptide and reveal the backbone amide populations for the peptide of interest.
This case illustrates a general rule when attempting to extract the first mass envelope in overlapping spectra. In general, for overlapping mass envelopes, if the separation between two peptide’s monoisotopic masses is X, then as long as there are no more than X −1 backbone amides exchanging, the deconvolution will completely extract the envelope for the peptide of lower mass from the heavier one. This is a significant advancement in analysis, as overlapping spectra often prevent more complete coverage of proteins, and the deconvolution step greatly improves our ability to analyze the lighter mass envelope. More peptides can now be analyzed, which will help increase coverage of the protein and increase the relevance of the results.
A front overlap that is known to have a monoisotopic mass five units lighter than the monoisotopic mass of sequence IYRDLKPENL is shown in Figure 7E. Although the overlap region appears to be less than the overlap in Figure 7C, the result of deconvoluting with the same upper and lower limits from Figure 7A (1260.60–1272.7, as illustrated by the dashed box in Fig. 7E) indicates a noticeable problem (Fig. 7F). The large M(0) signal followed by the negative M(1) clearly illustrates a physically unrealistic backbone amide deuteration profile. This occurs because the extra signal in the first few masses of the original mass envelope in Figure 7E causes a mismatch with the theoretical profile, which results in the unusual deconvolution result. As a consequence, it is inappropriate to attempt to deconvolute a peptide mass envelope by using only the original mass envelope range (1260.70–1273.70) when the M(0) of that mass envelope is clearly contaminated. This problem with deconvolution of front overlapping mass envelopes is in contrast to the problems with centroids. The centroid over the range 1260.70–1272.70 in Figure 7E is 3.82, less than 1% more than the uncontaminated centroid for Figure 7A. The deconvolution calculation is more robust when analyzing peptides with end overlapping mass envelopes then it is when analyzing for front overlapping mass envelopes, but the opposite is true for centroids.
One method for overcoming the problems with the front overlapping mass envelopes is to change the range for the deconvolution (Fig. 7G). If one changes the theoretical natural abundance isotope profile to match the range starting at the monoisotopic profile of the first peptide (1255.70) and continuing to the original end (1273.70) (as illustrated by the dashed box in Fig. 7G), then the same overlapping spectra may be separated into two distinct profiles if the general overlap rule holds. In this case, the overlap can be extracted (Fig. 7H), because the lighter mass envelope only has two backbone amides exchanging (and the distance between the two monoisotopic profiles is five), and the original mass envelope can be analyzed without difficulty. In addition, even though the lighter mass envelope is another peptide with different natural isotopic and fast exchanging side-chain profiles, the difference is usually small for peptides of nearly the same weight. Because of the similarity in theoretical profiles, the deconvolution does a good job of calculating the backbone amide exchange profile for it as well. Thus both the profiles can be extracted and analyzed without contamination effects, by a set of deconvolutions using the original range for the lighter mass envelope (Fig. 7C) and by shifting the second envelope’s theoretical profile to the start of the lighter mass envelope (Fig. 7G). Determining the correct range over which to deconvolute is thus shown to be critical in this calculation, and it assumes the M(0) of the overlapping peptide is known, which is often the case.
Separation of overlapping spectra in real data
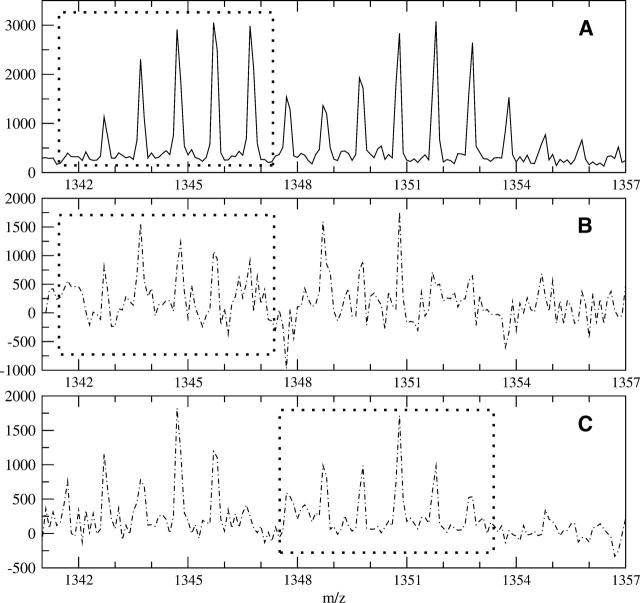
Figure 8 illustrates the application of using the deconvolution to extract both mass envelopes from an overlapping profile (separation of both an end overlap for the lighter peptide and a front overlap for the heavier peptide). Peptide FDRIKTLGTGSF (sequence 43–54) and peptide TKRFGNLKNGVN (sequence 278–289) of the C-subunit of PKA have similar monoisotopic masses: 1341.7117 and 1347.7497, respectively. They do have a noticeably different number of side-chain hydrogens exchanging (14 for peptide FDRIKTLGTGSF and 19 for peptide TKRFGNLKNGVN). Because of the exposed nature of these peptides in the C-subunit complex, the peptides broaden and overlap after a short amount of deuteration. Figure 8A shows the overlapped profile of both peptides after 30 sec of deuteration. The signal within the dashed box (1341.3–1347.3) is due solely to peptide FDRIKTLGTGSF, while the masses above that limit have signal from both peptides. The deconvolution of both the isotopic and side-chain profiles using the theoretical model for peptide FD RIKTLGTGSF is shown in Figure 8B. Although the spectrum signal to noise is lower than others previously shown, the signal is nonetheless decipherable. Populations at _M(1)–_M(5) are visible, with the M(5) peak a bit crowded. The M(6) peak, which at 1347.7 is the beginning of the contamination with the heavier peak, is significantly negative. The negative peak indicates a mismatch between our model and the mass envelope, which is due to the overlap in this case. The deconvolution reveals peptide FDRIKTLGTGSF has at least five backbone amide hydrogens exchanging at this time point, but the data are not consistent with a sixth site. This information could not be attained from a centroid of the original mass envelope using a partial centroid with limits from 1341.3–1347.3 (shown as the dashed box in Fig. 8B), as the overlap at the end skews the data. Thus, the determination of the backbone amide populations by deconvolution has increased the ability to interpret the data.
Figure 8.
Analysis of overlapping profiles using real data. (A) An overlapping spectra containing peptide FDRIKTLGTGSF (sequence 43–54) and peptide TKRFGNLKNGVN (sequence 278–289) of the C-subunit of PKA after 30 sec of deuteration. The two peptides have similar monoisotopic masses, 1341.7117 and 1347.7497, respectively, and overlap enough to cause analysis problems using only centroids. The dashed box shows the portion of the spectrum due solely to residues 43–54. (B) By using the theoretical profile for peptide FDRIKTLGTGSF, the deconvoluted signal between 1342.3 and 1347.3 is due solely to peptide FDRIKTLGTGSF, indicating up to five backbone amides exchanging (peaks within the dashed box). The sixth site is negative, showing a mismatch where the contamination with the heavier peptide begins. (C) Using the heavier peptide’s theoretical profile shifted over to the start of the first peptide produces a clean deconvolution for the peptide TKRF GNLKNGVN (peaks inside the dashed box). The second peptide also shows up to five backbone amides exchanging under experimental conditions.
Since the difference in the monoisotopic masses between the two peptides in Figure 8 is approximately six and the deconvolution of the first peptide revealed only five backbones exchanging, we have met the general overlap rule and can attempt extraction of the heavier peptide by the method described earlier. By shifting the theoretical profile for peptide TKRFGNLKNGVN to the beginning of the entire window (moving the profile to begin at 1341.7), we can completely extract the backbone amide populations from the second peptide. The result of this deconvolution is shown in Figure 8C. The signal in the range of 1347.3–1353.3 (dashed box in Fig. 8C) is now the properly calculated signal due to the backbone amides from peptide TKRFGNLKNGVN. Populations _M(0)–_M(5) are visible, indicating up to five backbone amides can exchange under the experimental conditions. The absence of a sixth population again suggests that only five sites are exposed to the solvent under the conditions. A centroid of the original mass envelope could also be done, which would reveal the total level of deuteration, but not the populations as shown here.
Back exchange correction for backbone amide exchange
Ideally, after the deconvolution of the isotopic and fast exchanging profiles, the result would be the complete backbone exchange during the experiment. Unfortunately, back exchange always occurs during the experiment to some extent, and this has the effect of greatly smoothing the populations. This is best illustrated by calculating the reverse of the normal deconvolution process for a theoretical peptide mass envelope, as it shows the smoothing process unambiguously. For example, consider a peptide mass envelope that has five backbone amide sites completely exchanged (black bar in Fig. 9A) and a back exchange factor of 33%. Solving for w n in Equation 7 over the range of n = 0 to n = 5 where x = 5 results in a binomial distribution (white bars in Fig. 9A). Clearly, the back exchange process has smoothed the backbone deuteron population from one distinct peak to a profile over five mass units, illustrating the dramatic differences in the population distributions before and after the back exchange. The centroid before back exchange is 5.00 D, while the centroid afterwards is 3.33 D, which is 0.67 times the original value, as expected for 33% back exchange.
Figure 9.
(A) A sample deuteration profile of sequence IYRDLKPENL before and after the back exchange during quench (assumes 33% back exchange). The black bar represents a profile where 100% of the peptide fragments have added five deuterons before back exchange. During quench, 33% of the deuterons are lost in a binomial process, with the resulting profile after represented by the white bars. (B) Two sample backbone amide exchange profiles of sequence IYRDLKPENL under two different experimental conditions are shown before (open symbols) and after (filled symbols) 33% back exchange. The original backbone profiles are quite different, but the back exchange smoothes the differences and makes the two trials look less distinguishable from each other (filled symbols). (C) The addition of the fast exchanging deuterationprofile causes additional broadening and smoothing of both trials, where filled squares and circles of B represent filled squares and open circles in C, respectively. (D) The final addition of the natural isotopic profiles to the total deuteration profile of C creates the simulated observable mass envelopes. Despite having significantly different backbone amide profiles, and thus significantly different exposure to the solvent, the two observable mass envelopes are quite similar and difficult to distinguish from one another.
Now consider the case of a peptide where there are two equally populated states in one experiment, and let us assume we know what the pre-back exchanged weights of these populations are. One state has three deuterons that exchanged under the experimental conditions and the other state has four (open squares in Fig. 9B). Instead of showing the Figure 9B spectra as bar charts, they are shown on grids for visual simplicity. The symbols are discreet and unitary, however, as it is impossible to have a backbone amide hydrogen exchange with a partial deuteron. This peptide consequently has a maximum of four deuterons exposed to the solvent under the experimental conditions. Both populations in the profile will back exchange according to the binomial model. To determine the back exchange–corrected result for the most deuterated population (w x), Equation 7 is used with x = 4, n = 4, F = 0.33, and B x = 0.50. Then, to calculate the other populations (w n) from n = 3 to n = 0 and x = 4, each pre-back exchange population is calculated by rearranging to solve for w n using Equation 8, to create the final observed backbone deuteration level (filled squares in Fig. 9B).
Suppose the same peptide, under different experimental conditions, has a different deuteration profile, one with four equally likely states (open circles in Fig. 9B). Now, the peptide has a maximum of five backbone amides exposed to the solvent, an increase over the previous set of experiments. This profile will also back exchange in the same random, binomial fashion; but because it has different starting points, the observed back exchanged profile will differ (filled circles in Fig. 9B). When the filled circle and square profiles are compared, the smoothing during back exchange becomes apparent; the back exchanged profiles are more similar than are the original profiles. Thus back exchange causes a backbone distribution with only two states and a maximum of four deuterons to become less distinguishable from a backbone distribution with four states and a maximum of five deuterons.
Both profiles have the same centroid before (3.50 D) and after (2.35 D) the simulated back exchange, but the biophysical differences are significant, because one sample has only four backbone amides sites exposed to the solvent and the other has five. Also, one sample has only two states populated, while the other has four. Assume, for example, the open circle profile in Figure 9B is a peptide of a protein by itself and the open square profile is the same peptide in its complex form. Let us further assume this peptide is at the interface with its partner in the complex. The difference between five and four solvent-accessible backbone amides is thus biologically significant, and quantification of this difference is important. Unfortunately, the open circle and square profiles are not what is observed; they must be extracted from the observed spectra by solving for B n over the range of n = 0 to n = x using Equation 8, given that w n is known. The reverse of the deconvolution process shows the total deuteration profile for this theoretical example, by combining the example fast exchanging profile (Fig. 2A) through a convolution with the filled profiles of Figure 9B, to reveal a new convoluted profile (Fig. 9C). Here the black squares are the total deuteration from the black square profile of Figure 9B, and the open circles are the total deuteration from the black circles of Figure 9B. The final observed mass envelopes for the two situations are revealed after convoluting the example natural isotopic abundance profile (Fig. 1A) with the results of Figure 9C (Fig. 9D, black bars from filled squares and white bars from open circles).
At first inspection, the two calculated mass envelope profiles in Figure 9D look remarkably similar, even though the underlying backbone deuteration distribution is quite different (open symbols in Fig. 9B). The mass envelope profiles have the exact same centroid (3.69) and thus are completely indistinguishable by centroid methods. They also have nearly the same shape. At their highest peaks (four deuterons), the difference between the two differ by only 2.6% in the mass envelope, while the differences in the underlying backbone deuteration profile differ by 25% at the same mass. Figure 9B–D, shows how each step of the process smoothes the differences, but the most dramatic effect is by the back exchange, because the back exchange process converts the backbone amide profiles to sums of binomials from loss of deuteration during back exchange. Originally, the backbone amide profiles only had two and four populations, respectively, but the final mass envelopes both have signal spread over eight populations. This broadening and smoothing has the general effect of obscuring important backbone differences in all real samples and complicates real spectral analysis. Determining the biological difference between the two states of a peptide relies on extracting small, observable differences, which is impossible with centroids but possible under the deconvolution method described here. In fact, high signal-to-noise in real data is necessary if this level of discrimination in backbone populations is to be achieved. Clearly, the higher the signal to noise that can be achieved, the better the chance there will be to distinguish populations after back exchange has occurred.
The effect of variation in the back exchange correction factor on mass envelopes
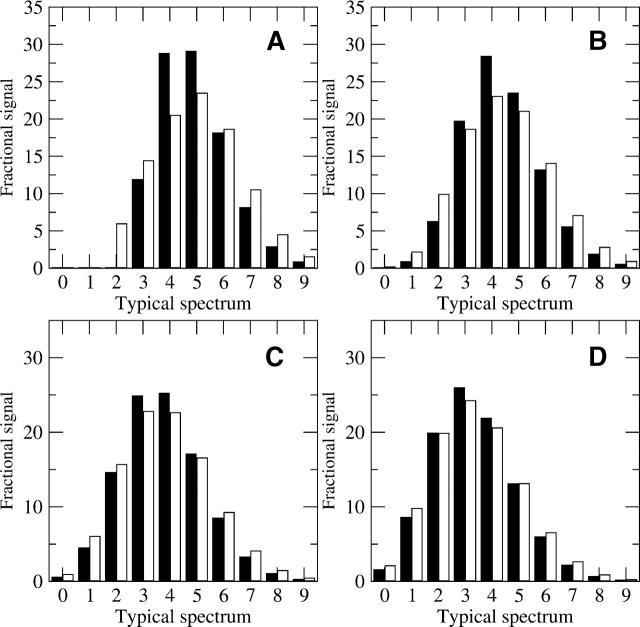
Because the back exchange process smoothes the results so noticeably, it is important to understand how variation in the back exchange correction factor affects the observed mass envelopes. Given the original backbone amide exchange profiles in Figure 9B (open symbols), the sample mass envelope illustrates the smoothing effect of increasing back exchange (Fig. 10). With no back exchange (0%), the differences between the two profiles are quite distinct (Fig. 10A, black bars from open squares, white bars from open circles). The largest difference in signal is >5.6% at the population with four deuterons, and the two profiles differ noticeably in their shape. The black bar mass envelope ranges from three to nine deuterons, while the white bar mass envelope ranges from two to nine. The lack of any population with two deuterons in the black bar mass envelope is noticeable and important. Briefly, it shows that the peptide represented by the black bars has at least three backbone amide sites completely exposed, whereas the peptide represented by the white bars must have some population with only two deuterons.
Figure 10.
(A_–_D) Examples of the difference between the mass envelopes for the two experimental conditions of sequence IYRDLKPENL (Fig. 9B) under different levels of back exchange. The back exchange level of each example for parts A_–_D is 0%, 15%, 33%, and 45%, respectively. As the back exchange level increases, the smoothing also increases, which minimizes differences between the two samples. In this case, the 0% level exhibits several important differences, while the 15% level retains some of those differences. By 33% back exchange, the differences are becoming obscure, and they are quite small by 45% back exchange. With 45% back exchange, the level of discrimination necessary to distinguish the two mass envelopes is only reached by high-resolution data. Simple inspection of the envelopes will not reveal the important differences between the two spectra in D, but removal of the natural isotopic and side-chain profiles to reveal the backbone deuteration profile will identify the differences between the two envelopes (as shown by the filled symbols in Figure 9B).
As the back exchange level is increased from zero to 15% (Fig. 10B), the profiles become much harder to distinguish. Both profiles have small populations with one and two deuterons, so the distinguishing characteristics in the low populations is minimized, but some differences are still important. At the signal with four deuterons, the difference between the two areas is still >5.3% of the total, a measurable amount. The mass envelope represented by the black bars is higher and more condensed around the center, while the mass envelope represented by the white bars is more spread out over more masses and lower at the center. Once the back exchange level reaches 33% (Fig. 10C), the differences become minor, and a back exchange level of 45% has very little differences between the observed spectra (Fig. 10D). Only one peak (with three deuterons) has a difference between the two mass envelopes of >1.5% with 45% back exchange. The two mass envelopes in Figure 10D are likely to look very similar under typical experimental conditions. With good signal-to-noise ratios, the small differences may be extracted by removing the natural isotopic abundance and side-chain profiles. Such quantitative analysis increases the ability to distinguish the two spectra, as shown by the differences in the backbone profiles (filled symbols in Fig. 9B). Reducing the back exchange is an important goal for better analysis, as it reduces loss of subtle distinctions across experimental conditions.
The effect of variation in the data on back exchange results
When solving for B n, instead of w n as calculated in Figures 9 and 10, the back exchange calculation in Equation 8 will explicitly determine the original backbone amide exchange profile, but it is very sensitive to errors in the observed weights. For example, if there is some uncertainty in the data because spectra have poor signal to noise, the back exchange correction result will be an amplification of the uncertainty. The uncertainty is proportional to the level of deuteration, with more uncertainty for the more highly deuterated peptides. This causes greater confidence in the analysis of peptides with little backbone exchange and less confidence in highly exchanged peptides.
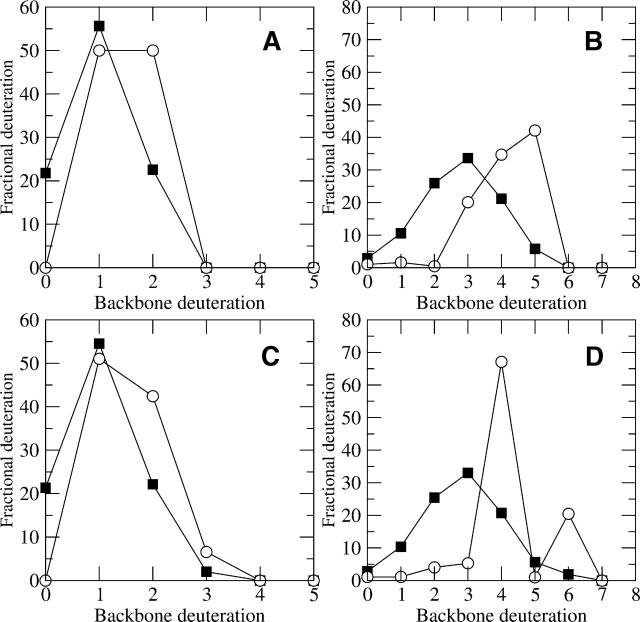
Consider the case of two different simulated peptides, one with only two solvent-accessible backbone amides, and the other with five, assuming 33% back exchange for both (filled squares in Fig. 11, A and B, respectively). The back exchange–corrected values (open circles) for the low exchanging peptide do not change as dramatically as do the corrected values for the highly deuterated peptide. In the peptide in Figure 11A, the increase at two deuterons for the back exchange–corrected value is about the same as the decrease in zero deuterons. In percentage terms, the increase at two deuterons goes from 22.6% to 50%, an increase by a factor of 2.2. In Figure 11B, the increase at five deuterons is much larger in percentage terms, going from 5.8% of the total signal to 42.1% after the back correction. This 7.3-fold increase suggests any variance across samples in the five deuteron population (up or down) will affect the back corrected value about seven times the observed backbone amide difference. Thus a small change in the observed backbone population could greatly affect the result.
Figure 11.
The effect of variation between trials on the resulting back exchange interpretations. (A_–_D) The filled squares represent simulated backbone amide exchange profiles (before back correction), while the open circles represent the back exchange–corrected results. Samples with low (A) and high (B) levels of backbone amide exchange are compared to alternate trials of each. (C) Another simulated trial of the same peptide as in A has a small signal at M(3). The resulting back exchange corrected profile (open circles) is similar between the two trials. (D) Another trial of the same peptide as in B with a small signal at M(6) has a very different back exchange corrected profile (open circles) from the previous one (B). The large differences in the two complicate interpretations of this peptide and suggest high confidence in the data is necessary in order to distinguish between small (but real) peaks and background noise.
Figure 11C represents a simulated duplicate analysis of the same peptide shown in Figure 11A, with a typical amount of variation between trials. The populations of backbone deuteration (closed symbols in both figures) are very similar, but a small population with three backbone deuterons is now present in Figure 11C. When the amount of deuteration is low, the back exchange–corrected populations (open circles in Fig. 11A,C) do not change much, although there is some variation. In contrast, Figure 11, B and D, show similar slight variations in the deuterated population except the peptide is more deuterated originally (closed symbols in Fig. 11B,D). In this comparison, the profiles are the same except for a small population with six deuterons in Figure 11D. This variation results in widely different back exchange corrected profiles (open circles in Fig. 11B,D). Clearly, the back exchange corrected profile in Figure 8D is physically unrealistic, and if it were obtained, one should consider that the indication of a small population at six deuterons may be due to noise.
The theoretical models must completely agree with the observed profile in order to have clear signal that properly separates small, yet real, signal from noise. This situation is quite uncommon in highly deuterated peptides and suggests that there will be less confidence in the results when determining the explicit back corrected backbone amide populations for highly deuterated peptides. The analysis is not as difficult for only slightly deuterated peptides, as shown in Figure 11, A and C, because the signal is spread over only a few populations. This suggests that studying less deuterated peptides (or faster time course experiments for highly solvent-accessible peptides) will result in more confident interpretations than those for highly deuterated peptides.
Comparison between FT deconvolution and maximum entropy
The MEM, although similar in outcome to the FT-based deconvolution method presented here, has some critical differences in assumptions that affect the result. While the deconvolution method presented in this article directly calculated the deuteration population levels based on the data from the mass spectrometer, the MEM requires the use of a user-defined parameter that specifies an expected noise level with which to process the data to determine the most probable result (Zhang et al. 1997). The main advantage of MEM is that it gives a conservative estimate of the deuteration profile consistent with the assumptions of the model. The disadvantage of MEM is that if the model is incorrect or incomplete, it will still return a highly plausible set of parameters, which may mislead the user. In addition, MEM smooths the data, which can minimize the populations that are far from the center of the distribution, due to the damping of populations where the standard deviation is high. The main advantage of the deconvolution procedure is that it explicitly displays the model as applied to a particular set of data and emphasizes problematic areas. The main disadvantage of the deconvolution method is the difficulty in determining accurate values where the data are noisy.
The MEM is slower than FT-based deconvolution of raw mass spectra data. To speed up the calculation, the data must first be integrated into line spectra, which may conceal problems. The FT-based deconvolution method described in this article does not require integration of the spectra into lines; it only requires the data be resampled into evenly spaced intervals. It also does not dampen the populations far from the mean, and thus it is more likely to accurately depict the real values in the most deuterated states. The choice between the two methods depends on whether the objective of the experiment is to determine the best set of parameters or to test the suitability of the model. In the analysis presented here, an accurate calculation of the most deuterated population is quite important, and thus the FT-based deconvolution is more appropriate.
Conclusion
We have demonstrated that the determination of the explicit number and level of backbone amide exchange in peptides from proteins by high-resolution MS experiments is possible and informative from a biological standpoint. This was accomplished by a deconvolution calculation that removes both the natural isotopic abundance as well fast exchanging side-chain deuterons from the observed MALDI-TOF MS mass envelope for any desired peptide. The result is the backbone amide populations due to the different deuterated states of the peptide. The reconstructed results based on the three parts of the model (natural isotopic profile, fast exchanging profile, and backbone amide exchange profile) result in excellent agreement for high-resolution data. Furthermore, by the deconvolution method, we were able to compare the fast exchanging side-chain model with the data and determine its validity for MALDI-TOF experiments. This method provides several new analysis tools beyond centroids to understand H/D exchange, including the ability to detect inconsistent data, as well as to separate some overlapping peptides, as is shown in simulated and real experiments. The deconvolution calculation is sensitive to both contamination and inconsistency in the mass envelope and thus detects problematic data more reliably than do other methods. Interpretation of good data is taken to a higher level with the calculation of deuterium population profiles, which give additional information on the minimum number of exchangeable backbone hydrogen atoms. When the data are not sufficient for use with this method, either a centroid analysis or MEM is more appropriate.
We have also presented a quantitative analysis of what happens during the back exchange process. Because back exchange is a binomially distributed process, different backbone amide profiles can look very similar when their MS mass envelopes are observed. This smoothing process is exacerbated by high levels of back exchange and demonstrates the importance of minimizing it. Finally, we have detailed how some of the variations between trials in the data can affect the back exchange corrected values, and how the change in results is dependent on the deuteration level. Consequently, the data need tobe of high quality with good signal to noise for high confidence in the results for highly deuterated peptides. With increasing quality and resolution abilities of new MS instruments, we can expect to generate more data with high signal to noise in the future, making the methods described here more broadly applicable in H/D analysis.
Materials and methods
Implementation of deconvolution theory
The DEX software package (http://biology.sdsc.edu/ccms/dex) is written in the C++ programming language, with the main deconvolution engine written in ANSI C. Included in this package is a program to calculate the natural isotopic profiles for any normal protein sequence. The FFTW library (Frigo and Johnson 2005; www.fftw.org), is used in the deconvolution, and the GRACE graphing package (Turner, Paul) (http://plasma-gate.weizmann.ac.il/Grace) is used for graphical visualization. Both programs are freely available. The DEX package source code is freely available for academic use from the authors of this article.
The data from most mass spectrometers are in nonuniform increments, so the observed data first has to be completely resampled into evenly spaced increments of 0.100 mass units by integration with linear interpolation for the end points. This greatly reduces the data points in the file but has shown to be of sufficient detail (10 data points between the peak offsets) for our analysis. The natural abundance profiles need to be normalized and arranged such that they have the same spacing as the observed data peaks.
The hypothesis behind the deconvolution method is the assumption that the observed spectra are a combination of the convolution of the natural abundance profile with the deuteration weights, and random noise (see Theory section). If the Fourier coefficient in the denominator of Equation 4 is very small and the numerator is not zero, the quotient can be either machine infinity or “not a number” on computers that properly implement the IEEE Standard 754–1985 for floating point arithmetic. This situation can only arise if the nonzero numerator is due to noise or if the spectrum does not match the physical model. DEX replaces any such quotients by the original numerator. This preserves an indication of the noise level of the observations while avoiding amplification of error. Noise is further reduced by the mathematical form of the convolution, which in effect treats each point as a weighted average over the number of points in the theoretical isotopic profile of the undeuterated species.
The deconvolution program uses only a few megabytes of memory and calculates the deuteration levels for all profiles quickly. On a single Intel Pentium 4 processor (2.6 GHz), the program spent only ~15 sec to integrate and deconvolute 40 mass spectra, each consisting of 26 peptides to analyze, or >1000 deconvolutions. The program’s inputs are the observed MS data file, resampled to 0.1 mass unit intervals and the normalized natural isotope profile for each known peptide present in the data. The natural isotope profile can be automatically generated from a sequence file by using a binomial distribution based on standard isotopic distributions or user-defined abundance frequencies for standard protein atoms. The program will look at each natural isotope profile and select an upper and lower bound to ensure that any completely deuterated sample would not have peaks beyond the selected range. This range is called the envelope and should be as large as the number of maximum exchangeable hydrogens plus the natural isotope profile for each peptide. We have found a length of 1.5 times the sequence length to be sufficient for the envelope. This is normally much longer than necessary but should cover extreme cases, and the higher mass part of the mass envelope need not be analyzed if the peaks do not extend that far, as contamination there will not affect the results of the lighter mass values.
As a reality check, we take 1.5 mass units of data before the monoisotopic mass as a buffer, but zero out the range from 1.5 to 0.5 mass units before the M(0) peak, because any points before 0.5 mass units from M(0) cause a problem due to overlap with other peaks that may be present. In cases of front overlap, it is suggested to change the range of the natural isotope profile to start with the range of overlapping peptide’s monoisotopic mass and continue through original peptide’s mass envelope (see Results and Discussion). Consider the example of a sequence 10 residues long with a monoisotopic mass of 1260.70. The envelope for deconvolution extends from 1259.20–1275.60 mass units, or a total of 165 data points for the observed spectra. The normalized natural isotope profile will have the same mass ranges (1259.20–1275.60) and number of points (165) as the observed MS data, with the value for each point set to zero except for the values corresponding to the monoisotopic mass peak and the higher mass populations.
Once the deconvolution has been calculated, there are several analysis and viewing options available. With the program GRACE, the user can view a succession of all the mass envelopes with both the original and deconvoluted result of one entire spectrum, or make a custom file containing only specific peptides for all the trials desired. The envelopes can be viewed one at a time, or multiple graphs can be stacked together to track the increasing exchange over time. For viewing purposes, the observed data between 1.5 and 0.5 units before the mono-isotopic mass is preserved, which is very helpful in detecting the existence of any problems from front overlap. Included in the package are programs to automatically evaluate the deconvoluted results by population weights or centroids. The previous method for determining the centroid simply summed all of the signal above the baseline over a user-defined range to calculate the centroid. DEX software is able to centroid only the signal corresponding with the correct masses for the peptide, not contamination signal that may intersperse between the peptide signal. This improves the centroid value noticeably, especially when centroiding mass envelopes where the noise is a considerable component of the overall signal. If the peaks are not quite correlated to the mass because of shifting upon detection, the program will automatically find the shifted peaks and adjust the profile accordingly. It is highly recommended to first visually inspect the graphs for inconsistencies (overlapping peptides, poor data quality) before interpreting the calculated data.
Signal-to-noise ratios, as discussed in Figure 3, were determined by dividing the area of the single highest signal in the mass envelope by the average background noise level. The average background noise level was determined by averaging all the points that were before, between, and after the peptide’s signal over the mass envelope range.
Acknowledgments
This work was supported by grant RO1GM70996 from the National Institute of General Medical Sciences. We thank Vineet Bafna for his help with the natural isotope abundance algorithms.
Abbreviations
- H/D exchange, hydrogen/deuterium exchange
- MS, mass spectrometry
- MALDI-TOF, matrix-assisted laser-desorption/ ionization time-of-flight
- ESI-qTOF, electrospray ionization time-of-flight
- FTICR, Fourier transform ion cyclotron resonance
- NMR, nuclearmagnetic resonance
- PKA, proteinkinase A;M(0), monoisotopic peak
- FT, Fourier transform
- FFT, fast Fourier transform
- MEM, maximum entropy method
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.051774906.
References
- Anand, G.S., Hughes, C.A., Jones, J.M., Taylor, S.S., and Komives, E.A. 2002. Amide H/2H exchange reveals communication between the cAMP and catalytic subunit-binding sites in the RIαsubunit of protein kinase A. J. Mol. Biol. 323**:** 377–386. [DOI] [PubMed] [Google Scholar]
- Anand, G.S., Law, D., Mandell, J.G., Snead, A.N., Tsigelny, I., Taylor S.S., Ten Eyck, L.F., and Komives, E.A. 2003. Identification of the protein kinase A regulatory RIα-catalytic subunit interface by amide H/2H exchange and protein docking. Proc. Natl. Acad. Sci. 100**:** 13264–13269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clauser, K.R., Baker, P., and Burlingame, A.L. 1999. Role of accurate mass measurement (± 10 ppm) in protein identification strategies employing MS or MS/MS and database searching. Anal. Chem. 71**:** 2871–2882. [DOI] [PubMed] [Google Scholar]
- Dempsey, C.E. 2001. Hydrogen exchange in peptides and proteins using NMR spectroscopy. Progr. Nuclear Magn. Reson. Spectr. 39**:** 135–170. [Google Scholar]
- Englander, S. 1993. In pursuit of protein folding. Science 262**:** 848–849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Englander, S.W. and Kallenbach, N.R. 1983. Hydrogen exchange and structural dynamics of proteins and nucleic acids. Q. Rev. Biophys. 16**:** 521–655. [DOI] [PubMed] [Google Scholar]
- Frigo, M., and Johnson, S.G. 2005. The design and implementation of FFTW3. Proc. IEEE. 93**:** 216–231. [Google Scholar]
- Gmeiner, W.H., Xu, I., Horita, D.A., Smithgall, T.E., Engen, J.R., Smith, D.L., and Byrd, R.A. 2001. Intramolecular binding of a proximal PPII helix to an SH3 domain in the fusion protein SH3Hck : PPIIhGAP. Cell. Biochem. Biophys. 35**:** 115–126. [DOI] [PubMed] [Google Scholar]
- Hirschman, I.I. and Widder, D.V. 1955. The convolution transform. Princeton University Press, Princeton, NJ.
- Hughes, C.A., Mandell, J.G., Anand, G.S., Stock, A.M., and Komives, E.A. 2001. Phosphorylation causes subtle changes in solvent accessibility at the interdomain interface of methylesterase CheB. J. Mol. Biol. 307**:** 967–976. [DOI] [PubMed] [Google Scholar]
- Hvidt, A. and Linderstrøm-Lang, K. 1954. Exchange of hydrogen atoms in insulin with deuterium atoms in aqueous solutions. Biochim. Biophys. Acta 14**:** 574–575. [DOI] [PubMed] [Google Scholar]
- Jeng, M. and Dyson J. 1995. Comparison of the hydrogen-exchange behavior of reduced and oxidized Escherichia coli thioredoxin. Biochemistry 34**:** 611–619. [DOI] [PubMed] [Google Scholar]
- Lanman, J., Lam, T.T., Barnes, S., Sakalian, M., Emmett, M.R., Marshall, A.G., and Prevelige Jr., P.E. 2003. Identification of novel interactions in HIV-1 capsid protein assembly by high-resolution mass spectrometry. J. Mol. Biol. 325**:** 759–772. [DOI] [PubMed] [Google Scholar]
- Law, D., Hotchko, M., and Ten Eyck, T.F. 2005. Progress in computation and amide hydrogen exchange for prediction of protein–protein complexes. Proteins 60**:** 302–307. [DOI] [PubMed] [Google Scholar]
- Lee, T., Hoofnagle, A.N., Kabuyama, Y., Stroud, J., Min, X., Goldsmith, E.J., Chen, L., Resing, K.A., and Ahn, N.G. 2004. Docking motif interactions in MAP kinases revealed by hydrogen exchange mass spectrometry. Mol. Cell. 14**:** 43–55. [DOI] [PubMed] [Google Scholar]
- Lide, D.R. 1995. CRC handbook of chemistry and physics. CRC Press, Boca Raton, FL.
- Mandell, J.G., Falick, A.M., and Komives, E.A. 1998a. Measurement of amide hydrogen exchange by MALDI-TOF mass spectrometry. Anal. Chem. 70**:** 3987–3995. [DOI] [PubMed] [Google Scholar]
- ———. 1998b. Identification of protein–protein interfaces by decreased amide proton solvent accessibility. Proc. Natl Acad. Sci. 95**:** 14705–14710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandell, J. G., Baerga-Ortiz, A., Akashi, S., Takio, K., and Komives, E.A. 2001. Solvent accessibility of the thrombin–thrombomodulin interface. J. Mol. Biol. 306**:** 575–589. [DOI] [PubMed] [Google Scholar]
- Nazabal, A., Laguerre, M., Schmitter, J.M., Vaillier, J., Chaignepain, S., and Velours, J. 2003. Hydrogen/deuterium exchange on yeast ATPase supramolecular protein complex analyzed at high sensitivity by MALDI mass spectrometry. J. Am. Soc. Mass Spectrom. 14**:** 471–481. [DOI] [PubMed] [Google Scholar]
- Paterson, Y., Englander, S.W., and Roder, H. 1990. An antibody binding site on cytochrome c defined by hydrogen exchange and two-dimensional NMR. Science. 249**:** 755–759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rockwood, A.L., Kushnir, M.M., and Nelson, G.J. 2003. Dissociation of individual isotopic peaks: Predicting isotopic distributions of product ions in MSn. J. Am. Soc. Mass Spectrom. 14**:** 311–322. [DOI] [PubMed] [Google Scholar]
- Smith, D., Deng, Y., and Zhang, Z. 1997. Probing the non-covalent structure of proteins by amide hydrogen exchange and mass spectrometry. J. Mass Spectrom. 32**:** 135–146. [DOI] [PubMed] [Google Scholar]
- Tuma, R., Coward, L.U., Kirk, M.C., Barnes, S., and Prevelige, P.E. 2001. Hydrogen–deuterium exchange as a probe of folding and assembly in viral capsids. J. Mol. Biol. 306**:** 389–396. [DOI] [PubMed] [Google Scholar]
- Wang, L. and Smith, D.L. 2005. Capsid structure and dynamics of a human rhinovirus probed by hydrogen exchange mass spectrometry. Protein Sci. 14**:** 1661–1672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weisstein, E.W. 1999. Convolution. http://mathworld.wolfram.com/Convolution.html.
- Yergey, J.A. 1983. A general-approach to calculating isotopic distributions for mass-spectrometry. Int. J. Mass Spectrom. Ion Proc. 52**:** 337–349. [DOI] [PubMed] [Google Scholar]
- Zhang, Z. and Smith, D.L. 1993. Determination of amide hydrogen exchange by mass spectrometry: A new tool for protein structure elucidation. Protein Sci. 2**:** 522–531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, Z., Post, C.B., and Smith, D.L. 1996. Amide hydrogen exchange determined by mass spectrometry: Application to rabbit muscle aldolase. Biochemistry 35**:** 779–791. [DOI] [PubMed] [Google Scholar]
- Zhang, Z., Guan, S., and Marshall, A.G. 1997. Enhancement of the effective resolution of mass spectra of high-mass biomolecules by maximum entropy-based deconvolution to eliminate the isotopic natural abundance distribution. J. Am. Soc. Mass Spectrom. 8**:** 659–670. [Google Scholar]