On the characterisation of the mechanism underlying passive activation of the Ca2+ release-activated Ca2+ current ICRAC in rat basophilic leukaemia cells (original) (raw)
Abstract
- Tight-seal whole-cell patch clamp experiments were performed to investigate the mechanism whereby passive depletion of stores activates the Ca2+ release-activated Ca2+ current (_I_CRAC) in rat basophilic leukaemia (RBL) cells.
- Passive depletion of stores was achieved by dialysing cells with different concentrations of Ca2+ chelators. Low concentrations generally evoked a submaximal _I_CRAC, which developed slowly and monophasically. Higher concentrations resulted in a biphasic current in which the initial slow monophasic component developed into a faster and bigger second phase.
- The kinetics of _I_CRAC as well as its final amplitude were not affected by Ca2+ chelators that had different affinities or speeds of binding.
- Exogenous Ca2+ binding ratios ≥ 16 670 were necessary to fully activate _I_CRAC. Because the Ca2+ binding ratio within the stores is presumably low, this indicates that other factors like Ca2+ transport across the stores membrane are rate limiting for passive store depletion.
- Heparin and Ruthenium Red both failed to affect passive Ca2+ leak from the intracellular stores.
- Treatment with sarco/endoplasmic reticulum Ca2+-ATPase (SERCA) pump blockers dramatically altered the kinetics of activation of biphasic currents, and increased the amplitude of monophasic ones.
- Our results suggest that SERCA pumps are very effective in preventing _I_CRAC from activating passively, and are responsible for the phasic nature of the current, its time course of development and its overall extent.
In a variety of different cell types, the process of emptying the inositol 1,4,5-trisphosphate (Ins_P_3)-sensitive intracellular Ca2+ store triggers Ca2+ entry across the plasma membrane, a process originally termed capacitative Ca2+ entry (Putney, 1986). Patch clamp experiments have established that store depletion opens plasmalemmal Ca2+ channels, the best characterized and most widely distributed of which is the Ca2+ release-activated Ca2+ current (_I_CRAC) (reviewed in Parekh & Penner, 1997).
_I_CRAC can be activated by several distinct mechanisms, all of which share the property of depleting the intracellular Ins_P_3-sensitive Ca2+ stores. Such mechanisms include an increase in intracellular Ins_P_3, inhibition of the SERCA pumps or exposure to the Ca2+ ionophore ionomycin (Hoth & Penner, 1992; Parekh & Penner, 1997). In order for these diverse manoeuvres to be effective, however, the cells must be dialysed with pipette solutions that contain high concentrations of Ca2+ chelators like EGTA or BAPTA. In fact, dialysis with 10 mm EGTA or BAPTA alone is sufficient to maximally activate _I_CRAC, a process referred to as passive depletion of stores (Hoth & Penner 1992). It has been suggested that passive depletion relies only on the endogenous leakage of Ca2+ from the stores. Cytoplasmic Ca2+ is strongly buffered and clamped at very low concentrations, so as Ca2+ leaks out from the stores, it will be captured by the chelator and cannot therefore be taken back up. In this way, the stores will gradually be drained of their Ca2+ (Hoth & Penner, 1992, 1993). However, this model has not been tested and some observations need to be clarified. Thus, considering that the known Ca2+ buffers within the stores have low affinity for Ca2+ (Pozzan et al. 1994), the expected Ca2+ binding ratio (Neher, 1995) within the stores is presumably low and roughly equivalent to a concentration of only a few micromolar of exogenous Ca2+ chelator. Dialysis with 0.5 mm EGTA will presumably buffer cytosolic Ca2+ at around 10 nm, and hence one might expect such low concentrations of cytoplasmic chelator (<< 10 mm) to passively deplete the stores. However, this is not the case. Furthermore, the potential role of SERCA pumps in passive store depletion is not considered. In view of the fact that passive depletion is widely used to study _I_CRAC (Fasolato et al. 1998; Kerschbaum & Cahalan, 1999; Fierro & Parekh, 1999), it is important to establish the underlying mechanism in order to be able to fully interpret the results. Clarification of the passive depletion mechanism will also add to our understanding of the Ca2+ transport mechanisms that operate on the stores.
In this report, we have investigated the ability of different concentrations of a given Ca2+ chelator to activate _I_CRAC. Furthermore, we have used Ca2+ chelators with different characteristics in order to establish whether apparent _K_d and/or speed of binding (_k_on) of the Ca2+ buffers have any impact on passive store depletion and the subsequent activation of _I_CRAC. We have also examined the role of SERCA pumps in this process. We find that passive depletion of stores is more complex than previously thought. _I_CRAC activates in either a mono- or biphasic manner, depending on chelator concentration. Furthermore, using passive depletion with millimolar concentrations of Ca2+ chelator, we find that SERCA pump activity is rather strong and is responsible for the phasic nature of the current, its time course of development and its overall extent. Our results highlight the critical role played by SERCA pumps in intracellular Ca2+ homeostasis and activation of _I_CRAC.
METHODS
Rat basophilic leukaemia (RBL-1) cells, which were kindly provided by Michael Pilot from the Max Planck Institute for Biophysical Chemistry in Göttingen, Germany, were cultured essentially as previously described (Parekh et al. 1997). Briefly, cells were maintained in medium containing Dulbecco's modified Eagle's medium, 10 % heat-inactivated fetal bovine serum and 3 % streptomycin-penicillin (all from Life Technologies), and kept in a 5 % CO2 humidified atmosphere at 37°C. Cells were trypsinized and then plated on glass coverslips at least 24 h before use. Patch clamp experiments were conducted in the tight-seal whole-cell configuration at room temperature (18-25°C) as previously described (Hamill et al. 1981; Fierro & Parekh, 1999). Patch pipettes were pulled from borosilicate glass (Hilgenberg), Sylgard coated and fire polished. Pipettes had DC resistances of 2.5-4 MΩ when filled with standard internal solution that contained (mm): caesium glutamate, 145; NaCl, 8; MgCl2, 1; Hepes, 10; pH 7.2 with CsOH. Depending on the experiment (described in the text), the Ca2+ chelators EGTA, BAPTA tetracaesium salt (BAPTA) or 5-5′-dimethyl BAPTA tetrapotassium salt (dimethyl BAPTA) (both from Molecular Probes), were added to this solution at specified concentrations, as sometimes was Ins_P_3 (30 μm), thapsigargin (Calbiochem) (4 μm), cyclopiazonic acid (100 μm), Ruthenium Red (100 μm) and heparin (1 mg ml−1). Thapsigargin (4 μm) was applied locally by means of a second pipette, placed within 30 μm of the cell. All chemicals were purchased from Sigma unless otherwise noted. A correction of +10 mV was applied for the subsequent liquid junction potential that arose from this glutamate-based internal solution. Extracellular solution contained (mm): NaCl, 145; KCl, 2.8; CaCl2, 10; MgCl2, 2; CsCl, 10; glucose, 10; Hepes, 10; pH 7.2 (NaOH). High-resolution current recordings were acquired and _I_CRAC was measured as described previously (Fierro & Parekh, 1999). Data are presented as means ±s.e.m., and statistical evaluation was carried out using Student's unpaired t test.
Analysis and curve fitting
The currents obtained following dialysis with different concentrations of Ca2+ chelator were either monophasic or biphasic (see Fig. 1_C_) and these developed after a delay of several tens of seconds. We measured the delay as the time after break-in when _I_CRAC had reached an amplitude twice the noise of the baseline current. We tried a variety of fits to the data (exponential, double exponential, polynomial, linear). None of these were able to reliably fit our data. In light of this, we arbitrarily fitted tangents to the steepest parts of the curves and found that two linear components could reasonably fit the biphasic currents whereas one linear component was sufficient for the monophasic ones. Although our fitting is an approximation at best, it sufficed for a qualitative inspection of the data and provided valuable information on the rate of activation of the current.
Figure 1. Effects of dialysing RBL-1 cells with different concentrations of Ca2+ chelators.
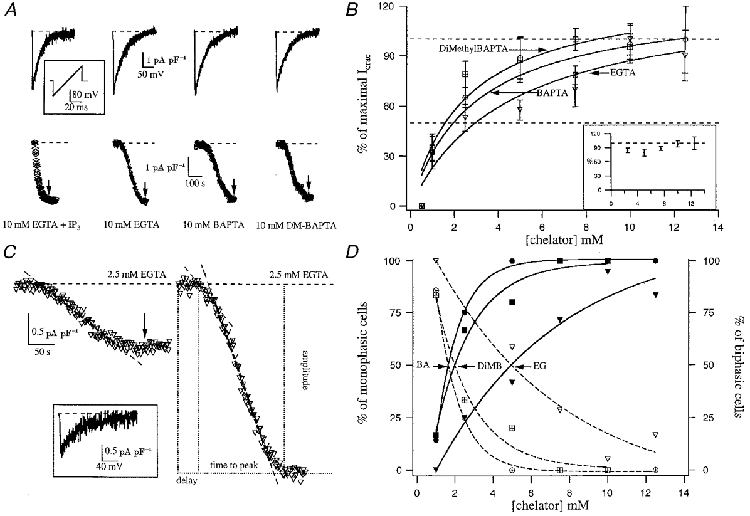
A shows ramp currents (upper panel) and the time course of _I_CRAC (measured at -80 mV; lower panel) following dialysis with 30 μm Ins_P_3 (IP3) + 10 mm EGTA (active depletion) or 10 mm EGTA, BAPTA or dimethyl (DM)-BAPTA (passive depletion). The inset shows the ramp protocol (-100 to +100 mV in 50 ms at 0.5 Hz). B plots the concentration-_I_CRAC relationship for the different chelators. Cells that did not respond have not been included in the analysis. The inset represents the dose-response curve for all cells that generated a biphasic current (see text for detailed description). C shows typical monophasic (left-hand panel) and biphasic currents (right-hand panel) that were obtained by dialysis with 2.5 mm EGTA. The inset shows the ramp current taken at the arrow, when _I_CRAC had reached steady state. The right-hand panel shows the parameters that we measured. D shows the relationship between chelator concentration and the percentage of cells that responded by generating either a monophasic or biphasic _I_CRAC. As chelator concentration increases, so does the fraction of cells that respond with biphasic _I_CRAC. EG, EGTA; BA, BAPTA; DiMB, dimethyl BAPTA.
RESULTS
Passive depletion of stores generates biphasic _I_CRAC
Figure 1_A_ compares the effects on _I_CRAC of depleting stores actively (cytoplasm was dialysed with 30 μm InsP3 and 10 mm EGTA) with passive depletion using 10 mm of three different Ca2+ chelators (EGTA, BAPTA and dimethyl BAPTA). The chelators have apparent _K_d values of 150, 225 and 150 nm, respectively, and on-rates of 1.5 × 106 M−1 s−1 for EGTA and 5 × 108 M−1 s−1 for BAPTA and dimethyl BAPTA (Martell & Smith, 1974; Harrison & Bers, 1987; Pethig et al. 1989). The current was measured by applying voltage ramps (-100 to +100 mV in 50 ms; see inset of Fig. 1_A_). For all cases, the inwardly rectifying, voltage-independent CRAC current was obtained with a reversal potential close to +50 mV (Fig. 1_A_, upper panel). _I_CRAC amplitude was measured from the ramps at -80 mV and plotted against time (Fig. 1_A_, lower panel). It can be seen that the overall extent of the current was similar using either active (Ins_P_3) or passive means to deplete the stores, but the kinetics of development were strikingly different (see text below).
We then constructed a dose-response curve to various concentrations of the three different Ca2+ chelators mentioned above. Figure 1_B_ summarizes the pooled data (fitted with a Michaelis-Menten-type equation) from cells which were dialysed with concentrations of EGTA (▿, _n_= 73) and BAPTA (^, _n_= 38) from 0.5 to 12.5 mm, and dimethyl BAPTA (□, _n_= 34) from 0.5 to 10 mm. Ca2+ chelator concentrations of 0.5 mm failed to generate any detectable current (_n_= 9). After dialysing cells with 1 mm Ca2+ chelator, _I_CRAC could be clearly discerned in 42 % of the cells with EGTA (_n_= 12), 71 % with BAPTA (_n_= 6) and 83 % with dimethyl BAPTA (_n_= 6). These currents could be fitted well with a single slow linear component (henceforth monophasic response) and ranged from -0.4 to -1.3 pA pF−1. Figure 1_C_ (left-hand panel) shows a typical monophasic response. The inset shows the I-V ramp, taken at the point indicated by the arrow.
_I_CRAC was routinely activated by dialysis with chelator concentrations from 2.5 to 12.5 mm, with a current amplitude ranging from -0.5 to -4.5 pA pF−1. Currents were larger than -1 pA pF−1 in most of the cases (97 out of 106 cells; 92 %), and all these cells exhibited a short slow phase that was invariably followed by a second faster developing phase (biphasic response). Figure 1_C_ (right-hand panel) shows a typical biphasic response. The two regions over which the current was developing could be represented by linear components. Although we cannot completely rule out the possibility that our monophasic currents were in fact biphasic with an initial small component lost in the noise, the fact that relatively large currents of around -1 pA pF−1 could clearly be seen to have only monophasic or biphasic components suggests this is unlikely.
Different current sizes were detected within the range from 2.5 to 12.5 mm Ca2+ buffer. Although current amplitudes tended to be larger as more Ca2+ chelator was used, big currents could occasionally be recorded with 2.5 mm Ca2+ chelator whereas small currents were sometimes measured even with 10 mm, where the peak amplitude was attained for all three dose-response curves (Fig. 1_B_). Monophasic responses occurred more frequently with ≤ 2.5 mm chelator than with higher concentrations. Increasing the concentration of chelator increased the likelihood that the second fast component would be present (biphasic response), and this is shown in Fig. 1_D_. In the inset of Fig. 1_B_, the dose-response curve is plotted only for cells that developed the secondary phase (_n_= 97, all chelators at each concentration have been lumped together because there was no significant difference between the amplitudes). Strikingly, the overall extent of _I_CRAC was the same irrespective of the chelator concentration, demonstrating that if the first slow phase develops into the second faster one, then _I_CRAC activates to its maximal extent. The dose-response curve of Fig. 1_B_ is therefore somewhat misleading because it does not take into account this key difference between mono- and biphasic current amplitudes.
Delay and time to peak of _I_CRAC are independent of both the nature of the Ca2+ chelator and different concentrations used
Figure 1_C_ defines various properties of _I_CRAC that we analysed in detail and some of which are plotted in Fig. 2. Figure 2_A_ summarises the relationship between _I_CRAC amplitude and delay (left panel) and time to peak (right panel). Each point represents a different concentration of EGTA. Except for 1 mm EGTA concentration (▴), once _I_CRAC started to develop, it reached its peak amplitude at a time that was independent of the EGTA concentration. This relationship also held when BAPTA or dimethyl BAPTA were used to deplete the stores instead (Fig. 2_B_ and C, respectively). Average delay and time to peak were, respectively, 77 ± 5 and 183 ± 7 s for EGTA (_n_= 73), 72 ± 5 and 177 ± 10 s for BAPTA (_n_= 38) and 79 ± 9 and 151 ± 12 s for dimethyl BAPTA (_n_= 34). These values were not significantly different (P > 0.1) between the different chelators or the various concentrations used.
Figure 2. Relationship between delay and time to peak for _I_CRAC following passive activation by dialysis with different concentrations of Ca2+ chelators.
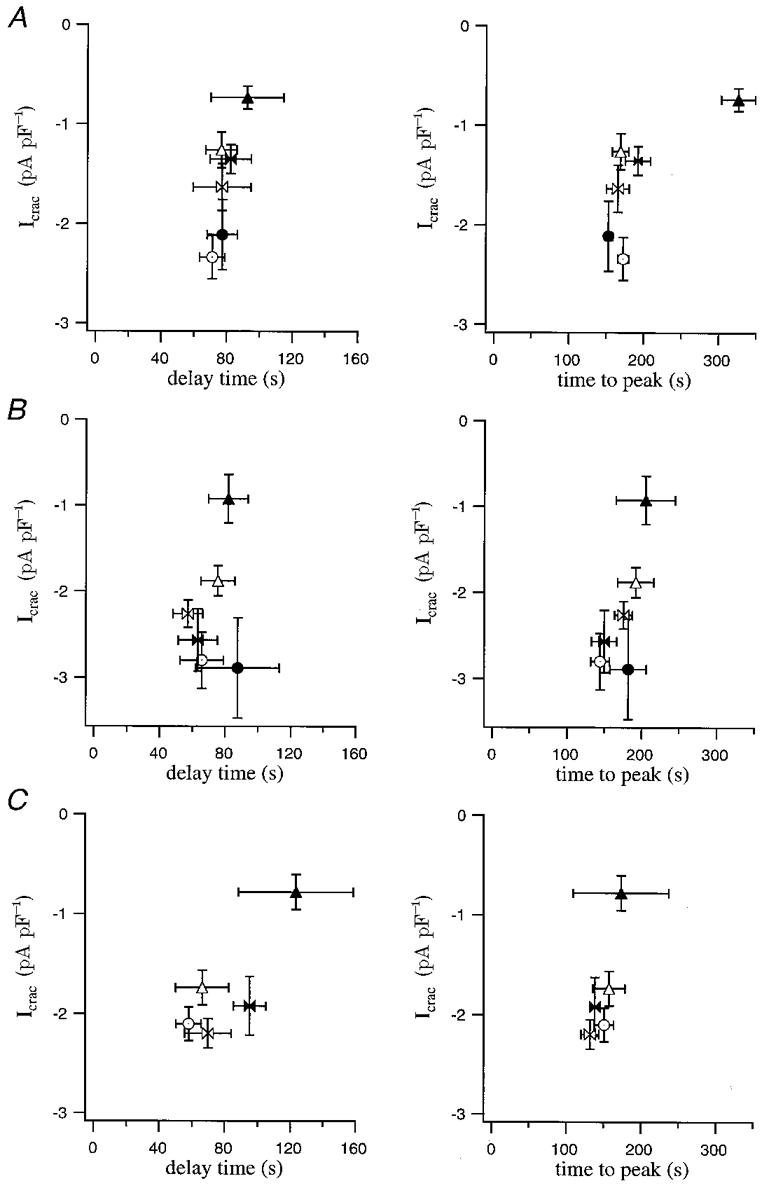
Each point represents the pooled data for a given chelator concentration. Filled triangles correspond to 1 mm; open triangles, 2.5 mm; filled butterfly, 5 mm; open butterfly, 7.5 mm; filled circle, 10 mm; open circle, 12.5 mm. In A the chelator analysed was EGTA, in B BAPTA and in C it was dimethyl BAPTA. For all concentrations and all chelators, there was no significant difference between delay or time to peak (P > 0.1) except for time to peak in 1 mm EGTA.
The monophasic response and the slow phase of the biphasic response correspond to the same phenomenon
Each phase of those biphasic currents that reached amplitudes larger than -1 pA pF−1 (_n_= 97) were fitted with a line. The rate of development of each phase (determined by the slope of the fits) as well as the duration was obtained from the linear fits for each Ca2+ chelator and at each concentration. The relative contribution of each phase to the final _I_CRAC amplitude was then calculated from these parameters. The results are summarized in Fig. 3_A-C_ for EGTA, BAPTA and dimethyl BAPTA, respectively. For biphasic responses, the rate of development of the current, the duration of each phase and the relative contribution to the final _I_CRAC amplitude was not significantly different when the different concentrations were compared (P > 0.1).
Figure 3. The relative contributions of the slow and fast phases to the overall amplitude of _I_CRAC in cells that generated a biphasic current.
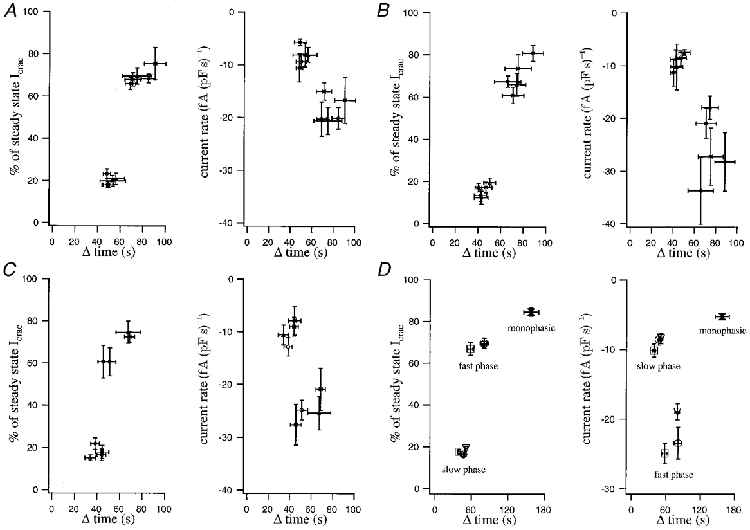
Each point represents a different concentration of chelator and is plotted against its duration after correcting for delay (Δ time). In A, EGTA was the chelator. The monophasic component accounted for around 20 % of the overall extent of the current, and there was no significant difference between the different concentrations of chelator (left-hand panel; P > 0.1). Similarly, the fast component accounted for around 70 % of the current and this fraction was independent of the chelator concentration (P > 0.1). The right-hand panel shows the rate of current development for the slow (uppermost set of points, around -7 fA (pF s)−1) and fast components (lower set of points; range of -20 fA (pF s)−1). B and C are similar plots but reflect BAPTA and dimethyl BAPTA, respectively. Because there were no significant differences in the fractional contributions of the slow and fast phases to the final extent of the current nor in the respective rate of current development between different chelator concentrations, we pooled all concentrations for each given chelator together. The results are summarized in D, where the left-hand panel represents the fractional contribution of each phase to the final extent of the current and the right-hand panel shows the rate of development of the currents for the two phases. Triangles correspond to EGTA, circles to BAPTA and squares to dimethyl BAPTA. For the fast phase, the points representing EGTA and BAPTA overlapped. Also included in the plots are the monophasic responses that were usually seen with chelator concentrations < = 2.5 mm. The data from all three chelators have been combined.
We therefore pooled together all concentrations for each chelator. Thus, when cells were dialysed with EGTA, the slow component had an amplitude that was 19 ± 1 % (_n_= 42) of the total current (lower triangle in Fig. 3_D_, left-hand panel). This contribution was maintained when either BAPTA (17 ± 1 %, _n_= 32, lower circle in Fig. 3_D_, left-hand panel) or dimethyl BAPTA (18 ± 1 %, _n_= 23, lower square in Fig. 3_D_, left-hand panel) was used to deplete the stores instead. The average duration of the slow phase was 51 ± 3 s for EGTA, 47 ± 3 s for BAPTA and 40 ± 3 s for dimethyl BAPTA. Similarly, the slow phase developed at an approximately constant rate (-9 ± 0.5 fA (pF s)−1, _n_= 97) and this was not changed by either the concentration of the Ca2+ chelator or its nature (Fig. 3_A-D_, right-hand panels).
The average duration of the fast phase was 80 ± 5 s for EGTA, 81 ± 7 s for BAPTA and 58 ± 5 s for dimethyl BAPTA. For EGTA, the fast phase had an amplitude that was 69 ± 1 % (_n_= 47) of the total current (upper triangle in Fig. 3_D_, left-hand panel). This contribution was also maintained when either BAPTA (70 ± 3 %, _n_= 33, upper circle in Fig. 3_D_, left-hand panel) or dimethyl BAPTA (67 ± 3 %, _n_= 26, upper square in Fig. 3_D_, left-hand panel) was used to deplete the stores instead. With EGTA, the rate of development of the second, fast phase (-19 ± 1 fA (pF s)−1, _n_= 47) was twice as fast as the slow phase and again this rate was not significantly different between the various EGTA concentrations that generated biphasic _I_CRAC (2.5 to 12.5 mm). The rates for the fast phase in BAPTA (-23 ± 2 fA (pF s)−1, _n_= 33) and dimethyl BAPTA (-25 ± 1 fA (pF s)−1, _n_= 26) were similar, although the overall level of variability was higher (Fig. 3_A-D_, right-hand panel).
Despite some slight differences, in general all the parameters analysed in this section were independent of either the nature of the Ca2+ chelator or of the concentration used. We therefore pooled all the currents with amplitudes smaller than -1 pA pF−1 (_n_= 39) and analysed their activation phase. Most of these cells were from experiments performed with 1 and 2.5 mm EGTA, and all of them (100 %) were monophasic. In these cells the activation phase acounts for 85 ± 2 % of the total _I_CRAC amplitude (Fig. 3_D_, left-hand panel), a value very close to the contribution of the slow and fast phase of the biphasic response, when they are considered together (87 %). Likewise, these monophasic currents develop, on average, in 158 ± 12 s at a mean current rate of -5 ± 0.5 fA (pF s)−1 (Fig. 3_D_, right-hand panel). Direct comparison of these values with those obtained for biphasic currents indicate that the monophasic response and the slow phase of the biphasic response correspond to the same phenomenon. Only for biphasic cells is a sort of ‘threshold’ reached and then the second fast phase is generated. This ‘threshold’ can be a consequence of an intrinsic component of the _I_CRAC activation mechanism and/or reflect the manner in which the stores are emptied. We tested the second hypothesis.
Phase-dependent roles for Ca2+ reuptake and Ca2+ leakage from the stores
Several factors govern the rate and extent of store emptying following dialysis with Ca2+ chelators. These include Ca2+ reuptake, Ca2+ leakage from the stores and the relative Ca2+ binding ratios of the cytosol and the lumen of the stores. However, considering that (1) the exogenous Ca2+ buffers, rather than the endogenous ones, will be the dominant cytoplasmic buffers under our conditions, (2) the intraluminal buffers have very low affinity for Ca2+, and therefore the Ca2+ binding ratio within the stores should be very low (around 10) when compared with the Ca2+ binding ratios of the internal solutions we have used (e.g. 16 670 for 2.5 mm EGTA) and (3) our results indicate that it is necessary to dialyse cells with a Ca2+-binding ratio> 16 670 to fully activate the current, the Ca2+ binding ratio can be ruled out as a rate-limiting factor for passive store emptying under our experimental conditions.
In order to determine roles for the two other factors (leak and reuptake) we compared the kinetics of development of _I_CRAC between passive depletion alone (10 mm EGTA), passive depletion in the presence of SERCA pump inhibitors (10 mm EGTA and either 100 μm cyclopiazonic acid (Inesi & Sagara, 1994) or 2 μm thapsigargin (Thastrup et al. 1989)) and rapid depletion using both Ins_P_3 and 10 mm EGTA together. We also attempted to block Ca2+ leakage from the stores by dialysing cells with 10 mm EGTA and either 1 mg ml−1 heparin, an inhibitor of the Ins_P_3 receptor (Ghosh et al. 1988), which fully inhibits Ins_P_3-mediated Ca2+ signalling in RBL cells (Parekh & Penner, 1995), or Ruthenium Red (100 μm), an inhibitor of intracellular Ca2+ release channels (Taylor & Broad, 1998). Both drugs, independently (data not shown) and in combination (_n_= 7, Fig. 4_B_ and C) failed to affect either the delay, the time to peak, the biphasic development of _I_CRAC, the rates of the fast and slow phases or the final extent of the current (Fig. 4_A_ (fourth trace), B and C). The leakage channels therefore do not correspond to either the Ins_P_3-gated or the ryanodine-sensitive ones.
Figure 4. The effects of SERCA pump inhibition on delay and rate of development of _I_CRAC.
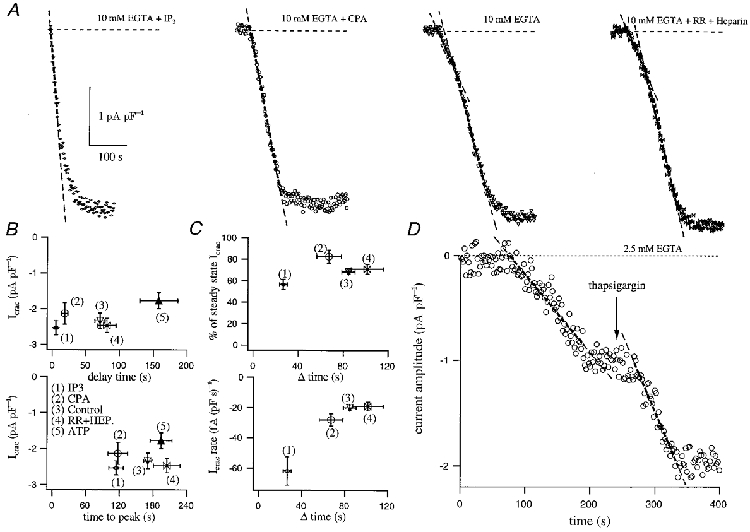
A compares the time course of development of _I_CRAC following dialysis with Ins_P_3 (IP3) + 10 mm EGTA (upper left), 10 mm EGTA + the SERCA blocker cyclopiazonic acid (CPA), 10 mm EGTA alone and 10 mm EGTA + heparin (HEP) + Ruthenium Red (RR). The delay before the current started as well as the time to peak are plotted against current amplitude for the various conditions in B. We analysed the fractional contribution of the fast phase of the current to the overall extent as well as its rate and these are plotted against their duration in C (upper and lower panels, respectively). D shows a cell which was dialysed with 2.5 mm EGTA and responded by generating monophasic _I_CRAC. Once the current had reached steady state, external application of the SERCA blocker thapsigargin both increased the size of the current and did so at a faster rate (dashed lines).
As shown in Fig. 4_A_, dialysis with 10 mm EGTA alone (_n_= 19) (third trace in Fig. 4_A_) activated _I_CRAC with the typical biphasic kinetics. Both the mean delay (71 ± 8 s) and the time to peak (170 ± 8 s) are shown in Fig. 4_B_. The second, faster component of the current accounted for 68 ± 2 % of the overall amplitude and developed at a rate of -20 ± 2 fA (pF s)−1 (Fig. 4_C_). Dialysis with Ins_P_3 and 10 mm EGTA (_n_= 14) resulted in an initially more rapid development of _I_CRAC, after a barely detectable delay (approximately 5 ± 2 s; Fig. 4_B_). In order to compare this rate of development directly with that evoked by passive depletion, we fitted the initial rate of development with a straight line. This was -62 ± 9 fA (pF s)−1, three times faster than the rate obtained with 10 mm EGTA alone (Fig. 4_A_ and C). The rapid phase was followed by a slower one which approached the steady-state amplitude exponentially. The fast phase accounted for 57 ± 5 % of the total amplitude of _I_CRAC (Fig. 4_C_). The slower second phase prolonged the overall duration of the development of the current, such that the time at which the current peaked was 114 ± 13 s after its onset (Fig. 4_C_).
When SERCA pumps were inhibited with either cyclopiazonic acid or thapsigargin (_n_= 6), the kinetics of _I_CRAC (activated by dialysis with 10 mm EGTA and the SERCA pump blocker) changed dramatically compared with 10 mm EGTA alone (Fig. 4_A_). Strikingly, the delay before the current activated now was significantly reduced by almost four-fold (to 18 ± 5 s, Fig. 4_B_). Importantly, the biphasic nature of the current, which was always seen with passive depletion using 10 mm EGTA, was not present in the majority of cells exposed to cyclopiazonic acid or thapsigargin (5 out 6 cells) (Fig. 4_A_). Instead, the rapid component developed almost straight away. It accounted for 83 ± 6 % of the overall amplitude of _I_CRAC but developed at a rate (-28 ± 4 fA (pF s)−1) similar to that seen with 10 mm EGTA alone (Fig. 4_C_, _P_= 0.075). Moreover, the time at which the current peaked 117 ± 17 s was not different to that seen with the combination of Ins_P_3 and 10 mm EGTA (Fig. 4_B_).
Assuming that Ca2+ leakage from the stores remains constant or at least does not increase when passive activation of _I_CRAC with millimolar concentrations of Ca2+ chelators is performed (which seems reasonable based on the findings of Hofer et al. 1996; Mogami et al. 1998), these results support the conclusion that SERCA pump activity is the rate-limiting factor that sets the delay before _I_CRAC activates under these conditions. Consistent with this notion, inclusion of 2 mm ATP in the recording pipette (together with 10 mm EGTA) substantially increased the delay (158 ± 28 s, _n_= 8) compared with control cells in which ATP was not present in the pipette (P < 0.001, Fig. 4_B_). However, dialysis with ATP did not affect the rate of development of the slow or fast phases nor did it change the fractional amplitude of either component (data not shown). Although we did not routinely include ATP in the recording pipette, glycolysis seems to provide sufficient ATP for the SERCA pumps to function (Mohr & Fewtrell, 1990), although probably not as effectively as they would with physiological concentrations of ATP (around 2 mm). Cytoplasmic ATP has been reported to increase Ca2+ leakage from the stores (Hofer et al. 1996), and hence one might expect it to accelerate the rate of store depletion and subsequent activation of _I_CRAC. Under our conditions, it appears that the enhanced SERCA pump activity in the presence of ATP dominates over a possible increase in leakage, rendering it harder to deplete the stores.
SERCA pump activity is also responsible for the final current amplitude of the small monophasic responses. Figure 4_C_ shows an example of a cell (_n_= 3 out of 5) that generated only a slowly developing monophasic _I_CRAC when dialysed with 2.5 mm EGTA. The current reached a submaximal steady state, at a rate typical for monophasic responding cells. External application of thapsigargin (4 μm), however, increased the amplitude of the current further, demonstrating that the submaximal _I_CRAC reflected a steady state between efflux from the stores and reuptake by SERCA pump activity. Strikingly, the rate at which _I_CRAC developed in the presence of thapsigargin was around twice (1.92 times) as fast as that in its absence, a ratio very close to that found between the rates for the fast and slow phases in biphasic responses (Fig. 4_B_). We therefore conclude that as soon the SERCA pumps are unable to take up Ca2+ into the stores or their efficiency becomes minimal, then the second fast phase is generated and this is determined mainly by Ca2+ leakage from the stores.
DISCUSSION
Our results shed new insight into the mechanism that underlies passive depletion of stores and subsequent activation of _I_CRAC. We have found that the current activates in either a monophasic or biphasic manner under these conditions, and this is dictated by the prevalent activity of SERCA pumps. The SERCA pumps determine which reponse type will be generated and can effectively attenuate the initial rate of development of _I_CRAC as well its final overall extent.
When passive depletion was performed with Ca2+ buffer concentrations from 2.5 mm, irrespective of the chelator used, the current showed the same behaviour. That is, a delay of around 73 ± 3 s (_n_= 145) elapsed before _I_CRAC started to activate and once it was activated, the activation time course was complex and consisted of at least two kinetically distinct phases. A slowly developing phase (duration of 47 ± 2 s, _n_= 97), probably reflecting low levels of store depletion due to a balance between Ca2+ efflux from the stores and immediate reuptake by SERCA pumps, was followed by a secondary rapid increase in current development (duration of 75 ± 3 s, _n_= 97), probably when reuptake was unable to compensate for leak. Leakage from the stores appears to be constant over a wide range of intraluminal Ca2+ concentrations (Hofer et al. 1996; Mogami et al. 1998) and therefore the switch from the slow phase to the fast phase of development of _I_CRAC seems to reflect an abrupt fall in SERCA pump activity. In agreement with this was the observation that the rate of development of the fast phase was unaffected by SERCA blockers (Fig. 4). Because similar results were obtained using either EGTA (_K_d of around 150 nm), BAPTA (_K_d of around 225 nm) and dimethyl BAPTA (_K_d 150 nm) (references in Results), this biphasic activation of the current was not a consequence of chelator affinity for Ca2+ nor of speed of Ca2+ binding.
Because the Ca2+ binding ratios of these chelator concentrations are 2 to 3.5 orders of magnitude larger than those found within the stores and that the leakage rate appears to be constant over a range of intraluminal Ca2+ concentrations (Hofer et al. 1996; Mogami et al. 1998), one might have expected low concentrations of chelators to be quite effective in activating _I_CRAC. This was not the case (Fig. 1_B_), and would appear to be due to the countering action of SERCA pumps because both the rate of development and size of the current could be subsequently increased by thapsigargin (Fig. 4_D_). We calculate a cytoplasmic Ca2+ concentration of roughly 3 nm with 1 mm EGTA and 0.3 nm with 10 mm EGTA, both of which are several orders of magnitude less than the measured intraluminal free Ca2+ within the stores (Hofer et al. 1996; Mogami et al. 1998). Despite this, 1 mm EGTA was much less effective in activating _I_CRAC than 10 mm. Hence passive depletion of stores is not determined simply by the Ca2+ gradient between stores and cytoplasm.
Perhaps the power of the SERCA pumps can best be seen in the following illustration. Concentrations of chelator ≤ 0.5 mm routinely failed to activate _I_CRAC at all. This corresponds to exogenous Ca2+ binding ratios of between 2000 and 5000 for the chelators we have employed. These are more than two orders of magnitude larger than the corresponding values thought to exist within the stores. In the presence of a constant leakage from the stores, the SERCA pumps are fully able to offset this discrepancy in Ca2+ binding ratios so that _I_CRAC does not activate at all. Because 1 mm EGTA activates a small _I_CRAC in a fraction of the cells, the pumps are in fact able to compensate a cytoplasmic Ca2+ binding ratio of almost 7000. A cartoon sketch summarising the interaction between Ca2+ leakage from the stores, cytoplasmic Ca2+ binding ratio and SERCA uptake is shown in Fig. 5.
Figure 5. Cartoon summary of interaction between leak and reuptake.
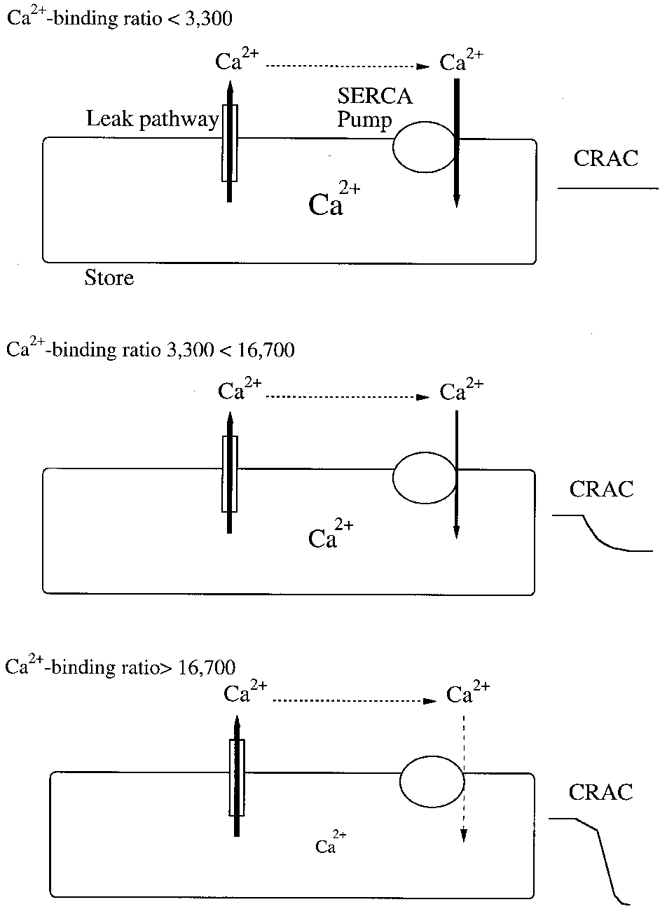
Top panel shows that Ca2+ efflux from the stores can be balanced by SERCA-mediated reuptake at a cytoplasmic Ca2+ binding ratio < = 3300 (corresponding to an EGTA concentration of < = 0.5 mm). Although the Ca2+ content of the stores may have fallen, _I_CRAC has not activated. Following exposure to moderate cytoplasmic buffers (0.5 to 2.5 mm, Ca2+ binding ratio 3300 to 16 700), SERCA pump activity decreases somewhat (depicted by the thinner arrow) and cannot fully compensate the continuous Ca2+ leakage from the stores. _I_CRAC activates to a submaximal extent and this is manifested as the typical monophasic current (middle panel). In the presence of high concentrations of chelators (> = 2.5 mm), pumps are initially operational, but then cease to function (dashed arrow). This results in full and uncompensated efflux of Ca2+ from the stores. Under these conditions, the majority of cells generate the biphasic _I_CRAC which develops to reach the maximal amplitude possible (bottom panel). In this model, we are considering only the effects of introducing Ca2+ chelators in their free form into the cytosol. Our analysis does not extend to the situation where mixtures of Ca2+-bound and free chelators are added simultaneously to clamp cytosolic Ca2+ at a predetermined value.
The estimated free Ca2+ concentrations in 1 and 10 mm EGTA are both well below the _K_d of the SERCA pump for Ca2+ (Pozzan et al. 1994), yet the pumps were operating rather well for 73 s in the presence of high EGTA and for several minutes in 1 mm EGTA. Even in the absence of ATP in the recording pipette and when cytosolic Ca2+ was strongly clamped at very low levels, SERCA pumps could adequately counter the leakage from the stores for several tens of seconds such that _I_CRAC did not activate. The reason why SERCA pumps are so effective, especially under these harsh conditions, is unclear. It is conceivable that the SERCA pumps in RBL cells have a very high affinity for cytosolic Ca2+ and can transport efficiently even when Ca2+ is extremely low. Alternatively, the pumps may be localised close to the leak channels and hence exposed to a higher local Ca2+ concentration than predicted from equilibrium conditions. Interestingly, the leak channels apparently transport Ca2+ at a rate only 4-5 times slower than maximal SERCA uptake (19 and 95 μm min−1; Mogami et al. 1998), and hence a low chelator concentration might not be able to fully suppress the Ca2+ signal close to the site of release when pumps are not operating at their maximal efficiency. Finally, the pumps may increase their activity in an attempt to compensate for the reduction in intraluminal Ca2+, as recently shown for pancreatic acinar cells (Mogami et al. 1998).
The biphasic development of _I_CRAC that we have seen with passive store depletion is not apparent when the stores are emptied with either Ins_P_3 or ionomycin in the presence of high EGTA concentrations. This probably reflects the fact that the efflux pathways activated by these agents (Ins_P_3-gated channels and ionophore-mediated transport) are large and sustained and hence the stores will be emptied rapidly. Both the monophasic and biphasic kinetics that we have observed with Ca2+ chelators require efflux from the stores (reflecting the endogenous leak pathway) to be relatively slow. Alterations in SERCA pump expression as well as their transport rates may therefore provide an effective way to control the rate of development of _I_CRAC.
We observed that submaximal _I_CRAC evoked by a low chelator concentration developed slowly, but further stimulation could accelerate the rate of activation and the amplitude of the current (see Fig. 4_B_, for example). Furthermore, a given stimulus was capable of evoking a range of _I_CRAC amplitudes and different stimuli could activate the current at different rates. Although we have not directly measured the Ca2+ concentration within the stores, our results are compatible with the notion that the Ca2+ sensor within the stores is able to respond in a gradual and apparently continuous manner, once the current starts to develop. This is consistent with previous studies that have demonstrated graded _I_CRAC to a non-metabolisable analogue of Ins_P_3 (Parekh et al. 1997; Huang & Putney, 1998), and a graded relationship between the fall in luminal Ca2+ and the rate of Ca2+ entry, monitored indirectly using fura-2 (Hofer et al. 1998).
Acknowledgments
This work was supported by the Wellcome Trust (grant no. 049236/Z/96/Z to A.B.P.). A.B.P. is the E. P. Abraham Research Fellow at Keble College, Oxford. We thank Professor Criss Hartzell for comments on the manuscript.
References
- Fasolato C, Pizzo P, Pozzan T. Delayed activation of the store-operated calcium current induced by calreticulin overexpression in RBL-1 cells. Molecular Biology of the Cell. 1998;9:1513–1522. doi: 10.1091/mbc.9.6.1513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fierro L, Parekh AB. The effects of interfering with GTP-binding proteins on the activation mechanism of calcium release-activated calcium current. Pflügers Archiv. 1999;437:547–552. doi: 10.1007/s004240050816. [DOI] [PubMed] [Google Scholar]
- Ghosh TK, Eis PK, Mullaney JM, Ebert CL, Gill DL. Competitive, reversible, and potent antagonism of inositol 1,4,5-trisphosphate-activated calcium release by heparin. Journal of Biological Chemistry. 1988;263:11075–11079. [PubMed] [Google Scholar]
- Hamill OP, Marty A, Neher E, Sakmann B, Sigworth F. Improved patch clamp techniques for high-resolution current recordings from cells and cell-free membrane patches. Pflügers Archiv. 1981;391:85–100. doi: 10.1007/BF00656997. [DOI] [PubMed] [Google Scholar]
- Harrison SM, Bers DM. The effect of temperature and ionic strength on the apparent Ca-affinity of EGTA and the analogous Ca-chelators BAPTA and dibromo-BAPTA. Biochimica et Biophysica Acta. 1987;925:133–143. doi: 10.1016/0304-4165(87)90102-4. [DOI] [PubMed] [Google Scholar]
- Hofer AM, Curci S, Machen TE, Schulz I. ATP regulates calcium leak from agonist-sensitive internal calcium stores. FASEB Journal. 1996;10:302–308. doi: 10.1096/fasebj.10.2.8641563. [DOI] [PubMed] [Google Scholar]
- Hofer A, Fasolato C, Pozzan T. Capacitative Ca2+ entry is closely linked to the filling state of internal Ca2+ stores: a study using simultaneous measurements of ICRAC and intraluminal Ca2+ Journal of Cell Biology. 1998;140:325–334. doi: 10.1083/jcb.140.2.325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoth M, Penner R. Depletion of intracellular calcium stores activates a calcium current in mast cells. Nature. 1992;355:353–356. doi: 10.1038/355353a0. [DOI] [PubMed] [Google Scholar]
- Hoth M, Penner R. Calcium release-activated calcium current in rat mast cells. The Journal of Physiology. 1993;465:359–386. doi: 10.1113/jphysiol.1993.sp019681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y, Putney JW., Jr Relationship between intracellular calcium store depletion and calcium release-activated calcium current in a mast cell line (RBL-1) Journal of Biological Chemistry. 1998;273:19554–19559. doi: 10.1074/jbc.273.31.19554. [DOI] [PubMed] [Google Scholar]
- Inesi G, Sagara Y. Specific inhibitors of intracellular Ca2+ transport ATPase. Journal of Membrane Biology. 1994;141:1–6. doi: 10.1007/BF00232868. [DOI] [PubMed] [Google Scholar]
- Kerschbaum HH, Cahalan MD. Single-channel recording of a store-operated Ca2+ channel in Jurkat T lymphocytes. Science. 1999;283:836–839. doi: 10.1126/science.283.5403.836. [DOI] [PubMed] [Google Scholar]
- Martell AE, Smith RM. Critical Stability Constants. Vol. 1. New York: Plenum Press; 1974. [Google Scholar]
- Mogami H, Tepikin AV, Petersen OH. Termination of cytosolic Ca2+ signals: Ca2+ reuptake into intracellular stores is regulated by the free Ca2+ concentration in the store lumen. EMBO Journal. 1998;17:435–442. doi: 10.1093/emboj/17.2.435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohr FC, Fewtrell C. The effect of mitochondrial inhibitors on calcium homeostasis in tumor mast cells. American Journal of Physiology. 1990;258:C217–226. doi: 10.1152/ajpcell.1990.258.2.C217. [DOI] [PubMed] [Google Scholar]
- Neher E. The use of Fura-2 for estimating Ca2+ buffers and Ca2+ fluxes. Neuropharmacology. 1995;34:1423–1442. doi: 10.1016/0028-3908(95)00144-u. [DOI] [PubMed] [Google Scholar]
- Parekh AB, Fleig A, Penner R. The store-operated calcium current ICRAC: Nonlinear activation by InsP3 and dissociation from calcium release. Cell. 1997;89:973–980. doi: 10.1016/s0092-8674(00)80282-2. [DOI] [PubMed] [Google Scholar]
- Parekh AB, Penner R. Activation of store-operated calcium influx at resting InsP3 levels by sensitization of the InsP3 receptor in rat basophilic leukaemia cells. The Journal of Physiology. 1995;489:377–382. doi: 10.1113/jphysiol.1995.sp021058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parekh AB, Penner R. Store depletion and calcium influx. Physiological Reviews. 1997;77:901–930. doi: 10.1152/physrev.1997.77.4.901. [DOI] [PubMed] [Google Scholar]
- Pethig R, Kuhn M, Payne R, Adler E, Chen TH, Jaffe L. On the dissociation constants of BAPTA-type calcium buffers. Cell Calcium. 1989;10:491–498. doi: 10.1016/0143-4160(89)90026-2. [DOI] [PubMed] [Google Scholar]
- Pozzan T, Rizutto R, Volpe P, Meldolesi J. Molecular and cellular physiology of intracellular calcium stores. Physiological Reviews. 1994;74:595–636. doi: 10.1152/physrev.1994.74.3.595. [DOI] [PubMed] [Google Scholar]
- Putney JW. A model for receptor-regulated calcium entry. Cell Calcium. 1986;7:1–12. doi: 10.1016/0143-4160(86)90026-6. [DOI] [PubMed] [Google Scholar]
- Taylor CW, Broad L. Pharmacological analysis of intracellular Ca2+ signalling: Problems and pitfalls. Trends in Pharmacological Sciences. 1998;19:370–375. doi: 10.1016/s0165-6147(98)01243-7. [DOI] [PubMed] [Google Scholar]
- Thastrup O, Dawson AP, Scharff O, Foder B, Cullen PJ, Drobak BK, Bjerrum PJ, Christensen SB, Hanley MR. Thapsigargin, a novel molecular probe for studying intracellular calcium release and storage. Agents and Actions. 1989;27:17–23. doi: 10.1007/BF02222186. [DOI] [PubMed] [Google Scholar]