Scoring profile-to-profile sequence alignments (original) (raw)
Abstract
Sequence alignment profiles have been shown to be very powerful in creating accurate sequence alignments. Profiles are often used to search a sequence database with a local alignment algorithm. More accurate and longer alignments have been obtained with profile-to-profile comparison. There are several steps that must be performed in creating profile–profile alignments, and each involves choices in parameters and algorithms. These steps include (1) what sequences to include in a multiple alignment used to build each profile, (2) how to weight similar sequences in the multiple alignment and how to determine amino acid frequencies from the weighted alignment, (3) how to score a column from one profile aligned to a column of the other profile, (4) how to score gaps in the profile–profile alignment, and (5) how to include structural information. Large-scale benchmarks consisting of pairs of homologous proteins with structurally determined sequence alignments are necessary for evaluating the efficacy of each scoring scheme. With such a benchmark, we have investigated the properties of profile–profile alignments and found that (1) with optimized gap penalties, most column–column scoring functions behave similarly to one another in alignment accuracy; (2) some functions, however, have much higher search sensitivity and specificity; (3) position-specific weighting schemes in determining amino acid counts in columns of multiple sequence alignments are better than sequence-specific schemes; (4) removing positions in the profile with gaps in the query sequence results in better alignments; and (5) adding predicted and known secondary structure information improves alignments.
Keywords: sequence profiles, profile–profile alignment, PSI-BLAST
The goal of homology modeling (also known as comparative modeling) is to build an accurate three-dimensional model of a protein of unknown structure from the experimentally determined structure of one or more evolutionarily related proteins. This requires identifying proteins of known structure homologous to the target sequence and producing accurate and complete sequence–structure alignments between them. Even when identifying the correct homolog is accomplished, sufficient alignment quality is often still a challenge when the sequence identities fall below 30% (Sauder et al. 2000).
Accurate sequence alignment between a target sequence and a parent structure to be used as template for modeling is now usually determined with the help of other protein sequences related to both target and parent sequence. Such multiple sequence information is often represented in some form of profile, a matrix of dimensions 20 × L (or 21 × L if information on gaps is contained in the profile), where L is usually the length of the target or query sequence. The profile contains information on the proportion of each amino acid in each column of a multiple sequence alignment of proteins related to the query sequence. Profiles were originally proposed by Gribskov et al. (1987) as a means for database search. They proposed that profiles could be constructed both from related sequences and using structural information to determine which amino acids were likely at each position of a known structure and to determine position-specific gap penalties. Somewhat later they also proposed using secondary-structure-specific substitution matrices and including surface accessibility in determining the profile (Luthy et al. 1991).
The use of profiles has greatly accelerated with the development of the PSI-BLAST program by Altschul et al. (1997). PSI-BLAST uses heuristics to search protein databases rapidly for sequences with good alignment scores to a query sequence. From these sequences and a pairwise amino acid substitution matrix (Henikoff and Henikoff 1993), a profile is constructed that contains the log-odds scores (relative to database frequency) of each amino acid at each position of the query sequence. This profile matrix is then used to search the same database again, but now the position-specific scores are used to evaluate alignments instead of pairwise amino acid comparisons. High-scoring sequences in the second round are used to build a new profile, and the iteration continues.
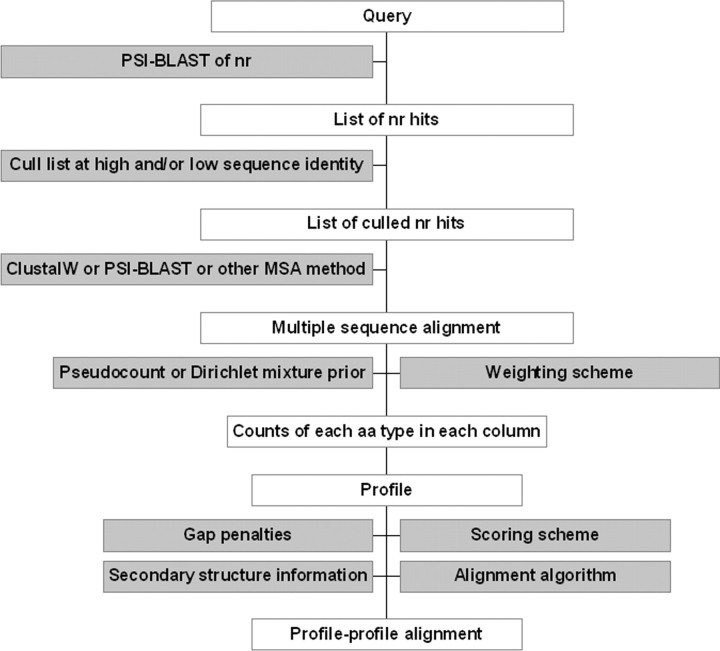
A generalization of profile-to-sequence database searches and alignments was proposed by Pietrokovski (1996). Instead of searching a database of sequences, one can create a database of profiles from the sequence database, each of which contains information on a protein family. This profile database can now be searched with a profile constructed from a query protein family of interest using profile-to-profile alignments. Several groups have published profile-to-profile alignment methods (Pietrokovski 1996; Rychlewski et al. 1998, 2000; Yona and Levitt 2002; Panchenko 2003; Sadreyev and Grishin 2003; von Öhsen and Zimmer 2003; von Öhsen et al. 2003). Most of these use the standard Smith-Waterman local alignment method (Smith and Waterman 1981), but they vary significantly in a number of important respects. A schematic of the profile–profile alignment procedure is shown in Figure 1 ▶.
Figure 1.
Scheme for profile–profile alignments.
The first of these is the procedure used to generate the initial profile. PSI-BLAST is usually used to search a large database of sequences, such as the nonredundant protein sequence database from NCBI (Wheeler et al. 2004). Some authors use multiple sequence alignments that can be generated by PSI-BLAST and derive a profile in the form of frequencies or log-odds from these alignments. Others use the log-odds profile generated by PSI-BLAST directly. In either case, building the profile entails choices of what sequences to include and how (how many rounds of PSI-BLAST, what _E_-value cutoffs, sequence weighting schemes [Henikoff and Henikoff 1994], etc.) and whether to use a substitution matrix or Dirichlet mixture (Sjolander et al. 1996) to augment the observed amino acid counts. The form of the profile also varies in terms of whether gaps are represented in each column (i.e., each position of the query or template sequence), and whether gaps in the query or template sequence are represented (i.e., columns that have a gap character in the generating query sequence).
The second major variation is the method for scoring the alignment of one column of the query profile against a column from a database or template profile. It is, in fact, rather surprising that there is no consensus on how this should be done, from either a theoretical or practical point of view. The methods include correlation coefficients, Euclidean distances (Pietrokovski 1996), sums over substitution matrices weighted by the query and template frequencies (von Öhsen and Zimmer 2003), scores based on information theory (Yona and Levitt 2002), and dot products of log-odds scores with log-odds scores (Pietrokovski 1996), frequencies with frequencies (Rychlewski et al. 2000), or frequencies or amino acid counts with log-odds scores (Sadreyev and Grishin 2003). With the Smith-Waterman algorithm (Smith and Waterman 1981), pairwise scores must on average be negative with the maximum score positive. Some scoring functions require a shift so that the Smith-Waterman algorithm can identify common regions as completely as possible without aligning unrelated regions, and this is discussed in some publications on profile–profile scoring methods.
A third variation occurs for gap penalties. Some methods, such as the BLOCKS database alignments of Pietrokovski (1996) and the core alignment method (Panchenko et al. 1999) used by Panchenko (2003), do not require gap penalties. A recent paper by Mittelman et al. (2003) investigated the different column–column scoring functions in generating short ungapped alignments. But local and global dynamic programming methods do require a gap penalty that must be carefully set to produce reasonable alignments. These parameters are usually optimized on a training set to go with the chosen column–column scoring function. Because the predominant use of profile–profile alignments is to generate a sequence–structure alignment, it is usually the case that a structure is known for the sequence used to build one of the profiles. From this structure, one can use the secondary structure as well as surface accessibility information.
Finally, profile–profile alignment is used to search databases of profiles, usually derived from sequences of known structure in the PDB, and to produce accurate sequence–structure alignments of the query sequence and template structure. Methods should therefore be tested both for their search sensitivity and specificity as well as their alignment accuracy and completeness. The size of benchmarks used and whether both search and alignment accuracy have been examined also vary among published methods.
In this paper, we explore some alternatives in each category described above with a large benchmark of structurally aligned protein pairs. We examine five issues: (1) seven different scoring functions for comparing two profile columns; (2) how to optimize gap penalties; (3) weighting schemes; (4) whether including fewer or more divergent sequences in each profile is helpful; and (5) whether adding a secondary-structure substitution matrix is beneficial. The benchmark we have derived is larger than most used in previously published profile–profile methods. This is necessary given the large variance in search efficacy and alignment accuracy each method exhibits over a test set.
Materials and methods
Test set
From SCOP 1.48 (Murzin et al. 1995), we derived a nonredundant subset in terms of sequence identity, scop148_40, in which no pair of sequences share >40% sequence identity. Domain definitions in this older version of SCOP are the same as more recent versions except for a small handful of proteins. Both the CE (Shindyalov and Bourne 1998) and DALI (Holm and Sander 1993) programs were used to create two sets of all possible family and superfamily (as defined by SCOP) pairwise structural alignments within scop148_40. With all DALI and CE alignments in hand, we used the following procedure to build a benchmark data set:
- For each protein structure alignment, we calculated the consensus alignment rates between DALI and CE, R = 2_N_both/(_N_CE + _N_DALI). Here _N_both is the number of aligned pairs in common between the CE and DALI alignments, and _N_CE and _N_DALI are the numbers of aligned residue pairs in the CE and DALI alignments, respectively. We calculated the average sequence identity of CE and DALI alignments, _ID_¯ = (_ID_CE + _ID_DALI)/2.
- All alignment pairs with _ID_¯ > 40% were discarded.
- Alignment pairs were selected for the test set from the remaining pairs with the following criteria: (a) R ≥ 0.9 or (b) consensus structural alignment length (_N_both) is >100, and the alignment length difference between CE and DALI is <20% of the average length of the CE and DALI alignments.
- We added some alignment pairs manually to compensate for low numbers at low sequence identity or for some SCOP families or superfamilies by relaxing the limitations used in step 3. In all cases, the consensus alignment length is greater than 40, and no pair with R < 0.5 is included in the data set.
The resulting data set contains 3441 alignment pairs, involving 1627 sequences that belong to 374 SCOP families and 128 superfamilies. The sequence identity range is 0%–35%. We call this group of alignments Set A (for “Accuracy”). About one-third of the pairs in Set A were selected randomly to be used as a training set (1136 pairs), with the rest serving as a testing set (2305 pairs).
To evaluate the database searching selectivity and sensitivity, we constructed Set S (for “search”), which was derived from Set A by using the following criteria: No more than two sequences in this data set belong to the same SCOP family, and no more than 10 sequences are from the same superfamily. Set S contains 665 sequences comprising 441,560 alignment pairs (in both directions). Of these, 3320 pairs are true positives, and all others are false positives. True positives were defined in such a way that either both sequences in the alignment belong to the same SCOP fold designation or they are both classified in SCOP as Rossmann-like folds. The Rossmann-like fold consists of a parallel β-sheet in the order 32145, often decorated by varying numbers of α-helices and additional sheet strands. In SCOP 1.48, there are 25 different folds annotated as Rossmann-like fold, and many of these are putatively homologous (Sadreyev and Grishin 2003).
Profile generation
PSI-BLAST (Altschul et al. 1997) was used to build multiple alignments through database searching. We used PSI-BLAST in two ways to build multiple sequence alignments. The first method was accomplished by searching a version of the nonredundant protein sequence database (Wheeler et al. 2004), nr, with low-complexity segments masked with the seg program (Wootton 1994; length parameter = 20) for five rounds with an _E_-value cutoff for both printing and inclusion in the position-specific scoring matrix of 0.002. The multiple sequence alignment was taken from the final round. We call these Last Round profiles.
Because the initial multiple alignment from PSI-BLAST usually contains many very closely related sequences, we culled the multiple alignments using a mutual sequence identity of 98% (PSI-BLAST culls sequences that are 98% identical or more to the query only). On the other hand, a PSI-BLAST multiple alignment may also contain very distantly related sequences. These sequences may create “noise” in building the profile, either because they are false positives, or because they are poorly aligned to the other sequences in the multiple alignment. We therefore created another set of multiple alignments in which not only redundant sequences were removed from the alignment, but also very distantly related sequences (sequence identity to query <15%) were also removed. We call these Cut Low Ident profiles.
Weighting schemes
An important step in building a profile from a multiple alignment is weighting each sequence in the alignment. We tested three well-established weighting schemes: (1) the Henikoff weighting scheme (Henikoff and Henikoff 1994), which is used in PSI-BLAST and many other profile-related applications; (2) PSIC weighting (Sunyaev et al. 1999), which is used in the COMPASS profile–profile alignment algorithm (Sadreyev and Grishin 2003); (3) an FFAS-like weighting scheme (Rychlewski et al. 2000) that we label Seq Divergence weighting.
In Henikoff weighting, for an amino acid at position m of sequence i, we first determine the subset of sequences that also have an amino acid in the same column of the multiple alignment. Each sequence in this subset may begin and end in different columns of the multiple alignment. We find the first column in which all of these sequences in the subset are represented either with an amino acid or an internal gap (i.e., excluding N- and C-terminal gaps). We call this _C_left. Similarly, we identify the last column of this subset in which all of these sequences are represented either with an amino acid or an internal gap. We call this _C_right. The weight of the amino acid at position m of sequence i is then
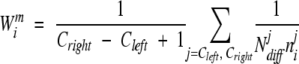 |
(1) |
|---|
where N jdiff is the number of different amino acids at alignment position j but considering only those sequences in the subset, and _n_ij is the total number of the same amino acid type as the residue of sequence i in alignment column j in the subset.
In PSIC weighting, the weight of sequence i at alignment position m with amino acid type a(i) is
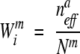 |
(2) |
|---|
where _N_m is the number of sequences that have amino acid a(i) at position m, n aeff is the effective count of amino acid a(i) at that position,
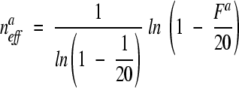 |
(3) |
|---|
where _F_a is the average number of different amino acid types per position in the sequences that have residue type a(i) at position m. To calculate _F_a, we use a similar procedure as with the Henikoff weighting. For PSIC, the subset is defined differently. It now includes only those sequences that have the same amino acid as sequence i, not all sequences that have an amino acid in the column. Once we have the subset of sequences, _C_left and _C_right are defined in the same way as in Henikoff weighting above. _F_a is then the number of different amino acids averaged over the columns from _C_left and _C_right, inclusive.
In the SeqDivergence weighting scheme, the weight of sequence i is
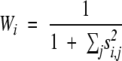 |
(4) |
|---|
where _s_i,j is the similarity score of sequences i and j,
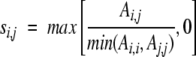 |
(5) |
|---|
and _A_i,j is the alignment score of sequence i and j calculated with the BLOSUM62 mutation matrix.
It should be noted that the Henikoff weighting method assigns the same weights to amino acids in a sequence that form the same subset, regardless of the different amounts of variation in each column. PSIC, on the other hand, assigns lower weights if many sequences have the same amino acid at a particular position. Whereas Henikoff and PSIC assign weights that vary along the sequence, SeqDivergence assigns a constant weight for each whole sequence.
We calculate “target” frequencies of the 20 amino acids at each position from the observed counts weighted with each weighting scheme listed above using the pseudocount method used in PSI-BLAST (Altschul et al. 1997). However, the Seq Divergence weighting scheme calculates these target frequencies by adding the “balanced family profile frequencies” (Rychlewski et al. 2000):
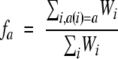 |
(6) |
|---|
where _f_a is the weighted fraction of amino acid type a (or gap) in the sequences aligned at a given position, _W_i is the weight of sequence i, and a(i) is the amino acid type in sequence i at this position. From CE structural alignments and following Rychlewski et al., we calculate the probability of a mutation from amino acid b to a (or deletion) _p_b,a, and then we use a pseudocount method to obtain amino acid target frequencies in a given position as
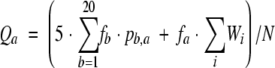 |
(7) |
|---|
where N is a normalization coefficient that ensures that
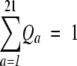
For the other methods we use the pseudocount method used in PSI-BLAST (Altschul et al. 1997) to calculate the amino acid target frequency at the given position.
Scoring functions
One of our goals is to test whether the choice of scoring function for aligning positions in two profiles affects sequence alignment accuracy and searching sensitivity and specificity. We implemented several scoring functions already discussed in the literature (Pietrokovski 1996; Rychlewski et al. 2000; Yona and Levitt 2002; Sadreyev and Grishin 2003; von Öhsen and Zimmer 2003; von Öhsen et al. 2003). The functions we have tested are very similar to those tested by Mittleman et al. (2003) in gapless profile–profile alignment tests.
Sum of pairs
These scoring functions use the summation of the products of frequencies for both columns for every combination of amino acid a and b. There are two variants of this function: one (Cross Product) multiplies the products by the corresponding log-odds elements of the substitution matrix BLOSUM62, _s_ab:
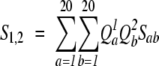 |
(8) |
|---|
The other function (Log Average) multiplies the products by the corresponding BLOSUM62 matrix amino acid substitution frequencies, _q_ab, and takes the logarithm to get the final profile–profile alignment scores (von Öhsen and Zimmer 2003; von Öhsen et al. 2003):
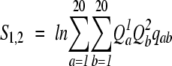 |
(9) |
|---|
_q_ab is the BLOSUM62 matrix frequency (calculated from the standard log-odds form) of amino acid a being aligned to amino acid b.
Dot product
This is the summation of the products of the frequencies or log-odds values for both columns. Two functions in this family have been tested, one (Dot P Freq) computes the product using frequencies:
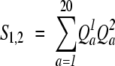 |
(10) |
|---|
and the second function (Dot P Odds) calculates the dot product using log-odds values:
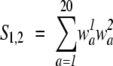 |
(11) |
|---|
where
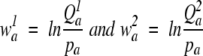
are log-odds values with _p_a as the background frequency of amino acid a.
Pearson’s correlation coefficient (CORREL)
This function was used in the LAMA method for profile–profile comparison (Pietrokovski 1996):
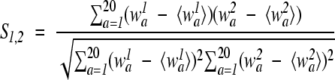 |
(12) |
|---|
Jensen-Shannon function
This score function, Jensen Shannon, was introduced by Yona and Levitt (2002). It involves the calculation of a divergence score and a significance score. The divergence score D is computed using the equation
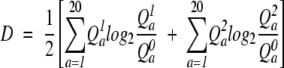 |
(13) |
|---|
where
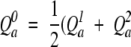
and the significance score S is calculated by
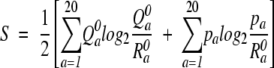 |
(14) |
|---|
where
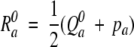
The final substitution score is the combination of the divergence score D and significance score S:
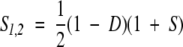 |
(15) |
|---|
Symmetric log-odds multinomial score
The score function used in COMPASS, Log Odds Multin, is a natural extension of PSI-BLAST for alignments of profiles with profiles (Sadreyev and Grishin 2003):
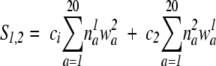 |
(16) |
|---|
where _n_a 1 and _n_a 2 are the effective counts for each amino acid in columns 1 and 2, which are calculated with the following formula (Pei et al. 2003; Sadreyev and Grishin 2003):
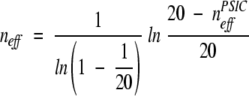 |
(17) |
|---|
And _c_1 and _c_2 are weighting parameters to balance the contribution of the two terms in the formula:
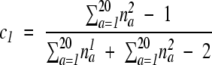 |
(18) |
|---|
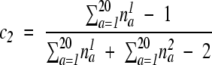 |
(19) |
|---|
A very similar function was suggested to us by Stephen Altschul (pers. comm.) in 2001.
Gap penalty and zero-shift parameters optimization
We use the Smith-Waterman local alignment algorithm to align profiles (Smith and Waterman 1981). This algorithm requires the average score between random pairs of positions from the two profiles to have a negative score, so that alignments do not extend into unrelated regions of the two profiles. Some of the scores described above yield only positive scores and therefore require a “zero-shift.” We used Set A as a training set of pairwise structure alignments to optimize the gap penalty parameters and zero-shift value in terms of alignment accuracy with respect to CE structural alignments.
Three parameters were used to monitor the alignment quality: _Q_Modeler, _Q_Developer, and _Q_Combined. _Q_Modeler and _Q_Developer were first introduced by us in Sauder et al. (2000) as _f_M and _f_D, standing for the quality of the alignment from a modeler’s point of view and the quality from a developer’s point of view. These values were renamed and used by Yona and Levitt (2002) and by Sadreyev and Grishin (2003), who used the Yona-Levitt names. We use the newer names here for sake of consistency with the later papers. _Q_Modeler is the fraction of correctly aligned positions in the profile–profile alignment, and _Q_Developer is the fraction of correctly aligned positions in the structural alignment. That is,
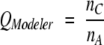 |
(20) |
|---|
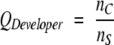 |
(21) |
|---|
where _n_C is the number of aligned pairs in common between the sequence and structure alignments, _n_A is the number of aligned pairs in the sequence (or profile–profile) alignment, and _n_S is the number of aligned pairs in the structure alignment. _Q_Modeler penalizes sequence alignments that are too long; that is, when _n_A ≫ _n_S. _Q_Developer penalizes sequence alignments that are too short; that is, when _n_A ≪ _n_S. Taken together, they give a picture of the good and bad features of a sequence alignment method. Yona and Levitt introduced another parameter, _Q_Combined, that penalizes sequence alignments that are either too long or too short. It is defined as
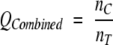 |
(22) |
|---|
where _n_T is the total number of unique alignment pairs in either the sequence or structure alignment or both. If a pair of residues is aligned in both the sequence and structure alignments, it is only counted once in _n_T. We have found that _Q_Combined is more useful as a parameter for optimizing gap parameters than either _Q_Modeler or _Q_Developer. Optimization based on _Q_Modeler results in very short alignments of the most highly conserved regions and hence low _Q_Developer scores, whereas optimization on _Q_Developer results in very long alignments often with low _Q_Modeler scores.
We optimized the gap penalties using _Q_Combined as the target function for several of the scoring schemes described above. For each scheme, we need to determine the optimal combination of zero-shift parameter and gap-open and gap-extension parameters. We optimized parameters on a combination of five gap-open values, five zero-shift values, and three gap-extension values, for a total of 75 sets. Gap-open candidates were determined based on the variation scale of column–column alignment scores; zero-shift candidates were assigned according to the average column–column score; and three gap-extension candidates were selected as 0.1, 0.075, and 0.05 × gap-open. If the best parameters (in terms of _Q_Combined) included one at the extremes of its range, then additional values beyond that extreme were tested. The resulting gap parameters are subsequently referred to as Full Opt Gaps.
This process of optimizing the parameters for each individual pair function by testing the whole training set on 75 parameter sets is very time-consuming. Rychlewski et al. (2000) have introduced a protocol for determining gap penalties and zero-shift parameters in their FFAS profile–profile alignment method by transforming column–column scores into the standard normal (μ = 0; σ = 1) distribution, and determining the gap penalties for scores that follow a standard normal distribution. We compared the results of this protocol to the optimization over 75 parameter sets (see Results).
In the Results section, we call the gap parameters determined by this procedure Fitted Gaps. In this procedure, every aligned pair has its own transformation as follows: First, the _L_1 columns of profile 1 are compared with the _L_2 columns of profile 2 using a particular scoring scheme (Cross Product, Jensen-Shannon, etc.), and the average μ and standard deviation σ of the _L_1 × _L_2 scores are calculated. The score for any pair of columns _S_1,2 is then transformed to the standard normal distribution:
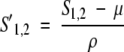 |
(23) |
|---|
The scoring function used to align the two profiles includes a constant zero-shift term to produce an average score that is negative:
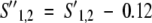 |
(24) |
|---|
The gap penalties as well as the zero-shift value used in this scheme are those provided by Rychlewski et al. (2000), optimized on the UCLA-DOE fold recognition benchmark (Fischer et al. 1996).
Gaps in profiles
PSI-BLAST produces profiles that are the length of the query sequence. That is, all columns in the multiple sequence alignment with a gap character in the query sequence are excluded from the profile. We used this method to create profiles we refer to as No Gaps In Query. We also created profiles that included these columns to test whether this procedure improves alignments of search selectivity. In the Results section, these profiles are referred to as Gaps In Query profiles.
Adding secondary structure similarity measures
A secondary structure substitution matrix was determined for use in profile–profile alignments as follows: Because the primary purpose for profile–profile alignments is usually to determine distant relationships between proteins of unknown structure and those of known structure, we have determined an asymmetric substitution matrix between predicted secondary structures and known structures. A similar substitution matrix for predicted versus experimental secondary structures has been used by Ginalski et al. (2003) in their ORFEUS server. Secondary structure for the proteins in Set A was predicted from output profiles from the last round of PSI-BLAST using the PSI-PRED program (Jones 1999), and the experimental secondary structures were determined from the corresponding PDB files with the program Stride (Frishman and Argos 1995). The substitution matrix was determined using a standard procedure (Henikoff and Henikoff 1993) from the structure alignments of proteins in Set A as determined by the program CE.
To use the secondary structure substitution matrix, we need to balance this matrix with the column–column scores for each scoring scheme. First, both the column–column scores and the secondary structure scores were adjusted to the standard normal distribution, as in the equation for _S_1,2 above. Second, we set the fraction of column–column score and secondary structure score from x of 0.50 to 0.90 in steps of 0.05:
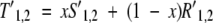 |
(25) |
|---|
where T is the total score and R is the secondary-structure matrix substitution score. This score is then shifted to the standard normal, and the zero-shift of 0.12 is used to produce the final score.
Results
Comparing seven functions
We compared the alignment accuracy and search sensitivity and specificity of seven profile–profile scoring schemes proposed previously. These scoring schemes are all functions of the frequencies in columns of multiple alignments of proteins in a particular family. These seven scoring functions are: (1) Cross Product, which is a sum over all pairs of amino acid types (20 × 20 = 400) from the two profiles of the frequencies multiplied by the log-odds score for that pair from the BLOSUM matrix; (2) Log Average (von Öhsen and Zimmer 2003; von Öhsen et al. 2003) uses the sum over the 400 products of the profile frequencies times the substitution frequency in the BLOSUM matrix, and then takes the log of this sum; (3) Dot P Freq is the dot product of the profile frequency vectors; (4) Dot P Odds is the dot product of the log-odds of the frequencies from the two profiles; (5) Correl (Pietrokovski 1996) is the Pearson’s correlation coefficient on the log-odds from the profile; (6) Jensen Shannon (Yona and Levitt 2002) is the Jensen-Shannon entropy of the profile; (7) Log Odds Multin (Sadreyev and Grishin 2003) uses the dot products of amino acid counts from one profile with the log-odds of the other profile.
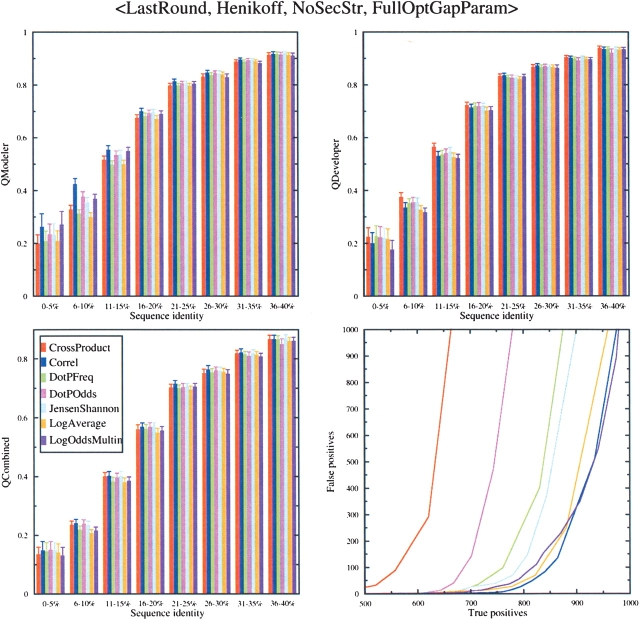
To compare these scoring functions fairly, we optimized the gap-open, gap-extension, and zero-shift parameters for each scheme independently of the others. We optimized the gap parameters based on the value of _Q_Combined, as described in Materials and Methods. _Q_Combined is the fraction of correct pairs aligned out of the total number of unique aligned pairs in either the predicted sequence alignment or structure alignment to which it is compared (Yona and Levitt 2002). The optimized parameters are listed in Table 1. A comparison of the alignment accuracy and search sensitivity-specificity for these functions is shown in Figure 2 ▶. At the top of the figure, other choices in the profile–profile alignment protocol that were used to generate the data in the figure are also listed. In the case of Figure 2 ▶, the Last Round multiple sequence alignments were used, the Henikoff weighting scheme was used, and no secondary structure information (No Sec Str) was included. In this figure and the subsequent figures, No Gaps In Query was used (see below). In Figure 2 ▶, we show the values of _Q_Modeler, _Q_Developer, and _Q_Combined as a function of sequence identity. _Q_Modeler is the fraction of correctly aligned pairs out of the number of aligned pairs in the predicted sequence alignment. _Q_Developer is the fraction of pairs in the structure alignment that are also aligned in the predicted sequence alignment.
Table 1.
Optimized parameters for scoring functions
| Function | Gap open | Gap extension | Zero shift |
|---|---|---|---|
| Cross Product | 0.81 | 0.06 | 0.92 |
| Correl | 1.39 | 0.07 | −0.21 |
| Dot P Freq | 0.07 | 0.005 | −0.05 |
| Dot P Odds | 226 | 11.3 | −42.2 |
| Jensen Shannon | 0.16 | 0.012 | −0.452 |
| Log Average | 0.45 | 0.033 | 0.06 |
| Log Odds Multin | 11 | 0.83 | 1.6 |
Figure 2.
Comparison of seven scoring functions for profile–profile alignment. Choices at specific stages of the alignment process are listed at the top of the figure and described in Materials and Methods. (Upper left) _Q_Modeler scores; (upper right) _Q_Developer scores; (lower left) _Q_Combined scores; (lower right) search capability as measured by the number of true positives vs. false positives. The legend given in the lower left figure applies to all four plots.
For _Q_Combined, the seven scoring functions all behave comparably at all levels of sequence identity, except perhaps the Log Average and Log Odds Multin functions, which perform at slightly lower accuracy at low sequence identity under these conditions (Last Round profiles, Henikoff weighting, No Sec Str). However, _Q_Modeler and _Q_Developer results show that for comparable values of _Q_Combined, the functions exhibit different behaviors. Some functions, such as Correl, Dot P Odds, Jensen Shannon, and Log Odds Multin, have shorter, more accurate alignments in terms of _Q_Modeler, and Correl and Log Odds Multin have lower values for _Q_Developer. Other functions may have lower _Q_Modeler, but longer alignments will produce higher _Q_Developer. The Cross Product function has the highest _Q_Developer. The results indicate that judging which scoring function is best depends on the criterion used.
The results for search specificity and sensitivity in Figure 2 ▶ (lower right panel) show that the searching abilities of the different functions differ significantly. The Log Odds Multin, Correl, and Log Average scoring functions perform significantly better than the other functions. For instance, Correl finds 850 true positives before the 100th false positive, compared with 560 for Cross Product.
We chose three functions for further analysis—the Log Odds Multin, Jensen Shannon, and Cross Product functions, because they perform well in at least one of the measures in Figure 2 ▶. Other functions could have been chosen.
Optimizing gap penalties and zero-shift parameter with the FittedGaps scheme
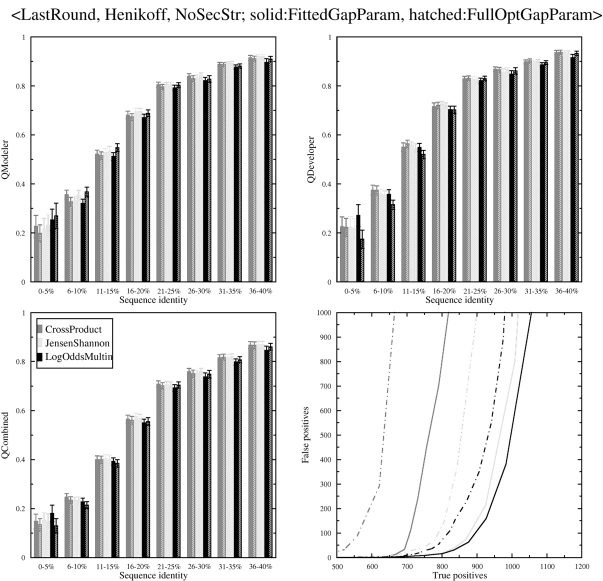
Because the parameter optimization is time-consuming and we wished to explore several other features of profile–profile alignment, we decided to test a method proposed by Rychlewski et al. (2000) for optimizing these parameters. They proposed establishing optimized gap and zero-shift parameters for column–column scores that follow a standard normal distribution with mean of 0.0 (without the zero-shift) and variance of 1.0, and normalizing any scoring system of interest to the standard normal. We tested this for the three functions we have chosen for further analysis, as shown in Figure 3 ▶. The standard-normal scheme works quite well, producing alignment quality in terms of _Q_Combined that is approximately equal to the fully optimized parameters over the full range of sequence identity. This was true without further optimization of the parameters proposed by Rychlewski et al. Starting from the parameters from Rychlewski et al., we optimized the parameters for each of the three scoring schemes. The best parameters were only slightly different from the Rychlewski parameters (data not shown). Whereas optimizing on _Q_Combined resulted in similar results between Fitted Gap Param and Full Opt Gap Param, the Log Odds Multin scoring function behaves differently under the two optimization schemes. For Full Opt Gap Param, as noted above, it exhibits higher _Q_Modeler and lower _Q_Developer than the others, whereas with Fitted Gap Param, it behaves more like the other functions. Fitted Gap Param improves the search capability of all three scoring functions shown in Figure 3 ▶. The reason is presumably that the column–column scores are adjusted individually for every pair of profiles to be aligned after calculation of their average column–column score and its standard deviation. Thus, for instance, two profiles with similar amino acid compositions will have relatively stricter gap parameters when compared with the adjusted column–column scores. This may reduce false positives, for instance, for all-α versus all-α structures.
Figure 3.
Comparison of Full Opt Gap Param vs. Fitted Gap Param for three scoring functions. Choices at specific stages of the alignment process are listed at the top of the figure and described in Materials and Methods. (Upper left) _Q_Modeler scores; (upper right) _Q_Developer scores; (lower left) _Q_Combined scores; (lower right) search capability as measured by the number of true positives vs. false positives. The legend given in the lower left figure applies to all four plots.
Improving profiles
We explored several issues in constructing the profiles for use in profile–profile alignments. These include the methods used to weight sequences used in calculating amino acid counts and frequencies in each column of the profile; the inclusion of positions that have a gap character in the query sequence used to build the profile; and whether the inclusion of the most distantly related sequences in a multiple alignment improved or degraded the quality of profiles, which we refer to as “sequence choice.” The inclusion of positions in the profile that contain a gap in the query in the multiple alignment did not result in improved alignments (data not shown).
We decided to test the issues of weighting with sequence choice together using the Log Odds Multin scoring function. The results are shown in Figure 4 ▶. We tested three weighting schemes, that of Henikoff and Henikoff used by PSI-BLAST (Henikoff and Henikoff 1994), that of Rychlewski et al. (2000) used in the FFAS programs, and the PSIC scheme (Sunyaev et al. 1999) used in COMPASS (Sadreyev and Grishin 2003). We refer to these three schemes as Henikoff weighting, Seq Divergence weighting, and PSIC weighting, respectively. The PSIC weighting scheme appears to be better than the Henikoff and Seq Divergence weighting schemes in both sequence alignment accuracy using all three quality scores and search sensitivity and specificity, for the Log Odds Multin column–column scoring function, regardless of what sequence choice scheme is used. The PSIC weighting also improves alignments with the other scoring functions (data not shown).
Figure 4.
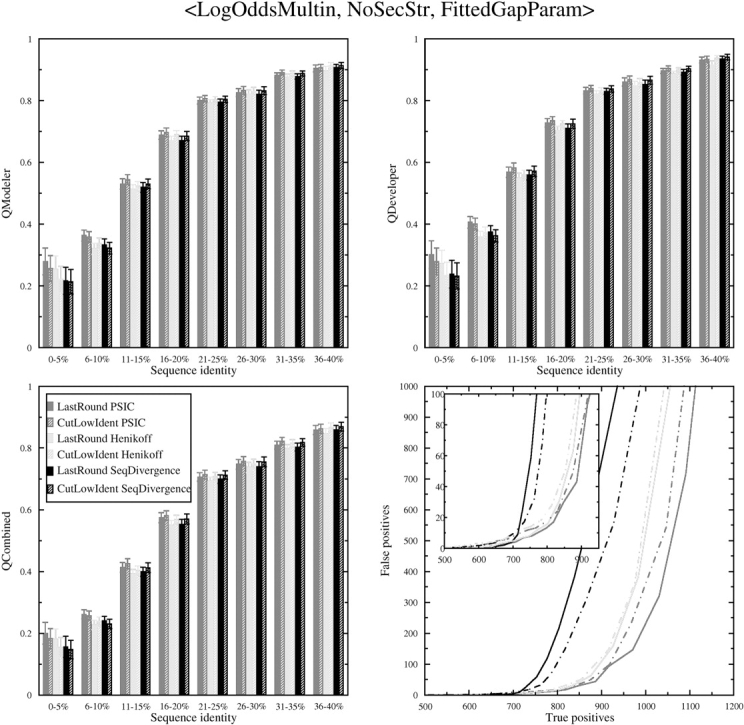
Comparison of three weighting schemes and two sequence-choice schemes for the Log Odds Multin scoring function. Choices at specific stages of the alignment process are listed at the top of the figure and described in Materials and Methods. (Upper left) _Q_Modeler scores; (upper right) _Q_Developer scores; (lower left) _Q_Combined scores; (lower right) search capability as measured by the number of true positives vs. false positives. The legend given in the lower left figure applies to all four plots.
It is not a given that including all available sequences related to a query will produce profiles that result in the most accurate sequence alignments and/or the highest specificity and sensitivity behaviors. For instance, adding sequences to the query profile that are further away from the hit sequence or profile than is the hit itself may add noise to the alignment. Very distantly related sequences may be aligned accurately over only short stretches of highly conserved sequence and misaligned everywhere else. This would tend to decrease the specificity of the profile. However, the results indicate that cutting out the lowest identity hits in the multiple sequence alignment tends to worsen the alignment accuracy for all three scoring functions. It improves the specificity/sensitivity for the Seq Divergence weighting scheme and worsens it slightly for the PSIC weighting, and has little effect on the Henikoff weighting scheme.
Adding secondary structure information
Because profile–profile alignments are often used to align sequences without a known structure to those with a known structure for the purpose of structure prediction, we decided to test whether comparing the predicted secondary structure of a query sequence (based on its profile) and the known secondary structure of another sequence would improve alignments. We used a set of structure alignments, predicted secondary structures on profiles based on the sequences in these alignments and the PSIPRED program (Jones 1999), and the known secondary structures of these proteins based on their experimental structures to derive a secondary structure substitution matrix. The Secondary Structure Substitution Matrix has the form:
 |
(26) |
|---|
where the rows represent predicted secondary structures, Helix, Coil, Sheet, respectively, and the columns represent experimental secondary structures in the same order. The values in the matrix are sensible, because Helix-for-Sheet substitutions are given the most negative values, and Sheet-for-Sheet the most positive value.
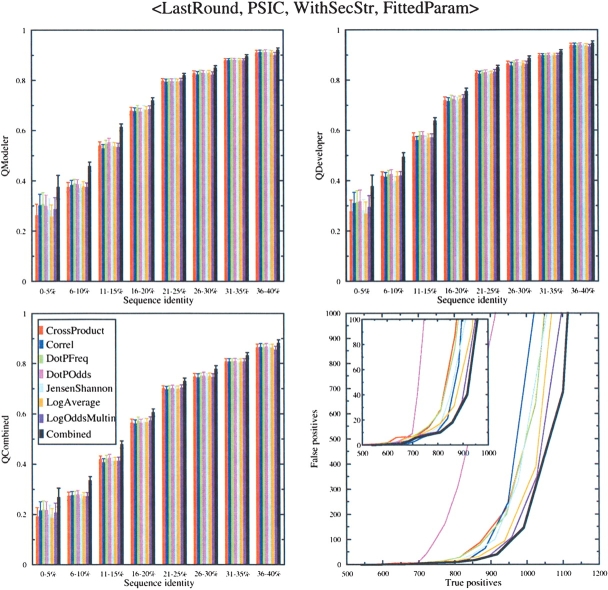
To use the secondary structure substitution matrix, we had to optimize the balance between the column–column scores and the secondary structure matrix scores. This was done as described in Materials and Methods. For the seven functions we studied, the weights of the secondary structure matrix (out of 100% total) were: Cross Product, 20%; Log Average, 30%; Dot P Freq, 35%; Dot P Odds, 20%; CORREL, 30%; Jensen Shannon, 25%; and Log Odds Multin, 30%. For all these functions, the use of the secondary structure matrix improved sequence alignment accuracy slightly. The results are shown in Figure 5 ▶. Secondary structure information improved the search capability of the Cross Product function significantly. It improved the results for the Log Odds Multin function only at low numbers of false positives (Fig. 5 ▶, inset).
Figure 5.
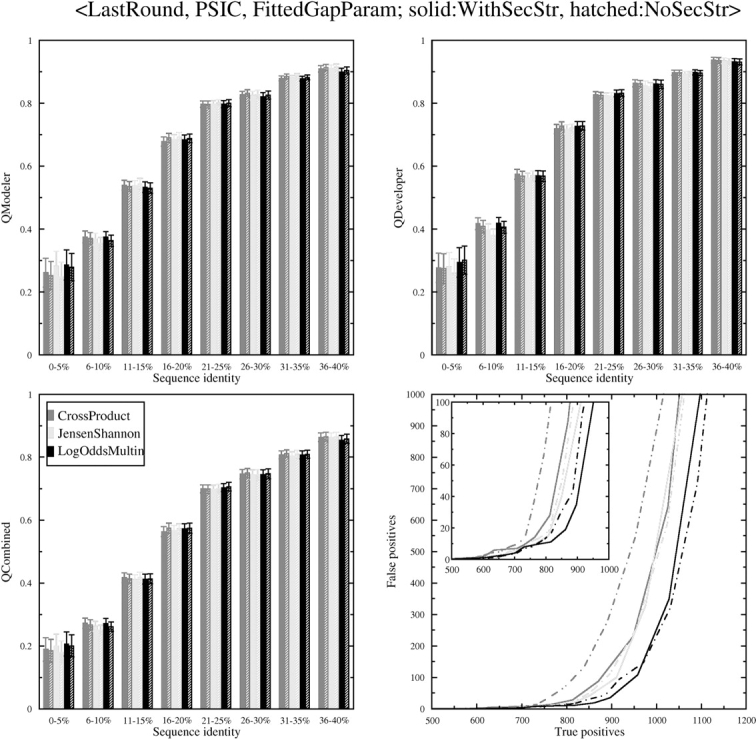
Effect of adding secondary structure substitution matrix to three scoring schemes. Choices at specific stages of the alignment process are listed at the top of the figure and described in Materials and Methods. (Upper left) _Q_Modeler scores; (upper right) _Q_Developer scores; (lower left) _Q_Combined scores; (lower right) search capability as measured by the number of true positives vs. false positives. The legend given in the lower left figure applies to all four plots.
Improving alignment accuracy
We have investigated several aspects of the profile–profile alignment process as shown in Figure 1 ▶. We have found that the PSIC weighting scheme, building the profile including no gaps in the query sequence, building the profile from the Last Round of PSI-BLAST, and adding secondary structure information each individually improves sequence alignment accuracy and search sensitivity and specificity. We have not investigated all combinations of these choices, and they may not be entirely independent. Nevertheless, to investigate their combined effect, we tested each of the seven scoring functions using PSIC weighting, Last Round multiple sequence alignments, no gaps in the query sequence, and with secondary structure information. This is shown in Figure 6 ▶. In terms of alignment accuracy, the Dot P Odds and Dot P Freq behave a little better than the others, and the Log Average and Cross Product slightly worse.
Figure 6.
Effect of combining protocol choices for all seven scoring functions. For the first three panels, “Combined” means taking the best scoring result of the seven scoring functions for each alignment pair. For the last panel, the scores of the seven functions were summed and used to sort the hits to form the true/false positive curve. Choices at specific stages of the alignment process are listed at the top of the figure and described in Materials and Methods. (Upper left) _Q_Modeler scores; (upper right) _Q_Developer scores; (lower left) _Q_Combined scores; (lower right) search capability as measured by the number of true positives vs. false positives. The legend given in the lower left figure applies to all four plots.
We also investigated the alignment accuracy if we picked the best alignment in terms of _Q_Combined out of the seven scoring functions for each aligned pair, and this is shown in the first three panels of Figure 6 ▶. The alignment accuracy in terms of _Q_Combined at low sequence identity improves from 20% to 27%. Of course, this is not possible when one does not know the correct alignment, but it does indicate that the seven scoring functions taken as a whole are sampling better alignments than any one of them is able to produce consistently. It may be possible that using threading techniques one might be able to pick out the best alignment most of the time, thus improving alignment accuracy.
The Log Odds Multin and Log Average functions perform better than others in terms of specificity and sensitivity, whereas the Dot P Odds behaves significantly worse. Because the scoring functions used to generate these data were all fitted to the standard normal, they are all approximately on the same scale. We therefore tried combining them in one score simply by adding the scores for all seven functions for each alignment pair. This results in better search sensitivity and specificity than any of the individual scores (Fig. 6 ▶, lower right panel). This result does not depend on any prior knowledge of the correct answer, and therefore could be used to improve search capability.
Discussion
Any structure prediction protocol involves several steps, and in any one step there may be several choices of algorithms or parameters to be made. It is often difficult to know what choices make a significant difference in the outcome of the calculations. The use of profile–profile alignments in comparative modeling has increased in recent years, and thus we have investigated several of the choices to be made in producing such alignments. Although it is difficult to investigate all combinations of alternatives, we have identified several trends that seem useful for improving alignments. These include using PSIC weighting, removing positions from the profile that contain gaps in the query, using all sequences from the multiple alignments generated from PSI-BLAST searches of the nonredundant protein sequence database, and using secondary structure information when available. It also seems to be the case that adjusting the scores relative to the gap penalty (or vice versa) for each profile–profile comparison, rather than having a global set of gap parameters, improves search sensitivity and alignment accuracy. Finally, the various scoring functions are all fairly similar to one another once the gap penalties have been optimized, although some functions behave differently with respect to length of alignments and accuracy per residue of the alignment.
Mittleman et al. (2003) recently published a similar study in which they compared column–column scoring methods in gapless alignments. They chose several functions either the same as or quite similar to those tested here, including Correl, Dot P Odds, Log Odds Multin, Cross Product, Jensen Shannon, and Dot P Freq. They used a test set of 1800 pairwise structure alignments with the DALI program, whereas we have used a set of protein pairs with consistent DALI and CE structure alignments to reduce noise due to choice of structure alignment method. When we used the Full Opt Gap Param parameters, the test set was 2305 pairs, and with the Fitted Gap Param parameters, it was 3441 pairs. They judged the alignment quality by the number of short fragments (of length 5 or 7) correctly aligned in the top 20 hits for each pair of profiles. This parameter is not directly comparable to _Q_Modeler, _Q_Developer, or _Q_Combined used here, but it is probably closest to _Q_Modeler, because there is no adjustment for the length of the structure alignment. The results in Mittleman et al. (2003) are quite similar to those here, with the log-odds-based methods (Dot P Odds, Log Odds Multin) and Jensen Shannon method behaving better than the others. This is encouraging considering the different protocols used for deriving the alignments and assessing their accuracy.
A key component in these results has been the use of a large benchmark of structural alignments of homologous proteins used in judging sequence alignment accuracy and search sensitivity and specificity. We have been able to give results with reasonably small uncertainties at all levels of sequence identity, to identify significant variations among methods chosen in each step of profile–profile alignment. This is in contrast to some smaller sets used when new methods are developed and in the CASP series of experiments, where the test sets are generally too small to reach firm conclusions, although some important trends have been identified (Bourne 2003; Venclovas et al. 2003). We have used the same principle in developing side-chain prediction (Canutescu et al. 2003) and loop modeling methods (Canutescu and Dunbrack Jr. 2003), and it appears to be becoming more the rule than the exception as recent efforts indicate (Mittelman et al. 2003).
Acknowledgments
We gratefully acknowledge support from NIH Grants R01-HG02302 to R.L.D. and CA06972 to Fox Chase Cancer Center, an appropriation from the Commonwealth of Pennsylvania, and the Pennsylvania Tobacco Settlement.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.03601504.
References
- Altschul, S.F., Madden, T.L., Schäffer, A.A., Zhang, J., Zhang, Z., Miller, W., and Lipman, D.J. 1997. Gapped BLAST and PSI-BLAST: A new generation of database programs. Nucleic Acids Res. 25 3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bourne, P.E. 2003. CASP and CAFASP experiments and their findings. Methods Biochem. Anal. 44 501–507. [PubMed] [Google Scholar]
- Canutescu, A.A. and Dunbrack Jr., R.L. 2003. Cyclic coordinate descent: A robotics algorithm for protein loop closure. Protein Sci. 12 963–972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canutescu, A.A., Shelenkov, A.A., and Dunbrack Jr., R.L. 2003. A graph-theory algorithm for rapid protein side-chain prediction. Protein Sci. 12 2001–2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer, D., Elofsson, A., Rice, D., and Eisenberg, D. 1996. Assessing the performance of fold recognition methods by means of a comprehensive benchmark. Pac. Symp. Biocomput. pp. 300–318. [PubMed]
- Frishman, D. and Argos, P. 1995. Knowledge-based protein secondary structure assignment. Proteins 23 566–579. [DOI] [PubMed] [Google Scholar]
- Ginalski, K., Pas, J., Wyrwicz, L.S., von Grotthuss, M., Bujnicki, J.M., and Rychlewski, L. 2003. ORFeus: Detection of distant homology using sequence profiles and predicted secondary structure. Nucleic Acids Res. 31 3804–3807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gribskov, M., McLachlan, A.D., and Eisenberg, D. 1987. Profile analysis: Detection of distantly related proteins. Proc. Natl. Acad. Sci. 84 4355–4358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henikoff, S. and Henikoff, J.G. 1993. Performance evaluation of amino acid substitution matrices. Proteins 17 49–61. [DOI] [PubMed] [Google Scholar]
- ———. 1994. Position-based sequence weights. J. Mol. Biol. 243 574–578. [DOI] [PubMed] [Google Scholar]
- Holm, L. and Sander, C. 1993. Protein structure comparison by alignment of distance matrices. J. Mol. Biol. 233 123–138. [DOI] [PubMed] [Google Scholar]
- Jones, D.T. 1999. Protein secondary structure prediction based on position-specific scoring matrices. J. Mol. Biol. 292 195–202. [DOI] [PubMed] [Google Scholar]
- Luthy, R., McLachlan, A.D., and Eisenberg, D. 1991. Secondary structure-based profiles: Use of structure-conserving scoring tables in searching protein sequence databases for structural similarities. Proteins 10 229–239. [DOI] [PubMed] [Google Scholar]
- Mittelman, D., Sadreyev, R., and Grishin, N. 2003. Probabilistic scoring measures for profile–profile comparison yield more accurate short seed alignments. Bioinformatics 19 1531–1539. [DOI] [PubMed] [Google Scholar]
- Murzin, A.G., Brenner, S.E., Hubbard, T., and Chothia, C. 1995. SCOP: A structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol. 247 536–540. [DOI] [PubMed] [Google Scholar]
- Panchenko, A.R. 2003. Finding weak similarities between proteins by sequence profile comparison. Nucleic Acids Res. 31 683–689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panchenko, A., Marchler-Bauer, A., and Bryant, S.H. 1999. Threading with explicit models for evolutionary conservation of structure and sequence. Proteins 37 133–140. [DOI] [PubMed] [Google Scholar]
- Pei, J., Sadreyev, R., and Grishin, N.V. 2003. PCMA: Fast and accurate multiple sequence alignment based on profile consistency. Bioinformatics 19 427–428. [DOI] [PubMed] [Google Scholar]
- Pietrokovski, S. 1996. Searching databases of conserved sequence regions by aligning protein multiple-alignments. Nucleic Acids Res. 24 3836–3845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rychlewski, L., Zhang, B., and Godzik, A. 1998. Fold and function predictions for Mycoplasma genitalium proteins. Fold. Des. 3 229–238. [DOI] [PubMed] [Google Scholar]
- Rychlewski, L., Jaroszewski, L., Li, W., and Godzik, A. 2000. Comparison of sequence profiles. Strategies for structural predictions using sequence information. Protein Sci. 9 232–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadreyev, R. and Grishin, N. 2003. COMPASS: A tool for comparison of multiple protein alignments with assessment of statistical significance. J. Mol. Biol. 326 317–336. [DOI] [PubMed] [Google Scholar]
- Sauder, J.M., Arthur, J.W., and Dunbrack Jr., R.L. 2000. Large-scale comparison of protein sequence alignment algorithms with structure alignments. Proteins 40 6–22. [DOI] [PubMed] [Google Scholar]
- Shindyalov, I.N. and Bourne, P.E. 1998. Protein structure alignment by incremental combinatorial extension (CE) of the optimal path. Prot. Eng. 11 739–747. [DOI] [PubMed] [Google Scholar]
- Sjolander, K., Karplus, K., Brown, M., Hughey, R., Krogh, A., Mian, I.S., and Haussler, D. 1996. Dirichlet mixtures: A method for improved detection of weak but significant protein sequence homology. Comput. Appl. Biosci. 12 327–345. [DOI] [PubMed] [Google Scholar]
- Smith, T.F. and Waterman, M.S. 1981. Identification of common molecular subsequences. J. Mol. Biol. 147 195–197. [DOI] [PubMed] [Google Scholar]
- Sunyaev, S.R., Eisenhaber, F., Rodchenkov, I.V., Eisenhaber, B., Tumanyan, V.G., and Kuznetsov, E.N. 1999. PSIC: Profile extraction from sequence alignments with position-specific counts of independent observations. Protein Eng. 12 387–394. [DOI] [PubMed] [Google Scholar]
- Venclovas, C., Zemla, A., Fidelis, K., and Moult, J. 2003. Assessment of progress over the CASP experiments. Proteins 53Suppl. 6: 585–595. [DOI] [PubMed] [Google Scholar]
- von Öhsen, N. and Zimmer, R. 2001. Improving profile–profile alignments via log average scoring. In Algorithms in bioinformatics, First International Workshop, WABI 2001 (eds. O. Gascuel and B.M.E. Moret), pp. 11–26. Springer-Verlag, Berlin.
- von Öhsen, N., Sommer, I., and Zimmer, R. 2003. Profile–profile alignment: A powerful tool for protein structure prediction. Pac. Symp. Biocomput. 252–263. [PubMed]
- Wheeler, D.L., Church, D.M., Edgar, R., Federhen, S., Helmberg, W., Madden, T.L., Pontius, J.U., Schuler, G.D., Schriml, L.M., Sequeira, E., et al. 2004.Database resources of the National Center for Biotechnology Information: Update. Nucleic Acids Res. 32 Database issue: D35–D40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wootton, J.C. 1994. Non-globular domains in protein sequences: Automated segmentation using complexity measures. Comput. Chem. 18 269–285. [DOI] [PubMed] [Google Scholar]
- Yona, G. and Levitt, M. 2002. Within the twilight zone: A sensitive profile–profile comparison tool based on information theory. J. Mol. Biol. 315 1257–1275. [DOI] [PubMed] [Google Scholar]