Controlled encapsulation of single cells into monodisperse picoliter drops (original) (raw)
. Author manuscript; available in PMC: 2009 Aug 1.
Published in final edited form as: Lab Chip. 2008 Jun 13;8(8):1262–1264. doi: 10.1039/b805456h
Abstract
Encapsulation of cells within picoliter-size monodisperse drops provides new means to perform quantitative biological studies on a single-cell basis for large cell populations. Variability in the number of cells per drop due to stochastic cell loading is a major barrier to these techniques. We overcome this limitation by evenly spacing cells as they travel within a high aspect-ratio microchannel; cells enter the drop generator with the frequency of drop formation.
While drop-based microfluidics1,2 promises breakthrough applications in biotechnology such as directed evolution,3 tissue printing4 and bead-based PCR in emulsions,5 it also facilitates many quantitative studies of biology at the most fundamental level, that of single cells. Because each cell can be made to reside within its own picoliter-volume drop, chemically isolated from all other drops, cell-secreted molecules rapidly achieve detectable concentrations in the confined fluid surrounding the encapsulated cell. Similarly, uptake of trace chemicals specific to individual cells can be probed due to their depletion within the confined extracellular fluid. Moreover, highly monodisperse drops of water in an inert and immiscible carrier fluid can be formed at rates of several kHz using microfluidic techniques,6 and these drops can be pair-wise combined,7 split in two,8 and selected based on the contents of individual drops.9,10
Despite their great potential, studies of single cells in drops suffer from an intrinsic limitation; because the process of loading cells into drops is purely random, the distribution is dictated by Poisson statistics. Thus, the probability of a drop containing k cells is λk exp(−λ) / k!, where λ is the average number of cells per drop, so the ratio of drops containing one cell to those containing two is 2/λ. This means that to minimize the number of drops that contain more than a single cell requires very low average loading densities, meaning that most drops actually contain no cells whatsoever. This constraint significantly reduces the number of usable drops; for example, only 15.6 % of all drops will contain one cell if no more than one in ten of the occupied drops can be allowed to hold two or more cells.
Recent work describes a method to passively sort drops containing single cells from smaller empty drops after each cell triggers its own encapsulation upon entering a narrow aqueous jet formed in a flow-focusing device.11 This clever mechanism can also be used to sort cells based on their size since, for this system, drops are always slightly larger than the cell they contain; however, to overcome the inherent limitations of stochastic encapsulation of cells within controlled-size (monodisperse) drops, one (and only one) cell should be present whenever a drop is generated. This can be achieved manually for each drop,12 or passively, and with a much higher throughput, by organizing cells in the direction of flow so that they enter the microfluidic nozzle with the same frequency at which drops form.
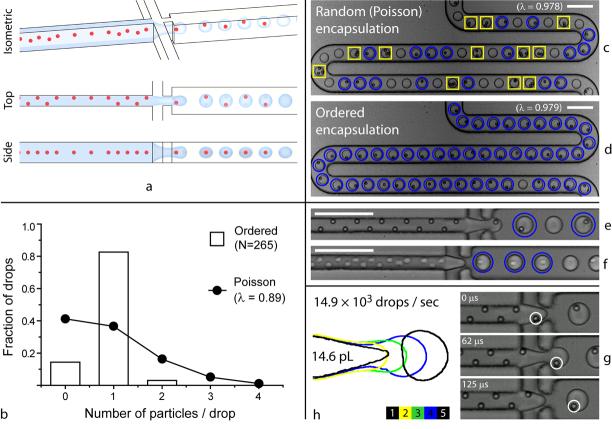
Here we report a method that causes cells to self-organize into two evenly-spaced streams whose longitudinal order is shifted by half the particle-particle spacing. This occurs when a high density suspension of cells or particles is forced to travel rapidly through a high-aspect ratio microchannel, where particle diameter is a large fraction of the channel narrow dimension (Fig. 1a). This phenomenon provides a purely passive method to controllably load single cells into drops, overcoming the intrinsic limitations set by Poisson statistics and ensuring that virtually every drop contains exactly one cell (Fig 1b and compare stochastic encapsulation, Fig. 1c, with ordered encapsulation, Fig. 1d, where 46 out of 47 drops contain a single bead).
Figure 1.
Ordered encapsulation. As depicted schematically in (a), hydrodynamic interactions cause particles to self-organize along one side of the microchannel or into a diagonal/alternating pattern. The uniform spacing in the direction of flow (see side view) leads to the formation of single-particle drops when the two lateral flows of oil pull drops from the aqueous stream (see isometric view) with the same (or slower) frequency that particles reach the microdrop generator (g). As the results for 0.89 beads per drop on average in (b) indicate, ordered encapsulation of beads (d-e) generates more single-particle drops (circles) and fewer empty (not marked) or multiple-particle drops (boxes) than would have been possible from (c) stochastic (Poisson) loading. With little or no loss in membrane integrity, cells also self-organize (f), where drops formed as in (h). Scale bars: 100 μm.
To demonstrate controlled single-cell microdrop generation, we used a flow-focusing geometry6 to emulsify concentrated suspensions of HL60 cells or 9.9-μm-diameter polystyrene beads immediately after they had traversed a 27-μm-wide × 52-μm-tall × 6-cm-long rectangular microchannel (Supplementary Methods online). Favorable conditions generated two main classes of organized behavior in the focusing channel preceding the drop generator (Fig. 1a, top view): either 1) particles were focused into the same streamline along one side of the channel, or 2) particles were arranged into an array that alternated from one side of the channel to the other (Fig. 1e for beads and Fig. 1f for cells). Recent advances in inertial sorting of particles in microfluidic devices describe four independent streams of particles in square channels.13 For the high-aspect ratio microchannel here, we have superimposed a tightly controlled additional degree of particle ordering that generates two particle trains with precisely staggered longitudinal spacing; this is critical for controlled loading of cells or beads into drops.
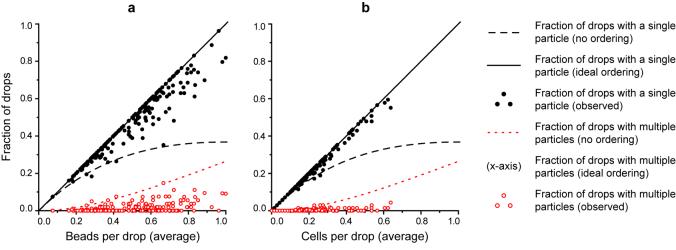
In Figure 2a (beads) and Figure 2b (cells), we report the resulting fractions of drops that contain a single particle (singles) and of drops that contain multiple particles (multiples) for concentrations between zero and one particles per drop. Nearly perfect single particle loading (maximum fraction of singles is λ) is achieved in all cases and the results are far superior to those expected from Poisson statistics, especially for high concentrations. By fitting the dependences of singles and multiples to linear functions of λ, we determine the ratio of singles to multiples to be 30.9 for beads and 56.5 for cells. From high-speed video recording, it is evident that most multiples resulted from particle aggregates that presumably formed when the initial batches of suspension were concentrated. Therefore, the rate of multiples should be proportional to λ, consistent with Figure 2. Moreover, perfect ordering appears limited only by these pre-existing particle aggregates.
Figure 2.
Fraction of drops that contain a single particle (singles) and of drops that contain more than one particle (multiples) vs. average number of particles per drop (λ) for (a) beads and (b) cells. Data points (experiment) are plotted alongside curves expected for perfect (ordered) and random (Poisson) encapsulation. Fractions of singles fit a linear trend versus concentration, where they occurred with a frequency of 0.937 λ for beads and 0.966 λ for cells (1 λ is ideal). Multiples should not occur for perfect ordering but resulted sporadically from pre-existing particle aggregates (0.0303 λ and 0.0171 λ for beads and cells, respectively). Each presented data point represents an analysis of 50 – 250 drops in one of many wide-field frames of video, chosen at regular intervals from high-speed videos up to 5 ½ minutes long, totaling 8.42 × 103 beads in 18.9 × 103 drops and 4.46 × 103 cells in 21.6 × 103 drops.
To confirm that the high aqueous flow rate required to induce self-ordering (aqueous flow rate was 10 μL/min for beads and 13 μL/min for cells) did not adversely affect the cells, we tested their survival rates after encapsulation and found that 92.9 % of cells retained membrane integrity, as compared with 96.2 % for controls (Supplementary Fig. 1 online).
The two above-mentioned patterns of self-organized behavior shared three distinctive characteristics: 1) each particle was separated from its nearest neighbor by a uniform spacing in the direction of flow, 2) particles were always found near the side walls of the channel, and 3) particles moved only in the direction of flow as a group. For our experimental conditions, the center-to-center spacing between adjacent particles focused on the same side of the channel was 48.2 ± 4.0 μm for beads and 33.5 ± 3.7 μm for cells, corresponding to velocities of 13.7 ± 0.1 cm/s and 20.6 ± 0.7 cm/s, respectively. In comparison, the longitudinal spacing between particles that self-organized into the alternating pattern was reduced to 24.4 ± 1.0 μm for beads and 19.0 ± 2.0 μm for cells, corresponding to velocities of 13.70 ± 0.04 cm/s and 21.1 ± 0.3 cm/s, respectively. The repulsive wall effect and the inertial lift towards the wall combine to restrict particles to certain streamlines in rectangular channels, but a complete explanation is still lacking as to why the high aspect ratio geometry has caused the four streams of particles observed for square channels to become two whose longitudinal order becomes synchronized.
To ensure single-particle drops, we adjusted the flow of oil to generate drops with a frequency not less than the frequency with which cells in the more closely-spaced alternating pattern of order arrived at the microdrop generator. More precisely, we set the flow of oil to 50 – 60 μL/min during bead experiments and 85 μL/min during cell experiments, causing 21.7-pL drops to form at 7.7 kHz for beads (Supplementary Video 1 online and Fig. 1g) and 14.6-pL drops to form at 14.9 kHz for cells (Supplementary Video 2 online and Fig. 1h).
The self-organizing phenomenon reported here will aid cell-in-drop applications whenever control of cell-occupancy is important. Quantitative studies of the secretion14 or uptake of trace amounts of bio-molecules by single cells can now be conducted much more conveniently. For example, to ensure that less than 2 % of the occupied drops are multiples, so that any misleading cross-talk between cells in the same drop is infrequent, Poisson statistics requires that cell suspension be diluted to λ = 0.040, so that only 3.84 % of all drops contain a single cell. Based on the data we report, the method presented here can provide over 20 times higher rates of single-cell drops for the same ratio of singles to multiples.
Applications that demand minimal numbers of empty drops in addition to a high ratio of single-cell drops to multiples would also benefit. For example, the creation of tissue-engineered constructs by “printing” cells onto a substrate as a spray of picoliter-size aqueous drops in air4 will receive a significant boost in resolution from this ability to control cell loading,15 allowing the narrowest possible lines to become the width of a single cell. Such ordered encapsulation becomes even more important for applications where streams of drops, each with single particles of two varieties, are combined to create larger drops carrying exactly one particle of each kind; the number of suitable drops for the above conditions would rise from 0.15 % without ordering to about 80 %, about 500 times higher.
Drop-based microfluidics is becoming a powerful technology with exciting applications in the fields of biology, biotechnology,3-5 computation16 and chemical analysis.17 The ability to apply these tools for high-throughput single-cell biology, cell analysis, and tissue engineering is extremely promising but has yet to be realized. The passively-controlled cell and particle encapsulation that we report here is a critical missing component to attain these goals.
Supplementary Material
Movie1
Movie2
Supplementary
Acknowledgments
This work was supported by the NIBIB (P41 EB002503), by the NSF (DMR-0602684 and DBI-0649865) and by the Harvard MRSEC (DMR-0213805). JFE was supported by an NIH Postdoctoral Fellowship (1F32EB007901), DDC was supported by an American Cancer Society Postdoctoral Fellowship (PF-07-237-01-CCE), and SK was supported by the Deutsche Forschungsgemeinschaft (DFG, KO 3572/1).
References
- 1.Whitesides GM. Nature. 2006;442:368–373. doi: 10.1038/nature05058. [DOI] [PubMed] [Google Scholar]
- 2.Teh S-Y, Lin R, Hung L-H, Lee AP. Lab on a Chip. 2008;8:198–220. doi: 10.1039/b715524g. [DOI] [PubMed] [Google Scholar]
- 3.Kelly BT, Baret J-C, Taly V, Griffiths AD. Chemistry Communications. 2007:1773–1788. doi: 10.1039/b616252e. [DOI] [PubMed] [Google Scholar]
- 4.Nakamura M, et al. Tissue Engineering. 2005;11:1658–1666. doi: 10.1089/ten.2005.11.1658. [DOI] [PubMed] [Google Scholar]
- 5.Margulies M, et al. Nature. 2005;437:376–380. doi: 10.1038/nature03959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Anna SL, Bontoux N, Stone HA. Applied Physics Letters. 2003;82:364–366. [Google Scholar]
- 7.Ahn K, Agresti JJ, Chong H, Marquez M, Weitz DA. Applied Physics Letters. 2006;88:264105. [Google Scholar]
- 8.Link DR, Anna SL, Weitz DA, Stone HA. Physical Review Letters. 2004;92:054503. doi: 10.1103/PhysRevLett.92.054503. [DOI] [PubMed] [Google Scholar]
- 9.Link DR, et al. Angewandte Chemie International Edition. 2006;45:2556–2560. doi: 10.1002/anie.200503540. [DOI] [PubMed] [Google Scholar]
- 10.Ahn K, et al. Applied Physics Letters. 2006;88:024104. [Google Scholar]
- 11.Chabert M, Viovy J-L. PNAS. 2008;105:3191–3196. doi: 10.1073/pnas.0708321105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.He M, et al. Analytical Chemistry. 2005;77:1539–1544. doi: 10.1021/ac0480850. [DOI] [PubMed] [Google Scholar]
- 13.Di Carlo D, Irimia D, Tompkins RG, Toner M. PNAS. 2007;104:18892–18897. doi: 10.1073/pnas.0704958104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Köster S, et al. Lab Chip. 2008;8:1110–1115. doi: 10.1039/b802941e. [DOI] [PubMed] [Google Scholar]
- 15.Calvert P. Science. 2007;318:208–209. doi: 10.1126/science.1144212. [DOI] [PubMed] [Google Scholar]
- 16.Prakash M, Gershenfeld N. Science. 2007;315:832–835. doi: 10.1126/science.1136907. [DOI] [PubMed] [Google Scholar]
- 17.Song H, Chen DL, Ismagilov RF. Angewandte Chemie International Edition. 2006;45:7336–7356. doi: 10.1002/anie.200601554. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Movie1
Movie2
Supplementary