A model for DNA replication showing how dormant origins safeguard against replication fork failure (original) (raw)
Abstract
Replication origins are ‘licensed' for a single initiation event before entry into S phase; however, many licensed replication origins are not used, but instead remain dormant. The use of these dormant origins helps cells to survive replication stresses that block replication fork movement. Here, we present a computer model of the replication of a typical metazoan origin cluster in which origins are assigned a certain initiation probability per unit time and are then activated stochastically during S phase. The output of this model is in good agreement with experimental data and shows how inefficient dormant origins can be activated when replication forks are inhibited. The model also shows how dormant origins can allow replication to complete even if some forks stall irreversibly. This provides a simple explanation for how replication origin firing is regulated, which simultaneously provides protection against replicative stress while minimizing the cost of using large numbers of replication forks.
Keywords: replication origins, dormant origins, replication licensing, computer modelling, MCM2–7
Introduction
In late mitosis and G1, MCM2–7 complexes are loaded onto replication origins to ‘license' them for a single initiation event (Blow & Dutta, 2005; Machida et al, 2005; Arias & Walter, 2007). MCM2–7 are thought to provide the essential helicase that unwinds DNA ahead of the replication fork. To prevent DNA from replicating more than once in a single cell cycle, it is essential that, once S phase starts, no further MCM2–7 are loaded onto the DNA. However, the inability to license new origins of replication during S phase creates the problem that if two converging forks stall irreversibly and there is no licensed replication origin already present between them, the intervening DNA cannot be replicated without some more complex event such as recombination.
Many licensed replication origins are not used during a normal S phase, but instead remain dormant and are passively replicated by forks from neighbouring origins (Taylor, 1977; DePamphilis, 1999; Santocanale et al, 1999; Dijkwel et al, 2002; Anglana et al, 2003; Li et al, 2003; Gilbert, 2007). Consistent with this, there are 10–20 times more MCM2–7 molecules loaded onto DNA in G1 than there are active replication origins (Burkhart et al, 1995; Donovan et al, 1997; Mahbubani et al, 1997; Edwards et al, 2002). These dormant origins can be activated when replication is inhibited, and become essential for complete replication and cell survival (Woodward et al, 2006; Ge et al, 2007; Courbet et al, 2008; Ibarra et al, 2008).
At present, it is unclear what induces the firing of dormant origins when forks are inhibited. One possibility is that this does not involve an active mechanism but occurs as a consequence of the stochastic nature of origin firing (Ge et al, 2007; Blow & Ge, 2008). Dormant origins normally have only a certain period of time to fire before they are passively replicated—and hence inactivated—by a fork from a neighbouring origin. When fork progression is slowed, it takes longer for the dormant origins to be passively replicated and therefore they have an increased probability of firing. The work described here uses a computer model to show that such a mechanism can provide levels of dormant origin activation that are similar to those seen in vivo, and it can thereby protect against the effects of fork stalling. This behaviour is obtained essentially ‘for free' simply by making origin firing stochastic and without the need for additional regulatory pathways.
Results And Discussion
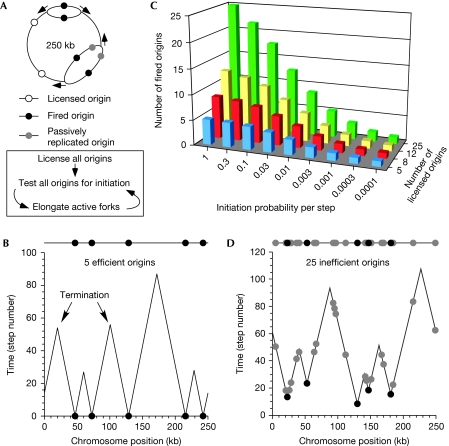
We modelled the behaviour of a typical replicon cluster (Jackson & Pombo, 1998; Berezney et al, 2000) in which 250 kb of DNA was replicated from five origins (Fig 1A). Except at the extreme ends of the chromosomes, any piece of DNA can potentially be replicated by either of two forks coming from opposite directions. To mimic this, and to eliminate end effects, the DNA in the model cluster was circularized.
Figure 1.
Modelling efficient and inefficient origins. (A) A diagram of a circular replicon cluster containing five origins. Two of these origins have fired and one has been passively replicated. Arrows show the direction of fork movement. The model sequence (initial origin licensing, followed by repeated steps of initiation and elongation) is shown below. (B) An example of replication of the cluster by five randomly spaced efficient origins (initiation probability per step=1). (C) The average initiation probability (_x_-axis) and the number of randomly spaced licensed origins per 250-kb cluster (_z_-axis) were varied. The average number of origins that fired was then determined (_y_-axis). (D) An example of replication of a cluster by 25 randomly spaced inefficient origins (mean initiation probability=0.003).
In the model, licensed replication origins were first created on the 250 kb DNA molecule. Origins were either distributed randomly or evenly spaced; actual cellular origin distribution probably falls between these extremes. Each origin was also assigned an initiation probability. In all the experiments shown here, the initiation probabilities of individual origins were distributed around a specified mean value (see Methods), meaning that within one cluster different origins have higher or lower initiation probabilities. This reflects the idea that, in cells, some origins are more efficient than others. Broadly similar results were obtained, however, when all the initiation probabilities in a cluster were set to the same value (data not shown).
Replication was then modelled in a series of discrete time steps, each corresponding to approximately 25 s of a real S phase. Each time step comprises an initiation stage and an elongation stage (lower panel of Fig 1A). In the initiation stage, a random test is performed on each licensed origin, based on its initiation probability, to determine whether it will initiate. An initiation probability of 0.05, for example, means that an origin has a 5% probability of firing in a time step. If an origin passes the test, it initiates a pair of forks and becomes unlicensed. After all licensed origins have been tested for initiation, all active replication forks are advanced 500 bp. If this causes two forks to converge, they terminate. If a fork passes over a licensed origin, the origin becomes unlicensed—‘passive replication'. The initiation–elongation sequence is repeated until replication of the 250-kb cluster is completed.
Fig 1B shows the replication profile of a typical cluster replicated by five randomly positioned efficient origins (initiation probability of one per step). All origins are initiated in the first step (black circles), and replication forks subsequently moved away from them; the peaks represent sites where forks terminated.
In living cells, the number of origins that are licensed and the probability with which they initiate are currently unknown. The model allows for variation in both parameters. For each set of simulation parameters, the model was run at least 10,000 times and average results were calculated. Fig 1C shows that when the number of origins was increased to 25 while maintaining an initiation probability of 1, then all 25 origins fired. However, when the initiation probability was reduced to 0.003 per step, then, on average, only 5 of the 25 licensed origins initiated during the replication of the whole cluster. Fig 1D shows an example of this, in which five origins fired in different time steps, and the other 20 remained dormant and were passively replicated (grey circles).
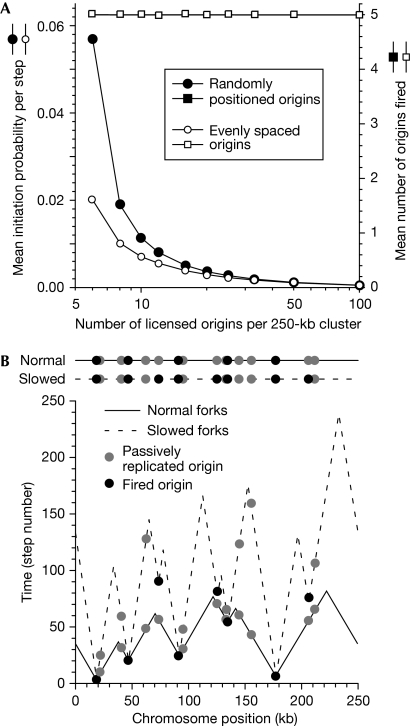
We varied the number of licensed origins and determined the initiation probabilities that are required to maintain an average of five origins firing in the 250-kb cluster. The circles in Fig 2A show how the initiation probabilities decrease as the total number of licensed origins increases. Slightly lower probabilities were required for evenly spaced replication origins as compared with randomly-positioned origins because when evenly spaced, unfired origins tend to be situated closer to termination events. Apart from the special case of highly efficient spaced origins, increasing the number of licensed origins in this way only slightly increased the total time required for complete replication of the origin cluster (supplementary Fig S1 online).
Figure 2.
Activating dormant origins. (A) Initiation probabilities were determined that maintained an average of five origins fired per 250-kb replicon cluster, whereas the number of licensed origins varied from 5 to 100. The average number of fired origins (squares) and the average initiation probability (circles) are plotted for randomly distributed (filled symbols) or evenly spaced origins (open symbols). The _x_-axis shows the number of licensed origins per cluster (log scale). (B) Example showing the effect of fork slowing. Sixteen randomly positioned origins were licensed with a mean initiation probability of 0.00508. The model was first run with a fork speed of 25% of normal (dashed lines) and the outcome with a normal fork speed was then derived (solid lines). Black circles, initiation events; grey circles, passively replicated origins.
We used this information to investigate the effect of fork slowing on origin usage. Sixteen randomly distributed origins were given a mean initiation probability of 0.00508 so that, on average, only five origins fired. The solid line in Fig 2B shows an example of replication under these conditions. The fork rate was then reduced to 25%, and the resultant replication profile is shown by the dashed line. The slow-moving forks took longer to reach the 11 origins that were passively replicated at the normal fork rate. Consequently, these 11 origins remained licensed for a longer period of time and 3 of them underwent initiation in later time steps. This is an example of dormant origins being activated by a ‘passive' mechanism in response to fork inhibition (Ge et al, 2007).
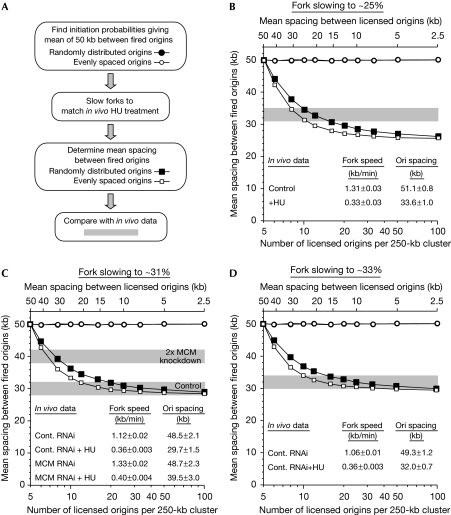
Next, we set out to fit the model to the results obtained when tissue culture cells were treated with hydroxyurea, which reduces the supply of dNTPs needed for DNA replication. DNA fibre analysis of human U2OS cells showed that 200 μM hydroxyurea reduced the replication fork rate to 25–33% of the controls and induced dormant origins to fire (Ge et al, 2007). Fig 3A shows a diagram of how the simulations were performed. Results from Fig 2A were used to establish conditions in which the number of licensed origins varied from 5 to 100 per 250 kb, whereas lowered initiation probabilities maintained an average of five origins fired per cluster (Fig 3B–D, circles). Fork speed was then reduced to mimic the effect of hydroxyurea (fork slowing to 25%, 31% or 33% of the appropriate controls for each experiment), and the number of origins that fired was determined (Fig 3B–D, squares). The results were then compared with three separate in vivo experiments (Fig 3B–D, grey shading). The data from Fig 3C were also plotted to show the number of origins fired and the origin efficiency (supplementary Fig S2 online). To match the in vivo data of Fig 3B, the model requires 8–16 licensed origins per 250-kb cluster, whereas to match the in vivo data of Fig 3C the model requires more than 12 licensed origins and Fig 3D requires more than 10 licensed origins. When chromatin-bound MCM2–7 in U2OS cells was reduced approximately twofold by short interfering RNA, the number of dormant origins was reduced, so the mean spacing between fired origins in the presence of hydroxyurea was only approximately 40 kb (Fig 3C, ‘2 × MCM knockdown'). To match these in vivo data, the model requires 6–9 licensed origins per 250-kb cluster. Assuming that a twofold reduction in chromatin-bound MCM2–7 leads to a twofold reduction in the number of licensed origins, this would imply that there are normally 12–18 licensed origins per cluster.
Figure 3.
Comparison of in vivo and in silico results. (A) Diagram showing the steps involved in modelling the in vivo data. (B–D) The number of licensed origins per 250-kb cluster was varied from 5 to 100; the mean initiation probability was also varied to maintain an average of five initiation events per cluster at normal fork rates (circles). The fork rate was then reduced to (B) 25%, (C) 31% or (D) 33% to match results obtained in vivo after treating U2OS cells with HU (Ge et al, 2007). For (C), the fork rate reduction to 31% was derived from the mean rates obtained with control and MCM RNAi. The mean spacing between fired origins is plotted (squares) for randomly distributed origins (open symbols) and evenly spaced origins (filled symbols). The matching in vivo data are presented within the relevant graph (values±s.e.m.) and the approximate origin spacing after HU treatment is indicated in grey (mean value±2 kb, to indicate the approximate experimental variability). In (C), the effect of an approximately twofold knockdown of chromatin-bound MCM2–7 is also presented (Ge et al, 2007). The _x_-axis at the bottom shows the number of licensed origins per 250-kb cluster (log scale); at the top, this is expressed as the mean spacing between licensed origins. Cont., control; HU, hydroxyurea; Ori, origin; RNAi, RNA interference.
Taken together, the model is in reasonable agreement with the experimental data if there are approximately 10–20 licensed origins per 250-kb cluster in U2OS cells. This means that licensed origins would be, on average, 12.5–25 kb apart (250/20–250/10 kb) and that there would be 1–3 dormant origins for each fired origin. This is well within the approximately 10-fold excess of MCM2–7 complexes over replication origins reported in various eukaryotic cells (Burkhart et al, 1995; Donovan et al, 1997; Mahbubani et al, 1997). One explanation for why there might be more MCM2–7 complexes than licensed origins is that there might be more than two MCM2–7 complexes present at each licensed origin. Alternatively, the number of dormant origins activated in response to hydroxyurea might be limited by checkpoint pathways that suppress origin firing. Consistent with this explanation, the in vivo experiment in which dormant origin activation was the smallest (Fig 3B) is the one in which fork slowing was the greatest, and so checkpoint activity was likely to be highest. The model's prediction of 1–3 dormant origins for each fired origin is therefore likely to represent the lower limit of the number of dormant origins actually present in vivo. Data from experiments showing that some dormant origins are activated following inhibition of checkpoint kinases also support this idea (Woodward et al, 2006; Ge et al, 2007).
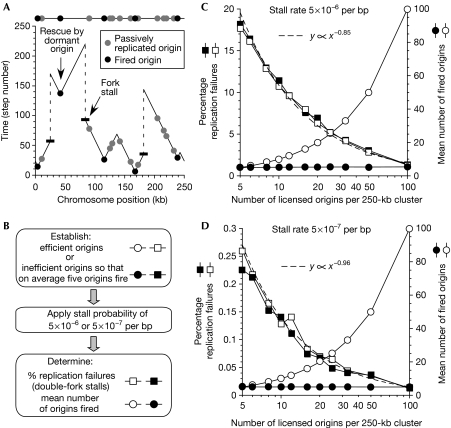
When replication forks encounter damaged DNA bases, crosslinks or tightly bound proteins, they can stall irreversibly (Dimitrova & Gilbert, 2000; Tercero & Diffley, 2001; Merrick et al, 2004). We modelled this by giving forks a certain probability of stalling at each base pair; an example is shown in Fig 4A. The rightward fork initiated at a map position of approximately 170 kb stalled after replicating just over 10 kb of DNA (indicated by a horizontal bar). This did not prevent the cluster from completing replication because the leftward fork initiated at a map position of 240 kb replicated all the DNA up to the stalled fork. In addition, the rightward fork initiated at approximately 5 kb and the leftward fork initiated at approximately 115 kb both stalled. This ‘double stall' of two converging forks might have made it impossible to replicate the intervening DNA; however, in this case, the presence of a dormant origin between the stalled forks, at approximately 40 kb, allowed all the intervening DNA to be replicated. This origin would not have fired if the adjacent forks had not stalled. When potential double-fork stalls are rescued by activation of a dormant origin in this manner, the total time taken to complete replication might often be significantly longer than would have been the case in the absence of fork stalling (Fig 4A; supplementary Fig S3 online).
Figure 4.
The effect of fork stalling. (A) An example showing the effect of fork stalling. Sixteen randomly positioned origins were licensed on a 250-kb cluster (mean spacing 15 kb) with a mean initiation probability of 0.00508 (five origins fired on average). The cluster was then replicated with a fork stall probability of 10−5 per base pair. Black circles, initiation events; grey circles, passively replicated origins; thick horizontal bars, fork stalls. (B–D) The number of licensed origins per 250-kb cluster was varied from 5 to 100; the mean initiation probability was also varied to maintain an average of five initiation events per cluster in the absence of fork stalling (filled symbols). The same number of licensed origins was also created and given an initiation probability of 1 (efficient origins; open symbols). Clusters were then replicated with fork stall probabilities of either (C) 5 × 10−6 or (D) 5 × 10−7 per base pair. The percentage of replication failures (squares) and the total number of fired origins (circles) are shown. Curve fitting was used to fit the number of replication failures (dashed lines).
We used a range of stall rates and measured how often complete replication failed owing to double stalls; Fig 4B summarizes the protocol. As in Figs 2 and 3, the number of licensed origins was varied from 5 to 100 per 250 kb, while lowered initiation probabilities maintained an average of five origins fired per cluster (Fig 4C,D, filled symbols). This was compared to the situation in which the same number of efficient origins (initiation probability of 1) was licensed (open symbols). Clusters were then replicated with a fork stall rate of either 5 × 10−6 (Fig 4C) or 5 × 10−7 (Fig 4D) per base pair. Increasing the number of licensed origins decreased the number of replication failures attributable to double-fork stalls (squares) at virtually the same rate whether the origins were efficient or inefficient. Curve fitting (dashed lines) showed that the percentage of replication failures was approximately inversely proportional to the number of licensed origins—that is, doubling the number of licensed origins approximately halves the probability of replication failure. The total number of inefficient origins firing under these circumstances increased only slightly owing to fork stalling (filled circles). Supplementary Fig S4 online shows that evenly spaced origins provide significantly more protection against replication failure than do randomly positioned origins over a range of stall rates. This is probably because the maximum distance between adjacent origins in a cluster, where double-fork stalls are most likely to occur, is minimized if origins are evenly spaced.
These results show that protection against double-fork stalling can be achieved by increasing the total number of licensed origins, and that it does not depend on whether these origins are efficient or whether they normally remain dormant. As it requires far fewer resources to assemble a licensed origin than it does to initiate a pair of replication forks (both of which probably comprise in excess of 50 polypeptides in addition to MCM2–7), it is clearly preferable to use inefficient origins, most of which will remain dormant. The protection given by replication origins against double-fork stalls can also help to explain why eukaryotes generally use far more replication origins than are strictly required to complete replication in the time allotted for S phase.
Although more complicated active mechanisms can be imagined for how origins in a replicon cluster are regulated, our model provides results that are in good agreement with experimental data simply by assigning origins a certain initiation probability per unit time. This shows that dormant origins can protect against double-fork stalls without the expense incurred by increasing the number of active replication forks. Given the potential simplicity of this control mechanism and the advantages it provides, we anticipate that the use of dormant replication origins will be widespread among various eukaryotic cells.
Methods
Computer modelling. The computer model (DormantOriSim) was written in Objective C using the Cocoa framework and the XCode 3 development environment. The model is controlled by a JBSPhaseController object that obtains model parameters from a graphical user interface. JBSPhaseController controls replication origins through a JBOriginController object and replication forks through a JBForkController object. During the simulation, JBOriginController first licenses replication origins, which are each represented by a JBOrigin object. Origins are distributed at random points on the DNA or else they are evenly spaced. Each JBOrigin contains information about its location, initiation probability and status (licensed/fired/passively replicated). Initiation probability is randomly determined from a mean value and a value that determines the variability around the mean, implemented so that the log of the initiation probability is normally distributed. Unless stated otherwise, for all experiments reported here, the log normal variability was set to 0.25 so that two standard deviations extended from 1/3 to 3 times the mean. Once the licensing phase is over, JBSPhaseController iteratively executes a series of S phase time steps. In each step, JBSPhaseController instructs JBOriginController to initiate licensed origins as appropriate and then instructs JBForkController to advance all the replication forks. JBOriginController performs a random test on each licensed origin based on its initiation probability. If the origin passes the test, the origin is converted to the fired state, and JBForkController is instructed to create a pair of JBFork objects representing the two forks initiated at that location. At initiation, each JBFork is assigned a distance at which it will stall, generated randomly through an exponential decay algorithm. When all origins have been tested, JBForkController instructs each JBFork to advance 500 bp. The 500-bp elongation distance was chosen so that in most cases no two origins that fire in the same time step are less than this distance apart. Each fork maintains a record of how far it has travelled and, if the movement would cause a JBFork to exceed its stall distance, it stalls irreversibly. If a JBFork passes over a licensed origin, it converts the origin to the ‘passively replicated' status. If the JBFork encounters another converging JBFork, both of them are terminated. The simulation continues until there are no more licensed origins and no more unstalled forks. JBSPhaseController keeps a full record of fork position and origin status for each time step for subsequent statistical analysis.
The integrity of the model was validated by using two methods. First, examples of all simulations were visually inspected using the graphical output shown in Figs 1B,D, 2B and 4A. Second, an extensive integrity check was performed by the program during all simulations, which included checking not only the relationship between the positions of all forks, origins and replicated DNA, but also that the status of origins was consistent with the replication map.
A working version of the model (for Mac OS 10.4 and above) and the source code (version 1.2.1) can be downloaded from http://www.dundee.ac.uk/lifesciences/blow/LabSite/Resources.html.
Origin spacing and fork rate measurements. Origin spacing was measured by DNA fibre analysis in previously published experiments (Ge et al, 2007). Fork rate was measured from fibres generated in these experiments by measuring the length of 100 individual, well-separated bromodeoxyuridine tracks and dividing it by the duration of the bromodeoxyuridine pulse. All other experimental details were as described.
Supplementary information is available at EMBO reports online (http://www.emboreports.org).
Supplementary Material
supplementary Information
Acknowledgments
We thank Tomo Tanaka and Margret Michalski-Blow for comments on the paper. This study was supported by Cancer Research UK grants C303/A7399 and C303/A4416.
Footnotes
The authors declare that they have no conflict of interest.
References
- Anglana M, Apiou F, Bensimon A, Debatisse M (2003) Dynamics of DNA replication in mammalian somatic cells: nucleotide pool modulates origin choice and interorigin spacing. Cell 114: 385–394 [DOI] [PubMed] [Google Scholar]
- Arias EE, Walter JC (2007) Strength in numbers: preventing rereplication via multiple mechanisms in eukaryotic cells. Genes Dev 21: 497–518 [DOI] [PubMed] [Google Scholar]
- Berezney R, Dubey DD, Huberman JA (2000) Heterogeneity of eukaryotic replicons, replicon clusters, and replication foci. Chromosoma 108: 471–484 [DOI] [PubMed] [Google Scholar]
- Blow JJ, Dutta A (2005) Preventing re-replication of chromosomal DNA. Nat Rev Mol Cell Biol 6: 476–486 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blow JJ, Ge XQ (2008) Replication forks, chromatin loops and dormant replication origins. Genome Biol 9: 244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burkhart R, Schulte D, Hu D, Musahl C, Gohring F, Knippers R (1995) Interactions of human nuclear proteins P1Mcm3 and P1Cdc46. Eur J Biochem 228: 431–438 [PubMed] [Google Scholar]
- Courbet S, Gay S, Arnoult N, Wronka G, Anglana M, Brison O, Debatisse M (2008) Replication fork movement sets chromatin loop size and origin choice in mammalian cells. Nature 455: 557–560 [DOI] [PubMed] [Google Scholar]
- DePamphilis ML (1999) Replication origins in metazoan chromosomes: fact or fiction? Bioessays 21: 5–16 [DOI] [PubMed] [Google Scholar]
- Dijkwel PA, Wang S, Hamlin JL (2002) Initiation sites are distributed at frequent intervals in the Chinese hamster dihydrofolate reductase origin of replication but are used with very different efficiencies. Mol Cell Biol 22: 3053–3065 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dimitrova DS, Gilbert DM (2000) Temporally coordinated assembly and disassembly of replication factories in the absence of DNA synthesis. Nat Cell Biol 2: 686–694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donovan S, Harwood J, Drury LS, Diffley JF (1997) Cdc6p-dependent loading of MCM proteins onto pre-replicative chromatin in budding yeast. Proc Natl Acad Sci USA 94: 5611–5616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards MC, Tutter AV, Cvetic C, Gilbert CH, Prokhorova TA, Walter JC (2002) MCM2–7 complexes bind chromatin in a distributed pattern surrounding the origin recognition complex in Xenopus egg extracts. J Biol Chem 277: 33049–33057 [DOI] [PubMed] [Google Scholar]
- Ge XQ, Jackson DA, Blow JJ (2007) Dormant origins licensed by excess MCM2 7 are required for human cells to survive replicative stress. Genes Dev 21: 3331–3341 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert DM (2007) Replication origin plasticity, Taylor-made: inhibition versus recruitment of origins under conditions of replication stress. Chromosoma 116: 341–347 [DOI] [PubMed] [Google Scholar]
- Ibarra A, Schwob E, Mendez J (2008) Excess MCM proteins protect human cells from replicative stress by licensing backup origins of replication. Proc Natl Acad Sci USA 105: 8956–8961 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson DA, Pombo A (1998) Replicon clusters are stable units of chromosome structure: evidence that nuclear organization contributes to the efficient activation and propagation of S phase in human cells. J Cell Biol 140: 1285–1295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li F, Chen J, Solessio E, Gilbert DM (2003) Spatial distribution and specification of mammalian replication origins during G1 phase. J Cell Biol 161: 257–266 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machida YJ, Hamlin JL, Dutta A (2005) Right place, right time, and only once: replication initiation in metazoans. Cell 123: 13–24 [DOI] [PubMed] [Google Scholar]
- Mahbubani HM, Chong JP, Chevalier S, Thömmes P, Blow JJ (1997) Cell cycle regulation of the replication licensing system: involvement of a Cdk-dependent inhibitor. J Cell Biol 136: 125–135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merrick CJ, Jackson D, Diffley JF (2004) Visualization of altered replication dynamics after DNA damage in human cells. J Biol Chem 279: 20067–20075 [DOI] [PubMed] [Google Scholar]
- Santocanale C, Sharma K, Diffley JF (1999) Activation of dormant origins of DNA replication in budding yeast. Genes Dev 13: 2360–2364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor JH (1977) Increase in DNA replication sites in cells held at the beginning of S phase. Chromosoma 62: 291–300 [DOI] [PubMed] [Google Scholar]
- Tercero JA, Diffley JF (2001) Regulation of DNA replication fork progression through damaged DNA by the Mec1/Rad53 checkpoint. Nature 412: 553–557 [DOI] [PubMed] [Google Scholar]
- Woodward AM, Gohler T, Luciani MG, Oehlmann M, Ge X, Gartner A, Jackson DA, Blow JJ (2006) Excess MCM2–7 license dormant origins of replication that can be used under conditions of replicative stress. J Cell Biol 173: 673–683 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
supplementary Information