The epidemiology of antibiotic resistance in hospitals: Paradoxes and prescriptions (original) (raw)
Abstract
A simple mathematical model of bacterial transmission within a hospital was used to study the effects of measures to control nosocomial transmission of bacteria and reduce antimicrobial resistance in nosocomial pathogens. The model predicts that: (i) Use of an antibiotic for which resistance is not yet present in a hospital will be positively associated at the individual level (odds ratio) with carriage of bacteria resistant to other antibiotics, but negatively associated at the population level (prevalence). Thus inferences from individual risk factors can yield misleading conclusions about the effect of antibiotic use on resistance to another antibiotic. (ii) Nonspecific interventions that reduce transmission of all bacteria within a hospital will disproportionately reduce the prevalence of colonization with resistant bacteria. (iii) Changes in the prevalence of resistance after a successful intervention will occur on a time scale of weeks to months, considerably faster than in community-acquired infections. Moreover, resistance can decline rapidly in a hospital even if it does not carry a fitness cost. The predictions of the model are compared with those of other models and published data. The implications for resistance control and study design are discussed, along with the limitations and assumptions of the model.
Antimicrobial resistance is a growing problem in many bacterial pathogens and is of particular concern for hospital-acquired (nosocomial) infections (1, 2). Frequently, the bacteria responsible for nosocomial infections are members of the normal, usually commensal bacterial flora that become pathogenic when they multiply in normally sterile sites, such as the lower respiratory tract or the blood. Thus, hospital-acquired infections often involve transmission from patients who carry the bacteria asymptomatically (or symptomatically) to other patients, some of whom then may become infected with the colonizing strain (3).
A number of interventions have been proposed and tried to limit nosocomial infections and particularly to stem the spread of antibiotic-resistant bacteria. Some of these measures, such as hand washing and barrier precautions, are designed to reduce overall transmission of bacteria within the hospital (4, 5). In some cases, hospitals have increased the prophylactic use of drugs other than those for which resistance is currently a problem, to prevent or terminate colonization with the resistant bacteria (6, 7). Another strategy has been “cycling” of formularies in a hospital or ward, whereby one class of antibiotics is used, where possible, for primary treatment of infections for a period of time, and then, as resistance to this class climbs, the policy switches to emphasize use of a second class of antibiotics, for which resistance is rare or absent (8–11). At the extreme, the use of all antibiotics has been curtailed in an effort to control the ascent of resistance to particular antibiotics (12, 13).
Although it generally is assumed that use of a particular antibiotic will be positively related to the level of resistance to that drug, most of these interventions have been conducted without quantitative expectations for the magnitude or time scale of their effects, and often without predetermined criteria for how to measure their success. Consequently, it is difficult to judge whether an intervention has been successful, compare the relative merits of different interventions, or identify the reasons particular interventions have succeeded while others have failed.
Mathematical models can provide such quantitative predictions, which naturally give rise to criteria for evaluating the interventions (9, 14–17). This report describes the structure and analysis of a simple mathematical model of hospital-transmitted bacterial pathogens. The analysis has two objectives: to make testable predictions about the transmission dynamics of resistant and sensitive nosocomial pathogens and to suggest and justify criteria for measuring the success of interventions to reduce resistance in hospitals. Toward these ends, we have not attempted to “fit” the model to the observations from a particular organism or hospital; rather, we describe the generic properties of a model intended for a range of hospital-acquired infections. In our numerical analysis of this model, we use parameter values derived from published studies to predict how the prevalence of resistant bacteria will change over time after various interventions. We conclude with a consideration of how well our model accounts for existing observations about the spread and control of drug-resistant bacteria and with suggestions about how the validity of this model can be tested.
Mathematical Model
The model is designed to describe the transmission dynamics of any one of several species of bacteria that commonly reside in or on the skin, respiratory passages, or digestive tracts of humans: e.g., Staphylococcus spp., Enterococcus spp., Escherichia coli, Klebsiella pneumoniae, and Enterobacter. Although generally commensal, these and other members of the normal human flora also can be responsible for symptomatic and even lethal infections. These bacteria are transmitted between patients in hospitals via direct contact between patients, through contamination of the institutional environment, or with the inadvertent help of human vectors (e.g., healthcare workers, HCWs) (18–20). The bacteria are continually confronted with antibiotics being used for prophylaxis or treatment (21, 22). As well as posing a risk of opportunistic infection, these species serve as a reservoir of antibiotic-resistance plasmids that are horizontally transmitted between strains and species of bacteria and are responsible for much of the multiple drug resistance in pathogenic bacteria (23–25).
The model shown in Fig. 1A considers the transmission dynamics of a single bacterial species and the use of two antimicrobial agents, called drug 1 and drug 2. Hereafter, the term bacteria refers to the single bacterial species under consideration. The structure of the model is similar to that of previous compartmental models (9, 16, 17, 26–31). The major difference from most of its predecessors (except ref. 15) is that in this model, a fraction (or possibly all) of the individuals that enter the institution already are colonized with the bacterial species of interest. This distinction has an important effect on the dynamics of nosocomial antibiotic resistance.
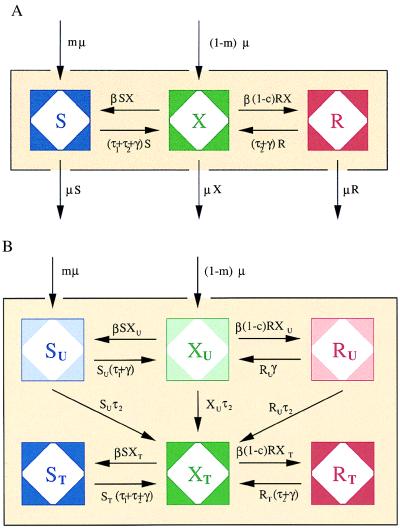
Figure 1.
(A) A compartment model of antibiotic-resistance in a hospital setting. See text for description and equations. (B) The extended model, in which patients are tracked by their treatment history (see text). Individuals are discharged at a constant rate μ from all compartments (not shown). For brevity, _S = S_T + SU; _X = X_T + XU; r = RT +RU.
Individuals may carry strains of these bacteria that are either sensitive (S) or resistant (R) to drug 1, or they may be free of these bacteria (X); here, X, S, and R, are the frequencies of the different host states as well as their designations. We assume that resistance to drug 2 is not present in the bacteria. Individuals enter the hospital either carrying sensitive bacteria, S, (a fraction m) or uncolonized with these species, X (a fraction 1-m); for some species, such as E. coli, m will be 1 or nearly 1, whereas for other species it will be less. Because antibiotics are used in hospitals to prevent or treat a wide range of conditions, we assume that patients will receive antibiotics at a rate independent of whether or not they are colonized by the bacterial species under consideration. Treatment with drug 1, which occurs at rate τ1 per day, clears carriage of sensitive bacteria, converting members of the S population into X, but has no effect on hosts bearing resistant bacteria. Treatment with drug 2, which occurs at rate _τ_2 per day, clears carriage of either sensitive or resistant bacteria. Spontaneous clearance of sensitive and resistant bacteria occurs at a rate γ per day. Individuals who are not carrying the sampled species (X) are colonized with sensitive bacteria at a rate proportional to the prevalence of hosts carrying sensitive bacteria and a rate constant β. Colonization with resistant bacteria occurs with rate constant β(1-c), where c denotes the fitness “cost” of resistance to drug 1. The average duration of stay in the institution is 1/μ days, and the total population of the hospital is kept steady by an admission rate of μ per day. The system is described by the following set of ordinary differential equations:
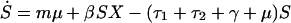
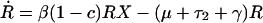
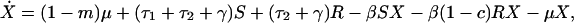
where a dot denotes differentiation with respect to time.
Fig. 1B shows an expanded form of this same model, which tracks individuals by their histories of drug 2 treatment. Here, each compartment (S, X, and R) from the simple model is broken into two compartments based on treatment history: those who have not received drug 2 (_S_U, _X_U, and _R_U) and those who have (_S_T, _X_T, and _R_T). The transmission dynamics are identical to those in the simple model, but by keeping track of individual treatment histories, we can now use this compartment model to evaluate the effect of treatment with drug 2 on the odds that individual patients will carry flora resistant to drug 1.
Results
Equilibria.
Patients colonized with sensitive bacteria are always present in this model, because they are constantly entering the hospital, and patients not colonized with the bacteria are also present, because of clearance of colonized individuals and, if m<1, the entry of already uncolonized individuals. Carriage of resistant bacteria will persist in the hospital under the condition:
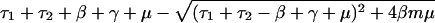
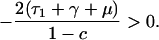 |
1 |
|---|
For the special case in which resistant and sensitive bacteria are equally transmissible (c = 0), this condition simplifies to:
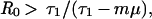
where _R_0 = β/(_τ_2 + μ + γ) is the basic reproductive rate of resistant bacteria in a hypothetical institution where all hosts entered uncolonized (X). Qualitatively, these conditions mean that endemic persistence of a population of bacteria resistant to drug 1 depends on having sufficiently high rates of: within-hospital bacterial transmission (β) and use of drug 1 (_τ_1), and sufficiently low: fitness cost of resistance (c), rates of entry of individuals carrying sensitive bacteria (m), turnover of the hospital population (μ), use of drug 2 (_τ_2), and spontaneous clearance of colonization (γ).
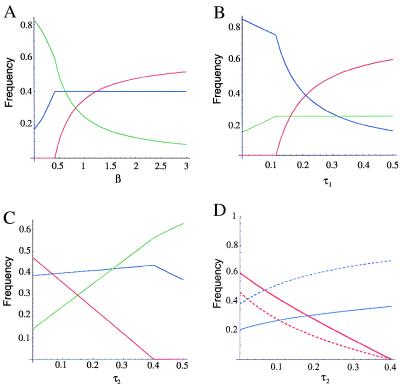
The equilibrium prevalence of colonization with bacteria resistant to drug 1 also depends on these parameters, in the same direction. Thus, for example, the model predicts that any procedure that reduces the rate (β) of between-host transmission of bacteria in the hospital, such as improved hygiene and barrier precautions, would reduce the prevalence of resistant infections, as illustrated in Fig. 2A. Although this result is unsurprising, the more interesting prediction is that as long as transmission is sufficient to maintain endemic persistence of resistant bacteria in the hospital, reducing transmission will only reduce resistant bacteria, and will have no effect on the prevalence of sensitive bacteria. This prediction is counterintuitive because reductions in transmission do not distinguish between bacterial types, but it can be understood as a consequence of the fact that resistant bacteria depend solely on within-hospital transmission, whereas sensitive bacteria maintain their prevalence by both “immigration” and transmission. Mathematically, the result simply states that the transmission rate does not appear in the expression for the equilibrium value of S, given in the legend of Fig. 2.
Figure 2.
Equilibrium prevalence of sensitive and resistant bacterial carriage predicted by the model, as a function of treatment and transmission variables. Equilibrium prevalences are given by:
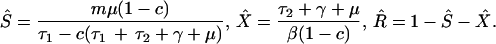
Sensitives are shown in blue; resistants in red; and uncolonized individuals in green. (A) Increased within-hospital transmission rates (β) increase the prevalence of sensitive bacteria, up to the threshold (given by Eq. 1) at which resistant bacteria are able to invade and persist endemically. Further increases in transmission rates increase the prevalence of resistant bacterial carriage but have no effect on the prevalence of carriage of sensitive bacteria. Thus, interventions to reduce transmission, such as barrier precautions and hand washing, are most likely to reduce carriage of resistant bacteria before they reduce carriage of sensitive, if they affect sensitive carriage at all. (B) Increased levels of treatment with drug 1 (_τ_1) result in higher prevalence of bacteria resistant to it and lower prevalence of sensitive bacteria. (C) Increased treatment with drug 2 (_τ_2) reduces prevalence of bacteria resistant to drug 1 but increases the prevalence of sensitives, up to the point at which resistants have been driven extinct; thereafter, it reduces the prevalence of sensitives. (D) Individuals treated with drug 2 are at higher risk of carriage of drug 1-resistant bacteria at equilibrium, although increased total use of drug 2 (_τ_2) reduces prevalence of drug 1-resistant carriage. Shown are prevalences of sensitive (blue) and resistant (red) bacteria in individuals who have been treated with drug 2 (solid curves) and those who have not (dashed curves). Parameters (except when parameter is varied along _x_-axis): β = 1.0/day, c = 0.05, μ = 1/(10 days), γ = 1/(30 days), m = 0.75, _τ_1 = 1/(5 days), _τ_2 = 1/(10 days).
Not surprisingly, the model also predicts that the prevalence of resistance to drug 1 would be directly related to the level of use of drug 1 (Fig. 2B). More surprising, on at least first consideration, is the prediction that increasing the use of drug 2, for which there is no resistance, would result in a reduction in the equilibrium prevalence of bacteria resistant to drug 1 (Fig. 2C). Stated another way, in the hospital at large, there should be a negative relationship between the use of drug 2 and the prevalence of resistance to drug 1.
Interestingly, at the level of individual patients, the anticipated relationship between treatment with drug 2 and resistance to drug 1 is precisely the opposite. Patients treated with drug 2 are more likely to carry bacteria resistant to drug 1 than those who have not been treated. Epidemiologists often present this individual association as a prevalence odds ratio (32):

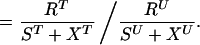
If this ratio is greater than 1, an individual who has been treated with drug 2 is more likely to carry bacteria resistant to drug 1 than someone who has not received drug 2. In the model of Fig. 1B, it can be proven that this odds ratio is always greater than 1; although this is algebraically messy in general, it can be seen more easily for the special case when c = 0; in this case, the odds ratio at equilibrium is given by:
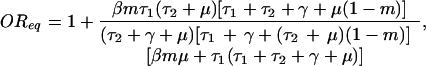
which is clearly greater than 1, because all terms of the fraction are positive. Thus, the model makes the counterintuitive prediction that use of drug 2 reduces the prevalence of resistance to drug 1 in the institution, while at the same time treatment with this second antibiotic increases any individual's odds of carrying resistant bacteria. This result is illustrated in Fig. 2D.
This result, too, is explained by the fact that many individuals enter the institution carrying sensitive bacteria. Treatment clears these sensitive bacteria, making it possible for them to be colonized by the resistant strain, which is endemic in the hospital. Therefore, individuals treated with drug 2 are at greater risk of acquiring the resistant strain than individuals who are not. However, in the hospital at large, treatment with drug 2 reduces the duration of carriage of bacteria resistant (or sensitive) to drug 1, thereby reducing the endemic prevalence of the resistant bacteria. In this sense, use of drug 2 has the same effect as infection control or any other measures that reduce the transmission of bacteria in the hospital.
These equilibrium results indicate how (in which direction) changes in transmission conditions and drug use within a hospital should affect levels of resistance. However, they do not provide information on how fast such effects will occur. Next we consider the dynamics of the model after an intervention.
Dynamics: Response of Hospital Populations to Interventions.
To estimate the rate at which hospital populations respond to interventions, it is necessary to use realistic values for key parameters of the model. Fortunately, the literature contains sufficient information to obtain realistic values of the most important of these parameters; see Table 1. In what follows, we describe the results of numerical solutions of the model by using parameters from the ranges in Table 1.
Table 1.
Values of some important parameters and published sources for these values
| Name | Meaning | Values | Source |
|---|---|---|---|
| 1/μ | Average duration of hospital stay | 7–20 days | (7, 13, 46, 54) |
| m | Proportion of admitted already colonized with sensitive bacteria | 20–100% | (55, 56) |
| 1/γ | Average time from admission or colonization until spontaneous clearance of bacterial carriage | 30–60 days | (39) |
| 1/λ | Average time from admission to colonization | 6–50 days | (3, 7, 39, 57, 58) |
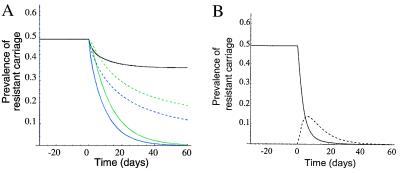
Fig. 3A illustrates the dynamics of colonization with sensitive and resistant bacteria after various interventions. The black curve shows the effects of reducing transmission (β) within a hospital by 30%, using nonspecific measures such as barrier precautions or hand washing. The green curves show the effects of discontinuing drug 1 use (solid) or of reducing it by half (dashed lines), using realistic parameter values. The blue curves show the effects of the same intervention, supplemented by an equivalent increase in use of drug 2. In each case, the response of the bacterial populations is rapid, taking place over a period of a few weeks to a few months.
Figure 3.
The prevalence of carriage of bacteria resistant to drug 1 changes rapidly over the weeks after changes in hospital practice (at day 0), starting from an equilibrium where only drug 1 was being used. Parameters: μ = 1/(10 days), γ = 1/(30 days), m = 0.75, c = 0. Before day 0: β = 1/day, τ 1 = 1/(5 days), _τ_2 = 0. (A) Effects of reducing transmission rates (β) by 30% (black curve), reducing the use of drug 1 (_τ_1) (green curves) by 50% (dashed) or 100% (solid), or replacing 50% (dashed) or 100% (solid) of use of drug 1 by use of drug 2 (blue curves). Addition of drug 2 makes the decline in resistance to drug 1 faster and larger than reduction of drug 1 alone. (B) Carriage of resistance to drug 1 after a switch from use of drug 1 only to use of drug 2 only (same as solid blue curve), in individuals who have (dashed curve) and have not (solid curve) received drug 2. After about 7 days, drug 2 treatment becomes a risk factor for drug 1 resistance, even though use of drug 2 is aiding in the reduction of resistance to drug 1 in the hospital.
This relatively rapid response to these interventions can be understood intuitively as the replacement of resistant bacteria by the drug-sensitive bacteria brought in by newly admitted patients. Because the average length of stay in most hospital units is on the order of a week or two (see Table 1), this turnover occurs quickly, so that when conditions become less favorable for maintaining resistant bacteria, they are rapidly replaced. The process also can be understood analytically. One way to measure the effect of an intervention is to consider changes in ρ, defined as the prevalence ratio of hosts carrying resistant to those carrying sensitive bacteria, ρ = R/S. This ratio changes at a rate
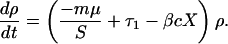
Thus, if a hospital were to discontinue the use of drug 1, and if the fitness difference between sensitive and resistant bacteria were relatively small (c ≈0), then the ratio would decline at a rate of at least mμ, the rate of admission of new individuals carrying sensitive bacteria. Using the values in Table 1, reasonable values of mμ fall between 0.01 and 0.15 day−1, corresponding to characteristic time scales between a week and 3 months. These time scales give rough upper bounds on the amount of time it should take for this ratio to fall by about 70% after discontinuation of use of drug 1. The slowest time scales correspond to bacteria that are rarely carried by admitted patients and to hospitals or units with very long average stays; the faster ones correspond to species, such as E. coli, that are commonly carried by incoming patients, and to units with shorter average stays. As the simulations show, changes that are less dramatic than a total cessation of use of a particular antibiotic produce slower changes in resistance, but still produce substantial results within a short period (months).
As a final consideration about dynamics, we re-examine the question of individual effects (as measured by the odds ratio for carrying resistant bacteria) versus population effects (as measured by the prevalence of resistance in the hospital). Switching from use of drug 1 to use of drug 2 in the hospital brings a faster, and more complete, reduction in drug 1 resistance than does a reduction in drug 1 alone, as illustrated by a comparison between the blue and green curves (Fig. 3A). However, during the period just after such a hospital-wide switch from drug 1 to drug 2 (as might occur in a hospital cycling program), individuals who have received drug 2 will be at increased risk of carrying resistance to drug 1. This dynamical result, shown in Fig. 3B, parallels the equilibrium result of Fig. 2D. Once again, the reason for this discrepancy is that use of drug 2 makes individuals who were previously carrying sensitive bacteria susceptible to acquiring resistant ones, thereby increasing individual risk; however, use of drug 2 at the population level helps to clear carriage of bacteria resistant to drug 1, thereby providing a benefit.
Discussion
This model makes a number of testable predictions. Of these, the most interesting are that: (i) use of an antibiotic for which resistance is not present will be positively associated at the individual level with carriage of bacteria resistant to another antibiotic but negatively associated at the population level with the prevalence of resistance to the other antibiotic; (ii) reductions in within-hospital bacterial transmission will disproportionately reduce the prevalence of resistant bacteria; and (iii) changes in the prevalence of resistance after a successful intervention will take place on a time scale of weeks to months, considerably faster than in community-acquired infections.
Epidemiologic studies in hospitals also have confirmed that a history of treatment with one antibiotic is frequently a risk factor for individual patients carrying bacteria resistant to another antibiotic. In many cases, there are simple explanations for this association, which do not involve the mechanisms proposed by our model; for example, resistance to the two antibiotics may be coded for by the same gene or mutation (e.g., two cephalosporins), or by different genes located on the same plasmid (33). Similarly, treatment with a drug to which all bacteria of a particular species are resistant may remove competing bacteria and promote overgrowth of the species of concern, which may in turn be resistant to other drugs. This appears to be the explanation for the observation that treatment with cephalosporins, which are ineffective against enterococci, is a risk factor for vancomycin-resistant enterococcus (VRE) (34, 35). However, the model predicts that such an association should be found even when these factors are not at work, and several studies have shown such associations (24, 36, 37); for example, ciprofloxacin use has been documented as a risk factor for plasmid-borne resistance to beta-lactams in enterobacteria, and for plasmid-borne vancomycin resistance in enterococci, although quinolone resistance is chromosomal. It is possible in principle that in each of these hospitals, bacteria resistant to quinolones also tended to carry other, plasmid-borne resistance genes, but none of the studies has reported whether such an association exists.
Prediction ii is easily tested in principle, but in practice it is rarely tested in its pure form, because most interventions designed to control resistance in a hospital combine general infection control measures with measures targeted specifically at resistant bacteria, such as antibiotic use restrictions or cohorting. Also, colonization levels with sensitive bacteria often are not reported. Nonetheless, the use of infection control measures or prophylaxis with unrelated antibiotics does seem to have a particularly strong effect on resistant bacteria (4, 5, 38).
Prediction iii is consistent with the results of a number of empirical studies, in which interventions in hospitals produce rapid reductions in levels of resistance (13, 38–41). Furthermore, this prediction contrasts with both the predictions of mathematical models (16, 42) and the empirical record (16, 43, 44) of responses to interventions designed to control resistance in community-acquired infections. Changes in the prevalence of resistant community-acquired infections typically occur over several years. It is also interesting to note that in this hospital infection model, unlike models of community-acquired infection (9, 16, 42, 45), the frequency of resistance can decline rapidly even when resistance carries no fitness “cost” for the bacteria. This occurs because sensitive bacteria enter the hospital with newly admitted patients, and this “immigration” allows sensitive bacteria to “wash out” resistant bacteria when there is not sufficient selective pressure to maintain resistance.
Each of the three key predictions of the model depend on the assumption that some or all individuals enter the hospital already colonized with antibiotic-sensitive bacteria of the species of interest. Thus, they are expected to hold for hospital-acquired, but not community-acquired infections, and this expectation is confirmed by available data. These predictions show that minor variations in the mathematical structure of models for community-acquired vs. hospital-acquired infections can result in substantial changes in predictions, suggesting that some conclusions of prior models, including those by the present authors, should be reconsidered before applying them to hospital situations (9).
These results suggest several principles for the choice of interventions to control resistance and the assessment of their success. The first principle is that successful interventions in hospitals should show measurable results within weeks to a few months, and studies should be designed to look for such rapid changes. A corollary is that if resistance does not decline on the scale of weeks to months after cessation of antibiotic use, one might suspect that a reservoir (e.g., contaminated surfaces in the hospital, patients with very long durations of stay, or hospital personnel) may be maintaining the prevalence of resistance at high levels.
The second principle is that it is important to measure the effects of antibiotic use both at the individual level (risk factors) and at the ecological level (population prevalence); equivalently, one should distinguish between the effects on an individual of his/her own treatment with an antibiotic, and the effects of use of that antibiotic by others in the hospital. Few studies measure both (for an exception see ref. 46); typically observational epidemiologic studies focus on individual risk factors, whereas intervention studies usually measure population prevalences. If one looked only at individual risk factors, an association between resistance to one antibiotic and prior use of a second might misleadingly suggest that resistance to the first could be reduced by curtailing use of the second. Similarly, risk factors in a study of an antibiotic cycling program might suggest that use of the second antibiotic was prolonging resistance to the first, while in fact it was speeding the decline of that resistance. The distinction between individual-level risks and population-level effects is well known in general (47) and has been elegantly described by Koopman and Longini (48) in the context of infectious disease epidemiology.
Mathematical models simplify some aspects of transmission dynamics to enhance understanding of other aspects. The present model may be compared with the recent model of Austin et al. (15); both describe the transmission dynamics of bacteria in a hospital or intensive-care unit, but the two papers focus on different aspects of the transmission process. Austin et al. (15) analyzed a model for the transmission dynamics of VRE in an intensive-care unit, using parameters estimated from Cook County Hospital in Chicago. The model considered some aspects of transmission not explicitly modeled here, in particular the dynamics of HCWs as vectors of contamination between patients. This study permitted the estimation of rates of VRE transmission from colonized patients to HCWs, and separately transmission from HCWs to uncolonized patients, and allowed the authors to compare the benefits of cohorting and barrier precautions to reduce the spread of VRE. An interesting prediction of their model was that the prevalence of contamination in HCWs may be low although the HCWs are responsible for much or all VRE transmission. In the unit studied, a 15% VRE colonization rate among admitted patients guaranteed the endemic persistence of VRE despite successful control measures.
The model in this paper was more detailed in its consideration of both sensitive and resistant bacteria and of treatment with different drugs, both those for which resistance is present and those for which it is not. This model therefore was able to separate the effects of treatment with different drugs on the prevalence of resistance, describe the contrast between individual-level and population-level effects, and make general statements about the direction and rapidity of changes in resistance after interventions. On the other hand, this paper did not consider the role of HCWs as vectors or attempt to estimate the parameters of the model for a particular hospital.
Finally, we consider the impact of some of the simplifying assumptions of our model. One such assumption is that individuals, once colonized with either sensitive or resistant bacteria, do not become colonized with the other type unless they are first cleared by treatment (or spontaneously). We have analyzed a model that relaxes this assumption and includes such “superinfection.” Although the algebra of the superinfection model is more complicated, the predictions remain qualitatively unchanged, except for prediction ii above. If superinfection is very common, and if transmission rates are also very high, then reductions in within-hospital transmission can have strange effects, in some cases actually increasing the total prevalence of resistance.
A second simplifying assumption is that individuals enter the hospital carrying sensitive bacteria or none at all, but not carrying resistant bacteria. All three predictions of the model continue to hold if a relatively small proportion of patients enter the hospital carrying resistant bacteria. If the proportion of patients entering with resistant bacteria is large, then the decline of resistance will, of course, be slower. In numerical runs of the model, we have found that if this proportion is very large (e.g., 30%), the odds ratio result, prediction i, will no longer hold, though it holds for lower values. Prediction ii holds for all parameters we have tried. A difference is that if individuals are allowed to enter the model already carrying resistant bacteria, then colonization with both resistant and sensitive bacteria is reduced as transmission rates are reduced. In summary, the model in its present form is a good approximation as long as the proportion of patients entering with resistant bacteria is modest compared with the endemic prevalence in the unit. In fact, the prevalence of colonization with resistant bacteria on admission ranges from a few percent to 15–18% in recent studies (35, 36, 49–52), which is considerably lower than the endemic prevalence in many cases. The model can be readily modified to quantitatively evaluate the consequences of having a greater fraction of the patients entering hospitals carrying resistant bacteria.
A more complex model also might include such factors as multiple bacterial species colonizing the same individual, the potential exchange of plasmid-borne multiple drug resistance, variation among patients in the length of hospital stay, and other factors. Because intensive-care units tend to be small, stochastic events may play an important part in the dynamics of resistance in these settings (14, 46). We believe that the particular model considered here (for which resistance to drug 2 is assumed to be absent) may be useful in understanding the short-term dynamics of resistance in hospitals but is almost certainly inappropriate for understanding longer-term or global trends in antibiotic resistance. In the longer run, of course, what one obtains in hospitals with respect to the dissemination of resistant bacteria will reflect what is happening in the community at large. The more appropriate models for regional, national, or global patterns of resistance over a number of years are the population genetic models (42, 53) and the compartment models (9, 17, 26, 27, 29, 45), in which importation of exogenous bacteria does not drive the population dynamics.
Because of the complexity of commensal bacterial communities within hosts and the variation in diseases and treatment among patients in any real hospital, we are skeptical of the ability of such models as these to “fit” accurately the data from a particular hospital. Rather, we believe that these models are primarily useful in identifying the key variables determining the prevalence of resistance in hospitals and its rate of change, making predictions for the population-level effects of interventions that can be tested in clinical studies, and identifying the key outcomes that should be measured in those studies.
Acknowledgments
We thank R. Antia, J. Freeman, J. Smith, and R. A. Weinstein for stimulating discussions and an anonymous referee for helpful comments. This work was supported by National Institutes of Health Grants GM19182 (M.L.), T32-AI0742 (C.T.B.), and GM33782 and AI40662 (B.R.L.).
Abbreviations
VRE
vancomycin-resistant enterococcus
HCW
healthcare worker
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Gaynes R, Monnet D. Ciba Found Symp. 1997;207:47–56. doi: 10.1002/9780470515358.ch4. ; discussion 56–60. [DOI] [PubMed] [Google Scholar]
- 2.Monnet D L, Archibald L K, Phillips L, Tenover F C, McGowan J E, Jr, Gaynes R P. Infect Control Hosp Epidemiol. 1998;19:388–394. doi: 10.1086/647837. [DOI] [PubMed] [Google Scholar]
- 3.Bonten M J, Weinstein R A. Infect Control Hosp Epidemiol. 1996;17:193–200. doi: 10.1086/647274. [DOI] [PubMed] [Google Scholar]
- 4.Gaynes R P, Weinstein R A, Smith J, Carman M, Kabins S A. Infect Control. 1983;4:221–224. doi: 10.1017/s0195941700058264. [DOI] [PubMed] [Google Scholar]
- 5.Slaughter S, Hayden M K, Nathan C, Hu T C, Rice T, Van Voorhis J, Matushek M, Franklin C, Weinstein R A. Ann Intern Med. 1996;125:448–456. doi: 10.7326/0003-4819-125-6-199609150-00004. [DOI] [PubMed] [Google Scholar]
- 6.Boyce J M. Infect Control Hosp Epidemiol. 1996;17:256–261. doi: 10.1086/647289. [DOI] [PubMed] [Google Scholar]
- 7.Brun-Buisson C, Legrand P, Rauss A, Richard C, Montravers F, Besbes M, Meakins J L, Soussy C J, Lemaire F. Ann Intern Med. 1989;110:873–881. doi: 10.7326/0003-4819-110-11-873. [DOI] [PubMed] [Google Scholar]
- 8.McGowan J E., Jr Infect Control. 1986;7:573–576. doi: 10.1017/s0195941700065401. [DOI] [PubMed] [Google Scholar]
- 9.Bonhoeffer S, Lipsitch M, Levin B R. Proc Natl Acad Sci USA. 1997;94:12106–12111. doi: 10.1073/pnas.94.22.12106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Momin F, Chandrasekar P H. Ann Intern Med. 1995;123:205–215. doi: 10.7326/0003-4819-123-3-199508010-00008. [DOI] [PubMed] [Google Scholar]
- 11.Kollef M H, Vlasnik J, Sharpless L, Pasque C, Murphy D, Fraser V. Am J Respir Crit Care Med. 1997;156:1040–1048. doi: 10.1164/ajrccm.156.4.9701046. [DOI] [PubMed] [Google Scholar]
- 12.Price D J, Sleigh J D. Lancet. 1970;2:1213–1215. doi: 10.1016/s0140-6736(70)92179-3. [DOI] [PubMed] [Google Scholar]
- 13.Dunkle L M, Naqvi S H, McCallum R, Lofgren J P. Am J Med. 1981;70:455–458. doi: 10.1016/0002-9343(81)90787-7. [DOI] [PubMed] [Google Scholar]
- 14.Austin D J, Bonten M J M, Weinstein R A, Slaughter S, Bergmans D C J, Stobberingh E E, Anderson R M. 39th ICAAC. Washington, DC: Am. Soc. Microbiol.; 1999. p. 706. [Google Scholar]
- 15.Austin D J, Bonten M J, Weinstein R A, Slaughter S, Anderson R M. Proc Natl Acad Sci USA. 1999;96:6908–6913. doi: 10.1073/pnas.96.12.6908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Austin D J, Kristinsson K G, Anderson R M. Proc Natl Acad Sci USA. 1999;96:1152–1156. doi: 10.1073/pnas.96.3.1152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Blower S M, Small P M, Hopewell P C. Science. 1996;273:497–500. doi: 10.1126/science.273.5274.497. [DOI] [PubMed] [Google Scholar]
- 18.Freeman J, McGowan J E., Jr J Infect Dis. 1978;138:811–819. doi: 10.1093/infdis/138.6.811. [DOI] [PubMed] [Google Scholar]
- 19.Weinstein R A. Bull NY Acad Med. 1987;63:337–344. [PMC free article] [PubMed] [Google Scholar]
- 20.Rao G G. Drugs. 1998;55:323–330. doi: 10.2165/00003495-199855030-00001. [DOI] [PubMed] [Google Scholar]
- 21.Hawkey P M. J Antimicrob Chemother. 1986;18, Suppl. C:133–139. doi: 10.1093/jac/18.supplement_c.133. [DOI] [PubMed] [Google Scholar]
- 22.Hoiby N, Jarlov J O, Kemp M, Tvede M, Bangsborg J M, Kjerulf A, Pers C, Hansen H. Lancet. 1997;349:167–169. doi: 10.1016/S0140-6736(96)09229-X. [DOI] [PubMed] [Google Scholar]
- 23.McGowan J E., Jr Rev Infect Dis. 1983;5:1033–1048. doi: 10.1093/clinids/5.6.1033. [DOI] [PubMed] [Google Scholar]
- 24.De Champs C, Rouby D, Guelon D, Sirot J, Sirot D, Beytout D, Gourgand J M. J Hosp Infect. 1991;18:5–13. doi: 10.1016/0195-6701(91)90088-p. [DOI] [PubMed] [Google Scholar]
- 25.Schwalbe R S, Hoge C W, Morris J G, Jr, O'Hanlon P N, Crawford R A, Gilligan P H. Antimicrob Agents Chemother. 1990;34:161–163. doi: 10.1128/aac.34.1.161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Blower S M, Porco T C, Darby G. Nat Med. 1998;4:673–678. doi: 10.1038/nm0698-673. [DOI] [PubMed] [Google Scholar]
- 27.Austin D J, Kakehashi M, Anderson R M. Proc R Soc London Ser B. 1997;264:1629–1638. doi: 10.1098/rspb.1997.0227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Austin D J, Bonten M J. Memorias do Instituto Oswaldo Cruz. 1998;93:587–588. doi: 10.1590/s0074-02761998000500005. [DOI] [PubMed] [Google Scholar]
- 29.Massad E, Lundberg S, Yang H M. Int J Biomed Comput. 1993;33:65–81. doi: 10.1016/0020-7101(93)90060-j. [DOI] [PubMed] [Google Scholar]
- 30.Sebille V, Chevret S, Valleron A J. Infect Control Hosp Epidemiol. 1997;18:84–92. doi: 10.1086/647560. [DOI] [PubMed] [Google Scholar]
- 31.Sebille V, Valleron A J. Computers Biomed Res. 1997;30:307–322. doi: 10.1006/cbmr.1997.1451. [DOI] [PubMed] [Google Scholar]
- 32.Freeman J, Hutchison G B. Am J Epidemiol. 1980;112:707–723. doi: 10.1093/oxfordjournals.aje.a113043. [DOI] [PubMed] [Google Scholar]
- 33.Falkow S. Infectious Multiple Drug Resistance. London: Pion; 1975. [Google Scholar]
- 34.Rao G G, Ojo F, Kolokithas D. J Hosp Infect. 1997;35:63–69. doi: 10.1016/s0195-6701(97)90169-9. [DOI] [PubMed] [Google Scholar]
- 35.Weinstein J W, Roe M, Towns M, Sanders L, Thorpe J J, Corey G R, Sexton D J. Infect Control Hosp Epidemiol. 1996;17:36–41. doi: 10.1086/647186. [DOI] [PubMed] [Google Scholar]
- 36.Morris J G, Jr, Shay D K, Hebden J N, McCarter R J, Jr, Perdue B E, Jarvis W, Johnson J A, Dowling T C, Polish L B, Schwalbe R S. Ann Intern Med. 1995;123:250–259. doi: 10.7326/0003-4819-123-4-199508150-00002. [DOI] [PubMed] [Google Scholar]
- 37.Wiener J, Quinn J P, Bradford P A, Goering R V, Nathan C, Bush K, Weinstein R A. J Am Med Assoc. 1999;281:517–523. doi: 10.1001/jama.281.6.517. [DOI] [PubMed] [Google Scholar]
- 38.Cosseron-Zerbib M, Roque Afonso A M, Naas T, Durand P, Meyer L, Costa Y, el Helali N, Huault G, Nordmann P. J Hosp Infect. 1998;40:225–235. doi: 10.1016/s0195-6701(98)90140-2. [DOI] [PubMed] [Google Scholar]
- 39.Boyce J M, Landry M, Deetz T R, DuPont H L. Infect Control. 1981;2:110–116. doi: 10.1017/s0195941700053881. [DOI] [PubMed] [Google Scholar]
- 40.Franco J A, Eitzman D V, Baer H. Am J Dis Children. 1973;126:318–321. doi: 10.1001/archpedi.1973.02110190280006. [DOI] [PubMed] [Google Scholar]
- 41.Lilly H A, Lowbury E J. J Antimicrob Chemother. 1978;4:545–550. doi: 10.1093/jac/4.6.545. [DOI] [PubMed] [Google Scholar]
- 42.Stewart F M, Antia R, Levin B R, Lipsitch M, Mittler J E. Theor Popul Biol. 1998;53:152–165. doi: 10.1006/tpbi.1997.1352. [DOI] [PubMed] [Google Scholar]
- 43.Arason V A, Kristinsson K G, Sigurdsson J A, Stefansdottir G, Molstad S, Gudmundsson S. Br Med J. 1996;313:387–391. doi: 10.1136/bmj.313.7054.387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Seppala H, Klaukka T, Vuopio-Varkila J, Muotiala A, Helenius H, Lager K, Huovinen P. N Eng J Med. 1997;337:441–446. doi: 10.1056/NEJM199708143370701. [DOI] [PubMed] [Google Scholar]
- 45.Austin D J, Kakehashi M, Anderson R M. Proc R Soc London Ser B. 1997;264:1629–1638. doi: 10.1098/rspb.1997.0227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Garber A M. Biometrics. 1989;45:797–816. [PubMed] [Google Scholar]
- 47.Morgenstern H. In: Modern Epidemiology. Rothman K J, Greenland S, editors. Philadelphia: Lippincott–Raven; 1998. pp. 459–480. [Google Scholar]
- 48.Koopman J S, Longini I M., Jr Am J Public Health. 1994;84:836–842. doi: 10.2105/ajph.84.5.836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.D'Agata E M, Venkataraman L, DeGirolami P, Burke P, Eliopoulos G M, Karchmer A W, Samore M H. Crit Care Med. 1999;27:1090–1095. doi: 10.1097/00003246-199906000-00026. [DOI] [PubMed] [Google Scholar]
- 50.Ostrowsky B E, Venkataraman L, D'Agata E M, Gold H S, DeGirolami P C, Samore M H. Arch Intern Med. 1999;159:1467–1472. doi: 10.1001/archinte.159.13.1467. [DOI] [PubMed] [Google Scholar]
- 51.Nishi J I, Shirao K, Ito H, Yoshinaga M, Yoshinaka H, Miyanohara H, Hirata S, Ogawa H, Kitajima I, Maruyama I, et al. Infect Control Hosp Epidemiol. 1998;19:107–109. doi: 10.1086/647776. [DOI] [PubMed] [Google Scholar]
- 52.Bonten M J, Slaughter S, Hayden M K, Nathan C, van Voorhis J, Weinstein R A. Crit Care Med. 1998;26:2001–2004. doi: 10.1097/00003246-199812000-00029. [DOI] [PubMed] [Google Scholar]
- 53.Levin B R, Lipsitch M, Perrot V, Schrag S, Antia R, Simonsen L, Walker N M, Stewart F M. Clin Infect Dis. 1997;24:S9–16. doi: 10.1093/clinids/24.supplement_1.s9. [DOI] [PubMed] [Google Scholar]
- 54.Bonten M J, Hayden M K, Nathan C, van Voorhis J, Matushek M, Slaughter S, Rice T, Weinstein R A. Lancet. 1996;348:1615–1619. doi: 10.1016/S0140-6736(96)02331-8. [DOI] [PubMed] [Google Scholar]
- 55.Barber M, Dutton A A C, Beard M A, Elmes P C, Williams R. Br Med J. 1960;1:12–16. doi: 10.1136/bmj.1.5165.11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Johanson W G, Jr, Pierce A K, Sanford J P, Thomas G D. Ann Intern Med. 1972;77:701–706. doi: 10.7326/0003-4819-77-5-701. [DOI] [PubMed] [Google Scholar]
- 57.Bonten M J, Gaillard C A, Johanson W G, Jr, van Tiel F H, Smeets H G, van der Geest S, Stobberingh E E. Am J Respir Crit Care Med. 1994;150:1332–1340. doi: 10.1164/ajrccm.150.5.7952561. [DOI] [PubMed] [Google Scholar]
- 58.Lucet J C, Chevret S, Decre D, Vanjak D, Macrez A, Bedos J P, Wolff M, Regnier B. Clin Infect Dis. 1996;22:430–436. doi: 10.1093/clinids/22.3.430. [DOI] [PubMed] [Google Scholar]