Synaptic depression enables neuronal gain control (original) (raw)
. Author manuscript; available in PMC: 2009 Aug 19.
Published in final edited form as: Nature. 2009 Jan 14;457(7232):1015–1018. doi: 10.1038/nature07604
Abstract
To act as computational devices, neurons must perform mathematical operations as they transform synaptic and modulatory input into output firing rate1. Experiments and theory suggest that neuronal firing typically represents the sum of synaptic inputs1-3, an additive operation, but multiplication of inputs is essential for many computations1. Multiplication by a constant produces a change in the slope, or gain, of the input-output relation, amplifying or scaling down the neuron's sensitivity to changes in its input. Such gain modulation occurs in vivo, during contrast invariance of orientation tuning4, attentional scaling5, translation-invariant object recognition6, auditory processing7 and coordinate transformations8,9. Moreover, theoretical studies highlight the necessity of gain modulation in several of these tasks9-11. While potential cellular mechanisms for gain modulation have been identified, they often rely on membrane noise and require restrictive conditions to work3,12-18. Because nonlinear components are used to scale signals in electronics, we examined whether synaptic nonlinearities are involved in neuronal gain modulation. We used synaptic stimulation and dynamic-clamp to investigate gain modulation in granule cells (GCs) in acute cerebellar slices. Here we show that when excitation is mediated by synapses with short-term depression (STD), neuronal gain is controlled by an inhibitory conductance in a noise-independent manner, allowing driving and modulatory inputs to be multiplied together. The nonlinearity introduced by STD transforms inhibition-mediated additive shifts in the input-output relation into multiplicative gain changes. When GCs were driven with bursts of high-frequency mossy fibre (MF) input, as observed in vivo19,20, larger inhibition-mediated gain changes were observed, as expected with greater STD. Simulations of synaptic integration in more complex neocortical neurons confirm that STD-based gain modulation can also operate in neurons with large dendritic trees. Our results establish that neurons receiving depressing excitatory inputs can act as powerful multiplicative devices even when integration of postsynaptic conductances is linear.
The way a neuron transforms signals can be captured by its input-output relation (Fig. 1a). A modulatory input can change the shape of this relation, thereby performing a mathematical operation on this transfer function. A shift along the input axis corresponds to an additive operation (+), while a change in slope corresponds to a multiplicative operation, or gain change (×). Cerebellar GCs are well suited for studying gain modulation because they have few synaptic inputs. Excitation comes from ~4 MFs, which can sustain rate-coded signals over a large bandwidth20 and exhibit STD19,21. Inhibition comes from Golgi cells, most of which is mediated by a modulatable tonic GABAA receptor (GABAR) conductance22. Since it is difficult to activate multiple inputs independently, and since we wanted to compare real synaptic inputs exhibiting frequency-dependent STD with artificial synaptic inputs without STD, we used dynamic-clamp to study synaptic integration. GCs are ideal for this because their soma and dendrites form a single electrical compartment, allowing dendritic inputs to be mimicked by somatic conductance injection13.
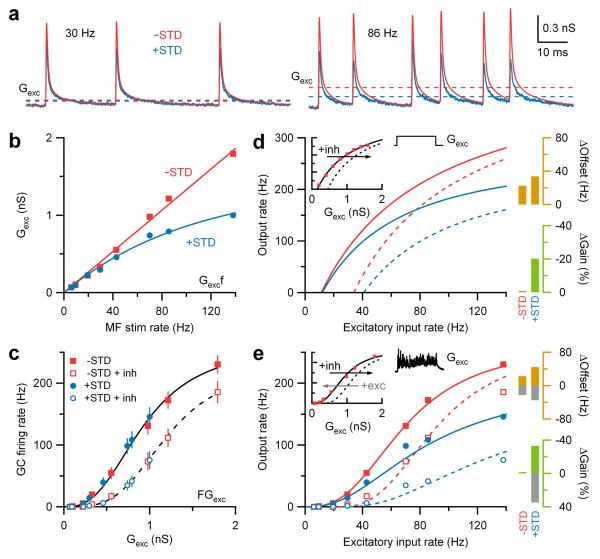
Figure 1. Synaptic depression enhances inhibition-mediated gain modulation.
a, Hypothetical neuronal input-output relation before (black) and after multiplicative gain modulation (green, ×) and an additive offset (orange, +).
b, Averaged AMPAR-mediated synaptic train exhibiting STD (blue trace) in response to Poisson stimulation (black ticks; f = 86 Hz) of single MF inputs. Red trace shows corresponding artificial synaptic train without STD.
c, The sum of 4 independent synaptic trains (each f = 86 Hz) with and without STD injected into a GC via dynamic clamp (_G_clamp) with and without tonic inhibition (black and gray; _G_inh = 500 pS). Right vertical ticks indicate spike times. Horizontal bars indicate output rate measurement window. _V_rest = −79 mV.
d, Average input-output relations (n = 9) with and without STD (blue and red) and tonic inhibition (open and closed symbols). Lines are fits to a Hill function (Eq. 5; Supplementary Table 1).
e, Gain (green) and offset (orange) changes due to STD (±STD) and inhibition (±inh) from fits in d.
We measured AMPA receptor (AMPAR)-mediated excitatory post-synaptic currents (EPSCs) from mature GCs at physiological temperature during Poisson-type stimulation of single MFs at different frequencies. These EPSC trains, which exhibited STD, were then converted to conductance (Fig. 1b, +STD, blue traces throughout). Artificial conductance trains without STD (−STD, red traces throughout), but with identical event timing, were constructed by adding a fixed amplitude synaptic conductance waveform at each stimulus time. The effects of STD on synaptic integration were then investigated by injecting the sum of 4 statistically independent conductance trains with the same mean MF rate into GCs using dynamic-clamp and measuring the mean output firing rate with and without STD (Fig. 1c). The resulting steady-state input-output relations revealed that STD had an almost purely multiplicative effect under control conditions (Fig. 1d). Multiplicative and additive transformations of the input-output relation were quantified by fitting the data to Hill-like equations16 (Fig. 1d; Supplementary Table 1) and measuring the change in slope (Fig. 1e; ΔGain, green) and the shift in the half maximal response (ΔOffset, orange). In the absence of STD, adding a tonic inhibitory conductance (Fig. 1c, _G_inh = 500 pS), close to the physiological value (438 ± 93 pS; n=10) produced a modest scaling of the input-output relation together with an additive shift13 (Fig. 1d, e). In contrast, the same level of inhibition produced a 4-fold larger gain change in the input-output relation when driven with depressing synapses. Moreover, this multiplicative scaling was nearly constant over the entire input range (Supplementary Fig. 1).
To understand how STD performs multiplicative gain modulation, we examined the frequency-dependence of the time-averaged excitatory conductances (_G_exc; Fig. 2a, dashed lines). Without STD, the relation between _G_exc and MF input rate (f) was linear (Fig. 2b). With STD, it became noticeably sublinear above 40 Hz and could be fit with an exponential function (Fig. 2b). To examine how _G_exc was integrated postsynaptically, we plotted the mean GC firing rate (F) as a function of _G_exc. We found that the _FG_exc relations with and without STD overlaid (Fig. 2c), indicating that _G_exc was integrated similarly for both cases. Thus the non-linearity between f and _G_exc introduced by STD underlies the enhanced gain modulation.
Figure 2. Synaptic depression transforms additive shifts into multiplicative gain modulation.
a, Average AMPAR-mediated synaptic trains with and without STD (blue and red) with their time-averaged conductances (_G_exc, dashed lines).
b, _G_exc versus MF rate f with and without STD. Red line is a linear fit (Eq. 3). Blue line is an exponential fit (Eq. 4).
c, Data in Fig. 1d plotted as output rate (F) versus _G_exc. Lines are Hill fits (Eq. 5).
d, Predicted input-output relations computed from G_exc_f relations in b, and experimentally measured GC _FG_exc relation generated with noise-free excitatory conductance steps (inset, red squares from Fig. 2b in ref. 13). Solid line in inset is a Hill fit, and dashed line is the same curve rightward shifted 0.3 nS along the _G_exc-axis. Bar graphs show changes in gain (green) and offset (orange) due to inhibition with and without STD.
e, Same as d, except control _FG_exc data (inset) is from c during noisy synaptic excitation. The predicted change in the input-output relation for STD match the experimental observations (blue symbols). Grey bars show gain and offset changes for a leftward shift of 0.3 nS to simulate excitation.
Since neuronal gain can be altered by synaptic noise3,13, we examined how STD transforms GC _FG_exc relations generated with noise-free conductance steps (Fig. 2d, inset13) and noisy synaptic conductances (Fig. 2e, inset). Hill equations were used to mimic _FG_exc relations (Fig. 2d-e insets) while linear and exponential functions were used to represent G_exc_f relations (Fig. 2b). These were then combined to predict the input-output relations. In the absence of STD, additive shifts in the _FG_exc relation produced a purely additive shift in the input-output relation (Fig. 2d-e), consistent with conductance performing an additive operation when the noise level is constant2,3. In contrast, when STD was present, additive shifts in the _FG_exc relation produced robust gain changes in the input-output relation for both noise-free or noisy excitation (Fig. 2d-e). Indeed, the gain change predicted from purely additive shifts in the _FG_exc relation accounted for most of that observed experimentally (Fig. 2e). This shows that STD transforms linear, additive modulation of the _FG_exc relation into multiplicative gain modulation of the input-output relation, irrespective of the presence of synaptic noise.
Our experimental results were reproduced in a conductance-based integrate-and-fire model that included short-term synaptic plasticity (Supplementary Fig. 2a-b) confirming the primary role of STD in gain modulation, rather than synaptic noise or other non-linear synaptic mechanisms, such as AMPAR activation via spillover23. Increasing the level of STD increased the inhibition-mediated gain reduction (Supplementary Fig. 2c-d). Conversely, increasing the level of tonic inhibition increased the size of the gain reduction at all levels of STD. We also observed gain modulation with phasic inhibitory conductances which are widespread in the CNS (Supplementary Fig. 3), confirming that STD-mediated gain modulation operates effectively with both phasic and tonic inhibition.
NMDA receptors (NMDARs) contribute to transmission at many central synapses and exhibit a nonlinear voltage-dependence. To examine, experimentally, how this synaptic component interacts with STD-based gain modulation, we measured the NMDAR component during Poisson stimulation of a single MF input and added it to the AMPAR conductance trains from the same GCs (Fig. 3a). The G_exc_f relations for the combined AMPAR and NMDAR components (Fig. 3b) were similar in shape to the AMPAR–only cases with and without STD (Fig. 2b), because the relationship between the mean NMDAR conductance and MF frequency was approximately linear (Fig. 3b, inset, and Supplementary Fig. 4). In the absence of AMPAR STD, 500 pS inhibition produced a slightly smaller gain reduction in the GC input-output relation (Fig. 3c-d, 7.1%) than the AMPAR component alone (Fig1 d-e, 12.6%), as predicted for noise-based gain modulation24. However, a robust inhibition-mediated gain reduction was observed with the depressing AMPAR component (Fig. 3d, 33.1%). These results show that synaptic activation of NR2C containing NMDARs in adult GCs25 is approximately linear with frequency and that this has little effect on STD-based gain modulation.
Figure 3. Gain modulation in the presence of synaptic NMDAR conductances.
a, Average AMPAR (blue) and NMDAR (black) synaptic conductance trains from the same 4 GCs during Poisson stimulation of individual MF inputs.
b, _G_exc versus MF rate (f) for AMPAR+NMDAR components with and without AMPAR STD. Red and blue lines are fits to Eqs. 3 and 4. Inset: G_exc_f relations for NMDAR with and without AMPAR STD (circles and squares).
c, Average input-output relations for AMPAR+NMDAR with and without AMPAR STD and tonic inhibition. Lines are Hill fits (Eq. 5).
d, Gain (green) and offset (orange) changes due to STD (±STD) and tonic inhibition (±inh) from fits in c.
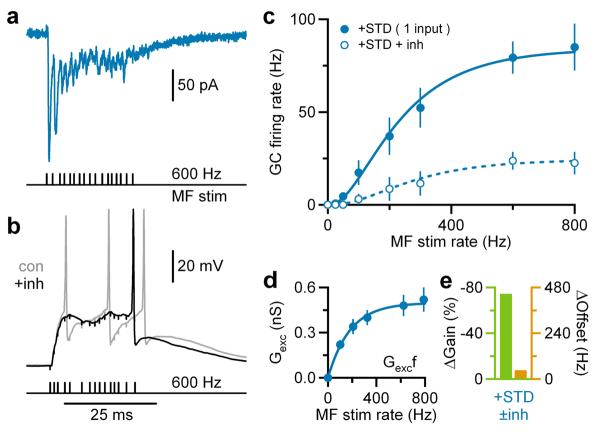
In vivo recordings show that finger extension20 and facial stimulation19 can produce high frequency bursts of MF firing. To examine whether STD-mediated gain modulation can operate under such conditions, we recorded from GCs while stimulating individual MFs with high frequency bursts to mimic activity in vivo19,20. This induced bursts of mixed AMPAR-NMDAR EPSCs under voltage-clamp, confirming reliable MF activation (Fig. 4a). In current-clamp, this produced GC firing19 from a potential of −75mV (Fig. 4b). Firing rate was measured from the 4th stimuli to allow time for EPSC depression to occur21. A 500 pS tonic inhibitory conductance reduced firing (Fig. 4b) and produced a robust reduction in neuronal gain (Fig. 4c) that was 2-fold larger than for the 4-fibre excitation (Fig. 3d and Fig. 4e). The powerful nonlinearity between _G_exc and f (Fig. 4d), combined with a purely additive shift in the _FG_exc relation, accounted for most of the inhibition-mediated gain change (Supplementary Fig. 5), confirming it was mediated predominantly by STD.
Figure 4. Gain modulation during broad bandwidth single mossy fibre stimulation.
a, Mixed AMPAR+NMDAR EPSCs in GCs during single MF, Poisson burst-like stimulation (black ticks) at −75mV. Stimulus artifacts subtracted.
b, Voltage responses to burst-like MF stimulation with and without tonic inhibition (±inh; black and gray; _G_inh = 500 pS) injected via dynamic clamp. Black horizontal bar indicates firing rate measurement window. _V_rest = −74mV.
c, Average GC input-output relation ±inh for single MF stimulation (n = 7) with Hill fits (Eq. 5).
d, Mean between relationship _G_exc and MF stimulation rate (f). Blue line is an exponential fit (Eq. 4).
e, Gain (green) and offset (orange) changes due to inhibition (±inh) computed from fits in c.
Several factors complicate the implementation of multiplicative operations in neurons with extensive dendritic trees. The large voltage fluctuations required for noise-based gain modulation3,13,16,17 are difficult to achieve with many inputs and heavy dendritic filtering, without precisely balanced excitation and inhibition3. Moreover, multiplication via nonlinear dendritic integration26 or a combination of noise and dendritic saturation17 requires spatially localized activation of synapses on a single dendritic branch, but these are usually distributed over the tree, making linear synaptic integration more likely26. To test whether the STD-mediated gain modulation can operate effectively in more complex neurons than GCs, we simulated synaptic integration in a neocortical layer 5 neuron model27 with hundreds of synaptic inputs, randomly distributed over the basolateral dendritic tree (Fig. 5a; Methods). These simulations show that inhibitory synaptic input can act as a powerful modulator of neuronal gain when excitation is mediated by depressing synapses and yet perform a largely additive operation when it is absent (Fig. 5b-e). These results demonstrate that multiplicative operations are possible in cells with large dendritic arbours under conditions of linear integration when excitation is mediated by depressing synapses.
Figure 5. Multiplicative gain modulation in a cortical layer 5 pyramidal neuron model.
a, Layer 5 neuron model with location of excitatory (red circles) and inhibitory (green) synaptic contacts. Bottom: black trace shows spiking during synaptic excitation and inhibition.
b, Top: conductance train for non-depressing unitary excitatory synaptic input. Bottom: input-output relation for non-depressing synaptic excitation (−STD, red) for control conditions (solid symbols) and various rates of synaptic inhibition (open symbols) together with Hill fits (Eq. 5).
c, Gain (green) and offset (orange) changes due to different inhibition rates (±inh) in absence of STD from fits in b.
d, As for b, but for depressing synaptic excitation (+STD, blue) together with Hill fits.
e, As for c, but for depressing synaptic excitation (+STD) from fits in d.
In vivo, MF-GC synapses typically operate at high frequencies20, where STD is pronounced19, although low frequency vestibular inputs are a notable exception, where STD is absent and linear transmission is preserved28. At 100 Hz, STD is mediated predominantly by AMPAR desensitization21. AMPARs can therefore act as nonlinear ‘molecular amplifiers’ that contribute to single cell computation. Although vesicle replenishment is rapid at MF release sites21, it will become limiting at higher frequencies and presynaptic STD will dominate. Presynaptic STD exhibits a range of frequency-dependencies across central synapses and can be modulated by long-term plasticity29, potentially allowing gain modulation to be matched to the operational frequency of the inputs.
Multiplication of driving and modulatory input conductance is most effective when synaptic depression has reached steady-state. Since EPSC depression occurs rapidly in GCs (τonset = 1.5 pulses)21, gain modulation will only require a 4-75 ms settling time (2τonset/frequency; 40-800 Hz), but at cortical synapses where STD occurs at lower frequencies gain modulation will be slower. STD-mediated gain modulation allows a modulatory conductance to scale a neuron's sensitivity to all of its driving inputs. This is distinct from the transient synaptic responses to changes in input rate, which allows signalling independent of absolute rate30. STD can therefore perform distinct multiplicative operations on different time scales: transient enhancement of the gain of dynamically changing inputs before STD has developed, and multiplication of all driving and modulatory inputs once depression has occurred.
Our findings show that the mathematical operation performed by a modulatory input on a particular set of driving inputs depends on their STD characteristics. This could allow input configuration specific, and thus context dependent computation at the level of a single neuron. The widespread incidence of STD, its compatibility with linear synaptic integration and the lack of dependence on synaptic noise, suggests that this cellular mechanism for gain modulation could be used to multiply inputs together in many different neuronal types in the brain.
Methods Summary
Whole-cell recordings were made from GCs at 35.3 ± 0.1°C (n=62) in rat cerebellar slices (P30-40). EPSC trains for conductance clamp were recorded during stimulation of a single MF input at random Poisson intervals (mean rate f = 6-138 Hz). The NMDAR EPSC component was isolated by recording in 5 μM NBQX. The AMPAR EPSC component was obtained by subtracting control and NBQX recordings. Conductance trains at each frequency were constructed by averaging 10 responses, subtracting stimulus artefacts, dividing by the holding potential and averaging responses from 4 different GCs. AMPAR, NMDAR, and tonic GABAR conductances with reversal potentials of 0 mV, 0mV and −75 mV, respectively, were injected into GCs using a dynamic-clamp amplifier. Inhibition was blocked with 10 PM SR95531. Direct activation of GC firing was achieved with single MF excitation using a 15-pulse Poisson stimulation (25-800 Hz). To minimize the effects of any time-dependent changes in excitability, MF excitation was randomized, control and tonic inhibition measurements interleaved and experiments were carried out within 15 minutes of going whole-cell. The cortical layer 5 neuron model27 was connected to 400 excitatory neurons and 30 inhibitory neurons using neuroConstuct (www.NeuroConstruct.org) and run on the NEURON simulator (www.neuron.yale.edu). Data is presented as mean ± s.e.m.
Methods
Parasagittal slices (200-250 μm) of the cerebellar vermis were prepared23,31,32 from Sprague-Dawley rats (P30-40) in ACSF solution containing (in mM): 125 NaCl, 2.5 KCl, 26 NaHCO3, 1.25 NaH2PO4, 2 CaCl2, 1 MgCl2, 25 glucose, 0.5 ascorbic acid (pH 7.4 when bubbled with 95% O2 and 5% CO2), or a low-sodium sucrose solution (in mM): 85 NaCl, 2.5 KCl, 26 NaHCO3, 1.25 NaH2PO4, 0.5 CaCl2, 4 MgCl2, 25 glucose, 63.4 sucrose, 0.5 ascorbic acid. In some preparations 1 mM kynurenic acid or 10 μM D-AP5 was added. After ~30 min incubation at 32°C, slices were transferred to ACSF solution at room temperature. Whole-cell recordings with a series resistance of 27.9 ± 1.3 MΩ (n=62) were made with an Axopatch 200B amplifier, filtered at 7-10 kHz, and digitized at 33-100 kHz using an InstruTech ITC-18 board and Axograph or NeuroMatic software (www.neuromatic.thinkrandom.com). GCs had a cell capacitance of 3.2 ± 0.1 pF (n=62) and a resting membrane potential of −78.5 ± 0.9 mV (n=52). Data was analysed using NeuroMatic within the Igor Pro environment (WaveMetrics, Oregon).
Synaptic conductance trains and dynamic clamp
Whole-cell recordings were made from GCs perfused with ACSF containing 0.3 μM strychnine and 10 μM SR95531 (Gabazine) to block inhibitory receptors, and 3 μM glycine to ensure NMDAR activation. Recordings of EPSC trains to be used for dynamic clamp were made at −54 or −60 mV, using fire-polished borosilicate micropipettes containing (in mM): 110 KmeSO3, 4 NaCl, 1.78 CaCl2, 0.3 Na-GTP, 4 Mg-ATP, 40 HEPES and 5 EGTA (pH 7.3), or in some cases: 90 CsCl, 10 NaCl, 1.78 CaCl2, 0.3 Na-GTP, 4 Mg-ATP, 40 HEPES, 5 EGTA and 5 TEA (pH 7.3). EPSCs were evoked by extracellular stimulation of a single MF input31 using Poisson stimulation trains (PSTs) of 250-2500 ms duration with a 1 ms minimum refractory interval. Ten repetitions of 4 statistically different PSTs were recorded from each MF-GC synapse at each frequency. Stimulus artefacts were removed by convolving a single stimulus artefact with the PST, and subtracting the resulting waveform from the averaged data. Synaptic current trains were converted to conductance trains by dividing by the holding potential, after correcting for the liquid junction potential13,32. Conductance trains with the same statistics from 4 different GCs were aligned and averaged, and had a mean conductance close to the population mean23,32. To create non-depressing AMPAR conductance trains, the first AMPAR response of each train was fit with the following multiple-exponential function:
| G(t)=(1−e−t∕τr)n[a1e−t∕τd1+a2e−t∕τd2+a3e−t∕τd3] | (1) |
|---|
where τr and τd1-3 are the time constants of the rising and decaying components, respectively. The resulting fit was then convolved with the given PST to create a non-depressing train (Fig. 1b, red trace).
Dynamic-clamp recordings and spike analysis
Slices were perfused with ACSF containing 10 μM SR95531 to block tonic GABAA-receptor (GABAR) currents. Dynamic-clamp recordings33,34 were made from GCs using fire-polished borosilicate micropipettes containing (in mM): 114 KmeSO3, 6 NaOH, 3 MgCl2, 0.02 CaCl2, 0.3 Na-GTP, 4 Na-ATP, 40 HEPES, 0.15 BAPTA (pH 7.3). A liquid junction potential of +6.3 mV (n=5) was corrected prior to gaining whole-cell access. During recordings, the resting membrane potential (_V_rest) was maintained near −80 mV using small amounts of holding current. Conductance trains were injected with a 3-channel SM1 amplifier (Cambridge Conductance, UK). Since GCs receive an average of 4 MF inputs, and often require more than one input to fire35,36, AMPAR conductance trains (and NMDAR conductance trains) from 4 statistically different PSTs were summated together at each input frequency f before injection into GCs via dynamic clamp as described below.
Unlike the AMPAR component, which follows a simple linear Ohmic relation with voltage, the NMDAR component introduced by the SM1 amplifier has a Boltzmann-like non-linearity that mimics the voltage-dependent Mg2+ block of the NMDA conductance measured in GCs (Supplementary Fig. 4). This non-linearity introduced by the SM1 amplifier required scaling of the NMDAR conductance waveforms so that the final peak value, after leaving the SM1 amplifier, matched that of GCs, as described by the following Boltzmann function:
| Gexc(V)=Gmax1+e−(V−V0.5)∕k | (2) |
|---|
where _G_max = 367.9 pS, _V_0.5 = −12.8 mV and k = 22.4 mV (n=6 cells; curve fit to data in Supplementary Fig. 4a). During the experiments, conductance trains at various f were injected in random order, and conditions with and without tonic inhibition (_G_inh = 500 pS; steps began 10 ms before onset of the synaptic input) were presented consecutively at each f. Some GCs were excluded since their output spike rate was too low or absent in the presence of STD and tonic inhibition (13/36 cells), preventing an accurate measurement of a gain change. This will tend to underestimate the gain change we report. Cells were also discarded if the heights of their action potentials changed more than 10% during the experiment (3/36 cells). For dynamic clamp experiments, GC output firing rate (F) was calculated from 100 ms after the onset to the end of the stimulus train. Action potentials were detected using a threshold-level detection set at 0 mV.
Granule cell excitation with mossy fibre stimulation
GCs were directly activated by stimulating single MF inputs with burst PSTs (f = 25-800 Hz; 1 ms minimum refractory interval) to mimic in vivo MF activity19,20. Bursts lasted for a period T = 15 / f seconds, consisting of approximately 15 stimuli. Average conductance and output spike rate were computed over the same period T, but starting from the time of the 4th stimulus, when STD reached approximate steady-state levels21. Recording conditions were the same as those described for the dynamic-clamp recordings, except _V_rest was maintained at −75mV rather than −80 mV since the majority of GCs (69%; n=22 of 32) either did not fire action potentials when stimulated from their resting potential or did not produce enough output spikes to compute an input-output relation in the range 25-800 Hz. Tonic inhibition was applied with dynamic clamp (_G_inh = 500 pS; steps began 75 ms before onset of the synaptic stimulation) and was alternated with control conditions at each f.
Data analysis
Plots of average excitatory conductance (_G_exc) versus MF input rate f (G_exc_f relations; Figs. 2b and 3b) were fit with a linear equation for AMPAR conductances without STD:
and an exponential function for AMPAR conductances with STD:
where λ is a frequency constant and m is a shared slope factor. At low frequencies (f << λ), these two equations are approximately equal. Plots of GC firing rate F versus _G_exc (_FG_exc relations) were well described by a Hill equation of the form:
| F(Gexc)=Fmax1+(Gexc50/Gexc)n+F0 | (5) |
|---|
where n is the exponent factor, _F_0 the firing rate offset, _F_max the maximum firing rate and _G_exc50 is the value of _G_exc at which F reaches half maximum. For n = 1, the relation is a simple saturating function (Fig. 2d, inset) and for n > 1, the relation is sigmoidal (Fig. 2c). Input-output relations (Figs. 1d, 3c and 4c) were also fit with Eq. 5, but with _G_exc(f) substituted for _G_exc, where _G_exc(f) was described by Eq. 3 for the AMPAR component without STD, and Eq. 4 for STD (λ and m held constant during the fits). Similar results were obtained by fitting a simple Hill function (Eq. 5), with f substituted for _G_exc, but the STD input-output data were less well described by this function than when Eqs 4 and 5 were combined, as theoretically predicted. Fits to input-output relations were compared using the F-ratio for the separate and combined data sets. All fits were significantly different (P << 0.05). The gain was calculated from the average slope (_F_′) of the fits between 5% and 75% its maximum value. An upper limit of 75% was used so that all computations of _F_′ were limited to the range of our experimental data. Changes in gain (ΔGain) were computed as follows:
| ΔGain=(F+a′−F−a′F−a′) | (6) |
|---|
where +a and −a denote conditions with and without inhibition (±inh) or with and without STD (±STD). Additive offset shifts (ΔOffset) were defined as the difference between the half-maximum frequencies of the fits for the two conditions +a and −a.
Neuronal models
A GC-like conductance-based integrate-and-fire (IaF) model was implemented in the NEURON simulation environment37 and was described by the following equation:
| −CmdVdt=(V−EL)Rm+D(t)GAMPAR(V−EAMBAR)+GGABAR(V−EGABAR) | (7) |
|---|
where Cm = 3.1 pF, the reversal potentials for the leak EL = −75 mV, AMPARs EAMPAR = 0 mV, GABARs EGABAR = −75 mV, and a membrane resistance Rm = 2.6 GΩ13,32. Spikes were generated when the model reached a threshold of −49 mV, at which time the voltage was set to 10 mV for one integration time step, then clamped to −75 mV for a refractory period of 2.5 ms. The AMPAR conductance was described by Eq. 1, using the following values computed from fits to our GC AMPAR conductance data: n = 11, τr = 0.10 ms, a1 = 2.23 nS, τd1 = 0.45 ms, a2 = 0.29 nS, τd2 = 2.88 ms, a3 = 0.08 nS and τd3 = 21.67 ms. For simulations with STD, whenever the IaF model received an excitatory input, the amplitude of the postsynaptic AMPAR response was multiplied by a scale factor δ (D → _D_δ)38. Between inputs, D recovered exponentially back to its initial value of 1.0 with a time constant τD = 40 ms. For simulations with phasic inhibitory input (Supplementary Fig. 3) the synaptic GABAR conductance was described by Eq. 1 using the following values: n = 8.34, τr = 0.14 ms, a1 = 53.02 nS, τd1 = 0.05 ms, a2 = 0.53 nS, τd2 = 6.90 ms and a3 = 0 (from unpublished data). The peak conductance was set to 663 pS to give a time averaged conductance of 500 pS at 100 Hz. Mean input rates were 50-150 Hz.
A model of a cortical layer 5 neuron27 was synaptically connected to 400 excitatory neurons and 30 inhibitory neurons using neuroConstuct39 (www.NeuroConstruct.org) and the code was automatically generated for the NEURON simulator37. Each excitatory connection cell had 3 synaptic contacts (to model 6 contacts with intermediate release probability)40 and inhibitory connections had 5 synaptic contacts (to model 10 synaptic inputs)41. Both input types were distributed randomly over the basolateral dendritic tree and soma to mimic layer 5-layer 5 connectivity. Excitatory synaptic inputs had a conductance time course described by two exponential functions (τrise = 0.3 ms, τdecay = 3 ms) and a peak conductance of 3 nS40 (i.e. 1 nS at each of the 3 synaptic contacts). Each presynaptic excitatory neuron was driven to fire an independent Poisson spike train (1-70 Hz) and the synaptic conductance was scaled by the level of STD, which was implemented as described previously using experimentally measured values for layer 5 pyramidal cell connections (Use = 0.5, τinact = 3 ms, τrecov = 500 ms)42. Inhibitory synaptic inputs had fixed conductances with a dual exponential time course (τrise = 0.3 ms, τdecay = 10 ms) and a peak conductance of 3.5 nS41. Presynaptic inhibitory neurons were driven with independent Poisson trains with mean rates 30-150 Hz. Reversal potentials for excitatory and inhibitory conductances were 0 mV and −75 mV respectively. Since the excitatory drive for non-depressing synapses was much higher than the more physiological depressing inputs, we carried out simulations with two different synaptic conductances (3 and 0.5 nS) for the non-STD case. 50 Hz inhibition produced a similar gain change for the two conductances (−11.7% and −10.9%, respectively), but the larger conductance gave a bigger gain change at 150 Hz as expected for noise-based gain modulation (−28.6% versus −22.9%). The 0.5 nS value was chosen for comparison because the excitatory input drive (0-70 Hz) better matched that of the STD case (0-60 Hz; Fig. 5b, d) than for 3 nS inputs, which saturated firing at input rates of only 12 Hz. Output firing rate was measured at steady-state. Input-output relations were fit with a simple Hill function similar to Eq. 5, but with input frequency f substituted for _G_exc, due to difficulty in defining the effective Gexc for a distributed input. ΔGain and ΔOffset were calculated from the fits as above, except for the −STD simulations, which exhibited little saturation of firing rate. In this case, ΔGain and ΔOffset were calculated assuming a maximum rate of 100 Hz. Since the model27 had an input resistance in the absence of synaptic input (11.5 MΩ) at the low end of that measured experimentally 9-123 MΩ (mean 36 MΩ)43, we repeated the simulations with a different model44 with a high input resistance (79 MΩ), which we modified to fire repetitively. We obtained similar results for the effects of inhibitory synaptic input on the input-output relation in the presence and absence of STD in the excitatory input (data not shown), although fewer presynaptic cells (100 excitatory and 20 inhibitory) were required to drive the model over a similar range of frequencies.
Supplementary Material
Supplementary Material
Acknowledgements
Supported by the Wellcome Trust, MRC (G0400598) and EU (EUSynapse, LSHM-CT-2005-019055). RAS is in receipt of a Wellcome Senior Research Fellowship. We thank Padraig Gleeson for help with neuroConstruct, Daniel Ward and Roby Kanichay for their experimental support, David Digregorio and Paul Kirkby for discussions and Alexander Arenz, David Attwell, Guy Billings, Emmanuelle Chaigneau, David DiGregorio, Mark Farrant, Federico Minneci and Koen Vervaeke for their comments on the manuscript.
References
- 1.Koch C. Biophysics of computation: Information processing in single neurons. Oxford University Press; 1999. p. 552. [Google Scholar]
- 2.Holt GR, Koch C. Shunting inhibition does not have a divisive effect on firing rates. Neural Comput. 1997;9:1001–13. doi: 10.1162/neco.1997.9.5.1001. [DOI] [PubMed] [Google Scholar]
- 3.Chance FS, Abbott LF, Reyes AD. Gain modulation from background synaptic input. Neuron. 2002;35:773–82. doi: 10.1016/s0896-6273(02)00820-6. [DOI] [PubMed] [Google Scholar]
- 4.Anderson JS, Lampl I, Gillespie DC, Ferster D. The contribution of noise to contrast invariance of orientation tuning in cat visual cortex. Science. 2000;290:1968–72. doi: 10.1126/science.290.5498.1968. [DOI] [PubMed] [Google Scholar]
- 5.Treue S, Martinez Trujillo JC. Feature-based attention influences motion processing gain in macaque visual cortex. Nature. 1999;399:575–9. doi: 10.1038/21176. [DOI] [PubMed] [Google Scholar]
- 6.Tovee MJ, Rolls ET, Azzopardi P. Translation invariance in the responses to faces of single neurons in the temporal visual cortical areas of the alert macaque. J Neurophysiol. 1994;72:1049–60. doi: 10.1152/jn.1994.72.3.1049. [DOI] [PubMed] [Google Scholar]
- 7.Ingham NJ, McAlpine D. GABAergic inhibition controls neural gain in inferior colliculus neurons sensitive to interaural time differences. J Neurosci. 2005;25:6187–98. doi: 10.1523/JNEUROSCI.0146-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Brotchie PR, Andersen RA, Snyder LH, Goodman SJ. Head position signals used by parietal neurons to encode locations of visual stimuli. Nature. 1995;375:232–5. doi: 10.1038/375232a0. [DOI] [PubMed] [Google Scholar]
- 9.Yakusheva TA, et al. Purkinje cells in posterior cerebellar vermis encode motion in an inertial reference frame. Neuron. 2007;54:973–85. doi: 10.1016/j.neuron.2007.06.003. [DOI] [PubMed] [Google Scholar]
- 10.Salinas E, Abbott LF. Transfer of coded information from sensory to motor networks. J Neurosci. 1995;15:6461–74. doi: 10.1523/JNEUROSCI.15-10-06461.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pouget A, Sejnowski TJ. Spatial transformations in the parietal cortex using basis functions. Journal of Cognative Neuroscience. 1997;9:222–237. doi: 10.1162/jocn.1997.9.2.222. [DOI] [PubMed] [Google Scholar]
- 12.Hansel D, van Vreeswijk C. How noise contributes to contrast invariance of orientation tuning in cat visual cortex. J Neurosci. 2002;22:5118–28. doi: 10.1523/JNEUROSCI.22-12-05118.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mitchell SJ, Silver RA. Shunting inhibition modulates neuronal gain during synaptic excitation. Neuron. 2003;38:433–45. doi: 10.1016/s0896-6273(03)00200-9. [DOI] [PubMed] [Google Scholar]
- 14.Gabbiani F, Krapp HG, Koch C, Laurent G. Multiplicative computation in a visual neuron sensitive to looming. Nature. 2002;420:320–4. doi: 10.1038/nature01190. [DOI] [PubMed] [Google Scholar]
- 15.Tiesinga PH, Jose JV, Sejnowski TJ. Comparison of current-driven and conductance-driven neocortical model neurons with Hodgkin-Huxley voltage-gated channels. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 2000;62:8413–9. doi: 10.1103/physreve.62.8413. [DOI] [PubMed] [Google Scholar]
- 16.Murphy BK, Miller KD. Multiplicative gain changes are induced by excitation or inhibition alone. J Neurosci. 2003;23:10040–51. doi: 10.1523/JNEUROSCI.23-31-10040.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Prescott SA, De Koninck Y. Gain control of firing rate by shunting inhibition: roles of synaptic noise and dendritic saturation. Proc Natl Acad Sci U S A. 2003;100:2076–81. doi: 10.1073/pnas.0337591100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fellous JM, Rudolph M, Destexhe A, Sejnowski TJ. Synaptic background noise controls the input/output characteristics of single cells in an in vitro model of in vivo activity. Neuroscience. 2003;122:811–29. doi: 10.1016/j.neuroscience.2003.08.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rancz EA, et al. High-fidelity transmission of sensory information by single cerebellar mossy fibre boutons. Nature. 2007;450:1245–8. doi: 10.1038/nature05995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.van Kan PL, Gibson AR, Houk JC. Movement-related inputs to intermediate cerebellum of the monkey. J Neurophysiol. 1993;69:74–94. doi: 10.1152/jn.1993.69.1.74. [DOI] [PubMed] [Google Scholar]
- 21.Saviane C, Silver RA. Fast vesicle reloading and a large pool sustain high bandwidth transmission at a central synapse. Nature. 2006;439:983–987. doi: 10.1038/nature04509. [DOI] [PubMed] [Google Scholar]
- 22.Semyanov A, Walker MC, Kullmann DM, Silver RA. Tonically active GABA A receptors: modulating gain and maintaining the tone. Trends Neurosci. 2004;27:262–9. doi: 10.1016/j.tins.2004.03.005. [DOI] [PubMed] [Google Scholar]
- 23.DiGregorio DA, Nusser Z, Silver RA. Spillover of glutamate onto synaptic AMPA receptors enhances fast transmission at a cerebellar synapse. Neuron. 2002;35:521–533. doi: 10.1016/s0896-6273(02)00787-0. [DOI] [PubMed] [Google Scholar]
- 24.Berends M, Maex R, De Schutter E. The effect of NMDA receptors on gain modulation. Neural Comput. 2005;17:2531–47. doi: 10.1162/089976605774320520. [DOI] [PubMed] [Google Scholar]
- 25.Cathala L, Misra C, Cull-Candy S. Developmental profile of the changing properties of NMDA receptors at cerebellar mossy fiber-granule cell synapses. J Neurosci. 2000;20:5899–905. doi: 10.1523/JNEUROSCI.20-16-05899.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.London M, Hausser M. Dendritic computation. Annu Rev Neurosci. 2005;28:503–32. doi: 10.1146/annurev.neuro.28.061604.135703. [DOI] [PubMed] [Google Scholar]
- 27.Kole MH, et al. Action potential generation requires a high sodium channel density in the axon initial segment. Nat Neurosci. 2008;11:178–86. doi: 10.1038/nn2040. [DOI] [PubMed] [Google Scholar]
- 28.Arenz A, Silver RA, Schaefer AT, Margrie TW. The contribution of single synapses to sensory representation in vivo. Science. 2008;321:977–80. doi: 10.1126/science.1158391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Markram H, Tsodyks M. Redistribution of synaptic efficacy between neocortical pyramidal neurons. Nature. 1996;382:807–10. doi: 10.1038/382807a0. [DOI] [PubMed] [Google Scholar]
- 30.Abbott LF, Varela JA, Sen K, Nelson SB. Synaptic depression and cortical gain control. Science. 1997;275:220–4. doi: 10.1126/science.275.5297.221. [DOI] [PubMed] [Google Scholar]
- 31.Silver RA, Cull-Candy SG, Takahashi T. Non-NMDA glutamate receptor occupancy and open probability at a rat cerebellar synapse with single and multiple release sites. J Physiol. 1996;494(Pt 1):231–50. doi: 10.1113/jphysiol.1996.sp021487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cathala L, Brickley S, Cull-Candy S, Farrant M. Maturation of EPSCs and intrinsic membrane properties enhances precision at a cerebellar synapse. J Neurosci. 2003;23:6074–85. doi: 10.1523/JNEUROSCI.23-14-06074.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Robinson HP, Kawai N. Injection of digitally synthesized synaptic conductance transients to measure the integrative properties of neurons. J Neurosci Methods. 1993;49:157–65. doi: 10.1016/0165-0270(93)90119-c. [DOI] [PubMed] [Google Scholar]
- 34.Sharp AA, O'Neil MB, Abbott LF, Marder E. Dynamic clamp: computer-generated conductances in real neurons. Journal of Neurophysiology. 1993;69:992–995. doi: 10.1152/jn.1993.69.3.992. [DOI] [PubMed] [Google Scholar]
- 35.D'Angelo E, De Filippi G, Rossi P, Taglietti V. Synaptic excitation of individual rat cerebellar granule cells in situ: evidence for the role of NMDA receptors. Journal of Physiology (London) 1995;482:397–413. doi: 10.1113/jphysiol.1995.sp020673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jorntell H, Ekerot CF. Properties of somatosensory synaptic integration in cerebellar granule cells in vivo. J Neurosci. 2006;26:11786–97. doi: 10.1523/JNEUROSCI.2939-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput. 1997;9:1179–209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- 38.Varela JA, et al. A quantitative description of short-term plasticity at excitatory synapses in layer 2/3 of rat primary visual cortex. J Neurosci. 1997;17:7926–40. doi: 10.1523/JNEUROSCI.17-20-07926.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gleeson P, Steuber V, Silver RA. neuroConstruct: A Tool for Modeling Networks of Neurons in 3D Space. Neuron. 2007;54:219–35. doi: 10.1016/j.neuron.2007.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Markram H, Lubke J, Frotscher M, Roth A, Sakmann B. Physiology and anatomy of synaptic connections between thick tufted pyramidal neurones in the developing rat neocortex. Journal of Physiology. 1997;500:409–40. doi: 10.1113/jphysiol.1997.sp022031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gupta A, Wang Y, Markram H. Organizing principles for a diversity of GABAergic interneurons and synapses in the neocortex. Science. 2000;287:273–8. doi: 10.1126/science.287.5451.273. [DOI] [PubMed] [Google Scholar]
- 42.Tsodyks MV, Markram H. The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability [published erratum appears in Proc Natl Acad Sci U S A 1997 May 13;94(10):5495] Proc Natl Acad Sci U S A. 1997;94:719–23. doi: 10.1073/pnas.94.2.719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Schwindt PC, O'Brien JA, Crill WE. Quantitative analysis of firing properties of pyramidal neurons from layer 5 of rat sensorimotor cortex. Journal of Neurophysiology. 1997;77:2484–2498. doi: 10.1152/jn.1997.77.5.2484. [DOI] [PubMed] [Google Scholar]
- 44.Mainen ZF, Joerges J, Huguenard JR, Sejnowski TJ. A model of spike initiation in neocortical pyramidal neurons. Neuron. 1995;15:1427–39. doi: 10.1016/0896-6273(95)90020-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material