A SNP discovery method to assess variant allele probability from next-generation resequencing data (original) (raw)
Abstract
Accurate identification of genetic variants from next-generation sequencing (NGS) data is essential for immediate large-scale genomic endeavors such as the 1000 Genomes Project, and is crucial for further genetic analysis based on the discoveries. The key challenge in single nucleotide polymorphism (SNP) discovery is to distinguish true individual variants (occurring at a low frequency) from sequencing errors (often occurring at frequencies orders of magnitude higher). Therefore, knowledge of the error probabilities of base calls is essential. We have developed Atlas-SNP2, a computational tool that detects and accounts for systematic sequencing errors caused by context-related variables in a logistic regression model learned from training data sets. Subsequently, it estimates the posterior error probability for each substitution through a Bayesian formula that integrates prior knowledge of the overall sequencing error probability and the estimated SNP rate with the results from the logistic regression model for the given substitutions. The estimated posterior SNP probability can be used to distinguish true SNPs from sequencing errors. Validation results show that Atlas-SNP2 achieves a false-positive rate of lower than 10%, with an ∼5% or lower false-negative rate.
In recent years, next-generation sequencing (NGS) technologies have propelled the rapid progress of genomics studies (Hillier et al. 2008; Srivatsan et al. 2008). Continuous improvement in NGS technologies are increasing the throughput while lowering costs, thus enabling ultra-large-scale sequencing efforts (Margulies et al. 2005; Shendure and Ji 2008). For example, the 1000 Genomes Project is aimed at sequencing more than 1000 human genomes to characterize the pattern of genetic variants (common and rare) in unprecedented detail (http://www.1000genomes.org/page.php) (Kaiser 2008). To realize this objective, it is essential that NGS technologies detect genomic variations accurately, including single nucleotide polymorphisms (SNPs), structural variations caused by insertions or deletions (indels), copy number variations (CNVs), and inversions or other rearrangements. However, the short read length and relatively high error rates present challenges to variant discovery from raw NGS data. While the error model for Sanger sequencing was well characterized (Ewing and Green 1998), systematic errors in NGS are not yet well studied, making it difficult to distinguish true genetic variations from the sequencing errors.
Currently, there are several methods available for detecting SNPs from NGS data, including Pyrobayes (Quinlan et al. 2008), POLYBAYES (Marth et al. 1999), MAQ (Li et al. 2008), SOAP (Li et al. 2009), VarScan (Ley et al. 2008; Koboldt et al. 2009), and other largely heuristic approaches (Wheeler et al. 2008). Pyrobayes-POLYBAYES recalibrates base-calling of all nucleotide positions from raw data, and then takes a Bayesian approach that incorporates the population polymorphism rates as priors to identify polymorphic sites. MAQ uses the consensus of the aligned reads to identify SNPs. While MAQ is able to achieve high sensitivity, it can result in an expected high false-positive rate due to intrinsic high probabilities of sequencing errors in NGS data (Li et al. 2008). VarScan and other available heuristic approaches that apply empirical covariate cutoffs can work well for specific projects, but become problematic with applications even with slight differences in underlying data.
In contrast to the efforts mentioned above, we have devised methods that consider individual platforms’ base-callers, taking advantage of the overall improvements in the base-calling algorithms. Our approach takes into account systematic errors of base substitutions on single reads by fitting training data sets using a logistic regression model that identified read sequence-related covariates in addition to the base quality scores. It further estimates the probability of variant alleles through a Bayesian method that integrates prior estimations of the overall sequencing error rate and an SNP rate with the results from the logistic regression model. Based on the output confidence score, users can tune the stringency of the SNP callings according to their own study designs. This method is implemented in our freely available software package, Atlas-SNP2.
Results
Overall workflow design
Atlas-SNP2 detects SNPs in genome resequencing data sets from different NGS technologies. There are three major steps in the overall workflow of Atlas-SNP2 (Fig. 1):
- A preprocessing step, to divide the reference genome into smaller pieces (ranging from a few hundred kilobases to a few hundred megabases in size, depending on computational resources available to the user), and to separate NGS reads into smaller batches (on the order of tens of thousands of reads per batch) for efficient computational resource management.
- A mapping step, to align the NGS reads to the reference sequence. These steps ensure the mapping accuracy and remove experimental artifacts such as duplicated reads.
- An SNP calling step, to detect single-nucleotide mismatches between the aligned reads and the reference sequence, and to estimate the posterior probability that the mismatch represents a true SNP.
Figure 1.
The overall workflow of the Atlas-SNP2 package. The reference genomic sequence and reads undergo an initial data processing step, whereby the reference sequence is split into smaller pieces and the reads into smaller batches. A combined BLAT and Cross_Match analysis was used to anchor and align reads back to the reference positions. All of the single nucleotide mismatches are parsed and assessed for their probabilities of being SNPs using the Atlas-SNP2 core statistical methods.
Preprocessing and mapping steps
Three main challenges to read mapping were addressed within the Atlas-SNP2 algorithm: (1) management of the computational resources, given the massive amount of NGS data (on the order of millions of reads); (2) accuracy of mapping, particularly in the presence of repeats and confounding factors such as sequencing errors and true variants; and (3) detection and removal of duplicated reads generated by technical artifacts introduced during the sequencing process. To reduce the computational requirements, as a preprocessing step we split the reference sequence into smaller pieces and divided the NGS reads into a number of batches, each with fewer reads (Methods). We anchored and aligned the reads onto the reference sequence using the established programs BLAT (Kent 2002) and Cross_Match (P Green, 1993; http://www.phrap.org) (Methods). To reduce the impact of mismapping of repeats, we discarded reads that had multiple best hits. Currently, all of the NGS sequencing platforms produce duplicated reads that often result in false-positive SNP calls (data not shown), because any amplification infidelity having occurred in early stages becomes overly represented. We detected and subsequently removed duplicated reads (Methods).
SNP calling step
We parsed all single nucleotide mismatches in individual reads reported by Cross_Match to establish a list of candidate SNP sites (which constitute our entire quality assessment sample space). For each candidate site, we evaluated the posterior probability of being a true SNP using a Bayesian method. It incorporated the error probabilities of mismatch bases inferred from single reads, and the depth-coverage information at the candidate site.
Characterization of the sequencing error model of 454 Life Sciences (Roche) data
It is important to thoroughly understand the systematic sequencing errors intrinsic to NGS technologies, which are specific to different sequencing-by-synthesis chemistries as well as different base-calling algorithms. The quality scores from current platform algorithms are often not accurate enough to differentiate true SNPs from sequencing errors. Nevertheless, significant biases in the error rates—as a function of the qualities of the interrogated base and the characteristic sequence context—are present in NGS data sets (Brockman et al. 2008; Dohm et al. 2008; Ossowski et al. 2008). Such biases can be detected and used to improve the ability to predict systematic sequencing errors.
We used a logistic regression model to estimate a classification value Pr(SNP)i for a given substitution on a single read i (Fig. 2) (Methods). The model incorporated information about the quality of the ascertained base and aspects of the neighboring sequence context relevant to systematic sequencing errors. Because of the earlier availability of multiple genome sequencing data sets generated using the 454 platform when we initiated this study, we first focused on the 454 platform as the initial model platform to test our method. Based on empirical observations, we identified a priori a set of variables that potentially affected the probability of a substitution being a sequencing error (Methods). We then trained the logistic regression model on a 454 platform data set of an Escherichia coli strain (K12 MG1655) (Supplemental Table S1; details are described in Methods) collected at Baylor College of Medicine-Human Genome Sequencing Center (HGSC), and identified a subset of variables that significantly elevated the probability to predict a sequence base as a SNP in a single read context (Table 1).
Figure 2.
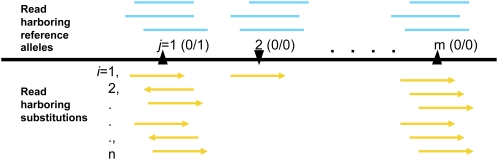
An illustration of the mapped reads at positions found with single base substitutions. (Blue) Reads with the reference alleles (the bases match those of the reference genomic sequence); (yellow) the variant alleles (that are the mismatches). With a reasonable average sequencing coverage, true SNPs are likely to be covered with more variant reads than false positives caused by sequencing errors.
Table 1.
Variables obtained from the training exercise that significantly increased the error probability of a substitution in 454 Titanium reads, and their respective coefficients in the logistic regression model
For the 454 Titanium platform, the four most significant predictors in the logistic regression model were as follows:
- The quality score of the substitution base call.
- Whether the base was involved in a “swap-base” event or a multi-nucleotide polymorphism (MNP) event. A “swap-base” is defined as two adjacent mismatch bases that invert their nucleotides when compared to the reference sequence (see Supplemental Fig. S1). These events result from “loss-of-synchrony” in the sequencing reactions.
- Whether the “neighboring quality standard” (NQS) passed the default threshold. To pass, the quality score of the mismatch base must be greater than 20, and the quality score for every base in the 5-base flanking sequence on either side must be greater than 15, which is referred to as “11-base NQS 20/15 threshold” (Altshuler et al. 2000; Brockman et al. 2008).
- The distance of the base from the 3′-end of the read, normalized against the entire read length (Table 1; Methods, Equation 1).
The significance of the “11-base NQS 20/15 threshold” was consistent with previous studies that empirically showed an increase in the false-positive rate in windows that fall below this threshold (Brockman et al. 2008).
Assessment of SNP probability for the variant alleles with a Bayesian framework
Following the initial error assessment based on single reads, we integrated the logistic regression results over all reads harboring the same substitution (i = {1, 2,…, n}) that mapped to the same position j (Fig. 2). Atlas-SNP2 estimated the posterior SNP probability of the substitution through a Bayesian formula that took into account prior probabilities of sequencing errors [prior(error)] and SNPs [prior(SNP)] among all the identified substitution loci from the interrogated genome (Methods, Equation 5).
The SNP predictor for a particular locus _j_—_Sj_—derived from the initial logistic regression, was used as a likelihood value for a given substitution site (Methods, Equation 4). The prior(error) and prior(SNP) were estimated as the proportion of SNPs and errors out of all the substitutions (i.e., in the sample space) (Supplemental Table S2; Methods). The Bayesian framework makes it possible to account for platform-specific systematic errors, genome-specific characteristics, and the depth-coverage variation among sequencing data sets. Therefore a more accurate posterior SNP probability estimation can be achieved.
The incorporation of the depth-coverage information is important (Methods). The classification of errors and SNPs conditional on the coverage of the variant reads (those reads harboring the substitution base) further improved our ability to make an accurate prediction. This is based on the rationale that the occurrence of errors with high read depth is much rarer than SNPs. Conditioning on the coverage information enables an extra layer of flexibility and sensitivity, as the coverage can vary greatly among different sites in the same study, and across different sequencing studies.
Tuning priors and validation with resequencing data of Staphylococcus aureus
We resequenced the genome of a well-characterized bacterial strain, Staphylococcus aureus (S. aureus) USA 300_TCH1516, using 454 Titanium chemistry for which a high-quality reference genome is available (accession no. NC_010079) (Supplemental Table S1; Methods). Mismatches identified in this process would be predominantly NGS sequencing errors, as it is extremely rare to find true mutations in the exact same strain. Additionally, we mapped the same set of reads onto the reference sequence of a genetically different strain—S. aureus USA 300_FPR3757 (accession no. NC_007793) (Supplemental Table S1; Methods). Excluding the sequencing errors defined above, the remaining mismatches constituted SNPs between these two different strains. The defined “errors” and “SNPs” allowed us to tune and validate the performance of our method, in particular tuning the prior(SNP|c) and prior(error|c).
At an average coverage of ∼31.6× (Supplemental Table S1; Methods), ∼99% of the reference genomic sequences were covered at least once, with ∼96% of the reads uniquely mapped. We defined a set of 33,802 “errors” and 84 “SNPs” (Supplemental Table S1).
We applied three sets of prior SNP probability and prior error probability for the preliminary tuning of the performance of Atlas-SNP2 (Supplemental Table S2; Methods). The parameters reflected different estimations of the sequencing error and SNP rates. In each set of prior parameters, in bins with fewer than three variant reads at a given locus (i.e., extremely low coverage), the prior SNP probability was set to be much smaller than prior error probability; in contrast, in bins with three variant reads or more (i.e., high coverage), the prior SNP probability was set to be much higher than prior error probability.
In the bins with at least three variant reads, we achieved an ∼10% false-positive rate and ∼5% false-negative rate by using all three different sets of prior values (Fig. 3; Methods). Using either the “set 1” or the “set 2” parameters listed in Methods and Supplemental Table S2, we reached the 10% level of performance by selecting different cutoffs of the posterior SNP probability. The “set 1” parameters enabled higher resolutions in posterior SNP probability to differentiate the properties; whereas the “set 2” parameters compressed most of the data points in the high end of the distribution of posterior SNP probability, and therefore neither the false-positive rate nor the false-negative rate would be improved by increasing the cutoff until it reached 0.8. This was due to the predominant effect of the priors when strong assumptions were made. It became worse when the “set 3” parameters were applied.
Figure 3.
The validation results in S. aureus data with at least three variant reads when three different sets of priors were used for tuning purposes. We used three sets of priors (Supplemental Table S2) in Equation 5 for SNP probability assessment. (A) The false-positive rate (FP) and false-negative rate (FN) can be evaluated using our defined SNPs and errors (described in Methods). The results indicate that a 10% false-positive rate and a 5% false-negative rate can be achieved when using either the “set 1” or the “set 2” parameters, while “set 1” enables a smoother resolution. (B) The FP/[FP + true-positives (TP)] is plotted against the posterior SNP probability cutoff for results obtained using “set 1” priors.
Depth-coverage variation was the main factor affecting the false-positive rate and false-negative rate. In the total 173 false-positives that our method identified with posterior probability greater than 0.5, 25% had posterior probability greater than 0.9. They all had more than two variant reads with high base quality scores and high read alignment qualities (data not shown), possibly owing to variables that Atlas-SNP2 has not fully modeled. Meanwhile, when there were fewer than three variant reads per locus, there was less power to confidently make a variant allele call, thereby increasing the false-negative rates significantly.
Extension to the Illumina platform, and SNP discovery performance comparison in both platforms
We applied a similar process of training and validating on an Illumina data set. The statistically significant predictors in the logistic model are similar to those in the 454 platform with the exception of the “swap-base” variable (Supplemental Methods; Supplemental Table S3).
We compared the SNP discovery performance of Atlas-SNP2 against that of VarScan (Koboldt et al. 2009) and of MAQ (Li et al. 2008) in both the 454 and Illumina platforms. We selected S. aureus data sets from both sequencing platforms for the validation analysis. VarScan uses a heuristic decision tree approach that can be applied to both 454 and Illumina platforms. For the 454 platform, Atlas-SNP2 had comparable sensitivity with VarScan, while the specificity was 9% lower than VarScan. The high specificity of VarScan could be achieved only when the sequencing read coverage was sufficiently high (as in the S. aureus 454 data set, with an average read coverage = 31×), because it required a high read coverage cutoff (the default read coverage cutoff is 10). Atlas-SNP2 showed an advantage of having the higher sensitivity in low-coverage 454 data sets, which is applicable to most of the sequencing projects of large genomes when using the 454 platform. Moreover, Atlas-SNP2 produces a probability score estimated for each SNP discovery, which can be beneficial for various downstream disease association studies and population genetics studies; even candidate loci with lower posterior probabilities than the cutoff provide uncertainty assessment information that can be used during analysis. Other heuristic decision tree approaches in general lack such estimations.
For Illumina data, Atlas-SNP2 demonstrated significant improvement over both VarScan and MAQ when the read-depth coverage was high (which is the case for most of the Illumina sequencing data sets) (Table 2). Our results indicate that the Atlas-SNP2 had ∼10% higher sensitivity than MAQ and VarScan, while the similarly high specificity was achieved.
Table 2.
Atlas-SNP2 performance comparison with VarScan (Koboldt et al. 2009) and MAQ (Li et al. 2008) when applied in 454 and Illumina platforms
Application to SNP detection in Watson genome sequencing data
The Watson genome sequence data was the first individual genome studied using NGS technologies (Wheeler et al. 2008). The sequencing was carried out using 454 platform at ∼7.4-fold diploid coverage (equivalent to ∼3.7-fold haploid coverage), and bases were initially called with the 454 GS FLX base-caller. We later re-called bases of the entire data set with the improved version of the 454 Titanium base caller (Leonardo V2008B1), which was consistently used throughout this study.
Using Atlas-SNP2, we mapped the 106.5 million re-called reads back to the human reference genome sequence (NCBI Build 36), identified ∼13 million single-base substitutions, and then evaluated the posterior SNP probability.
Atlas-SNP2 assessed the SNP probability for 13,498,188 total identified substitution sites with the “set 1” and “set 2” priors. Consistent with results from S. aureus reads, the “set 1” priors enabled a reasonably high resolution for distinguishing SNPs from errors (Table 3). We found more than 2.6 million SNPs with posterior probabilities greater than 0.9, when they had more than three variant reads mapped to the loci. In addition, a large number of data points in the bins of 0.4–0.5 reflected the quality and the coverage of the variant reads: 53,656, 349,151, and 385,393 SNPs were found in bins with coverage ≥3, =2, and =1, respectively. SNPs in the coverage bins with at least three variant reads were expected to have reasonably high confidence (Table 3), whereas the SNPs found with only one or two reads became more ambiguous. It was indicated by the significant reduction in the percentage of loci confirmed when checking against dbSNP—92.6% versus 49.8%—in these two categories. In practice, users can tune the desired levels of stringencies by choosing whether to include the more ambiguous calls.
Table 3.
Application of Atlas-SNP2 to the 454 Watson genomic sequence data
In summary, we identified about 2.66 million SNPs when there were more than two variant reads—2.6 million having high confidence and the rest having intermediate confidence (Table 3, dark blue and light blue boxes). The relative low sensitivity of detecting heterozygous SNP was limited by the average depth of coverage (Table 3). Among the 2.66 million SNPs, when compared to independent Affymetrix 500K Array genotyping results, we achieved a high genotype concordance rate of 99.2% when measuring the variant loci including both homozygotes and heterozygotes. When the 734,544 lower-quality loci were included (Table 3, gray boxes), the concordance rate remained at 99.2%.
Discussion
High error rates of NGS technologies present a challenge for the accurate detection of genetic variants. Here, we devised an approach that predicts error probabilities of mismatches in single reads using logistic regression followed by a Bayesian rule to combine the likelihood estimation from multiple reads mapped to the same locus with prior SNP probabilities. In this study, we initially selected the 454 Titanium as our platform because of the availability of multiple whole-genome resequencing data sets. We used reads from resequencing the E. coli K12 MG1655 genome for logistic regression model training to obtain an error predictor incorporating not only the base quality scores generated by the 454 base-caller, but also additional variables that took into account local sequence contexts. We verified our model by applying it to the analysis of both the S. aureus USA 300_TCH1516 genome and the Watson genome sequencing data sets.
An important factor in planning genome sequencing projects is the depth coverage, which directly determines the cost. In this study, our method was tuned to the depth coverage in order to provide a guideline for future sequencing project design. Our validation experiment in S. aureus demonstrated that we could reduce both the false-positive and false-negative rates to ∼10% in loci where there were more than two variant reads. Our simulation data suggested that at 12.5× average depth coverage for diploid genome sequencing, ∼90% of the genome would be covered by at least three reads for each haploid (Supplemental Fig. S3; Wheeler et al. 2008). We showed that Atlas-SNP2 requires just three or more reads for haploid sequencing, which is an attractive feature for whole-genome sequencing projects with relatively low coverage.
Atlas-SNP2 is portable across platforms and flexible enough to evolve along with platform updates. The framework of Atlas-SNP2 is suitable for dealing with multiple NGS data types. Specifically, the logistic regression model can accommodate different NGS platforms and different versions of NGS chemistry/base-callers after certain retraining. As a proof-of-concept, we applied Atlas-SNP2 to the Illumina platform by retraining the logistic regression model on an Illumina data set and demonstrated that our overall approach could be extended to other NGS platforms.
In this study, we used two available bacterial genome resequencing data sets for training and tuning purposes. We plan to further refine the model with well-characterized genomic data sets with higher genomic complexities. With many large-scale resequencing projects under way, larger training data sets will become available. Applications of Atlas-SNP2 to these new data sets will improve the package by iterative re-training.
Methods
Bacterial data sets used in the training and validation experiments
E. coli substrain K12.MG1655 and S. aureus substrain USA300_TCH1516 that were previously sequenced and finished to high accuracy using Sanger method were resequenced using the 454 platform. The reads were processed with the 454 base-caller (version Leonardo V2008B1) to produce base calls and quality metrics. The reference genome sequences were obtained from NCBI (E. coli K12.MG1655, accession no. NC_000913; S. aureus USA 300_TCH1516, accession no. NC_010079). Any identified mismatches were defined as sequencing errors. Each set of reads was also mapped to an alternative reference genome of a genetically different strain of the same species: E. coli DH10B (accession no. NC_010473) and S. aureus USA 300_FPR3757 (accession no. NC_007793), respectively. After identifying the sequencing errors by first mapping the reads to their genetically identical reference genome, the remaining mismatches were defined as the initial set of SNPs. Subsequently, to improve our SNP identification stringency, we mapped one high-quality reference genomic sequence from one strain to the high-quality reference genomic sequence from the second strain, for E. coli and S. aureus, respectively. These lists were intersected with both the initial sets of SNPs from the 454 and Illumina SNP data. Finally, we obtained 147 SNPs for E. coli data and 84 SNPs for S. aureus from both the 454 and Illumina data sets, which are in almost perfect concordance with that published before as discussed in details below.
Two previous publications have identified and reported the genetic variations between the two E. coli strains and the two S. aureus strains, respectively. Durfee et al. (2008) reported 105 SNPs in genic regions (listed in Table S2 of Durfee et al. 2008) and 42 SNPs in intergenic regions, so the total number of SNPs in Durfee et al. (2008) was 147 for E. coli. (detailed genomic coordinates for the SNP loci were not provided.) For the two S. aureus strains, Highlander et al. (2007) described in the main text that there were 92 SNPs and two 4-base deletions. Their Supplemental Table 2, however, listed that six deletions, two insertions, and 83 SNPs for _S. aureus_—a total of 91 polymorphisms—were identified. The SNP genomic positions given by Highlander's Supplemental Table 2 used USA300-MR as the reference, whereas our SNP positions used FP3757 as the reference, so the genomic position information could not be used for comparison.
We used BLAT and Cross_Match to uniquely map 98.2% of the E. coli and 95.8% of the S. aureus reads back to their respective reference genome sequences, resulting in an average coverage of ∼18× for E. coli and 31× for S. aureus (Supplemental Table S1). Slightly lower read mapping yields were achieved when the genome sequences of the related strains were used (93.1% for E. coli DH10B, and 95.8% for S. aureus USA300_FPR3757) (Supplemental Table S1). The E. coli DH10B sequence, with only 93.2% of the reference genome covered yielded a greater genetic difference between its reference and resequenced genomes.
The E. coli data set was used as training data after a resampling process that produced 10,000 data points for errors and SNPs. The S. aureus data set was used as validation data as well as for tuning parameters, because of a closer genomic composition (such as GC content) to the human genome.
Watson genome 454 platform sequencing data
Wheeler et al. (2008) sequenced the entire genome sequence of Watson with an average read coverage of ∼7.4× using the 454 platform. We re-called all the Watson genomic sequence reads with the same version of the base-caller (Leonardo V2008B1) used in processing the bacterial sequencing reads.
We also obtained the approximately 500,000 Watson genotypes determined using Affymetrix 500K genotyping microarrays (Wheeler et al. 2008) for validating the variant calls from our method. The genotypes were converted into A/C/G/T nucleotides using the Affymetrix map file and further checked against the HapMap-CEU genotypes by allele frequency matching. After filtering, 476,087 SNPs were retained for comparisons.
Mapping and aligning the reads to genomic sequences
A fundamental issue in read mapping is related to the presence of repeat sequences in the resequenced genome. Owing to the nature of genome assemblies, repeat sequences are occasionally collapsed into a single place in the reference genome. This process occurs in both draft and finished assemblies. As a result, a read from a repeat region in the resequenced genome can be mapped incorrectly to the reference genome, generating false-positive SNPs. A recent duplication in the resequenced genome (not found in the reference genome) can also lead to such errors. To reduce false positives due to such cases, we regard a read to be “ambiguously mapped” if it has multiple best hits, or if the mismatch rate of the best hit is larger than a predefined cutoff value (e.g., the ratio of the best hit to the second best hit exceeds 99%), which is based on the idea developed in POLYBAYES (Marth et al. 1999).
Detecting duplicated reads
In the 454 sequencing, some shotgun fragments share the same 5′ starting position. They can account for up to 60% of the overall NGS data obtained from the production centers. This creates a skewed coverage distribution that may subsequently bias the error model and thus substantially increases the number of false-positive SNP discoveries (data not shown). Currently, the simplistic approach is to detect the duplicates and remove all of them except the best quality read at a given position. In the future iterations, it is worth exploring whether there is any additional value to retaining some of the duplicates satisfying certain criteria, which might maintain the data integrity while maximizing high-quality coverage.
Logistic regression to improve base error prediction in sequencing reads
We used a logistic regression model to improve the accuracy of error estimation from each read. The model was trained on E. coli K12.MG1655 reads. We identified a priori a set of predictors based on empirical observations and results from other references (Brockman et al. 2008; Dohm et al. 2008), including raw quality score, swap (a Boolean variable), 11-base NQS 20/15 threshold (a Boolean variable), homopolymers, GC content, relative position from each end, NQS, the immediate flanking nucleotides, and the specific substitution classifications. A generalized linear model was used in the statistical training process, and a stepwise procedure was primarily used for model selection to achieve a balance between model parsimony and prediction accuracy. We chose only the variables with significant _P_-values.
The results from our training experiments are shown in Table 1. In the current version for 454 Titanium and base-caller Leonardo V2008B1, and as shown in Equation 1, the most significant predictors in the model were
- The quality score of the substitution base.
- Whether the base is involved in “swap-base” (a phenomenon defined as that two adjacent mismatch bases invert their nucleotides relative to the reference sequence) or multi-nucleotide polymorphism (MNP) events.
- A Boolean variable indicating whether the NQS passes the default requirement (i.e., the quality score of the substitution base call is greater than 20, and the quality score of each of the five flanking bases on either side is greater than 15—“11-base NQS 20/15 threshold”).
- The relative distance of the base from the 3′-end of the read, normalized by read length.
The inferred logistic regression model with overall significance is

We note that the new Titanium base-caller had much improved performance in dealing with homopolymers, which in previous versions caused the base-caller to overcall or undercall the number of contiguous bases from 454 data (Brockman et al. 2008). Our training results indicate that homopolymers no longer contribute significantly to increase the sequencing error probability in 454 reads. This is consistent with the vendor's feedback.
The base-call error probability for a given read is

Bayesian framework that considers all mapped reads to assess variant allele probability for a locus
We derived the locus error probability estimation as
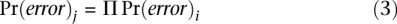
for all reads i = {1, 2, …, n} with the same substitution that are mapped to a particular locus j; and derive the locus SNP probability as

We use Sj to stand for Pr(SNP)j, which refers to the measured signal at the locus j.
The multiplication step assumes that error bases are fully stochastic and therefore arise independently of one another. This assumption, to a certain extent, may cause inaccuracy when total sequencing read coverage varies, and this inaccuracy is difficult to model with read coverage variations. We applied a Bayesian framework to try to take the read coverage variation into consideration in order to further improve our variant allele probability estimation at a given locus. Equation 5 is shown below.

Pr(SNP|Sj, c)j is the posterior variant allele probability at locus j when signal is Sj at a specific variant read coverage, c; Pr(Sj|SNP, c) and Pr(Sj|error, c) are inferred from the probability density distribution of Sj for SNPs and errors at a specific variant read coverage c that can be derived empirically from our E. coli training data set, as illustrated in Supplemental Figure S2; prior(SNP|c) and prior(error|c) are the prior estimations of the substitution SNP rate and the error rate when conditioned on the variant read coverage, respectively. In this paper, we used three sets of parameters (Supplemental Table S2). In particular, when there are two or more reads with the same variants, “set 1” priors were set as prior(SNP|c) = 0.9 and prior(error|c) = 0.1; “set 2” priors were prior(SNP|c) = 0.99 and prior(error|c) = 0.01; and “set 3” priors were prior(SNP|c) = 0.999 and prior(error|c) = 0.001.
Atlas-SNP2 software download and documentation
Atlas-SNP2 and its documentation are available for download at http://www.hgsc.bcm.tmc.edu/cascade-tech-software-ti.hgsc.
Acknowledgments
We thank Bingshan Li, Stephen Richards, Xiang Qin, Erica Sodergren, Jeffrey Reid, and Kim Worley for the discussions on 454 sequencing errors. We also thank Stephanie Kreml, Matthew Neil Bainbridge, Aniko Sabo, and Lara Bull for their help in testing Atlas-SNP2 and providing useful feedbacks from the applications. We also thank Andrew Jackson, Dajiang Liu, Momiao Xiong, and Rui Chen for their review of the manuscript. This work was funded by the National Human Genome Research Institute, National Institutes of Health, under grants 5U54HG003273 and 1U01HG005211-0109.
Footnotes
References
- Altshuler D, Pollara VJ, Cowles CR, Van Etten WJ, Baldwin J, Linton L, Lander ES. An SNP map of the human genome generated by reduced representation shotgun sequencing. Nature. 2000;407:513–516. doi: 10.1038/35035083. [DOI] [PubMed] [Google Scholar]
- Brockman W, Alvarez P, Young S, Garber M, Giannoukos G, Lee WL, Russ C, Lander ES, Nusbaum C, Jaffe DB. Quality scores and SNP detection in sequencing-by-synthesis systems. Genome Res. 2008;18:763–770. doi: 10.1101/gr.070227.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dohm JC, Lottaz C, Borodina T, Himmelbauer H. Substantial biases in ultra-short read data sets from high-throughput DNA sequencing. Nucleic Acids Res. 2008;36:e105. doi: 10.1093/nar/gkn425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durfee T, Nelson R, Baldwin S, Plunkett G, III, Burland V, Mau B, Petrosino JF, Qin X, Muzny DM, Ayele M, et al. The complete genome sequence of Escherichia coli DH10B: Insights into the biology of a laboratory workhorse. J Bacteriol. 2008;190:2597–2606. doi: 10.1128/JB.01695-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewing B, Green P. Base-calling of automated sequencer traces using phred. II. Error probabilities. Genome Res. 1998;8:186–194. [PubMed] [Google Scholar]
- Highlander SK, Hulten KG, Qin X, Jiang H, Yerrapragada S, Mason EO, Jr, Shang Y, Williams TM, Fortunov RM, Liu Y, et al. Subtle genetic changes enhance virulence of methicillin resistant and sensitive Staphylococcus aureus. BMC Microbiol. 2007;7:99. doi: 10.1186/1471-2180-7-99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillier LW, Marth GT, Quinlan AR, Dooling D, Fewell G, Barnett D, Fox P, Glasscock JI, Hickenbotham M, Huang W, et al. Whole-genome sequencing and variant discovery in C. elegans. Nat Methods. 2008;5:183–188. doi: 10.1038/nmeth.1179. [DOI] [PubMed] [Google Scholar]
- Kaiser J. DNA sequencing. A plan to capture human diversity in 1000 genomes. Science. 2008;319:395. doi: 10.1126/science.319.5862.395. [DOI] [PubMed] [Google Scholar]
- Kent WJ. BLAT—the BLAST-like alignment tool. Genome Res. 2002;12:656–664. doi: 10.1101/gr.229202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koboldt DC, Chen K, Wylie T, Larson DE, McLellan MD, Mardis ER, Weinstock GM, Wilson RK, Ding L. VarScan: Variant detection in massively parallel sequencing of individual and pooled samples. Bioinformatics. 2009;25:2283–2285. doi: 10.1093/bioinformatics/btp373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ley TJ, Mardis ER, Ding L, Fulton B, McLellan MD, Chen K, Dooling D, Dunford-Shore BH, McGrath S, Hickenbotham M, et al. DNA sequencing of a cytogenetically normal acute myeloid leukaemia genome. Nature. 2008;456:66–72. doi: 10.1038/nature07485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Ruan J, Durbin R. Mapping short DNA sequencing reads and calling variants using mapping quality scores. Genome Res. 2008;18:1851–1858. doi: 10.1101/gr.078212.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R, Li Y, Fang X, Yang H, Kristiansen K, Wang J. SNP detection for massively parallel whole-genome resequencing. Genome Res. 2009;19:1124–1132. doi: 10.1101/gr.088013.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margulies M, Egholm M, Altman WE, Attiya S, Bader JS, Bemben LA, Berka J, Braverman MS, Chen YJ, Chen Z, et al. Genome sequencing in microfabricated high-density picolitre reactors. Nature. 2005;437:376–380. doi: 10.1038/nature03959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marth GT, Korf I, Yandell MD, Yeh RT, Gu Z, Zakeri H, Stitziel NO, Hillier L, Kwok PY, Gish WR. A general approach to single-nucleotide polymorphism discovery. Nat Genet. 1999;23:452–456. doi: 10.1038/70570. [DOI] [PubMed] [Google Scholar]
- Ossowski S, Schneeberger K, Clark RM, Lanz C, Warthmann N, Weigel D. Sequencing of natural strains of Arabidopsis thaliana with short reads. Genome Res. 2008;18:2024–2033. doi: 10.1101/gr.080200.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quinlan AR, Stewart DA, Stromberg MP, Marth GT. Pyrobayes: An improved base caller for SNP discovery in pyrosequences. Nat Methods. 2008;5:179–181. doi: 10.1038/nmeth.1172. [DOI] [PubMed] [Google Scholar]
- Shendure J, Ji H. Next-generation DNA sequencing. Nat Biotechnol. 2008;26:1135–1145. doi: 10.1038/nbt1486. [DOI] [PubMed] [Google Scholar]
- Srivatsan A, Han Y, Peng J, Tehranchi AK, Gibbs R, Wang JD, Chen R. High-precision, whole-genome sequencing of laboratory strains facilitates genetic studies. PLoS Genet. 2008;4:e1000139. doi: 10.1371/journal.pgen.1000139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheeler DA, Srinivasan M, Egholm M, Shen Y, Chen L, McGuire A, He W, Chen YJ, Makhijani V, Roth GT, et al. The complete genome of an individual by massively parallel DNA sequencing. Nature. 2008;452:872–876. doi: 10.1038/nature06884. [DOI] [PubMed] [Google Scholar]