To Pool, or Not to Pool? (original) (raw)
IN this issue of Genetics, Futschik and Schlötterer (2010) present one of the first and the most systematic explorations of the relative merits of pooling vs. individual sequencing for several genetics applications. They argue that pooling individuals is often more effective both for SNP discovery and for the estimation of allele frequencies (and thus for population genomic analyses) and as a result can be more cost effective because less sequencing effort is required to obtain the same precision of estimates. While the authors' results are strictly correct for the models that they examine, application of the innovative and powerful statistical framework that they have developed may be used to show that, for a wide range of applications, pooling is in fact less desirable than individual sequencing. Given the prevalence and importance of current and future whole-genome sequencing projects, it is worthwhile to carefully consider these results.
The authors begin by considering SNP detection and comparing pooling experiments to individual sequencing. Building upon the work of Eberle and Kruglyak (2000), they derive both type I and type II errors under both schemes. The authors find, as expected, that the relative efficiency of pooling depends upon not only expected coverage, but also upon the minimum number of reads required for allele calling. The trade-off in power is clear: pooling is less efficient when coverage is small, whereas individual sequencing becomes less efficient with higher expected coverage. However, regardless of the assumed model of sequencing errors, SNP calling from pools is shown to be accompanied by a tremendously high probability of sequencing errors, unless the minimum coverage depth required to make a call is quite high.
And herein lies the major drawback of the pooling approach. The authors propose two possible corrections to address this unacceptably high error rate: (1) naturally, if an unbiased estimate of sequencing error is known, this estimate could be used as a correction in subsequent analysis; and (2) in the likely absence of this knowledge, the authors propose a minimum required allele frequency for inclusion of a site in SNP-based analyses. Based on the assumption that sequencing errors will be rare if this minimum frequency is sufficiently large, this approach resigns itself to the loss of a tremendous amount of information—notable particularly given the importance of low-frequency alleles in population genetics analyses ranging from the detection of patterns of hitchhiking (Maynard-Smith and Haigh 1974), to the quantification of positive (Przeworski 2002) and purifying selection (Charlesworth et al. 1993), to the estimation of demographic parameters (e.g., Thornton and Andolfatto 2006).
Perhaps more importantly, the precise application modeled by the authors, “SNP detection,” might subtly differ from the application that many readers may consider performing themselves. The application of the Futschik and Schlötterer model has the goal of discovering markers, which can subsequently be assayed in future experiments. This application is, of course, an important one, particularly in systems that have not yet seen much genomic analysis. Conversely, it is an experiment of essentially no utility in systems such as the human or fly, where SNP discovery has been extensively performed. Importantly, the key idea behind this experiment is that discovered SNPs are “exchangeable.” The user cares only about the total number of markers discovered and is untroubled by the fact that, if the experiment were repeated many times, the precise SNPs discovered would change with each experiment.
In the context of human genetics, for example, the more common experiment is often called “medical resequencing” and follows a general structure: N individuals who have some common disorder are sequenced, as are K individuals free of the disorder. The experiment determines whether these N individuals also share certain “kinds” of mutations (stop codons, replacement sites, etc.) disproportionately. In this experiment, the precise individuals sequenced and the precise variants discovered matter, and because of that, one comes to a very different conclusion about the relative merits of pooling. Futschik and Schlötterer's machinery may in fact be used to show that pooling is always less efficient than individual sequencing for this application.
In the medical resequencing experiment, the N individuals with a disorder are often “limiting”; i.e., there is not an infinite pool of individuals with that particular disorder. The N individuals are perhaps all the samples that will ever be available to the investigator. Fundamentally, this experiment seeks a complete catalog of the variants in those N individuals. For example, consider a human sample where N = 100 and the population mutation rate, θ = 4_N_μ per site, is ∼0.001 (International HapMap Consortium 2005). In such an experiment, we expect to find 0.00587 segregating sites per site (Watterson 1975). For >90% of the SNPs identified to be “real,” the error rate for the whole experiment necessarily must be <0.00065 per site. Because individuals are diploid, we assume the following base calling “rule”: We call a site heterozygous if at least six reads are seen from each allele and the minor allele constitutes at least 15% of the total reads. Otherwise, we call the majority allele homozygous, provided at least six reads agree. Using this base-calling rule and modifying the authors' equation 3 appropriately,
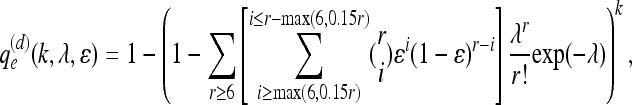
it is easy to show that if we sequence each individual to an average 30x depth, then the false positive rate per site is less than 0.00051, whenever the per base sequencing error is less than 1.4%. It is also easy to show
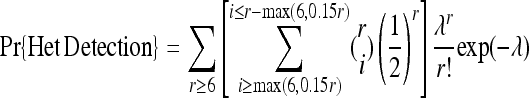
that 99.45% of all heterozygotes will be detected by these rules, and effectively all of the homozygous sites will be correctly called. This experiment requires a total sequencing burden of 100 × 30 = 3000 reads per base. There is no pooling experiment with 3000 reads per base that can begin to approach this performance at realistic error rates.
If we were to pool all 100 samples together, and sequence the pool to a 3000× depth, we may ask the minimum depth necessary to call a variant to achieve a per-site error rate of <0.00065. If the per-read error rate is, for example, between 0.001 and 0.01, then the minimum depth to call a variant will range from 11 at the low end to 50 at the high end. At the low end, 11% of all singleton heterozygotes will be dropped. At the high end, nearly 100% of the singleton heterozygotes, 100% of the doubletons, and 75% of the tripletons will be dropped. Thus, ∼29% of all variants will be lost at an error rate of 1% per base per read (phred 20). Making smaller pools helps if the error rate is sufficiently small, but not at realistic error rates. If pools of size 10 each are sequenced to a depth 300×, a rule of five reads will suffice at an error rate of 0.001, whereby the per-base false-positive rate meets our threshold and almost no variants are lost. However, if the error rate per read is closer to 1%, it will take at least 12 reads of the minor allele to achieve a sufficiently low error rate, and once again ∼28% of the variants will be missed from each pool. It is important to note that to make these calculations we have assumed that each DNA in the pool is at exactly equal molar concentration (i.e., there is no variance due to pooling). This is an unrealistic assumption and amounts to a best-case scenario for pooling.
The earliest published pooled sequencing experiments are obtaining similar results. Druley et al. (2009) built a site-specific error model, trimmed all but the 10 most reliable bases from each read, and obtained a per base error rate of ∼0.003 (much worse than modeled here), while detecting only one singleton in pools expected from neutral theory to contain ∼12. When analyzing pools of 88 samples, Out et al. (2009) were able to detect 3 out of 5 known singletons, but did not report any statistics concerning false positive rates.
Apart from variant identification itself, the primary interest of generating whole-genome polymorphism data for population genetics analyses generally revolves around an accurate characterization of the allele-frequency spectrum. Ignoring for a moment minimum allele-frequency corrections, for individual-based sequencing most of the sampling variance in the frequency spectrum stems directly from the selection of individuals. Thus, by including a large number of individuals in a given pool, this sampling error may be dramatically reduced. By way of quantifying frequency-spectrum-based inference under these different approaches, the authors compare the estimation of two commonly used scaled-mutation parameters (θ_W_ and θπ). In the absence of sequencing error, pooling results in more accurate estimation for large pools. However, sequencing error rates (1% per site per base) suggest that, for a pool sequenced to 300× depth [as depicted by the black line in Figure 5 of Futschik and Schlötterer] the necessary b to control for sequencing error is 11, not 3. Quite clearly the advantage of pooling for parameter estimation is beginning to disappear at b = 3 and is dramatically reduced for anything other than the largest imaginable pools at b = 11. Furthermore, new biases are introduced: some chromosomes in a pool may not be sequenced, and others may be multiply sequenced.
Employing a model similar to Lynch's (2009), Futschik and Schlötterer clearly demonstrate that, when individual DNAs can be pooled in exactly equal molar concentrations, estimation of allele frequencies for high-frequency alleles is always more efficient in pools. However, one of the greatest technical challenges to the pooling approach is obtaining equal molar concentrations (Craig et al. 2009). As Futschik and Schlötterer show in Figure 8, when realistic variance in DNA concentrations are assumed, pools must be very large (hundreds of individuals) for the allele-frequency estimation to be more efficient in pools than by individually sequencing 10 alleles to a 10× depth. Of course, it is not at all clear why any investigator would ever attempt to estimate allele frequency by sequencing 10 alleles to a 10× depth. A more realistic experiment might sequence 100–1000 samples to a 30× depth. Of course, for pools to perform better than individual sequencing for this application, the pools must be drawn from much larger populations, e.g., from thousands to tens of thousands of individuals, which again implies that the samples are not themselves limiting. More pointedly, when sequencing pools of hundreds to thousands of individuals, there is no possibility of individual variant detection. All rare alleles will be lost. The only SNPs that can be “called” are those at a very high minor allele frequency in the general population. Thus, the proper competitor experiment is not really “individual sequencing,” which would detect rare minor alleles, but instead “individual genotyping.” If only high minor allele-frequency SNPs can be assayed, the most straightforward experiment is simply to genotype them in all samples, efficiently and inexpensively, and avoid sequencing altogether. This trade-off—sequencing pools large enough for efficient allele-frequency estimation and thus destroying the ability to assay rare alleles—is just one of many trade-offs associated with a pooling approach.
Finally, although dismissed by Futschik and Schlötterer as an acceptable trade-off in light of the perceived relative advantages of pooling, it is significant to note that haplotype information is necessarily being sacrificed under this approach as well. While this may indeed be a necessary price for a cost-effective and accurate characterization of SNP frequencies in a population of interest, it should not be disregarded as insignificant. A number of recent methodological advancements in population genetics—ranging from the inference of demographic (Davison et al. 2009) and recurrent selection parameters (e.g., Jensen et al. 2008) to the identification of both complete and incomplete selective events (e.g., Hudson et al. 1994; Sabeti et al. 2007; Pavlidis et al. 2010)—revolve around patterns of linkage disequilibrium. Additionally, given the seemingly indistinguishable effects of selection and demography on the site frequency spectrum, recent theoretical work has argued for the importance of linkage disequilibrium in distinguishing among population genetics models (e.g., Stephan et al. 2006). At worst, this absence of LD information may greatly limit the value of pooled sequencing in evolutionary analyses, independent of the loss of low-frequency alleles. At best, the loss of LD information may represent a new challenge for theoretical and computational population geneticists to develop a novel class of test statistics designed to utilize this future wealth of cost-effective pooled data generation.
Although the authors do demonstrate several genetic applications when pooling performance can be better than individual sequencing, assuming realistic error rates, those applications are relatively narrow and always involve significant trade-offs. For many applications, individual sequencing must always be preferred. Thus, the work by Futschik and Schlötterer is significant as it represents a careful and systematic comparison between two competing methodologies and identifies trade-offs that ought to be carefully considered by the multiple fields utilizing next-generation sequencing technologies—from medical application to conservation genetics to population genomics.
References
- Charlesworth, B., M. T. Morgan and D. Charlesworth, 1993. The effect of deleterious mutations on neutral molecular variation. Genetics 134 1289–1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craig, J. E, A. W. Hewitt, A. E. McMellon, A. K. Henders, L. Ma et al., 2009. Rapid inexpensive genome-wide association using pooled whole blood. Genome Res. 19 2075–2080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison, D., J. K. Pritchard and G. Coop, 2009. An approximate likelihood for genetic data under a model with recombination and population splitting. Theor. Popul. Biol. 75 331–345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Druley, T. E., F. L. M. Vallania, D. J. Wegner, K. E. Varley, O. L. Knowles et al., 2009. Quantification of rare allelic variants from pooled genomic DNA. Nat. Methods. 6:(4) 263–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eberle, M., and L. Kruglyak, 2000. An analysis of strategies for discovery of single nucleotide polymorphisms. Genet. Epidemiol. 19 S29–S35. [DOI] [PubMed] [Google Scholar]
- Futschik, A., and C. Schlötterer, 2010. The next generation of molecular markers from massively parallel sequencing of pooled DNA samples. Genetics 186 207–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson, R. R, K. Bailey, D. Skarecky, J. Kwiatowski and F. J. Ayala 1994. Evidence for positive selection in the superoxide dismutase (Sod) region of Drosophila melanogaster. Genetics 136 1329–1340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International HapMap Consortium, 2005. A haplotype map of the human genome. Nature 437 1299–1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen, J. D., K. R. Thornton and P. Andolfatto, 2008. An approximate Bayesian estimator suggests strong recurrent selective sweeps in Drosophila. PLoS Genet. 4 e1000198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch, M., 2009. Estimation of allele frequencies from high-coverage genome-sequencing project. Genetics 182 295–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maynard Smith, J., and J. Haigh, 1974. The hitch-hiking effect of a favourable gene. Genet. Res. 23 23–25. [PubMed] [Google Scholar]
- Out, A. A., I. J. van Minderhout, J. J. Goeman, Y. Ariyurek, S. Ossowski et al., 2009. Deep sequencing to reveal new variants in pooled DNA samples. Hum. Mutat. 30:(12) 1703–1712. [DOI] [PubMed] [Google Scholar]
- Pavlidis, P., J. D. Jensen and W. Stephan, 2010. Searching for footprints of positive selection in whole-genome SNP data from non-equilibrium populations. Genetics 185 907–922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Przeworski, M., 2002. The signature of positive selection at randomly chosen loci. Genetics 160 1179–1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabeti, P. C., P. Varilly, B. Fry, J. Lohmueller, E. Hostetter et al., 2007. Genome-wide detection and characterization of positive selection in human populations. Nature 449 913–918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephan, W., Y. Song and C. H. Langley, 2006. The hitchhiking effect on linkage disequilibrium between linked neutral loci. Genetics 172 2647–2663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton, K. R., and P. Andolfatto, 2006. Approximate Bayesian inference reveals evidence of a recent, severe bottleneck in a Netherlands population of Drosophila melanogaster. Genetics 172 1607–1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watterson, G. A., 1975. On the number of segregating sites in genetical models without recombination. Theor. Popul. Biol. 7 256–276. [DOI] [PubMed] [Google Scholar]