A General Model of Synaptic Transmission and Short-Term Plasticity (original) (raw)
. Author manuscript; available in PMC: 2011 Feb 8.
SUMMARY
Some synapses transmit strongly to action potentials (APs), but weaken with repeated activation; others transmit feebly at first, but strengthen with sustained activity. We measured synchronous and asynchronous transmitter release at “phasic” crayfish neuromuscular junctions (NMJs) showing depression and at facilitating “tonic” junctions, and define the kinetics of depression and facilitation. We offer a comprehensive model of presynaptic processes, encompassing mobilization of reserve vesicles, priming of docked vesicles, their association with Ca2+ channels, and refractoriness of release sites, while accounting for data on presynaptic buffers governing Ca2+ diffusion. Model simulations reproduce many experimentally defined aspects of transmission and plasticity at these synapses. Their similarity to vertebrate central synapses suggests that the model might be of general relevance to synaptic transmission.
INTRODUCTION
Information processing and control capabilities of nervous systems depend on a diversity of transmitter release properties. Synapses can be strong but depress rapidly, or facilitate powerfully from near silence, with important consequences for circuit function. Presynaptic terminals of crustacean NMJs are well suited for electrophysiological recording, biochemical manipulation, and fluorescent tracking of chemical mediators. “Phasic” and “tonic” motor neuron junctions at crayfish leg extensor muscles differ 1000-fold in initial efficacy–phasic synapses depress while transmission at tonic synapses can grow 1000-fold during normal activity. These fast glutamatergic junctions span the range of short-term synaptic plasticity observed at vertebrate central synapses (Atwood and Karunanithi, 2002).
Differences in size, number, or density of active zones (Bradacs et al., 1997; King et al., 1996; Msghina et al., 1998), metabolic activity (Nguyen et al., 1997), Ca2+ entry or local Ca2+ concentration ([Ca2+]i) during an AP (Msghina et al., 1999), and in the size of the readily releasable pool (RRP) (Millar et al., 2002) cannot explain functional differences between phasic and tonic synapses. In contrast, transmitter release to step rises in [Ca2+]i imposed by photolysis of photosensitive chelators differs considerably (Millar et al., 2002, 2005), reflecting a difference in a Ca2+-sensitive priming step–rendering docked vesicles immediately available for release only at phasic synapses.
Previous analysis was limited by the paucity of quantitative data on plasticity at these junctions. Here we characterize phasic depression and tonic facilitation and the time courses of synchronous and asynchronous transmitter release. We offer a comprehensive model simulating these characteristics. Calculations of AP-evoked release were refined by considering diffusion of Ca2+ from Ca2+ channel arrays (Matveev et al., 2002, 2004, 2006; Tang et al., 2000; Yamada and Zucker, 1992) toward secretory and priming targets in the presence of recently defined endogenous buffers (V. Matveev and J.-W. Lin, personal communication; Vyshedskiy and Lin, 2000). With uniform synaptotagmin and buffer parameters but distinct priming parameters in phasic and tonic synapses we could reproduce kinetics of transmitter release and synaptic plasticity.
Our model can also explain effects of presynaptically injected or photolytically produced exogenous buffers on short-term plasticity (Kamiya and Zucker, 1994; Tang et al., 2000) and the recovery of transmission following RRP depletion by broadened APs (Lin and Fu, 2005). We address limitations of previous models, attempt to harmonize them with each other and experimental results, indicate how processes combine to produce a strongly accelerating facilitation at tonic synapses, and question the interpretation of the RRP at depressing synapses.
RESULTS
Part I. Experimental Findings
Release Rate and Depression at Phasic Synapses
Release in Normal Medium
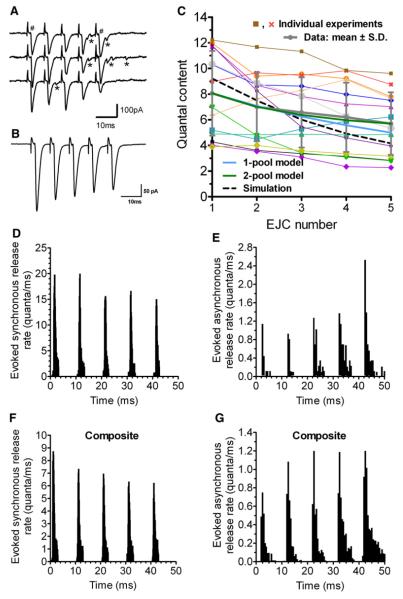
In normal van Harreveld’s (NVH) solution, focal extracellular recordings from a presynaptic bouton (Figure 1) show strong transmission with no failures but a drop in quantal content in successive responses (Bradacs et al., 1997; Msghina et al., 1998; Wojtowicz et al., 1994). Average quantal amplitudes, recorded as miniature excitatory junctional currents (mEJCs), remain constant. Depression to five impulses at 100 Hz was modest, with quantal content falling 34% ± 30% (mean ± standard deviation [SD], n = 14).
Figure 1. Evoked Release at Phasic Synapses.
Responses toa five-spike 100 Hz train, recorded as focal extracellular potentials reporting postsynaptic current, in NVH.
(A) Sample traces from one preparation; #, synchronous release; *, asynchronous release.
(B) Average of 100 trials in the same preparation.
(C) Averaged responses from 14 preparations (thin colored lines), with global average ± SD (thick gray line), predictions from a simple model of depletion from a single pool (thick blue line), or from two independent pools (thick green line), and simulations from our full model (dashed line).
(D) Synchronous release rates during EJCs from one preparation, estimated by deconvolution of EJC with average mEJC; 0.1 ms bins (full dataset in Figure S1).
(E) Asynchronous release rates from the same preparation, estimated by counting mEJCs between EJCs ; 0.5 ms bins (full dataset in Figure S2).
(F and G) Composite synchronous and asynchronous release rates from 11 synapses.
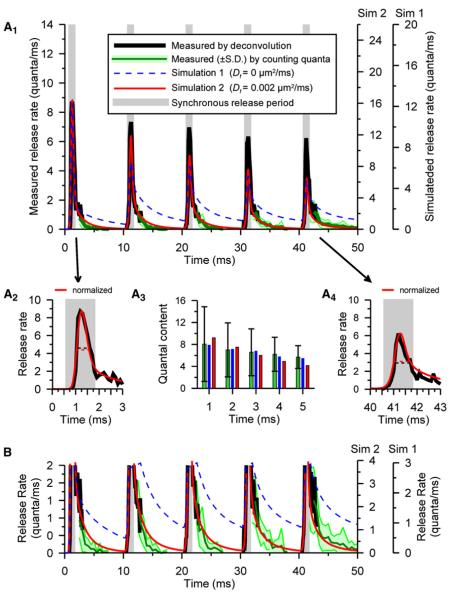
An increased mEJC frequency follows synchronous multiquantal releases. We measured release rate during the synchronous release period (Figure 1D and Figure S1 [available online]) by deconvolution of averaged EJCs (Figure 1B) with averaged mEJCs. Asynchronous release was evaluated by counting single quanta (Figures 1E and S2). Figure 2A1 shows release rates estimated by both methods; Figure 2B magnifies asynchronous release and also plots ±1 SD. The methods agree where the measurements overlap. As synchronous release drops, asynchronous release grows in a train.
Figure 2. Measured and Simulated Release from Phasic Synapses in NVH.
Responses tofive stimuli at 100 Hz.
(A1) Release rates averaged from 11 preparations estimated by deconvolution (black line) or by counting mEJPs (green line ± SD shown as light green area). Simulation 1 (dashed blue line, “fast buffer” diffusion constant [_Df_] of 0) and simulation 2 (solid red line, Df = 0.002 μm2/ms) rescaled to overlay peak rates (16.4 and 12.3 quanta/ms) on measured peak release rate (8.7/ms).
(A2 and A4) Magnified synchronous release periods (gray regions in all panels) for first and fifth responses from (A1), showing measurements and simulation 2: the fifth response is broader (wider half width, horizontal dashed lines) and begins earlier than the first response.
(B) Expansion of (A1) showing asynchronous release.
(A3) Quantal contents (green bars, ±SD) and simulations (in blue for Df = 0 and red for Df = 0.002 μm2/ms); first quantal contents: 8.06 (experimental), 7.91 (simulation 1), and 9.21 (simulation 2).
Quantal contents were calculated (Figure 2A3) by integrating release rate during the synchronous release period (defined in Experimental Procedures) and confirmed by dividing successive average EJC areas by average mEJC area. Quantal contents drop less (to 74.5% ± 26.9% of the first quantal content of 8.06 ± 6.80; Figure 2A3) than peak release rates (to 71.4% in Figure 2A1) because the half-width of synchronous release in the first response (Figure 2A2) is a bit less than for the fifth response (Figure 2A4).
Depression in Cs+-Ringer
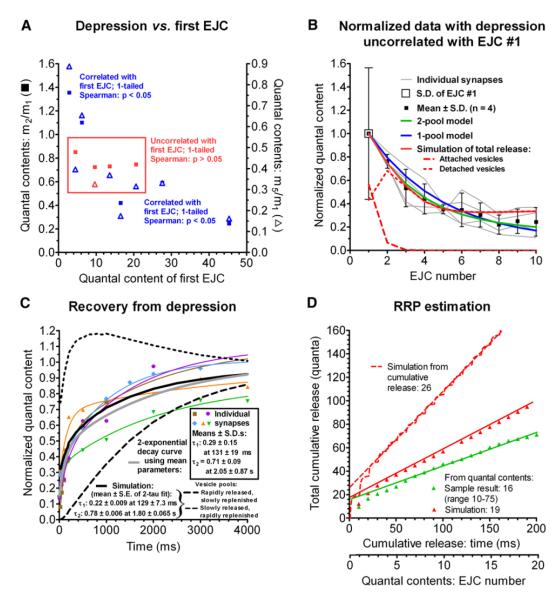
To characterize depression, we enhanced it by prolonging APs in a bathing medium with Cs+ substituted for K+ (Millar et al., 2002). Responses to ten stimuli at 100 Hz were quite variable (Figure 3A), even if normalized to the first response (Figures S3A and S3B). Depression was negatively correlated with initial quantal content (p < 0.01, Spearman r = −0.83 for second and fifth EJCs, n = 9), as expected if it arises from vesicle depletion. Weaker synapses showed a net facilitation on the second response, whereas stronger synapses depressed the most. Restricting attention to four synapses of intermediate strength, depression was more uniform and uncorrelated with first EJC (block in Figure 3A). Average data from these synapses (solid gray lines in Figure S3v, A and B) had smaller SDs (Figure S3C), especially if normalized to the first response (Figure S3D). We regard these intermediate synapses as “typical” phasic synapses (Figure 3B).
Figure 3. Depression at Phasic Synapses in Cesium Ringer.
Growth of, and recovery from, depression at nine phasic synapses stimulated ten times at 100 Hz.
(A) Correlation between depression of the second (squares, left ordinate) or fifth responses (triangles, right ordinate) and initial quantal content. Four synapses with intermediate depression uncorrelated (p > 0.05) with initial amplitude (symbols within box) were used for analysis.
(B) Responses averaged from 20 trials for individual boutons (gray lines), means ± SDs for all synapses (black symbols), simple single-pool (blue line) and two-pool (green line) depletion models, and simulations of our model (solid red line); the latter is separated into release from willingly (W, dashed line) and reluctantly released (V, dotted line) pools.
(C) Recovery from depression in five boutons (colored symbols, averages of 20 trials), showing double exponentials (r2 ≥ 0.97) fitted to each (colored lines). The global average (thick gray line) is a double exponential using parameters averaged from these fits (boxed values). Simulated recovery (black line) is separated into vesicle pools W (dashed line) and V (dotted line). For double-exponential fits, the amplitude and time constant of each exponential is indicated (±SDs for data; ±SEs for simulation parameters).
(D) Cumulative quantal content from simulations (red symbols) used to estimate RRP (red line) from 20-AP 100 Hz train, and an example of experimental data (green symbols and line). Dashed line shows larger RRP estimated from simulation of total cumulative release, including asynchronous release.
We studied recovery from depression in synapses in which the fifth response was between 32% and 40% of the first EJC, resembling our “typical” synapses. Conditioning trains were followed by stimuli at intervals from 5 ms to 4 s after the train (Figure 3C); recovery followed a double-exponential time course.
Synaptic depression is usually attributed to depletion of one or more pools of vesicles available for release (collectively called the RRP). RRP is estimated by plotting cumulative quantal content in a train versus stimulus number and extrapolating to the ordinate the final slope when release has reached steady state (Schneggenburger et al., 1999). Pooldepletion models of depression require an estimate of RRP size. Our measurements of phasic RRP size fell between 10 and 75 (41 ± 23), similar to results of Millar et al. (2002). Figure 3D shows a sample RRP determination.
Release Rate and Facilitation at Tonic Synapses
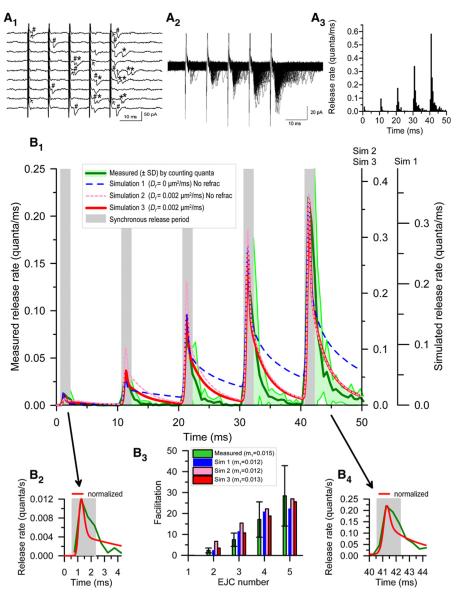
Tonic synapses are the opposite of phasic synapses–they start out nearly silent but facilitate tremendously. Focal recordings in NVH reveal occasional single-quantal responses to the first stimulus (quantal content 0.015 ± 0.011, corresponding to a probability of release per active zone of 0.00075 if there are 20 per bouton; Msghina et al., 1998), whereas asynchronous release is virtually nonexistent (Figures 4A1and 4A2); synchronous and asynchronous release grow strongly in subsequent responses.
Figure 4. Measured and Simulated Release at Tonic Synapses.
Measured and simulated release from tonic synapses stimulated five times at 100 Hz in NVH.
(A1) Sample focal extracellular EJCs; #, synchronous release; †, second element of a rare two-quantum synchronous response; *, asynchronous release; ↖, nerve terminal potential.
(A2) Superimposed traces (500) from another preparation, showing synchronous and asynchronous release.
(A3) Histogram of release rates from the preparation of (A1); full dataset in Figure S3.
(B1) Release rates (green line ±SD shown as light green area) averaged from 13 synapses. Gray regions mark synchronous release periods. Lines are model simulations with Df = 0 (simulation 1, dashed blue line) or 0.002 μm2/ms (simulation 2, dotted pink line) without refractoriness, and Df = 0.002 μm2/ms with refractoriness (simulation 3, solid red line), scaled so peak rates (0.365 [simulation 1] and 0.45 [simulations 2 and 3] quanta/ms) overlap measured peak release rate (0.22 quanta/ms) in the fifth response.
(B2 and B4) Enlarged first and fifth responses, respectively, from (B1).
(B3) Measured (means ± SDs) and predicted facilitation; measured m1 = 0.015 ± 0.011 (n = 13); simulated m1 = 0.012–0.013.
Overlapping quanta are extremely rare, so release rate may be estimated from histograms of synaptic delays to all quantal responses (Figures 4A3 and S4). Figure 4B1 shows average release time course (±SD). Quantal contents (Figure 4B3) were estimated by counting quanta in the synchronous release period and confirmed by dividing average EJC area by average mEJC area. Facilitation was defined as the fractional increase of the quantal content of a subsequent response, mn, compared with that of the first, m1, using Fn =mn/m1 – 1. Facilitation of quantal content (28.4 ± 14.4 for the fifth response, with a quantal content of 0.15 ± 0.11 for the first EJC) exceeded that of peak release rate (22.4 ± 13.4), due to broadening of the release period (Figures 4B2 and 4B4).
Excitatory junctional potentials (EJPs) were also recorded intracellularly from the muscle fiber used for focal recording. Quantal contents were estimated by counting uniquantal responses for early stimuli (Figure S5B), while, for later stimuli, EJP amplitude (Figure S5A) was divided by average mEJP amplitude; when both methods could be used, they agreed closely. Facilitation derived from this data (Figure S5C) was similar to that from extracellular recordings.
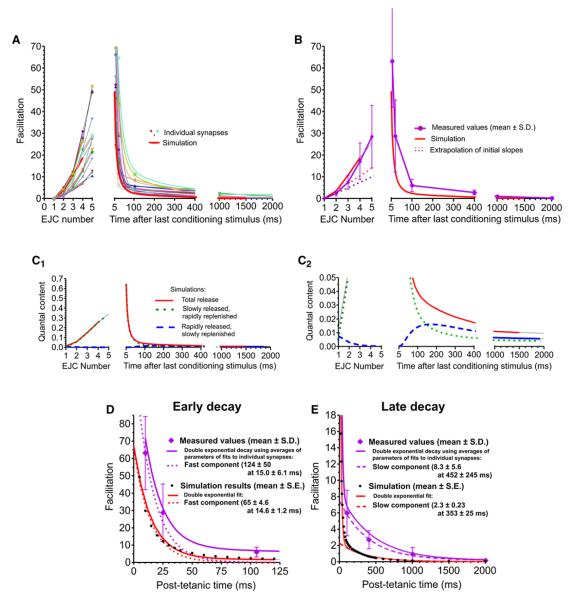
Figure 5A illustrates an accelerating accumulation of facilitation and its posttetanic biexponential decay in individual experiments; Figure 5B plots average behavior.
Figure 5. Facilitation at Tonic Synapses.
Growth of, and recovery from, facilitation at tonic synapses stimulated five times at 100 Hz.
(A) Data from 13 focal extracellular recordings (symbols, and thin colored lines, which for decay are two-exponential fits), compared with simulation (thick red lines).
(B) Averaged results ±SDs (purple lines and symbols) and simulation (red lines); dashed lines show initial growth rates of facilitation, illustrating acceleration.
(C1 and C2) Predicted release from the rapidly and slowly released vesicle pools (dashed blue and dotted green lines, respectively) and total release (solid red lines); (C2) expands foot of (C1) to reveal the rapidly released pool.
(D and E) Fast and slow phases of facilitation decay at two timescales showing measured averages (purple diamonds with SDs), double-exponential fit (solid purple line, parameters averaged from fits in [A]), and fast and slow components of this fit (dotted and dashed purple lines, respectively). Simulated results (small black circles) are shown with a double-exponential fit (solid red line) and fast and slow components (dotted and dashed red lines, respectively). The components of fits are unrelated to vesicle pools in model simulations.
Part II. A Comprehensive Model of Transmitter Release
The Release Scheme
Our model of synaptic transmission began with the scheme proposed by Millar et al. (2002), shown as grayed portions of Figure 6; they added a Ca2+-dependent priming process to the binding of five Ca2+ ions to synaptotagmin (Bollmann et al., 2000; Schneggenburger and Neher, 2000) to account for strong facilitation. This scheme had six parameters: on and off rates (kon and koff) for synaptotagmin binding, a cooperativity factor b, a fusion rate γ, and on and off rates for the priming process, kprime and kupr. Ca2+ binding to C2A and C2B domains occurs independently but with identical kinetics (Chapman, 2008).
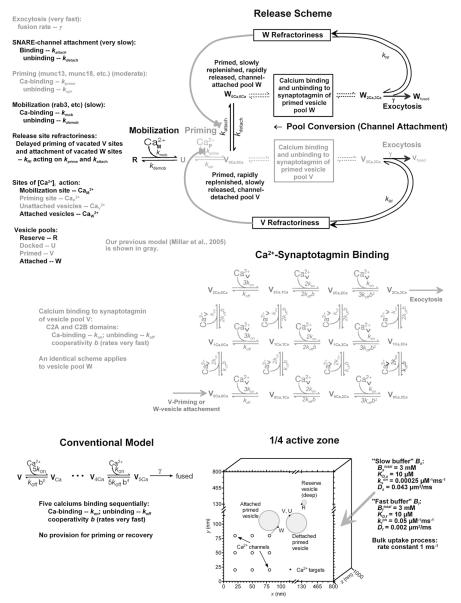
Figure 6. Reaction and Geometrical Schemes Used for Simulations.
The complete release scheme includes mobilization of vesicles from a reserve pool (R) to a docked, unprimed pool (U), molecular priming to vesicles unattached to a Ca2+ channel (V), and conversion to vesicles coupled to a Ca2+ channel (W). Primed vesicle pools are released by only one isoform of synaptotagmin binding three Ca2+ ions to C2A domains and two Ca2+ ions to C2B domains with positive cooperativity (reducing off-rates). Upon full binding, exocytosis occurs at rate γ. All transitions except exocytosis are reversible, and mobilization and priming are Ca dependent. A vesicle cannot be released from a vacated site for a time determined by refractoriness, implemented by reducing the priming or conversion rate in proportion to the fractional loss of vesicles in the pool from which exocytosis occurred. New model provisions are in black; those in Millar et al. (2005) are in gray. The conventional synaptotagmin model (Bollmann et al., 2000; Schneggenburger and Neher, 2000) is shown for comparison. The sketch indicates dimensions and locations of Ca2+ channels and vesicles in pools R, U, V, and W, the sites of Ca2+ action on those pools (small dots), and properties of endogenous buffers and uptake.
(B) Growth of facilitation (B1) in a train of five APs at 100 Hz, and its subsequent decay (B2), from Tang et al. (2000) (in black) with simulations (in red). Circles and solid lines, control experiments; squares and dashed lines, after injection of fura-2 as an exogenous buffer. Quantal content of first simulated response is 0.12. In (B1), error bars represent SDs.
(C1) Rapid production of exogenous buffer by flash photolysis of diazo-2 reduces facilitation after a 50 Hz train of ten APs; inset shows data from Kamiya and Zucker (1994). Left plot: facilitation of EJPs in the train (data, squares; simulation, dashed red line). Right plot: late decay of facilitation; controls without photolysis (open circles with exemplar SDs, and simulation as solid red line) versus responses after photolysis (filled circles with exemplar thicker SDs, and simulation as dashed red line).
(C2) Decay of augmentation following 200 APs at 50 Hz, tested at 0.5 Hz (from Kamiya and Zucker, 1994). Only augmentation remains 2 s after train; its reduction by diazo-2 photolysis 50 ms before the fourth test peaks after a 0.5 s delay. Open circles with SDs represent controls (no photolysis), whereas filled circles with thick SDs represent responses after photolysis. The solid red line represents simulated control responses, whereas the dashed red line represents simulated responses after photolysis. Inset: measurements (circles) and simulations (lines).
(D) Recovery of a releasable pool measured by paired stimulation with APs prolonged 9-fold by TEA; data (filled circles) and simulations (in red) with (solid line) and without (dashed line) refractoriness. Time is plotted logarithmically, as in the inset illustrating junctional currents from Lin and Fu (2005).
We modified this scheme to encompass features of depression. We allowed for refilling pool U of docked but unprimed vesicles from a reserve pool, R. Mobilization of vesicles from R to U was made Ca dependent, as suggested for other preparations (Gomis et al., 1999; Schneggenburger et al., 2002). This added two parameters, kmob and kdemob. Finally, instead of the number of unprimed (U) and primed (V) vesicles being fixed at average RRP sizes (Millar et al., 2002, 2005), only the initial total number of vesicles in all pools (R + U + V + W) was fixed. We recorded from larger phasic boutons, similar in size to average tonic boutons, so we assumed 20 active zones per bouton (Msghina et al., 1998); 600 vesicles per active zone (Wojtowicz et al., 1994) gives 12,000 vesicles per bouton.
The dual-component nature of depression (Figures 3B and 3C) resembles that of vertebrate glutamatergic synapses (Neher and Sakaba, 2008). There, depression initially develops faster and then slower than a single exponential, as if two vesicle pools are depleted at different rates, due to different release probabilities, and depression also recovers with two time constants. After a short train depleting only the first pool, recovery proceeds at the slower rate, as if the willingly released pool recovers more slowly than the reluctantly released pool.
Phasic junctions behave similarly, as shown by fits to single- and dual-pool models used for vertebrate synapses (Wölfel et al., 2007; Zucker et al., 1999). These simple models have no provision for facilitation, priming, or mobilization. Each pool is characterized by a resting size S (dependent on filling and reverse rates k+ and _k_− from a fixed reserve pool), and a constant fraction F of that pool is released by each AP. Following stimulation, each pool recovers at rate _k_−. S, F, and _k_− of the one-pool model were derived by fitting an exponential to recovery and from quantal contents of the first two responses, m1 and m2 (see Supplemental Experimental Procedures). The six parameters of the dual-pool model required estimation of the steady state of depression as well as m1 and m2, two time constants of recovery, and the resting sizes of the two pools, SA and SB. Their sum was set to 58, the average RRP of phasic synapses (Millar et al., 2002). Dual-pool models provided better fits to data from individual synapses (data not shown), as well as to composite data (Figures S3 and 3B). As at vertebrate synapses, the rapidly depleted pool was the slowest to recover.
Rather than propose independent pools, we adopted the suggestion of Neher and Sakaba (2008) that puts the pools in series (Figure 6). The idea is that the first pool (V) consists of molecularly primed and releasable vesicles uncoupled from a Ca2+ channel, so that release probability to an AP is low. Vesicles in the second pool (W) are attached to a Ca2+ channel, where their exposure to higher [Ca2+]i increases release probability. If priming is faster than transit between pools V and W, which Neher and Sakaba (2008) call “positional priming,” the relationship between release probability and recovery rate follows. This adds two more parameters, kattach and kdetach, to the model. A final modification, release site refractoriness, will be introduced later.
Release by APs
We simulate AP-evoked release by calculating the different magnitudes and time courses of [Ca2+]i at the targets governing mobilization, priming, and triggering secretion of V and W vesicles. Symmetry (Matveev et al., 2002, 2006; Tang et al., 2000; Yamada and Zucker, 1992) permits representation of a bouton as a rectilinear volume with x,y dimensions of a quarter active zone on its synaptic face and the surrounding region halfway to the next active zone, and a z depth to the back of the bouton, based on ultrastructural data (details in Supplemental Experimental Procedures).
Calcium Channels
APs admit Ca2+ with a time course dependent on channel kinetics and AP waveform. We use a Ca2+ current time course, ICa(t), derived from a Hodgkin-Huxley model of invertebrate P/Q-type Ca2+ channels (Llinás et al., 1981, 1982; Llinás, 1999) driven by an AP recorded presynaptically (Beaumont et al., 2002; Millar et al., 2005); channel kinetics were adjusted for 18°C. The resulting time course resembled a Gaussian, so a closely fitting Gaussian (with SD = 0.25 ms) was used for ICa(t). We assumed a single-channel conductance of 2.7 pS, based on recent vertebrate measurements (Li et al., 2007) and earlier invertebrate data (Llinás, 1999). Single-channel current peaked at 0.35 pA and admitted 0.35 fcoul (or 1.8 × 10−21 mol) of Ca2+ per AP. This is about half the estimate used in previous simulations (Matveev et al., 2002; Tang et al., 2000), so the number of channels per active zone was increased from four to nine per quarter active zone and arranged in a square array (Figure 6).
Buffers and Pumps
The profile of Ca2+ concentration, Ca2+(x,y,z,t) (or simply Ca2+), is governed by Ca2+ influx into boutons, its diffusion with binding to fixed and mobile endogenous (and sometimes exogenous) buffers, and its active removal. Analysis of presynaptic Ca2+ transients reveals a slowly binding buffer, Bs, and a fast equilibrating buffer, Bf (Lin et al., 2005; V. Matveev and J.-W. Lin, personal communication). Our simulations used values for total amounts (Bstotal and Bftotal), on rates (kson and kfon), and affinities (_K_D,s and _K_D,f) that are in the middle of ranges inferred experimentally (Table 1). For the fast buffer, kfon and _K_D,f were similar to those of a poorly mobile buffer from chromaffin cells (Xu et al., 1997) after adjustment for crayfish ionic strength, and the overall buffer ratio (Bstotal/KD,s + Bftotal/KD,f) agreed with data from Tank et al. (1995).
Table 1.
Parameters Common to All Simulations
| Geometrical Factors and Vesicle Number | |
|---|---|
| Simulation volume | 800 × 800 × 1000 nm |
| Ca channel locations (x,y) | (20,20) (20,50) (20,80) (50,20) (50,50) (50,80) (80,20) (80,50) (80,80) |
| Vesicles in all pools | 12,000 per bouton |
| Endogenous Buffers and Uptake | |
| Bstotal | 3 mM |
| KD,s | 10 μM |
| kson | 0.00025 μM−1ms−1 |
| Ds | 0.043 μm2/ms |
| Bftotal | 3 mM |
| KD,f | 10 μM |
| kfon | 0.05 μM−1ms−1 |
| Df | 0.002 μm2/ms |
| Uptake rate | 1 ms−1 |
| Secretory Trigger | |
| kon | 0.18 μm−1ms−1 |
| koff | 0.5 ms−1 |
| b | 0.4 |
| Secretory Trigger | |
| Calcium Influx and Uptake | |
| Gaussian areaa | 1.8 × 10−21 mol/channel |
| Gaussian SDb | 0.25 ms |
| Channels/active zone | 36 |
| Uptake ratec | 1 ms−1 |
Diffusion constants of endogenous buffers cannot be determined from volume-averaged Ca2+ indicator measurements. Because the slow buffer kinetics resembled those of parvalbumin in the presence of the ~3 mM [Mg2+]i in crayfish cytoplasm (Günzel and Galler, 1991), we assumed a diffusion constant of 0.043 μm2/s as measured for parvalbumin in neurons (Schmidt et al., 2003a); mobile parvalbumin is also present at the calyx of Held (Müller et al., 2007). If all endogenous buffers were highly mobile, Ca2+ would be rapidly shuttled from active zones, blunting synaptic facilitation arising from any mechanism (Matveev et al., 2002, 2004, 2006). Because relatively immobile buffers are ubiquitous in neurons (see Matveev et al., 2004), we initially set Df = 0, but later modified it to Df = 0.002 μm2/s to account for data on asynchronous release.
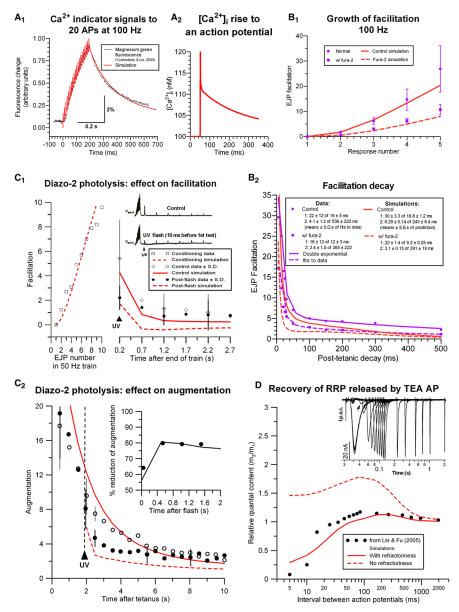
Previous simulations (Fogelson and Zucker, 1985; Matveev et al., 2002, 2004, 2006; Tang et al., 2000; Yamada and Zucker, 1992) removed Ca2+ by a surface pump. However, as [Ca2+]i approaches its resting level, pumps become diffusion limited by the reverse gradient they establish (Stockbridge and Moore, 1984), retarding removal so that resting [Ca2+]i is not reached for a very long time. This property has no effect on brief simulations but caused trouble for simulations of long trains or recovery times. A linear uptake process more accurately reproduced recovery of [Ca2+]i at crayfish motor terminals (Vyshedskiy and Lin, 2000). Figure 7A1 compares simulated and measured effects of a 0.2 s 100 Hz AP train on Ca2+ indicator fluorescence. We included 200 μM of an indicator with kon = 0.5 μM−1ms−1 and _K_D = 6 μM to match the magnesium green (Mg-green) used in the experiments. With an uptake rate of 1.0 ms−1, simulations decayed with time constants of 86 and 310 ms, close to experimental time constants of 84 ± 30 and 390 ± 153 ms. The fast decay arises from Ca2+ binding to the slow buffer; the slower component is due to uptake.
Figure 7. Simulating Results from Opener Synapses.
(A1) Mg-green fluorescence (in black) from Vyshedskiy and Lin (2000) to a train of 20 APs at 100 Hz compared with our simulation (scaled and overlaid as red trace). The ordinate applies to the simulation; the scale bar applies to data.
(A2) Predicted volume-averaged [Ca2+]i elevation to a single AP in a bouton.
The amplitude of Mg-green fluorescence change (Δ_F_) depends on the amount of [Ca2+]i increase and also on resting [Ca2+]i, and especially [Mg2+]i, which alters the effective Ca2+ affinity of Mg-green. Without precise knowledge of [Mg2+]i, it is impossible to predict Δ_F_. The ratiometric indicator fura-2 has been used to estimate that an AP elevates presynaptic [Ca2+]i by 9 ± 6 nM (Tang et al., 2000) at crayfish motor terminals. We simulated this measurement by including a buffer with measured KD = 0.36 μM and kon = 0.27 μM−1ms−1 (based on koff of Naraghi, 1997) at a concentration of 80 μM, which mimicked fura-2 effects on facilitation (see below and Figure 7B). The predicted rise in global [Ca2+]i (Figure 7A2) was 11 nM (excluding the sharp “spike” in [Ca2+]i, which fura-2 is unable to detect due to its slow kon and koff). The agreement with experiment supports our choice of number of Ca2+ channels per active zone.
Locations of Targets of Ca2+ Action
We now could predict the spatiotemporal profile of Ca2+ to neural activity. Effects on transmission depend on positions of the Ca2+ sensors governing release, which were varied within narrow ranges that seemed functionally defensible.
CaW
Because vesicles are docked in a circle surrounding the perimeter of the active zone (Cooper et al., 1996), Ca2+ was assumed to trigger secretion at an attached vesicle at position CaW(x,y,z) located 12–20 nm away in all x,y,z directions, or a diffusion distance of 20–35 nm, from a corner Ca2+ channel (Figure 6). This is a point partway up the vesicle surface: 66°–90° up from its contact with the plasma membrane, at a putative synaptotagmin bound to synaptobrevin in an imagined circle of docked SNAREs, with a lateral distance of 17–28 nm separating the center of the SNARE ring from the channel through its attachment to a syntaxin in the SNARE circle, and recognizing that Ca2+ must diffuse around many SNARE-associated proteins.
CaV and CaP
The locus of the secretory target for unattached vesicles, CaV(x,y,z), was made more distant, 34–55 nm in x and y directions from the corner channel and 20 nm beneath the membrane, or 52–80 nm from the channel mouth. This would correspond to where a vesicle first docks at the membrane; it was also taken as the priming site, CaP(x,y,z).
CaM
Mobilization from the reserve pool should occur further away, CaM(x,y,z), at vesicles near the plasma membrane but not yet docked. This point was 50–65 nm away in all dimensions (87–112 nm distant) from a corner Ca2+ channel.
We now describe our attempts to explain the behavior of phasic and tonic synapses.
Simulations of Phasic Synapses
Release in NVH
We aim to explain all aspects of phasic synapse behavior with a single set of parameters. We initially supposed that the fast buffer, Bf, was fixed (Df = 0). The parameters in Table 1 and under Sim 1 in Table 2, selected as described in Supplemental Experimental Procedures, produced reasonable fits to synchronous release time course and depression of quantal content in NVH (Figure 2A1, simulation 1), as well as depression and its recovery in Cs+-Ringer and responses to [Ca2+]i steps from the photolysis experiments of Millar et al. (2005) (Figure S6). However, simulations using these parameters overpredicted asynchronous release in a train (Figure 2B).
Table 2.
Parameters Particular to Individual Simulations
| Phasic Synapses | Tonic Synapses | Opener Neuromuscular Junctions | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | Sim1 Fixed_Bf_ (Df = 0) | Sim 2(±R) Mobile_Bf_ (Df = 0.002) | Sim 1,NR Fixed_Bf_ (Df = 0) | Sim 2,NR Mobile_Bf_ (Df = 0.002) | Sim3 Mobile_Bf_ (Df = 0.002) | AfterInjectingFura-2 | BeforePhotolysingDiazo-2 | AfterPhotolysingDiazo-2 | Plus TEA |
| Ca2+ Targets (Relative to Ca2+ Channel at [80,80]) | |||||||||
| CaM(x,y,z) (nm) | (65,65,65) | (50,50,50) | (50,50,50) | (50,50,50) | (50,50,50) | (50,50,50) | (50,50,50) | (50,50,50) | (50,50,50) |
| CaP(x,y,z) (nm) | (40,40,20) | (34,34,20) | (51,51,20) | (47,47,20) | (48,48,20) | (55,55,20) | (55,55,20) | (55,55,20) | (55,55,20) |
| CaV(x,y,z) (nm) | (40,40,20) | (34,34,20) | (51,51,20) | (47,47,20) | (48,48,20) | (55,55,20) | (55,55,20) | (55,55,20) | (55,55,20) |
| CaW(x,y,z) (nm) | (15,15,15) | (15,15,15) | (15,15,14) | (16,16,16) | (18,18,18) | (12,12,12) | (15,15,15) | (15,15,15) | (12,12,12) |
| Resting Vesicle Pool Sizesa | |||||||||
| R (Reserve) | 11,938 | 11,936 | 11,999 | 11,991 | 11,997 | 11,930 | 11,912 | 11,912 | 11,988 |
| U (Unprimed but docked) | 35 | 27 | 0.48 | 9 | 3.1 | 67 | 83 | 83 | 9.0 |
| V (Primed, unattached) | 18 | 29 | 0.03 | 0.054 | 0.12 | 3 | 5.1 | 5.1 | 3.2 |
| W (Primed and attached) | 9 | 8 | 0.013 | 0.006 | 0.012 | 0.095 | 0.082 | 0.082 | 0.10 |
| Exogenous Buffer | |||||||||
| Bitotal (μM) | 80 | 500 | 100 | ||||||
| KD,i (μM) | 0.36 | 4.4 | 0.15 | ||||||
| kion (μM−1ms−1) | 0.27 | 0.017 | 0.5 | ||||||
| Di (μm2/ms) | 0.036 | 0.025 | 0.025 | ||||||
| Mobilization, Priming, Attachment, and Refractoriness | |||||||||
| kmob (μM−1ms−1) | 7.2 × 10−5 | 5.0 × 10−5 | 2.19 × 10−4 | 6.8 × 10−6 | 3.0 × 10−5 | 8.45 × 10−4 | 7.0 × 10−4 | 7.0 × 10−4 | 3.0 × 10−4 |
| kdemob (ms−1) | 0.0025 | 0.0022 | 0.0024 | 0.0009 | 0.012 | 0.015 | 0.010 | 0.010 | 0.040 |
| kprime (μM−1ms−1) | 0.023 | 0.028 | 0.00074 | 0.022 | 0.018 | 0.006 | 0.0045 | 0.0045 | 0.015 |
| kupr (ms−1) | 0.0054 | 0.0032 | 0.039 | 0.45 | 0.048 | 0.016 | 0.0088 | 0.0088 | 0.0050 |
| kattach (ms−1) | 0.00043 | 0.00015 | 0.0002 | 0.00013 | 0.00091 | 0.00030 | 0.00012 | 0.00012 | 0.000304 |
| kdetach (ms−1) | 0.00082 | 0.00051 | 0.001 | 0.0011 | 0.0091 | 0.0097 | 0.0099 | 0.0099 | 0.0097 |
| kRf (ms−1) | 0.10 | 0.10 | – | – | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 |
Secretory cells, neurons, and nerve terminals often contain a poorly diffusible Ca2+ buffer (Helmchen et al., 1996, 1997; Lee et al., 2000; Ohana and Sakmann, 1998; Schmidt et al., 2003b). There is no evidence that this buffer is completely immobile–results are consistent with a mobility between 0 and 0.005 μm2/ms. Proteins should move at this rate, and although they might interact with internal membranes and structural proteins, they should not be absolutely fixed. Allowing Bf to diffuse slowly, with Df = 0.002 μm2/ms, dramatically improved the fit of simulations to synchronous and asynchronous phasic release (simulation 2 in Figures 2A1 and 2B and Table 2). Simulated peak release rates (right-hand ordinates) were somewhat higher than experimental peaks (left ordinate), which are blunted by histogram binning. Simulations also predicted an observed broadening and decreased minimal delay in release with successive APs (Figures 2A2 and 2A4). A slight overprediction of broadening compensated an underprediction of depression in peak release rate; hence, simulated depression of quantal contents matched observations (Figure 2A3).
Asynchronous release simulations were also within experimental variation (light green regions of Figure 2B). A realistic Bf mobility allowed Ca2+ to diffuse from primed vesicles quickly enough to fit the decay of synchronous release and the low asynchronous release rate. As synchronous release depressed, asynchronous release accumulated. This “anomalous property” of depression is often seen (Zucker and Regehr, 2002). It arises from accumulation of “residual calcium” at sites affecting release from pool V (CaR,CaU/CaV), which is almost entirely responsible for asynchronous release. The refinement of parameters needed to optimally fit AP-evoked release with nonzero Df (column 2 ofTable 2 and Figure 2) also improved the fit (Figure S6) of simulated photolysis responses to results (Millar et al., 2005).
Depression in Cs+-Ringer
We simulated responses in Cs+-Ringer by increasing duration of Ca2+ influx, ICa(t), to match the measured increase in quantal content from 8 to 12. Simulated depression and recovery fell within experimental observations (Figures 3B and 3C). Experimentally, depression decayed with a fast component of amplitude 29% ± 15% and time constant 131 ± 19 ms; and a slow component of 71% ± 9% at 2.05 ± 0.87 s (means ± SDs of fits to each experiment). Simulations recovered similarly (22% ± 0.9% at 129 ± 7.3 ms, and 78% ± 0.6% at 1.08 ± 0.065 s, means ± standard errors [SEs] of the estimates).
These kinetics imply two pools of immediately releasable vesicles (V and W). Simulations placed synaptotagmin in the channel-detached V pool (as well as the unprimed U pool) 52 nm away from the nearest Ca2+ channel (Table 2); for the channel-attached pool (W), this distance was 36 nm. Figures 3B and 3C show contributions of pools V and W to depression and its recovery. Attached vesicles are exhausted rapidly but recover slowly, due to slow rates of vesicle-channel attachment/detachment. Detached vesicles undergo an early facilitation and then depress gradually, but recover quickly, due to rapid repriming. In simulations of modest depression in NVH, pool V also evinced facilitation early in the train. This would explain why some synapses showed a small early facilitation, both in NVH (Figure 1C) and in Cs+-Ringer (Figures 3A and S3A).
We reproduced experiments for RRP estimation by stimulating 20 times at 100 Hz and plotting either quantal content of successive EJCs versus EJC number, or total release including asynchronous release versus time (Figure 3D). The quantal content simulation extrapolated to 19, within our measured range (10–75). Plotting total cumulative release produced a higher estimate of 26; Stevens and Williams (2007) showed a similar effect on RRP estimates when asynchronous release is included.
Simulations of Tonic Synapses
Tonic synapses behave very differently from phasic synapses, but we could simulate results with the same model by adjusting mobilization, priming, and attachment rates (Table 2). As with phasic synapses, simulated time course of release to APs using a fixed fast buffer (Df = 0) met with failure–asynchronous release was much too high (simulation 1 in Figure 4B1). Allowing Bf to diffuse slowly (Df = 0.002 μm2/ms, simulation 2) improved the fit to results. If release site refractoriness was included (simulation 3; see section at end of Results), asynchronous release came almost entirely from pool V and fell almost entirely within 1 SD of average measurements.
Like phasic synapses, simulated release rates of the largest response were higher than measured peaks, which are seriously underestimated by the 0.5 ms bins needed to measure the low release rates of tonic synapses. Synchronous release durations were narrower than those estimated experimentally (which are artifactually broadened by binning; Figures 4B2 and 4B4); this compensated for the higher peaks, so simulated and measured quantal contents were close (0.012–0.013 versus 0.015 ± 0.011 for the first response). Simulations also reproduced the decrease in minimal synaptic delay and increase in synchronous release duration seen in response to later stimuli. The amount of simulated facilitation (22.4, 27, and 25.6 for simulations 1, 2, and 3) was also close to results (28.4 ± 14.4, Figure 4B3). Finally, simulated responses to step [Ca2+]i elevations (Figure S7)–using parameters optimized to fit AP-evoked release with non-zero Df and refractoriness–fit results of photolysis experiments as well as, or in some aspects better than, the simulations of Millar et al. (2005). The need for refractoriness is explained at the end of Results.
Simulations also matched the growth of facilitation in a train and its subsequent decay (Figure 5A). Although we obtained satisfactory fits with all three simulations (Df = 0 or 0.002 μm2/ms, and with refractoriness), we only illustrate simulations with non-zero Df and refractoriness that were needed to fit other results. Acceleration of facilitation (Figure 5B) arose from pool V (Figure 5C1), due to mobilization and priming (see Discussion). The early loss of pool W (Figure 5C2) depresses the initial growth of facilitation, contributing to accelerated growth.
Facilitation decayed with two components (Figure 5D); we fitted a double-exponential to data from each synapse (the thin lines of Figure 5A) and formed a composite from averages of the amplitudes and time constants. Experimentally, facilitation decayed with a rapid component of 124 ± 50 magnitude and 15 ± 6.1 ms time constant and a slow component of 8.3 ± 5.6 amplitude and 452 ± 245 ms time constant (means ± SDs of fits to each experiment). Simulations decayed with similar time constants (14.6 ± 1.2 and 353 ± 25 ms, estimates ±SEs of two components). The amplitudes (65 ± 4.6 and 2.3 ± 0.23) were similar to the data, less than the means but nearly within the SDs. The difference (not significant) is due to the somewhat larger acceleration of experimental facilitation. Figure 5A confirms that simulated decay falls within the range of experimental data.
The two phases of facilitation decay arise from the recovery times of the two pools (Figure 5C). The recovery of pool V is determined by the interaction of mobilization and especially priming with the diffusion of Ca2+ away from these targets, whereas the recovery of pool W mainly reflects the time required for vesicle attachment to Ca2+ channels and the rate of Ca2+ removal.
Extending the Model to Fit Other Results
The utility of modeling in explaining both phasic and tonic transmission prompted us to examine its potential for simulating other results. Synaptic plasticity has been studied extensively at crayfish opener NMJs (Bittner, 1989); we therefore attempted to reproduce properties of this preparation.
Exogenous Buffers and Facilitation
Effects of exogenous buffers constrain possible mechanisms underlying facilitation (Matveev et al., 2002, 2004, 2006). Opener and tonic facilitation are similar (cf. Figures 5 to 7B), but quantal content is higher at opener boutons, e.g., 0.13 (Bittner and Kennedy, 1970) rather than 0.015. For opener simulations (Figure 7B), we adjusted tonic synapse parameters to increase unprimed (U), detached (V), and channel-attached (W) vesicle pools (Table 2). The duration of Ca2+ influx, ICa(t), was increased 30%, while total influx remained unchanged, reflecting cooler experimental conditions (15°C). On adding 80 μM of a buffer Bi with kion = 0.27 μM−1ms−1 and KD,i = 0.36 μM to match the properties of fura-2 (Tang et al., 2000), and using the measured fura-2 diffusion rate of Di = 0.036 μm2/ms (Baylor and Hollingworth, 1988), simulations replicated experimental results (Tang et al., 2000): facilitation was reduced (to 39% in simulations versus 40% experimentally), the fast component of decay was accelerated (16.8 to 9.2 ms in simulations versus 19 ± 5 ms to 12 ± 3 ms experimentally), while slow decay was essentially unchanged (243 to 291 ms in simulations versus 536 ± 222 ms to 365 ± 222 ms experimentally).
Diazo-2 Photolysis, Facilitation, and Augmentation
We simulated effects on facilitation and augmentation of photolyzing the presynaptically injected caged buffer diazo-2 (Kamiya and Zucker, 1994). These experiments were performed on an opener muscle region with less facilitation, so we adjusted parameters to fit the growth of facilitation and its decay, while including 500 μM unphotolyzed diazo-2 with kion = 0.017 μM−1ms−1 and KD,i = 4.4 μM (Adams et al., 1989; adjusted for crayfish ionic strength), which reduced transmission by the amount observed experimentally. Uptake was reduced to 0.2 s−1 in accord with the temperature used (cf. Tank et al., 1995) and the slower decay of facilitation observed in these experiments. We simulated diazo-2 photolysis by producing 100 μM high-affinity photoproduct (kion = 0.5 μM−1ms−1 and KD,i = 0.15 μM) 10 ms before the first posttetanic test stimulus. Simulated facilitation dropped by a percentage similar to experimental result (60% and 59%, respectively, Figure 7C1). Unfacilitated release (at late recovery times) was also reduced, but by less (42% reduction from first conditioning response). Augmentation is a slower form of plasticity seen after a longer conditioning train, which was probed by photolysis 50 ms before a fourth posttetanic stimulus at 0.5 Hz after facilitation had subsided. Photolysis reduced augmentation in simulations and experiments (Figure 7C2), but only after a delay reflecting augmentation’s slow reaction to [Ca2+]i. In our model, this comes from the kinetics of mobilization, which underlie this form of plasticity. Mobilization parameters were adjusted to match facilitation in the train, but were not altered to fit effects of diazo-2 photolysis.
Recovery of Transmission with TEA-Broadened APs Suggests Release Site Refractoriness
Lin and Fu (2005) prolonged APs with tetraethylammonium (TEA), causing massive transmitter release from the opener inhibitor. A subsequent stimulus released almost nothing, suggesting that the RRP had been emptied; recovery occurred quickly, within 50 ms. These synapses facilitate like excitatory ones (Atwood and Bittner, 1971), so we adapted our tonic model to simulate these experiments, prolonging ICa(t) and total influx 9-fold to duplicate observed increases in presynaptic [Ca2+]i transients and transmission (Vyshedskiy and Lin, 2000), while ICa(t) duration in the test pulse was reduced to half (as seen experimentally), recovering with a 50 ms time constant. We were unable to replicate the results with any combination of release parameters; instead, the continuing priming required for facilitation resulted in enhanced release to a closely following test stimulus (Figure 7D). To simulate experimental results, we had to invoke a refractory process, as suggested for several other synapses (Zucker and Regehr, 2002), in which sites from which either Ca-attached (W) or detached (V) vesicles had been released remained unable to accept a new primed vesicle for some time (Figure 6), determined by rate constant kRf =10s−1. Identical refractoriness was included in all simulations of opener and tonic synapses (Figures 4, 5, 7, and S7), whereas phasic synapse simulations (Figures 2, 3, and S6) included a briefer refractoriness (kRf = 100 s−1), similar to that observed at hippocampal synapses whose behavior resembles phasic NMJs (Dobrunz et al., 1997).
DISCUSSION
A Comprehensive Model
Crayfish NMJs behave much like other synapses. APs evoke synchronized release followed by a dribble of vesicle fusions. At phasic synapses, strong release undergoes two-component depression, deepened by increasing release and recovering with two time constants, while asynchronous release grows during a train. At weak synapses, facilitation is the rule, rising and falling with two kinetic components, with similar changes in asynchronous release; tonic NMJs are unusual only in the depth of their initial weakness and the robustness of subsequent facilitation. Our experimental results document, in some detail, these properties, that otherwise resemble those of other preparations (Zucker and Regehr, 2002).
Our main accomplishment was to develop a unified model of synaptic transmission that accounts quantitatively for release kinetics to step rises in [Ca2+]i by caged Ca2+ photolysis, kinetics of synchronous and asynchronous transmitter release, changes in synaptic delay and synchronous release duration in a train, the kinetics of two components of tetanic depression and posttetanic recovery when depression dominates, behavior to long trains used to estimate RRP size, the effect of including asynchronous release on RRP estimates, recovery from rapid emptying of the RRP by prolonged APs, facilitation in a train and its two-component recovery when facilitation dominates, the appearance of augmentation following longer trains, and the effects on facilitation and augmentation of exogenous buffers preinjected or produced by photolysis. A relatively simple model reproduces a wealth of synaptic phenomenology.
Previous Models
Most models focus on one type of synapse and one property of transmission and try to explain it by a single mechanism. For example, facilitation, which at crayfish NMJ is clearly not due to increased Ca2+ entry in successive APs (Tank et al., 1995), was initially attributed to Ca2+ acting nonlinearly at the secretory trigger (synaptotagmin), where a small residual [Ca2+]i would augment asynchronous release and facilitate evoked release by summating with [Ca2+]i increments in APs to produce elevated [Ca2+]i peaks. Early simulations (data not shown) confirmed conclusions that this mechanism alone cannot achieve large facilitation with a small increase in asynchronous release (Zucker and Regehr, 2002). Saturation of endogenous buffers underlies part of facilitation at some (Blatow et al., 2003), but not all (Rozov et al., 2001), mammalian central synapses. However, our simulations (data not shown) confirmed previous findings (Matveev et al., 2004) that if this buffer is mobile, exogenous buffers strongly accelerate the early decay but greatly prolong the late component of facilitation, contradicting observations (Figure 5B2); and if this buffer is immobile, unrealistically high buffer concentrations and separation of Ca2+ channels from secretory targets are required, and the growth of facilitation fails to accelerate.
Models of Ca2+ adducing facilitation to a separate target have also been proposed. In one, Ca2+ acts on two targets downstream of synaptotagmin with kinetics that generate fast and slow facilitation (Matveev et al., 2006). This model was as good as ours in describing the growth and decay of facilitation and effects of exogenous buffers, but simulations of diazo-2 photolysis reduced unfacilitated release as much as facilitated release, unlike experimental results. Moreover, this model introduced additional processes that have no physiological correlate and could not account for depression at all. In another model (Matveev et al., 2002), we allowed Ca2+ to act on one target to facilitate release with two components that arose from Ca2+ diffusion characteristics. But this model required immobile buffers with fast kinetics that are inconsistent with data on presynaptic buffer properties (Lin et al., 2005; V. Matveev and J.-W. Lin, personal communication) and required a high local tortuosity severely restricting Ca2+ diffusion and an unrealistic fura-2 immobilization.
Most models of facilitation and depression at vertebrate synapses (Zucker and Regehr, 2002) have been descriptive rather than mechanistic in nature (e.g., Dittman et al., 2000) and are therefore of an entirely different class of model from ours, which attempts to derive synaptic behavior from underlying physiological mechanisms interacting with measured physical processes. The vertebrate literature is rich with quantitative explorations of processes that could underlie facilitation or depression (see Neher and Sakaba, 2008, for a recent review). Our notions of depression arising from sequential two-pool depletion, with Ca2+-dependent mobilization from a reserve pool and “positional priming” reflecting association of primed vesicles with Ca2+ channels, as well as release site refractoriness, which Neher and Sakaba call “site clearing,” and our basic formulation of the exocytic process, are all borrowed from this literature. For this reason we think it likely that our explanations of transmitter release and short-term plasticity are as applicable to vertebrate neuronal synapses as to crustacean NMJs.
In contrast to approaches in which model parameters were relatively unconstrained, we began with extensive data that impose stringent constraints on endogenous buffers and pumps (Lin et al., 2005; V. Matveev and J.-W. Lin, personal communication) and chose unvarying parameters consistent with those constraints. We used a realistic model of synaptotagmin, separating Ca2+ binding to C2A and C2B domains and choosing parameters similar to those used by others and agreeing with kinetic biochemical data (Bollmann et al., 2000; Chapman, 2008; Schneggenburger and Neher, 2000). We avoided more complex allosteric models or multiple synaptotagmin isoforms (Lou et al., 2005; Sun et al., 2007), because our data do not require them and there is no evidence for them at crustacean synapses, but we cannot exclude them either. We included Ca2+-dependent priming as in Millar et al. (2005), consistent with accumulating molecular evidence (Neher and Sakaba, 2008), because we found no other way to produce massive facilitation of initially silent synapses. Priming is rapid in tonic synapses, slow at phasic synapses, and intermediate at opener synapses (Table 2). To this we add a Ca2+-dependent mobilization process, a little slower at phasic than at tonic and opener synapses, which both contributes to facilitation and replenishes vesicles from a reserve pool to restore transmission after depression. We allowed for two releasable vesicle pools to account for the two-component nature of depression. Finally, release site refractoriness was included to fit responses to long APs at facilitating synapses and was incorporated into all simulations, albeit with a faster rate at phasic synapses.
To activate these processes, we calculated the Ca2+ concentration profile in a space defined by ultrastructural measurements, entering through Ca2+ channels with experimentally determined properties and diffusing past buffers whose properties were experimentally delimited. This is quite different from models that “back-calculate” from a release scheme the local magnitude and time course of Ca2+ concentration that would be necessary to account for release to APs or that assume that local Ca2+ time course is identical to that of Ca2+ influx (e.g., Bollmann et al., 2000; Bollmann and Sakmann, 2005; Schneggenburger and Neher, 2000). We chose distinct locations for Ca2+ targets in mobilization, priming, and secretion of primed vesicles that were within narrow, realistic ranges but that necessarily result in differences in the local magnitudes and temporal profiles of Ca2+ at their locations. Exogenous buffer kinetics and mobilities were also experimentally grounded. All simulations of one synapse (tonic, phasic, different opener populations used in fura-2 and diazo-2 studies, and inhibitor synapses used in the TEA study) used one set of parameter values and Ca2+ target locations. Only with such severe constraints was such extensive modeling possible; yet despite them, it was successful, and because of them, it is meaningful.
We do not claim that the model is complete, perfect, or unique in being able to account for properties of synaptic transmission. The model is not stochastic–it ignores spatial heterogeneity and temporal fluctuations, diffusional barriers, and nonuniform tortuosity, as well as effects of interactions between neighboring active zones (Cooper et al., 1996). It does not constrain release to a single vesicle at a time in an active zone, as has been proposed at both crayfish NMJs (Zucker, 1973) and vertebrate central synapses (Korn et al., 1982; Stevens and Wang, 1995), nor does it limit the number of dockable vesicles that can be accommodated by an active zone (Stevens and Wesseling, 1999). Thus, it cannot be used to simulate the binomial nature of transmitter release statistics. Although we could not explain depression by depletion of a single uniform pool of releasable vesicles, there is no evidence that there are only two discrete pools rather than a continuum of states of vesicle priming. Like others, we respect the value of parsimony in our formulation. It has been suggested that at mammalian synapses, “positional priming” or attachment of molecularly primed vesicles to Ca2+ channels, is also Ca2+ dependent (Neher and Sakaba, 2008), and that might be true for crayfish synapses. At the calyx of Held, this process is thought to be chiefly responsible for the replacement of secreted vesicles, and the latest models include no separate mobilization process. Our simulations with Ca2+-dependent vesicle-channel association without mobilization of reserve vesicles did not produce facilitation and recovery with the properties of tonic synapses, so we rejected this alternative. A combination of the two models might work better than either alone, but we presented the simplest model that accounts for all the results we considered. Our goal was a comprehensive but simple framework integrating processes proposed to underlie the full diversity of common forms of short-term synaptic plasticity, to facilitate further experimental exploration of synaptic mechanisms and their regulation.
Meaning of the RRP
One question arising from our study is: which of our vesicle pools represents the RRP? Although we reproduced experiments used to estimate RRP (Figure 3D), the RRP derived from extrapolating cumulative release versus response number or time (19) did not correspond to any (combination) of the underlying pools, which were U = 27, V = 29, and W = 8. Because W is rapidly exhausted, the RRP estimate reflects mainly pool V, and to some extent pool U if it replenishes pool V quickly enough, but it clearly underestimates either or both of them. It may well be that RRP is a fuzzy concept, extractable from data but not rigorously corresponding to any physical vesicle pool.
Regulation of Synaptic Properties
Perhaps the most interesting aspect of opener synapses is that the properties of boutons from this single motor neuron vary across the muscle from being nearly silent with enormous facilitation, like tonic extensor synapses, to transmitting strongly with only moderate facilitation, midway toward phasic synapses (Bittner, 1968; Parnas et al., 1982). This fascinating feature of neural development implies graded posttranscriptional regulation of the proteins responsible for mobilization of reserve vesicles, vesicle attachment, or positional priming, and especially molecular priming of newly docked vesicles at different boutons of a single neuron.
EXPERIMENTAL PROCEDURES
Animals and Preparation
Freshwater crayfish (Procambarus clarkii; 5–6 cm) from Atchafalaya Biological Supply (Raceland, LA) or Niles Biological (Sacramento, CA) were kept in an approved poikilotherm facility. We used the carpopodite extensor preparation, innervated by tonic and one phasic excitatory motor axons. Anatomical and physiological features of this muscle have been described (Bradacs et al., 1997; Msghina et al., 1998). It was dissected and pinned on a Sylgard disc in a 4 ml chamber and superfused at 1 ml/min with NVH at 18°C–20°C containing (in mM) 195 NaCl, 5.4 KCl, 13.5 CaCl2, 2.6 MgCl2, and 10 Na-HEPES buffer (pH 7.4).
Electrophysiology
EJPs were recorded by impaling extensor fibers with a sharp microelectrode (10–20 MΩ, filled with 3 M KCl). EJP amplitudes in a tetanus were measured by subtracting peak amplitude from the falling phase of the previous EJPs (Figure S5A).
Loose macro-patch recordings (Cooper et al., 1995; Dudel, 1981; Wojtowicz et al., 1994) of EJCs were obtained from single boutons made visible by exposure for 3 min to 3 mM 4-(4-diethylaminostyryl)-N-methylpyridinium iodide (4-Di-2-Asp; Molecular Probes, Eugene, OR) (Cooper et al., 1995). Patch pipettes were beveled at 30° to a 6 × 10 μm opening, fire-polished, filled with saline, and placed over a well-defined tonic or phasic bouton.
Motor axons were stimulated with an electrode of 10–15 μm opening placed on an axon on the muscle surface. 4-Di-2-Asp stains the larger tonic axon more brightly (Bradacs et al., 1997). We averaged 20 sweeps at phasic synapses and at least 50 sweeps at tonic synapses. Successive five-pulse trains were separated by at least 10 s, and longer trains by at least 30 s.
EJCs were recorded in voltage clamp mode with an SEC-05LX amplifier (NPI Electronic GmbH, Tamm, Germany) modified for macro-patch applications, low-pass filtered at 5 kHz, and digitized at 10 kHz using pClamp (Axon Instruments, Foster City, CA). Data reduction was performed with Excel (Microsoft, Redmond, WA).
Data Analysis
Calculating Quantal Content and Rates of Synchronous and Asynchronous Release
At phasic synapses, release rate was estimated by deconvolution (Millar et al., 2005; Van der Kloot, 1988) of averaged evoked responses (Figure 1B) with quantal waveforms derived by averaging isolated mEJCs from the same preparation, using F[n(t)] = F[EJC]/F[mEJC], with F representing Fourier transforms of release rate n(t) at time t, EJCs, and mEJCs, respectively. Igor Pro (WaveMetrics, Lake Oswego, OR) produced the inverse Fourier transform of F[n(t)] to get n(t).
This procedure yielded positive release rates for 3–5 ms, beginning 0.6 ms after the presynaptic AP (the minimal synaptic delay), measured from the negative peak of the presynaptic nerve terminal potential (NTP) (Katz and Miledi, 1965). Over 90% of release occurred between 0.6 and 1.8 ms after the NTP (Figure S1); this was taken as the synchronous release period, corresponding to release contributing to the amplitude of intracellularly recorded EJPs (Landò and Zucker, 1994). Release rate integrated over this period yielded quantal contents, which were estimated independently by dividing averaged EJC areas by averaged mEJC area from each preparation; the estimates agreed within 10%. Deconvolution results were divided into 0.1 ms bins, and a composite histogram of release rate from all phasic synapses within each time bin was produced.
Asynchronous releases occurring >3–5 ms after the NTP were undetectable by deconvolution. Single quanta were discernable in individual traces, usually beginning 2.5 ms after the NTP until the next stimulus. Release rate in this period was calculated by counting quanta in each time bin and dividing by number of traces times the bin width (Figure S2), then forming a composite histogram from all synapses. Early asynchronous release was measurable by both methods, and close agreement at individual synapses (Figures S1 and S2) and the composite results (Figures 2A1 and 2B) provided a consistency check of the two methods.
Tonic release rate was estimated by counting mEJCs (Figures 4A1 and 4A2) and forming histograms binned at 0.5 ms of their synaptic delays from the NTP (Figures 4A3 and S3). Over 90% of release occurred within 0.6–2.3 ms (Figure S4), and this was taken as the quantal content of evoked synchronous release in Figures 4B3 and 5. Larger quantal contents were calculated from ratios of EJC area to averaged mEJC area. When both methods could be used they agreed within 10%. For quantal analysis of intracellular recordings (Figure S5), larger EJP amplitudes were divided by average mEJP amplitude in electrotonically compact fibers, where mEJP histograms fell well above noise level. Average EJPs for small responses were below the noise level, but multiple releases were so rare that quantal content could be estimated from the fraction of traces with failures. The two methods gave comparable results for intermediate EJPs. Phasic EJPs were unsuitable for quantal content estimation because of contamination by local active responses (partial APs), and their short duration and large size precluded accurate correction for nonlinear summation (Jack et al., 1975; Martin, 1976).
Calculating Phasic RRP Size
We estimated RRP content by the rapid depletion technique (Millar et al., 2002; Schneggenburger et al., 1999) in which a 100 Hz train of 20 stimuli produced depression reaching steady state in Ringer with Cs+ substituted for K+. Cumulative EJC quantal content was plotted versus stimulus number, and a line fitted to the last five events extrapolated to the ordinate to estimate the number of quanta in the RRP.
Analysis and Simulations
Extensive details are included in Supplemental Experimental Procedures. We outline equations for one- and two-pool depletion models and our implementation of transmitter release reactions, describe the publicly available “calcium calculator” (CalC) software used to implement partial differential equations for diffusion and reaction of Ca2+ and buffers, and describe procedures followed for parameter selection.
Supplementary Material
01
Figure S1. Synchronous Evoked Release Rates at Phasic Synapses Estimated by Deconvolution
Averaged responses to a 5-spike 100-Hz train from 100 focal extracellular recordings were deconvolved with the averaged waveform of at least 10 isolated mEJCs at 11 synapses; 0.1 ms bins. Time is measured from the arrival of the presynaptic AP (the negative peak of the nerve terminal potential). A composite histogram formed from responses at all phasic synapses is also shown (lower right).
Figure S2. Asynchronous Evoked Release Rates at Phasic Synapses
Histograms of synaptic delays to individual mEJCs in focal extracellular responses to a 5-spike 100-Hz train; 0.5 ms bins. Each panel shows number of traces used for counting quanta. Gray bars mark periods when individual quanta are obscured by stimulus artifacts or when release is too synchronous to discern individual quanta. A composite histogram formed from responses at all phasic synapses is on the lower right.
Figure S3. Different Ways of Selecting and Representing Depression in Phasic Synapses
(A) Depression to 10 APs at 100 Hz in cesium Ringer from 9 synapses, showing averages of 20 trials from individual preparations in gray, with solid lines from synapses with depression correlated with first EJC and dashed lines from synapses with no such correlation; black symbols show means ± SDs. Blue and green lines plot 1-pool and 2-pool depletion models derived from averaged responses of all synapses during trains and all synapses used for measuring recovery at various times after a train.
(B) The same data as in (A), but responses for each synapse have been normalized to the first EJP. The normalized responses were averaged and used with averages of normalized recovery curves to generate 1-pool and 2-pool depletion models.
(C) Data from 4 synapses showing depression uncorrelated with first EJC were analyzed as in (A), and fitted with 1- and 2-pool models based on depression of the average responses and recovery from averaged recovery data.
(D) Data selected as in (C), but averaging normalized responses during the train, and fitting 1- and 2-pool models to these using recovery rates derived from averaged normalized recovery curves. In all cases, 2-pool models provide a better fit to the data.
Figure S4. Evoked Release Rates at Tonic Synapses
Histograms from 13 synapses of synaptic delays to individual mEJCs in focal extracellular responses from 50 to 500 trials to a 5-spike 100-Hz train; 0.5 ms bins. Gray bars mark periods obscured by stimulus artifacts. A composite histogram formed from responses at all tonic synapses is shown on lower right.
Figure S5. Tonic Facilitation from Intracellularly Recorded EJPs
(A) Superimposed responses to one to five stimuli at 100 Hz; averages of 100 traces; line with arrows shows measurement of 5th EJP amplitude.
(B) Four traces to a single stimulus from the same experiment, used for counting quantal responses.
(C) Average facilitation ± SDs from 14 intracellular and 13 focal extracellular measurements.
Figure S6. Phasic Synapse Responses to Spatially Uniform Step Rises in [Ca2+]i
Simulations assume a fast buffer diffusion constant (Df) of 0.002 μm2/ms with refractoriness of 10 ms time constant (solid lines), or without refractoriness (thick dashed gray lines), and with Df = 0 and no refractoriness (dotted lines).
(A) simulated time courses of release rate to a 2.8 μM [Ca2+]i step are overlaid on experimental results for such a step from Millar et al. (2005) in light gray.
(B-E) simulated maximum release rates (B), cumulated release for 30 ms (C), time to peak release rate (D), and delay to first quantal release (E) are plotted using line styles as in (A), along with experimental results from Millar et al. (2005) shown as filled circles. The open circles represent the data plotted in (A). The plateaus in (C) reflect lack of well-defined peak release time in simulations to weak flashes.
Figure S7. Tonic Synapse Responses to Spatially Uniform Step Rises in [Ca2+]i
Simulations assume a fast buffer diffusion constant (Df) of 0.002 μm2/ms with refractoriness of 100 ms time constant (solid lines), or without refractoriness (thick dashed gray lines), and with Df = 0 and no refractoriness (dotted lines).
(A) simulated time courses of release rate to a 1.6 μM [Ca2+]i step are overlaid on results for steps between 1.4 and 2.5 μM from Millar et al. (2005) in light gray.
(B-E) simulated maximum release rates (B), cumulated release for 100 ms (C), time to peak release rate (D), and delay to first quantal release (E) are plotted using line styles as in (A), along with experimental results from Millar et al. (2005) shown as filled circles. The open circles represent the data plotted in (A). The rough fits of simulations to time course histograms reflect the sparseness of responses in tonic synapses, requiring the experimental histogram to be formed from all our data to [Ca2+]i steps above 1.4 μM. Simulated times to peak are not well defined for weak flashes.
Table S1. Parameters Used in 1- and 2-Pool Models of Depression (Figure S3).
ACKNOWLEDGMENTS
We are grateful to Victor Matveev for valuable discussion and help with programming and for updating CalC to include additional provisions that we requested, and to him and Jen-Wei Lin for sharing unpublished results. Russell English provided valuable technical assistance. This work was supported by NSF grants 0413936 and 0533533.
Footnotes
REFERENCES
- Adams SR, Kao JPY, Tsien RY. Biologically useful chelators that take up Ca2+ upon illumination. J. Am. Chem. Soc. 1989;111:7957–7968. [Google Scholar]
- Atwood HL, Bittner GD. Matching of excitatory and inhibitory inputs to crustacean muscle fibers. J. Neurophysiol. 1971;34:157–170. doi: 10.1152/jn.1971.34.1.157. [DOI] [PubMed] [Google Scholar]
- Atwood HL, Karunanithi S. Diversification of synaptic strength: presynaptic elements. Nat. Rev. Neurosci. 2002;3:497–516. doi: 10.1038/nrn876. [DOI] [PubMed] [Google Scholar]
- Baylor SM, Hollingworth S. Fura-2 calcium transients in frog skeletal muscle fibres. J. Physiol. 1988;403:151–192. doi: 10.1113/jphysiol.1988.sp017244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaumont V, Zhong N, Froemke RC, Ball RW, Zucker RS. Temporal synaptic tagging by Ih activation and actin: involvement in long-term facilitation and cAMP-induced synaptic enhancement. Neuron. 2002;33:601–613. doi: 10.1016/s0896-6273(02)00581-0. [DOI] [PubMed] [Google Scholar]
- Bittner GD. Differentiation of nerve terminals in the crayfish opener muscle and its functional significance. J. Gen. Physiol. 1968;51:731–758. doi: 10.1085/jgp.51.6.731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bittner GD. Synaptic plasticity at the crayfish opener neuromuscular preparation. J. Neurobiol. 1989;20:386–408. doi: 10.1002/neu.480200510. [DOI] [PubMed] [Google Scholar]
- Bittner GD, Kennedy D. Quantitative aspects of transmitter release. J. Cell Biol. 1970;47:585–592. doi: 10.1083/jcb.47.3.585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blatow M, Caputi A, Burnashev N, Monyer H, Rozov A. Ca2+ buffer saturation underlies paired pulse facilitation in calbindin-D28k-containing terminals. Neuron. 2003;38:79–88. doi: 10.1016/s0896-6273(03)00196-x. [DOI] [PubMed] [Google Scholar]
- Bollmann JH, Sakmann B. Control of synaptic strength and timing by the release-site Ca2+ signal. Nat. Neurosci. 2005;8:426–434. doi: 10.1038/nn1417. [DOI] [PubMed] [Google Scholar]
- Bollmann JH, Sakmann B, Borst JG. Calcium sensitivity of glutamate release in a calyx-type terminal. Science. 2000;289:953–957. doi: 10.1126/science.289.5481.953. [DOI] [PubMed] [Google Scholar]
- Bradacs H, Cooper RL, Msghina M, Atwood HL. Differential physiology and morphology of phasic and tonic motor axons in a crayfish limb extensor muscle. J. Exp. Biol. 1997;200:677–691. doi: 10.1242/jeb.200.4.677. [DOI] [PubMed] [Google Scholar]
- Chapman ER. How does synaptotagmin trigger neurotransmitter release? Annu. Rev. Biochem. 2008;77:615–641. doi: 10.1146/annurev.biochem.77.062005.101135. [DOI] [PubMed] [Google Scholar]
- Cooper RL, Stewart BA, Wojtowicz JM, Wang S, Atwood HL. Quantal measurement and analysis methods compared for crayfish and Drosophila neuromuscular junctions, and rat hippocampus. J. Neurosci. Methods. 1995;61:67–78. doi: 10.1016/0165-0270(95)00024-o. [DOI] [PubMed] [Google Scholar]
- Cooper RL, Winslow JL, Govind CK, Atwood HL. Synaptic structural complexity as a factor enhancing probability of calcium-mediated transmitter release. J. Neurophysiol. 1996;75:2451–2466. doi: 10.1152/jn.1996.75.6.2451. [DOI] [PubMed] [Google Scholar]
- Dittman JS, Kreitzer AC, Regehr WG. Interplay between facilitation, depression, and residual calcium at three presynaptic terminals. J. Neurosci. 2000;20:1374–1385. doi: 10.1523/JNEUROSCI.20-04-01374.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobrunz LE, Huang EP, Stevens CF. Very short-term plasticity in hippocampal synapses. Proc. Natl. Acad. Sci. USA. 1997;94:14843–14847. doi: 10.1073/pnas.94.26.14843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudel J. The effect of reduced calcium on quantal unit current and release at the crayfish neuromuscular junction. Pflugers Arch. 1981;391:35–40. doi: 10.1007/BF00580691. [DOI] [PubMed] [Google Scholar]
- Fogelson AL, Zucker RS. Presynaptic calcium diffusion from various arrays of single channels. Implications for transmitter release and synaptic facilitation. Biophys. J. 1985;48:1003–1017. doi: 10.1016/S0006-3495(85)83863-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gomis A, Burrone J, Lagnado L. Two actions of calcium regulate the supply of releasable vesicles at the ribbon synapse of retinal bipolar cells. J. Neurosci. 1999;19:6309–6317. doi: 10.1523/JNEUROSCI.19-15-06309.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Günzel D, Galler S. Intracellular free Mg2+ concentration in skeletal muscle fibres of frog and crayfish. Pflugers Arch. 1991;417:446–453. doi: 10.1007/BF00370938. [DOI] [PubMed] [Google Scholar]
- Helmchen F, Imoto K, Sakmann B. Ca2+ buffering and action potential-evoked Ca2+ signaling in dendrites of pyramidal neurons. Biophys. J. 1996;70:1069–1081. doi: 10.1016/S0006-3495(96)79653-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helmchen F, Borst JG, Sakmann B. Calcium dynamics associated with a single action potential in a CNS presynaptic terminal. Biophys. J. 1997;72:1458–1471. doi: 10.1016/S0006-3495(97)78792-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack JJB, Noble D, Tsien RW. Electric Current Flow in Excitable Cells. Clarendon Press; Oxford: 1975. pp. 55–66. [Google Scholar]
- Kamiya H, Zucker RS. Residual Ca2+ and short-term synaptic plasticity. Nature. 1994;371:603–606. doi: 10.1038/371603a0. [DOI] [PubMed] [Google Scholar]
- Katz B, Miledi R. The measurement of synaptic delay, and the time course of acetylcholine release at the neuromuscular junction. Proc. R. Soc. Lond. B. Biol. Sci. 1965;161:483–495. doi: 10.1098/rspb.1965.0016. [DOI] [PubMed] [Google Scholar]
- King MJ, Atwood HL, Govind CK. Structural features of crayfish phasic and tonic neuromuscular terminals. J. Comp. Neurol. 1996;372:618–626. doi: 10.1002/(SICI)1096-9861(19960902)372:4<618::AID-CNE9>3.0.CO;2-7. [DOI] [PubMed] [Google Scholar]
- Korn H, Mallet A, Triller A, Faber DS. Transmission at a central inhibitory synapse. II. Quantal description of release, with a physical correlate for binomial n. J. Neurophysiol. 1982;48:679–707. doi: 10.1152/jn.1982.48.3.679. [DOI] [PubMed] [Google Scholar]
- Landò L, Zucker RS. Ca2+ cooperativity in neurosecretion measured using photolabile Ca2+ chelators. J. Neurophysiol. 1994;72:825–830. doi: 10.1152/jn.1994.72.2.825. [DOI] [PubMed] [Google Scholar]
- Lee SH, Rosenmund C, Schwaller B, Neher E. Differences in Ca2+ buffering properties between excitatory and inhibitory hippocampal neurons from the rat. J. Physiol. 2000;525:405–418. doi: 10.1111/j.1469-7793.2000.t01-3-00405.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li L, Bischofberger J, Jonas P. Differential gating and recruitment of P/Q-, N-, and R-type Ca2+ channels in hippocampal mossy fiber boutons. J. Neurosci. 2007;27:13420–13429. doi: 10.1523/JNEUROSCI.1709-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin JW, Fu Q. Modulation of available vesicles and release kinetics at the inhibitor of the crayfish neuromuscular junction. Neuroscience. 2005;130:889–895. doi: 10.1016/j.neuroscience.2004.10.023. [DOI] [PubMed] [Google Scholar]
- Lin JW, Fu Q, Allana T. Probing the endogenous Ca2+ buffers at the presynaptic terminals of the crayfish neuromuscular junction. J. Neurophysiol. 2005;94:377–386. doi: 10.1152/jn.00617.2004. [DOI] [PubMed] [Google Scholar]
- Llinás R. A Model for Chemical Transmission. Oxford University Press; Oxford: 1999. The Squid Giant Synapse. [Google Scholar]
- Llinás R, Steinberg IZ, Walton K. Presynaptic calcium currents in squid giant synapse. Biophys. J. 1981;33:289–321. doi: 10.1016/S0006-3495(81)84898-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llinás R, Sugimori M, Simon SM. Transmission by presynaptic spike-like depolarization in the squid giant synapse. Proc. Natl. Acad. Sci. USA. 1982;79:2415–2419. doi: 10.1073/pnas.79.7.2415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lou X, Scheuss V, Schneggenburger R. Allosteric modulation of the presynaptic Ca2+ sensor for vesicle fusion. Nature. 2005;435:497–501. doi: 10.1038/nature03568. [DOI] [PubMed] [Google Scholar]
- Martin AR. The effect of membrane capacitance on non-linear summation of synaptic potentials. J. Theor. Biol. 1976;59:179–187. doi: 10.1016/s0022-5193(76)80031-8. [DOI] [PubMed] [Google Scholar]
- Matveev V, Sherman A, Zucker RS. New and corrected simulations of synaptic facilitation. Biophys. J. 2002;83:1368–1373. doi: 10.1016/S0006-3495(02)73907-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matveev V, Zucker RS, Sherman A. Facilitation through buffer saturation: constraints on endogenous buffering properties. Biophys. J. 2004;86:2691–2709. doi: 10.1016/S0006-3495(04)74324-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matveev V, Bertram R, Sherman A. Residual bound Ca2+ can account for the effects of Ca2+ buffers on synaptic facilitation. J. Neurophysiol. 2006;96:3389–3397. doi: 10.1152/jn.00101.2006. [DOI] [PubMed] [Google Scholar]
- Millar AG, Bradacs H, Charlton MP, Atwood HL. Inverse relationship between release probability and readily releasable vesicles in depressing and facilitating synapses. J. Neurosci. 2002;22:9661–9667. doi: 10.1523/JNEUROSCI.22-22-09661.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Millar AG, Zucker RS, Ellis-Davies GC, Charlton MP, Atwood HL. Calcium sensitivity of neurotransmitter release differs at phasic and tonic synapses. J. Neurosci. 2005;25:3113–3125. doi: 10.1523/JNEUROSCI.4717-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Msghina M, Govind CK, Atwood HL. Synaptic structure and transmitter release in crustacean phasic and tonic motor neurons. J. Neurosci. 1998;18:1374–1382. doi: 10.1523/JNEUROSCI.18-04-01374.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Msghina M, Millar AG, Charlton MP, Govind CK, Atwood HL. Calcium entry related to active zones and differences in transmitter release at phasic and tonic synapses. J. Neurosci. 1999;19:8419–8434. doi: 10.1523/JNEUROSCI.19-19-08419.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller M, Felmy F, Schwaller B, Schneggenburger R. Parvalbumin is a mobile presynaptic Ca2+ buffer in the calyx of held that accelerates the decay of Ca2+ and short-term facilitation. J. Neurosci. 2007;27:2261–2271. doi: 10.1523/JNEUROSCI.5582-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naraghi M. T-jump study of calcium binding kinetics of calcium chelators. Cell Calcium. 1997;22:255–268. doi: 10.1016/s0143-4160(97)90064-6. [DOI] [PubMed] [Google Scholar]
- Neher E, Sakaba T. Multiple roles of calcium ions in the regulation of neurotransmitter release. Neuron. 2008;59:861–872. doi: 10.1016/j.neuron.2008.08.019. [DOI] [PubMed] [Google Scholar]
- Nguyen PV, Marin L, Atwood HL. Synaptic physiology and mitochondrial function in crayfish tonic and phasic motor neurons. J. Neurophysiol. 1997;78:281–294. doi: 10.1152/jn.1997.78.1.281. [DOI] [PubMed] [Google Scholar]
- Ohana O, Sakmann B. Transmitter release modulation in nerve terminals of rat neocortical pyramidal cells by intracellular calcium buffers. J. Physiol. 1998;513:135–148. doi: 10.1111/j.1469-7793.1998.135by.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parnas I, Parnas H, Dudel J. Neurotransmitter release and its facilitation in crayfish muscle. V. Basis for synapse differentiation of the fast and slow type in one axon. Pflugers Arch. 1982;395:261–270. doi: 10.1007/BF00580788. [DOI] [PubMed] [Google Scholar]
- Rozov A, Burnashev N, Sakmann B, Neher E. Transmitter release modulation by intracellular Ca2+ buffers in facilitating and depressing nerve terminals of pyramidal cells in layer 2/3 of the rat neocortex indicates a target cellspecific difference in presynaptic calcium dynamics. J. Physiol. 2001;531:807–826. doi: 10.1111/j.1469-7793.2001.0807h.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt H, Brown EB, Schwaller B, Eilers J. Diffusional mobility of parvalbumin in spiny dendrites of cerebellar Purkinje neurons quantified by fluorescence recovery after photobleaching. Biophys. J. 2003a;84:2599–2608. doi: 10.1016/S0006-3495(03)75065-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt H, Stiefel KM, Racay P, Schwaller B, Eilers J. Mutational analysis of dendritic Ca2+ kinetics in rodent Purkinje cells: role of parvalbumin and calbindin D28k. J. Physiol. 2003b;551:13–32. doi: 10.1113/jphysiol.2002.035824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneggenburger R, Neher E. Intracellular calcium dependence of transmitter release rates at a fast central synapse. Nature. 2000;406:889–893. doi: 10.1038/35022702. [DOI] [PubMed] [Google Scholar]
- Schneggenburger R, Meyer AC, Neher E. Released fraction and total size of a pool of immediately available transmitter quanta at a calyx synapse. Neuron. 1999;23:399–409. doi: 10.1016/s0896-6273(00)80789-8. [DOI] [PubMed] [Google Scholar]
- Schneggenburger R, Sakaba T, Neher E. Vesicle pools and short-term synaptic depression: lessons from a large synapse. Trends Neurosci. 2002;25:206–212. doi: 10.1016/s0166-2236(02)02139-2. [DOI] [PubMed] [Google Scholar]
- Stevens CF, Wang Y. Facilitation and depression at single central synapses. Neuron. 1995;14:795–802. doi: 10.1016/0896-6273(95)90223-6. [DOI] [PubMed] [Google Scholar]
- Stevens CF, Wesseling JF. Identification of a novel process limiting the rate of synaptic vesicle cycling at hippocampal synapses. Neuron. 1999;24:1017–1028. doi: 10.1016/s0896-6273(00)81047-8. [DOI] [PubMed] [Google Scholar]
- Stevens CF, Williams JH. Discharge of the readily releasable pool with action potentials at hippocampal synapses. J. Neurophysiol. 2007;98:3221–3229. doi: 10.1152/jn.00857.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stockbridge N, Moore JW. Dynamics of intracellular calcium and its possible relationship to phasic transmitter release and facilitation at the frog neuromuscular junction. J. Neurosci. 1984;4:803–811. doi: 10.1523/JNEUROSCI.04-03-00803.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J, Pang ZP, Qin D, Fahim AT, Adachi R, Südhof TC. A dual-Ca2+-sensor model for neurotransmitter release in a central synapse. Nature. 2007;450:676–682. doi: 10.1038/nature06308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang Y, Schlumpberger T, Kim T, Lueker M, Zucker RS. Effects of mobile buffers on facilitation: experimental and computational studies. Biophys. J. 2000;78:2735–2751. doi: 10.1016/s0006-3495(00)76819-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tank DW, Regehr WG, Delaney KR. A quantitative analysis of presynaptic calcium dynamics that contribute to short-term enhancement. J. Neurosci. 1995;15:7940–7952. doi: 10.1523/JNEUROSCI.15-12-07940.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Kloot W. Estimating the timing of quantal releases during end-plate currents at the frog neuromuscular junction. J. Physiol. 1988;402:595–603. doi: 10.1113/jphysiol.1988.sp017224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vyshedskiy A, Lin JW. Presynaptic Ca2+ influx at the inhibitor of the crayfish neuromuscular junction: a photometric study at a high time resolution. J. Neurophysiol. 2000;83:552–562. doi: 10.1152/jn.2000.83.1.552. [DOI] [PubMed] [Google Scholar]
- Wojtowicz JM, Marin L, Atwood HL. Activity-induced changes in synaptic release sites at the crayfish neuromuscular junction. J. Neurosci. 1994;14:3688–3703. doi: 10.1523/JNEUROSCI.14-06-03688.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wölfel M, Lou X, Schneggenburger R. A mechanism intrinsic to the vesicle fusion machinery determines fast and slow transmitter release at a large CNS synapse. J. Neurosci. 2007;27:3198–3210. doi: 10.1523/JNEUROSCI.4471-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu T, Naraghi M, Kang H, Neher E. Kinetic studies of Ca2+ binding and Ca2+ clearance in the cytosol of adrenal chromaffin cells. Biophys. J. 1997;73:532–545. doi: 10.1016/S0006-3495(97)78091-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada WM, Zucker RS. Time course of transmitter release calculated from simulations of a calcium diffusion model. Biophys. J. 1992;61:671–682. doi: 10.1016/S0006-3495(92)81872-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zucker RS. Changes in the statistics of transmitter release during facilitation. J. Physiol. 1973;229:787–810. doi: 10.1113/jphysiol.1973.sp010167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zucker RS, Regehr WG. Short-term synaptic plasticity. Annu. Rev. Physiol. 2002;64:355–405. doi: 10.1146/annurev.physiol.64.092501.114547. [DOI] [PubMed] [Google Scholar]
- Zucker RS, Kullmann DM, Bennett M. Release of neurotransmitters. In: Zigmond MJ, Bloom FL, Landis SC, Roberts JL, Squire LR, editors. Fundamental Neuroscience. Academic Press; San Diego: 1999. pp. 155–192. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
01
Figure S1. Synchronous Evoked Release Rates at Phasic Synapses Estimated by Deconvolution
Averaged responses to a 5-spike 100-Hz train from 100 focal extracellular recordings were deconvolved with the averaged waveform of at least 10 isolated mEJCs at 11 synapses; 0.1 ms bins. Time is measured from the arrival of the presynaptic AP (the negative peak of the nerve terminal potential). A composite histogram formed from responses at all phasic synapses is also shown (lower right).
Figure S2. Asynchronous Evoked Release Rates at Phasic Synapses
Histograms of synaptic delays to individual mEJCs in focal extracellular responses to a 5-spike 100-Hz train; 0.5 ms bins. Each panel shows number of traces used for counting quanta. Gray bars mark periods when individual quanta are obscured by stimulus artifacts or when release is too synchronous to discern individual quanta. A composite histogram formed from responses at all phasic synapses is on the lower right.
Figure S3. Different Ways of Selecting and Representing Depression in Phasic Synapses
(A) Depression to 10 APs at 100 Hz in cesium Ringer from 9 synapses, showing averages of 20 trials from individual preparations in gray, with solid lines from synapses with depression correlated with first EJC and dashed lines from synapses with no such correlation; black symbols show means ± SDs. Blue and green lines plot 1-pool and 2-pool depletion models derived from averaged responses of all synapses during trains and all synapses used for measuring recovery at various times after a train.
(B) The same data as in (A), but responses for each synapse have been normalized to the first EJP. The normalized responses were averaged and used with averages of normalized recovery curves to generate 1-pool and 2-pool depletion models.
(C) Data from 4 synapses showing depression uncorrelated with first EJC were analyzed as in (A), and fitted with 1- and 2-pool models based on depression of the average responses and recovery from averaged recovery data.
(D) Data selected as in (C), but averaging normalized responses during the train, and fitting 1- and 2-pool models to these using recovery rates derived from averaged normalized recovery curves. In all cases, 2-pool models provide a better fit to the data.
Figure S4. Evoked Release Rates at Tonic Synapses
Histograms from 13 synapses of synaptic delays to individual mEJCs in focal extracellular responses from 50 to 500 trials to a 5-spike 100-Hz train; 0.5 ms bins. Gray bars mark periods obscured by stimulus artifacts. A composite histogram formed from responses at all tonic synapses is shown on lower right.
Figure S5. Tonic Facilitation from Intracellularly Recorded EJPs
(A) Superimposed responses to one to five stimuli at 100 Hz; averages of 100 traces; line with arrows shows measurement of 5th EJP amplitude.
(B) Four traces to a single stimulus from the same experiment, used for counting quantal responses.
(C) Average facilitation ± SDs from 14 intracellular and 13 focal extracellular measurements.
Figure S6. Phasic Synapse Responses to Spatially Uniform Step Rises in [Ca2+]i
Simulations assume a fast buffer diffusion constant (Df) of 0.002 μm2/ms with refractoriness of 10 ms time constant (solid lines), or without refractoriness (thick dashed gray lines), and with Df = 0 and no refractoriness (dotted lines).
(A) simulated time courses of release rate to a 2.8 μM [Ca2+]i step are overlaid on experimental results for such a step from Millar et al. (2005) in light gray.
(B-E) simulated maximum release rates (B), cumulated release for 30 ms (C), time to peak release rate (D), and delay to first quantal release (E) are plotted using line styles as in (A), along with experimental results from Millar et al. (2005) shown as filled circles. The open circles represent the data plotted in (A). The plateaus in (C) reflect lack of well-defined peak release time in simulations to weak flashes.
Figure S7. Tonic Synapse Responses to Spatially Uniform Step Rises in [Ca2+]i
Simulations assume a fast buffer diffusion constant (Df) of 0.002 μm2/ms with refractoriness of 100 ms time constant (solid lines), or without refractoriness (thick dashed gray lines), and with Df = 0 and no refractoriness (dotted lines).
(A) simulated time courses of release rate to a 1.6 μM [Ca2+]i step are overlaid on results for steps between 1.4 and 2.5 μM from Millar et al. (2005) in light gray.
(B-E) simulated maximum release rates (B), cumulated release for 100 ms (C), time to peak release rate (D), and delay to first quantal release (E) are plotted using line styles as in (A), along with experimental results from Millar et al. (2005) shown as filled circles. The open circles represent the data plotted in (A). The rough fits of simulations to time course histograms reflect the sparseness of responses in tonic synapses, requiring the experimental histogram to be formed from all our data to [Ca2+]i steps above 1.4 μM. Simulated times to peak are not well defined for weak flashes.
Table S1. Parameters Used in 1- and 2-Pool Models of Depression (Figure S3).