Is there a sex difference in accelerometer counts during walking in older adults? (original) (raw)
. Author manuscript; available in PMC: 2015 Mar 1.
Published in final edited form as: J Phys Act Health. 2013 Feb 8;11(3):626–637. doi: 10.1123/jpah.2012-0050
Abstract
Background
Accelerometers have emerged as a useful tool for measuring free-living physical activity in epidemiological studies. Validity of activity estimates depends on the assumption that measurements are equivalent for males and females while performing activities of the same intensity. The primary purpose of this study was to compare accelerometer count values in males and females undergoing a standardized 6-min walk test.
Methods
The study population was older adults (78.6 ± 4.1 years) from the AGES-Reykjavik Study (N = 319). Participants performed a 6-min walk test at a self-selected fast pace while wearing an ActiGraph GT3X at the hip. Vertical axis counts·s−1 was the primary outcome. Covariates included walking speed, height, weight, BMI, waist circumference, femur length, and step length.
Results
On average, males walked 7.2% faster than females (1.31 vs. 1.22 m·s−1, p < 0.001) and had 32.3% greater vertical axis counts·s−1 (54.6 vs. 39.4 counts·s−1, p < 0.001). Accounting for walking speed reduced the sex difference to 19.2% and accounting for step length further reduced the difference to 13.4% (p < 0.001).
Conclusion
Vertical axis counts·s−1 were disproportionally greater in males even after adjustment for walking speed. This difference could confound free-living activity estimates.
Keywords: Physical activity, 6-minute walk test, accelerometry, AGES-Reykjavik Study
Introduction
The use of accelerometers to measure physical activity during free-living has become common in epidemiological studies. Although accelerometers have limitations—they cannot yet reveal what specific activities people are performing, for example—they are generally considered superior to activity questionnaires, as they provide rich, quantitative physical activity data.1 Accelerometers can provide overall measures of physical activity (total counts, average counts·min−1 during weartime), but are also used to measure intensity-specific information based on sex independent cutpoints that reflect metabolic equivalents (sedentary time, time spent in moderate-to-vigorous physical activity).
One of the largest studies to use accelerometers was the National Health and Nutrition Examination Survey (NHANES),2 in which participants were asked to wear a uniaxial accelerometer at the hip for 7 days. An important finding of NHANES 2003-2004, based on analysis of vertical axis accelerometer data, was a substantial sex difference in physical activity across all ages, with males averaging 10-30% greater counts·min−1 during weartime than females.3 Studies using questionnaire-based physical activity measures have in some cases reported comparable sex differences in physical activity4, 5 but in other cases reported similar activity levels in males and females.6, 7
While it is possible that large sex differences such as those reported from NHANES 2003-2004 reflect differences in activity levels, it is also plausible that accelerometers record a greater signal for males than females for activities of similar intensity, such as walking at a given speed. Gait characteristics and anthropometric measures are highly dependent on sex8-10 and could contribute to sex differences in accelerations produced at the hip while walking. For example, Smith et al. showed that older males averaged 34.9 mm vertical center of mass (COM) displacement while older females averaged 28.8 mm.11 Crosbie et al. reported similar results, with males averaging 11% greater COM displacement at a preferred pace and 26% greater COM displacement at a self-selected fast pace.12 It seems probable that greater vertical COM displacements require greater vertical accelerations, which could result in inflated accelerometer count values for males. Similarly, males average longer step lengths than females during walking.8, 9, 11 One would expect that longer steps would result in males producing greater accelerometer counts·step−1, while also averaging fewer steps·s−1 when maintaining a given speed. Whether these effects counterbalance or one dominates depends on the relationship between step length and counts·step−1, which to our knowledge has not been characterized. Finally, there are well-characterized sex differences in body composition, including both the amount and distribution of skeletal muscle and fat.13, 14 Males have greater lean mass and females have greater adiposity; males have more fat at the abdomen, while females carry more fat at the hips and lower body.14 Such factors could coincide with sex differences in three-dimensional motion at the hip during walking.
Accelerometer validation studies aimed at developing energy-expenditure prediction equations or establishing intensity cut-points have been small and of low power, and have generally pooled male and female participants together rather than directly test for sex effects.15-18 One small validation study (n = 25) with the uniaxial Caltrac accelerometer reported 30-35% greater counts·min−1 in males across a range of walking speeds, while oxygen consumption was similar by sex.19 In a somewhat larger study (n = 50) with the uniaxial Computer Science and Applications, Inc. (CSA) monitor, Freedson et al. reported no significant sex difference in counts·min−1 during walking and jogging at set speeds, although count averages were consistently higher for males while oxygen consumption was not.20 Conversely, Brooks et al. reported females averaging 15.9% higher CSA counts than males while walking 5.6% faster and expending 2.7% greater kcal·kg−1·km−1.21 Each of these studies focused on healthy adults and used uniaxial accelerometer positioned to detect vertical axis motion. We are not aware of any larger studies that have tested for sex differences in accelerometry output during walking using triaxial devices.
The purpose of this study is to compare accelerometer output for males and females recorded during a fast 6-min walk test in a sample of older adults from the Age, Gene/Environment Susceptibility (AGES)-Reykjavik Study. Accounting for walking speed differences, we assess the relationship between sex and counts·s−1 in the vertical axis as well as the anteroposterior (AP) axis, mediolateral (ML) axis, and 3D vector magnitude (3D VM), a composite of all three axes. Further, we examine whether a potential sex difference in counts·s−1 during walking could be explained by anthropometric measures or gait characteristics that differ by sex.
Methods
Study Population
The study population was older adults from the Age, Gene/Environment Susceptibility (AGES)-Reykjavik Study. The Reykjavik Study cohort originally comprised a random sample of 30,795 men and women born in 1907-1935 and living in Reykjavik, Iceland, in 1967. A total of 19,381 people attended, resulting in 71% recruitment rate. Between 2002 and 2006, the AGES-Reykjavik Study re-examined a random sample of 5,764 survivors of the original cohort.22 The AGES-Reykjavik Study was approved by the institutional review boards of the National Institute on Aging, the National Bioethics Committee (VSN:00-063), and the Data Protection Authority. Written informed consent was obtained from all study participants. The comprehensive baseline examination included a detailed medical history, physical examination, physical performance tests, body composition examination, cognitive tests, laboratory screening tests, and questionnaires on health-related behaviors. An additional follow-up examination (AGESII) started in 2007 and was completed in 2011. Between April 2009 and July 2010 an accelerometry sub-study was added in which participants who did not have severe cognitive dysfunction, based on standardized testing with the Mini-Mental Status Examination,23 were asked to wear an accelerometer for 7 days and perform a 6-min walk test.
Measures
Walking test
AGESII participants in the accelerometry substudy (n = 658) who met additional inclusion criteria performed a 6-min walk test along a 20-m track while wearing an accelerometer. Exclusion criteria included use of an assistive device for walking (n = 80); ECG abnormalities (n = 7), reported heart attack, angioplasty of the coronary arteries, or heart surgery within the last 3 months (n = 5); reported chest pain, shortness of breath, or fainting in the past 3 months (n = 67); other medical exclusions (n = 17); and other physical problems (n = 57). Scheduling conflicts in the clinic resulted in 27 participants not performing the 6-min walk test, and 56 participants refused for various reasons. Of the 342 participants who performed the 6-min walk test, 9 stopped to rest during the test at least once and were thus excluded from the analysis. For one participant, the accelerometer was programmed to store counts each minute rather than each second, making it impossible to precisely select the 360 s of walking. Accelerometer data was not available for 7 participants, one accelerometer failed to record motion in one axis, and 5 participants were missing one or more covariates, resulting in an analytic sample of 319 participants (153 males, 166 females).
Participants were instructed to walk as many laps as possible in the time allowed. Cones were placed at each end of a walking course and participants were asked to walk around the outside of the cones at the end of each halflap. Total distance covered during the 6-min walk test was calculated based on number of laps completed and additional distance walked during the last unfinished lap. Average walking speed was calculated by dividing total distance covered during the 6-min walk test by six minutes.
Accelerometry
ActiGraph GT3X accelerometers (ActiGraph, LLC; Pensacola, FL) were worn at the right hip while participants performed the 6-min walk test. The accelerometers are sensitive to motion in all three axes—vertical, AP, and ML—and were programmed to record “counts,” an arbitrary unit of acceleration. The devices have an internal sampling frequency of 30 Hz and were programmed to record count values in 1-s intervals.
Average counts·s−1 during the walk test was calculated by dividing total counts by duration of the test. Counts·s−1 were calculated for each axis of accelerometer data, and 3D VM counts·s−1 was calculated as the square root of the sum of the squares of counts in all three axes.
Average counts·m−1 during the walk test was also used as a measure of accelerometer output per unit distance walked. This variable was calculated by dividing total counts in each axis by total distance walked.
All accelerometry data was processed using customized software written in MATLAB R2006a (The MathWorks, Inc.; Natick, Massachusetts).
Covariates
Covariates used in the analysis included average walking speed during the 6-min walk test (m·s−1), height (cm), weight (kg), BMI, waist circumference (cm), femur length (cm), and step length (cm). Height and weight were measured using a precise digital scale and BMI was calculated as weight divided by squared height in meters. Waist circumference was measured at the largest protrusion of the abdomen when viewed from the side while participants were standing. Femur length was obtained from the CT scout view. Step length was calculated from the observed number of steps taken during a fast-paced 6-m walk test (step length = 600 cm / number of steps). All anthropometric data was obtained as previously described.22
Statistical Analysis
Data were analyzed using R version 2.13.1 (http://www.r-project.org). Independent-sample t-tests with α = 0.05 were used to compare accelerometer averages for males and females. Multiple linear regression was used to test the relationship between sex and accelerometer counts·s−1, accounting for covariates. Pearson correlation coefficients were used to characterize associations between walking speed and counts·s−1 in each accelerometer axis. Propensity score analyses were performed to compare accelerometer measurements between subgroups of males and females matched on body size and walking speed. For this analysis, propensity scores were computed using logistic regression, using height, weight, step length, and walking speed. Matching was performed through the “Matching” package in R, using one-to-one caliper matching without replacement.24
Results
Demographics, along with average walking speed and accelerometer averages during the 6-min walk test, are shown in Table 1. On average, males walked 7.2% faster than females and had 32.3% greater vertical axis counts·s−1 (54.6 vs. 39.4 counts·s−1, p < 0.001). Per meter walked, males averaged 40.8 and females averaged 31.5 vertical axis counts, a 25.7% difference (p < 0.001). In the AP and ML axes, counts·s−1 and counts·m−1 were similar by sex, while males had greater 3D VM counts·s−1 and counts·m−1. Vertical axis counts·m−1 was positively associated with walking speed (Beta = 28.5, r = 0.549, p < 0.001), as were AP axis counts·m−1 (Beta = 4.3, r = 0.113, p = 0.043) and 3D VM counts·m−1 (Beta = 21.3, r = 0.432, p < 0.001).
Table 1.
Demographics and 6-min walk test results.
| Variable | Males **(n = 153)**Mean (SD) | Females **(n = 166)**Mean (SD) | % Diff | p |
|---|---|---|---|---|
| Demographics | ||||
| Age (years) | 78.8 (3.7) | 78.5 (4.5) | 0.4 | 0.463 |
| Height (cm) | 176.4 (6.3) | 162.1 (5.6) | 8.4 | <0.001 |
| Weight (kg) | 83.1 (14.3) | 68.9 (13.0) | 18.7 | <0.001 |
| BMI (kg·m−2) | 26.6 (3.9) | 26.2 (4.6) | 1.5 | 0.357 |
| Waist circumference (cm) | 101.4 (10.5) | 96.5 (12.9) | 5.0 | <0.001 |
| Femur length (cm) | 48.3 (2.3) | 44.5 (2.1) | 8.2 | <0.001 |
| Step length (cm) | 65.4 (6.5) | 55.3 (6.2) | 16.7 | <0.001 |
| 6-min walk test | ||||
| Distance walked (m) | 473.1 (75.2) | 440.4 (68.9) | 7.2 | <0.001 |
| Walking speed (m·s−1) | 1.31 (0.21) | 1.22 (0.19) | 7.2 | <0.001 |
| Vertical axis counts·s−1 | 54.6 (18.6) | 39.4 (15.2) | 32.3 | <0.001 |
| Vertical axis counts·m−1 | 40.8 (9.6) | 31.5 (9.5) | 25.7 | <0.001 |
| AP axis counts·s−1 | 34.2 (12.4) | 33.0 (11.5) | 3.6 | 0.341 |
| AP axis counts·m−1 | 25.8 (7.5) | 26.9 (8.1) | −4.2 | 0.207 |
| ML axis counts·s−1 | 15.7 (10.7) | 14.4 (9.2) | 8.6 | 0.246 |
| ML axis counts·m−1 | 12.1 (8.0) | 12.0 (7.9) | 0.8 | 0.936 |
| 3D VM counts·s−1 | 69.5 (20.8) | 56.8 (16.2) | 20.1 | <0.001 |
| 3D VM counts·m−1 | 52.2 (9.9) | 45.9 (9.3) | 12.8 | <0.001 |
A further comparison of vertical axis countsy·s−1 across the range of walking speeds was performed (Table 2). Cut-points for walking speed quartiles were based on the full sample. Within each quartile males and females had similar walking speeds while males had greater vertical axis counts·s−1 (p < 0.01 for all quartiles).
Table 2.
Comparison of walking speed and vertical axis counts·s−1 during 6-min walk test for males and females, within walking speed quartiles.
| Walking speed (m·s−1) | Vertical axis counts·s−1 | |||||||
|---|---|---|---|---|---|---|---|---|
| Quartile, speed | **Males**Mean (SD) | _Females_Mean (SD) | % Diff | p | _Males_Mean (SD) | _Females_Mean (SD) | % Diff | p |
| Q1, 0.75-1.11 m·s−1 | 1.02 (0.09) | 1.00 (0.10) | 2.0 | 0.579 | 33.8 (11.4) | 26.2 (11.1) | 25.3 | 0.004 |
| Q2, 1.11-1.28 m·s−1 | 1.21 (0.04) | 1.20 (0.05) | 0.8 | 0.918 | 47.1 (8.7) | 39.3 (10.5) | 18.1 | <0.001 |
| Q3, 1.28-1.39 m·s−1 | 1.33 (0.03) | 1.33 (0.04) | 0.0 | 0.362 | 54.4 (12.1) | 44.2 (11.1) | 20.7 | <0.001 |
| Q4, 1.39-1.88 m·s−1 | 1.53 (0.13) | 1.51 (0.09) | 1.3 | 0.400 | 70.7 (15.9) | 57.0 (11.7) | 21.5 | <0.001 |
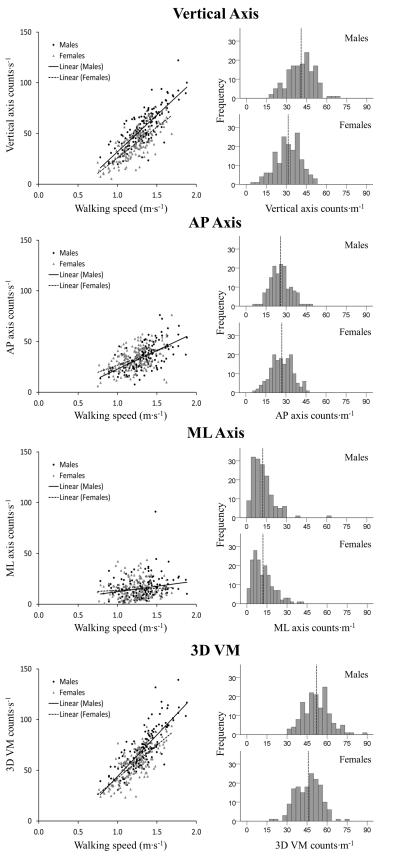
Figure 1 shows linear relationships between accelerometer output and walking speed and distributions of counts·m−1 for each accelerometer axis and 3D VM. Pearson correlation coefficients for the association between each accelerometer measure and walking speed were as follows, for the full sample (males/females): vertical axis, 0.79 (0.81/0.76); AP axis, 0.55 (0.62/0.47); ML axis, 0.16 (0.21/0.08); and 3D VM, 0.80 (0.82/0.76). P-values for all correlations with walking speed were < 0.01 except ML counts·s−1 in males (p = 0.01) and in females (p = 0.31).
Figure 1.
Scatterplots of counts·s−1 vs. walking speed (left) and histograms of counts·m−1 (right) during 6-min walk test for vertical axis, AP axis, ML axis, and 3D VM. Dotted lines on histograms represent the mean.
In an effort to identify an anthropometric variable or gait characteristic responsible for greater counts·s−1 in males than females, multiple linear regression was performed, using sex as a predictor, counts·s−1 as the outcome, and testing various covariates (Table 3). In the vertical axis, males had 15.2 greater counts·s−1 than females, a 32.3% difference; after accounting for walking speed (Model 2), the sex difference was reduced to 9.08 counts·s−1, or 19.2%. Both height (Model 3) and weight (Model 4) were borderline significant covariates and had the effect of increasing the sex difference, while step length (Model 8) was positively associated with counts·s−1 and reduced the sex difference to 6.31 counts·s−1, or 13.4%. In a model with all non-redundant covariates (Model 9), the sex difference was 9.64 counts·s−1, or 20.5%.
Table 3.
Multiple linear regression for sex predicting counts·s−1 in vertical and AP axis and 3D VM, accounting for various covariates.
| Vertical Axis | AP Axis | 3D VM | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Variables | R 2 | Beta (SE) | p | % Diff | R 2 | Beta (SE) | p | % Diff | R 2 | Beta (SE) | p | % Diff |
| 1 | Sex | 0.167 | −15.2(1.90) | <0.001 | 32.3 | 0.003 | −1.27 (1.34) | 0.340 | 3.6 | 0.105 | −12.7 (2.08) | <0.001 | 20.1 |
| 2 | Walk speed | 0.687 | 67.0 (2.92) | <0.001 | 0.302 | 32.7 (2.81) | <0.001 | 0.666 | 73.4 (3.19) | <0.001 | |||
| Sex | −9.08 (1.20) | <0.001 | 19.2 | 1.69(1.15) | 0.142 | −5.1 | −6.01 (1.31) | <0.001 | 9.5 | ||||
| 3 | Walk speed | 0.691 | 67.4 (2.92) | <0.001 | 0.304 | 32.5 (2.82) | <0.001 | 0.667 | 73.7 (3.20) | <0.001 | |||
| Height | −0.19 (0.10) | 0.052 | 0.09 (0.09) | 0.356 | −0.11 (0.11) | 0.318 | |||||||
| Sex | −11.8 (1.82) | <0.001 | 24.9 | 2.92 (1.76) | 0.097 | −8.6 | −7.52 (1.99) | <0.001 | 11.9 | ||||
| 4 | Walk speed | 0.690 | 66.1 (2.95) | <0.001 | 0.318 | 33.9 (2.82) | <0.001 | 0.666 | 73.7 (3.24) | <0.001 | |||
| Weight | −0.08 (0.04) | 0.060 | 0.11 (0.04) | 0.006 | 0.02 (0.05) | 0.629 | |||||||
| Sex | −10.3 (1.36) | <0.001 | 21.9 | 3.44 (1.30) | 0.009 | −10.1 | −5.67 (1.49) | <0.001 | 8.9 | ||||
| 5 | Walk speed | 0.688 | 66.3 (2.99) | <0.001 | 0.320 | 34.4 (2.84) | <0.001 | 0.667 | 74.2 (3.26) | <0.001 | |||
| BMI | −0.15 (0.14) | 0.277 | 0.38(0.13) | 0.004 | 0.17(0.15) | 0.254 | |||||||
| Sex | −9.21 (1.20) | <0.001 | 19.6 | 2.02(1.14) | 0.078 | −6.0 | −5.87(1.31) | <0.001 | 9.2 | ||||
| 6 | Walk speed | 0.689 | 66.0 (3.01) | <0.001 | 0.320 | 34.7 (2.86) | <0.001 | 0.667 | 74.3 (3.29) | <0.001 | |||
| Waist circ. | −0.07 (0.05) | 0.165 | 0.14 (0.05) | 0.004 | 0.06 (0.06) | 0.305 | |||||||
| Sex | −9.52 (1.24) | <0.001 | 20.5 | 2.56 (1.18) | 0.030 | −7.8 | −5.66 (1.35) | <0.001 | 8.9 | ||||
| 7 | Walk speed | 0.688 | 67.1 (2.93) | <0.001 | 0.303 | 32.6 (2.82) | <0.001 | 0.666 | 73.5 (3.20) | <0.001 | |||
| Femur length | −0.22 (0.27) | 0.410 | 0.14 (0.26) | 0.580 | −0.09 (0.29) | 0.769 | |||||||
| Sex | −9.91 (1.56) | <0.001 | 21.1 | 2.23 (1.50) | 0.140 | −6.6 | −6.34 (1.71) | <0.001 | 10.2 | ||||
| 8 | Walk speed | 0.695 | 61.1 (3.51) | <0.001 | 0.326 | 26.3 (3.36) | <0.001 | 0.679 | 65.7 (3.81) | <0.001 | |||
| Step length | 0.33 (0.11) | 0.003 | 0.35 (0.11) | <0.001 | 0.43 (0.12) | <0.001 | |||||||
| Sex | −6.31 (1.51) | <0.001 | 13.4 | 4.69 (1.44) | 0.001 | −14.1 | −2.39 (1.63) | 0.144 | 3.8 | ||||
| 9 | Walk speed | 0.704 | 59.8 (3.52) | <0.001 | 0.343 | 27.8 (3.38) | <0.001 | 0.685 | 65.8 (3.84) | <0.001 | |||
| Height | −0.24 (0.11) | 0.037 | −0.14 (0.11) | 0.197 | −0.30 (0.12) | 0.016 | |||||||
| Weight | −0.04 (0.05) | 0.372 | 0.13 (0.05) | 0.004 | 0.07 (0.05) | 0.174 | |||||||
| Step length | 0.40 (0.11) | <0.001 | 0.37 (0.11) | <0.001 | 0.50 (0.12) | <0.001 | |||||||
| Sex | −9.64 (1.88) | <0.001 | 20.5 | 4.91 (1.80) | 0.007 | −14.6 | −4.86 (2.05) | 0.019 | 7.8 |
In the AP axis, the unadjusted sex difference in counts·s−1 was not significant. Weight, BMI, and waist circumference (Models 4-6) were all positively associated with AP axis counts·s−1, and in models with these covariates, females had greater counts·s−1 (borderline significant). Step length was a strong predictor of AP axis counts·s−1, and including this covariate (Model 8) increased the sex difference to 4.69 counts·s−1, or 14.1%. In Model 9, the sex difference was 4.91 counts·s−1, or 14.6% (p = 0.007).
In 3D VM, males had 12.7 greater counts·s−1 than females, a 20.1% difference. Including walking speed (Model 2) reduced the difference to 6.02 counts·s−1, or 9.5%. Other covariates with the exception of step length did not alter the sex effect. Accounting for step length (Model 8) rendered the sex difference not significant (2.39 counts·s−1, or 3.8%). In Model 9, the difference was 4.86 counts·s−1, or 7.8% (p = 0.019).
Results are not shown here for the ML axis because ML axis counts·s−1 were generally lower in magnitude, weakly associated with walking speed, and similar in males and females in all regression models. These results are available in the Supplementary Table.
Including age in regression models did not alter the sex effect. Accounting for walking speed, age was not a significant predictor of counts·s−1 for vertical axis, AP axis, ML axis, or 3D VM (data not shown).
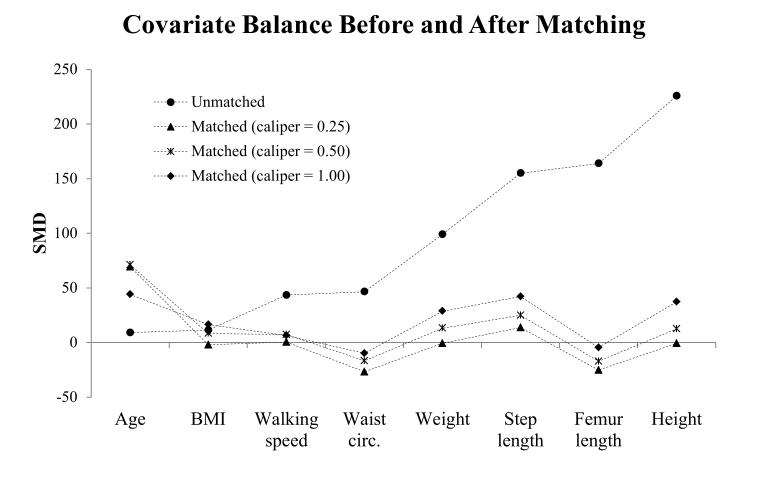
Propensity score matching was used to further test whether the sex differences in accelerometer measurements were secondary to sex differences in height, weight, step length, and walking speed. One-to-one matching without replacement with a caliper of 0.25 resulted in excellent covariate balance, but a small number of successful matches; increasing the caliper to 0.50 and 1.00 resulted in more matches at the expense of covariate balance (Figure 2). Estimates of the sex difference in accelerometer counts·s−1 in each axis using the three different caliper values are shown in Table 4, alongside the estimates obtained from multiple linear regression.
Figure 2.
Standardized mean differences (SMD) between males and females for each covariate, unmatched and after propensity score matching based on height, weight, step length, and walking speed. Positive values indicate higher SMD for males.
Table 4.
Estimates of sex differences in accelerometer counts·s−1 in each axis using propensity score matching, alongside results obtained from multiple linear regression.
| Vertical axis counts·s−1 | AP axis counts·s−1 | 3D VM counts·s−1 | |||||
|---|---|---|---|---|---|---|---|
| Method | n | Estimate (SE) | P | Estimate (SE) | P | Estimate (SE) | P |
| PSM, caliper = 0.25 | 58 | −8.43 (4.34) | 0.052 | 8.09 (2.34) | <0.001 | −2.24 (4.48) | 0.617 |
| PSM, caliper = 0.50 | 66 | −7.80 (4.43) | 0.078 | 6.91 (2.33) | 0.003 | −2.67 (4.54) | 0.556 |
| PSM, caliper = 1.00 | 82 | −10.4 (3.76) | 0.006 | 6.77 (2.38) | 0.004 | −4.75 (4.17) | 0.255 |
| MLR, Model 9a | 319 | −9.64 (1.88) | <0.001 | 4.91 (1.80) | 0.007 | −4.86 (2.05) | 0.019 |
Discussion
To our knowledge, this is the first study to test for and try to explain a sex difference in triaxial accelerometer measurements during walking. Using data from 319 older adults in the AGES-Reykjavik Study, we report a sex difference in vertical axis accelerometer counts·s−1 during fast walking. After accounting for walking speed differences, males averaged 9.08 greater counts·s−1, or 545 greater counts·min−1, than females. Considering that walking is the most common form of exercise in middle-aged and older adults,25 this sex difference could influence the assessment of physical activity in free-living populations using accelerometers, affecting both overall measures of physical activity and intensity-specific measures.
The question of whether the sex difference reported in our study is a confounding effect that could bias free-living activity measurements, or whether it reflects some physiologically meaningful difference in walking intensity, warrants discussion. Higher vertical axis counts·s−1 in males indicates that males have greater vertical accelerations at the hip than females during walking, which is in agreement with documented sex differences in vertical COM displacement during walking.11, 12 Whether sex differences in vertical COM displacement and vertical accelerometer counts coincide with similar differences in energy expenditure is not entirely clear. This is one limitation of our study: energy expenditure was not measured, and therefore we were able to compare counts relative to walking speed, but not relative to metabolic cost. Studies have generally shown males and females to have similar energy expenditure per unit body weight while walking at similar speeds.20, 21, 26-30 The 1983 study by Waters et al. is of particular interest, as it showed that the energy cost of walking is dependent on age but does not differ by sex in young or old adults.26 We suspect that the sex difference in vertical axis counts·s−1 observed in our study may arise from sex differences in vertical COM displacement or other gait characteristics. Additional studies to characterize the relationships among walking speed, vertical COM displacement, accelerometer measurements, and metabolic cost are warranted to test this hypothesis.
We expected height to play some role in the observed sex difference in vertical axis counts·s−1. After adjustment for walking speed, height was a borderline significant predictor of vertical axis counts·s−1, but the association was negative—taller persons had lower counts·s-1−1. Therefore height could not explain why males had greater vertical axis counts·s−1 than females. However, step length was positively associated with vertical axis counts·s−1, and accounting for step length along with walking speed attenuated the sex difference from 19.2% to 13.4%. This reduction is reasonable, considering that step length and vertical axis counts·s−1 were positively correlated and males averaged longer steps than females at any given walking speed. In our data, the positive association between step length and vertical axis counts·s−1 in the same regression model as walking speed shows that the dual effects of longer step lengths—greater counts·step−1 and fewer steps·s−1 for a particular speed—result in a net increase in vertical axis counts·s−1.
Sex differences in 3D VM counts·s−1 were less pronounced compared to the vertical axis. Accounting for walking speed, percent differences in counts·s−1 between males and females in the vertical axis, AP axis, and 3D VM were 19.2%, −5.1% (NS), and 9.5%, respectively. Further adjustment for step length resulted in sex differences of 13.4%, −14.1%, and 3.8% (NS), respectively. Notably, 69.5% of the variance in vertical axis counts·s−1 was explained by walking speed, sex, and step length, while these parameters explained only 32.6% of the variance in AP counts·s−1, suggesting that motion in the AP axis is affected by characteristics, including biomechanical features, not measured in our study. Further investigation is needed to identify determinants of AP axis counts·s−1 during walking. Our results could be taken to support the use of 3D VM rather than a single accelerometer axis, as sex differences are reduced relative to the vertical axis, while a reasonably tight association with walking speed is preserved. Moreover, triaxial measurements are reportedly more sensitive to low-intensity and non-walking activities than vertical-axis measurements alone.31
Propensity score matching allowed us to compare accelerometer measurements within small subsets of male and female participants matched on height, weight, step length, and walking speed. Estimates of the sex difference in counts·s−1 in each axis were generally similar to those obtained from multiple linear regression. Males averaged higher vertical axis output, females higher AP axis output, and males slightly higher 3D VM. These results support the notion that the sex differences observed were unrelated to body size, but rather stemmed from unmeasured sex differences in walking biomechanics.
The impact of a systematic sex difference in accelerometer measurements on free-living estimates of physical activity is important to consider. The walking-speed adjusted difference in vertical axis counts·s−1 of 19.2% can be considered a maximum effect size for measures of overall physical activity, and would correspond to a free-living activity profile consisting entirely of walking. The difference would decrease with increasing percentage of counts stemming from non-walking activities, assuming measurement equivalence for such activities. As for intensity measures, such as MVPA min·d−1, the effect is somewhat harder to quantify. One can appreciate that an average sex difference of 545 counts·min−1 during walking could result in considerable separation above and below the standard MVPA cutpoint of 2020 counts·min−1. Indeed, in our full sample, 87.6% of males and only 65.1% of females achieved an average count value corresponding to MVPA intensity. Estimates of sedentary time should be robust to sex differences in counts, as even the slowest walkers in our sample averaged far more than 100 counts·min−1 (1.67 counts·s−1).3 Sex differences in free-living data should be interpreted cautiously. Depending on the activity variable used, a portion of the difference may reflect a difference in measurement rather than the underlying behavior.
Although not a primary focus of our study, we were surprised to observe a positive association between vertical axis counts·m−1 and walking speed. Calculated as total counts divided by distance walked, or equivalently as counts·s−1 divided by walking speed, counts·m−1 was intended to serve as a walking-speed-independent variable that could be directly compared for males and females despite the fact that males walked faster. Mathematically, this variable remained dependent on walking speed because the linear relationship between vertical axis counts·s−1 and walking speed, over the range of 0.75 to 1.88 m·s−1, included a significant intercept. The positive association between counts·m−1 and walking speed means that a given distance walked quickly produces greater total counts than the same distance walked slowly. For illustrative purposes, our data suggests that, for a given duration, a man walking 1.1 m·s−1 would walk 9.5% farther than a man walking 1.0 m·s−1 but would accumulate 16.4% greater vertical axis counts. The linear relationship between vertical axis counts·s−1 and walking speed, including a negative intercept that renders counts·m−1 also dependent on walking speed, is present (although not discussed) in other reports.17, 32, 33 Notably, the relationship between energy expenditure per unit distance and walking speed is reportedly nonlinear, sloping slightly downward towards a speed of optimal efficiency and then increasing towards a speed at which running becomes more efficient than walking.27, 34-36
We emphasize that although this study was motivated by an accelerometer report showing males to be more active than females across all age groups,3 our study population was limited to older adults, ages 73-92. We cannot say whether a similar difference is present in younger age groups. We encourage other investigators that may already have accelerometry data during timed distance walking to conduct similar analyses to determine whether a sex difference is present, and whether it is similarly strong, in other age groups. Similarly, we propose a more general study to identify other explanatory factors. In our analysis, we observed a negative association between height and vertical axis counts·s−1, positive associations between weight-related measures and AP axis counts·s−1, and positive associations between step length and vertical axis, AP axis, and 3D VM counts·s−1. We tested only a small number of simple anthropometric measures, along with step length; other walking parameters could also be related to accelerometer output. Similar studies should also be conducted for accelerometers worn at different anatomical positions, such as the chest, upper arm, wrist, and thigh. Considering several reports of activity measurements favoring females for the CSA accelerometer,21, 37 sex differences should also be examined for activity monitors from various manufacturers. Once characterized, statistical approaches to correct for confounding factors in accelerometer measurements should be developed. In order for accelerometry to be considered truly objective, measurements must not systematically differ by sex or across other demographic subgroups.
In summary, the current accelerometry study showed that older males accumulate greater vertical axis counts·s−1 during walking than older females. Walking speed and step length explained some of the sex difference in vertical counts, but further research is needed to understand how other biomechanical factors explain variation in triaxial accelerometer measurements during walking. Given that walking is the most common form of physical activity, investigating systematic differences in accelerometer measurements will improve the use of this technology as an objective measure of physical activity.
Supplementary Material
Supplemental Table
Acknowledgment
This study has been funded by NIH contract N01-AG-1-2100, the NIA Intramural Research Program, Hjartavernd (the Icelandic Heart Association), and the Althingi (the Icelandic Parliament). The study is approved by the Icelandic National Bioethics Committee, VSN: 00-063. The researchers are indebted to the participants for their willingness to participate in the study.
Funding: This study was funded by NIH contract N01-AG-1-2100, the NIA Intramural Research Program, Hjartavernd (the Icelandic Heart Association), and the Althingi (the Icelandic Parliament)
Footnotes
Conflicts of Interest No financial disclosures or conflicts of interest were reported by any authors.
References
- 1.Chen KY, Bassett DR., Jr. The technology of accelerometry-based activity monitors: current and future. Med Sci Sports Exerc. 2005;37(11 Suppl):S490–500. doi: 10.1249/01.mss.0000185571.49104.82. [DOI] [PubMed] [Google Scholar]
- 2.Centers for Disease Control and Prevention, National Center for Health Statistics [Accessed February 6, 2012];About the National Health and Nutrition Examination Survey. Available at: http://www.cdc.gov/nchs/nhanes/about_nhanes.htm.
- 3.Troiano RP, Berrigan D, Dodd KW, Masse LC, Tilert T, McDowell M. Physical activity in the United States measured by accelerometer. Med Sci Sports Exerc. 2008;40(1):181–188. doi: 10.1249/mss.0b013e31815a51b3. [DOI] [PubMed] [Google Scholar]
- 4.Tucker JM, Welk GJ, Beyler NK. Physical Activity in U.S. Adults: Compliance with the Physical Activity Guidelines for Americans. Am J Prev Med. 2011;40(4):454–461. doi: 10.1016/j.amepre.2010.12.016. [DOI] [PubMed] [Google Scholar]
- 5.Goodwin RD. Association between physical activity and mental disorders among adults in the United States. Prev Med. 2003;36(6):698–703. doi: 10.1016/s0091-7435(03)00042-2. [DOI] [PubMed] [Google Scholar]
- 6.Pratt M, Macera CA, Blanton C. Levels of physical activity and inactivity in children and adults in the United States: current evidence and research issues. Med Sci Sports Exerc. 1999;31(11 Suppl):S526–533. doi: 10.1097/00005768-199911001-00007. [DOI] [PubMed] [Google Scholar]
- 7.Hootman JM, Macera CA, Ham SA, Helmick CG, Sniezek JE. Physical activity levels among the general US adult population and in adults with and without arthritis. Arthritis Rheum. 2003;49(1):129–135. doi: 10.1002/art.10911. [DOI] [PubMed] [Google Scholar]
- 8.Kerrigan DC, Todd MK, Della Croce U. Gender differences in joint biomechanics during walking: normative study in young adults. Am J Phys Med Rehabil. 1998;77(1):2–7. doi: 10.1097/00002060-199801000-00002. [DOI] [PubMed] [Google Scholar]
- 9.Ko SU, Tolea MI, Hausdorff JM, Ferrucci L. Sex-specific differences in gait patterns of healthy older adults: Results from the Baltimore Longitudinal Study of Aging. J Biomech. 2011;44(10):1974–1979. doi: 10.1016/j.jbiomech.2011.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.McDowell MA, Fryar CD, Ogden CL, Flegal KM. Anthropometric reference data for children and adults: United States, 2003-2006. National health statistics reports; no 10. National Center for Health Statistics; Hyattsville, MD: [PubMed] [Google Scholar]
- 11.Smith LK, Lelas JL, Kerrigan DC. Gender differences in pelvic motions and center of mass displacement during walking: stereotypes quantified. J Womens Health Gend Based Med. 2002;11(5):453–458. doi: 10.1089/15246090260137626. [DOI] [PubMed] [Google Scholar]
- 12.Crosbie J, Vachalathiti R. Synchrony of pelvic and hip joint motion during walking. Gait Posture. 1997;(6):237–248. [Google Scholar]
- 13.Abe T, Kearns CF, Fukunaga T. Sex differences in whole body skeletal muscle mass measured by magnetic resonance imaging and its distribution in young Japanese adults. Br J Sports Med. 2003;37(5):436–440. doi: 10.1136/bjsm.37.5.436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Geer EB, Shen W. Gender differences in insulin resistance, body composition, and energy balance. Gend Med. 2009;6(Suppl 1):60–75. doi: 10.1016/j.genm.2009.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Crouter SE, Clowers KG, Bassett DR., Jr. A novel method for using accelerometer data to predict energy expenditure. J Appl Physiol. 2006;100(4):1324–1331. doi: 10.1152/japplphysiol.00818.2005. [DOI] [PubMed] [Google Scholar]
- 16.Jakicic JM, Winters C, Lagally K, Ho J, Robertson RJ, Wing RR. The accuracy of the TriTrac-R3D accelerometer to estimate energy expenditure. Med Sci Sports Exerc. 1999;31(5):747–754. doi: 10.1097/00005768-199905000-00020. [DOI] [PubMed] [Google Scholar]
- 17.Hendelman D, Miller K, Baggett C, Debold E, Freedson P. Validity of accelerometry for the assessment of moderate intensity physical activity in the field. Med Sci Sports Exerc. 2000;32(9 Suppl):S442–449. doi: 10.1097/00005768-200009001-00002. [DOI] [PubMed] [Google Scholar]
- 18.Swartz AM, Strath SJ, Bassett DR, Jr., O’Brien WL, King GA, Ainsworth BE. Estimation of energy expenditure using CSA accelerometers at hip and wrist sites. Medicine and Science in Sports and Exercise. 2000;32(9):S450–S456. doi: 10.1097/00005768-200009001-00003. [DOI] [PubMed] [Google Scholar]
- 19.Balogun JA, Martin DA, Clendenin MA. Calorimetric validation of the Caltrac accelerometer during level walking. Phys Ther. 1989;69(6):501–509. doi: 10.1093/ptj/69.6.501. [DOI] [PubMed] [Google Scholar]
- 20.Freedson PS, Melanson E, Sirard J. Calibration of the Computer Science and Applications, Inc. accelerometer. Med Sci Sports Exerc. 1998;30(5):777–781. doi: 10.1097/00005768-199805000-00021. [DOI] [PubMed] [Google Scholar]
- 21.Brooks AG, Gunn SM, Withers RT, Gore CJ, Plummer JL. Predicting walking METs and energy expenditure from speed or accelerometry. Med Sci Sports Exerc. 2005 Jul;37(7):1216–1223. doi: 10.1249/01.mss.0000170074.19649.0e. [DOI] [PubMed] [Google Scholar]
- 22.Harris TB, Launer LJ, Eiriksdottir G, et al. Age, Gene/Environment Susceptibility-Reykjavik Study: multidisciplinary applied phenomics. Am J Epidemiol. 2007;165(9):1076–1087. doi: 10.1093/aje/kwk115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Folstein MF, Folstein SE, McHugh PR. “Mini-mental state”. A practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res. 1975;12(3):189–198. doi: 10.1016/0022-3956(75)90026-6. [DOI] [PubMed] [Google Scholar]
- 24.Sekhon JS. Multivariate and propensity score matching software with automated balance optimization: The Matching Package for R. J Stat Softw. 2011;42(7):1–52. http://www.jstatsoft.org/v42/i07/. Jasjeet S. Sekhon (2011) [Google Scholar]
- 25.U.S. Department of Health and Human Services . Physical activity and health: a report of the surgeon general. Centers for Disease Control and Prevention; Atlanta, GA: 1996. pp. 87–142. [Google Scholar]
- 26.Waters RL, Hislop HJ, Perry J, Thomas L, Campbell J. Comparative cost of walking in young and old adults. J Orthop Res. 1983;1(1):73–76. doi: 10.1002/jor.1100010110. [DOI] [PubMed] [Google Scholar]
- 27.Waters RL, Mulroy S. The energy expenditure of normal and pathologic gait. Gait Posture. 1999;9(3):207–231. doi: 10.1016/s0966-6362(99)00009-0. [DOI] [PubMed] [Google Scholar]
- 28.Gleim GW, Stachenfeld NS, Nicholas JA. The influence of flexibility on the economy of walking and jogging. J Orthop Res. 1990;8(6):814–823. doi: 10.1002/jor.1100080606. [DOI] [PubMed] [Google Scholar]
- 29.Loftin M, Waddell DE, Robinson JH, Owens SG. Comparison of energy expenditure to walk or run a mile in adult normal weight and overweight men and women. J Strength Cond Res. 2010 Oct;24(10):2794–2798. doi: 10.1519/JSC.0b013e3181cc26cd. [DOI] [PubMed] [Google Scholar]
- 30.Hall C, Figueroa A, Fernhall B, Kanaley JA. Energy expenditure of walking and running: comparison with prediction equations. Med Sci Sports Exerc. 2004 Dec;36(12):2128–2134. doi: 10.1249/01.mss.0000147584.87788.0e. [DOI] [PubMed] [Google Scholar]
- 31.Midorikawa T, Tanaka S, Kaneko K, et al. Evaluation of low-intensity physical activity by triaxial accelerometry. Obesity (Silver Spring) 2007 Dec;15(12):3031–3038. doi: 10.1038/oby.2007.361. [DOI] [PubMed] [Google Scholar]
- 32.Leenders NY, Nelson TE, Sherman WM. Ability of different physical activity monitors to detect movement during treadmill walking. Int J Sports Med. 2003;24(1):43–50. doi: 10.1055/s-2003-37196. [DOI] [PubMed] [Google Scholar]
- 33.John D, Tyo B, Bassett DR. Comparison of four ActiGraph accelerometers during walking and running. Med Sci Sports Exerc. 2010;42(2):368–374. doi: 10.1249/MSS.0b013e3181b3af49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Waters RL, Lunsford BR, Perry J, Byrd R. Energy-speed relationship of walking: standard tables. J Orthop Res. 1988;6(2):215–222. doi: 10.1002/jor.1100060208. [DOI] [PubMed] [Google Scholar]
- 35.Martin PE, Rothstein DE, Larish DD. Effects of age and physical activity status on the speed-aerobic demand relationship of walking. J Appl Physiol. 1992;73(1):200–206. doi: 10.1152/jappl.1992.73.1.200. [DOI] [PubMed] [Google Scholar]
- 36.Ralston HJ. Energy-speed relation and optimal speed during level walking. Int Z Angew Physiol. 1958;17(4):277–283. doi: 10.1007/BF00698754. [DOI] [PubMed] [Google Scholar]
- 37.King GA, Torres N, Potter C, Brooks TJ, Coleman KJ. Comparison of activity monitors to estimate energy cost of treadmill exercise. Med Sci Sports Exerc. 2004 Jul;36(7):1244–1251. doi: 10.1249/01.mss.0000132379.09364.f8. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental Table