Interpreting principal component analyses of spatial population genetic variation (original) (raw)

. Author manuscript; available in PMC: 2014 Apr 16.

Published in final edited form as: Nat Genet. 2008 Apr 20;40(5):646–649. doi: 10.1038/ng.139

Abstract

Nearly thirty years ago, Cavalli-Sforza et al pioneered the use of principal components analysis (PCA) to summarise data on variation in human gene frequencies across continental regions [1]. Cavalli-Sforza et al produced maps representing each Principal Component (PC), and found these maps exhibited highly distinctive patterns, including gradients and sinusoidal waves. They interpreted these patterns as resulting from specific migration events, such as the migration of agriculturalists out of the Near East [1, 2, 3]. Cavalli-Sforza et al’s results have been highly influential (e.g. [4]), and controversial [5, 6, 7, 8, 9], and PCA has become heavily used in population genetics (e.g. [10, 11, 12, 13]). Despite its widespread use, the behavior of PCA with data exhibiting continuous spatial variation, such as might exist within human continental groups, has been little studied. Here, using empirical and theoretical approaches, we find that the distinctive patterns observed by Cavalli-Sforza et al resemble sinusoidal mathematical artifacts that arise generally when PCA is applied to spatial data, implying that the patterns are not necessarily due to population movements. Our results aid the interpretation of PCA results from large-scale analyses of human genetic variation, and suggest that PCA will be helpful in correcting for continuous population structure in association studies.

Cavalli-Sforza et al’s 1994 “The History and Geography of Human Genes” [3] stands as a classic text in human population genetics, synthesizing a decades-long survey of human genetic variation. These ground-breaking datasets stimulated development of methods that are now widely used, such as the application of Principal Components Analysis (PCA) to population genetic variation. In essence, Cavalli-Sforza et al collected count data for each genetic variant (“allele”) at numerous genetic loci from population samples at many geographic locations, and produced for each allele an allele-frequency map, a spatially-interpolated map representing variation in allele frequency across space. They then used PCA, a general method for obtaining low-dimensional summaries of high-dimensional data, to distill the many allele-frequency maps into a smaller number of “synthetic maps", which for brevity we refer to as PC-maps. Intuitively, the first few PC-maps summarize the allele-frequency maps, in that each allele-frequency map can be well approximated by a linear superposition of the PC-maps (indeed one view of PCA is that it aims to produce PC-maps with this property).

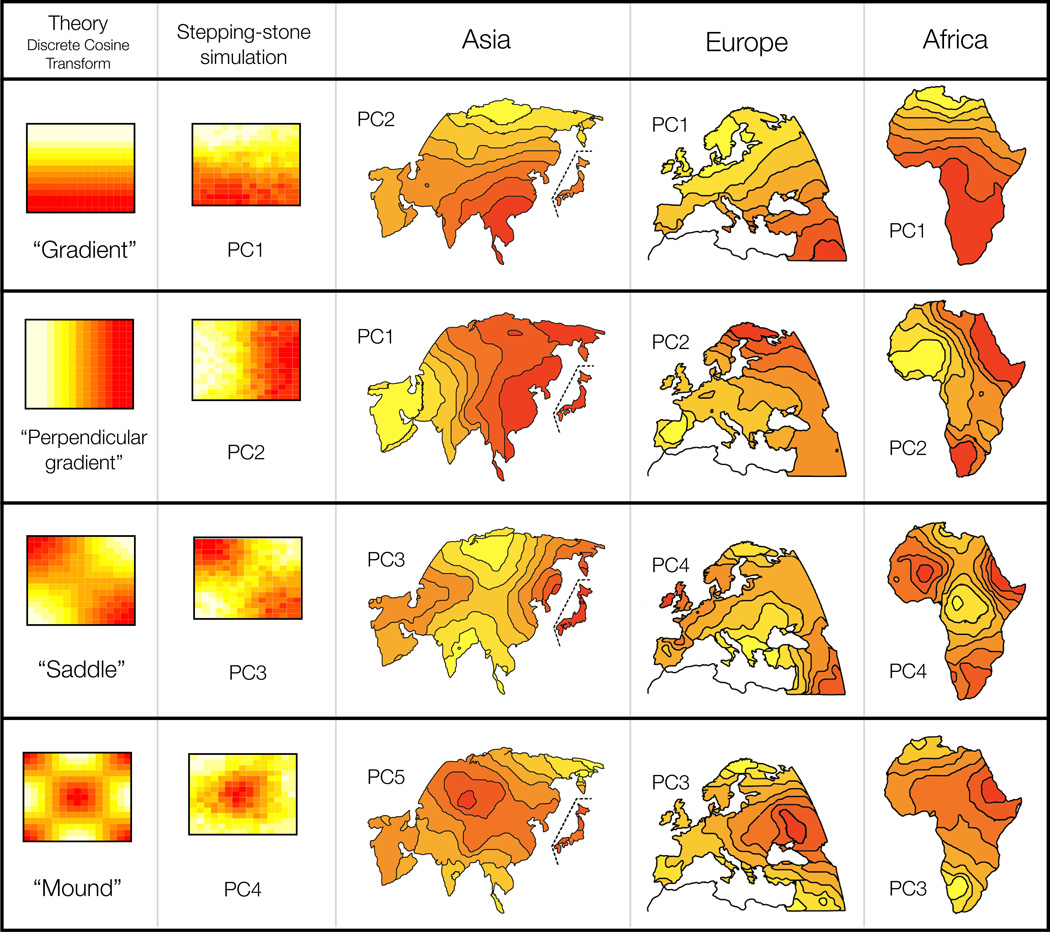
Figure 1 shows PC-maps for Asia, Europe and Africa from [2, 3]. In interpreting these maps, Cavalli-Sforza and colleagues suggest that “if there is a radiation of circular or elliptic lines from a specific area, a [population] expansion is a possible explanation; and its place of origin must be the center of the radiation.” (p. 295 [3]). They also suggest centripetal population movements as an alternative explanation. Examples of their explanations for the European PC-maps in Figure 1 include: expansion of agriculturalists out of the Near East (Europe PC1); migrations of Mongoloid Uralic speakers from northwestern Asia (Europe PC2); migration of the carriers of the proto-Indo-European Kurgan culture in Europe (Europe PC3); and an expansion from Greece (Europe PC4).

Figure 1.

Figure 1

Comparison of PC-maps of [3] with theoretical and empirical predictions. The first column shows the theoretical expected PC-maps for a class of models in which genetic similarity decays with geographic distance (see text for details). The second column shows PC-maps for population genetic data simulated with no range expansions, but constant homogeneous migration rate in a 2-dimensional habitat. The columns marked Asia, Europe, and Africa are redrawn from the originals of [3]. Each map is marked by which PC it represents. The order of maps in each of the last three columns was chosen to correspond with the shapes in the first two columns.

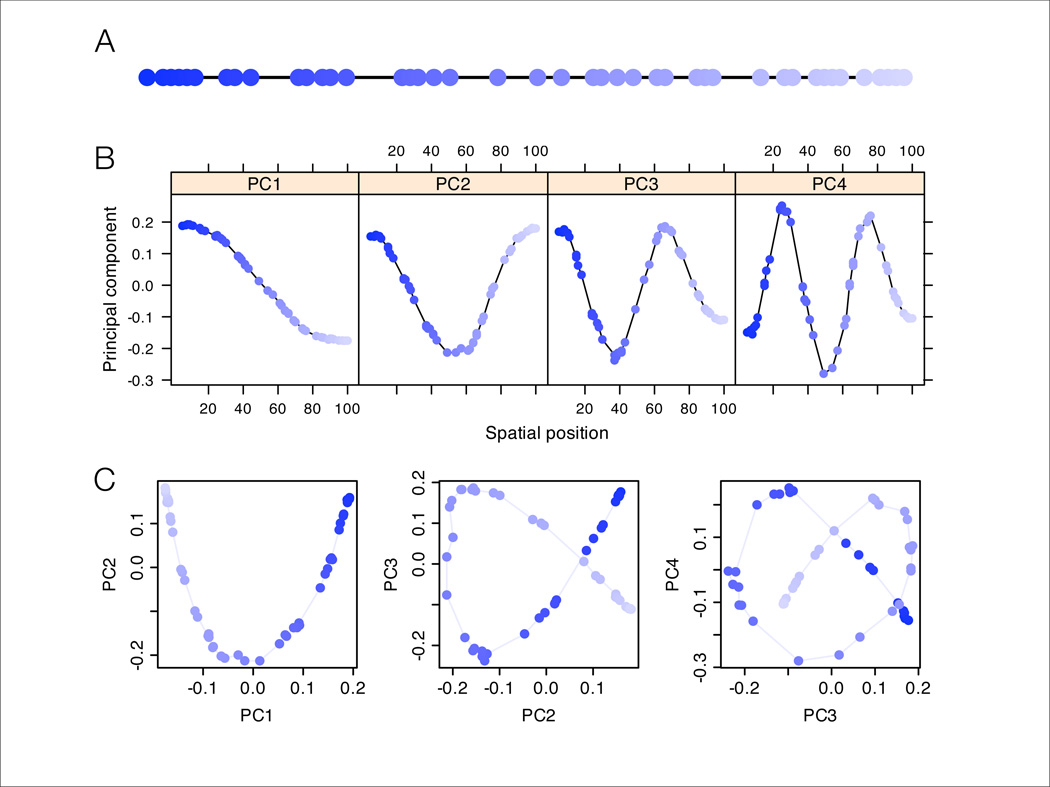
Since the basis for Cavalli-Sforza et al’s interpretive guidelines is unclear, we performed simulations to investigate whether such specific migration events are necessary to explain the observed patterns. Specifically, we performed PCA on data simulated under population genetics models without range expansions, assuming a constant homogeneous short-range migration process across both time and (2-dimensional) space. The results showed highly distinctive structure. For example, the first two PC-maps exhibit large-scale orthogonal gradients, and the next two exhibit “saddle” and “mound” patterns (fig. 1). The same four basic patterns occurred consistently in the first few PC-maps across multiple simulations, although not always in the same order (fig. S1). Results for the analogous 1-dimensional habitat setting are even more structured, resembling sinusoidal functions of increasing frequency (fig. 2B, fig. S2). Thus PC-maps exhibit local peaks and troughs even when underlying migration patterns are homogeneous across time and space. This implies that interpretation of local features of the PC-maps as necessarily reflecting specific localized historical migration events is inappropriate. Furthermore, the first few PC-maps obtained by Cavalli-Sforza et al in Asia, Europe, and Africa show, with minor exceptions, highly structured patterns strikingly similar to those from our simulations (fig. 1,fig. S1).

Figure 2.

Figure 2

Results of PCA applied to data from a one-dimensional habitat. (A) Schematic of the one-dimensional habitat, with circles marking sampling locations and shades of blue marking order along the line. (B) One-dimensional PC-maps (i.e. plots of each PC element against the geographic position of the corresponding sample location). (C) Biplots of PC1 vs. PC2, PC2 vs. PC3, and PC3 vs. PC4. Colors correspond to those in Panel A. In many datasets without spatially referenced samples, the colors and the lines connecting neighboring points would not be observed; here they are shown to aid interpretation.

In fact, these highly structured patterns are mathematical artifacts that arise generally when PCA is applied to data exhibiting a “spatial” covariance structure (i.e. where covariances between locations tend to decay with distance, fig. S3A). In population genetic data, a spatial covariance structure will arise when genetic similarity tends to decrease with distance, which would be expected under a wide range of demographic scenarios, including both equilibrium isolation-by-distance models [14] and non-equilibrium models involving population expansions [15, 16]. For intuition into why sinusoidal patterns emerge in PC-maps, we note that the common description of PCA, as searching for directions that explain the most variance in the data, is perhaps not especially helpful here, as these directions are in a very high dimensional mathematical space and not geographic space. Instead recall the property of PC-maps mentioned above: it should be possible to accurately approximate any of the allele-frequency maps using a linear superposition of the first few PC-maps. PC-maps that contain sinusoidal functions of increasing frequency accomplish this in a sensible way: the low-frequency patterns in the first few PC-maps allow for a coarse approximation by reflecting changes in allele frequencies across large spatial scales, while higher-frequency patterns in subsequent PC-maps allow for refinement of the coarse approximations by capturing finer-scale changes.

Mathematically, the explanation for the highly structured patterns is that covariance matrices from spatial data have eigenvectors related to sine waves of increasing frequency [17, 18, 19], and PC-maps are direct visual representations of such eigenvectors (see Supplemental Material). To give three specific examples, consider a situation where the covariance between two populations depends only on the geographic distance between them, and assume that sufficient genetic data (loci/alleles) are available to accurately estimate this covariance structure. Then:

  1. If populations are regularly spaced on a line, then their covariance matrix has a “Toeplitz” structure1(e.g. fig. S3B), and the eigenvectors of any (large) Toeplitz matrix are known to be closely approximated by sinusoidal functions [19]. A well-studied special case occurs when the covariance between populations decays exponentially with distance2, where the eigenvectors are approximately the columns of the discrete cosine transform (DCT) matrix [17, 18].
  2. If populations are regularly spaced around a circle, then their covariance matrix has a “circulant” structure3 (e.g. fig. S3B). The eigenvectors of any circulant matrix are the columns of the discrete Fourier transform matrix [19], which are sinusoidal functions of increasing frequency.
  3. If populations are located on a 2-dimensional regular grid, as in Cavalli-Sforza et al’s analyses, the covariance matrix has a “block Toeplitz with Toeplitz blocks” form (e.g. fig. S3B), with eigenvectors that are approximated by the two-dimensional DCT commonly used in image compression4 [18]. The first two eigenvectors are commonly two orthogonal gradients, and the next two have a “saddle” and a “mound” shape (fig. 1). Higher order eigenvectors relate to 2-dimensional sinusoidal functions of increasing frequency (fig. S4).

We note also that in time-series analysis, where problems often arise that are analogous to analysis of one-dimensional spatial data taken at regular intervals, it has long been recognized that PCs are closely approximated by the columns of the discrete Fourier transform matrix [20].

Although Cavalli-Sforza et al performed PCA on population allele frequency estimates, PCA can also be applied to individual genotype data [12]. The results above apply equally to this context: just as spatial covariance among populations will produce sinusoidal-like PC-maps, so will spatial covariance among individuals. However, in this setting geographical information may not be available for each individual, making PC-maps difficult to produce. Instead PCA results are commonly visualized by producing biplots of one PC against another. Under uniform sampling from a 1-dimensional habitat with homogeneous migration, this results in biplots of sinusoidal functions of differing frequencies, producing characteristic patterns known as Lissajous curves [21, 22] (fig. 2C). In particular, the first of these biplots shows a pattern known as the “horseshoe effect” (e.g. [23]). For the analogous 2-dimensional setting, because PC1 and PC2 are typically orthogonal gradients, a biplot of the first 2 PCs essentially reproduces the geographic arrangement of sampled individuals (explaining PCA results on genetic variation in Arabidopsis [24] for example), and biplots involving later PCs have intricate patterns analogous to Lissajous curves (fig. S5).

Since the above empirical and theoretical results involve unrealistically simplistic scenarios, we assessed robustness by examining PC-maps for more complex scenarios involving heterogeneous migration processes and irregular sampling of populations across space. Detailed features of the PC-maps were influenced by both factors. Changing the sampling scheme or details of migration can produce a range of continuous distortions of the idealized sinusoidal shapes. Since quantifying this effect is difficult, we instead provide several examples for illustration. Anisotropic migration (i.e. migration is not equal in all directions, fig. S6) and irregularly spaced populations (fig. S7) both distort the PC-maps, and change their order. The direction of the gradient in the first PC-map is influenced by habitat shape (e.g. in fig. 2, PC1 in Africa and Asia are both along the longer axis of the continent), as has also been noted in climatological data [25], and by migration patterns (e.g. under anisotropic migration in a square habitat the gradient in PC1 aligns with the axis of least migration, fig. S6). However, sinusoidal-like patterns consistently emerge. Even when sampling locations are highly clustered within the continuous habitat (a common sampling design in practice, because of logistical challenges to obtaining spatially uniform samples in many species, [26]), the first PCs separate out the clusters as if the sample were obtained from discrete sub-populations, and subsequent PCs show sinusoidal patterns within clusters (fig. S8).

We also examined how quantity of data affects PCA results. With limited data sinusoidal patterns can still emerge. For example, such patterns occur in PC1 and PC2 (figs. S9, S10) from only 62 amplified fragment length polymorphism (AFLP) markers typed in 105 individuals from the ring species complex of greenish warblers (Phylloscopus trochiloides, see supplementary text, [27]). However, limited data can lead to less well-defined (or entirely absent) sinusoidal patterns, particularly in higher PC-maps (e.g. PC3 for the same dataset; fig. S9). In general, amounts of data needed to recover sinusoidal patterns will depend on the strength of the population structure (e.g. the amount of differentiation among sampled populations). Thus, for a fixed number of loci, higher effective migration rates, which tend to reduce population structure, lead to less well-defined sinusoidal patterns (fig. S11).

In summary: i) when analyzing data with a spatial covariance structure, PCA produces highly structured results relating to sinusoidal functions of increasing frequency; ii) in as far as PCA results depend on the details of a particular data set, they are affected by factors in addition to the actual underlying spatial population structure, such as the distribution of sampling locations and the amount of data available. These conclusions are supported not only by the results we present here, but by extensive empirical results from other fields where PCA has been applied to spatial data, including pattern analysis of natural images [28], ecology [23] and climatology [25, 29, 30, 31].

Both features i) and ii) above limit the utility of PCA to draw inferences about underlying processes, a fact previously noted in climatology ([25, 29, 30, 31]). In particular, interpreting gradient and wave-like patterns in PC-maps as signatures of historical migration events is problematic because such patterns arise quite generally under a simple condition: that genetic similarity decays with distance. This finding has important implications for interpretation of PCA in population genetics generally, and for Cavalli-Sforza et al’s PCA analyses in particular. Not only is this simple condition likely to be satisfied under many possible models, but, since Cavalli-Sforza et al used spatial interpolation to estimate allele frequencies, their data could satisfy this condition even if absent in the underlying allele frequencies [6, 8]. (Indeed use of interpolation may partly explain the striking similarity between Cavalli-Sforza et al’s PC-maps and those predicted by theory, particularly in Asia where their analysis was based on fewer samples. That said, recent analyses of European data without interpolation also show perpendicular gradients in PC1 and PC2 [32].)

Regarding the specific question of a Neolithic expansion in Europe, we emphasize this paper is not about whether or not such an expansion occurred; a full consideration of this would require a synthesis of multiple types of evidence from many diverse sources (see review in [33] and e.g. [34, 35, 9, 36, 37, 38, 39]). It is true that the NW-SE slope of the PC1 gradient in Europe suggests that this may be the direction of greatest genetic variation in Europe (although a careful analysis would have to take account of the fact that other factors, including the shape of the continent, could also influence the slope direction). However, if a Neolithic expansion could explain this, it is but one of many possible explanations.

For another example of how our results aid interpretation of PCA, consider the data from Linz et al [13] who found that PC-maps from Heliobactor pylori show similar patterns to those in Cavalli-Sforza et al’s human data and who use this as part of an argument that genetic patterns of H. pylori reflect a shared migrational history with humans. There are good reasons to suspect genetic variation in H. pylori will have been influenced by human migrations. However our results show that similar patterns in PC-maps of two groups does not imply a shared migrationary history; indeed, if each group shows an underlying spatial covariance structure, then similar patterns will often occur in the top few PC-maps even if their histories are independent (e.g. fig. S1).

Despite its limitations for inferring underlying processes that have produced population structure, PCA is undoubtedly an extremely useful tool for investigating and summarising population structure, and we anticipate that it will play a prominent role in the analysis of ongoing genome-wide studies of human genetic variation. Results presented here provide a helpful context for evaluating PCA results, essentially providing a “null” expectation against which observed PCs may be compared and contrasted. On the one hand, a close correspondence between observed and expected PCs may suggest an underlying continuous spatial covariance structure. On the other hand, departures from this null may also be useful, perhaps pointing towards a more discrete ”cluster-like” population structure [12], or to other important structure in the data, such as genotyping error or regions of high linkage disequilibrium [40].

Finally, our results provide some intuitive support for the use of PCA to address the problem of spurious associations produced by population structure in genome-wide association studies [41, 11]. In essence, the problem is that if phenotype mean (or risk) varies among subpopulations, then alleles that have no mechanistic connection to phenotype, but differ in frequency among subpopulations, will be “spuriously” associated with phenotype [42]. Although this problem has been studied mostly in the context of discrete subpopulations, it applies also to continuous (e.g. spatial) variation [43]. One commonly used PCA-based solution [11] controls for stratification by including the first few PCs as covariates in a regression. In populations showing a discrete, cluster-like, structure the first few PCs typically separate out the clusters [12], and so this solution corresponds to allowing for phenotype mean to vary among subpopulations. Our work shows that, for spatially-continuous populations, the PCA-based approach is conceptually similar to modeling smooth geographical trends in phenotype mean, a recognized technique in spatial epidemiology [44]. For example, if PC1 and PC2 are orthogonal gradients in space, including them in a regression essentially controls for latitude and longitude, and allows for linear trends in phenotype across space; including higher-order PCs allows for more flexible spatial trends. While some practical issues remain, including how many PCs should be used (supplementary text) and how best to employ the PCs [24], this analogy between the PCA-based and spatial-statistics approaches gives an intuitively appealing justification for using PCA to control for spurious associations in spatially-structured populations. It also has two important practical advantages over simply using geographic information on each individual directly. First, PCA can be used even when geographic information is not available. Second, PCA will control for continuous population structure even when geographic position does not correlate well with genetic background (as is typical in the United States, for example).

Methods

Simulations

For our population-genetics simulations we assumed a model of D demes that are arranged in a regular square lattice (for two-dimensional habitat) or a line (one-dimensional habitat). Each deme has effective population size 2_N_ gametes, and, backwards in time, in each generation, a proportion, m, of gametes swap places with an equal number of gametes in each neighboring deme (e.g. for the 2-d simulations, demes internal on the lattice have four neighbors; demes on the edge have three neighbors; demes in the corners have two neighbors). We assume the population has reached equilibrium (i.e, the population has been evolving in this way for a long time).

We applied PCA to both “population-based” data (as in Cavalli-Sforza et al [1, 2, 3]) and “individual-based” data (as in [12]). For generating population-based data sets, we sampled n individuals from Ds of the D demes, and simulate for each individual data at L independent, bi-allelic polymorphic loci. Assuming independence of loci corresponds to migration of alleles rather than of whole gametes. We experimented with different spatial arrangements of the Ds demes, but for the results shown here (figs. 1, S1,S3,S5,S6), we use a regular square lattice of Ds = 15 × 15 demes embedded in a larger D = 31 × 31 lattice of demes. Allele frequencies in each deme are stimated from the n sampled individuals in that deme, to create a Ds × L data matrix of allele frequency estimates. For the one-dimensional simulations we report individual-based, rather than population-based PCA. We sampled n diploid individuals randomly from the D demes, and the data matrix consists of an n × L genotype matrix. See Supporting Online Material for additional details.

Principal components analysis

To calculate principal components on our simulated data, we use bi-allelic loci and include only the frequency of one of the two alleles. To compute the PCs, we apply the prcomp function of the R statistical package [45] to a matrix based on allele counts. In accord with Cavalli-Sforza’s method for creating PCA maps, we do not scale the allele frequencies when conducting population-based PCA; however our methods differ from Cavalli-Sforza et al’s in that we applied PCA directly to the observed allele-frequency matrix rather than using allele frequencies spatialy interpolated on a dense grid. This avoids problems with interpolation altering underlying spatial covariance patterns [6]. For individual-based PCA we use an approach similar to that of Patterson et al [12], in that we scale the genotype values across individuals at each locus to have unit variance. For the analysis of AFLP data from greenish warblers, we coded each typed marker by using an indicator variable with 0 or 1 indicating the absence or presence of an AFLP band, respectively. We then normalized each indicator variable to have mean zero and unit variance before applying PCA (again similar to [12], see Supporting Online Material for more detail).

Supplementary Material

Supp Info

Acknowledgements

We acknowledge G. Coop, M. Przeworski, Y. Guan, M. Barber, and C. Becquet for helpful comments on a draft of this manuscript and D. Witonsky for pointing out the connection to Lissajous figures. Funding for this research was provided by an NSF postdoctoral research fellowship in bioinformatics (JN) and NIH grant RO1 HG02585-01 (MS).

Footnotes

1

A Toeplitz matrix is a matrix whose (i, j)th element Xij depends only on (j — i).

2

Specifically, each element Xij of the matrix equals ρ|i–j| for some constant ρ.

3

A circulant matrix is a Toeplitz matrix in which each row is obtained from the row above it by a right cyclic shift; that is, by moving the last element of the row to the start of the row.

4

Indeed, the 2-D DCT is central to the popular JPEG image compression algorithm, and much of its efficacy is due to the fact that the 2-D DCT basis functions so closely approximate the PCA basis (also known as the Karhunen-Loeve basis) without having basis vectors that are specific to each dataset (as in PCA).

Author contributions

J.N. and M.S. jointly designed the analyses and interpreted results. J.N. performed the analyses and researched the applications of PCA in other fields. J.N. and M.S. wrote the paper.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supp Info