The contribution of genetic variants to disease depends on the ruler (original) (raw)

. Author manuscript; available in PMC: 2015 Nov 1.

Published in final edited form as: Nat Rev Genet. 2014 Sep 16;15(11):765–776. doi: 10.1038/nrg3786

Preface

Our understanding of the genetic basis of disease has evolved from descriptions of overall heritability or familiality to identifying large numbers of risk loci. One can quantify the impact of such loci on disease using a plethora of measures, which can guide decisions on new experiments, for example, whether to focus on the biology of identified variants or put more effort into discovering novel variants. However, different measures can attribute varying degrees of importance to a variant. We consider and contrast the most commonly used measures, specifically the heritability of disease liability, approximate heritability, sibling recurrence risk, overall genetic variance using a log relative risk scale, the area under the receiver-operating curve for risk prediction, and the population attributable fraction, and give guidelines for their use that should be explicitly considered when assessing the contribution of genetic variants to disease.

Introduction

A rapidly growing number of genetic loci have been detected for disease and other traits. These include high-risk Mendelian loci from next-generation sequencing studies and many highly replicated low penetrance variants from genome-wide association studies (GWAS).1,2 Two important questions that follow are to what degree do such loci and variants impact the overall burden of disease, and how many variants remain to be discovered.3 This can be assessed using a number of measures, many of which have been developed with different goals and within traditionally disparate fields—such as quantitative genetics and epidemiology—whose boundaries are now blurring in the post-genomics era (Figure 1). The quantitative genetics approach calculates measures such as heritability of disease liability or sibling recurrence risk explained by genetic variants. A more epidemiologic or translational approach might assess their impact on the overall genetic variance (using a log relative risk (logRR) scale), the area under the receiver-operating curve (AUC) for risk prediction, or the population attributable fraction (PAF).4–6

Figure 1. Different measures of genetic effects on disease.

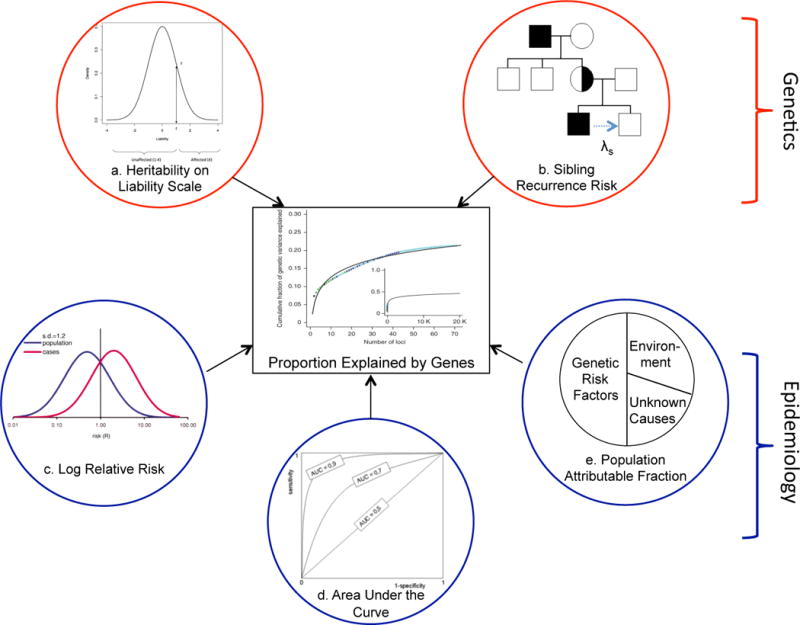
Figure 1

A number of different measures can be used to assess how much known genetic factors contribute to the overall genetic variation in disease. These include: a. heritability, b. sibling relative risk, c. log relative risk genetic variance, d. area under the receiver operating curve (AUC), and e. population attributable fraction. These measures have their bases in traditionally distinct disciplines such as quantitative genetics and epidemiology, which have recently begun to coalesce. While the latter were originally developed to address different questions, they are presently being repurposed to assess how much genetic variation cab be explained. We compare these measures via simulation and applications.

Each of these measures can be calculated as a proportion to quantify how much of the underlying genetic basis of disease is explained by known risk loci. The heritability explained is most commonly calculated as the proportion of variance in disease explained by risk loci relative to the overall heritability.5,7 The proportion of the sibling recurrence or the logRR genetic variance explained by the loci provides a similar measure of their impact on disease. The AUC indicates how well known risk loci classify diseased individuals; dividing this measure by the maximum attainable AUC for a genetic risk predictor calculated from the heritability quantifies the proportion of maximum AUC explained.4 Finally, the PAF approximates the proportion by which disease incidence or death would be reduced in a population in the absence of the identified genetic risk factors.

While all these measures are valid and have the same bounds (ranging from 0 to 100%), for a given dataset they may give different messages about the impact of risk variants on disease. This has resulted in contrasting and confusing use of these measures in the literature. For example, the same association results for the Crohn’s disease variants in NOD2 are reported to explain between 1–2% of heritability8, 5.1% of genetic risk9 and 18.2% of the PAF.9 In other words, the apparent proportion of disease ‘explained’ by risk variants can vary widely across measures, so which measure one uses can result in very different interpretations among geneticists and epidemiologists.

Here, we compare six measures used to assess how much of the genetic basis of disease is explained by risk variants to understand their similarities and differences. We estimate the heritability of liability, approximate heritability, sibling recurrence risk, logRR genetic variance, AUC and PAF explained across a range of risk allele frequencies and relative risks via empirical calculations and application to data from studies of breast cancer, Crohn’s disease, rheumatoid arthritis and schizophrenia. We describe the interrelationships among these measures and give guidance for their appropriate calculation and interpretation when assessing the overall impact of genetic contributions to disease. Finally, we provide an online tool to calculate these measures from association study summary statistics: risk allele frequency and relative risks.

Measures of genetic impact for individual risk loci

Scale matters

A key difference between the measures considered here is the scale on which they are measured (Box 1, Table 1). Assessing the contribution of individual loci to disease risk on the observed (binary) scale is not very informative as the relationship between increasing burden of risk loci and probability of disease is highly non-linear.10,11 Therefore, transformations are made to more informative scales, such as the liability of risk scale or the log-risk scale. Quantitative geneticists commonly use the liability scale to evaluate the genetic basis underlying disease variability in a population.12 By contrast, epidemiologists more often use log relative risk models for estimation of genetic effects on disease. As shown below, these different perspectives, ensuing model choices, and calculated measures can ultimately affect inferences and conclusions. That is, the measure of an apparent contribution made by a given locus can depend on the ruler.

Box 1. A matter of scale.

The contribution of genetic loci to disease can hinge on the scale used to assess risk (e.g., observed, log, or liability scales). On the observed scale, the risk of disease (D) for individuals carrying zero, one, or two copies of risk variant B are Pr(D|bb) = kbb, Pr(D|Bb) = kbbRRBb, and Pr(D|BB) = kbbRRBB. Here, kbb is the baseline risk among non-carriers and RRG is the relative risk for carrying genotype G∈(Bb, BB) in comparison to the bb genotype. Then the probability of disease given genotype from a multiplicative model on the observed risk scale is Pr(D|G)=kbbRRBbxBbRRBBxBB, where XG is a (0,1) indicator of which genotypes one caries. The overall risk of disease (K) is K = E_[Pr(D)] = Σ_GPr(D|G)Pr(G) = kbb((1−p)2 + 2_p_(1−p)RRBb + p_2_RRBB), where p is the risk variant (B) frequency. When RRBb, RRBB, and K are known this can be rearranged to estimate kbb. The overall relative risk due to multiple independent variants can be modeled by extension in which kbb is replaced by the probability of disease in individuals carrying no risk variants. This model is appealing because it is mathematically tractable, but it is not constrained so some combinations of parameters can generate a probability of disease greater than 1.11,21 For this reason, it is not the model of choice when considering multiple risk loci. Instead it can be converted to an additive model on the log risk scale.

log(Pr(D|G))=log(kbb)+log(RRBb)xBb+log(RRBB)xBB.

Another possibility is to use the liability risk scale, which assumes that individuals have a latent continuous liability of risk for disease reflecting both genetic and non-genetic risk factors12. Disease occurs when the total phenotypic liability exceeds a threshold (i.e., a sufficient number of risk factors are present). For complex diseases, numerous risk factors each of modest effect are expected. The residual variation in liability between individuals of each genotype class at any given risk locus is assumed to have a standard normal distribution about different mean liabilities wbb, wBb, and wBB for the genotype classes bb, Bb, and BB. The observed disease risks for each genotype class are converted into thresholds on the liability scale. The difference between the genotype thresholds equals the differences between the mean distributions with a common threshold for disease. The liability risk model is mathematically tractable, easily generalizes to multiple risk loci, and is constrained so that the probability of disease does not exceed 1. Moreover, the contribution of individual risk loci can be parameterized in terms of the variance they explain, which provides a general framework since many different combinations of allele frequency and effect size can generate the same contribution to variance. For these reasons, the liability risk model is usually the model of choice when considering multiple risk loci21,40–44.

Table 1.

Unified approach showing how measures of a genetic variant’s impact on disease are grounded in different scales of risk. For each scale, the genotype risk values can be used to calculate the corresponding means and variances.

Genotypea
Measures bb Bb BB
General notation
Population frequencyb (1−p)2 2p(1−p) p2
Genotype riskc wbb wBb wBB
Mean genotype risk (M)d (1−p)2 wbb 2p(1−p) wBb p2 wBB
Variance of genotype risk (V)d (1−p)2 (wbb − M)2 2p(1−p) (wBb − M)2 p2 (wBB −M)2
Scale-specific genotype risks
Observed riske kbb kbb RRBb kbb RRBB
Relative risk 1 RRBb RRBB
Log relative risk 0 log(RRBb) log(RRBB)
Liability thresholdf −Φ−1(1−kbb) −Φ−1 (1−kbb RRBb) −Φ−1 (1−kbb RRBB)
Quantitative genetics notation
Genotype risk −a d = wBb−(wbb+wBB)/2 a = wBB − (wbb+wBB)/2
Deviations from the meang
Total −a−M = −2p(a+(1−p)d) d−M = a((1−p) −p)+d(1−2p(1−p)) a−M = 2(1−p)(a−pd)
Additiveh −2pα ((1−p) −p)α 2(1−p)α
Dominance −2p2d 2p(1−p)d 2(1−p)2d

Proportion of heritability explained

Using the methods and notation in Table 1 and Box 1, we can estimate the proportion of phenotypic variance on the liability scale explained by risk variant i as h2L[i] =VAL[i]/VPL = VAL[i]/(VGL[i] + 1),13,14 where h2L[i] is the heritability explained, V*L[i] is the additive (*=A), phenotype (*=P), genetic (*=G) variance. On this scale we only consider the additive contribution from the locus (VAL[i]), which allows for comparison with existing estimates of heritability of liability derived from family data (h2L).13,15,16 Furthermore, under the assumption of a small relative risk (RR) for variant B (i.e., RRBb is close to 1) and a multiplicative model on the observed scale (i.e., RRBb2 = RRBB), an approximate heritability is given by h2L-approx[i] = 2p(1−p)(RRBb−1)2/v2, where p is the frequency of risk allele B.18,21,22 Here v is the mean liability of diseased individuals, approximated as z/K where z is the height of the standard normal distribution at the threshold T that truncates the proportion K, T= Φ−1(1−K) (i.e., the overall disease risk; Box 1). Then h2L[i]/h2L (or h2L-approx[i]/h2L) estimates the proportion of total heritability explained by the ith risk variant.

Sibling recurrence risk explained

The impact of a risk variant can also be quantified relative to the overall sibling recurrence risk (λS)9. Siblings share VAO/2 + VDO/4 of risk17, where VAO and VDO are the additive and dominance genetic variance on the observed risk scale. Thus, the increased risk attributable to the ith risk variant is λS[i]=1+VAO[i]2+VDO[i]4K2. From Table 1 we can estimate VAO[i] = k2bb2*p(1−p)(p*(RRBB−RRBb)+(1−p)*(RRBb−1))2, and VDO[i] = k2bbp2(1−p)2(RRBB+1−2*RRBb)2. The ratio of λs[i] to λS indicates the impact of a variant on the sibling recurrence risk, where λS is generally obtained from published estimates. However, λs[i]/λS can give nonsensical values under the null hypothesis. When λs[i] =1 the ratio incorrectly suggests that the ith variant contributes to the genetic risk, and when λS =1 the ratio equals 1. Instead, the ratio of logarithms (log(λs[i])/log(λS)) has been proposed9. Here, when λs[i]=1 the ratio of logs appropriately indicates no contribution of the ith genetic variant to risk. And the ratio of logs gives values more uniformly distributed across the range of (0,1). Of course, shifting scales results in a quantitatively different measure.

Genetic variance on log relative risk scale

From a more epidemiological perspective, one can calculate the contribution of a risk variant to overall genetic variation on the logRR scale. From Table 1, the genetic variance attributable to the ith risk variant on the logRR scale is VGlog_[i_] = (1−_p)2M2 + 2 p(1−_p)(log (RRBb) − M)2 + _p_2(log (RRBB) − M)2, where M is the mean value of log relative risk, M= 2p(1−p) log(RRBb) + p2 log(RRBB). Assuming a multiplicative model this simplifies to. For a polygenic disease with numerous risk alleles, the distribution of logRR in the population tends towards normal with variance VGlog. Thus, the fraction of the genetic risk explained by a single allele is given by VGlog[i]/VGlog. In practice VGlog is assumed to approximately equal 2log().18–20 Note that VGlog should not be estimated as log(—the recurrence risk to monozygotic twins—because λMZ≈λs2 is an asymptotic result that only holds for diseases of high prevalence (e.g., K > 0.1) and low heritability,21 and otherwise can give nonsensical results.

Proportion of area under the curve

We can also determine how much of the maximum possible AUC attainable with a risk prediction model based on all genetic information is explained by the ith risk variant. We can first estimate the AUC for the ith variant using the variance it explains the liability scale (h_2_L[i])4 AUCL[i]=Φ((x−v)hL[i]2hL[i]2(1−hL[i]2x(x−T)+1−hL[i]2v(v−T))), where x = −z/K, T is the population threshold and v = −x * K(1−K) (as described above and in Box 1).13 Next, we determine the maximum attainable AUC by substituting into the above equation the overall heritability h_2_L (for example, estimated from twin studies)4. While the AUC upper bound is 1.0, the AUC attainable with genetic factors will generally be lower. Then, we can estimate the proportion of the max AUC explained by the risk variants as the proportional AUC, pAUC = [(AUCL[i]−0.5)/(AUCMax−0.5)]2. We square this measure because it is related to the square root of heritability, allowing comparisons with other measures that are visually more intuitive to interpret. This measure will generally range from 0 (AUC=0.5) to 1 (AUC=1).

Population attributable fraction

The PAF assesses how much disease can be ‘attributed’ to a genetic risk variant. This is commonly used to approximate the public health implications of modifying or removing an exposure. While we cannot currently intervene to remove or nullify risk variants, genetic PAFs are often used to estimate how much disease can be attributed to the risk variants. We can calculate this from the ratio of the disease due to a risk variant (that is, subtracting off the baseline risk) divided by the overall risk,

From Box 1, kbb=K((1−p)2+2p(1−p)RRBb+p2RRBB), so

PAF=1−1(1−p)2+2p(1−p)RRBb+p2RRBB=2p(1−p)(RRBb−1)+p2(RRBB−1)1+2p(1−p)(RRBb−1)+p2(RRBB−1).

These equations highlight that the PAF is the effect of ‘removing’ the genetic risk variant on the overall risk of disease. Note that previous work gives an incorrect equation for the PAF19.

Comparison of measures for single variants

We first evaluated how the above measures assess the impact of a single genetic variant on disease. Specifically, we calculated the measures across a range of risk allele frequencies (RAFs) and genetic relative risks (RRs) for carrying one additional risk allele. We assume an overall disease risk in the population of 0.01 and a sibling recurrence risk of 5—which are consistent with an overall genetic heritability on the liability scale of 55%—and a multiplicative model of genotype RRs. Note that we present calculations for PAF separately because it generally gives estimates an order of magnitude larger than the other measures. The proportion of genetic risk explained by all measures is similar and quite limited for variants that are less common and/or have modest effects on disease (Figure 2). However, these measures diverge as the RAF increases—up to a point—and as the RRs increase. The conventional heritability estimate always suggests one of the smallest impacts of the genetic variants on disease, irrespective of RAF and RR (Figure 2, red line). Similar values are given by the approximate heritability when RR < 1.5, but this increasingly overestimates the heritability as the RR increases, as expected from its derivation. The sibling recurrence risk explained suggests the largest contribution of the genetic variants to disease when RAF ≤ 0.25, but then a smaller amount for larger RAF (Figure 2, green line). An opposite trend is seen for the logRR genetic variance explained, which is lower than the sibling recurrence risk when RAF < 0.25 and then larger for more common risk variants. Finally, the pAUC consistently indicates one of the highest estimates of genetic basis of disease explained (Figure 2, orange line). While these differences may seem slight, they are only so for individual variants. Aggregated across numerous risk variants, substantially larger differences in the measures become apparent, as shown in the following applications.

Figure 2. Empirical evaluation of measures of genetic effects.

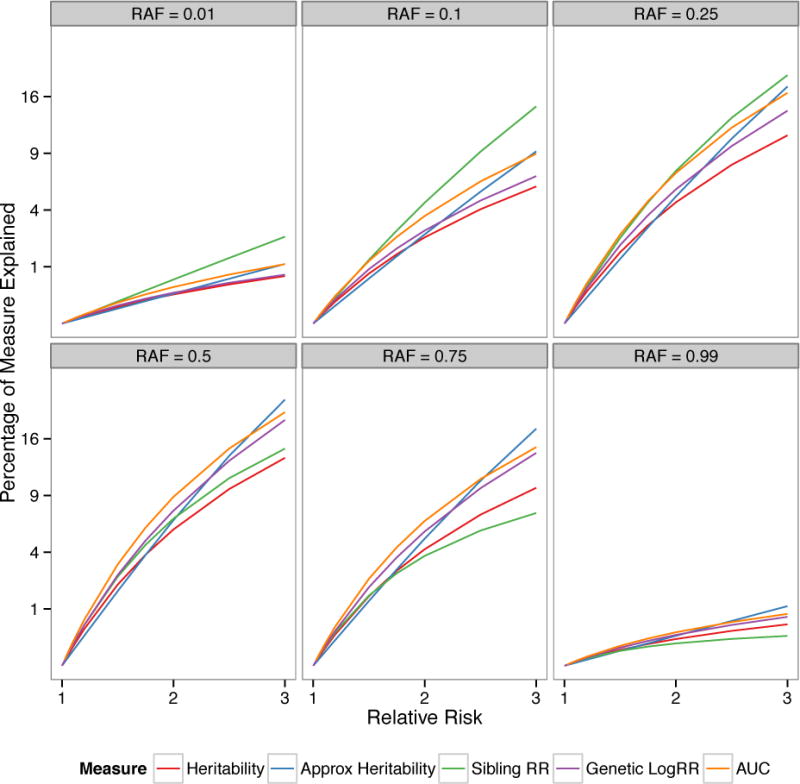
Figure 2

Comparison of heritability, approximate heritability, sibling relative risk, log relative risk genetic variance, and area under the curve (AUC) explained across a range of complex disease architectures. The measures are calculated for a single causal variant with risk allele frequency (RAF) = 0.01, 0.10, 0.25, 0.50, 0.75, and 0.99 and genetic relative risk (RR) ranging from 1.0 to 3.0 (assuming multiplicative model). The overall disease risk is assumed = 0.01, and the total sibling relative risk = 5, which gives an overall genetic heritability on the liability scale = 0.55 and a maximum AUC = 0.95. The percentage of heritability, sibling risk, and logRR genetic variance explained is quite modest for low RRs and small RAF, but as these increase the measures start to materially differ. Heritability is always one of the smallest measures, and is overestimated by the approximate heritability as the RR increases. The sibling relative risk and AUC are generally the largest measures for lower RAFs.

Contribution of multiple risk loci to disease

To determine the contribution of multiple risk loci to disease from summary statistics, the methods for individual loci can be aggregated if they are independent. Specifically, for heritability on the liability scale, approximate heritability, sibling relative risk, and logRR genetic variance, an aggregate score is calculated from the sum of the contributions calculated for each locus. Similarly, the aggregate heritability of liability is used to calculate AUC. To calculate the PAF due to multiple risk variants, one cannot simply add together the single variant PAFs because this ignores the fact that most individuals will carry multiple risk alleles. In fact, summing single variant PAFs can quickly give an overall PAF > 100%. Instead, we can calculate a joint PAF across multiple variants, which restricts the total PAF due to all risk variants ≤ 100%. Specifically, if we assume that the risk variants are independent of each other and that their combined effects on disease are multiplicative, a joint estimate of PAF is given by PAFTotal = 1−∏i(1−PAFi).

Application to complex diseases

To further explore how these measures can imply different impacts of genetic variants on disease, we calculate them across studies of breast cancer, Crohn’s disease, rheumatoid arthritis, and schizophrenia. We selected these diseases because they have been well studied to date and have a range of underlying genetic architectures. For each disease, we selected those loci previously reported in the literature as independently associated with disease, and identified the reported risk allele, its frequency, and its relative risk—estimated by the odds ratio. More specifically, for breast cancer the loci were obtained from the NHGRI catalog (http://www.genome.gov/gwastudies), and for the other three diseases we used the SNPs that were reported and selected as independent by the corresponding publications. While the criteria for SNP selection varies depending on the publications and ongoing work continues to discover novel loci for these traits, the SNPs considered here provide a sufficient view of the differences in the measures and including additional SNPs should not materially affect our findings.

Breast cancer

GWAS have detected a relatively large number of low-risk, common variants for breast cancer (http://www.genome.gov/gwastudies). We evaluate here 65 SNPs that appear independently associated with breast cancer using a linkage disequilibrium filter of r2 < 0.2 among Europeans within 100kb of the most associated SNP. Based on the literature we assume that the baseline disease risk = 12% and the sibling recurrence risk (λS) = 2.022; these are consistent with heritability of liability = 60%. Benchmarked against these values, almost all of the risk variants individually explain less than 0.5% of the total variation in heritability, sibling recurrence risk, logRR genetic variance, and pAUC (Figure 3a, Table 2, Supplemental Table 1). As expected, the variants with larger effects on breast cancer (1.3 < RR ≤ 2) explain a larger proportion of these measures (Figure 3a, blue lines). The breast cancer approximate heritability and heritability explained are lower than the other measures, and the sibling recurrence risk is the largest—in agreement with our empirical calculations. All breast cancer variants combined are estimated to explain: 13% of the approximate heritability; 18% of heritability; 19% of the AUC; 21% of the logRR genetic variance; and 22% of the sibling recurrence risk (Figure 3a, Table 2). The similarity among the latter four measures reflects the uniformly low penetrance and high frequency across the risk variants. Moreover, the relatively high proportion of these measures explained reflects the high baseline risk but modest sibling relative risk for breast cancer in the population.

Figure 3. Application of measures to four diseases.

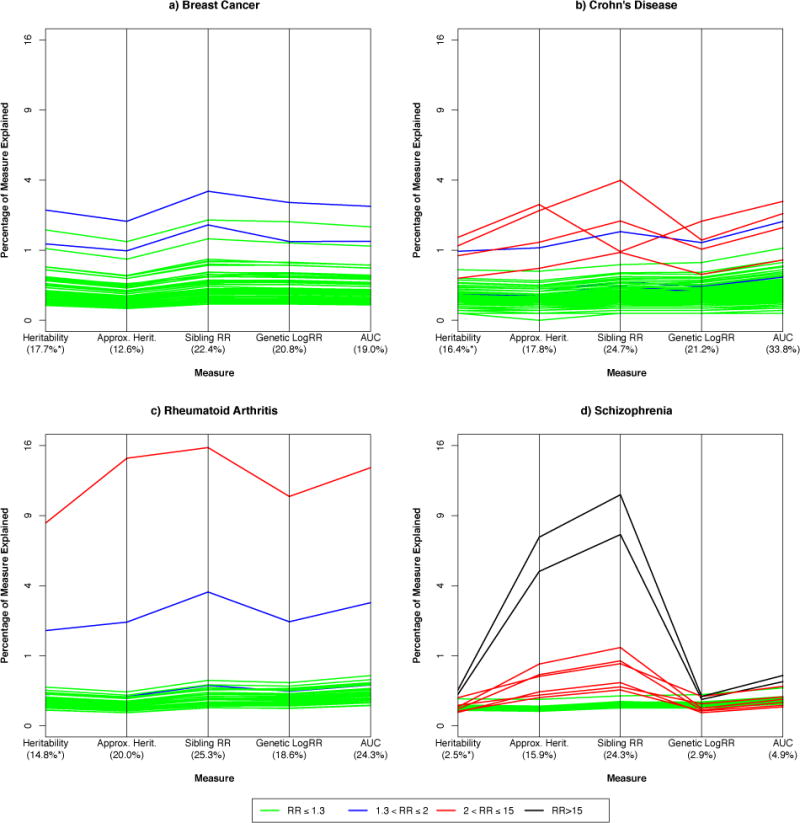
Figure 3

Comparison of commonly used measures for assessing the impact of known risk variants on four diseases: a. breast cancer (65 variants), b. Crohn’s disease (143 variants), c. rheumatoid arthritis (36 variants), and d. schizophrenia (32 variants). The measures are: heritability explained; approximation of heritability explained; sibling recurrence risk explained; logRR genetic variance explained; and the proportion of area under the curve (pAUC). Each line corresponds to an individual risk variant, indicating the percentage of each measure (e.g., total variability) it explains. Lines are different colors depending on the relative risk (estimated by the odds ratio, OR) for each variant. The percentage axes are on a squared scale.

Table 2.

Measures of overall impact of risk variants on different diseases with a range of underlying genetic architectures.a

Disease Risk Variant [i] RAFb RRb Heritability Sibling Recurrence LogRR Area Under the Curve PAF g
h2L[i]c h2L[i]/h2L d h2L[i]apprx/h2L d λS[i] log(λS[i])/log(λS) e VGlog(RR[i])/2log(λS) e AUC[i] pAUC[i] f
Breast Cancer
rs2943559 0.07 1.13 0.07% 0.12% 0.08% 1.001 0.16% 0.14% 0.51 0.13% 1.80%
rs10771399 0.90 1.20 0.22% 0.36% 0.27% 1.003 0.39% 0.45% 0.52 0.39% 28.1%
rs2180341 0.21 1.41 1.49% 2.47% 2.00% 1.02 3.39% 2.83% 0.57 2.65% 15.2%
All variants (m=65) – – 10.70% 17.74% 12.62% 1.17 22.39% 20.78% 0.65 18.98% 95.2%
Crohn’s
rs12103 0.18 1.09 0.03% 0.04% 0.03% 1.001 0.05% 0.05% 0.51 0.07% 3.1%
rs11209026 0.93 2.37 1.02% 1.40% 2.73% 1.023 0.96% 2.00% 0.58 2.88% 80.8%
rs5743293 0.02 3.10 0.82% 1.13% 2.45% 1.10 3.99% 1.31% 0.57 2.32% 9.5%
All variants (m=143) – – 11.85% 16.38% 17.84% 1.78 24.73% 21.16% 0.77 33.8% 100%
Rheumatoid Arthritis
rs5029937 0.04 1.40 0.13% 0.20% 0.17% 1.01 0.33% 0.24% 0.53 0.34% 3.1%
rs2476601 0.10 1.94 1.17% 1.85% 2.19% 1.07 3.65% 2.21% 0.58 3.09% 16.4%
rs6910071h 0.22 2.88 5.30% 8.38% 14.59% 1.33 15.77% 10.72% 0.67 13.6% 50.0%
All variants (m=36) – – 9.34% 14.76% 20.10% 1.57 25.25% 18.60% 0.72 24.3% 99.3%
Schizophrenia
rs171748 0.47 1.08 0.04% 0.05% 0.04% 1.001 0.06% 0.06% 0.52 0.10% 7.0%
rs17504622 0.05 1.24 0.06% 0.08% 0.08% 1.003 0.12% 0.10% 0.52 0.15% 2.3%
16p11.2 CNV (duplication) 0.0003 26.0 0.16% 0.20% 4.85% 1.18 7.45% 0.14% 0.53 0.40% 1.4%
All variants (m=32) – – 2.02% 2.50% 15.92% 1.69 24.26% 2.87% 0.61 4.93% 90.9%

Crohn’s disease

At least 140 modest—and three additional high-risk—variants have been reported as independently associated with Crohn’s disease.23 We assume that the baseline risk of Crohn’s = 0.5%, the sibling recurrence risk = 10.3, and the heritability of liability = 72%24. For the low risk, common variants similar patterns are observed as with breast cancer: heritability < logRR genetic variance < sibling recurrence risk (Figure 3b, Table 2, Supplemental Table 2). For the high-risk variants (2<RR<15), however, there is more variation in these measures, reflecting different combinations of RRs and RAFs (Figure 3b, red lines). Specifically, the common allele of rs11209026—which is the wild-type allele corresponding to the uncommon IL23R coding variant protective for Crohn’s—has a relatively large effect (RR=2.4) but is extremely common (RAF=0.93), a combination that explains the most individual heritability (1.4%) but lower sibling recurrence risk (0.97%) (Table 2). In contrast, rs5743293 has an even larger effect (RR=3.07) but is less common (RAF=0.02) so it explains slightly less heritability (1.1%) but substantially higher sibling recurrence risk (4.0%) (Table 2). Taken together, the 143 Crohn’s risk variants account for approximately 16.4% of the heritability, but explain a larger proportion of the sibling recurrence risk (25%), and an even larger proportion of the AUC (34%) (Figure 3b, Table 2). The higher pAUC estimates across all of the risk variants reflect in part the low baseline risk of disease (0.5%).

Rheumatoid arthritis (RA)

Here we evaluate 36 risk variants reported as being independently associated with RA, and assume a disease risk = 1% and sibling recurrence risk = 6.0, which together are consistent with heritability of liability of 63%.16 Even with so few risk variants we observe a similar proportion of disease explained as for Crohn’s (Figure 3c, Supplemental Table 3). This is due to the substantial impact of a single variant on all of the measures: rs6910071 at the HLA-DRB1E locus (Figure 3c, red line). This variant has a large effect on RA (RR=2.88) and is common (RAF=0.22), so it accounts for an estimated 8% of the heritability, 16% of sibling recurrence risk, 11% of logRR genetic variance, and 14% of the AUC (Table 2). The two-fold range between heritability and sibling recurrence risk leads to a substantial difference in the overall measures of genetic variation explained: 15% of heritability but 25% of sibling recurrence risk. Thus, single common variants of large effect can result in different estimates across these measures. We note that the latest GWAS for RA reports 101 associated loci25.

Schizophrenia

Here we consider 24 GWAS risk variants reported for schizophrenia.26,27. We also consider eight rare copy number variants (CNV) that substantially increase risk of this disease (Figure 3d, Supplemental Table 4).28–30 Here we benchmark using baseline disease risk = 1%, sibling recurrence risk = 8.8, together consistent with heritability of liability of 81%.31 As above, the common low risk variants explain a small percentage of the measures evaluated here (Figure 3d—green lines). By contrast, the CNVs give extremely different results across these measures (Figure 3d, red and black lines). This is especially apparent for the CNVs at 16p11.2 and 22q11, which both are rare (RAF=0.0003) and have very large effects on schizophrenia (RRs>25). Due to their rarity these explain a modest proportion of heritability, genetic variance, and AUC (<0.5%); but their large impact on disease results in much higher proportions of approximate heritability (>5%) and sibling recurrence risk (>7.5%) (Figure 3d, Table 2). Thus, when looking at all 32 schizophrenia variants (24 GWAS and 8 CNVs), estimates of the heritability, sibling recurrence risk, logRR genetic variance, and AUC explained give very different messages about the variants’ impact on this disease. While the variants explain only 2.5–3% of heritability or logRR genetic variance, and 5% of AUC, they are estimated to account for up to five times as much of the approximate heritability and ten times as much of the sibling recurrence risk (Figure 2d, Table 2). The large increase for the approximate heritability was expected as this measure departs from heritability for large RRs. But it was somewhat surprising to see such a large departure between the sibling recurrence risk and logRR genetic variance explained. Although the sibling recurrence risk is generally always larger than the logRR genetic variance, the rarity and extremely large effects for the CNVs results in these two seemingly similar measures giving drastically different results.

Population attributable fraction: a problematic measure

The PAF can also be used to assess the impact of genetic factors on disease, but this measure has a number of limitations.32 The PAF estimates how much disease might be reduced if a risk factor was removed from a population. In our empirical comparisons, the PAF generally gave estimates an order of magnitude larger than the other measures even when the RAF=0.01 and the RR is low. As the RAF increases beyond 0.50, the PAF is the one measure that continues to increase since it directly depends on the RAF. Even for a single variant, as the RAF and RR increase, the PAF can approach the upper bound of 100%. For example, in our breast cancer application a variant (rs10771399) with a large RAF (0.90) but a modest impact on disease (RR=1.20) has a very large PAF (28%) (Table 2). Similarly, if a rare genetic variant is protective for disease, the other (extremely common) allele can give a very large PAF. For example, the protective IL23R coding variant (rs11209026) for Crohn’s (minor allele frequency=0.07%, RR=0.42)23 yields a PAF of an astonishing 81% (i.e., for the risk allele, RAF = 0.93, RR=1/0.42=2.37) (Table 2). By contrast, our schizophrenia application shows how a rare variant (CNV at 16p11.2, RAF = 0.0003) with an enormous effect size (RR=26.0) can have a relatively small PAF (=1.4%) (Table 2). Looking at all of the risk variants combined, the PAF for the four diseases are all > 90% (and 100% with just half of the Crohn’s disease risk variants) (Table 2, Supplemental Tables 1–4).

The combined PAF also exhibits a computational anomaly: the apparent impact of each additional risk variant depends on which variants have already been incorporated into this measure. For example, assume that there are two genetic variants for a disease, and each has an individual PAF of 0.50, and a corresponding combined PAF of 0.75 (=1−(1−0.5)2). An intervention that eliminates the effect of a risk variant at any one of these risk loci would decrease the incidence of disease in the population by half. An intervention at the second locus would further reduce the disease incidence by half in the remaining population, or by a quarter in the original population. The order in which the exposure is removed will impact the magnitude of its apparent effect on the combined PAF. In other words, the apparent impact of a given risk variant on the combined PAF depends on what has already been discovered. Novel variants from less versus more well studied traits will appear to have a larger effect, even if the risk variants have the same magnitude of association and risk allele frequency. Moreover, the combined PAF for multiple low penetrance risk SNPs is not analogous to that obtained by removing a single high-risk environmental exposure from a population, such as reducing smoking to lower rates of lung cancer. The difference here depends not only on the number of risk factors, but also on their penetrance and prevalence, as well as their potential for modification or therapeutic intervention. As the number of known risk loci continues to increase—many of which are quite common—essentially everyone in the population will carry a number of risk alleles. Then any preventative treatment directed at countering the risk loci would have to be applied to almost the entire population.

Measures depend on the baseline disease risk

Of the measures evaluated here, heritability depends on the baseline disease risk (K). In practice, pAUC may be directly estimated, but here it is calculated from the heritability of liability, which is calculated from the reported risk allele frequency and RR and hence also depends on K. For a given RR, these both increase with increasing K as the RR is expressed relative to the risk in the wild type homozygote, which depends on K. The proportion of heritability and pAUC explained is actually lower with increasing K, and so these depend on the value assumed for K. By contrast, the sibling recurrence risk, logRR genetic variance, and PAF do not depend upon K, which is an advantage of these measures since defining K is not always straightforward. Nevertheless, the possible range in K—which can be determined from the literature—will generally be quite small for most diseases. For example, for breast cancer K ranges from 10–15%, for Crohn’s Disease 0.3–0.5%, for RA 1% to 3.6%, and for schizophrenia 0.5–1%. Such ranges may have limited impact on the proportion of heritability and AUC explained, which would thus be relatively robust to misspecification of K. We note that, although sibling recurrence risk, logRR genetic variance, and PAF do not appear to depend on K, there is a built-in assumption that the baseline disease risk is the same in the family data used to calculate sibling risk as in the population used to calculate the contribution to risk from an individual variant, since any relative risk is expressed relative to a baseline. Violation of this assumption may generate misleading results.

To complicate matters further, there is some confusion in the literature about the definition of the baseline risk, reflecting in part the merging of disciplines. Falconer defines K as the incidence of a binary trait12 “or, in the context of human disease, the prevalence”13. Both incidence (i.e., the rate at which new cases occur in a time period) and prevalence (i.e., the proportion of the population that is affected by a disease at any one time) have very precise meanings in epidemiology. In fact, the relevant benchmark for calculation of heritability of liability is the lifetime morbid risk (LMR), the lifetime probability of being affected or lifetime incidence. Most likely the confusion arises because in the context of idealized populations germane to logical thinking in quantitative genetics theory, the parameters prevalence and LMR would be the same. In practice they can be very different. For example, schizophrenia is a disorder with a relatively early age of onset and long average mean life expectancy after diagnosis (although reduced compared to the general population) and so annual incidence, prevalence, and lifetime morbid risk differ considerably at 2.5, 46, and 72 per 10,000, respectively33. As another example, consider motor neuron disease, for which the median age at onset is ~60 years and life expectancy is only 2–5 years. Here, estimates of incidence, prevalence, and lifetime morbid risk of are 0.3, 0.6, and 25 per 10,000, respectively34. For less common disorders, the assessment of LMR (or prevalence or incidence) and risk to relatives are associated with considerable sampling variance, and estimates of heritability of liability and sibling relative risk can vary substantially between studies. Finally, in addition to the baseline disease risk, study design and time-dependent effects could also affect the measures considered here.

Focus on the mean or variance?

Another important point to consider when contrasting the different measures is whether emphasis should be placed on assessing the effect of variants on the mean risk in a population or the genetic variation. Under a simple additive model, the effect on the mean and variance are 2pa and 2p(1−p)a2, respectively (see Table 1, assuming d=0). So a variant at or near fixation (p close to one) can have a relatively large effect on the mean and no effect on variation. Thus, for a given effect size, ‘intervening’ on more common variants may help reduce disease regardless of how much variance is explained. Nevertheless, if there are many risk variants for disease it will be effectively impossible to remove or affect all of them to decrease risk. In this case it does not make sense to use measures (e.g., PAF) that focus on the mean. Instead, we recommend using measures that help understand and explain variation around the mean, which is a key component of genetic risk prediction.

Extensions and additional measures

Our focus is on measures for a limited number of variants, in which we extend the one-locus methods to multiple loci under the assumption of independence among risk variants. Hence, usually the most associated locus from a region is used. Necessarily, this requires some arbitrary threshold on linkage disequilibrium which becomes increasingly unsatisfactory as more associated loci are identified. To overcome this, associated loci can be fit together in a regression analysis and the variance explained accounting for the interdependence between loci can be estimated. If the sample for discovery of the associated loci is used, then there may be some inflation of variance explained compared to if the contribution was estimated from an independent sample drawn from the same population. Genomic risk profile scoring15,35 is one strategy used to test the efficacy of associated SNPs identified in one sample for the contribution to variance in another sample. Briefly, risk alleles and their effect sizes identified by a GWAS conducted in a discovery sample are used to generate genomic profile risk scores (GPRSs) in an independent target sample, using SNPs whose p-values in the discovery sample are below some user-defined threshold of statistical significance. A GPRS is calculated for each individual in the target sample as the sum of the count of risk alleles weighted by the effect size in the discovery sample. The profile score is evaluated through regression of the target phenotype on the GPRS after accounting for other known covariates. The efficacy statistic is frequently Nagelkerke’s R2 or AUC, although expression on the liability scale may be more interpretable36.

To account for the correlational structure among loci and estimate the overall proportion of variance attributable to variants genome-wide, one can use more complex mixed models that jointly fit all variants5,37. Such methods estimate the variance attributable to all variants together, the so-called chip-heritability (or SNP-heritability). One can also partition this variance based on annotation of variants, for example those in loci identified as associated with disease versus all remaining variants. Here, one fits the genetic contribution from known loci as one random effect and the genetic contribution from all other loci as another. Then the ratio of these will provide an estimate of how much known risk variants explain the overall chip-heritability. These different components of heritability explained by genetic variants are illustrated in Figure 4.

Figure 4. Aspects of disease heritability: known, hiding, and missing.

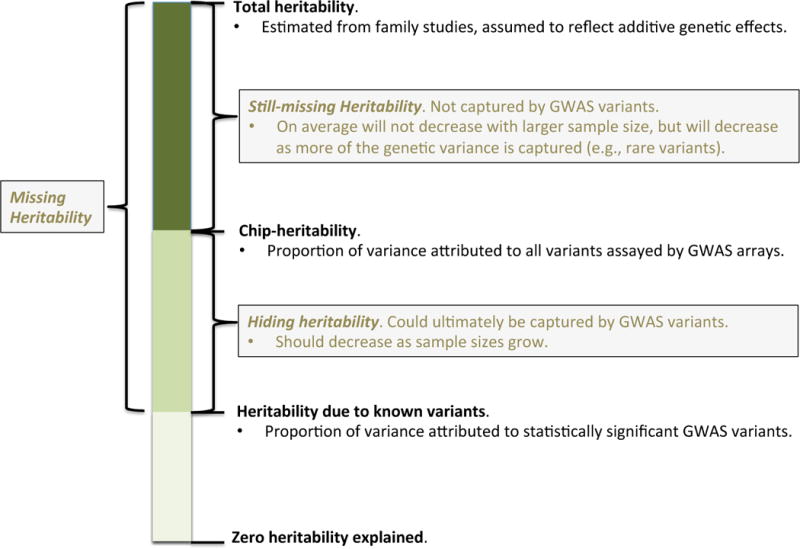
Figure 4

A growing proportion of the total heritability estimated from family studies can be explained by known variants detected in existing genome-wide association studies (bottom). This is one of the key measures considered here. The remaining heritability can be broken into that which is ‘hiding’ versus ‘still missing’. The hiding heritability can be estimated from genome-wide arrays using the Genetic Relatedness Estimation through Maximum Likelihood (GREML) model. The still-missing heritability is that which may remain even after genome-wide association studies, reflecting for example genetic different architectures (e.g., rare variants). Note that the total heritability may be biased upward due to confounding by non-additive genetic or non-genetic factors.

Note that genetic variation as evaluated here is not the only measuring stick for the utility of identified risk variants. A set of variants may have good clinical utility in a particular context (i.e. for some patients) while not explaining much variation in the population and vice-versa. Moreover, a number of measures besides the AUC have been proposed to assess the risk prediction properties of known variants.38 However, since many of these measures do not yield a single, bounded summary value and are context dependent they are not useful for assessing genetic variation per se.

Conclusions and future perspectives

In genetic studies it is a common and useful practice to quantify the contribution to risk of disease of each associated variant, the total for all associated variants, and the additional contribution compared to previous studies. Quantifying such successes across research projects can be hampered if different studies use different measures. Here we present the different measures side-by-side and compare the similarity and differences of these commonly used measures. We provide an online tool to calculate these measures from association study summary statistics.

Although geneticists and epidemiologists often interpret different measures of the impact of risk variants on disease as providing similar information, as shown here they are not interchangeable and can give quite different messages. For common, low risk variants the measures are fairly uniform. But for risk variants with a range of allele frequencies and relative risks, heritability explained is often substantially lower than sibling recurrence risk and logRR genetic variance. For rare, high-penetrance variants, the approximate heritability16 and sibling recurrence risk can be an order of magnitude larger than other measures. The pAUC may be larger or smaller than the other measures depending on the nature of the risk alleles, and the PAF gives much larger estimates than all other measures and has philosophical and computational limitations. As we move into the era of discovering both common and rare variants with varying penetrance for disease, we recommend that investigators focus primarily on the heritability of liability or logRR genetic variance explained since these appear to give estimates that are less sensitive to rare, high risk variants than the other measures considered here.

While the measures of the contribution to risk considered here may have similar underlying intentions, they can be on different scales and include different types and amounts of information. Depending on the measure, the apparent impact of genetic variants can hinge on the assumed overall risks of disease, which despite their apparent simplicity are often difficult to pin down. All measures considered here except the PAF can be expressed relative to a maximum specified by parameters measured in twin or family studies, the “denominator” (for example, total heritability, sibling recurrence risk, max AUC). The denominator measures are themselves difficult to estimate, may be contaminated by non-genetic factors, and for less common diseases are subject to considerable sampling variance39. Moreover, these denominator estimates can be study context dependent due to real differences reflecting environmental factors such as country, age, year and many other complexities of real-life data. Valid comparison of the numerator and denominators requires that samples have been drawn from the same population. Thus, we recommend that investigators undertake sensitivity analyses that explore how their results vary when using a range of assumed underlying risks. The important take home message is that given such uncertainty, the concept of individual loci “explaining” disease is less straightforward than it may appear at first sight and hence all quantifications should be considered in terms of benchmarking rather than as precise measures. In addition, calculating multiple different measures may provide valuable information about how sensitive results are to the underlying assumptions.

Genetic and epidemiologic study designs and analytic methods have nicely coalesced to help investigators detect large numbers of risk variants for complex diseases. However, the different views of these disciplines can shade the interpretation and apparent implications of such findings. By presenting side-by-side the different models and measures used to assess the impact of genetic variants on disease, we highlight their strengths and weaknesses and make a number of recommendations for their use. With this information—and with software provided as an online tool to calculate the measures considered here—one can judge what is truly meant when a study concludes that genetic variants explain or account for a particular proportion of disease.

Supplementary Material

Supplemental Table 1

Supplemental Table 2

Supplemental Table 3

Supplemental Table 4

Online summary.

Acknowledgments

We thank Cara Nolan and Beben Beyamin for developing the companion website, Matthew Robinson for generating the figure in Box 1, Thomas Hoffmann for help plotting Figure 3, and Jinghua Liu for LD filtering of the breast cancer SNPs. This work is supported by NIH grants R01 CA088164 and U01 CA127298 and Australian National Health and Medical Research Council grants 613602, 613601, 1011506, 1050218, 1048853.

Glossary

Area under the receiver operating characteristic curve (AUC)

The receiver operating characteristic curve for a predictor (for example a genetic test) plots the proportion of cases correctly identified by the test versus the proportion of controls incorrectly classified as cases. The AUC indicates the probability that a factor (for example, a genetic risk score) will predict a higher risk of disease in a randomly selected case than in a control

Genetic architecture

The number of risk alleles underlying disease their allele frequency spectrum, effect sizes and mode of interaction

Genetic variance

The variance of trait values that can be ascribed to genetic differences among individuals. The total genetic variance of a trait can be dissected into additive dominance and other components

Genomic risk profile

A predicted measure of genetic risk for individuals constructed from a set of loci whose risk alleles and their effect sizes have been estimated in an independent sample.

Heritability

The proportion of phenotypic variation in a population that is attributable to genetic variation among individuals.

Liability of disease

An underlying or latent continuous variable such that those with a liability above a threshold are considered diseased. The quantitative trait of liability reflects both genetic and environmental factors.

Linkage disequilibrium

A measure of whether alleles at two loci coexist in a population in a non-random fashion. Alleles that are in linkage disequilibrium are found together on the same haplotype more often than would be expected by chance.

Mendelian locus

A genetic locus the alleles of which have discrete effects on the phenotype which obeys Mendel’s laws of segregation and independent assortment

Overall disease risk

The lifetime probability that an individual is affected by disease.

Population attributable fraction

Also called the population attributable risk. For a given disease risk factor and population, the population attributable risk is the fraction by which the incidence rate of the disease in the population would be reduced if the risk factor was eliminated

Sibling recurrence risk

The ratio of the probability that a sibling of an individual affected by a disease will also be affected compared to the risk of disease in the general population.

Biographies

John Witte is Professor of Epidemiology and Biostatistics and Associate Director of the Institute for Human Genetics at the University of California, San Francisco. His research program encompasses a synthesis of methodological and applied genetic epidemiology, with the overall aim of deciphering the mechanisms underlying complex diseases and traits. His current methods work is focused on the design and statistical analysis of next-generation sequencing and genetic association studies. He is applying these methods to studies of cancer, birth defects, and pharmacogenomics.

Peter Visscher is Professor of Quantitative Genetics at the University of Queensland, and a senior principal research fellow of the National Health and Medical Research Council in Australia. His research is at the interface of quantitative genetics, statistical genetics, population genetics, human genetics, animal genetics, evolution, bioinformatics and genetic epidemiology. His current research focuses on estimation and dissection of complex-trait variation in human populations, through the development of new statistical genetics methods for estimation and prediction, and applications to quantitative traits and disease in human populations.

Naomi Wray is Professor of Psychiatric Genetics at the University of Queensland and a senior research fellow of the National Health and Medical Research Council in Australia. Her Ph.D. and early postdoctoral work was on the prediction of rates of inbreeding in populations undergoing selection. Currently, she leads a research programme in psychiatric genomics. Recent research has focused on the application of quantitative genetics methods to psychiatric disorders, including the estimation of genetic variation in liability to disease and prospects and limitations to make predictions of individual risk from genetics data.

Footnotes

Further Information

Companion website for calculating measures considered here to quantify the contribution of disease risk variants, INDI-V online tool: cnsgenomics.com/software/INDI-V

Competing interests

The authors declare no competing interests.

References

Explores the relationship between heritability on disease and liability scales

A formal derivation of the relationship between disease risk in relatives and heritability plus a thoughtful exploration of scenarios and caveats

Explains variance explained by a single locus on the disease and liability scale

A clear presentation of the log relative risk model

Considers the limitations of the population attributable fraction

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Table 1

Supplemental Table 2

Supplemental Table 3

Supplemental Table 4