A Comparison between Accelerated Failure-time and Cox Proportional Hazard Models in Analyzing the Survival of Gastric Cancer Patients (original) (raw)

. 2015 Aug;44(8):1095–1102.

Abstract

Background:

Gastric cancer is the one of the most prevalent reason of cancer-related death in the world. Survival of patients after surgery involves identifying risk factors. There are various models to detect the effect of risk factors on patients’ survival. The present study aims at evaluating these models.

Methods:

Data from 330 gastric cancer patients diagnosed at the Iran cancer institute during 1995–99 and followed up the end of 2011 were analyzed. The survival status of these patients in 2011 was determined by reopening the files as well as phone calls and the effect of various factors such as demographic, clinical, treatment, and post-surgical on patients’ survival was studied. To compare various models of survival, Akaike Information Criterion and Cox-Snell Residuals were used. STATA 11 was used for data analyses.

Results:

Based on Cox-Snell Residuals and Akaike Information Criterion, the exponential (AIC=969.14) and Gompertz (AIC=970.70) models were more efficient than other accelerated failure-time models. Results of Cox proportional hazard model as well as the analysis of accelerated failure-time models showed that variables such as age (at diagnosis), marital status, relapse, number of supplementary treatments, disease stage, and type of surgery were among factors affecting survival (P<0.05).

Conclusion:

Although most cancer researchers tend to use proportional hazard model, accelerated failure-time models in analogous conditions — as they do not require proportional hazards assumption and consider a parametric statistical distribution for survival time — will be credible alternatives to proportional hazard model.

Keywords: Accelerated failure-time models, Akaike information criterion, Cox proportional hazard model, Cox-Snell residuals, Gastric cancer

Introduction

Gastric cancer is the one of the most prevalent reason of cancer-related death in the world. Now, gastric cancer contains 10% of cancers in the world and is one of the most common kinds of cancers (1). According to the statistics of Iran Cancer Institute, gastric cancer is the third most common cancer between Iranian women after breast cancer and the most common cancer between Iranian men (2–6).

Gastric cancer is usually treated with surgery, radiotherapy, or chemotherapy. The elementary treatment of gastric cancer in initial stages is surgery; so it is considered as the prime treatment for cancer. Chemotherapy and radiotherapy will be used as supplementary treatments, if necessary. In advanced stages of the disease, surgical procedures, radiotherapy and chemotherapy are also used for the treatment but they do not usually achieve good outcomes. The odds of patients’ complete recovery depend on the surgery but the time when the disease passes through the mucous membrane, it is possible lymph nodes Metastases and relapse in spite of the total surgery, which has been performed on the patient (7, 8).

One of the most important prognostic indicators which is considered after surgery and for patients with gastric cancer is an increase in patients’ survival rate especially the 5-year survival rate. Gastric cancer is difficult to treatment unless cancer is diagnosed at an elementary stage. Unfortunately, because early gastric cancer causes few symptoms, the cancer is usually advanced when the diagnosis is made. So conventional treatment such as surgery, chemotherapy and radiation therapy are not impressive in increasing the patients’ survival rate (9, 10). For this reason, the 5-year survival rate for gastric cancer after surgery is reported to be less than 10% (11–15). The increase in these patients’ survival rate after surgery involves identifying various factors, including individual, clinical, diagnostic and therapeutic.

There are various statistical methods to assess the effects of various factors on survival of cancer patients including parametric and Cox semi-parametric regression models. These models are divided into two basic categories: Proportional Hazard (PH) model and Accelerated Failure-time (AFT) model. In the proportional hazard regression model, the effect of covariates is obtained on the hazard function. In this case, if baseline hazard is considered parametric, one of the Weibull, exponential and Gompertz models will be achieved. If the baseline hazard is considered non-parametric, the Cox proportional hazard model will be obtained. In the accelerated failure-time regression model, the effect of covariates on the logarithm of the survival time is assessed. The obtained models in this case include generalized gamma, Log-logistic, Log-normal, Weibull and exponential. Weibull and exponential are the only parametric regression models which have both a proportional hazards and an accelerated failure-time representation.

The proportional hazard model does not need to consider a specific probability distribution for the survival time; therefore, it is the most helpful model in analyzing survival data. But the efficiency of the model is severely dependent to proportional hazards assumption and, for this reason, The Cox model is often called proportional hazards model. In occasions where the proportional hazard model is not acceptable, estimates derived from Cox model will lead to an improper fitting of the model and incorrect inferences (16–22). Accelerated failure-time models are especially important in such situations. These models—due to having a parametric distribution for the survival times—make statistical inference more accurate and lead to an proper fitting of the model (23).

Factors affecting the survival of cancer patients are often identified by Cox proportional hazard model (14, 24–30). Neither have these studies generally tested proportional hazards assumption nor did they try to identify a proper model as an alternative to proportional hazards model.

In this study in addition to comparing various survival models as well as identifying an alternative accelerated failure-time model for the Cox proportional hazards model Akaike Information Criterion (AIC) and Cox-Snell Residuals have been used to assess various survival models.

Materials and Methods

In this historical study, 330 patients with Gastric cancer with the following data were studied: 1) the patients had been hospitalized and had undergone surgery during 1995–99 in surgical wards of Iran Cancer Institute 2) these patients had information in the archives of the hospital, and in their files their phone numbers and addresses were available for further follow-ups. The survival status of these patients in 2011 was determined by reopening the files as well as phone calls. The survival time of these patients after surgery was determined and those patients who were still alive at the end of study time or the ones whose information were not available after a specific time were considered right-censored.

The effects of demographic variables such as Age, Sex, and Marital status, and clinical data of the disease including Lymph node metastases, Liver metastases, Distance metastases; Disease stage (I-II-III-IV); and Type and extent of gastrectomy (Total-Subtotal-Distal-Partial-Proximal) as well as post-surgical and treatment variables including relapse and the number of supplementary treatments (surgery - radiotherapy - chemotherapy or a combination of them) on patients’ survival were evaluated and compared among various models.

To compare different survival models, Akaike Information Criterion (AIC) and Cox-Snell Residuals were applied. Cox-Snell Residuals is a graphical scale for evaluating the fitness of Proportional hazard and accelerated failure-time models; the short deviation of residuals from the straight line through the origin with a slope of 1, the more appropriate fitness of the survival model (18, 20, 31). Graphical methods are often associated with visual error. For a better decision, thus, Akaike information criterion (AIC) can be used along with Cox-Snell residuals. Akaike information criterion (AIC) is used to measure the goodness of models’ fitness, and the smaller it is, the better it is (17, 18, 32–34). Note that a direct comparison of the AIC cannot be made between parametric models and semi-parametric model because the likelihoods differ. Akaike information criterion (AIC) for the models used in this study has been calculated according to the following formula:

where p is the number of model parameters and L is the model likelihood function (17, 34, 35). The smaller the Akaike information criterion (AIC) is, the more efficacious the model will be in identifying the risk factors (34). Moreover, in order to facilitate the comparison of the variables’ variances used in the model in this study, the standardized variability, calculated as sv=se(β^)β^, was used to standardize the variance of estimated parameters (in this equation se(β̂) is the standard error of parameter and β̂ is the coefficient of parameter in the survival model). To determine the disease stage, TNM (7th edition) was employed (36). STATA 11 software was used for all analyses and the significance level was set at 5%.

Results

Overall, 228 patients were male (69.1%) and 315 (95.45%) were married. The mean of age was 65.41 ± 10.56 years for women and 65.7 ± 11.22 years for men. Two hundred thirty-nine patients (72.4%) died by the end of the study and the rest were right censored. The survival median time of these patients was 16.33 months. The patients’ five-year survival rate was 0.21.

Totally, 192 patients (58.2%) had metastases out of which 12.5% suffer from liver metastases and 66.67% suffered from lymph nodes metastases. Forty-three patients (13.03%) had a relapse and 8.48% had undergone Proximal Gastrectomy, 8.79% had undergone Partial Gastrectomy, 3.03% had undergone Distal Gastrectomy, 27.27% had undergone Subtotal Gastrectomy and 52.42% of patients had undergone Total Gastrectomy. The analysis of disease stage revealed that 58.79% of patients were in stage IV, 16.36% in stage III, 18.18% in stage II and 6.67% stage I of disease. 20.3% of patients had not received any supplementary treatments whereas, 23.03% of the patients had received one supplementary treatment, 30.61% of the patients had received two supplementary treatments and 26.06% of the patients had received three supplementary treatments.

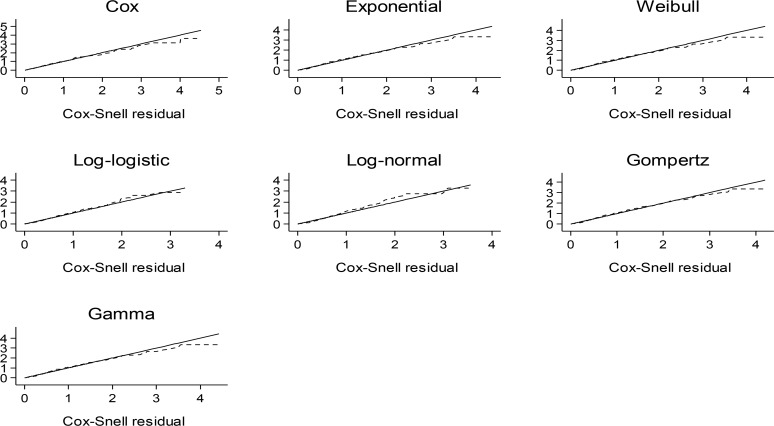
Referring to the figure analysis of Cox-Snell residuals for accelerated failure-time models and Cox proportional hazard model represents approximately equal fitness of accelerated failure-time models compared with proportional hazard model (Fig. 1).

Fig. 1:

Fig. 1:

The Cox-Snell residuals in the considered Cox proportional hazard and accelerated failure-time models

Among accelerated failure-time models, the exponential, Gompertz and Weibull proved better fitness to the data. Akaike information criterion confirms these results too (Table 1).

Table 1:

The comparison results of the risk factors between the Cox proportional hazard and accelerated failure-time models (First category is considered as a reference group).

Risk factors COX HR(SV) Exponential RR(SV) Weibull RR(SV) Log-logistic RR(SV) Log-normal RR(SV) Gompertz HR(SV) Gamma RR(SV)
Sex
Male
Female 1.02(7.69) 1.02(8.49) 1.02(8.45) 1.04(5.68) 0.90(1.22) 1.02(8.23) 1.02(8.35)
Age 1.03(0.22) 1.03(0.22) 1.03(0.22) 1.04(0.26) 1.02(0.30) 1.03(0.22) 1.03(0.22)
Marriage
Married
Single 0.39(0.48) 0.38(0.45) 0.38(0.45) 0.29(0.48) 0.49(0.48) 0.39(0.46) 0.38(0.45)
Relapse
No
Yes 1.52(0.47) 1.49(0.49) 1.49(0.49) 1.65(0.57) 1.44(0.60) 1.48(0.50) 1.50(0.49)
Metastases
No
Yes 1.08(4.32) 1.05(6.57) 1.05(6.73) 1.88(1.81) 1.16(2.28) 1.06(6.87) 1.12(6.95)
Lymph nodes Metastases
No
Yes 1.07(2.27) 1.07(2.17) 1.07(2.22) 1.46(1.31) 1.32(1.15) 1.08(2.05) 1.16(2.27)
Liver Metastases
No
Yes 1.59(0.85) 1.59(0.84) 1.60(0.82) 1.66(1.10) 1.20(1.86) 1.55(.89) 1.61(0.82)
Distance Metastases
No
Yes 1.72(0.57) 1.72(0.57) 1.74(0.56) 1.57(0.99) 1.24(1.30) 1.68(0.60) 1.74(0.56)
Stage
I
II 1.27(1.40) 1.27(1.37) 1.28(1.36) 1.45(1.34) 1.16(1.85) 1.26(1.42) 1.28(1.36)
III 2.13(0.44) 2,12(0.44) 2.13(0.44) 2.41(0.56) 1.55(0.64) 2.07(0.46) 2.14(0.44)
IV 1.85(1.28) 2.01(1.13) 2.02(1.12) 1.60(2.38) 1.34(2.58) 1.96(1.17) 2.03(1.12)
Number of Supplementary Treatment
0
1 0.53(0.32) 0.54(0.33) 0.54(0.33) 0.27(0.25) 0.39(0.19) 0.54(0.34) 0.54(0.34)
2 0.29(0.16) 0.30(0.17) 0.30(0.17) 0.12(0.14) 0.24(0.12) 0.31(0.17) 0.30(0.18)
3 0.22(0.15) 0.24(0.15) 0.24(0.15) 0.10(0.12) 0.19(0.11) 0.24(0.16) 0.24(0.16)
Type of Gastrectomy
Total
Subtotal 1.08(2.10) 1.06(2.68) 1.06(2.67) 1.07(3.57) 0.96(3.50) 1.06(2.61) 1.06(2.66)
Distal 0.49(0.62) 0.48(0.59) 0.48(0.59) 0.56(1.12) 0.68(0.89) 0.50(0.62) 0.48(0.59)
Partial 0.88(1.82) 0.89(1.97) 0.88(1.94) 0.73(1.15) 0.85(1.28) 0.89(2.09) 0.88(1.94)
Proximal 0.54(0.42) 0.55(0.43) 0.54(0.42) 0.52(0.57) 0.61(0.45) 0.56(0.44) 0.54(0.42)
AIC 2351.65** 969.14 971.10 973.74 1023.24 970.70 973.10

Furthermore, Table 1 shows Cox proportional hazard model and accelerated failure-time models analyses of risk factors according to the standardized variations, hazard ratio (HR) and relative risk (RR) for all variables.

According to Akaike information criterion, the exponential (AIC=969.14) and Gompertz (AIC=970.70) models are more efficient than other models. The results of Cox proportional hazard model and accelerated failure-time models (except log-logistic and log-normal) do not show much difference in terms of variables’ significance. Although the hazard rate in proportional hazard model is virtually the same as the results of accelerated failure-time models, the exponential and Gompertz models had better results according to Akaike information criterion.

Results of Cox proportional hazard model and analyses of exponential, Weibull, Gompertz, and gamma accelerated failure-time models showed that variables of age (at diagnosis), marital status, relapse, number of supplementary treatments, disease stage, and type of surgery are among the effective factors on the survival of patients with gastric cancer (P <0.05). Unlike the similarity between proportional hazard model results and the results of accelerated failure-time models, the analysis of log-normal and log-logistic accelerated failure-time models also revealed that only variables of age (at diagnosis), marital status, relapse, and number of supplementary treatments were among the effective factors on the survival of patients with gastric cancer (P <0.05). Disease stage and type of surgery were not identified as risk factors by these models. Variables of sex, metastases, lymph node metastases, liver metastases, and distance metastases did not have any significant effect on patients’ survival in any of the studied models.

Discussion

To investigate the effect of different variables on the survival of cancer patients, most cancer researchers tend to use proportional hazard proportional hazard model rather than accelerated failure-time models. A systematic review on cancer journals indicates that only 5% of studies in which proportional hazard model was used, investigated the required assumptions for this model (37). The lack of proportional hazards assumption causes the results of model to be unreliable and biased; therefore, accelerated failure-time models such as generalized gamma, Log-logistic, Log-normal, Gompertz, Weibull and exponential can be better choices in such circumstance. As accelerated failure-time models consider a statistical distribution for survival time and they do not need proportional hazards assumption (PH), they are suitable alternatives to proportional hazard model.

In this study, the results of Cox proportional hazard model and accelerated failure-time models were compared to analyze the survival of patients with gastric cancer who had undergone surgery.

To compare these models, Cox-Snell residuals and Akaike information criterion (AIC) were used. The analysis of Cox-Snell residuals (Fig. 1) revealed that accelerated failure-time models and Cox proportional hazard model had approximately equal fitness. Among accelerated failure-time models, exponential, Weibull and Gompertz were good choices. Moreover, the analysis of models based on Akaike information criterion (AIC) (Table 1) showed that the exponential and Gompertz models were the best alternatives for Cox proportional hazard model. There was not a significant difference between accelerated failure-time models and proportional hazard model in identifying factors affecting the survival of patients with gastric cancer except log-normal and log-logistic which showed higher AIC than other accelerated failure-time models.

The analyses of accelerated failure-time models and proportional hazard model showed that variables of age (at diagnosis), marital status, relapse, number of supplementary treatments, disease stage, and type of surgery were among the effective factors on the survival of patients with gastric cancer (P <0.05). These results are consistent with the results of many studies in this field (13, 14, 30, 38, 39). Moreover, variables of sex, metastases, lymph node metastases, liver metastases, and distance metastases did not have any significant effect on patients’ survival in any of the studied models. Based on the criteria presented in this study (AIC & Cox-Snell), exponential and Gompertz models are the best parametric alternatives for Cox proportional hazard model. This issue is consistent with most studies conducted on patients with gastric cancer (40–42). In some studies, however, Weibull model has been considered as the good model but as exponential model is a specific case of Weibull; again, the results of these studies are confirming the results of the present research (40).

Conclusion

Although using Cox proportional hazard model has come to the fore by most researchers in medical and cancer fields, results of accelerated failure-time models have often been more valid and have had minor bias since these models have better fitness in similar conditions due to a specific statistical distribution for the survival time and their not having need to PH assumption. Accelerated failure-time models will also be reliable alternatives to Cox proportional hazard model where this assumption is not made. In addition, accelerated failure-time models may offer some benefits.

Based on asymptotic results, accelerated failure-time models lead to more efficient parameters than proportional hazard model. With a reduction in sample size, relative efficiency may further change in favor of accelerated failure-time models. When empirical information is adequate, accelerated failure-time models can prepare some insights into the form of the baseline hazard.

Ethical considerations

Ethical issues (including plagiarism, informed consent, misconduct, data fabrication and/or falsification, double publication and/or submission, and redundancy) have been completely observed by the authors.

Acknowledgements

The authors gratefully acknowledge the financial support for this work provided by Tehran University of Medical Sciences. The authors declare that there is no conflict of interests.

References