Unraveling the drivers of MERS-CoV transmission (original) (raw)

Significance

Since it was discovered in 2012, Middle East respiratory syndrome coronavirus (MERS-CoV) has infected more than 1,700 persons, one-third of whom died, essentially in the Middle East. Persons can get infected by direct or indirect contact with dromedary camels, and although human-to-human transmission is not self-sustaining in the Middle East, it can nonetheless generate large outbreaks, particular in hospital settings. Overall, we still poorly understand how infections from the animal reservoir, the different levels of mixing, and heterogeneities in transmission have contributed to the buildup of MERS-CoV epidemics. Here, we quantify the contribution of each of these factors from detailed records of MERS-CoV cases from the Kingdom of Saudi Arabia, which has been the most affected country.

Keywords: epidemic dynamics, mathematical modeling, zoonotic virus, animal reservoir, outbreaks

Abstract

With more than 1,700 laboratory-confirmed infections, Middle East respiratory syndrome coronavirus (MERS-CoV) remains a significant threat for public health. However, the lack of detailed data on modes of transmission from the animal reservoir and between humans means that the drivers of MERS-CoV epidemics remain poorly characterized. Here, we develop a statistical framework to provide a comprehensive analysis of the transmission patterns underlying the 681 MERS-CoV cases detected in the Kingdom of Saudi Arabia (KSA) between January 2013 and July 2014. We assess how infections from the animal reservoir, the different levels of mixing, and heterogeneities in transmission have contributed to the buildup of MERS-CoV epidemics in KSA. We estimate that 12% [95% credible interval (CI): 9%, 15%] of cases were infected from the reservoir, the rest via human-to-human transmission in clusters (60%; CI: 57%, 63%), within (23%; CI: 20%, 27%), or between (5%; CI: 2%, 8%) regions. The reproduction number at the start of a cluster was 0.45 (CI: 0.33, 0.58) on average, but with large SD (0.53; CI: 0.35, 0.78). It was >1 in 12% (CI: 6%, 18%) of clusters but fell by approximately one-half (47% CI: 34%, 63%) its original value after 10 cases on average. The ongoing exposure of humans to MERS-CoV from the reservoir is of major concern, given the continued risk of substantial outbreaks in health care systems. The approach we present allows the study of infectious disease transmission when data linking cases to each other remain limited and uncertain.

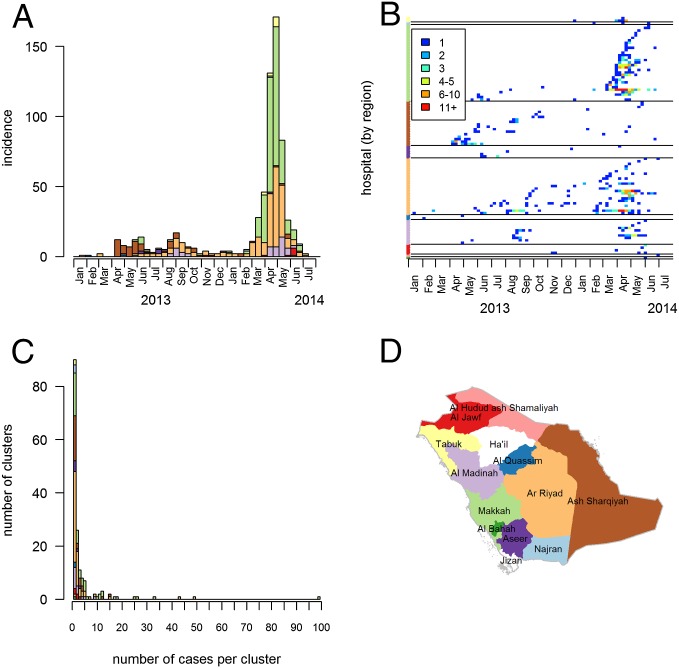
Despite the occurrence of 1,728 laboratory-confirmed cases and 624 deaths (1) since the virus was first isolated in 2012, transmission of the Middle East respiratory syndrome coronavirus (MERS-CoV) remains poorly understood. Dromedary camels play a role in transmission (2), but the nature and extent of human exposure to camels is not well defined. Despite multiple reintroductions from the reservoir, there has been no sign of the continuous exponential growth in human case numbers that is the typical signature of the start of a pandemic. Furthermore, most infections have occurred in Middle Eastern countries on the Arabian Peninsula, with ∼75% of cases reported by the Kingdom of Saudi Arabia (KSA). Spatial expansion to other areas has been limited. Although these simple observations suggest that MERS-CoV is not presently capable of self-sustaining transmission in humans (at least in the Middle East), large clusters of human cases, typically in health care settings, have been documented (3). Notably, in March to May 2014, KSA experienced a large, rapidly growing outbreak affecting many hospitals and spanning multiple regions of the country (Fig. 1) (4, 5).

Fig. 1.

Fig. 1.

The epidemic of MERS-CoV in KSA between January 1, 2013, and July 31, 2014. (A) Biweekly number of MERS-CoV laboratory-confirmed infections per region. (B) Weekly number of cases in the different hospitals and over time. The color of dots indicates the weekly number of cases. Colors on the y axis indicate the region of the hospital. (C) Distribution of the number of cases per cluster. (D) Map of the KSA. Colors in A, B, and C match the color of regions in D.

A number of studies have attempted to characterize the human-to-human transmission of MERS-CoV and the contribution of the reservoir from the analysis of specific features of the epidemic—for example, cluster sizes (6), epidemic time series in clusters (7), transmission trees in few large clusters (8, 9), or the proportion of MERS-CoV cases with no known human source of infection (5, 10)—sometimes restricted to one or more large outbreaks (5, 8, 9). Such an approach simplifies inference but comes with a number of limitations. First, by restricting analysis to simple features of the epidemic, strong assumptions about the underlying transmission process are often required, such as assuming that cases with no known source of infection are infected by the reservoir (5–7, 10), that clusters are closed epidemics independent of each other (6, 7, 10), or that transmission rates are constant over time (6). In addition, analysis restricted to large outbreaks may bias estimates of human-to-human transmission upward. A coherent and holistic picture of MERS-CoV epidemic dynamics therefore remains elusive, reflected, for instance, in published estimates of the proportion of infections due to the animal reservoir varying from a few percent (5) to 55% (10).

Here, to obtain a comprehensive picture of MERS-CoV transmission dynamics, we developed a general framework to analyze detailed epidemiological records of all MERS-CoV cases reported between January 1, 2013, and July 31, 2014 in KSA, a time frame that included the largest outbreaks of MERS-CoV reported to date. The framework makes it possible to relax the simplifying assumptions often made in past work about the epidemic process (e.g., independence of clusters, unknown sources of infection being interpreted as infections from the reservoir). It builds on methods used to reconstruct transmission trees from case data (11, 12) but greatly expands them by allowing estimation of the generation time distribution, multiple and heterogeneous levels of transmission, and changing risks of infection from a zoonotic reservoir.

Results

Between January 1, 2013, and July 31, 2014, 681 MERS-CoV patients were identified in KSA. The first outbreak was reported in the region of Ash Sharqiyah in April to May 2013 followed by an outbreak in Riyadh in July to September 2013 (Fig. 1). The largest outbreak in March to May 2014 principally affected Makkah region (mostly Jeddah) and Riyadh. Combined, these two regions accounted for 78% (n = 294 in Makkah region and 235 in Riyadh) of cases. Fig. 1_B_ shows how cases clustered over space, time, and according to the hospital (n = 98) in which they were treated, diagnosed, and/or tested. We identify 162 clusters, where a cluster is defined as a group of cases who were treated, diagnosed, and/or tested in the same hospital, with a time lag between two consecutive cases of at most 21 d. The distribution of cluster sizes is highly skewed (Fig. 1_C_).

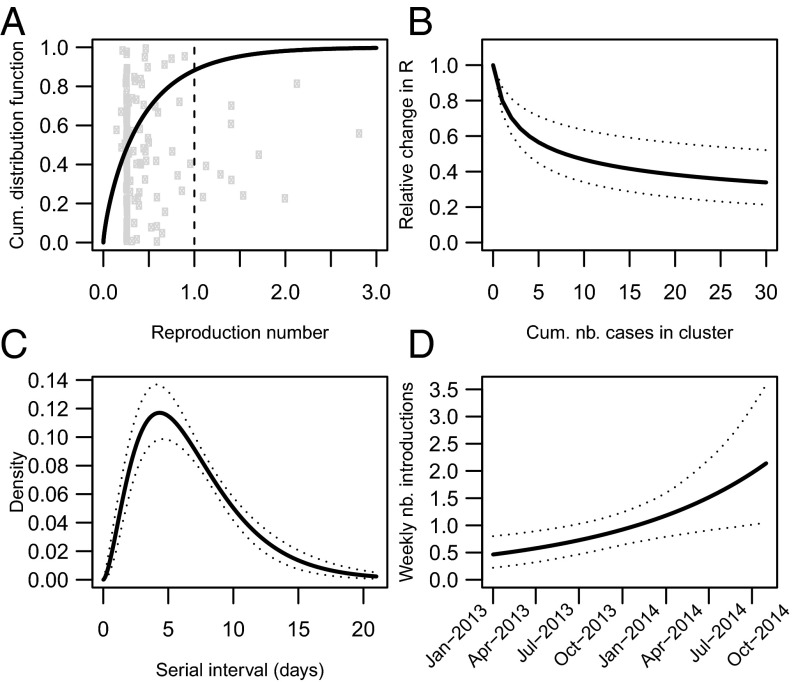
We were able to characterize the overall pattern of transmission by estimating the within-cluster reproduction numbers (i.e., average number of secondary cases generated by a case in their cluster), the within-region reproduction number (i.e., average number of secondary cases in other clusters of the region), and the between-region reproduction number (i.e., average number of secondary cases in other regions) (Materials and Methods). Fig. 2_A_ shows the distribution of the initial within-cluster reproduction number, RC. It has a mean of 0.45 [95% credible interval (CI): 0.33, 0.58] but with substantial heterogeneity between clusters (SD: 0.53; 95% CI: 0.35, 0.78). The initial within-cluster reproduction number is over 1 in 12% (95% CI: 6%, 18%) of clusters. We can also assess where each cluster falls within this distribution (Fig. 2_A_). We find that the within-cluster reproduction number at a point in time is a declining function of the cumulative number of cases that have accrued in the cluster by that time (Fig. 2_B_). We estimate that, after 10 cases, the within-cluster reproduction number is on average 47% (95% CI: 34%, 63%) of its initial value (Fig. 2_B_).

Fig. 2.

Fig. 2.

Transmission characteristics of MERS-CoV in KSA. (A) Cumulative distribution function of the within-cluster reproduction number at the start of a new cluster (black line). Gray dots show the posterior mean for each cluster. (B) Variations in the within-cluster reproduction number as a function of the cumulated number of cases in the cluster (solid line: posterior mean; dotted lines: 95% CI). (C) Distribution of the serial interval of MERS-CoV (solid line: posterior mean; dotted lines: 95% CI). (D) Weekly number of introductions from the reservoir during the study period (solid line: posterior mean; dotted lines: 95% CI).

The within-region reproduction number RR is estimated at 0.24 (95% CI: 0.19, 0.29). This suggests that clusters of the same region are not necessarily closed epidemics independent of each other but that there can be substantial transmission between them. In contrast, clusters from different regions appear to be largely independent of each other (between-region reproduction number RO: 0.05, 95% CI 0.02, 0.09).

We estimate that the serial interval (delay between symptom onset in a case and symptom onset in the persons they infect) of MERS-CoV has a mean of 6.8 (95% CI: 6.0, 7.8) days and a SD of 4.1 (95% CI: 3.4, 5.0) days (Fig. 2_C_).

We estimate that the weekly number of introductions from the reservoir grew by approximately fourfold during the study period: from 0.5 (95% CI: 0.2, 0.8) reported cases per week infected by the reservoir in early 2013 to 2.1 (95% CI: 1.0, 3.6) in mid-2014 (Fig. 2_D_).

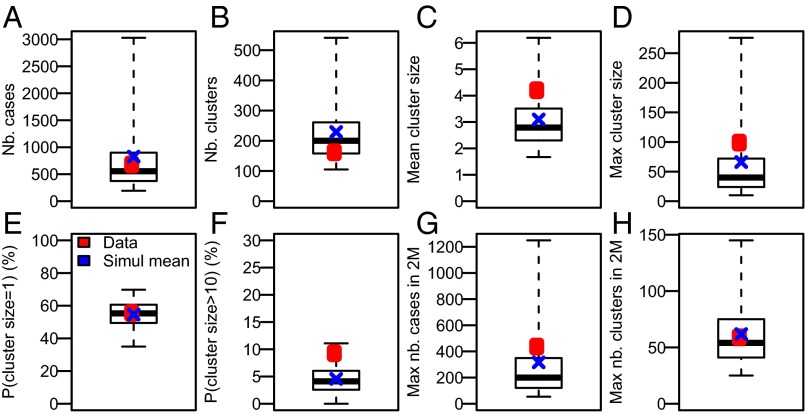
We explore the ability of our model to reproduce MERS-CoV epidemic dynamics in KSA by using the model to simulate epidemics from January 1, 2013. We find that the model satisfyingly reproduces the distribution of the number of cases (Fig. 3_A_), of the number of clusters (Fig. 3_B_), and of the size of these clusters (Fig. 3 C–F). The model can also generate explosive outbreaks over short time periods similar to what was observed in Spring 2014 (Fig. 3 G and H).

Fig. 3.

Fig. 3.

Model adequacy. Observed values (red dot) and values predicted by the model from 10,000 simulations (blue cross: mean; black boxplot gives quantiles 2.5%, 25%, 50%, 75%, 97.5%). (A) Number of cases. (B) Number of clusters. (C) Mean cluster size. (D) Maximum cluster size. (E) Probability that a cluster is of size 1. (F) Probability that the size of a cluster is larger than 10. (G) Maximum number of cases over a 2-mo period. (H) Maximum number of clusters over a 2-mo period.

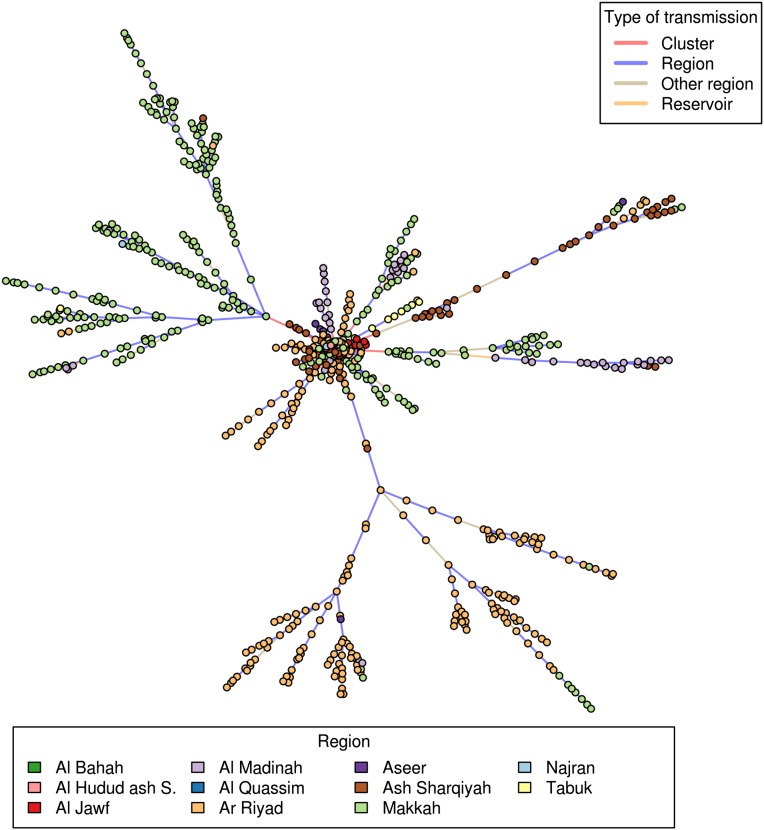
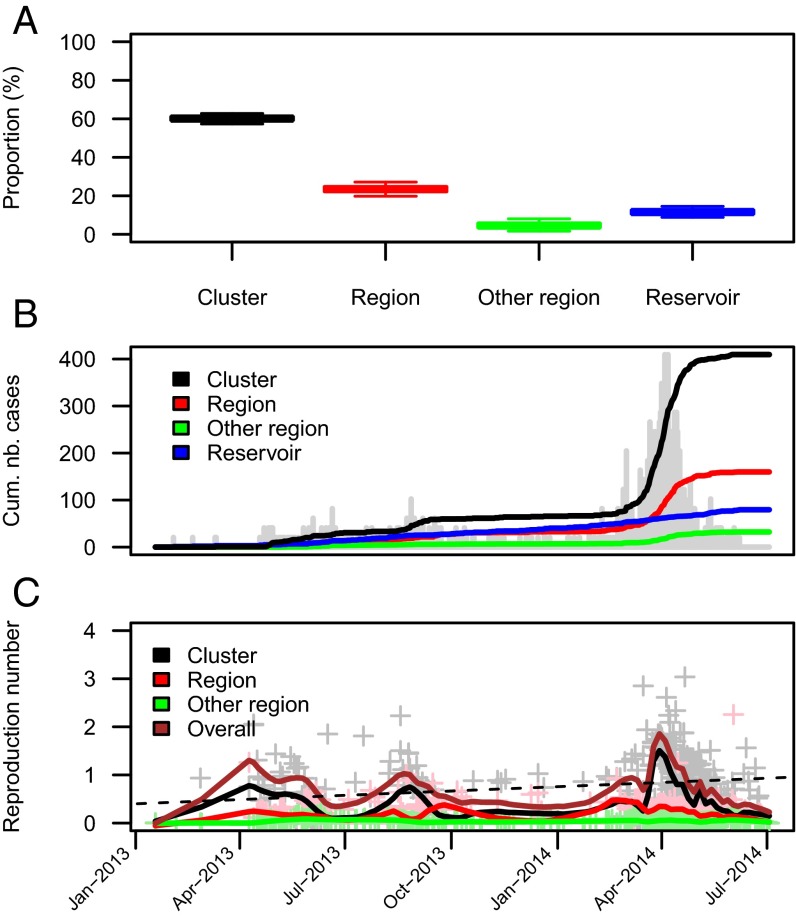
We can also use the model to reconstruct the transmission tree and probabilistically determine the likely source of infection of each case. Fig. 4 shows an example of an inferred transmission tree. Fig. 5 presents summary statistics calculated from a sample of 500 such trees. We estimate that 12% (95% CI: 9%, 15%) of the cases were infected via exposure to the animal reservoir, 60% (95% CI: 57%, 63%) were infected in their cluster, 23% (95% CI: 20%, 27%) were infected by cases from other clusters in their region, and only 5% (95% CI: 2%, 8%) from cases of other regions (Fig. 5_A_). This finding is illustrated in Fig. 4 where the different regional outbreaks appear to be largely independent. In particular, there is very little transmission between Riyadh and Makkah regions. Fig. 5_B_ shows the time series of the reconstructed cumulative number of cases by source of infection. It suggests that infections from the reservoir have occurred repeatedly over the study period. In contrast, within-cluster infections are concentrated in time during three substantial outbreaks that occurred in May 2013, September 2013, and March to May 2014. The last of these outbreaks involved by far the largest contribution of within-cluster and within-region transmission. These three peaks of transmission are apparent in Fig. 5_C_, which presents reconstructed trends in individual reproduction numbers. The smoothed overall reproduction number peaked at 1.9 in March to April 2014. Fig. 4 also shows that, although most introductions generated few secondary infections, a small number of them had a disproportionate contribution to the epidemic. We estimate that three zoonotic infections were responsible for 464 (95% CI: 376, 532) MERS-CoV cases during this time period, indicating large heterogeneity in the length of chains of human-to-human transmission.

Fig. 4.

Fig. 4.

A reconstructed transmission tree consistent with the data. Each dot represents a case. The large central dot represents the animal reservoir.

Fig. 5.

Fig. 5.

Relative contributions of the different routes of transmission. (A) Proportion of cases by inferred route of transmission. (B) Temporal trend in the cumulated number of cases by inferred route of transmission. Trends in the daily number of cases appear in gray. (C) Temporal trend in the estimated reproduction number for the different routes of transmission. Gray, pink, and green crosses give estimates of within-cluster, within-region, and between-region reproduction numbers for individual cases, respectively. These summary statistics were derived from the probabilistic reconstruction of 500 transmission trees consistent with the data like the one plotted in Fig. 4.

Discussion

In this paper, we studied the spatiotemporal clustering of MERS-CoV cases in KSA, the country that has been the most affected by MERS-CoV. The framework we developed made it possible to analyze all surveillance data in a coherent and integrated manner, in contrast to previous studies that have examined individual aspects of the observed epidemiology (for example, cluster sizes). Our analysis has resulted in a more holistic characterization of MERS-CoV epidemiology in KSA.

Surveillance data for zoonotic infections such as MERS-CoV or avian influenza are often challenging to interpret because it is rarely possible to reliably identify the source of infection of each case. If multiple clusters of cases are detected in the same area and time period, it is unclear whether we should assume that they are independent introductions of the virus from the reservoir or that they belong to the same chain of transmission. If no human source of infection has been identified, does it mean that the case was infected by the reservoir? The answer depends on the quality of the epidemiological investigation, which may vary geographically and over time. A strength of our approach is that we do not need to assume that clusters are completely independent of each other. Instead, we can estimate the degree of epidemiological linkage between clusters and assess how that linkage varies by the geographic separation of clusters (within vs. between region). Our algorithm for identifying clusters was deliberately designed to be liberal in linking cases, to match the way surveillance data are collected. However, we found that the clusters thus identified were highly relevant epidemiological units in that we estimate that two-thirds of human-to-human transmissions occurred within clusters. The clusters we identified also stratified observed heterogeneity in transmission intensity well. We estimated that there was substantial transmission between clusters within the same region, validating our prior belief that clusters cannot be treated as independent, but little transmission between regions. Another strength of our approach is that it does not require that the source of infection of a case (human or animal) to be known to ascertain the contribution of the animal reservoir in the overall epidemic.

We found that a majority of MERS-CoV cases (88%) reported during this time period were due to human-to-human transmission. Different strategies may be considered to evaluate the relative contribution of the animal-to-human and human-to-human transmission First, one can perform thorough epidemiological investigations of MERS-CoV patients to ascertain their likely source of infection. Second, viral genetic sequences can be used to assess the number of independent introductions of the virus in an area. Third, analysis and modeling of the spatiotemporal clustering of MERS-CoV patients as performed here can be used to better characterize the dynamics of spread. Each of these approaches has limitations. Epidemiological investigation may struggle to identify sources of infection when modes of zoonotic exposure remain poorly characterized and when multiple exposures are possible. Although the number of concurrent viral lineages may be inferred from sequence data, the origin of these lineages (e.g., animal reservoir vs. humans from other regions) may be harder to ascertain. Last, modeling relies on spatiotemporal locality to link cases and may be sensitive to assumptions about the mechanisms of spread. Given these limitations, substantial insights may be gained by running these analyses independently and then carefully comparing their findings (7, 13). In that respect, the large Jeddah outbreak in March to May 2014 offers an interesting opportunity. A thorough field investigation of MERS-CoV patients in the outbreak concluded that the proportion of cases infected by the reservoir was likely to be very small (3 out of 112 of MERS-CoV patients who were not health care workers and had exploitable data) (5). This is largely consistent with our analysis that estimates that 5 (95% CI: 2–11) cases in this outbreak were infected by the reservoir. These results are also corroborated by the analysis of seven sequences isolated during the Jeddah outbreak that were found to be largely homogeneous, all falling within a single clade (4). For the 2014 Riyadh outbreak, concurrently circulating viruses were found to be distributed across at least 6 different clades (4), which is roughly consistent with our estimate of 4 (95% CI: 1, 8) introductions from the reservoir in that outbreak. Compared with epidemiological investigations that are thorough but limited in time and space (5), the analysis of surveillance data presented here makes it possible to get a more comprehensive picture of MERS-CoV transmission across KSA for an 19-mo time period. Although transmission was relatively quickly controlled in most clusters, our study highlights that few clusters acted as major amplifiers of the epidemic. Ensuring a consistent response is quickly implemented in all clusters is essential to reduce the burden of MERS-CoV.

In the absence of detailed data documenting infection control measures implemented during MERS-CoV outbreaks, it is not possible to estimate the intrinsic transmissibility of MERS-CoV in the absence of interventions (the basic reproduction number _R_0). We can only estimate the reproduction number seen in individual outbreaks, an estimate that implicitly incorporates the effects of the interventions in place. Our study shows that, for the level of control implemented in KSA, MERS-CoV epidemics are not self-sustaining in that country. However, one needs to be cautious when extrapolating from this study to countries with more limited health care resources. Analogies exist with the recent Ebola epidemic in West Africa; previous Ebola outbreaks were contained after at most few hundred cases, arguably leading to a false sense of security that all future outbreaks would also be readily contained. Like Ebola, MERS-CoV also exhibits high levels of heterogeneity in onward infection rates from case to case and hospital to hospital. Indeed, given MERS-CoV infections are not as consistently clinically severe as Ebola, case finding and effective contact tracing might be more challenging in a large-scale outbreak in a resource-poor setting. Furthermore, evolutionary theory suggests that pathogens that are most at risk for evolving high levels of transmissibility are those that are already moderately transmissible; predicted probabilities of major epidemics increase nonlinearly as reproduction numbers approach 1 and case numbers increase (14). Our approach, like other methods that reconstruct the transmission tree from case data (11, 12), can quantify trends in the effective reproduction number. However, more detailed models and data are needed to decipher the mechanisms explaining these trends. For example, is the declining trend in the within-cluster reproduction number (Fig. 2_B_) due to control measures or to other mechanisms such as depletion of susceptibles? Answering this question will require detailed data on control measures but also on the structure of hospitals (number of wards and number of beds per ward, bed occupancy, etc.).

This study has a number of limitations. Like for most emerging infectious diseases, reporting of MERS-CoV cases is imperfect and has changed over time. For example, the case definition changed on May 13, 2014 to allow for wider testing of suspect cases (15). Underreporting and variations in testing protocols can potentially bias estimates. To evaluate the robustness of our findings to these issues, in a sensitivity analysis, we restricted the study to 495 cases (73%) that were detected through passive surveillance (Table S1), that is, the surveillance type that was most stable over time. Even though one-third of cases were removed, results remained roughly unchanged with the proportion of infections from the reservoir increasing slightly from 12% (95% CI: 9%, 15%) to 17% (95% CI: 13%, 20%). In particular, exponential growth in the risk of spillover was robust to the surveillance subset (Table S1). This suggests that the quantified increase was not a mere surveillance artifact and that there was indeed a growing MERS-CoV epidemic in the reservoir at the time of the study. We also explored sensitivity of our findings to the presence of atypically large clusters and found that our estimates changed little when we removed 102 cases from the most affected hospital from the analysis (Table S2). We modeled temporal variations in introductions from the reservoir with a Poisson distribution that had a time-varying mean. However, introductions may occur in clumps. To explore this possibility, we considered an alternative scenario in which the daily number of introductions was modeled with a negative-binomial distribution characterized by high overdispersion. We found this had little impact on our estimates (Table S3). We cannot rule out the possibility that some of the human-to-human transmission events we inferred could actually be animal-to-human transmission events even though our population level estimates are consistent with other data sources.

Table S1.

Parameter estimates when analysis uses the 681 cases detected by passive and active surveillance (baseline) and when it is restricted to the 495 cases detected by passive surveillance

Variable Summary statistic 681 cases from passive-plus-active surveillance (baseline) 495 cases from passive surveillance
Serial interval Mean 6.8 (6.0, 7.8) 7.6 (6.4, 9.0)
SD 4.1 (3.4, 5.0) 4.8 (3.8, 6.1)
Reproduction numbers
Within cluster Initial mean R C 0.45 (0.33, 0.58) 0.36 (0.24, 0.51)
Initial SD σ C 0.53 (0.35, 0.78) 0.55 (0.33, 0.90)
Probability it starts >1 12% (6%, 18%) 10% (4%, 16%)
Value after 10 cases (relative to starting value) 47% (34%, 63%) 46% (32%, 68%)
Within region R R 0.24 (0.19, 0.29) 0.22 (0.17, 0.29)
Between region R O 0.05 (0.02, 0.09) 0.04 (0.004, 0.09)
Risk of introduction from reservoir
Nb at start of study period (weekly) 0.5 (0.2, 0.8) 0.4 (0.2, 0.7)
Nb at end of study period (weekly) 2.1 (1.0, 3.6) 2.4 (1.2, 3.9)
Exponential growth rate α (daily) 0.003 (0.001, 0.005) 0.003 (0.001, 0.005)
Source of infection, %
Within cluster 60% (57%, 63%) 57% (54%, 60%)
Within region 23% (20%, 27%) 22% (18%; 26%)
Between region 5% (2%, 8%) 4% (0.4%, 8%)
Reservoir 12% (9%, 15%) 17% (13%, 20%)

Table S2.

Parameter estimates for the baseline analysis and for an analysis that excludes 102 cases from the hospital with the largest number of cases

Variable Summary statistic Baseline Excluding cases from the hospital with the largest number of cases
Serial interval Mean 6.8 (6.0, 7.8) 7.1 (6.2, 8.2)
SD 4.1 (3.4, 5.0) 4.4 (3.6, 5.4)
Reproduction numbers
Within cluster Initial mean R C 0.45 (0.33, 0.58) 0.46 (0.34, 0.60)
Initial SD σ C 0.53 (0.35, 0.78) 0.53 (0.33, 0.81)
Probability it starts >1 12% (6%, 18%) 12% (6%, 19%)
Value after 10 cases (relative to starting value) 47% (34%, 63%) 43% (28%, 64%)
Within region R R 0.24 (0.19, 0.29) 0.26 (0.20, 0.32)
Between region R O 0.05 (0.02, 0.09) 0.05 (0.02, 0.10)
Risk of introduction from reservoir
Nb at start of study period (weekly) 0.5 (0.2, 0.8) 0.4 (0.2, 0.7)
Nb at end of study period (weekly) 2.1 (1.0, 3.6) 2.1 (1.1, 3.6)
Exponential growth rate α (daily) 0.003 (0.001, 0.005) 0.003 (0.001, 0.005)
Source of infection, %
Within cluster 60% (57%, 63%) 56% (53%, 59%)
Within region 23% (20%, 27%) 26% (21%; 30%)
Between region 5% (2%, 8%) 5% (0.2%, 10%)
Reservoir 12% (9%, 15%) 13% (10%, 16%)

Table S3.

Parameter estimates for the baseline analysis where the daily number of introductions follows a Poisson distribution and for an alternative model where it follows a negative-binomial distribution with high overdispersion (k = 0.2)

Variable Summary statistic Poisson (baseline) Negative binomial
Serial interval Mean 6.8 (6.0, 7.8) 6.8 (6.0, 7.7)
SD 4.1 (3.4, 5.0) 4.1 (3.4, 5.0)
Reproduction numbers
Within cluster Initial mean R C 0.45 (0.33, 0.58) 0.44 (0.32, 0.58)
Initial SD σ C 0.53 (0.35, 0.78) 0.52 (0.35, 0.78)
Probability it starts >1 12% (6%, 18%) 12% (6%, 19%)
Value after 10 cases (relative to starting value) 47% (34%, 63%) 46% (34%, 64%)
Within region R R 0.24 (0.19, 0.29) 0.24 (0.19, 0.30)
Between region R O 0.05 (0.02, 0.09) 0.06 (0.02, 0.10)
Risk of introduction from reservoir
Nb at start of study period (weekly) 0.5 (0.2, 0.8) 0.5 (0.2, 1.0)
Nb at end of study period (weekly) 2.1 (1.0, 3.6) 1.6 (0.7, 3.3)
Exponential growth rate α (daily) 0.003 (0.001, 0.005) 0.002 (0.000, 0.004)
Source of infection, %
Within cluster 60% (57%, 63%) 60% (57%, 63%)
Within region 23% (20%, 27%) 24% (20%, 28%)
Between region 5% (2%, 8%) 6% (3%, 9%)
Reservoir 12% (9%, 15%) 10% (7%, 13%)

Although health care facilities can amplify transmission of MERS-CoV, we still poorly understand the factors that facilitate human-to-human transmission in health care settings and in the community, and that may therefore explain the heterogeneity in transmission intensity we have characterized. In a number of nosocomial outbreaks, a large proportion of cases had comorbidities (3, 5) that have been suggested to increase susceptibility to infection or disease severity. Another possibility is that certain aerosolizing medical procedures in hospitals facilitate spread. Unfortunately, we were unable to test these hypotheses here as information on comorbidities and hospital practices was unavailable. It is important that we address such knowledge gaps to strengthen outbreak control in the future.

The ongoing exposure of the humans to MERS-CoV is of major concern, with the risk of a major epidemic growing larger the longer exposure remains unchecked. Understanding the medical, health care, and social factors that facilitate high levels of human-to-human transmission and lead to large outbreaks is critical to continued containment of the ongoing threat posed by MERS-CoV.

Materials and Methods

Data.

The KSA Ministry of Health routinely collects detailed information on all patients with laboratory-confirmed MERS-CoV infection through multiple sources that include MERS-CoV case report forms, laboratory report forms, and clinical records. The database contains the following for each case: the reason for testing, whether the case had symptoms meeting the MERS-CoV case definition at the time of testing, clinical status (hospitalized, home isolation, discharged, or deceased), demographic information, date of symptom onset, and hospital where treated, diagnosed, and/or tested. The study period is January 1, 2013, to July 31, 2014.

We partition MERS-CoV cases into clusters. A cluster is defined as a group of cases who were treated, diagnosed, and/or tested in the same hospital, with a time lag between two consecutive cases of at most 21 d. These clusters thus encompass not just nosocomial infections that occurred within the hospital but also infections that may have occurred in the catchment area of the hospital (either from another person in the community or from the animal reservoir).

The data are available in Dataset S1.

Modeling the Risk of MERS-CoV Infection.

The reproduction number R (i.e., the mean number of secondary cases generated by a human case) is decomposed into mutually exclusive categories arising from within-cluster transmission (R C), from within-region transmission (R R, i.e., transmission to other clusters of the region), and from between-region transmission (R O, i.e., transmission to clusters of other regions). To capture the dynamics of transmission and control within clusters, we assume that, when a new cluster c starts, the within-cluster reproduction number RCc(0) in that cluster is drawn from a Gamma distribution with mean R C and SD σ_C_. After C t cases, the within-cluster reproduction number is RCc(Ct)=RCc(0)(1+Ct)−γ (16, 17). Decline in the within-cluster reproduction number could be due to control measures and/or to other factors such as the natural depletion of susceptible individuals.

We explore scenarios where the risk of infection from the reservoir could be constant or increase exponentially over time.

Statistical Inference.

In a Bayesian setting, we develop a data augmentation strategy to estimate parameters of the model (18–21). The source of infection of each case (reservoir or another human case of the dataset) is considered as augmented data. Markov chain Monte Carlo sampling is used to explore the joint posterior distribution of parameters and augmented data (18–22).

Technical details are given in Supporting Information.

Notation

The serial interval is the time lag between symptom onset in a MERS-CoV human case and symptom onset in the persons they infect. We denote ωs the proportion of secondary cases with onset date s days after the onset date of the infecting case. We assume the serial interval has a Gamma distribution with a mean and SD that are estimated from the data.

We denote H the number of hospitals in the study and Q the number of regions. There are Hq hospitals in region q. Hospital h is in region qh.

N MERS-CoV cases are observed during the study period, allocated to C different clusters. Case n has symptom onset on day tn and is allocated to cluster cn associated with hospital hn. Cluster c starts on day Tc with a cumulative number of cases up to day t equal to mc(t).

A General Model of Transmission of MERS-CoV in KSA

Here, we present a general model for the transmission of MERS-CoV in KSA.

Human-to-Human Transmission.

Consider case n that belongs to cluster cn and is associated with hospital hn with symptom onset on day tn. The number of secondary cases generated by case n is RC,n in hospital hn (cluster cn), RR,n in other hospitals of the region, and RO,n in hospitals of other regions.

We assume that RR,n and RO,n are drawn from a Poisson distribution with mean RR (within-region reproduction number) and RO (between-region reproduction number), respectively. Parameters RR and RO are estimated from the data. We assume that secondary cases generated in other hospitals of the same region (or in hospitals of other regions) are uniformly distributed among these hospitals.

To capture the dynamics of transmission and control within clusters, we assume that the within-cluster reproduction number varies from cluster to cluster and depends on the cumulated number of cases in the cluster. Denote RCc(m) the within-cluster reproduction number in cluster c after m cumulated cases. We assume that the within-cluster reproduction number at the start of the cluster RCc(0) is drawn from a Gamma distribution with mean RC and SD σC that are estimated from the data. Furthermore, after m cumulated cases, we have the following:

where parameter γ captures the decay in the within-cluster reproduction number as cases accumulate (16, 17). This decay could be due to control measures and/or to other factors such as the natural depletion of susceptible individuals.

Transmission from the Animal Reservoir.

We denote αt the mean number of infections from the reservoir on day t, which is parameterized with an exponential model:

where E0 is the expected number of infections from the reservoir at the start of the study period (i.e., January 1, 2013) and α is the exponential growth rate (we do not constrain α to be >0).

Inference

A key challenge for the estimation of model parameters is that the source of infection of cases is unknown. This means it is difficult to write down the likelihood of the parameters. In the first subsection of this section, we show how to calculate the likelihood when the source of infection of cases is known. In the second subsection, we present a data augmentation framework that can cope with uncertainty about the source of infection.

Likelihood When the Source of Infection of Cases Is Known.

Let us first consider the scenario where the source of infection sn is known for each case n. This assumption will be relaxed in the next section. By notation, if case n was infected by a human case, sn is equal to the ID of the infector; otherwise, sn=0.

With this information, the number of secondary cases of the different types is known for each case:

RR,n=∑i:ci≠cn,qi=qnδ(si=n),

where δ(si=n)=1 if si=n and 0 otherwise.

Furthermore, the number of introductions from the reservoir on day t is as follows:

The contribution of case n to the transmission part of the likelihood is as follows:

Lntrans=Ppois{RC,n|Rccn[mcn(tn)]}Ppois(RR,n|RR)Ppois(RO,n|RO)×(Hqn−1)−RR,n(H−Hqn)−RO,n×∏i:si=nω(ti−tn).

The first line gives the probability of the number of secondary cases of different types. The second line gives the probability a secondary case drawn in the region or in other regions will end up in a given hospital. The third line gives the density of the generation time distribution.

The contribution to the likelihood of introducers with onset on day t is as follows:

Ltintro=Ppois(It|αt)(H)−It,

where the first term is the probability of the number of introductions on that day and the second one is the probability each introducer will end up in a given hospital.

Heterogeneity of transmission at the cluster level is captured by the following:

Lcluster=∏cPgamma[RCc(0)|mean=RC,SD=σC].

Finally, the likelihood is as follows:

L=Lcluster∏tLtintro∏nLntrans.

A Bayesian Data Augmentation Strategy to Deal with Uncertainty in the Source of Infection.

In practice, the source of infection sn of case n is unobserved, which means that the likelihood of the parameters, presented in the previous section, is no longer available.

Here, we set up a Bayesian data augmentation strategy to deal with this uncertainty (18–22). In this framework, the source of infection sn of case n is considered as augmented data (or nuisance parameter). In a Bayesian setting, the joint posterior distribution of the parameters and the augmented data are explored by Markov chain Monte Carlo sampling.

Prior Distributions.

We assume flat priors for all parameters.

Markov Chain Monte Carlo Algorithm.

We develop a Markov chain Monte Carlo algorithm to explore the joint posterior distribution of parameters and augmented data. The algorithm has the following updates.

Updates of parameters.

A standard Metropolis Hastings step is performed to update parameters on the log scale (22).

Update of the source of infection of case i.

A Metropolis Hastings step is implemented (22). To improve mixing, rather than drawing the source uniformly from the possible sources, we define a proposal that makes best use of available data. In the proposal, each possible source n (where n = 0 corresponds to the reservoir) is allocated the weight:

wn={RCω(ti−tn)if cn=ciRRω(ti−tn)if cn≠ci and qn=qiROω(ti−tn)if qn≠qiβif n=0 (reservoir),

with β=0.05. The proposal probability that the source of case i is source n is as follows:

Implementation.

The algorithm is run for 100,000 iterations with a burn in of 5,000, storing 1 out of 10 iterations. Convergence is visually assessed. One run with 100,000 iterations takes about 30 min on a desktop.

Sensitivity Analysis

Analysis Restricted to MERS-CoV Infections Detected Through Passive Surveillance.

Patients in the database were defined as being detected via passive surveillance if the reason for testing included “MERS” or “Suspected MERS based on symptoms” and as being detected via active surveillance if the reason for testing was “Case contact,” “Household contact,” “Health care worker,” or “Other.”

In the main analysis, we consider n = 681 human MERS-CoV infections detected in KSA through passive (n = 495) and active surveillance (n = 186). Here, analysis is restricted to the n = 495 cases detected through passive surveillance and distributed across 89 hospitals (Table S1).

Analysis Excluding the Hospital with the Largest Number of Cases.

To assess sensitivity of our estimates to the presence of large clusters, we rerun the analysis excluding the hospital with the largest number of cases. Estimates are provided in Table S2.

Analysis Under the Assumption That the Daily Number of Introductions Follows a Negative-Binomial Distribution.

We modeled temporal variations in introductions from the reservoir with a Poisson distribution that had a time-varying mean. However, introductions may occur in clumps. To explore this possibility, we considered an alternative scenario in which the daily number of introductions was modeled with a negative-binomial distribution characterized by high overdispersion (k = 0.2). Estimates are provided in Table S3.

Measure of Overdispersion in the Within-Cluster Reproduction Number

We estimate that the within-cluster reproduction number has a mean of 0.45 (95% CI: 0.33, 0.58) with substantial heterogeneity between clusters (SD: 0.53; 95% CI: 0.35, 0.78). This level of heterogeneity corresponds to an overdispersion parameter k equal to 0.77 (95% CI: 0.36, 1.46).

It should be noted that this estimate cannot be directly compared with estimates of k investigating case-to-case heterogeneity in transmission (8) because we are estimating cluster-to-cluster heterogeneity in transmission, not case-to-case heterogeneity in transmission.

Data

Dataset S1 provides the data used in this analysis as an Excel table. The first line of the spreadsheet provides the ID of the hospital. The second line of the spreadsheet provides the region of the hospital. The first column indicates the date. Each cell contains the number of cases with onset in a specific hospital and for a given date.

Supplementary Material

Supplementary File

Acknowledgments

We acknowledge funding from the Medical Research Council, the National Institute for Health Research Health Protection Research Unit Programme, the Laboratory of Excellence Integrative Biology of Emerging Infectious Diseases, the European Union Seventh Framework Programme (FP7/2007-2013) under Grant 278433-PREDEMICS, the National Institute of General Medical Sciences Models of Infectious Disease Agent Study Initiative, the Bill and Melinda Gates Foundation, and the AXA Research Fund.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary File