Model of Cellular and Network Mechanisms for Odor-Evoked Temporal Patterning in the Locust Antennal Lobe (original) (raw)
. Author manuscript; available in PMC: 2010 Jul 21.
Summary
Locust antennal lobe (AL) projection neurons (PNs) respond to olfactory stimuli with sequences of depolarizing and hyperpolarizing epochs, each lasting hundreds of milliseconds. A computer simulation of an AL network was used to test the hypothesis that slow inhibitory connections between local neurons (LNs) and PNs are responsible for temporal patterning. Activation of slow inhibitory receptors on PNs by the same GABAergic synapses that underlie fast oscillatory synchronization of PNs was sufficient to shape slow response modulations. This slow stimulus- and neuron-specific patterning of AL activity was resistant to blockade of fast inhibition. Fast and slow inhibitory mechanisms at synapses between LNs and PNs can thus form dynamical PN assemblies whose elements synchronize transiently and oscillate collectively, as observed not only in the locust AL, but also in the vertebrate olfactory bulb.
Introduction
Odor stimulation evokes complex temporal patterns of activity in the mitral cells of the vertebrate olfactory bulb (Kauer, 1974; Kauer and Shepherd, 1977; Chaput and Holley, 1980; Meredith, 1986, 1992) and projection neurons (PNs) of the insect antennal lobe (Burrows et al., 1982; Christensen and Hildebrand, 1987; Laurent and Davidowitz, 1994). These patterns, recently characterized in locust, consist of alternating epochs of excitation (characterized by Na+ spikes), inhibition (PN activity is reduced or subthreshold), and quiescence. Different odors can evoke different temporal patterns in one PN, and one odor can evoke different patterns in simultaneously recorded PNs (Laurent and Davidowitz, 1994; Wehr and Laurent, 1996; Laurent et al., 1996). These patterns are consistent across trials.
The slow temporal structure of PN responses occurs independently of any temporal patterning in the olfactory input. It rather results from the intrinsic dynamics of interacting excitatory PNs and inhibitory local neurons (LNs). Unpatterned electrical stimulation of the olfactory afferent axon tract evoked different temporal response patterns in simultaneously recorded PNs (Wehr and Laurent, 1999). In addition, activation of spatially different groups of afferents with otherwise identical electrical stimuli produced different response patterns in individual PNs. The complex synaptic organization of the antennal lobe network must therefore, by itself, provide the mechanisms underlying odor-specific slow temporal patterning. In a recent theoretical study, it was shown that heteroclinic structures in the phase space of a dynamical system representing the antennal lobe network can underlie patterns of PN activity that resemble those observed in vivo (Laurent et al., 2001). The specific mechanisms underlying these slow temporal structures, however, remain unknown. This issue is explored here.
The dynamical properties of a network consisting of interacting excitatory and inhibitory neurons depend, in part at least, on the dynamics of synaptic transmission between its elements. Previous pharmacological experiments with the locust antennal lobe showed that fast inhibition mediated by LNs can be blocked by applicationof the GABA-activated chloride channel blocker picrotoxin (MacLeod and Laurent, 1996; MacLeod et al., 1998; Stopfer et al., 1997). Picrotoxin blocks fast IPSPs, thereby desynchronizing PNs and thus the antennal lobe output. Remarkably, however, this manipulation spared the slow patterning of individual PN responses to odors (MacLeod and Laurent, 1996; MacLeod et al., 1998; Stopfer et al., 1997). In particular, picrotoxin did not block the slow phases of inhibition observed in PNs before, between, or following bursts of odor-evoked activity. Pharmacological blockers of the vertebrate GABAB receptor did not affect this slow inhibition (K. MacLeod and G.L., unpublished data). This pharmacological analysis, however, does not exclude the possible presence of metabotropic GABA receptors, for insect and vertebrate receptor/channel pharmacology can differ significantly. Bicuculline, for example, fails to block fast and picrotoxin sensitive GABA-mediated inhibition in most insects. These experimental results simply indicate the existence of slow inhibitory mechanisms, whose action may be to shape the slow evolution of antennal lobe dynamics. These slow mechanisms must be synaptic because long-lasting PN inhibition can occur in the absence of any preceding spiking by the inhibited neuron (e.g., see Figure 1; Laurent et al., 1996). Thus, AHP-type mechanisms as well as reciprocal inhibition can be excluded as necessary functional features.
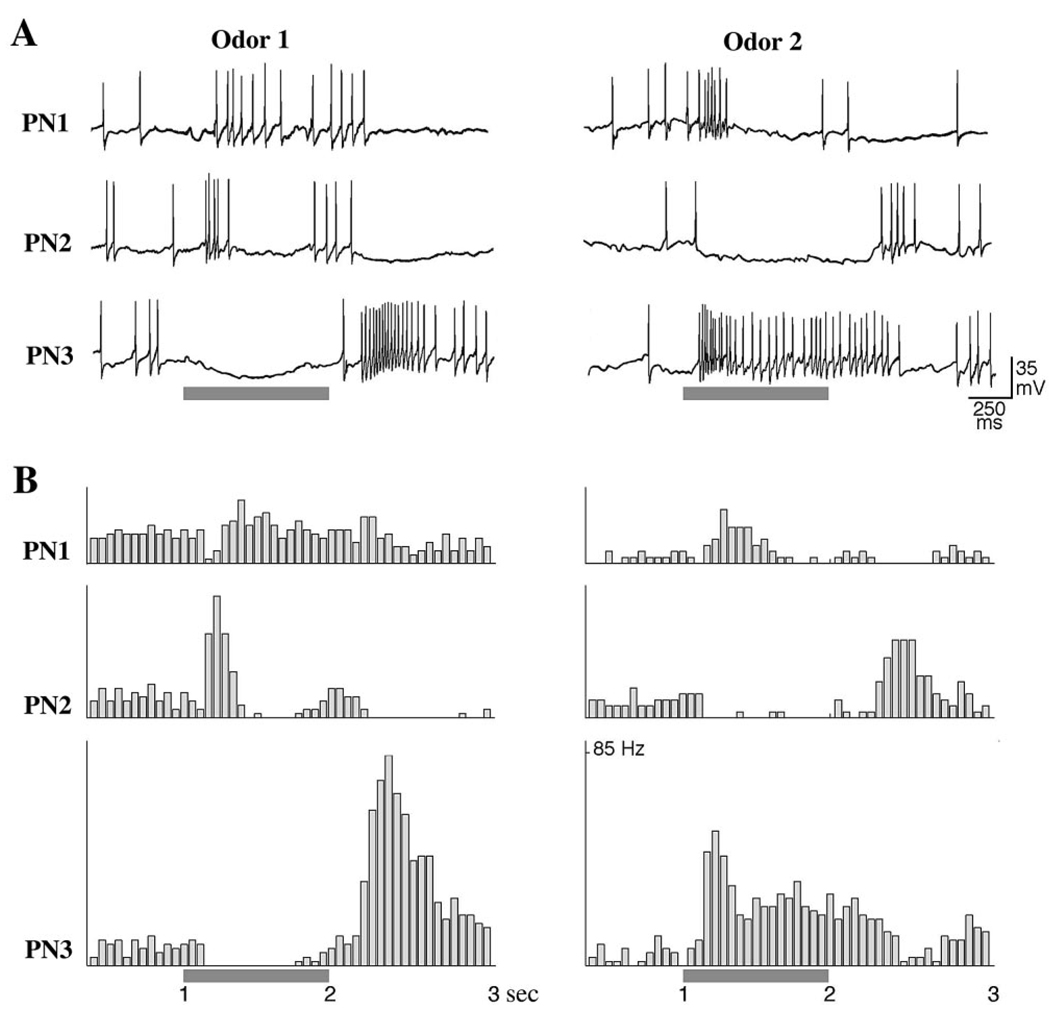
Figure 1. Odor-Specific Slow Temporal Patterns in Locust PNs.
Simultaneous intracellular recordings from 3 PNs show odor-specific slow temporal patterns. The odor responses in each PN are shown for two different stimuli (gray bars).
(A) PNs membrane potentials.
(B) PSTHs corresponding to the spike trains shown in (A), (12 trials).
Our goal here is to build on our previous model of the antennal lobe, initially designed to investigate the fine temporal structure of spike synchronization during olfactory stimulation (Bazhenov et al., 2001 [this issue of _Neuron_]). This model showed that fast GABAergic inputs from LNs to PNs are sufficient to cause transient PN synchronization. Stimulus-specific shaping of LN activity depended to a large extent on lateral LN-LN inhibition. We now extend this model by including strong slow inhibition of PNs by LNs to explore the hypothesis that such mechanisms, with a time constant of a few hundred milliseconds, can account for the stimulus-specific slow temporal patterning of PN responses. Our results lead us to predict the existence and characteristics of slow inhibitory conductances in the LNs. Because the phenomena described here are observed in the vertebrate olfactory bulb also, our model may help us understand general rules of early olfactory circuit dynamics, important for odor coding.
Results
In Vivo Recordings
Locust PNs normally fire in response to more than one odorant, typically with distinct odor-specific slow temporal patterns (Laurent et al., 1996). Figure 1 shows responses elicited by two odors in three simultaneously recorded PNs. PN1 is initially inhibited but rapidly resumes firing throughout the response to the first odor, whereas it fires vigorously only at the beginning of the second odor. PN2 fires over two phases separated by a silence in response to the first odor, whereas it is strongly hyperpolarized by the second odor. PN3 shows sustained inhibition followed by rebound to the first odor, but strong phasic-tonic excitation by the second odor. These patterns are reliable; the same sequences of excitation, inhibition, and relative quiescence are evident each time each odor is presented (Figure 1B). Such PN responses underlie a dynamic ensemble representation of odors in the antennal lobe.
Stimulus-Evoked Responses in PN-LN Network Model
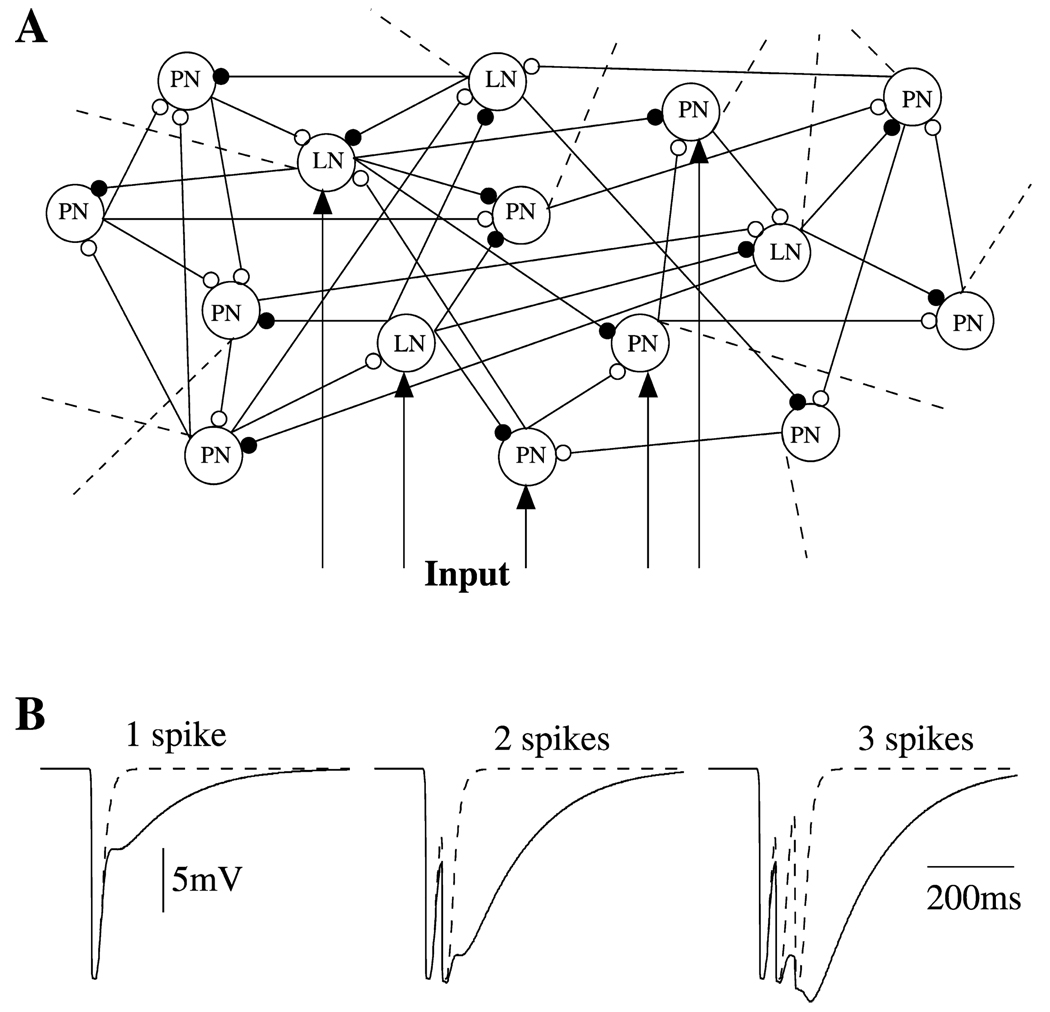
To study the possible origin of odor-evoked slow temporal patterns in PN responses, we constructed a network model consisting of 90 PNs and 30 LNs (see Figure 2A), as previously introduced (Bazhenov et al., 2001). In the present study, the contribution of slow inhibitory receptors between LNs and PNs was enhanced so that activity during normal stimulation would be sufficient to activate them. The enhanced inhibition is illustrated in Figure 2B, where the IPSP in a postsynaptic PN is plotted in response to 1, 2, or 3 Ca2+ spikes in a presynaptic LN (see also Experimental Procedures).
Figure 2. Network Properties.
(A) A simulated network model consisted of 90 PNs and 30 LNs. All interconnections were random with probability 0.5. Forty percent of PNs and 30% of LNs were stimulated by current pulses. Dashed lines illustrate connections to the rest of the network.
(B) Fast GABAA IPSPs (dashed line) and the sum of fast GABAA and slow GABA IPSPs (solid line) are shown for three different inputs—different numbers of presynaptic spikes.
Upon stimulus presentation, PN activity in the model became synchronized at about 25 Hz, in agreement with experimental data (Laurent and Davidowitz, 1994). Between stimuli, PNs displayed irregular low-frequency firing (not visible in Figure 3B), caused by random synaptic “noise” included in each model neuron (see Experimental Procedures). The absence of synchronization and low firing rates in PNs during this time were reflected in field potentials, which became flat after a stimulus ended (Figure 3A).
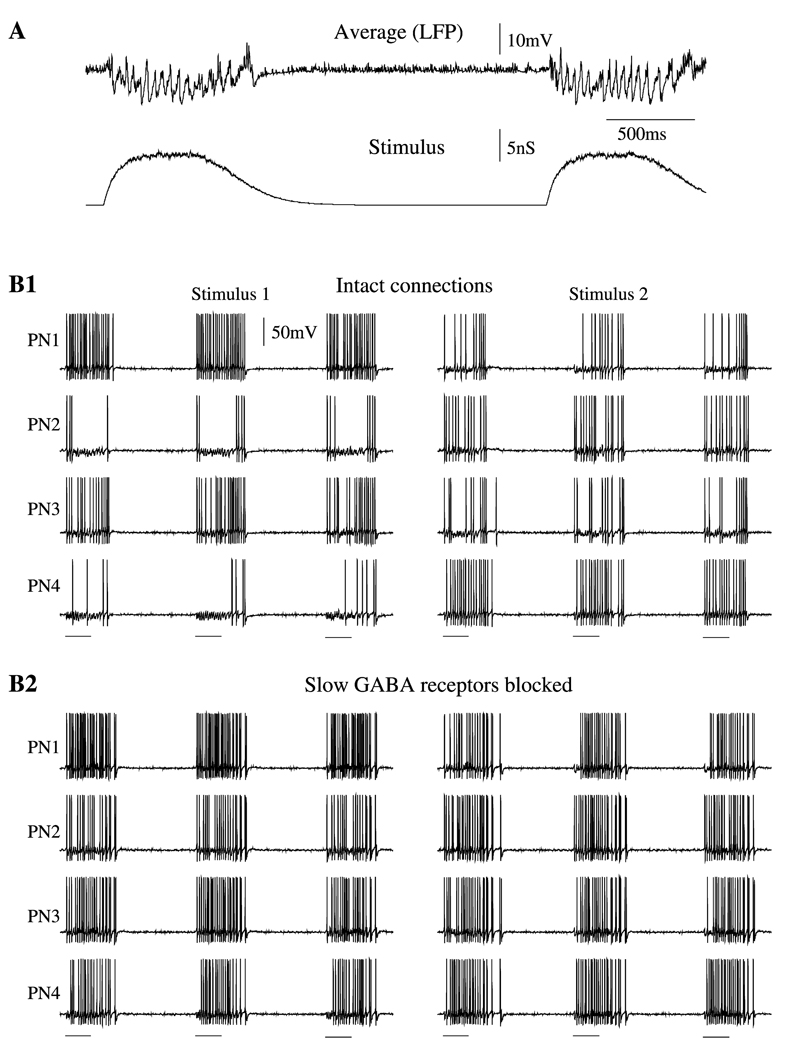
Figure 3. Oscillation in Response to External Stimulation.
(A) Two sequential stimuli each lasting 500 ms were delivered with 2500 ms delay to a randomly selected subset of PNs and LNs (40% and 30% of the total populations, respectively). Field potential oscillations (upper panel) and stimulus (lower panel) are shown.
(B) Effect of slow inhibition on temporal patterning. Four representative examples of PNs are shown in response to three presentations of two different stimuli. Stimuli (500 ms duration) are marked by horizontal bars.
(B1) Stimulus-specific slow temporal structure was found in the network with intact slow inhibition.
(B2) Blocking the slow inhibitory receptors eliminated temporal patterning.
The role of slow inhibitory receptors is illustrated in Figure 3B. It shows 4 representative PNs during repeated presentations of two different stimuli. With slow inhibition intact (Figure 3B1), each stimulus induced characteristic slow temporal structures in the response patterns of each individual PN. This structure usually consisted of alternating depolarizing epochs when Na+ spikes were generated, and hyperpolarizing epochs, when only subthreshold oscillations (caused by periodic IPSPs) were evident. Each epoch usually lasted a few hundred milliseconds. The model of slow inhibition used in our simulations required that a few presynaptic LN spikes arrive sequentially to reach significant receptor activation (see Experimental Procedures). This condition also determined the timescale of temporal patterning—from 100 ms to 500 ms—also in agreement with data obtained in vivo (see Figure 1). The slow patterns differed among PNs and were stimulus specific (Figure 3B1). Figure 3B2 shows the responses of the same subset of neurons when only the slow inhibitory receptors between LNs and PNs had been blocked: the slow temporal structure was eliminated from PN spike trains; PNs all showed similar responses that did not change when a new stimulus was applied. Thus, these results suggest that the slow, odor-specific modulation of PN firing during olfactory stimulation observed in vivo (Figure 1) can emerge from the activation of slow inhibitory receptors between LNs and PNs.
Effect of Picrotoxin-Induced Disinhibition in LN-PN Network
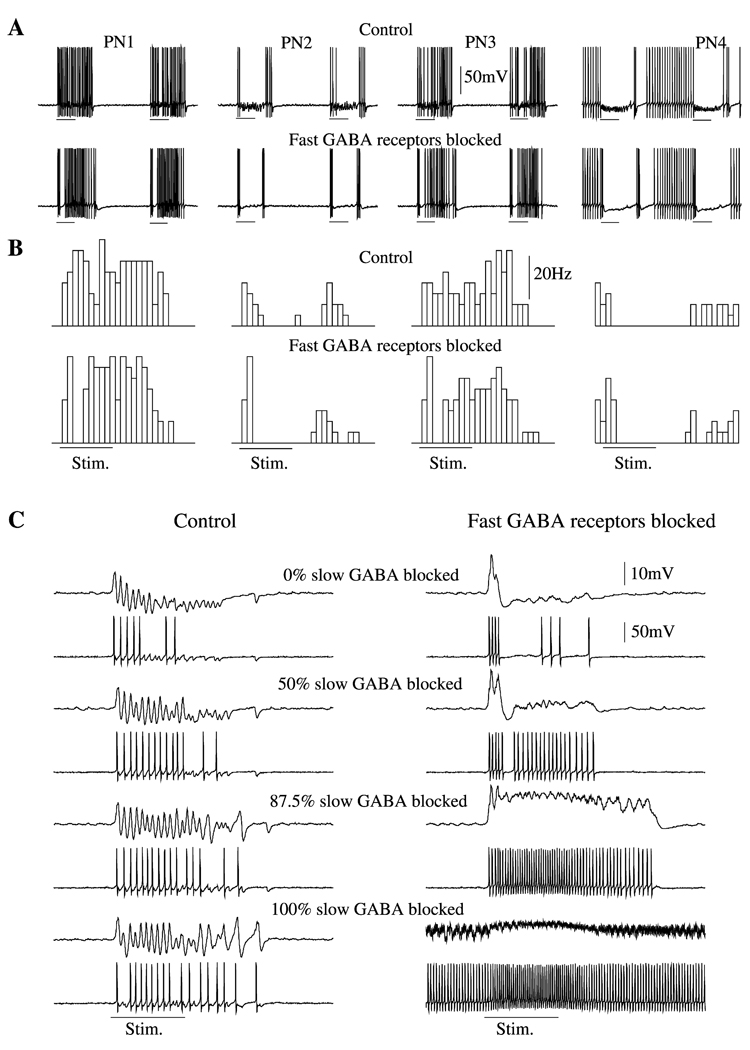
It has been shown in locusts that application of the GABA-activated chloride channel antagonist picrotoxin (PCT) eliminates odor-evoked synchronous PN oscillations while sparing the slow temporal structure of their spike trains (MacLeod and Laurent, 1996; MacLeod et al., 1998). To examine this dissociation in our network model, we first blocked 98% of the fast inhibition between LNs and PNs (the peak conductance for all fast inhibitory synapses was reduced by a factor of 50) while keeping slow inhibitory receptors intact. Figure 4A shows activity in 4 representative PNs under intact and disinhibited network conditions. Reducing the conductance of fast GABAergic receptors between LNs and PNs by 98% eliminated the fast, periodic inhibitory drive to PNs, leading to their desynchronization. In the disinhibited network, the local field potential was almost flat, except for the first 100–200 ms of stimulation, when a positive peak was evoked (see Figure 4C). This peak reflects intense asynchronous responses in many PNs right after stimulus onset. In some cases stimulus termination was followed by an increase in PN firing rate, leading to a second peak in the field potential. This offset response was partially the result of the slow stimulus decay used in our model (see Figure 3A). When, after stimulus offset, many LNs became hyperpolarized below Ca2+ spike generation threshold, some PNs fired at a higher frequency, producing the depolarizing peak in the field potential. Figure 4B shows average peristimulus time histograms (PSTHs) for the four neurons in Figure 4A. In spite of the induced desynchronization, the slow temporal patterns of individual PN responses remained essentially intact.
Figure 4. Disinhibition in LN-PN Network.
(A) Four representative PNs from intact (upper panels) and disinhibited (lower panels) networks. In disinhibited network, peak conductance for GABAA synapses was reduced by a factor of 50. It was not completely eliminated because it is likely that, in physiological experiments with PCT, a small fraction of the fast inhibitory channels remained unaffected. Slow inhibition was preserved in both models.
(B) PSTHs (four trials) for the same neurons from intact (upper panels) and disinhibited (lower panels) networks. The slow temporal structure was remained intact after fast inhibitory receptors were blocked.
(C) The maximal conductance for slow inhibitory receptors was gradually decreased from 100% to zero in intact (left) and disinhibited (right) networks. When both fast and slow inhibitions were blocked (right, bottom), PNs continued to fire even between stimuli. Top trace, LFP, and second trace down, PN.
Slow Inhibition and PN Response Patterning
In a network with intact fast inhibition, reducing the peak conductance for slow inhibitory receptors increased the field oscillatory power (Figure 4C). This resulted from the loss of the slow temporal structure of PN spike trains: activated PNs could generate spikes at most cycles of the network oscillation. Even though some of these spikes were not synchronized with the ensemble response (Bazhenov et al., 2000), the total number of spikes contributing to the field potential at each cycle was larger than that in the intact network. Reducing slow inhibition also eliminated the progressive hyperpolarization of the local field potential typically observed in vivo during the first 200–500 ms of odor presentation (e.g., Wehr and Laurent, 1999, figure 2a). If, in addition, fast inhibition was blocked, the firing rate increased and synchronization disappeared (Figure 4C, right).
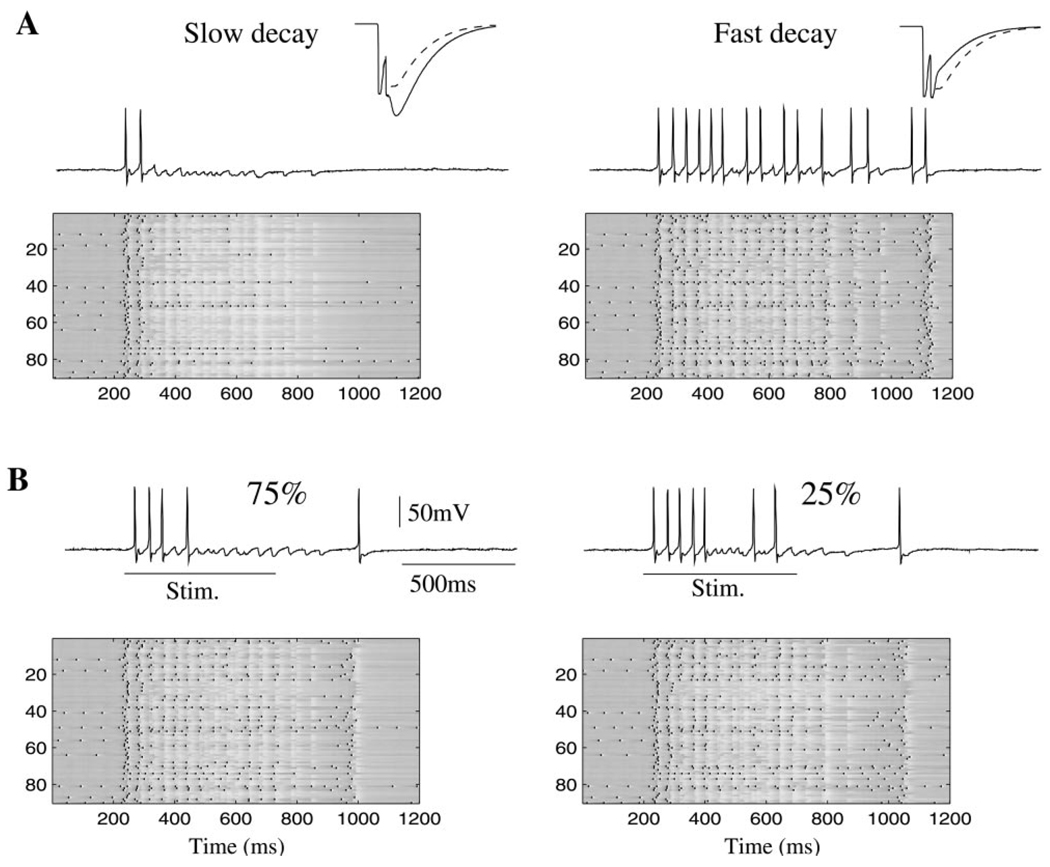
We next explored the role of the off time constant of slow inhibition. Figure 5A shows the network response and one representative PN in the model with an increased (left) or decreased (right) decay time constant. The insets in each figure illustrate the kinetics of the modified synapses (solid lines) compared to control ones (dashed lines) for doublets of presynaptic spikes (see Experimental Procedures). Slow inhibition grew significantly when the time constant was increased, reducing network activity after the first 100–150 ms of stimulation. Decreasing the decay time constant had the opposite effect, causing most activated PNs to fire continuously.
Figure 5. Effect of Kinetic Parameters and Spatial Density of Slow Inhibitory Receptors.
(A) Increase (left) or decrease (right) in decay time constant for slow inhibition significantly decrease or increase, respectively, the network response. Insets show slow IPSPs in response to 2 presynaptic spikes before modification (dashed line) and after modification (solid line).
(B) Increase (left) or decrease (right) of the density of slow GABAergic interconnections led to relatively small changes in PN activity. In 2D panels, y axis represents PN label (1–90).
Changing the probability of finding a slow inhibitory connection between each LN and PN had surprisingly little effect on the network and each PN’s response. In our previous simulations, slow inhibitory synapses were distributed with a probability of 0.5 (identical to that of fast inhibitory synapses; see Experimental Procedures). We changed this probability to 0.75 (Figure 5B, left) or 0.25 (Figure 5B, right) while keeping the distribution of fast inhibitory synapses unchanged. In either case, the slow temporal structure of the spike trains in a majority of PNs appeared to be unchanged (Figure 5B, compare individual PN responses in two-dimensional panels). These findings indicate that the presence of a certain number of slow inhibitory synapses is essential to gener-ate realistic PN spike trains in the network, but that the absolute number of these slow synapses may not be critical.
Slow Inhibition and Response Specificity
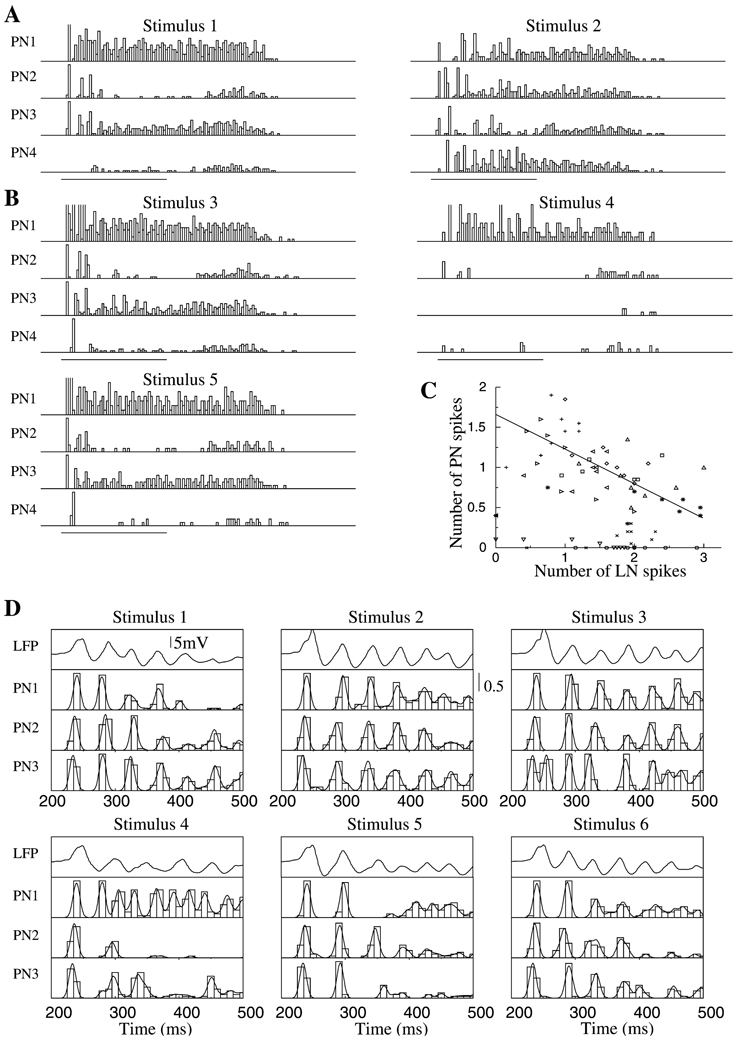
As shown experimentally, the existence of stimulus-specific slow temporal patterns in PN spike trains contributes to an observer’s ability to discriminate among different stimuli using single PN responses (MacLeod and Laurent, 1996; Stopfer et al., 1997; Laurent et al., 1996), particularly if these stimuli are similar to one another. Here we examined the role of slow inhibition in generating slow temporal patterns sufficient for stimulus discrimination. Figure 6A shows the responses (PSTHs) of 4 PNs to two different stimuli, as in Figure 3B. When stimulus 1 was applied, PNs 1–3 had peaks of activity right after the stimulus onset. PN4 displayed little activity during the stimulus, except for a firing rate increase 200 ms after stimulus termination. When stimulus 2 was presented, these neurons showed different response patterns, as typically observed experimentally (Laurent et al., 1996).
Figure 6. Temporal Structure of PN Activity during Different Stimuli.
PSTHs for 4 representative PNs during five stimulus presentations are shown.
(A) The same two stimuli as in Figure 3B are shown—identical PNs but different LNs were stimulated.
(B) Spatially overlapping stimuli: 50% overlap between stimuli 3 and 4 and 90% overlap between stimuli 3 and 5.
(C) Total number of Ca2+ spikes in all presynaptic LNs versus number of spikes in their postsynaptic PN at each cycle of population oscillations. Different symbols indicate results for different PNs.
(D) Field potential (top) and 3 different PNs are shown in response to six different stimuli. First six cycles of network oscillations following stimulus onset are presented.
Stimuli 1 and 2 shown in Figure 6A were arranged to directly activate identical subsets of PNs but different subsets of LNs. To analyze how the “spatial” overlap between stimuli affects the slow temporal patterns of PNs, we changed the subsets of stimulated PNs as well: for example, there was a 50% spatial overlap between the sets of stimulated PNs and LNs for stimuli 3 and 4 and a 90% overlap for stimuli 3 and 5 (Figure 6B). PSTHs constructed from responses to stimuli 3 and 4 were clearly different. As the spatial overlap between inputs increased, however, the slow temporal structures of PN spike trains became more similar, making discrimination tightly dependent on the temporal resolution used to assess similarity between firing patterns and PSTHs. This initial approach did not consider the fine relational structure of PN spikes that provides an additional dimension for odor discrimination (Laurent, 1996; Wehr and Laurent, 1996; Stopfer et al., 1997; Bazhenov et al., 2001); the fine structure will be examined below.
To examine the relationship between the activity pattern of a given PN and those of its presynaptic LNs, we first identified, for each PN, all LNs presynaptic to it and counted the total number of Ca2+ spikes produced by these LNs in the time window between two nearest peaks of the field potential. Figure 6C plots the calculated PN versus LN activity. This graph indicates that there was a negative correlation (R = −0.2) between LN and PN firing. Greater numbers of LN spikes during specific epochs of a response led to stronger slow inhibition, resulting in a reduction of PN firing. The slow modulation of PN firing patterns during a response is thus a reflection of the dynamic activation patterns of the LNs presynaptic to them.
Fine Temporal Structure of PN Firing
The temporal patterns studied above occurred on a time scale of a few hundred milliseconds and were controlled by the activation of slow inhibitory synapses between LNs and PNs. To examine whether the probabilities of PN firing on individual cycles of the network oscillations were also stimulus specific, we next analyzed the fine temporal structure of PN responses. We found that, as observed experimentally (Wehr and Laurent, 1996), the firing probabilities of PNs displayed 20 Hz oscillations phase-locked to the field potential and across different neurons. Figure 6D shows the firing probabilities of 3 representative PNs for six different stimuli. These, but not all, PNs fired reliably at the first cycle of the network response; the firing probability of each PN then changed over the course of the response in a stimulus-specific manner. Similar to data recorded in vivo (Wehr and Laurent, 1996), model PNs fired with a high probability during specific cycles but never during other cycles. For example, PN1 fired synchronously with the field potential during cycle 3 in response to stimuli 1, 2, 3, and 6 but always skipped this cycle in response to stimulus 5. PN3 fired at every cycle in synchrony with the field potential during stimulus 2 but missed some cycles during stimuli 4 and 5. Slow temporal patterning was also evident: PN1 fired during every cycle in response to stimuli 3 and 4; when stimulus 1, 5, or 6 were presented, however, the activity of this neuron was significantly reduced, starting from the third cycle. PN2 fired during every cycle for stimuli 2 and 3, but its activity was much reduced during cycles 4–6 of stimuli 1 and 5. Note also that, in some cases, a PN fired spikes that were not synchronized with the field potential. For example, PN1 fired during every cycle in response to stimuli 4 and 6; however, starting from cycle 3, spike timing relative to the field potential maxima varied from one trial to another. This shows that, although this PN did not skip cycles, its contribution to the ensemble response was reliable only during specific cycles.
We showed previously that PN desynchronization results from the reduction of fast inhibitory input from presynaptic LNs (MacLeod and Laurent, 1996; MacLeod et al., 1998; Bazhenov et al., 2001). Thus, both increases and decreases of activity in the population of presynaptic LNs affects postsynaptic PNs: reducing LN output leads to PN desynchronization caused by the reduction of fast inhibition, whereas increasing LN output leads to a greater activation of slow inhibitory receptors, causing PN hyperpolarization. The spiking and phase-locking of PNs during odor-evoked responses thus result from a balance between fast and slow inhibition.
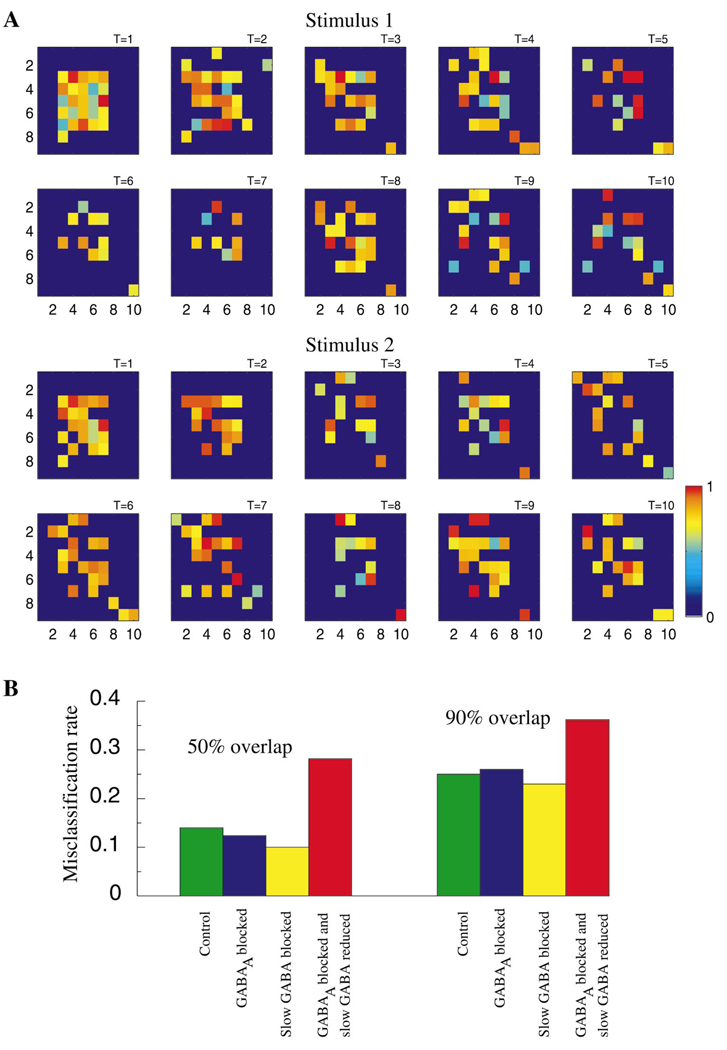
Figure 7A illustrates the spatiotemporal dynamics of the entire PN population during stimulation with two odors (stimulus 1 and 2) over T = 10 cycles of the LFP oscillation. For each stimulus, the set of PNs responding with action potentials evolved throughout the duration of the odor presentation; while some neurons fired throughout (e.g., stimulus 1: row 3, column 7), others displayed action potentials only during specific cycles of the network oscillation (e.g., stimulus 1: row 7, column 5). In most cases, even if a neuron fired throughout the response, the degree of synchronization between its action potentials and the LFP oscillation (indicated by color) changed over time. Stimuli 1 and 2 overlap by 90%. At stimulus onset, therefore, the PN assemblies are very similar. Starting from the second cycle, however, the initial clusters of activated PNs dissolved, making the representations of each stimulus more distinctive. This suggests that, as observed in the zebrafish (Friedrich and Laurent, 2001), antennal lobe dynamics amplify small differences between odor representations by progressively reducing spatial overlap over the duration of single stimuli.
Figure 7. Temporal Structure of PN Responses and Stimulus Discrimination.
(A) Spatiotemporal dynamics of the PNs during two different stimulus presentations (90% spatial overlap between stimuli). Each plot (9 × 10) corresponds to one cycle of the field potential oscillation (10 cycles are shown for each stimulus). Light color shows the presence of an action potential and characterizes its phase relative to the nearest peak of the field potential (red corresponds to precise synchronization—zero phase shift, light blue indicates a spike occurring precisely between two peaks of the field potential—±π phase shift). Dark blue color indicates silent cells.
(B) Misclassification rate calculated for all PNs using cluster algorithm (τ = 200 ms). Intact network (green); maximal conductance for GABAA synapses reduced by factor of 50 (blue); slow inhibitory receptors blocked (yellow); maximal conductance for GABAA synapses reduced by factor of 50 and maximal conductance for slow inhibitory receptors reduced by factor of 8 (red). Stimuli with different degrees of spatial overlap (50% and 90%) are shown. Misclassification rate of 0.5 indicates a complete loss of discriminability.
To quantify how fast and slow forms of inhibition affect an observer’s ability to classify different responses as caused by specific stimuli, we used a clustering algorithm (MacLeod et al., 1998; see also Experimental Procedures) to compare responses in intact and disinhibited networks. The misclassification rate was calculated using single-neuron responses (i.e., discarding correlation between PNs and LNs) and for stimuli that overlapped by 50% and 90% (i.e., 50% and 90% overlap between initially activated LN and PN subsets). Four conditions were compared: (1) intact network; (2) fast inhibition blocked by 98% (gblock = gGABAA/50); (3) slow inhibition eliminated; (4) fast and slow inhibition both reduced by factors of 50 and 8, respectively (blocking both fast and slow inhibition completely caused the network to be overexcited, as shown in Figure 4C). Figure 7B shows that eliminating fast GABAergic inhibition did not affect an observer’s ability to discriminate between stimuli using single PN spike trains, as observed in experiments with picrotoxin application (MacLeod et al., 1998). Surprisingly, blocking slow inhibition alone also did not reduce discriminability. However, when both fast and slow inhibitions were reduced, the misclassification rate increased significantly. This result suggests that both fast and slow inhibition can individually contribute to a high level of discriminability. The potential role of the slow temporal structure for stimulus classification becomes clear after the fast inhibition has been blocked and vice versa.
Discussion
Application of the GABA-activated chloride channel antagonist picrotoxin to the antennal lobe of the locust eliminates odor-elicited PN synchronization and, hence, 20–30 Hz field potential oscillations (MacLeod and Laurent, 1996. Complex slow temporal patterns of PN activity (sequences of depolarizing and hyperpolarizing epochs, each lasting a few hundred milliseconds), however, were found to be resistant to PCT application, indicating that at least two forms of inhibition are present in the antennal lobe (MacLeod and Laurent, 1996; MacLeod et al., 1998). We explored here the hypothesis that slow inhibitory receptors—yet unidentified, but indicated by analysis of intracellular recordings (MacLeod and Laurent, 1996)—can underlie this slow patterning. We used an existing model of GABAB receptor kinetics (Dutar and Nicoll, 1988; Destexhe et al., 1996) to describe slow inhibition in the antennal lobe. We modified some of this model’s parameters so as to cause significant receptor activation after only 2–3 rather than 5–6 presynaptic spikes, as required in models of the thalamus (Destexhe et al., 1996). This modification was required given the low peak frequency of LN output (20–30 Hz).
Slow Inhibition and PN Firing Patterns
As previously reported, stimulus-dependent temporal variations of activity in the LN population can produce the fine (cycle-by-cycle) structure of transient PN synchronization (Bazhenov et al., 2001). Reducing the number of LN spikes during a given oscillation cycle reduces synchrony in postsynaptic PNs and, thus, oscillatory power in the field potential. By contrast, when the number of activated LNs exceeds a certain value, the PN postsynaptic to these LNs fires a spike that is synchronized with the population response. Thus, temporal variations in the distribution of activated LNs can create a corresponding temporal variation in the structure of the global PN output. These variations are mainly controlled by inter-LN inhibition and LN spike adaptation (Bazhenov et al., 2001).
We now show that slow inhibition with decay time constants of a few hundred milliseconds can further organize PN output by creating realistic slow temporal patterns (alternating active and inactive epochs) within PN spike trains, while preserving the fine structure of spike synchronization. When slow inhibition was reduced or eliminated, this slow, large-scale temporal structure was abolished; PNs either fired at each cycle of the network oscillations for as long as a stimulus was present (and some time after stimulus termination) or were silent but displayed subthreshold oscillations. Analysis of the fine temporal structure of PN spike trains in the intact network model shows that PNs, at each cycle of stimulus-evoked oscillatory activity, could (1) produce a spike that was synchronized with the network; (2) produce a spike that was not synchronized; or (3) just skip the cycle and produce no spike. This structure, comprising both fast and slow modulations of PN spike output, was stimulus and PN specific, as observed experimentally. Note that the identities of active neurons (the “spatial” code) contribute to this coding scheme: some olfactory neurons never spike in response to a given stimulus while others do. However, the set of responding neurons is not fixed but evolves over time in a stimulus-dependent manner. This dynamic depends on the stimulus and on synaptic interconnections within the antennal lobe; changes in the balance between excitatory and inhibitory inputs to a given LN modulate its activity, which affects the firing rate and spike timing of its postsynaptic PNs. These results are consistent with earlier models of competition among olfactory glomeruli caused by lateral inhibition (Linster et al., 1994; Kerszberg and Masson, 1995).
Our model of information coding does not rely explicitly on spike phase in contrast to other models in which information is coded by relative time delays between spikes arriving from different neurons (Hopfield, 1995). Our model proposes that downstream neurons detect the presence of synchrony among spikes across PNs. This synchrony could, for example, be utilized by “coincidence detector” mechanisms in the locust mushroom body (Laurent and Naraghi, 1994). This hypothesis is supported by results showing a loss of information in spike trains evoked by different odors in locust β-lobe neurons after PN synchrony is abolished by application of PCT within the antennal lobe (MacLeod et al., 1998).
Slow versus Fast Inhibition
Blocking fast inhibition in our model mimicked experimental results obtained with PCT application. In the absence of fast inhibition, the field potential contained no oscillatory power but contained some DC component right after stimulus onset. The absence of oscillatory power was not the result of the neurons’ silence, but rather of PN desynchronization. Analysis of individual PN spike trains, however, showed that the large-scale temporal structure remained intact after PCT application, as observed experimentally (Stopfer et al., 1997; MacLeod et al., 1998). When the slow inhibitory conductance was progressively reduced in our model, PN responses changed markedly. In a network with intact fast inhibition, reducing slow inhibition eliminated slow temporal patterns while preserving spike synchronization. The oscillatory power of the field potential increased as more PNs contributed to the population response at each oscillation cycle. In a network where fast inhibition was blocked, reducing slow inhibition transformed PN responses to high-frequency firing that could persist even beyond stimulus offset. This shows that the slow inhibition used in our model is necessary and sufficient not only to obtain realistic slow temporal structures but also to explain the results of in vivo experiments, obtained under PCT application (MacLeod and Laurent, 1996; MacLeod et al., 1998).
Furthermore, the waveform of the field potential in the disinhibited model (large onset peak but no oscillation) matched those recorded in physiological experiments with novel stimulus applications, i.e., under conditions where oscillatory synchronization had not yet been established by repeated stimulation (see below; Stopfer and Laurent, 1999). This result suggests that the initial absence of oscillatory responses to novel odors may be due to initially weak inhibitory synapses between LNs and PNs. Facilitation of fast GABAergic synapses between LNs and PNs during repetitive stimulus presentations might thus be sufficient to explain the progressive refinement of ensemble representations of odors over repeated stimulation (Stopfer and Laurent, 1999). This prediction can now be tested experimentally.
Slow Inhibition and Stimulus Discrimination
Slow inhibition provides an important means to discriminate odors. In the locust antennal lobe, information carried by about 90,000 afferent axons is compressed to about 800 output fibers (PNs) (Laurent, 1996). This compression involves the transformation of odor codes from an identity to an identity-temporal reference frame. It appears that both fast and slow features of PN spike patterns play a role in odor coding (MacLeod and Laurent, 1996; Stopfer et al., 1997). In zebrafish, the slow temporal patterning in mitral cells (the functional analogs in the olfactory bulb of antennal lobe PNs) appears to play a major role in the decorrelation of odor representations, a process that helps reduce overlap between similar representations over the duration of single stimuli (Friedrich and Laurent, 2001). Our model predicts that similar decorrelation can be found in the locust antennal lobe. This model shows that during stimulation with spatially overlapping stimuli, the initial clusters of activated PNs disappeared; representations that were initially similar became decorrelated, thus increasing stimuli separation (Figure 7A).
We tested our model antennal lobe network’s ability to discriminate between stimuli. Blocking only fast inhibition did not affect the discriminability of single PN spike trains evoked by different odors (Figure 7B). This result is in agreement with experimental data obtained in vivo (MacLeod et al., 1998). We previously reported a larger increase in the rate of misclassifications after partially blocking fast GABAergic connections in a model where the effect of the slow inhibitory receptors was essentially absent (Bazhenov et al., 2001). Surprisingly, eliminating slow inhibition while keeping fast inhibitory connections intact did not affect the network’s ability to discriminate among stimuli. The fine temporal structure (alternation of epochs with or without precise synchronization between PN spikes and field potential oscillations) was sufficient to separate even responses evoked by spatially overlapping stimuli. Our results suggest that fast and slow inhibition in the antennal lobe constitute complementary mechanisms for stimulus encoding and discrimination. Thus, the existence of stimulus-specific information across a wide range of time-scales enables a decoder to categorize and identify odors appropriately, even in the absence of some normal response features.
Our model of olfactory sensory processing is sensitive to small differences between stimuli even when these stimuli evoke activity in significantly overlapping ensembles of neurons. This sensitivity does not necessarily reduce the robustness of stimulus representations to noise or input fluctuations. Olfactory stimuli provide a prolonged input to the sets of antennal lobe neurons. Thus, we speculate that a stimulus does not simply set the initial state of a fixed dynamical system, but instead that each stimulus creates a new and unique dynamical system (Laurent et al., 2001). This dynamical system has a stimulus-specific global attractor that determines its spatiotemporal response pattern or trajectory. Internal noise and input current fluctuations can in fact be useful as they help the dynamical system find the global at-tractor.
Short-Term Plasticity
It was shown recently that, during initial stimulation with novel odors, the fine temporal structure is absent from PN spike trains; this structure emerges only after repeated or prolonged stimulation (Stopfer and Laurent, 1999). Results from our model suggest progressive strengthening of initially weak GABAA synapses between LNs and PNs may cause this effect. In disinhibited networks, individual neurons fire at higher rates, leading to strong activation of slow inhibitory receptors, thus increasing their effectiveness in organizing slow temporal patterns. This patterning appears critical for preliminary identification of a novel odor (Stopfer and Laurent, 1999) and weak, fast inhibition may be critical for raising the sensitivity of the naive system in conditions where no prediction can be made about forthcoming stimuli. Once a given odor has been detected (and thus coarsely encoded), modifying the intrinsic and synaptic properties of the antennal lobe neurons during subsequent presentations of the same odor via an increase in fast GABAergic inhibition (Bazhenov et al., unpublished data), leads to the appearance of the coordinated fine temporal structures in PN ensembles that is essential for precise odor identification (Stopfer et al., 1997). This phenomenon may also contribute to the identification of odors at low concentrations that may produce relatively weak responses in the antennal lobe network. Our model now enables us to test these ideas and investigate the mechanisms underlying fast “adaptation” in its most general form, in a sensory system during realistic stimulation conditions. Long-term synaptic plasticity in the olfactory network may further reorganize spatiotemporal patterns of activity. A model of olfactory memory based on altering lateral inhibition in the honeybee’s antennal lobe has been proposed (Linster and Masson, 1996). Further experiments are needed to establish conditions for long-term synaptic modifications in the antennal lobe.
Experimental Procedures
Each PN and LN was modeled by a single compartment that included voltage- and Ca2+-dependent currents described by Hodgkin-Huxley kinetics (Hodgkin and Huxley, 1952):
| CmdVdt=−gL(V−EL)−Iint−Isyn, | (1) |
|---|
where V is the membrane potential, Cm is the membrane capacitance, gL is the leakage conductance, EL is the leak reversal potential, Iint is a sum of active intrinsic currents (Ijint) and Isyn is a sum of synaptic currents (Ijsyn).
Intrinsic Currents
For the LNs we included a transient Ca2+ current IN (Laurent et al., 1993), a calcium-dependent potassium current IK(Ca) (Sloper and Powell, 1978), a fast potassium current IK (Traub and Miles, 1991), and a potassium leak current IKL. For the PNs we included a fast sodium current INa (Traub and Miles, 1991), a fast potassium current IK (Traub and Miles, 1991), a transient potassium A current IA (Huguenard et al., 1991), and a potassium leak current IKL.
The expressions for voltage- and Ca2+-dependent transition rates for all currents are given in Bazhenov et al. (2001).
Synaptic Currents
All synaptic currents were calculated according to
| Isyn=gsyn[O](t)(V−Esyn), | (2) |
|---|
where gsyn is the peak conductance, Esyn is the synaptic reversal potential, and [_O_](_t_) is the fraction of open channels. The reversal potentials were EnACh = 0 mV for cholinergic synapses, EGABA = −70 mV for fast GABAergic synapses, and EK = −95 mV for slow inhibitory synapses.
Fast GABA and nicotinic cholinergic synaptic currents were modeled by first-order activation schemes (see review in Destexhe et al., 1994):
| d[O]dt=α(1−[O])[T]−β[O]. | (3) |
|---|
The release of transmitter [_T_] for cholinergic synapses was modeled by a square pulse [_T_](_t_) = Aθ(t0 + tmax − t)θ(t − t0) with duration tmax = 0.3 ms and amplitude A = 0.5 triggered when the presynaptic voltage crosses 0 mV. For GABAergic (nonspiking) synapses we used a model with gradient activation [_T_](_t_) = 1/(1 + exp(−(V(t) − V0)/σ)), with V0 = −20 mV and σ = 1.5. The rate constants for all kinetic equations are given in Bazhenov et al. (2001).
Slow inhibitory receptors were introduced to investigate the slower (hundreds of milliseconds) temporal structure of PN activity. In our previous simulations, we introduced slow hyperpolarizing synaptic currents to prevent unrealistic overexcitation when fast GABAergic synapses were blocked (Bazhenov et al., 2001). Here, we both increased the peak conductance of the slow inhibition and modified its kinetic parameters, to ensure its activation during stimulus-evoked oscillations in the intact network.
Slow inhibitory receptors were modeled by a higher-order reaction scheme with kinetics similar to the model introduced for thalamocortical GABAB receptors (Dutar and Nicoll, 1988; Destexhe et al., 1996; Bazhenov et al., 1998):
| Islow-inh=gslow-inh[G]4[G]4+K(V−EK),d[G]dt=r3[R]−r4[G],d[R]dt=r1(1−[R])[T]−r2[R][T]=Aθ(t0+tmax−t)θ(t−t0), | (4) |
|---|
where [_R_](_t_) is the fraction of activated receptors, [_G_](_t_) is the concentration of receptor-coupled G proteins, EK = −95 mV is the potassium reversal potential, A = 0.5, tmax = 0.3 ms. The rate constants were _r_1 = 1 mM−1ms−1, _r_2 = 0.0025 ms−1, _r_3 = 0.1 ms−1, _r_4 = 0.06 ms−1, and K = 100 µM4.
Peak synaptic conductances were gGABAA = 0.4 µ_S_ between LNs; gGABAA = 0.8 µ_S_ between LNs and PNs; gslow-inh = 0.8 µ_S_ between LNs and PNs; gnACh = 0.3 µ_S_ between PNs and LNs; gnACh = 0.35 µ_S_ between PNs.
Figure 2B shows a computed fast GABAA IPSP alone (dashed line), and the sum of GABAA and slow GABA IPSPs (solid line) upon receiving 1, 2, or 3 presynaptic Ca2+ spikes. After 2 spikes the slow component of the IPSP dominated when compared to the effect of fast IPSP. Further increasing the number of incoming spikes produced a less dramatic change. The receptors were saturated after 4–5 presynaptic Ca2+ spikes (data not shown).
Network Geometry and Stimulation
We simulated a network of 90 PNs and 30 LNs, as in Bazhenov et al. (2001) (Figure 2A). All interconnections were random with a probability of 0.5. These probabilities are larger than those estimated from experimental data (G.L., unpublished data). However, in a network with more realistic neuron numbers (about 900 PNs and 300 LNs; Laurent, 1996), these probabilities would be rescaled to 0.05–0.1 (Bazhenov et al., 2001; Golomb and Hansel, 2000). Some of the intrinsic parameters of the neurons in the network were initialized with random variability to test for reliability. Also, small-amplitude currents in the form of Gaussian noise (σ ≈ 10%) were introduced into each cell to cause random and independent membrane potential fluctuations. To simulate odor stimulation, a randomly selected fraction of LNs and PNs was activated by a current pulse with a rise time constant of 100 ms and a decay time constant of 200 ± 100 ms. This current was simulated as total synaptic current produced by N = 200 independent Poisson distributed spike trains with an average rate of 100 Hz. The random current fluctuations were 5%–10% of its peak amplitude. Setting correlations among some of the otherwise independent Poisson-distributed spike trains resulted in little or no change in response patterns. The local field potential was calculated by averaging membrane potentials over the whole population of 90 PNs.
Computational Experimental Procedures
All simulations were performed using a fourth-order Runge-Kutta [RK(4)] integration method and in some cases an embedded Runge-Kutta [RK6(5)] method (Enright et al., 1995). The time step was 0.04 ms. Source C++ code was compiled on an Intel PC using GCC compiler (ver. 2.7.2.1). A simulation of 1 s of real time took about 15 min.
Cluster Analysis
Spike trains with duration T were divided into nonoverlapping bins of duration τ and the number of spikes in each bin was counted. Each trial was then represented by a vector in n = T/τ dimensional vector space. Repeated presentations of the same stimulus produced a set of points in this space and the centroid of this set was calculated. Two different stimuli were used to produce different clusters each defining a centroid. The Euclidean distances from each trial to the two centroids were then calculated and plotted against each other, as in MacLeod et al. (1998). Bins between 50 ms and 200 ms were tested to ensure the results were not dependent on the bin size.
Electrophysiology
Young adult locusts (Schistocerca americana) were immobilized with one antenna intact. The brain was exposed, desheathed, and continually superfused with oxygenated locust saline, as previously described (Laurent and Davidowitz, 1994).
Odor Stimulation
Odorants, 2–3 microliters of cherry (Bell Flavors) and spearmint (Flavco), were applied to small strips of filter paper and kept in separate cartridges. Desiccated and filtered air puffs (0.3 liter min−1) were delivered through the cartridges and then to the antenna by separate pipettes (1 cm inner diameter). Pipettes were placed 2–3 cm in front of the antenna. A10 cm diameter vacuum funnel placed 5 cm behind the antenna constantly drew background air over the antenna and rapidly vented the odors.
Recordings
Intracellular recordings from projection neurons were made using sharp glass micropipettes (200 MΩ, Sutter P87 horizontal puller, Novato, CA) filled with 0.5 M potassium acetate and amplified with DC amplifiers (Axon Instruments, Foster City, CA). Data were stored on digital audiotape (DAT 8 channel, 5 kHz sampling/channel, Micro Data, Woodhaven, NY) and analyzed off-line using NBM116L hardware, LabVIEW (National Instruments, Austin, TX) and MatLab (The MathWorks) software.
Acknowledgments
This research was supported by The Howard Hughes Medical Institute (M.B. and T.J.S.), The Sloan Center for Theoretical Neurobiology (Salk Institute [M.B. and T.J.S.] and Caltech [M.S. and G.L.]), the NIDCD (M.S. and G.L.), and the DOE (grant DE-FG03-96ER14592).
References
- Bazhenov M, Timofeev I, Steriade M, Sejnowski TJ. Cellular and network models for intrathalamic augmenting responses during 10 Hz stimulation. J. Neurophysiol. 1998;79:2730–2748. doi: 10.1152/jn.1998.79.5.2730. [DOI] [PubMed] [Google Scholar]
- Bazhenov M, Stopfer M, Rabinovich M, Huerta R, Abarbanel HDI, Sejnowski TJ, Laurent G. Model of transient oscillatory synchronization in the locust antennal lobe. Neuron. 2001;30:553–567. doi: 10.1016/s0896-6273(01)00284-7. this issue. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burrows M, Boeckh J, Esslen J. Physiological and morphological properties of interneurons in the deutocerebrum of male cockroaches which respond to female pheromone. J. Comp. Physiol. A. 1982;145:447–457. [Google Scholar]
- Chaput M, Holley A. Single unit responses of olfactory bulb neurons to odor presentation in awake rabbits. J. Physiol. 1980;76:551–558. [PubMed] [Google Scholar]
- Christensen T, Hildebrand J. Male-specific, sex phero-mone-selective projection neurons in the antennal lobes of the moth Manduca sexta. J. Comp. Physiol. A. 1987;160:553–569. doi: 10.1007/BF00611929. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Mainen ZF, Sejnowski TJ. Synthesis of models for excitable membranes, synaptic transmission and neuromodulation using a common kinetic formalism. J. Comp. Neurosci. 1994;1:195–230. doi: 10.1007/BF00961734. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Bal T, McCormick DA, Sejnowski TJ. Ionic mechanisms underlying synchronized oscillations and propagating waves in a model of ferret thalamic slices. J. Neurophysiol. 1996;76:2049–2070. doi: 10.1152/jn.1996.76.3.2049. [DOI] [PubMed] [Google Scholar]
- Dutar P, Nicoll RA. A physiological role for for GABAB receptors in the central nervous system. Nature. 1998;332:156–158. doi: 10.1038/332156a0. [DOI] [PubMed] [Google Scholar]
- Enright WH, Higham DJ, Owren B, Sharp PW. A survey of the explicit Runge-Kutta method. 1995 Available from ftp://ftp.cs.toronto.edu/pub/reports/na/cs-94-291.ps.Z. [Google Scholar]
- Friedrich R, Laurent G. Dynamical optimization of odor representations by slow temporal patterning of mitral cell activity. Science. 2001;291:889–894. doi: 10.1126/science.291.5505.889. [DOI] [PubMed] [Google Scholar]
- Golomb D, Hansel D. The number of synaptic inputs and the synchrony of large, sparse neuronal networks. Neural Comp. 2000;12:1095–1139. doi: 10.1162/089976600300015529. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. Lond. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hopfield JJ. Pattern recognition computation using action potential timing for stimulus representation. Nature. 1995;376:33–36. doi: 10.1038/376033a0. [DOI] [PubMed] [Google Scholar]
- Huguenard JR, Coulter DA, McCormick DA. A fast transient potassium current in thalamic relay neurons: kinetics of activation and inactivation. J. Neurophysiol. 1991;66:1305–1315. doi: 10.1152/jn.1991.66.4.1304. [DOI] [PubMed] [Google Scholar]
- Kauer JS. Response patterns of amphibian olfactory bulb neurons to odor stimulation. J. Physiol. Lond. 1974;243:695–715. doi: 10.1113/jphysiol.1974.sp010772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kauer JS, Shepherd GM. Analysis of the onset phase of olfactory bulb unit responses to odour pulses in the salamander. J. Physiol. Lond. 1977;272:495–516. doi: 10.1113/jphysiol.1977.sp012056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerszberg M, Masson C. Signal-induced selection among spontaneous oscillatory patterns in a model of honeybee olfactory glomeruli. Biol. Cybern. 1995;72:487–495. [Google Scholar]
- Laurent G. Dynamical representation of odors by oscillating and evolving neural assemblies. Trends Neurosci. 1996;19:489–496. doi: 10.1016/S0166-2236(96)10054-0. [DOI] [PubMed] [Google Scholar]
- Laurent G, Davidowitz H. Encoding of olfactory information with oscillating neural assemblies. Science. 1994;265:1872–1875. doi: 10.1126/science.265.5180.1872. [DOI] [PubMed] [Google Scholar]
- Laurent G, Naraghi M. Odorant-induced oscillations in the mushroom bodies of the locust. J. Neurosci. 1994;14:2993–3004. doi: 10.1523/JNEUROSCI.14-05-02993.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurent G, Seymour-Laurent KJ, Johnson K. Dendritic excitability and a voltage-gated calcium current in locust non-spiking local interneurons. J. Neurophysiol. 1993;69:1484–1498. doi: 10.1152/jn.1993.69.5.1484. [DOI] [PubMed] [Google Scholar]
- Laurent G, Wehr M, Davidowitz H. Temporal representations of odors in an olfactory network. J. Neurosci. 1996;16:3837–3847. doi: 10.1523/JNEUROSCI.16-12-03837.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurent G, Stopfer M, Friedrich RW, Rabinovich M, Volkovskii A, Abarbanel H. Odor encoding as an active, dynamical process: experiments, computation, and theory. Annu. Rev. Neurosci. 2001 doi: 10.1146/annurev.neuro.24.1.263. in press. [DOI] [PubMed] [Google Scholar]
- Linster C, Masson C. A neural model of olfactory sensory memory in the honeybee’s antennal lobe. Neural Comp. 1996;8:94–114. [Google Scholar]
- Linster C, Marsan D, Masson C, Kerszberg M. Odor processing in the bee: a preliminary study of the role of central input to the antennal lobe. In: Cowan JD, Tesauro G, Alspector J, editors. Advances in Neural Information Processing Systems 6. San Francisco, CA: Morgan Kaufman; 1994. pp. 527–534. [Google Scholar]
- Meredith M. Patterned response to odor in mammalian olfactory bulb: the influence of intensity. J. Neurophysiol. 1986;56:572–597. doi: 10.1152/jn.1986.56.3.572. [DOI] [PubMed] [Google Scholar]
- Meredith M. Neural circuit computation: complex patterns in the olfactory bulb. Brain Res. Bull. 1992;29:111–117. doi: 10.1016/0361-9230(92)90014-o. [DOI] [PubMed] [Google Scholar]
- MacLeod K, Laurent G. Distinct mechanisms for synchronization and temporal patterning of odor-encoding neural assemblies. Science. 1996;274:976–979. doi: 10.1126/science.274.5289.976. [DOI] [PubMed] [Google Scholar]
- MacLeod K, Backer A, Laurent G. Who reads temporal information contained across synchronized and oscillatory spike trains? Nature. 1998;395:693–697. doi: 10.1038/27201. [DOI] [PubMed] [Google Scholar]
- Sloper JJ, Powell TPS. Ultrastructural features of the sensori-motor cortex of the primate. Phil. Trans. R. Soc. Lond. B Biol. Sci. 1978;285:124–139. [PubMed] [Google Scholar]
- Stopfer M, Laurent G. Short-term memory in olfactory network dynamics. Nature. 1999;402:664–668. doi: 10.1038/45244. [DOI] [PubMed] [Google Scholar]
- Stopfer M, Bhagavan S, Smith BH, Laurent G. Impaired odour discrimination on desynchronization of odour-encoding neural assemblies. Nature. 1997;390:70–74. doi: 10.1038/36335. [DOI] [PubMed] [Google Scholar]
- Traub RD, Miles R. Neuronal Networks of the Hippocampus. Cambridge: Cambridge University Press; 1991. [Google Scholar]
- Wehr M, Laurent G. Odor encoding by temporal sequences of firing in oscillating neural assemblies. Nature. 1996;384:162–166. doi: 10.1038/384162a0. [DOI] [PubMed] [Google Scholar]
- Wehr M, Laurent G. Relationship between afferent and central temporal patterns in the locust olfactory system. J. Neurosci. 1999;19:381–390. doi: 10.1523/JNEUROSCI.19-01-00381.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]