A Tobit Variance-Component Method for Linkage Analysis of Censored Trait Data (original) (raw)
Abstract
Variance-component (VC) methods are flexible and powerful procedures for the mapping of genes that influence quantitative traits. However, traditional VC methods make the critical assumption that the quantitative-trait data within a family either follow or can be transformed to follow a multivariate normal distribution. Violation of the multivariate normality assumption can occur if trait data are censored at some threshold value. Trait censoring can arise in a variety of ways, including assay limitation or confounding due to medication. Valid linkage analyses of censored data require the development of a modified VC method that directly models the censoring event. Here, we present such a model, which we call the “tobit VC method.” Using simulation studies, we compare and contrast the performance of the traditional and tobit VC methods for linkage analysis of censored trait data. For the simulation settings that we considered, our results suggest that (1) analyses of censored data by using the traditional VC method lead to severe bias in parameter estimates and a modest increase in false-positive linkage findings, (2) analyses with the tobit VC method lead to unbiased parameter estimates and type I error rates that reflect nominal levels, and (3) the tobit VC method has a modest increase in linkage power as compared with the traditional VC method. We also apply the tobit VC method to censored data from the Finland–United States Investigation of Non–Insulin-Dependent Diabetes Mellitus Genetics study and provide two examples in which the tobit VC method yields noticeably different results as compared with the traditional method.
Introduction
Variance-component (VC) linkage analysis (Amos 1994; Almasy and Blangero 1998) is an attractive, nearly mode-of-inheritance–free method for the mapping of genes that influence quantitative traits. Simulation studies (Amos et al. 1996; Williams and Blangero 1999) have shown that the VC method has increased power to map genes as compared with relative-pair–based methods, such as the Haseman-Elston method (Haseman and Elston 1972) and the sib-pair method of Kruglyak and Lander (1995). The increased power of the VC method is due, in part, to its ability to analyze data on all relatives in a family simultaneously. Another attractive feature of the VC method is its flexible modeling structure, which allows one to accommodate and test multiple genetic and environmental effects and interactions. The flexible structure of the VC method allows one to model measured covariate effects in the mean structure and to incorporate unmeasured genetic and environmental effects (as well as potential interactions) in the covariance structure. One can estimate parameters by using maximum-likelihood procedures, and one can construct linkage tests by examining the variance-parameter estimates associated with the unmeasured genetic effects of the model.
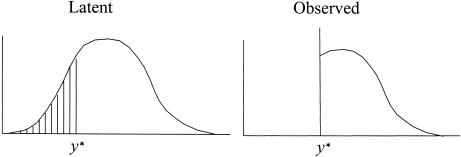
The traditional VC method assumes that, within a family, the quantitative-trait data either follow or can be transformed to follow a multivariate normal distribution. Studies have shown that violation of this assumption can lead to biased parameter estimates (Amos et al. 1996) and an increase in false-positive linkage findings (Allison et al. 1999; Blangero et al. 2001). Violation of this assumption can occur for many reasons, but one potential cause is trait censoring. We show an example of trait censoring in figure 1. Here, the latent distribution of the trait data is normal. However, for some reason, latent trait values less than some threshold y* are observed to be at y*. Therefore, the data are censored at y*.
Figure 1.
Example of censoring for a normally distributed trait. Latent trait values truly less than y* are observed at y*.
Trait censoring can arise in several ways. The trait assay may fail to detect values smaller (or larger) than some general threshold y*. We have observed this phenomenon in the genetic analysis of coronary artery calcification (a predictor of coronary artery disease) in the Rochester Family Heart Study (Maher et al. 1996; Bielak et al. 2001). One way to measure the amount of coronary artery calcification consists of using an imaging procedure, such as electron-beam computer tomography (Agatston et al. 1990). This procedure takes digital cross-section slides of a subject’s heart and, utilizing the slide pixels that contain calcium, determines the amount of coronary artery calcification. However, Bielak et al. (2001) considered coronary artery calcification as present only when at least four contiguous slide pixels contained calcium. Therefore, coronary artery calcium levels corresponding to fewer than four contiguous slide pixels were not observed and were assumed to be 0. In the Bielak et al. (2001) data set, ∼50% of the coronary artery calcium data were censored at this threshold.
Trait censoring may also arise from subject-specific thresholds, owing to factors such as medication. For example, in the study of cholesterol, doctors likely will place a subject with truly high cholesterol on medication, seeking to reduce that subject’s observed cholesterol such that it is in a normal range. Therefore, the true latent cholesterol of the subject is almost certainly greater than or equal to the observed value. The subject’s trait value is then censored at the observed value, owing to medication. We have observed this phenomenon in the genetic analyses of cholesterol, high-density lipoprotein ratio (HDLR) (which is the ratio of high-density lipoprotein:total cholesterol), and triglyceride (TG) in the Finland–United States Investigation of Non–Insulin-Dependent Diabetes Mellitus Genetics (FUSION) study (Valle et al. 1998). Approximately 30% of these trait data are censored at subject-specific thresholds, owing to anti-lipid medication.
Proper analysis of censored trait data by the VC method requires correct modeling of the censoring event. If the censoring event is ignored and one analyzes the trait data with the assumption that the observed trait distribution is normal, then parameter estimates from the VC method likely will be biased. For the censoring example in figure 1, our results show that analysis of the observed data when censoring is ignored leads to an overestimate of the mean of the trait and an underestimation of the variance of random effects. Also, failure to account for the censoring event leads to the false impression of increased trait similarity among relatives and can lead to an increase in false-positive linkage findings.
To support linkage analysis for these situations, we have extended the traditional VC method to accommodate censored data. To do this, we use the work of Tobin (1958), who developed a regression-based method for the analysis of censored normal data when independent observations are assumed. To account for censoring, as shown in figure 1, Tobin defined the likelihood of a censored observation y* as the probability that the observed value is ⩽y*. By doing this, Tobin accounted for the possibility that the latent value of a censored observation is actually smaller than the observed value y*. We have modified the method of Tobin to account for censored normal trait data among related individuals by using random effects. Our method, which we call the “tobit VC method,” has all the benefits of the traditional VC method, but it properly accounts for censoring in quantitative-trait data within families and can accommodate both global and subject-specific censoring thresholds.
In subsequent sections, we develop the traditional and tobit VC methods and describe the methods’ similarities and differences. We describe estimation procedures and develop statistical tests for detecting linkage at a major-gene locus. We also compare and contrast the characteristics of the tobit and traditional VC methods for accommodating censoring by applying both methods to simulated censored data. Finally, we illustrate the use of the tobit VC model by applying it to censored trait data from the FUSION study.
Methods
Derivation of Traditional VC Method Using a Generalized-Linear-Mixed-Model Framework
We derive the traditional VC method using the generalized-linear-mixed-model framework of Breslow and Clayton (1993). We show this derivation in order to illustrate the differences between the traditional VC method and the subsequent tobit VC method. Consider a family of n relatives. Let y j denote the trait value of the j_th relative and let 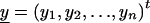 denote the trait data for the entire family. We model y j as the sum of independent effects due to both measured and unmeasured factors. Measured factors (covariates) are directly observable and can include such effects as age and gender. We let X j denote a vector of such covariates for the j_th relative. For unmeasured factors, we assume effects due to unmeasured major-gene (MG), polygene (PG), and subject-specific environmental (E) effects. We assume the subject-specific random effects MG j, PG j, E j for the j_th relative are independent and normally distributed with means 0 and variances σ2_mg, σ2_pg, and σ2_e, respectively.
denote the trait data for the entire family. We model y j as the sum of independent effects due to both measured and unmeasured factors. Measured factors (covariates) are directly observable and can include such effects as age and gender. We let X j denote a vector of such covariates for the j_th relative. For unmeasured factors, we assume effects due to unmeasured major-gene (MG), polygene (PG), and subject-specific environmental (E) effects. We assume the subject-specific random effects MG j, PG j, E j for the j_th relative are independent and normally distributed with means 0 and variances σ2_mg, σ2_pg, and σ2_e, respectively.
Let U _j_=MG j+PG j denote the total unmeasured genetic effects for the _j_th relative and let 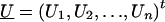 indicate the set of unmeasured genetic effects for the family. Conditional on U , _y_1,y_2,…,y n are independent normal random variables with mean
indicate the set of unmeasured genetic effects for the family. Conditional on U , _y_1,y_2,…,y n are independent normal random variables with mean 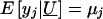 and variance
and variance 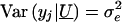 . We model μ_j by using the linear mixed model
. We model μ_j by using the linear mixed model

where β denotes a vector of regression coefficients for the covariates. For simplicity, we assume that X j contains an intercept.
To construct the likelihood of 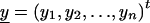 , we condition on U such that
, we condition on U such that
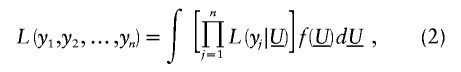
owing to the independence of y_1,y_2,…,y n conditional on U. Given our assumption of the conditional trait normality of 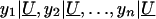 ,
,
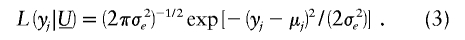
The final step in the construction of likelihood (2) requires the specification of the distribution of 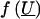 . We assume that
. We assume that 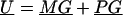 has a multivariate normal distribution with mean vector 0 and covariance matrix Σ=σ2_mg_·Π+σ2_pg_·2Φ. The matrix Π is the n_×_n matrix with (j,k)th element π_jk_, which denotes the proportion of alleles shared identical by descent (IBD) at the major gene by relatives j and k; generally, we cannot observe π_jk_ but can efficiently estimate this proportion by using a multipoint algorithm (e.g., see Lander and Green 1987; Fulker et al. 1995) that uses available marker data and a known marker map. The matrix 2Φ is the n_×_n matrix with (j,k)th element 2φ_jk_, which is defined as the expected proportion of genes shared IBD by relatives j and k.
has a multivariate normal distribution with mean vector 0 and covariance matrix Σ=σ2_mg_·Π+σ2_pg_·2Φ. The matrix Π is the n_×_n matrix with (j,k)th element π_jk_, which denotes the proportion of alleles shared identical by descent (IBD) at the major gene by relatives j and k; generally, we cannot observe π_jk_ but can efficiently estimate this proportion by using a multipoint algorithm (e.g., see Lander and Green 1987; Fulker et al. 1995) that uses available marker data and a known marker map. The matrix 2Φ is the n_×_n matrix with (j,k)th element 2φ_jk_, which is defined as the expected proportion of genes shared IBD by relatives j and k.
Given the derivation of the likelihood for one family in equations (2) and (3), the construction of the full likelihood for the trait data of I independent (unrelated) families is the product of such likelihoods for all I families
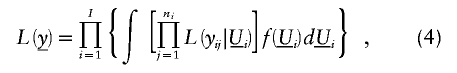
in the obvious notation.
We can use likelihood (4) to test the hypothesis of linkage at the major gene _H_0:σ2_mg_=0 versus H A:σ2_mg_>0 by constructing a likelihood-ratio statistic that is 2loge of the ratio of the likelihood fit under the alternative and null hypotheses. Because the null hypothesis is on the boundary of the parameter space, the likelihood-ratio statistic is asymptotically distributed as a (1/2):(1/2) mixture of χ21 and a point mass at 0 under the null hypothesis of no linkage (Self and Liang 1987). As an alternate statistic, we can calculate the LOD score (Morton 1955), which is log10 of this likelihood ratio.
Tobit VC Method
The tobit VC method requires the modification of likelihood (3) to account for the censoring event. Here, we assume that censoring results in setting all trait values less than some threshold y* equal to y* (fig. 1). Extension of the tobit VC method to other censoring events (e.g., subject-specific thresholds owing to medication) is straightforward.
Following Tobin (1958), the tobit likelihood 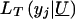 takes one of two forms, depending on whether the observed y j is equal to or greater than y*:
takes one of two forms, depending on whether the observed y j is equal to or greater than y*:
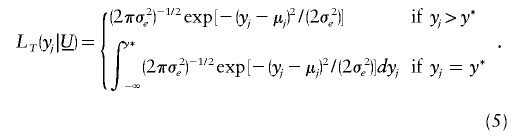
When y _j_>y*, 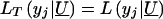 in likelihood (3) (for the traditional VC method). However, when y _j_=y*,
in likelihood (3) (for the traditional VC method). However, when y _j_=y*, 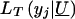 models the probability that y j_⩽_y* and thereby accommodates the censoring event.
models the probability that y j_⩽_y* and thereby accommodates the censoring event.
Specifying 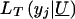 and assuming that U follows the same multivariate normal distribution described above, we obtain the full likelihood for I families for the tobit VC method:
and assuming that U follows the same multivariate normal distribution described above, we obtain the full likelihood for I families for the tobit VC method:
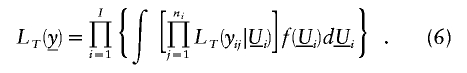
As before, we can apply likelihood (6) to test for linkage.
Unlike likelihood (4) (for the traditional variance-component method), the integrals in likelihood (6) do not have a closed-form solution, which complicates inference. To resolve this issue, we apply the numerical-integration method of adaptive Gaussian quadrature (Pinheiro and Bates 1995) as implemented in the SAS procedure PROC NLMIXED. We choose the number of quadrature points, Q, at which the function will be evaluated. With _Q_=1, adaptive Gaussian quadrature of likelihood (6) corresponds to a Laplace approximation (Breslow and Clayton 1993). As Q increases, the approximation of the integral in likelihood (6) becomes more accurate. However, the complexity of the maximization algorithm also increases, which leads to longer computer run times. Therefore, we choose a Q value that suitably approximates the likelihood but allows efficient computation. Our analyses to date suggest that _Q_=5 quadrature points is adequate for accurate likelihood approximation and allows reasonably efficient computation.
Simulations
We performed computer simulations with data sets of 400 sib trios, to compare the characteristics of the traditional and tobit VC methods for the analysis of censored normal data. We simulated trait data for a sib trio by use of mixed model (1) and the covariance matrix Σ. We generated trait data assuming an assortment of trait models that varied the values of σ2_mg_, σ2_pg_, and σ2_e_, resulting in traits with different values of overall genetic heritability 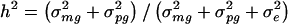 and major-gene heritability
and major-gene heritability 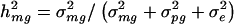 . After we simulated the latent trait values, we censored those values below a threshold that corresponded to the 25th percentile of the latent population distribution.
. After we simulated the latent trait values, we censored those values below a threshold that corresponded to the 25th percentile of the latent population distribution.
To simulate marker data, we first placed the major gene at the center of a 110-cM chromosome. We simulated a 10-cM map of 12 genetic markers each with four equally frequent alleles. At each locus, we randomly assigned alleles to the parents of a sib trio, after which we generated offspring genotypes by assuming the Haldane mapping function. We then removed the genotypes of the parents from the data set.
We analyzed the censored data by using both the traditional VC method, which ignores censoring, and the tobit VC method, which models censoring. We estimated IBD sharing at the major-gene locus by using the Lander-Green algorithm (Lander and Green 1987) as implemented in Genehunter (Kruglyak et al. 1996). We tested the linkage hypothesis _H_0:σ2_mg_=0 versus H A:σ2_mg_>0 by fitting likelihoods (4) (for the traditional VC method) and (6) (for the tobit VC method) using the SAS procedure PROC NLMIXED.
To determine whether the traditional and tobit VC methods had appropriate size under the null hypothesis of no linkage, we performed simulations assuming trait models with overall genetic heritability _h_2 of 0.25, 0.33, 0.50, or 0.75 and the major-gene heritability _h_2_mg_=0. For each model, we assumed that the trait originated from mixed model (1) when an intercept and no covariates are also assumed. For each trait model, we analyzed 3,000 replicate data sets.
We also performed simulations that compared the power of the traditional and tobit VC methods and that assessed the bias of the parameter estimates  . We considered trait models 1, 2, 3, and 4 with respective
. We considered trait models 1, 2, 3, and 4 with respective  parameter values of (0.20, 0.80, 1.00), (0.40, 2.60, 1.00), (0.50, 0.50, 1.00), and (1.00, 2.00, 1.00), corresponding to
parameter values of (0.20, 0.80, 1.00), (0.40, 2.60, 1.00), (0.50, 0.50, 1.00), and (1.00, 2.00, 1.00), corresponding to  values of (0.10, 0.50), (0.10, 0.75), (0.25, 0.50), and (0.25, 0.75). We analyzed 1,000 replicate data sets under each trait model. To ensure proper power comparisons between the traditional and tobit VC methods for a given trait model, we adjusted for each method’s empirical size under the corresponding null trait model, which assumed the same _h_2 but assumed _h_2_mg_=0.
values of (0.10, 0.50), (0.10, 0.75), (0.25, 0.50), and (0.25, 0.75). We analyzed 1,000 replicate data sets under each trait model. To ensure proper power comparisons between the traditional and tobit VC methods for a given trait model, we adjusted for each method’s empirical size under the corresponding null trait model, which assumed the same _h_2 but assumed _h_2_mg_=0.
To determine the impact that censoring had on covariate estimates, we conducted additional simulations that incorporated covariates into the trait model with 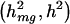 =
= 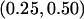 . We assumed two covariates, one binary and the other continuous and normally distributed. We set the binary regression coefficient βB = 0.20 and the normal regression coefficient βN = 0.50 and simulated 500 additional replicate data sets. We again analyzed the data sets by using both the traditional and tobit VC methods.
. We assumed two covariates, one binary and the other continuous and normally distributed. We set the binary regression coefficient βB = 0.20 and the normal regression coefficient βN = 0.50 and simulated 500 additional replicate data sets. We again analyzed the data sets by using both the traditional and tobit VC methods.
Application to FUSION Data Set
We analyzed a subset of the FUSION replicate data set; this subset, FUSION2, consists of 558 affected siblings in 238 sibships. These families were assayed for a variety of diabetes-related quantitative traits. Here, we focus on HDLR and TG. After transforming the traits to approximate normality, we performed a genome scan using the traditional VC method. We estimated IBD along the genome by using the Lander-Green algorithm (Lander and Green 1987) as implemented in Genehunter (Kruglyak et al. 1996). Analyses revealed an interesting linkage signal for HDLR on chromosome 2 and for TG on chromosome 20.
The original analyses of these traits assumed no censoring. However, ∼30% of the affected siblings were on anti-lipid medication. For medicated subjects, such treatment is expected to increase the level of HDLR and decrease the level of TG. Even though medicated subjects in the FUSION study were asked to stay off their anti-lipid medication 24 h prior to data collection, lingering effects of medication may influence these quantitative traits such that observed values are different from latent values.
To determine the impact that censoring had on results for these traits, we applied our tobit VC method to the HDLR data on chromosome 2 (with an average intermarker distance of 8.3 cM) and the TG data on chromosome 20 (with an average intermarker distance of 1.8 cM). For medicated subjects, latent trait values for HDLR were assumed to be less than or equal to observed values, and latent trait values for TG were assumed to be greater than or equal to the observed values. No restrictions were made on the trait values of nonmedicated subjects. We assumed the normality of latent trait values for both analyses.
Results
Empirical Type I Error Rates
In table 1, we show the empirical significance levels at α=0.05 and α=0.01 and the mean likelihood-ratio statistic across the 3,000 replicate data sets for each trait model. Under the null hypothesis of no linkage, the likelihood-ratio statistic asymptotically follows a (1/2):(1/2) mixture of χ21 and a point mass of 0. Therefore, the expected value of the likelihood-ratio statistic should be 0.50.
Table 1.
Empirical Type I Error Rates of VC Methods for Testing of _H_0:σ2_mg_=0 versus H A:σ2_mg_>0 under 25% Trait Censoring[Note]
| Traditional VC Method | Tobit VC Method | |||||
|---|---|---|---|---|---|---|
| Empirical Type I Error Rate When | Empirical Type I Error Rate When | |||||
| Overall TraitHeritabilitya | α = .05 | α = .01 | Mean LRStatisticb | α = .05 | α = .01 | Mean LRStatisticb |
| _h_2=.25 | .0570 | .0107 | .5177 | .0510 | .0090 | .5051 |
| _h_2=.33 | .0577 | .0120 | .5266 | .0487 | .0097 | .4859 |
| _h_2=.50 | .0590 | .0137 | .5590 | .0506 | .0103 | .5024 |
| _h_2=.75 | .0663 | .0183 | .5635 | .0503 | .0097 | .4788 |
On the basis of empirical P values and the mean likelihood-ratio statistic, all four trait models show that the traditional VC method has elevated empirical type I error relative to the nominal in testing for linkage of a quantitative trait with 25% censoring. We expect this finding, considering that, when censoring is ignored, the observed trait values within sib trios appear to be more similar than the corresponding latent values. Type I error for the traditional VC method increased with an increase in overall genetic heritability _h_2. For nominal α=0.05, the type I error ranged between 0.0570 (when _h_2=0.25) and 0.0663 (when _h_2=0.75). For nominal α=.01, the type I error ranged between 0.0107 (when _h_2=0.25) and 0.0183 (when _h_2=0.75). Increased overall genetic heritability leads to increased trait similarity among relatives, which can lead to an increase in false-positive linkage findings at a major-gene locus. Whereas the traditional VC method has elevated type I error, the tobit VC method’s type I error rates for the four trait models closely mirror those of the nominal at α=0.05 and α=0.01.
Empirical Power for Detecting Linkage
In table 2, we show the empirical power of the traditional and tobit VC methods for testing the linkage hypothesis _H_0:σ2_mg_=0 versus H A:σ2_mg_>0 at α=0.05 and α=0.01 across 1,000 replicate data sets for each of the four different trait models described in the “Methods” section. For a trait model with specific _h_2 and h_2_mg , we determined the critical regions for rejecting the linkage hypothesis under the traditional and tobit VC methods using the corresponding type I error results when the same _h_2 and _h_2_mg_=0 are assumed.
Table 2.
Empirical Power of VC Methods for Testing of _H_0:σ2_mg_=0 versus H A:σ2_mg_>0 under 25% Trait Censoring for Four Trait Models[Note]
| Empirical Powerb for | ||||
|---|---|---|---|---|
| TraditionalVC Method | Tobit VCMethod | |||
| Trait Modela | α=.05 | α=.01 | α=.05 | α=.01 |
| Model 1 (_h_2=.50; _h_2_mg_=.10) | .2467 | .0904 | .2744 | .0925 |
| Model 2 (_h_2=.75; _h_2_mg_=.10) | .3010 | .1020 | .3230 | .1480 |
| Model 3 (_h_2=.50; _h_2_mg_=.25) | .7800 | .5340 | .8240 | .5730 |
| Model 4 (_h_2=.75; _h_2_mg_=.25) | .8820 | .6800 | .9200 | .7640 |
As expected, our results show that the power of both VC methods to detect linkage at the major gene increases as the variance due to the major gene increases. However, our results also show that the tobit VC method has somewhat greater power to detect linkage, as compared with the traditional VC method, for all four trait models at both significance levels of α. The power discrepancy between the two VC methods increases as the variance due to the major gene increases. Therefore, the tobit VC method will be a particularly important tool for the mapping of genes with high heritability that influence censored traits.
Effect of Censoring on Variance and Heritability Estimates
Table 3 reveals the mean parameter estimates for both VC methods when 25% trait censoring is assumed. The traditional VC method severely underestimates the true values of σ2_mg_, σ2_pg_, and σ2_e_ for all four trait models. Estimates of σ2_mg_, σ2_pg_, and σ2_e_ for the four trait models averaged 58%–65%, 56%–57%, and 68%–76% of the true values, respectively. We expected this finding, because the traditional VC method assumes that the overall variance of the observed (censored) distribution is correct. Because the variance of the observed distribution is smaller than the overall variance of the latent distribution, the traditional VC method yields variance-parameter estimates that severely underestimate the true variance-parameter values in the latent distribution.
Table 3.
Mean Parameter Estimates of VC Methods under 25% Trait Censoring for Four Trait Models[Note]
| Mean ParameterEstimate (Mean SE) for | |||
|---|---|---|---|
| Parametera | True Value | Traditional VC Method | Tobit VC Method |
| Model 1: | |||
| σ2_mg_ | .20 | .129 (.098) | .214 (.168) |
| σ2_pg_ | .80 | .448 (.140) | .783 (.241) |
| σ2_e_ | 1.00 | .679 (.078) | 1.003 (.132) |
| h_2_mg | .10 | .099 (.070) | .103 (.076) |
| _h_2 | .50 | .453 (.084) | .493 (.085) |
| Model 2: | |||
| σ2_mg_ | .40 | .261 (.181) | .421 (.309) |
| σ2_pg_ | 2.60 | 1.485 (.285) | 2.512 (.469) |
| σ2_e_ | 1.00 | .763 (.148) | 1.040 (.231) |
| h_2_mg | .10 | .103 (.066) | .108 (.070) |
| _h_2 | .75 | .695 (.059) | .738 (.058) |
| Model 3: | |||
| σ2_mg_ | .50 | .292 (.116) | .496 (.199) |
| σ2_pg_ | .50 | .283 (.146) | .503 (.252) |
| σ2_e_ | 1.00 | .677 (.077) | 1.001 (.131) |
| h_2_mg | .25 | .233 (.079) | .248 (.084) |
| _h_2 | .50 | .459 (.086) | .499 (.087) |
| Model 4: | |||
| σ2_mg_ | 1.00 | .624 (.211) | 1.030 (.356) |
| σ2_pg_ | 2.00 | 1.120 (.300) | 1.900 (.488) |
| σ2_e_ | 1.00 | .759 (.148) | 1.040 (.231) |
| h_2_mg | .25 | .250 (.073) | .261 (.076) |
| _h_2 | .75 | .695 (.061) | .737 (.059) |
The traditional VC method also yields mean estimates of the overall genetic heritability h_2 = (σ2_mg + σ2_pg_)/(σ2_mg_ + σ2_pg_ + σ2_e_) that are somewhat smaller than the true simulated values for each trait model. For the four trait models, h_2 estimates based on the traditional VC method averaged 90%–93% of the true value. However, we also found that, for each trait model, the traditional VC method yields estimates of the major-gene heritability 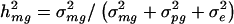 that were close to the true value. This result was surprising, especially considering that the estimates of σ2_mg, σ2_pg_, and σ2_e_ are each biased by a different factor with respect to their true values. However, σ2_mg_ and σ2_mg_+σ2_pg_+σ2_e_ are biased by approximately the same factor, which explains why mean parameter estimates of _h_2 are biased whereas mean parameter estimates of h_2_mg are unbiased.
that were close to the true value. This result was surprising, especially considering that the estimates of σ2_mg, σ2_pg_, and σ2_e_ are each biased by a different factor with respect to their true values. However, σ2_mg_ and σ2_mg_+σ2_pg_+σ2_e_ are biased by approximately the same factor, which explains why mean parameter estimates of _h_2 are biased whereas mean parameter estimates of h_2_mg are unbiased.
For the tobit VC method, parameter estimates were unbiased for all models (table 3). The SEs of the variance estimates for the tobit VC method are larger than those of the traditional VC method. We expected this finding, because the tobit method properly accounts for the uncertainty within the data whereas the traditional method ignores it. This finding appears to be in contrast with our power results, which show the tobit VC method to be more powerful than the traditional VC method for the simulation studies considered. However, the size of the traditional VC test is inflated, so we cannot examine the SEs of the major-gene variance parameter to check for power in the simulation study. As described earlier (see the “Empirical Power for Detecting Linkage” subsection), we adjusted for the incorrect size of the traditional VC method when we performed our power calculations.
Effect of Censoring on Regression-Coefficient Estimates
The effects that censoring had on regression-coefficient estimates for the traditional and tobit VC methods are shown in table 4. The traditional VC method underestimates βB and βN. Estimates of βB and βN averaged 74.5% and 74.2% of the true simulation values, respectively. Censoring of the latent trait distribution restricts the range of possible trait values in the observed distribution. This phenomenon gives the false impression that mean effects due to covariates are smaller than they actually are, which attenuates the covariate estimates toward 0.
Table 4.
Mean Parameter Estimates of VC Methods under 25% Trait Censoring for Trait Model with Covariates[Note]
| Mean ParameterEstimate (Mean SE) for | |||
|---|---|---|---|
| Parametera | True Value | Traditional VC Method | Tobit VC Method |
| βB | .20 | .149 (.061) | .200 (.080) |
| βN | .50 | .371 (.043) | .500 (.057) |
| σ2_mg_ | .50 | .299 (.114) | .512 (.199) |
| σ2_pg_ | .50 | .251 (.132) | .460 (.248) |
| σ2_e_ | 1.00 | .690 (.076) | 1.020 (.131) |
| h_2_mg | .25 | .241 (.077) | .262 (.083) |
| _h_2 | .50 | .443 (.085) | .487 (.088) |
Whereas the traditional VC method underestimates the true values of βB and βN for censored data, the tobit VC method returns unbiased estimates of the two regression coefficients. As with the variance estimates, the SE of the tobit-based regression-coefficient estimates are larger than those based on the traditional VC method, since the former method properly accounts for the uncertainty of the censored trait data.
Analysis of FUSION Data Set
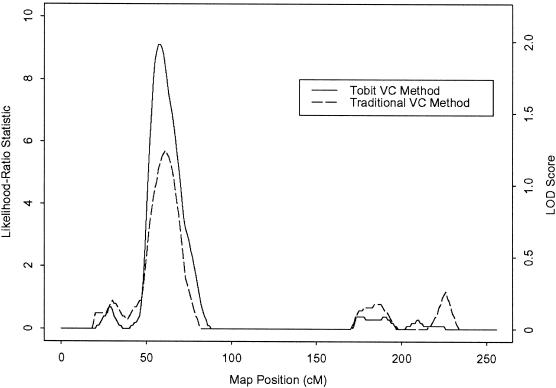
Figure 2 compares the traditional and tobit VC analyses for HDLR on chromosome 2. Both analyses yield similar patterns of linkage evidence across the chromosome; however, the tobit VC method provides increased evidence for linkage in the region previously identified by the traditional VC method. The tobit VC method yields a maximum LOD score of 1.98, at 58 cM (asymptotic _P_=.0013), whereas the traditional VC method yields a maximum LOD score of only 1.24, at 60 cM (_P_=.0085). Examination of HDLR data of medicated subjects reveals 19 sibships that show increased evidence of linkage when censoring is modeled using the tobit VC method. In these siblings, the modeling of censoring strengthens the linkage signal by either increasing the trait similarity of pairs who share two alleles IBD at the locus or decreasing the similarity of pairs who share no alleles IBD at the locus.
Figure 2.
VC analyses of HDLR on chromosome 2. For the tobit method, the maximum likelihood-ratio statistic is 9.1 (maximum LOD score 1.98), at 58 cM; for the traditional method, the maximum likelihood-ratio statistic is 5.7 (maximum LOD score 1.24), at 60 cM.
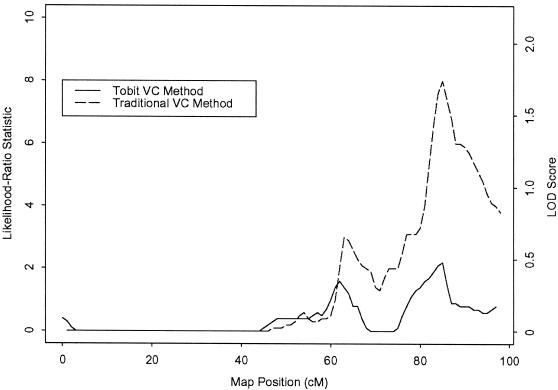
Figure 3 shows the traditional and tobit VC analyses for TG on chromosome 20. As with the HDLR analyses on chromosome 2, the tobit and traditional VC methods show similar linkage patterns along the chromosome; however, the tobit VC method shows reduced evidence of linkage at the peak previously identified by the traditional VC method. Whereas the traditional VC method yields a maximum LOD score of 1.74, at 84 cM (_P_=.0023), the tobit VC method yields a maximum LOD score of only 0.48, at 85 cM (_P_=.0690). Several sibships that previously supplied evidence for linkage when censoring was ignored provide little evidence when we now account for anti-lipid medication.
Figure 3.
VC analyses of TG on chromosome 20. For the tobit method, the maximum likelihood-ratio statistic is 2.2 (maximum LOD score 0.48), at 85 cM; for the traditional method, the maximum likelihood-ratio statistic is 8.0 (maximum LOD score 1.74), at 84 cM.
Discussion
Trait censoring can arise in genetic studies in a variety of traits. Common analytical methods for quantitative-trait mapping, such as the traditional VC method, fail to account for censoring; this can lead to biased parameter estimates and invalid tests of linkage. Here, we present a tobit VC method that should be a useful tool for the mapping of genes that influence censored quantitative traits. For the simulation settings considered, we show that analysis of censored quantitative data by the tobit VC method yields unbiased parameter estimates and empirical false-positive linkage findings that reflect the nominal. In contrast, analysis of such traits by the traditional VC method leads to severely biased parameter estimates, modestly elevated false-positive rates for linkage, and modestly decreased linkage power relative to the tobit VC method.
Besides being a useful test for linkage, the tobit VC method could also be valuable as a family-based test for linkage disequilibrium at a candidate gene that influences a censored trait. Fulker et al. (1999) and Abecasis et al. (2000) showed how the traditional VC method can be used for the testing of linkage disequilibrium when a normally distributed quantitative trait is assumed. Both groups tested for the association of alleles at the trait-influencing candidate gene by incorporating them as covariates in the mean structure of the model while simultaneously accounting for linkage in the covariance structure. Our results show that covariate estimates from the traditional VC method are attenuated toward 0 when censoring exists and is ignored. Therefore, tests of linkage disequilibrium by the traditional VC method may yield incorrect results for censored trait data. Because covariate estimates obtained using the tobit VC method are unbiased, we plan to extend the tobit method, to test for linkage disequilibrium of censored traits by methods analogous to those of Fulker et al. (1999) and Abecasis et al. (2000).
In the simulations that we have described, we assumed that the lower 25% of the trait data were censored. We also performed simulations under the assumptions of less (10%) and more (50%) extensive censoring. Our results showed that the traditional VC method yields biased parameter estimates for these levels of censoring, with the bias becoming more severe as censoring increases. This result is expected because an increase in censoring reduces the range of possible observed values of the trait distribution and decreases the overall trait variance. The traditional VC method’s type I error rate for detecting linkage also increases as censoring increases, owing to an increase in false similarity of observed trait values among relatives. In contrast, the tobit VC method yielded unbiased parameter estimates at all levels of censoring tested and had empirical type I error rates that reflected the nominal rates. For all levels of censoring analyzed, the tobit VC method consistently was more powerful than the traditional VC method for detecting linkage. However, the power to detect linkage by both VC methods decreased with an increase in censoring, which is expected owing to the increased amount of uncertainty in the trait data.
Methods for censored trait data assume independence of the latent and censored trait values. Violation of this assumption may yield biased parameter estimates and elevated type I error rates (e.g., see Williams and Lagakos 1977). For our tobit analyses, censoring due to medication likely violated this assumption. The correlation between latent and censored trait values is dependent on the drug effect. For our FUSION examples, the effect of anti-lipid medication is quite variable, so, although correlation likely exists between latent and censored trait values, the correlation is likely weak. To investigate the effect that such correlation had on tobit results, we performed additional simulations in which we assumed that subjects in the lower 25% of the trait distribution were on medication. We then simulated the censored trait value from the latent trait value (with the censored trait value being greater than the latent trait value), assuming a correlation of 0.4, 0.75, or 1. For correlations of 0.4 and 0.75, the tobit method returned unbiased parameter estimates and had appropriate type I error. Therefore, for the correlation that likely exists in our FUSION example, we believe that this dependence will not have a serious deleterious effect on results. When the correlation was 1 (perfect linear relationship between latent and censored trait values), the tobit method returned variance-parameter estimates that were slightly inflated. However, the corresponding type I error rates appeared to be close to the nominal levels. Therefore, even when the latent and censored trait values are completely dependent, the simulations support the idea that the tobit method will yield accurate tests of linkage.
Because fitting the tobit VC method requires numerical integration, the method is more computationally intensive than the traditional VC method. If one approximates the tobit-based likelihood by using five quadrature points, then the tobit VC method requires approximately four to five times as much computer time to fit a model as compared with the traditional VC method for the cases that we considered. To reduce the amount of time for the tobit method, one could perform the analyses with the assumption of a smaller number of quadrature points. We repeated our simulations for the case of _h_2=0.75 and _h_2_mg_=0.25 but now assumed only one quadrature point for analysis (which corresponds to a Laplace approximation). For one quadrature point, the tobit VC method required approximately the same amount of computer time as the traditional VC method. The analyses based on one quadrature point had similar linkage power and type I error rates as compared with the same tobit analyses performed using five quadrature points, but we observed bias in the mean variance and heritability estimates. These results suggest that one could use a Laplace approximation to perform a computationally efficient genome scan for the identification of linked regions of interest. However, one should then reanalyze the regions of interest by using more quadrature points, to obtain more-accurate estimates of genetic and nongenetic effects.
For the situations considered in the present article, our analyses suggested that _Q_=5 quadrature points were sufficient to approximate the likelihood accurately for the tobit VC method. In other situations, the number of quadrature points needed for accurate likelihood approximation will depend on such factors as family size and degree of censoring. As family size increases, we would expect to need fewer quadrature points for accurate likelihood approximation; as the degree of censoring increases, we likely will need more quadrature points. In the SAS procedure PROC NLMIXED, one can adaptively select the number of quadrature points needed for a given data set. We strongly recommend using this feature of the procedure, to ensure an accurate likelihood approximation.
We understand that the chosen significance levels for testing the linkage hypothesis in the present study are much less stringent than those commonly used in a linkage analysis of a genetic trait. However, the goal of the present article was to compare and contrast the characteristics of the traditional and tobit VC methods. From our results, we felt that these empirical significance levels were appropriate for such comparisons. Such data sets also yielded the additional benefit of computational simplicity relative to both larger and selected data sets.
We have developed the tobit VC method under the assumption that the latent distribution of the trait data is multivariate normal within families. We could also extend the method to accommodate censored traits with other known latent distributions, both continuous (e.g., gamma) and discrete (e.g., Poisson). Assuming the censoring event in figure 1, we must determine the probability of a censored and a noncensored observation given the latent distribution of interest. We can accomplish this by using the latent distribution’s probability and cumulative density/mass functions. These probability and cumulative functions replace the respective functions of the normal distribution in likelihood (5). One can then fit the models of interest by using adaptive Gaussian quadrature or some other numerical-integration inference method. Extensions to subject-specific thresholds are straightforward.
As we have shown with the tobit VC method, one can use the generalized-linear-mixed-model framework that has been proposed by Breslow and Clayton (1993) to develop VC methods for the mapping of genes that influence many types of nonnormally distributed trait data. We intend to use this framework to develop VC methods for the mapping of genes that influence dichotomous (e.g., presence/absence of disease), polychotomous, and count data (Epstein et al. 2001). In the case of disease data, we will base the linkage test on a logistic VC model. This proposed disease-mapping method has the advantage that it accommodates multiple genetic and environmental effects.
Acknowledgments
We thank our colleagues in the FUSION study for allowing us to present results from the analysis of FUSION data. We thank Drs. Lawrence Bielak and Richard Watanabe for their helpful comments. We also thank two anonymous reviewers for their constructive and thoughtful observations. This work was supported by a University of Michigan Rackham Predoctoral Fellowship (to M.P.E.) and National Institutes of Health grants R29 CA76404 (to X.L.) and R01 HG00376 (to M.B.).
References
- Abecasis GR, Cardon LR, Cookson WOC (2000) A general test of association for quantitative traits in nuclear families. Am J Hum Genet 66:279–292 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agatston AS, Janowitz WR, Hildner FJ, Zusmer NR, Viamonte M Jr, Detrano R (1990) Quantification of coronary artery calcium using ultrafast computer tomography. J Am Coll Cardiol 15:827–832 [DOI] [PubMed] [Google Scholar]
- Allison DB, Neale MC, Zannolli R, Schork NJ, Amos CI, Blangero J (1999) Testing the robustness of the likelihood-ratio test in a variance-component quantitative-trait loci–mapping procedure. Am J Hum Genet 65:531–544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almasy L, Blangero J (1998) Multipoint quantitative-trait linkage analysis in general pedigrees. Am J Hum Genet 62:1198–1211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amos CI (1994) Robust variance-components approach for assessing genetic linkage in pedigrees. Am J Hum Genet 54:535–543 [PMC free article] [PubMed] [Google Scholar]
- Amos CI, Zhu DK, Boerwinkle E (1996) Assessing genetic linkage and association with robust components of variance approaches. Ann Hum Genet 60:143–160 [DOI] [PubMed] [Google Scholar]
- Bielak LF, Sheedy PF II, Peyser PA (2001) Coronary artery calcification measured at electron-beam CT: agreement in dual scan runs and change over time. Radiology 218:224–229 [DOI] [PubMed] [Google Scholar]
- Blangero J, Williams JT, Almasy L (2001) Variance component methods for detecting complex trait loci. In: Rao DC, Province MA (eds) Genetic dissection of complex traits. Academic Press, London, pp 151–182 [DOI] [PubMed] [Google Scholar]
- Breslow NE, Clayton DG (1993) Approximate inference in generalized linear mixed models. J Am Stat Assoc 88:9–25 [Google Scholar]
- Epstein MP, Lin X, Boehnke M (2001) Variance-component linkage methods for non-normally distributed trait data. Am J Hum Genet Suppl 69:A228 [Google Scholar]
- Fulker DW, Cherny SS, Cardon LR (1995) Multipoint interval mapping of quantitative trait loci, using sib pairs. Am J Hum Genet 56:1224–1233 [PMC free article] [PubMed] [Google Scholar]
- Fulker DW, Cherny SS, Sham PC, Hewitt JK (1999) Combined linkage and association sib-pair analysis for quantitative traits. Am J Hum Genet 64:259–267 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haseman JK, Elston RC (1972) The investigation of linkage between a quantitative trait and a marker locus. Behav Genet 2:3–19 [DOI] [PubMed] [Google Scholar]
- Kruglyak L, Daly M, Reeve-Daly M, Lander E (1996) Parametric and nonparametric linkage analysis: a unified multipoint approach. Am J Hum Genet 58:1347–1363 [PMC free article] [PubMed] [Google Scholar]
- Kruglyak L, Lander ES (1995) Complete multipoint sib-pair analysis of qualitative and quantitative traits. Am J Hum Genet 57:439–454 [PMC free article] [PubMed] [Google Scholar]
- Lander ES, Green P (1987) Construction of multilocus genetic linkage maps in humans. Proc Natl Acad Sci USA 84:2363–2367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maher JE, Raz JA, Bielak LF, Sheedy PF II, Schwartz RS, Peyser PA (1996) Potential of quantity of coronary artery calcification to identify new risk factors for asymptomatic atherosclerosis. Am J Epidemiol 144:943–953 [DOI] [PubMed] [Google Scholar]
- Morton NE (1955) Sequential tests for the detection of linkage. Am J Hum Genet 7:277–318 [PMC free article] [PubMed] [Google Scholar]
- Pinheiro JC, Bates DM (1995) Approximations to the log-likelihood function in the nonlinear mixed-effects model. J Comput Graph Stat 4:12–35 [Google Scholar]
- Self SG, Liang K-Y (1987) Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under non-standard conditions. J Am Stat Assoc 82:605–610 [Google Scholar]
- Tobin J (1958) Estimation of relationships for limited dependent variables. Econometrica 26:24–36 [Google Scholar]
- Valle T, Tuomilehto J, Bergman RN, Ghosh S, Hauser ER, Eriksson J, Nylund SJ, Kohtamaki K, Toivanen L, Vidgren G, Tuomilehto-Wolf E, Ehnholm C, Blaschak J, Langefeld CD, Watanabe RM, Magnuson V, Ally DS, Hagopian WA, Ross E, Buchanan TA, Collins F, Boehnke M (1998) Mapping genes for NIDDM: design of the Finland–United States Investigation of NIDDM Genetics (FUSION) study. Diabetes Care 21:949–958 [DOI] [PubMed] [Google Scholar]
- Williams JS, Lagakos SW (1977) Models for censored survival analysis: constant sum and variable sum models. Biometrika 64:215–224 [Google Scholar]
- Williams JT, Blangero J (1999) Comparison of variance components and sibpair-based approaches to quantitative trait linkage analysis in unselected samples. Genet Epidemiol 16:113–134 [DOI] [PubMed] [Google Scholar]