Mechanical switching and coupling between two dissociation pathways in a P-selectin adhesion bond (original) (raw)
Abstract
Many biomolecular bonds exhibit a mechanical strength that increases in proportion to the logarithm of the rate of force application. Consistent with exponential decrease in bond lifetime under rising force, this kinetically limited failure reflects dissociation along a single thermodynamic pathway impeded by a sharp free energy barrier. Using a sensitive force probe to test the leukocyte adhesion bond P-selectin glycoprotein ligand 1 (PSGL-1)–P-selectin, we observed a linear increase of bond strength with each 10-fold increase in the rate of force application from 300 to 30,000 pN/sec, implying a single pathway for failure. However, the strength and lifetime of PSGL-1–P-selectin bonds dropped anomalously when loaded below 300 pN/sec, demonstrating unexpectedly faster dissociation and a possible second pathway for failure. Remarkably, if first loaded by a “jump” in force to 20–30 pN, the bonds became strong when subjected to a force ramp as slow as 30 pN/sec and exhibited the same single-pathway kinetics under all force rates. Applied in this way, a new “jump/ramp” mode of force spectroscopy was used to show that the PSGL-1–P-selectin bond behaves as a mechanochemical switch where force history selects between two dissociation pathways with markedly different properties. Furthermore, replacing PSGL-1 by variants of its 19-aa N terminus and by the crucial tetrasaccharide sialyl LewisX produces dramatic changes in the failure kinetics, suggesting a structural basis for the two pathways. The two-pathway switch seems to provide a mechanism for the “catch bond” response observed recently with PSGL-1–P-selectin bonds subjected to small-constant forces.
Noncovalent interactions among large multidomain proteins underlie most adhesive functions in biology. Well known prototypes are the complexes formed between the selectin family of adhesion receptors, e.g., P-selectin expressed on activated endothelial cells or platelets, and their glycosylated ligands, e.g., the leukocyte mucin P-selectin glycoprotein ligand 1 (PSGL-1). Referred to as “bonds,” these interactions transiently interrupt rapid transport of leukocytes in blood flow and enable cells to perform a rolling exploration of vessel walls during the inflammatory response (1, 2). Most of our knowledge about how selectin bonds behave under stress has come from observing the decay in a number of receptor-bearing particles (cells or microspheres) tethered to walls by adhesive ligands in flow chambers. Held under nearly constant “force clamp” conditions, particles tethered by ligand/selectin bonds release at progressively faster rates with increasing shear forces in high flow (3–5) but, at the same time, exhibit an unexpected shear threshold in slow flow below which particles also detach very quickly (6, 7). Recently tested by both flow chamber and atomic force microscope (AFM) techniques in a similar force clamp mode, the lifetimes of PSGL-1–P-selectin attachments were found to first increase with initial application of small forces before crossing over to decrease at higher forces (8), suggesting an explanation for the shear-threshold behavior. Yet, in contrast to the force clamp assays of lifetime, fast steady-speed detachment of P-selectin–ligand bonds with an AFM (9, 10) and the biomembrane force probe (BFP) (11) have demonstrated a kinetically limited failure with forces rising in proportion to the logarithm of the force rate, as expected for an exponential decrease in bond lifetime under force (12), apparently missing the unusual reversal in lifetime and leaving the mechanism of reversal obscure.
To unravel the complex dynamics of PSGL-1–P-selectin failure over time frames from 0.001 sec to >1 sec and force levels from 1 to 200 pN, we have used the biomembrane force probe with a combination of the conventional “steady ramp” and a new “jump/ramp” mode of force spectroscopy (Fig. 1). We find that force history can select between two pathways for dissociation with very different kinetics. Pulled with slow steady ramps starting from zero force, PSGL-1–P-selectin bonds are weak and break rapidly at very small forces, indicating a low-impedance failure pathway with a fast dissociation rate. By comparison, when pulled in the same way under fast force ramps, PSGL-1–P-selectin bonds become strong and break at forces rising in proportion to the logarithm of the loading rate, demonstrating a high-impedance failure pathway. Revealing a mechanical switching between pathways, a quick initial jump to a small force blocks the low-impedance pathway and allows bonds to fail only along the high-impedance pathway, even if then pulled very slowly. Replacing PSGL-1 by variants of its 19-aa N terminus (13) and by the crucial tetrasaccharide sialyl LewisX (sLeX) produces significant changes in the impedances to dissociation along the two pathways.
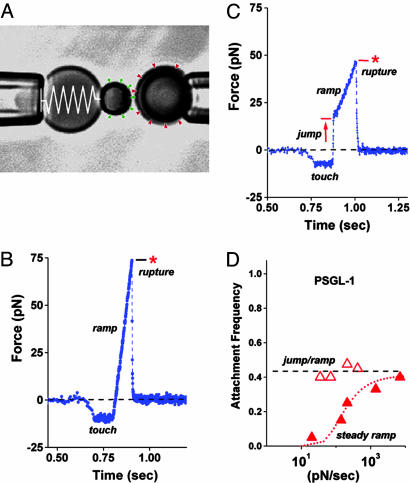
Fig. 1.
Videomicrograph (A) of the BFP (labeled by the “spring” on the left) juxtaposed with a 4-μm target microsphere; force-time plot (B) from a steady ramp test of a P-selectin–PSGL-1 bond; force time plot (C) from a jump/ramp test of a P-selectin–PSGL-1 bond; comparison of the perceived frequencies (D) of BFP tip-target attachments in jump/ramp and steady ramp tests of P-selectin–PSGL-1 bonds. (A) Pressurized by pipette suction, a PEG-biotinylated red blood cell acts as the elastic transducer for force in the BFP. To form an active tip, a 2-μm glass bead was bound with P-selectin (“green pins”) as well as PEG biotin and then attached to the transducer with streptavidin. With the PSGL-1 ligands (“red wedges”) linked covalently to a target glass bead (on the right) in the same way, bonds to P-selectin were formed and broken by moving the target into and out of contact with the BFP tip by using a piezo-mounted pipette. (B) A steady ramp test shows the BFP response during target approach “soft” touch, then retraction at fixed speed. Formed at touch, a PSGL-1–P-selectin bond failed at ≈75 pN under the force ramp of ≈700 pN/sec. (C) A jump/ramp test shows the BFP response during target approach, touch, then a rapid retraction abruptly switched after 0.004 sec to slow retraction. Again formed at touch and surviving the jump in force (at ≈5,000 pN/sec), a PSGL-1–P-selectin bond failed at ≈50 pN under the final force ramp of ≈140 pN/sec. (D) Frequencies of tip-surface attachments in steady ramp tests appeared to increase with ramp rate (filled red triangles), whereas frequencies in the jump/ramp tests were essentially independent of ramp rate (open red triangles). The dotted red curve estimates the apparent frequency that would be perceived if some attachments went undetected under steady ramps within the first force bin (≈10–12 pN), assuming rapid dissociation (≈10 pN/sec) along a separate pathway that could be blocked by a 20- to 30-pN jump in force.
Materials and Methods
PSGL-1 Ligands and P-Selectin. Soluble fucosylated PSGL-1 and constructs (SGP-3, GP-1) of its 19-aa N terminus were generously provided by Ray Camphausen (Thios Pharmaceuticals, Emeryville, CA). Isolation of these materials and other details are provided in the refs. 13 and 14. P-selectin was purchased as a soluble Fc chimera along with a biotinylated form of sLeX (b-sLeX) from GlycoTech (Gaithersburg, MD).
Linkage to Glass Microspheres. To immobilize a PSGL-1 ligand and P-selectin on separate microspheres, one as a target and the other as the BFP tip, 2- and 4-μm-size glass spheres were functionalized with a very low concentration of either the ligand or a combination of P-selectin plus a large amount of polyethylene glycol (PEG)-biotin to provide strong bonding to the BFP transducer (a PEG-biotinylated red cell) via streptavidin. As described (15), the microspheres were first bound with mercapto-silane groups. Then, mono-and bifunctional (thiol-and amine-reactive) PEGs (Shearwater, Huntsville, AL) were used to anchor PEG-biotin and the P-selectin or the PSGL-1 ligands. To achieve rare-discrete bond formation, the numbers of reactive P-selectin (and ligand) sites were kept well below the detection limit of ≈40/μm2 in our fluorescence assay.
BFP Instrument. Assembly of the BFP force transducer begins by pressurizing a PEG-biotinylated red blood cell into a spherical shape with a micropipette and then attaching the streptavidinated/protein-decorated glass bead (left of Fig. 1 A). The pipette suction sets the red cell membrane tension and, when scaled by a measured geometrical prefactor (16), establishes the BFP spring constant k_f (force/capsule extension) to an accuracy of 10% over a range of 0.2–2 pN/nm. Approach, touch, and retraction of the target to/from the BFP tip are controlled by a computer-driven linear-piezo translator coupled to a micropipette that holds the target. The force history applied to a bond involves first selecting the BFP spring constant and then programming the time course for piezo retraction of the target bead after touch. Enabled by fast video processing, the BFP tip and target are tracked simultaneously along the pulling direction at time intervals of 0.0006 sec and at a displacement resolution of approximately ±5 nm. The “steady ramp” mode (Fig. 1_B_) is performed by separation at constant speed Vt after 0.1 sec of “soft” (approximately –10 pN) touch. In the “jump/ramp” mode (Fig. 1_C_), the “jump” in force is achieved by pulling at a very fast speed (typically ≈20,000 nm/sec, equivalent to a force ramp of ≈5,000 pN/sec) for a preset time (e.g., 5–6 msec to reach ≈25 pN). Then, within 0.6 msec, the retraction speed is abruptly lowered to produce the desired slower “steady ramp.” Varying piezo retraction speeds from 40 to 33,000 nm/sec and BFP spring constants from 0.25 to 1.54 pN/nm, nominal force ramps can be programmed from ≈10 to 50,000 pN/sec in experiments. The actual force rates r_f experienced by bonds are quantified by measuring the slope of the applied force versus time (Δ_f/Δ_t). When pulled at extremely fast speeds ≥20,000 nm/sec, a viscous contribution due to probe damping augments the BFP elastic force as described and quantified (15). Correction for the added-viscous force is made by using the product of the damping factor (ξ ≈ 0.0005 pN-sec/nm) measured for the BFP and the pulling speed, i.e., f ≈ _f_elastic + ξ _V_t. Up to ≈1,000 pN/sec in loading rate, a BFP spring constant of _k_f ≈ 0.25 pN/nm is used and sets the unaveraged force resolution at, SD ≈ ± 1–2 pN. At faster rates, the optimum conditions for both force resolution and damping are obtained by increasing the spring constant to values predetermined by the nominal loading rate (15), giving a resolution in force of ± 4–5 pN SD at 10,000 pN/sec and ± 10–11 pN SD at 30,000 pN/sec.
Tests of specific P-selectin interactions were performed in a microscope chamber that contained Hepes 10 mM, NaCl 150 mM, and 1 mM CaCl2. The impingement force at surface touch is set by feedback control to ≈–10 (± 1) pN and typically held for 0.1 sec (see Fig. 1 B and C). In the tests reported here, the ratios (frequencies) of specific tip-surface attachments ranged from ≈1–4 per 10 touches in repeated bead–bead contacts. For controls, P-selectin probes were tested against nonspecific PEG-protein beads in Ca2+ and against PSGL-1 beads in Ca2+ free buffer plus 10–20 mM EDTA. In both controls, the frequencies of attachments dropped to ≈2–3 per 100 touches, and the attachments broke at small force, confirming that the interactions between PSGL-1 and P-selectin beads were specific in the presence of calcium.
Results
Failure of P-Selectin–PSGL-1 Bonds Under Steady Ramps of Force. We first probed P-selectin–PSGL-1 bonds by linear force ramps rf (pN/sec). Over a large range from 300 to 30,000 pN/sec, all of the rupture force histograms exhibited a prominent peak. Seen emerging in Fig. 2_B_ and fully formed in Fig. 2_C_, the similarly shaped peak shifted to higher force in direct proportion to Loge(rf), consistent with previous fast-loading experiments (9–11). The dashed red curves in Fig. 2 B and C show probability densities for kinetically limited failure (11, 12) predicted by a failure rate that increases exponentially under force, i.e., _k_rup(f) = (1/_t_off) exp(f/_f_β). A simple generic function, p(y) = exp[y – exp(y) + 1], was used to obtain the force distribution at each loading rate rf through the parameterization, y ≡ f/_f_β – Log[rf/(_f_β/_t_off)]. Consistent with the model postulated by Bell many years ago (17), this generic distribution is the characteristic signature for dissociation along a single pathway impeded by a sharp free-energy barrier (12). Accordingly, the rate of failure or “off rate” increases _e_-fold when force reaches a scale _f_β defined by the ratio of thermal energy k_B_T (≈4.08 pN nm at room temperature) to the average length _x_β gained in the pulling direction upon passing the barrier, i.e., f_β = k_B_T/x_β. For a steady ramp of force and an exponential dependence on force, the failure rate increases exponentially with time, which leads to a single peak in the probability density at force _f_β Log[rf/(_f_β/_t_off)]. Hence, the upward shift in histogram peaks from ≈70 to >150 pN over a range of force rates from ≈300 to 30,000 pN/sec implied a force scale of _f_β ≈ 18 ± 0.5 pN (equivalent to a length _x_β ≈ 0.226 ± 0.01 nm) for exponentiation of kinetics that appeared to begin from an unstressed rate of 1/_t_off ≈ 0.37 ± 0.07/sec for dissociation along the single pathway. As shown by the dashed red curves in Fig. 2, probability densities calculated with these parameters closely match the force statistics local to histogram peaks, which supported the exponential model for increase in failure rate under fast loading conditions (see Supporting Text and Fig. 6, which are published as supporting information on the PNAS web site, for details on the method used to fit distributions to the measured force histograms.)
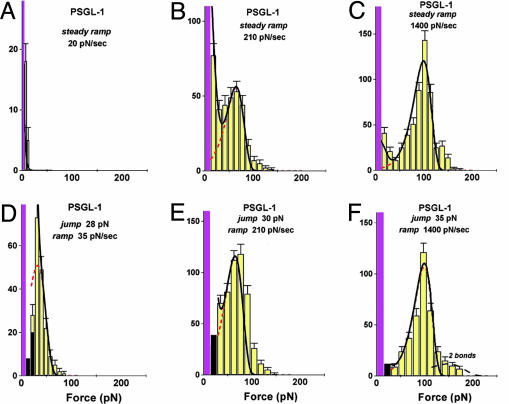
Fig. 2.
Force histograms for PSGL-1–P-selectin bonds ruptured under steady ramps (A_–_C) and under jump/ramps (D_–_F). Forces in the first bin include tests without detection of an attachment, which causes the first bin (magenta) to rise off-scale. As shown by a 40–45% attachment frequency for D_–_F in contrast to <10% for A, ≈25% for B, and ≈33% for C, the quick initital jumps in force to ≈20–30 pN captured numerous bonds otherwise missed because of fast failure along a low-impedance pathway within the time increment defined by the first bin (see Fig. 1_D_). (The few bonds that broke during the jump phase are shown by the dark bins in D_–_F.) After force jumps or under fast steady ramps, the force distributions are seen to agree with the probability densities (dashed red curves) predicted for kinetically limited failure along a single pathway (labeled 2) defined by the failure rate, _k_2rup ≈ (0.37 ± 0.07pN/sec) exp(f/18 ± 0.5 pN). Superimposed as solid black curves are the probability distributions computed by using the master equation for the two-pathway switch described in the text. To match the histograms for both steady ramp and jump/ramp modes at all loading rates, the two-pathway dissociation was modeled by a fast rate of _k_1rup ≈ 8–12 pN/sec along low-impedance pathway 1 and a switch to high-impedance pathway 2 in the range of ≈20–25 pN. [It appears that a few (<20% in all cases) double bonds led to the small tails of very high forces, as shown by the predicted distribution added to the histogram in F.]
Based on the fast steady ramp experiments, the rates of PSGL-1–P-selectin bond failure were found to rise significantly from ≈17/sec at 70 pN to >1,400/sec at 150 pN. On the other hand, for the kinetics of failure along this single pathway to be consistent over all rates, the positions of the most frequent rupture force in force histograms should continue to move down in proportion to the logarithm of loading rate and then reach zero force at a steady ramp equal to the force scale _f_β multiplied by the unstressed off rate 1/_t_off, i.e., rf o = _f_β/_t_off ≈ 6 pN/sec. Contrary to this expectation, the most frequent forces for PSGL-1–P-selectin failure (distribution peaks) remained at zero force for ramps up to nearly 300 pN/sec (e.g., note the large peak near zero force for 240 pN/sec in Fig. 2_B_), even while a prominent second peak began to appear. In addition, the prominent peak completely vanished with ramps below 100 pN/see (see Fig. 2 A) and, as illustrated in Fig. 1_D_, the apparent frequency of attachment dropped dramatically.
Tests of P-Selectin–PSGL-1 Bonds Under Steady Ramps After a Jump in Force. The disappearance of bond strength under slow loading, the coexistence of two force peaks at intermediate loading rates, and finally, a paramount single peak moving to higher force under fast loading, all provided strong evidence for the existence of two failure pathways consistent with the biphasic dependence of lifetime on force that was observed previously under force clamp conditions (1). Still, the separate kinetic properties of the pathways remained to be defined. The crucial question was whether the pathways emanated from one or two distinct bound states, the later offering a possibility to switch from one failure pathway to the another.
To test the origin of two-pathway dynamics, we probed PSGL-1–P-selectin bonds with the new “jump/ramp” mode (see Fig. 1_C_). As shown by the rupture force distributions in Fig. 2 D–F, failure along the low-impedance pathway seemed to almost completely vanish when a steady ramp was preceded by a rapid jump to 20–30 pN within 5–6 msec. After fast jumps in force, continued pulling with even slow ramps produced force distributions that were in agreement with the generic probability density p[y(f)] for kinetically limited failure along a single high-impedance pathway, which now covered a span in force rate from ≈30 to 30,000 pN/sec. Varying the jump heights between 10 and 40 pN, we found that a jump to 20–30 pN effectively prevented attachments from quickly failing and, at the same time, increased the apparent frequency of attachment to a level nearly independent of the force rate as shown in Fig. 1_D_. Evidently captured by the force jump, the bonds were then restricted to fail along a single pathway impeded by a sharp free-energy barrier in the pulling direction. Thus, the combination of steady ramp and jump/ramp tests demonstrated the operation of a switch between the two dissociation pathways triggered by fast application of 20–30 pN of force to the bond.
Modeling the Dynamics of Pathway Switching. To quantify the dynamics of switching between pathways, we used a model that assumes that bond failure originates from two possible bound-state configurations defined by the occupancies _S_1(t), _S_2(t), and proceeds to failure through two forward-unbinding events at rates _k_1rup, _k_2rup. For a low probe spring constant as used here, rebinding becomes extremely unlikely as pulling force rises above ≈10 pN (11). So the likelihood of bond survival over time [_S_B(t) ≡ _S_1 + _S_2] is described by a first-order master equation that involves only unbinding from each configurational state,
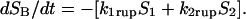
However, the possibility of inner conversion or exchange between the two bound states adds an additional complexity represented by two more rates _k_12, _k_21 that govern the exchange between states, ±(_k_21_S_2 – _k_12_S_1). As a result, the master equation for bond survival is split into two separate equations describing the evolution of each bound state (see Supporting Text). In general, analysis of data using these two equations can be very challenging given four transition rates (_k_1rup, _k_2rup, _k_12, _k_21) with arbitrary dependencies on force. Yet, guided by the clear demonstration of a high-impedance pathway under fast steady ramps and in all jump/ramp tests, we assumed that the failure rate along this pathway (labeled 2) could be defined by the exponential, _k_2rup ≈ (0.37/sec) exp(f/18 pN). Doing so, we then found that all force histograms from both testing modes could be matched over the entire range of loading rates by simply (i) treating the failure rate _k_1rup along the low-impedance pathway 1 as effectively constant and (ii) postulating that the inner conversion between bound states is very fast. In this way, the bound states were assumed to remain thermally equilibrated with an initial occupancy ratio set by a small difference Δ_E_21 in energy level between the states. To provide a simple mechanism for pathway switching, the energy difference between bound states was assumed to shift in proportion to force as a consequence of a small length Δ_x_12 gained in the transition from state 1 to state 2. Thus, beginning from the unstressed ratio defined by Φo ≡ exp(Δ_E_21/k_B_T), the occupancies of the two bound states shift with increase in force to follow the ratio,
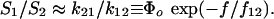
The force scale _f_12 ≡ k_B_T/Δ_x_12 governs the force span for changing the occupancy ratio by _e_-fold; therefore, the initial difference in energy level and the force _f_12 define an equal-occupancy crossover at the force, _f_196 = _f_12 (Δ_E_21/k_B_T). With rapid inner conversion between states and deterministic switching by force, the likelihood of bond survival (_S_1 + _S_2) in two-pathway failure is reduced to a single first-order differential equation in time governed by an effective force-dependent rate of failure,
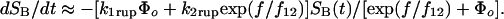
Specifying the force history f(t), this equation was integrated to provide the probability densities that were fit to the rupture force histograms for all ramp rates in both modes of force application (illustrated in Supporting Text). The close agreement is demonstrated by the black solid curves in Fig. 2 (and later in Fig. 4 A–D). Given the exponential relation found for the failure rate _k_2rup along pathway 2, these correlations yielded a failure rate along the low-impedance pathway 1 of _k_1rup ≈ 8–12/sec. Switch from pathway 1 to pathway 2 was found to occur within a small span of force set by _f_12 ≈ 4–6 pN and centered at a crossover _f_⊗ ≈ 20–24 pN. From the ratio of crossover force _f_⊗ to _f_12, the difference in energy between the two bound states was estimated to be small, Δ_E_21 ≈ 4–5 k_B_T, which is clearly consistent with the hypothesis of rapid inner conversion.
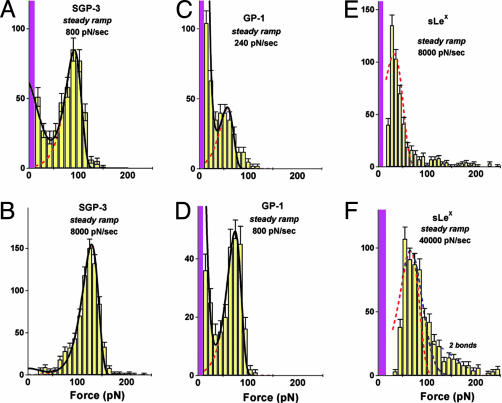
Fig. 4.
Force histograms obtained from steady ramp tests of SGP-3–P-selectin bonds (A and B), GP-1–P-selectin bonds (C and D), and b-sLeX–P-selectin bonds (E and F). Superposed in A_–_D are the probability distributions computed for the two-pathway switch (solid dark curves) as well as the kinetically limited pathway distributions (dashed red curves). (A and B) Match of the two-pathway model to the data for SGP-3–P-selectin bonds gave parameters similar to those obtained for PSGL-1–P-selectin bonds (see Fig. 6): i.e., a rate of _k_1rup ≈ 7–13/sec for dissociation along the first pathway and switch to the second pathway above ≈20–30 pN defined by the failure rate, _k_2rup ≈ (0.2 ± 0.1/sec) exp(f/16 ± 0.5 pN). (C and D) Optimal match to the data for GP-1–P-selectin bonds yielded a rate of _k_1rup ≈ 50 ± 10/sec along pathway 1, followed by a switch to pathway 2 above ≈20 pN defined by the rate _k_2rup ≈ (0.3 ± 0.1/sec) exp(f/14 ± 0.5 pN). (E and F) Superimposed (dotted red curve) on the data for b-sLeX–P-selectin bonds are probability densities for a single kinetically limited pathway defined by the failure rate _k_rup ≈ (90 ± 10/sec) exp(f/20 ± 1 pN). Also shown in E is the broadening (dotted blue curve) expected from error (σexp ≈± 10–11 pN) in force detection with the large BFP stiffness needed for ultrafast loading. Similarly, a gap appears between the magenta bin and the lowest forces detected because of the limitation by video framing rate (≈1,500/sec) at very fast pulling speeds. [Again, a few (<20% in all cases) double bonds seem to account for the tails of very high forces, as shown by the predicted distribution added to the histogram in F.]
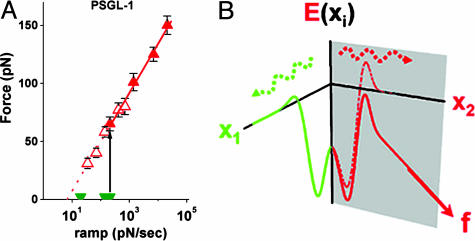
Cumulated in the plot shown in Fig. 3_A_, the most frequent forces in histograms remain at zero (green truncated wedges) for slow loading rates and then at ≈300 pN/sec, shift abruptly to ≈70 pN to follow a linear proportionality to Loge(ramp rate) with faster loading speeds (red solid triangles). The abrupt transition in bond strength is the dynamical consequence of the switch between failure pathways under steady ramps. Also plotted in Fig. 3_A_, the most frequent forces from jump/ramp histograms (red open triangles) follow the same linear dependence on Loge(rf) but beginning from a slow loading rate of 35 pN/sec. Taken together, the dynamical transition at ≈300 pN/sec and its suppression by a fast jump to 20–30 pN are direct manifestations of a switch between the two dissociation pathways. Fig. 3_B_ shows a conceptual energy landscape consistent with the phenomenology of the two-pathway switch.
Fig. 3.
The most frequent forces (highest peaks in histograms) obtained from steady ramp and jump/ramp tests of PSGL-1–P-selectin bonds are plotted as functions of log10(ramp rate). Conceptual energy landscape for a two-pathway switch. In A, the solid green wedges and solid red triangles are the force positions for the highest peaks under steady ramps (see Fig. 2 A_–_C), which show an abrupt change in the expected value of bond strength (from solid green wedges to solid red triangles) near 300 pN/sec. The open red triangles are force positions for the single peaks found in histograms under steady ramps after jumps to ≈20–30 pN. Continuing the linear proportionality down to ≈35 pN/sec, the most frequent rupture forces in jump/ramp tests overlap precisely with the solid red triangles at loading rates >300 pN/sec. Consistent with the dynamical transition in bond strength under steady ramp loading, jumps to ≈20–30 pN in <0.01 sec blocked access to the initial low-impedence pathway, allowing failure only along the high-impedance pathway. In our model of the two-pathway switch, the initial pathway is closed off when the occupancy ratio of the two bound configurations is quickly inverted. (B) Conceptual energy contours along two pathways in configuration space originating from separate bound states that couple in different ways to the pulling force, as modeled by the single master equation in the text. The energy contour along pathway 1 is viewed as essentially orthogonal to the pulling direction, so that force has little effect on failure rate. In contrast, the energy contour along pathway 2 is aligned significantly with the pulling direction (but need not be coparallel). Key to the switching mechanism, the small difference in energy levels between the two bound states is shifted by the force from favoring pathway 1 to pathway 2.
Probing the Structural Determinants of Pathway Switching. To examine the role of ligand structure in the two pathway dissociation, we replaced PSGL-1 by variants of its 19-aa N terminus and the tetrasaccharide b-sLeX. Requiring Ca2+ like native PSGL-1 interactions, the 19-aa N terminus has been shown to be sufficient for binding to P-selectin provided that a fucosylated and sialylated oligosaccharide (related to sLeX) is present at Thr-16 (14). Moreover, the binding affinity is enhanced to varying degrees by sulfation (13, 18, 19) of three tyrosine residues at positions 5, 7, and 10. Therefore, we tested strengths of P-selectin bonds to two 19-mer polypeptides linked with sLeX at the Thr-16 position (13), one fully sulfated at all three tyrosines (called SGP-3) and the other with no tyrosine sulfation (called GP-1), and also to the simple carbohydrate b-sLeX.
Probed by steady ramps between 100 and 50,000 pN/sec, force distributions for SGP-3 bonds to P-selectin were found to be similar to those obtained for PSGL-1 yielding the same two pathway behavior with almost the same rate of failure for the low-impedance pathway 1 (cf. Fig. 4 A and B). Even so, there were modest changes in the parameters describing the high-impedance pathway 2, _f_β ≈ 16 ± 0.5 pN and 1/_t_off ≈ 0.2 ± 0.1/sec. In contrast, major changes were found in steady ramp tests of GP-1 and b-sLeX bonds to P-selectin. First, for GP-1, there was a large increase in the fraction of bonds failing near zero force even under fast ramps of ≈103 pN/sec, indicating a very fast dissociation along the low-impedance pathway 1, but at the same time, a prominent peak appeared signifying a high-impedance pathway as for PSGL-1–P-selectin (cf. Fig. 4_D_). When correlated to the two-pathway model (cf. Fig. 4 C and D), quite different parameters were needed to match the GP-1–P-selectin distributions over the range of steady ramps from ≈100 to 10,000 pN/sec. Most significant, the rate of GP-1–P-selectin failure along the low-impedance pathway 1 was found to be 5-fold faster (_k_1rup ≈ 50 ± 10/sec) than for PSGL-1–P-selectin. Also, the switching between pathways seemed to occur at a slightly lower force, and again, the force scale for exponentiation of the rate along the high-impedance pathway 2 was lower than for PSGL-1–P-selectin, i.e., _f_β ≈ 14 ± 0.5 pN. Next, for s-LeX bonds to P-selectin, the most striking outcome was that only a single failure pathway could be detected in tests. Indeed, force peaks moved above zero force only when the s-LeX–P-selectin bonds were subjected to very fast loading rates of 8,000 pN/sec and 40,000 pN/sec (Fig. 4 E and F). Intriguingly, the force distributions look like phantom images of the high-impedance pathway in PSGL-1–P-selectin, exhibiting a similar shift (_f_β ≈ 18–20 pN) of the peak location with change in Loge(ramp rate). Concomitantly, nearly 100-fold faster ramps were required to reach strengths comparable to PSGL-1–P-selectin interactions, and an unstressed failure rate of ≈90–100/sec was needed to correlate the kinetically limited probability density to the force histograms (compare dotted red curves in Fig. 4 E and F). To emphasize the differences between P-selectin bonds to PSGL-1, GP-1, and sLeX, the mean lifetimes derived from the analyses of failure statistics are plotted as continuous functions of force in Fig. 5_A_.
Fig. 5.
The mean lifetimes of PSGL-1–P-selectin, GP-1–P-selectin, and b-sLeX–P-selectin bonds plotted as continuous functions of force (A) and correlation of the two-pathway model to the mean lifetimes measured for neutrophil and PSGL-1 bead tethers to P-selectin in a flow chamber under different shear rates (data from ref. 8) (B). (A) Needed to match histograms under steady ramp and jump/ramp force histories (see legend of Fig. 2 for PSGL-1–P-selectin and legend of Fig. 4 for GP-1–P-selectin and b-sLeX–P-selectin), the mean rates of failure are continuous functions of applied force, the reciprocals being equivalent to the mean lifetimes expected at constant force. The red dashed line defines the lifetime if restricted to dissociation along the high-impedance pathway for PSGL-1–P-selectin. (B) Using the force scale _f_β = 18 pN for rate exponentiation along pathway 2, the two-pathway model was fit to the data from ref. 8, assuming that the cell and bead attachments in the flow chamber experiments were held by an average of two bonds. The solid black curve shows the lifetime for one bond predicted by the two-pathway parameters: _k_1rup ≈ 7/sec, _k_2rup = (0.45/sec) exp(f/18 pN), and a crossover in force at ≈15–20 pN. The dashed black curve shows the lifetime 〈_t_〉 expected for two of these bonds that equally share the force f and fail randomly; i.e., 〈_t_〉= [_k_rup(f) + 2 _k_rup(f/2)]/[2 _k_rup(f) _k_rup(f/2)], where _k_rup(f) defines the failure rate for one bond.
Conclusions and Discussion
Perhaps similar in design, both P- and L-selectin bonds have exhibited an unexpected rise and fall of lifetime when tested under constant force–clamp conditions (cf. Fig. 5_B_; refs. 8 and 20). Labeled as a “catch-slip” bond, this type of phenomenological behavior was proposed in a model proposed by Dembo et al. (21) many years ago. It was thought that pulling with small force could first tighten a bond, extending its lifetime, and then higher forces could lower a principal energy barrier to speed up failure of the bond. Here, probing PSGL-1–P-selectin bonds with “steady ramp” and “jump/ramp” modes of force spectroscopy, we have shown that the “catch-slip bond” behavior arises from a mechanochemical switch, and that the switching dynamics involve an important coupling between molecular components of the PSGL-1 N-terminal binding domain. Of particular note is that sLeX–P-selectin bonds, although strong only under very fast loading, seem to fail along a single dissociation pathway. Yet, even with no tyrosine sulfation, the combination of polypeptide and carbohydrate branches in GP-1 enables two-pathway switching. As an indication of the important coupling between the N-terminal branches, the failure rate along the high-impedance pathway in GP-1–P-selectin is slowed 100-fold relative to that in sLeX–P-selectin interactions, leading to much greater strength under fast loading. Although GP-1 lacks the numerous sites for hydrogen bonding and water bridges provided by tyrosine sulfates, x-ray crystallographic studies of SGP-3 (13) suggest that several nonpolar interactions may still remain between the peptide branch and the lectin domain of P-selectin as well as a couple of hydrogen bonds. Perhaps these residual interactions strengthen the carbohydrate interaction. However, the lack of tyrosine sulfation is also significant and seems to impact bond lifetime under slow loading perhaps by increasing impedance along the initial-fast pathway. The mechanical strengthening of the extremely weak carbohydrate–P-selectin interaction by the polypeptide backbone and the effect of tyrosine sulfation are consistent with the hierarchy of affinities measured in previous studies of P-selectin binding to constructs of PSGL-1 in solution (13, 18, 19). Viewed overall, the insights obtained from dynamic rupture of the PSGL-1–P-selectin adhesion bond not only provide better understanding of adhesive functions but also indicate how force can act to signal, switch, and catalyze chemical activities inside cells.
Supplementary Material
Supporting Information
Acknowledgments
This work was supported by National Institutes of Health Grants HL65333, HL31579 (to E.E.), and AI44902 (to C.Z.).
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: PSGL-1, P-selectin glycoprotein ligand 1; sLex, the tetrasaccharide sialyl LewisX; b-sLex, biotinylated form of sLeX; PEG, polyethylene glycol; BFP, biomembrane force probe.
References
- 1.McEver, R. P. (2001) Thromb. Haemostasis 86, 746–756. [PubMed] [Google Scholar]
- 2.McEver, R. P. (2002) Curr. Opin. Cell Biol. 14**,** 581–586. [DOI] [PubMed] [Google Scholar]
- 3.Alon, R., Hammer, D. A. & Springer, T. A. (1995) Nature 374**,** 539–542. [DOI] [PubMed] [Google Scholar]
- 4.Alon, R., Chen, S., Puri, K. D., Finger, E. B. & Springer, T. A. (1997) J. Cell Biol. 138**,** 1169–1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Smith, M. J., Berg, E. L. & Lawrence, M. B. (1999) Biophys. J. 77**,** 3371–3383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Finger, E. B., Puri, K. D., Alon, R., Lawrence, M. B., von Andrian, U. H. & Springer, T. A. (1996) Nature 379**,** 266–269. [DOI] [PubMed] [Google Scholar]
- 7.Lawrence, M. B., Kansas, G. S., Kunkel, E. J. & Ley, K. (1997) J. Cell Biol. 136**,** 717–727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Marshall, B. T., Long, M., Piper, J. W., Yago, T., McIver, R. P. & Zhu, C. (2003) Nature 423**,** 190–193. [DOI] [PubMed] [Google Scholar]
- 9.Fritz, J., Katopodis, A. G., Kolbinger, F. & Anselmetti, D. (1998) Proc. Natl. Acad. Sci. USA 95**,** 12283–12288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hanley, W., McCarty, O., Jadhav, S., Tseng, Y., Wirtz, D. & Konstantopoulos, K. (2003) J. Biol. Chem. 278**,** 10556–10561. [DOI] [PubMed] [Google Scholar]
- 11.Evans, E. & Williams, P. (2002) in Physics of Bio-Molecules and Cells, Les Houches: Ecole d'Ete de Physique Théorique, eds. Flyvberg, H., Jülicher, F., Ormos, P. & David, F. (EDP Sciences–Springer, Paris), Vol. 75, pp. 145–185. [Google Scholar]
- 12.Evans, E. & Ritchie, K. (1997) Biophys. J. 72**,** 1541–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Somers, W. S., Tang, J., Shaw, G. D. & Camphausen, R. T. (2000) Cell 103**,** 467–479. [DOI] [PubMed] [Google Scholar]
- 14.Sako, D., Comess, K. M., Barone, K. M., Camphausen, R. T., Cumming, D. A. & Shaw, G. D. (1995) Cell 83**,** 323–331. [DOI] [PubMed] [Google Scholar]
- 15.Evans, E., Leung, A., Hammer, D. & Simon, S. (2001) Proc. Natl. Acad. Sci. USA 98**,** 3784–3789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Evans, E., Ritchie, K. & Merkel, R. (1995) Biophys. J. 68**,** 2580–2587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bell, G. I. (1978) Science 200**,** 618–627. [DOI] [PubMed] [Google Scholar]
- 18.Leppänen, A., Mehta, P., Ouyang, Y.-B., Ju, T., Helin, J., Moore, K. L., van Die, I., Canfield, W. M., McEver, R. P. & Cummings, R. D. (1999) J. Biol. Chem. 274**,** 24838–24848. [DOI] [PubMed] [Google Scholar]
- 19.Leppänen, A., White, S. P., Helin, J., McEver, R. P. & Cummings, R. D. (2000) J. Biol. Chem. 275**,** 39569–39578. [DOI] [PubMed] [Google Scholar]
- 20.Sarangapani, K. K., Yago, T., Klopocki, A. G., Lawrence, M. B., Fieger, C. B., Rosen, S. D., McEver, R. P. & Zhu, C. (2003) J. Biol. Chem. 279**,** 2291–2298. [DOI] [PubMed] [Google Scholar]
- 21.Dembo, M., Tourney, D. C., Saxman, K. & Hammer, D. (1988) Proc. R. Soc. London 234**,** 55–83. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information