Measuring the Elasticity of Clathrin-Coated Vesicles via Atomic Force Microscopy (original) (raw)

Abstract

Using a new scheme based on atomic force microscopy (AFM), we investigate mechanical properties of clathrin-coated vesicles (CCVs). CCVs are multicomponent protein and lipid complexes of ∼100 nm diameter that are implicated in many essential cell-trafficking processes. Our AFM imaging resolves clathrin lattice polygons and provides height deformation in quantitative response to AFM-substrate compression force. We model CCVs as multilayered elastic spherical shells and, from AFM measurements, estimate their bending rigidity to be 285 ± 30 k_B_T, i.e., ∼20 times that of either the outer clathrin cage or inner vesicle membrane. Further analysis reveals a flexible coupling between the clathrin coat and the membrane, a structural property whose modulation may affect vesicle biogenesis and cellular function.

INTRODUCTION

The formation, transformation, and recycling of clathrin-coated vesicles (CCVs) play a central role in receptor-mediated endocytosis at the cell surface and in intracellular trafficking from the _trans_-Golgi network (1–4). CCVs are involved in the uptake of molecules essential to cell function, the regulation of signaling receptors at the plasma membrane, cellular invasion by certain pathogens, and the movement of materials between cell compartments. To first approximation, one can consider CCVs as having an outer clathrin protein coat linked by adaptor proteins (APs) and other macromolecules to an inner lipid membrane vesicle to which cargo-laden receptors are attached. The dynamical cycle of coated vesicle production and cargo delivery involves myriad protein-protein and protein-lipid interactions (5–9). Defects in CCV-related trafficking correlate with a number of human diseases (3,8), including premature atherosclerosis, disorders in iron metabolism, and neurological problems. However, many aspects of CCV structure and function are not yet fully understood. In this study, we advance the use of atomic force microscopy (AFM) and investigate the mechanical structure of the coated vesicles. Knowledge of the mechanical properties of CCV components (10) may provide insight into the mechanisms by which highly curved vesicles bud from plasma membranes of much lower curvature.

AFM, which has imaging capability with sub-nanometer resolution and force manipulation capability from tens of pico-Newtons (pN) to several nano-Newtons, has become a potent research tool (11–15). Since AFM can be used to study samples in aqueous environments, it can be particularly advantageous for biological investigations. Electron microscopy (EM) historically has been used to obtain structural information about CCVs and clathrin lattices, most recently to furnish remarkable atomic-resolution images of clathrin cages (16–18). We now show how a novel implementation of AFM, together with appropriate modeling and data analysis, provides additional information about the mechanical structure and energetic organization of CCVs. We demonstrate that the bending rigidity of bovine brain CCVs is only ∼20 times that of the clathrin lattice or vesicle membrane alone, implying a flexible coupling between the outer clathrin coat and inner membrane. The CCV rigidity would be approximately one order-of-magnitude greater than this value if the coupling were infinitely stiff, whereas in the limit of very weak coupling CCV rigidity would be about the same order as that of the membrane and coat alone. In principle, the rigidity of the vesicles can be up- or downregulated by changing the mechanical properties of coat constituents, which may have mechanistic significance for the internalization of CCVs and their transport to, and fusion with, endocytic compartments.

MATERIALS AND METHODS

AFM methods and tip reconstruction

To facilitate this investigation, we developed new AFM-related techniques and a novel data analysis scheme to replace a traditional indentation approach for nanomechanical measurements. Variable-force contact mode and gentle tapping-mode AFM studies both were performed using a Nanoscope IV controller, PicoForce Multimode platform, and either a PicoForce or a type-E scanner head (Veeco/Digital Instruments, Santa Barbara, CA). To achieve a suitable condition for CCV/substrate attachment, freshly peeled mica was incubated in a concentration gradient of MES-buffered CaCl2 (<20 mM) at room temperature for several minutes. Excess solution was rinsed away and a high purity, fresh CCV sample (19) of clathrin concentration ∼0.15 mg/ml, in 100 mM MES-NaOH (pH = 6.5) buffer, was quickly introduced, after which CCVs were allowed to adsorb for several minutes. The samples were rinsed and reimmersed in the same buffer, and imaged using either tapping mode, under resonance Q-factor control enhancement, or contact mode with varying force levels. Similar biological AFM optimization was also carried out recently in our AFM facility for studies of rhodopsin in visual membranes (20). Basic AFM instrumentation and optimization procedures have also been described elsewhere (21,22).

AFM scanners were calibrated using silicon gratings (TGT series, MikroMasch, Portland, OR). The spring constants of soft silicon nitride cantilevers, nominally 0.01N/m or 0.03 N/m, were determined by thermal fluctuation methods (23) in a PicoForce MultiMode AFM (Thermal Turn, Veeco/Digital Instruments). Tips with nominal radius of <20 nm were preselected by the method of blind-tip reconstruction (24) using images of thin niobium calibration films (25), and were rechecked from sample images to detect tip modifications that might have occurred during our measurements. Sharp probe tips (of radius <∼5 nm) were chosen when we wished to resolve CCV polygonal facets via tapping-mode imaging, while blunt tips (of radius ∼15 nm), selected to reduce CCV damage, were used to quantify CCV compression via contact-mode imaging. Although the soft CCV samples result in certain scan artifacts and image noise, our implementation of the blind tip reconstruction routines still gives good estimates of the tip profiles in the direction along the scanlines.

AFM data acquisition and analysis

We developed a new scheme of data acquisition and analysis to obtain the CCV height response when the compression force is changed, either continuously or discontinuously, by a combination of a gradual drift of free cantilever voltage and sudden feedback voltage setpoint jumps. A continuous drift was induced by a slight temperature mismatch between the fluid sample cell and the injected exchange buffer, which slowly changes the voltage from the position detector measuring the laser beam reflected off the cantilever before sample-surface contact. To determine the profile of the force applied during imaging, we recorded several force-distance measurements interspersed with a series of imaging scans. The steady drift typically was ∼0.5 pN per scanline. Corresponding AFM images were analyzed scanline-by-scanline to extract force-dependent information.

New programs were developed in MathCad (MathSoft, Cambridge, MA) to identify CCV particles from each scanline, and the heights of isolated particles over the flat mica surface were determined by standard curve-fitting procedures. Particle heights from scanlines of neighboring force values were binned together to determine the average particle height for each scan force group. Because the AFM tip scans past CCVs with varying amounts of offset to their centers, a geometric conversion is required to obtain the average height of the CCV population from the apparent particle size distribution. For contact geometry between hard spherical CCVs of radius R randomly positioned on the mica surface and an AFM tip of radius r, the particles seen along scanlines have an apparent, height probability density,

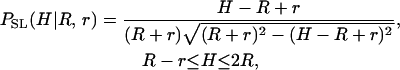graphic file with name M1.gif (1)

which is nonzero only in the indicated range of H, and features a weak divergence at H_→2_R. Accordingly, we define and evaluate via standard calculus a geometrical transformation function, _f_t(R, r); e.g.,

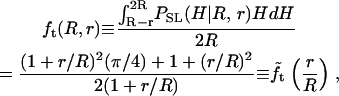graphic file with name M2.gif (2)

which, as shown below, can be used to relate the apparent and actual CCV heights.

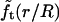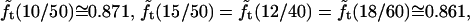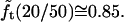The quantity Inline graphic turns out to be very slowly varying for values of r/R close to 0.3, which pertains to our AFM CCV compression experiments, where r ∼ 15 nm and R ∼ 50 nm. For example, Inline graphic and Inline graphic Thus, when the CCVs have size-probability density _P_CCV(R), we propose that the average height of the CCV particles measured along the scanlines, 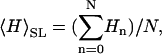Inline graphic is approximated very well by

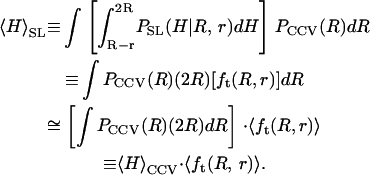graphic file with name M7.gif (3)

In other words, we can regard _f_t(R, r) in Eqs. 2 and 3 as a constant and deduce the average height of the CCV population, 〈_H_〉CCV, from

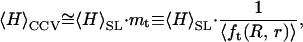graphic file with name M8.gif (4)

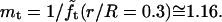where Inline graphic Because of the relative invariance of 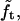Inline graphic the same multiplier can be used when the CCV particles are somewhat compressed between the AFM tip and substrate.

Shell models for CCV elasticity

We model intact CCVs as thin shells with liposome-type elastic energy, compressed between two flat plates that represent the substrate and AFM tip. Consequently, we approximate the energy change arising under the conditions of our AFM measurements as (26–30)

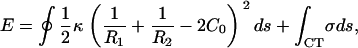graphic file with name M11.gif (5)

where _R_1 and _R_2 are the two principle radii of curvature, _C_0 represents intrinsic curvature, κ is the local bending modulus, and σ denotes the average interaction energy, per unit area, of the surface of a CCV when contacting the mica substrate or AFM tip. Note that the first (closed) integration is over the entire surface but the second integration (marked by CT) covers only the CCV areas that are in direct contact with the confining surfaces. The true energy-deformation relationship is very complex, and approximations are adopted here that allow us to capture leading-order terms with respect to relevant shape changes. We also ignore possible higher-order linear or nonlinear responses, e.g., involving local variations in shell thickness (31–33) or due to discrete lattice features (34) (see Appendix for a full discussion).

By using functional minimization procedures (29,35–37), we are able to solve for altered CCV shapes corresponding to minimal energy, for given AFM contact imaging and force constraints. We focus on elastic deformations under uniaxial compression. As shown in earlier publications, these fall within two classes: (1) oblate spheroids (30,36,38,39); and (2) smoothly-linked, piecewise, surfaces of constant mean curvature (29,40). Our detailed analysis (see Appendix) provides additional equations and numerical evaluations to calculate the CCV bending rigidity from the deformation height 〈_H_〉, taking into account an interaction energy parameter ɛ, for given compression force _F_tip. Although the shapes of oblate spheroids correspond to lower energies for larger values of ɛ, the constant mean curvature (CMC) vesicle energies turn out to be lower than those of oblate spheroids for the range of CCV compression corresponding to our measurements. Thus, the expression for CCV rigidity relevant to our AFM measurements is

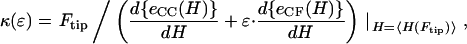graphic file with name M12.gif (6)

where _e_CC(H) and _e_CF(H) are functions related to the constant curvature (CC) elastic and contact flat (CF) surface energies, respectively (see Eq. A7). Thus, the energy of the CMC structures is proportional to _e_CMC(H) ≡ _e_CC(H) + ɛ · _e_CF(H), ɛ being a unitless parameter related to the ratio of σ/κ in Eq. 5. Were the value of ɛ known, then _κ_CCV could be readily determined from Eq. 6. The unknown ɛ leads to a curve, κ(ɛ), for each data pair of CCV height and force. Therefore, we can the use the range of experimental measurement {_F_tip, 〈_H_〉} to generate a series of κ(ɛ) curves and, from their intercepts, determine the converging values (κ ± stdκ, ɛ ± stdɛ) as the best estimates for our CCV sample.

For comparison, we similarly calculated the bending rigidity when an oblate spheroidal shape is assumed for the distorted vesicle, using values of compression from our measurements. Based on Eq. 5, such deformation is found to require higher energy than when a vesicle is distorted into the CMC shape. Hence, for a given applied force and discerned compression, such use of the spheroidal shape approximation would underestimate the rigidity of the CCVs.

Bending elasticity of composite shells

The bending rigidity of a uniform solid sheet scales with the cubic power of its thickness, as we neglect the CCV lattice discreteness in analogy to the properties of nanotube composites (34,41), following from classical moment of inertia calculations. For pure bending, the bending rigidity of a rod increases as the fourth power of increasing diameter. For out-of-plane bending of a large homogeneous sheet, the bending rigidity shows a basic cubic power dependence on the thickness. However, this relationship is modified for a layered composite. Consider, for example, the sheet to be a composite structure of total thickness h composed of two equal, uniformly separated, slabs of thickness t connected by ideal, stiff, noninteracting supports. These rigid supports form an intermediate layer that mechanically couples the outer layer and the inner layer completely together so that, upon composite bending, both will experience bending with respect to the common single neutral surface (NS) midway between the two slabs. For such a strong intermediate layer, the supports must have both a stiffness that opposes changes in the layer separation and a shear rigidity that opposes relative layer sliding. Assuming a strong coupling layer and pure bending with respect to a single NS, we find that the bending rigidity of the composite is increased over that of an individual slab by a factor G(h, t), given as

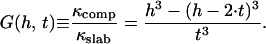graphic file with name M13.gif (7)

For h/t ∼5, such as for a CCV (see below), the _G_-factor would be ∼100 for a strongly coupled composite form. However, in the limit that the intermediate layer is made of weak supports, it could behave like a liquid and provide no structural rigidity. With such a weak coupling layer, the inner and outer slabs could slip with respect to each other, and each would bend with respect to its own NS. Then, instead of the value given by Eq. 7, we would have G = 2, independent of the slab separation height. Therefore, the bending rigidity of the composite depends strongly on the interslab coupling. Thus, by comparing CCV rigidity with the rigidities of the inner membrane layer and outer clathrin lattice, one can probe the nature of clathrin-membrane coupling.

RESULTS AND DISCUSSION

AFM visualization of clathrin polygons

To visualize the topological structure of the clathrin coats, we selected sharp probe tips and adopted a particularly gentle, noncontact, AFM tapping mode scheme (21). Highly purified bovine brain CCVs (19) were stored cold (0–4°C) in 0.1 M MES-NaOH (pH 6.5) buffer and used while fresh. Since CCV integrity and energetic properties can be salt- and pH-dependent, all AFM measurements in this study were performed in the same MES solution. We searched for an appropriate material to use as a functional AFM substrate, and discovered that Ca2+-pretreated mica would adsorb our CCVs without causing their collapse. High purity CCV samples were essential, as impurities directly compete for substrate and AFM tip surface.

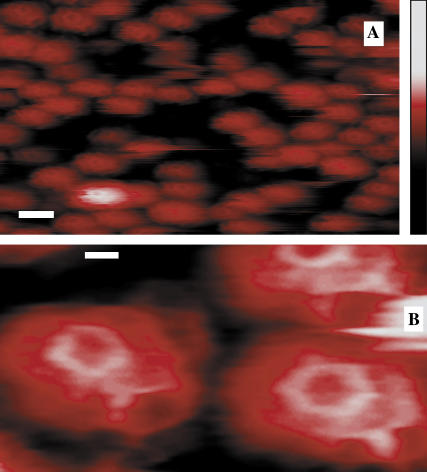
Our low-force tapping-mode imaging showed the polygonal lattice structures previously seen only from electron microscopy (16–18). We resolved coat elements with representative pentagonal and hexagonal facets having a lattice bond length of 18 ± 2 nm and heights mostly between 80 and 100 nm (Fig. 1).

FIGURE 1.

FIGURE 1

Topographical images of CCVs on a Ca2+-pretreated mica substrate, obtained by soft tapping mode AFM under fluid. (A) A representative field (scale bar = 100 nm) of unprocessed image showing clathrin CCVs mostly between 80 and 100 nm in height (color-scale, right, 0–250 nm), obtained by using a sharpened and clean silicon nitride tip (r ∼3 nm). (B) A bandpass-filtered and contrast-enhanced image area showing a CCV pentagon (left) and a hexagon (right). Scale bar = 20 nm.

Clathrin polygonal facets were seen only when sharpened and clean silicon-nitride (SiN) AFM tips (of <5 nm radius) were used to reduce tip convolution. This visualization of pentagonal and hexagonal facets (Fig. 1 B) confirms the fidelity of our CCV samples under the chosen measurement conditions.

CCV compression by AFM tips

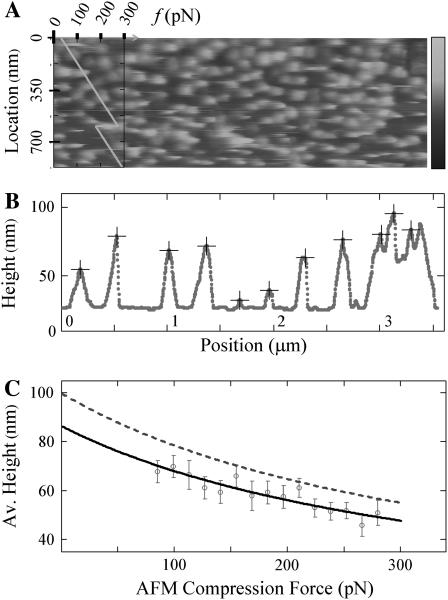
We next used AFM contact mode imaging to apply quantitatively varying levels of compressive force and measured CCV compression between the substrate and the AFM tips. Compression force level was allowed to increase gradually and was subjected to sudden decreases at selected locations (to test for vesicle height recovery) by varying the contact set point value. We used relatively blunt AFM tips (of ∼15 nm radius) to reduce CCV damage, and line-by-line image analyses to extract force-dependent features. We found that CCV heights correlate with the compression force in the range of ∼50–280 pN (Fig. 2 A), before CCV damage becomes visible (bottom of Fig. 2 A). Along each scanline, particles can be readily identified (Fig. 2 B) and they correspond to section profiles of the CCVs. When the height values of these scanline particles were grouped according to the AFM contact force, we found that the mean value declined smoothly for higher tip force, whereas the standard deviation of the height does not change significantly (Fig. 2 C). We routinely monitored the AFM imaging scan rate and feedback parameters to determine equilibrium imaging results, i.e., those where the response of the CCVs depends only on changes in AFM compression force. Related AFM imaging techniques could be used to discern features that are kinetic-, viscous-, and/or rate-dependent, but such nonelastic features are not subjects of current analysis.

FIGURE 2.

FIGURE 2

AFM contact mode imaging of CCVs under elastic compression. (A) A portion of a contact-mode AFM image when the imaging force changes over a range of ∼40–300 pN at a rate of ∼0.5 pN per scanline (or per second), obtained by using a relatively blunt silicon nitride AFM tip (r ∼15 nm). The force profile (scale, top left corner), showing a controlled reduction of 100 pN, is plotted (diagonal line) to indicate the AFM compression force at each scanline location (left vertical scale). Grayscale on the right indicates topographic height range to 200 nm. (B) A filtered set of CCV particle profiles (+ signs), tracked along a particular scanline by curve fitting to reduce the effects of noise and lattice struts. (C) The average particle height, estimated for CCVs from scanlines grouped together according to compression force. Solid curve is a linear fit of this force to the inverse of the average height. The dashed line is the average height for the CCV population calculated from the solid line after a geometric correction (Eq. 4).

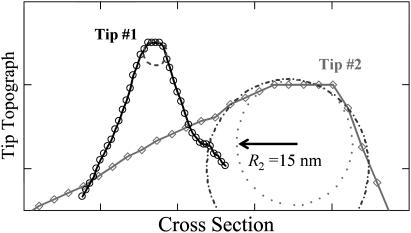
To further quantify CCV compression, we devised a geometric conversion function to account for the fact that the AFM tip generally does not pass over a vesicle center (see Materials and Methods). This conversion depends, rather weakly, on the tip size relative to CCV size (Eqs. 2–4). We implemented a blind tip reconstruction procedure (24) to estimate the tip shape from the scanned images. From Fig. 2 A, the reconstruction suggested a blunt tip with a 15 nm radius at the sharpest point and asymmetric 30–60° cone angles (Fig. 3). (Similarly, from Fig. 1 A we reconstructed a cross section of a sharp tip of 3 nm radius and of ∼30° cone angle, which explains why the clathrin polygons were well resolved in the tapping mode studies.) Therefore, with the geometric conversion approximated by a simple 16% increase, our variable-force imaging data revealed that the average height of the CCV population decreases with increasing AFM compression force approximately as Δ(1/〈_H_〉) ∝ f (Fig. 2 C). The average CCV height is consistent with an uncompressed CCV diameter of ∼100 nm when the data are extrapolated to zero AFM contact force, but this height is reduced to ∼65 nm at a force of 200 pN.

FIGURE 3.

FIGURE 3

Scanline cross sections of AFM tips determined by blind-tip reconstruction procedures (24). The sharp tip (Tip #1) for tapping-mode images (Fig. 1 A) has a radius of ∼3 nm (dashed circle). The blunt tip (Tip #2) for contact-mode images (Fig. 2 A) is more asymmetric and can be fit to a radius of between 15 nm (_dash_-dotted circle) and 21 nm (dotted circle).

CCV bending rigidity via shell elasticity model

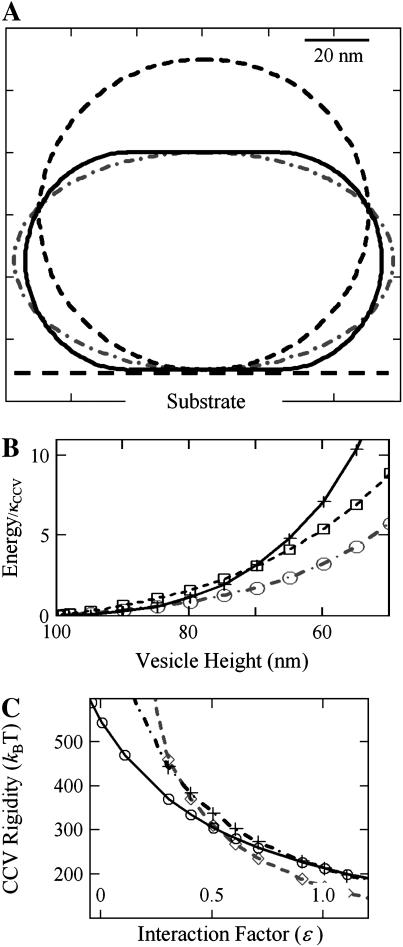
We modeled the three-dimensional elastic deformations of CCVs compressed between two parallel planes defined by the substrate and AFM tip (see Materials and Methods). The CCVs were approximated by elastic shells having either oblate shape or as being constructed from several smoothly linked surfaces of constant mean curvature (CMC surfaces) (Fig. 4 A). To calculate the deformation, the shells are subjected to the constraint of constant surface area, but the total internal volume is allowed to relax (see Appendix). We implemented mathematical calculations that relate the bending rigidity of the vesicle membrane, _κ_CCV, to both the height compression and an energy parameter, ɛ, which accounts for interactions between the CCVs and the mica surface and AFM tip (Eq. 6). In Fig. 4, A and B, we show that, for relatively strong interactions and a moderately large degree of CCV compression, CCVs have smaller total energies when described by CMC surfaces, as compared with shapes of oblate spheroids. However, when the attractive energy between CCVs and substrate and tips is small, and when the compression is small, the lowest energy shape is that of an oblate spheroid (Fig. 4, A and B). Our analysis (Materials and Methods, and Appendix) thus demonstrates how the compression of CCVs depends sensitively on both CCV sample conditions and substrate/tip characteristics.

FIGURE 4.

FIGURE 4

Rigidity analysis of elastic shell models of CCVs (see Materials and Methods, as well as Appendix). (A) Calculated cross sections of CCV shape with axial symmetry perpendicular to the substrate (dashed line, uncompressed CCV at 2_R_0 = 100 nm diameter; solid line, vesicles formed from CMC surfaces, at a deformed height of 70 nm; _dash_-dotted line, oblate spheroidal representation of deformation to the same compressed height of 70 nm). (B) The total bending and surface energy of the CCV shapes shown in panel A in units of bending rigidity, as a function of the vesicle height reduction (+ sign, oblate spheroids; ○ and □, CMC surfaces under different contact interactions with parameter value of ɛ = 0.5 and 1.0, respectively). (C) CCV rigidity calculation, using the measured data in Fig. 2 C and following the force balance relationship given in Eq. 6. The ⋄, +, and ○ signs pertain to height data for compression forces of 75, 175, and 275 pN, representative of the whole data range. The three curves converge near the result _κ_CCV = 285 _k_BT, ɛ = 0.6.

By using measured CCV compressions for the range of applied force shown in Fig. 2 C, we deduced the bending rigidity, _κ_CCV, and simultaneously determined the value of the interaction parameter ɛ. Calculations were performed for CMC structures using Eq. 6 and related mathematical expressions (see Appendix). By taking three data pairs (corresponding to low, medium, and high force, which span the whole data range), we find that associated rigidity curves intersect near the common values _κ_CCV = 285 ± 30 k_B_T, and ɛ = 0.6 ± 0.1 (Fig. 4 C). The parameter ɛ is related to the interaction energy between the flat surfaces of the distorted CCV structure (CMC) and the mica substrate and AFM tip with which they are in contact. The value ɛ = 0.6 suggests that, for the sample conditions in our study, the magnitude of this attractive energy is ∼40% of the energy needed to bend equivalent spherical caps into the planar surfaces of the CMC vesicle.

We expect the CMC shape to be fairly close to that which truly is the shape requiring minimal compression energy. To quantify the impact of CCV shape minimization on rigidity estimates, we also calculated _κ_CCV when making a spheroidal shape approximation (See Appendix). Under the conditions of our CCV measurements, oblate spheroids require higher deformation energy than do the correct CMC shapes (Fig. 4 B). Consequently, the spheroid shape approximation provides estimates of CCV rigidity as 178, 132, and 101 k_B_T, respectively, from the height data corresponding to compression forces of 75, 175, and 275 pN (Fig. 4 C). Therefore, the spheroidal shape results in an underestimation of _κ_CCV of ∼40% for smaller deformations to 70% for larger deformations. We have also shown that the effects of water and buffer permeability on CCV shape changes are of minimal concern in our analyses, but water movement might be important in other situations (see Appendix).

Molecular coupling between clathrin net and lipid vesicle

What is the significance of the rigidity value determined above? The answer lies in CCV structural anatomy and can be examined within the context of a shell rigidity model (Fig. 5). Each CCV can be thought of as a composite structure which, according to average dimensions inferred from electron microscopy (16–18), has a coat thickness of ∼27 nm divided into three layers: 1), the polygonal clathrin lattice (CL, t ≅ 4.5 nm); 2), a vesicle membrane of mostly lipids and cargo proteins (VM, t ≅ 4.5 nm); and 3), a connecting layer (≅18-nm thick) containing APs and other associated coat proteins, cytoplasmic regions of membrane proteins, and certain inward-pointing domains of clathrin chains. In terms of mechanics, layers #1 and #2 are of approximately equal thickness and happen to have similar individual bending rigidities, that is, _κ_CL ≅ 20 k_B_T (10,42) and _κ_VM = 10–30 k_B_T (26,28). The intermediate region, #3, mainly provides mechanical coupling between the clathrin lattice and vesicle membrane, but may also contain interconnections that give rise to enhanced intralayer bending resistance.

FIGURE 5.

FIGURE 5

Composite shell rigidity model of a CCV. (A) Cartoon of a 100-nm CCV with average dimensions obtained from EM reconstitutions (16–18), highlighting the flexible interlayer coupling inferred here from the measured rigidity of the CCVs. (B) Composite shell of the CCV (total thickness, h ≅ 27 nm), where the clathrin lattice (layer 1: t ≅ 4.5 nm) and vesicle membrane (layer 2) are approximately equal thickness and have similar bending rigidity. The connecting layer (layer 3) provides a partially rigid mechanical coupling whose variation can strongly modulate the rigidity of the CCV.

The character of the coupling between inner membrane and clathrin shell strongly affects the overall bending rigidity of the composite CCVs. Were the connecting layer to provide totally rigid linkage in the radial direction (but no intralayer connectivity), the CCV would be ∼100-times more rigid than each sublayer. In contrast, CCV rigidity would be only twice that of the membrane should the intermediate layer offer no resistance and behave as a liquid. From the measured value of _κ_CCV and estimates of _κ_CL and _κ_VM, we find that the ratios _G_CCV/CL ≡ _κ_CCV/_κ_CL and _G_CCV/VM ≡ _κ_CCV/_κ_VM lie within the range 10–30, varying mainly with the value of _κ_VM. These _G_-values are considerably smaller than the value predicted for rigid connections between the layers, but an order-of-magnitude larger than were there no support (Eq. 7). We thus can infer that the intermediate protein layer in bovine CCVs provides only partially rigid mechanical coupling between the membrane and the clathrin lattice. Although on small length scales the membrane undoubtedly is heterogeneous due to, e.g., the existence of lipid rafts (22,43,44) during cargo-loading, this conclusion is unlikely to be altered by such considerations. Additionally, although unequal individual rigidities for layers #1 and #2 would shift the location of the neutral surface of bending (Fig. 5 B), they would do so in predicable ways and the composite CCV rigidity would scale more-or-less linearly with the component rigidities. In the unlikely case that elastic coupling between the coat and inner vesicle membrane can be totally ignored, the measured rigidity would be that of the protein coat, alone, for sufficiently weak compression, increasing as the layers make stronger contact. Note, also, that the probable sources of error in our deduced rigidity value (discussed in the Appendix) are unlikely to affect the qualitative conclusion that the intermediate layer only partially (i.e., weakly) couples the clathrin lattice to the lipid membrane.

A possible cause of the flexibility of the interlayer connections is that the bundles of three clathrin distal segments and terminal domains, resolved by EM (16,17) as pointing inward toward APs, buckle relatively easily. Another possibility is misaligned or incomplete AP linkage to other CCV constituents. Consequently, CCVs containing tissue-specific membrane elements and carrying differing endocytotic cargo, might have interlayer couplings of differing mechanical strength. Mechanical factors can affect the formation of clathrin cages (10,42), the creation and recycling of coated vesicles (45), and, by extension, other intracellular membrane trafficking mechanisms similar to clathrin-dependent processes. The measured value, _κ_CCV = 285 k_B_T, is consistent, also, with a significant increase in the rigidity of the clathrin-containing coat due to the binding of clathrin-associated proteins. In this case, although the coupling might be weak, the stiff outer coat might bend the plasma membrane by steric mechanisms. Interactions between specific proteins and particular membrane constituents that increase intrinsic membrane curvature (46–48) might also play a role in vesicle blebbing, in which case weak coupling to an adaptable clathrin lattice, where the links between triskelia could be easily broken, would be advantageous. The large deformations involved in our AFM measurements correspond to energy increases from a fraction of, to a few times, _κ_CCV (Fig. 4 B). However, biological CCV shape transformations more likely progress step-by-step, each of which involves only a small number of triskelia and a localized membrane patch.

The possibility to change the mechanical coupling between coat and membrane could provide CCVs the adaptability to undergo cycles of assembly/disassembly and shape transformation associated with endocytosis or _trans_-Golgi trafficking. Association of AP2 complexes with clathrin in a nascent-coated pit (49) might serve this purpose. If, as seems to be the case, the interlayer coupling is flexible, its modulation can substantially impact the dynamic cycling of membrane-trafficking organelles. The relatively high value of clathrin-coated pit rigidity obtained by expanding the plasma membrane with surfactants (50) perhaps is indicative of a stronger interlayer coupling at this earlier stage of clathrin-coat formation. Other observations indicate that clathrin-dependent trafficking processes are sensitive to environmental conditions (51), are subject to stochastic fluctuations (52–55), and are compatible with cellular regulation (8,56). Interlayer mechanical coupling could be involved in these, as well as other, dynamic aspects of trafficking within cells.

CONCLUDING REMARKS

We have demonstrated here the use of a new method, based on atomic force microscopy (AFM), to determine the mechanical rigidity of clathrin-coated vesicles (CCVs). The novelty of this AFM scheme involves applying a controlled but variable force to the CCVs and then relating their deformations to their elastic modulus. Our new approach depends only on contact-mode scanning, with force gradually increasing from a very low value to a value close to, but not exceeding, the sample damage threshold. This method has advantages over traditional indentation approaches which, especially for nonuniform samples, are subject to problems such as piezo drift, creep, and hysteresis.

We also have created mathematical models that link applied forces, via coat mechanics and vesicle water/buffer permeability, to corresponding CCV shape changes. To our knowledge, this is the first direct nanomechanical measurement on CCVs. It yields information about the specific rigidity of the molecular entities linking the outer protein coat to the inner lipid membrane. Variants of our AFM technique may have applications in other studies directed toward understanding the mechanical structure of both biological and synthetic nanometric complexes.

Acknowledgments

We thank Dr. Dan Sackett and Dr. Emilios Dimitriadis, and Ed Wellner, Sylvain Ho, and Suber Chi for their assistance. We also thank Drs. Jonathan Silver, Nicole Morgan, Alan Burns, Tinh Nguyen, Terry Phillips, Richard Leapman, and Evan Eisenberg for insightful comments.

This work was supported in part by extramural grant NS29051 (to E. M. L.) and intramural funds from the National Institutes of Health, Department of Health and Human Services.

APPENDIX

Elastic shell model for CCVs

We model intact CCVs as composite shells with liposome-type elastic energy, given in a first approximation as Eq. 5, which is (26–30)

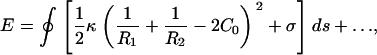graphic file with name M14.gif (A1)

where _R_1 and _R_2 are the two principle radii of curvature, _C_o represents intrinsic curvature, κ is the local bending modulus, and the integration is over the entire surface. The σ term represents, in general, both a vesicle surface tension contribution and the direct interaction energy between CCV surface and the substrate/AFM tip surfaces. Here, however, we restrict our consideration to the simplified case denoted by Eq. 5 in the Materials and Methods section where we use an averaged interaction energy per unit area for the any part of CCV surface in direct contact with substrate or tip and assume that the surface expansion modulus is sufficiently large that surface area is conserved, even if some surface tension arises during CCV compression. An extended discussion of the approximations of this model appears later in this Appendix.

Functional energy minimization (29,35–37) in the absence of deformation force yields a spherical shell of which the radius is set by the total surface area, that is, 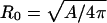Inline graphic= 50 nm for a CCV of average size. Without loss of generality, we can choose _C_0 = 1/_R_0 and set the energy minimum to zero. We further restrict our attention to uniaxial compression of CCVs between two flat plates representing the substrate and AFM tip. Elastic deformations obtained from functional minimization are expected to be rotationally symmetric and to conserve total surface area. We encounter two relevant classes of deformed shapes: 1), oblate spheroids (30,36); and 2), smoothly-linked, piecewise, surfaces of constant mean curvature (CMC) (29,40) (Fig. 4 A). With surface area conservation, the shape profile in both cases is uniquely defined by the reduced shell height, H < 2_R_0 (we presume that the CCVs lie with their long axes parallel to the substrate when compressed vertically).

For oblate spheroids, the shape equation for the radius coordinate, ρ, as a function of the angular coordinate θ, is well known to be (38)

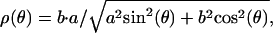graphic file with name M16.gif (A2)

where the short axis, a = H/2 at θ = 0, and the long axis, b = b(a) ≥ a at θ = π/2, follow from conservation of vesicle surface area, e.g.,

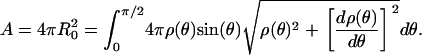graphic file with name M17.gif (A3)

Further, standard surface geometry provides relationships for two principle radii _R_1(θ) and _R_2(θ) as (38,39)

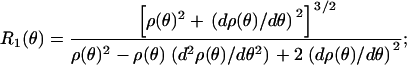graphic file with name M18.gif (A4)
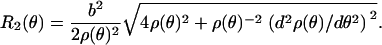graphic file with name M19.gif (A5)

Moreover, the elastic energy, as a function of deformation, is given as

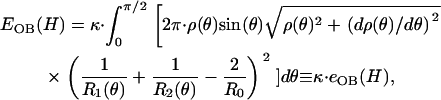graphic file with name M20.gif (A6)

where the energy function, _e_OB, increases as the height is reduced (see Fig. 4 B).

For vesicles modeled by surfaces of constant mean curvature (CMC), CCV height compression presumes two flat disks of radius _r_CF where the vesicles contact the mica substrate and AFM tip. If ω is taken to represent the average interaction energy per unit surface area of CCV in direct contact with these two planes, and if we assume that all the noncontact CCV surfaces have the same mean curvature, mc ≤ 1/_R_0, we then find, in contrast to Eq. A6,

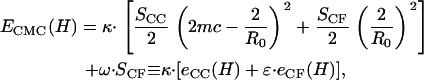graphic file with name M21.gif (A7)

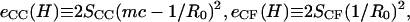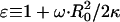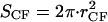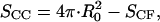where Inline graphic SCC is the area of the noncontact constant curvature (CC) surface, and SCF is the combined area of the two contact flat (CF) surfaces. The interaction factor Inline graphic is smaller than unity when the substrate and AFM tip attract CCVs with an averaged contact energy, ω ≡ 〈_σ_〉 < 0. The terms SCF and SCC are, respectively, Inline graphic and Inline graphic where the latter provides a relationship between mean curvature, mc, and disk radius, _r_CF. The shape equation for the noncontact CMC surface is satisfied by a segment of the so-called Delaunay's nodoids (37) (Fig. 4 A), and can be parameterized as

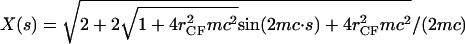graphic file with name M26.gif (A8)
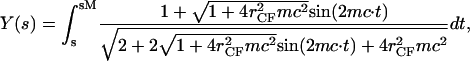graphic file with name M27.gif (A9)

where s is the cross-section contour length ranging from 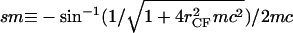Inline graphic to sM ≡ π/4_mc_ for the upper-right quadrant. The up-down reflection symmetry and axial symmetry around the vertical center line complete the entire CMC surface. This noncontact CMC surface joins the flat disks at edges X(x = sm) = _r_CF, corresponding to dY(s)/ds = 0 and dX(s)/ds = 1 at s = sm; it is continuous at Y(s = sM) = 0, corresponding to dY(s)/ds = 1 and dX(s)/ds = 0 at s = sM. The entire piecewise CMC surface is smooth, i.e. there is no discontinuity in slope.

In the case of zero compression, Eqs. A8 and A9 yield the spherical limit with _r_CF = 0, mc = 1/_R_0, and sM – sm = π/2_R_0. With increasing compression, we have the basic relationships for area conservation and the reduced height H < 2_R_0, e.g.,

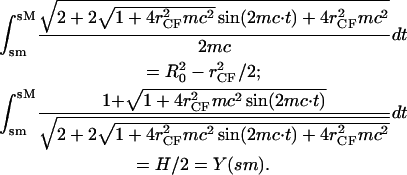graphic file with name M29.gif (A10)

From these relations we numerically determined the functions, _r_CF(H) and mc(H), and then evaluated _e_CC(H) and _e_CF(H) appearing in Eq. A7, providing the quantity 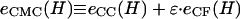Inline graphic for different values of the interaction factor ɛ (see Fig. 4 B).

To determine the bending rigidity modulus κ from our CCV height measurement via AFM, we use the force balance relation consistent with functional minimization (35–37), e.g.,

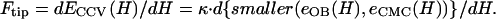graphic file with name M31.gif (A11)

Our energy functions show that there is a complicated crossover regime where the lower energy surface switches between piecewise CMC and the oblate spheroid shapes. Lower energy is required to distort the oblate spheroid shapes when CCV compression is small (<∼15%), corresponding to forces of <∼50 pN (Fig. 4 B). But, for larger compression (and most values of ɛ < 1), the piecewise CMC surface has lower elastic energy than the corresponding oblate ellipsoid shape. Therefore, for calculations applicable to our CCV measurements, the force follows from Eq. A11 with a substitution of Eq. A7. Finally, to simultaneously extract the bending rigidity κ and the interaction parameter ɛ, we rearrange Eq. A11 to obtain our main result, Eq. 6, appearing in Materials and Methods. To assess the robustness of the rigidity estimate when different approximations are used in CCV shape minimization, we calculated the apparent rigidity via Eq. A11 from _e_OB(H) for oblate spheroid shapes. Results were obtained for several values of experimentally observed compressions. Comparison with the corresponding CMC surface results indicated differences in deduced _κ_CCV of between 40% and 70%.

Effect of water permeability on CCVs

We need to justify that the intra-CCV water stress buildup, although existing transiently before CCV volume relaxation during compression, does not alter the equilibrium vesicle shapes that are imaged in our AFM scans and used for our rigidity calculations. While the clathrin lattice features 20-nm-size openings that should be permeable to water and ionic buffer constituents, the inner membrane vesicle could act as an enclosure that requires a finite time period to expel water in order that the internal volume is reduced to that of the energy-minimizing shape. In this subsection, we quantify the characteristic time of water permeation across the CCV membrane, and show it to be much shorter than the time during which a CCV is compressed by the AFM tip. Consequently, it is valid to ignore constraints on vesicle volume changes by water pressure when undertaking our equilibrium CCV shape calculations.

Earlier studies of lipid membranes indicated that the water permeation constant, measured as _P_=V/(Aτ) (where τ is the average residence time of a water molecule inside a unilamellar vesicle of volume V and surface area A), depends on lipid composition and increases with elevated carbon-carbon bond unsaturation in the hydrocarbon chains. Reported values of P at 25°C range from ∼155, to ∼330, to ∼412 _μ_m/s for single-component PC lipids 18:0–18:1n-9, 18:0–18:3n-3, and 18:0–22:6n-3, respectively (57). By inverting this expression, we find that the water contained in the aqueous core of a CCV would have an average intravesicle residence time,

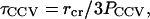graphic file with name M32.gif (A12)

where _r_cr ≅ 23 nm is the radius of the aqueous core of a 100-nm-diameter CCV, taking into account that the coat thickness totals ∼27 nm (see Fig. 5). To obtain a value for _P_CCV, we note that brain CCVs are highly enriched in polyunsaturated lipids (58,59), containing hydrocarbon chains such as 20:4n-6 and 22:5n-3, averaging approximately two carbon-carbon double bonds per chain (59). The lipid composition of the membrane is not fully known, and it is unclear how the protein components affect water permeation. For example, the vesicle surface might be occluded by receptors and linkage proteins, resulting in sites of low water permeability. On the other hand, CCVs may contain molecules such as aquaporins that facilitate water transport, as well as mechanically sensitive water transporters. Although an investigation of these aspects of vesicle physiology might be very interesting and informative, we here focus on the contributions of the lipids, and make a conservative guess that _P_CCV is of the order 100 _μ_m/s. Correspondingly, we can estimate from Eq. A12 that _τ_CCV is of the order of (23 nm)/(3 × 100 _μ_m/s) ≅ 0.1 ms. Because water flow is simply the net flux of water diffusion biased in direction by driving forces such as hydrostatic and osmotic pressure differences, this average intravesicular water residence time should set a relevant timescale for water diffusion out of the CCV membrane during AFM compression.

To look quantitatively at water expulsion during AFM compression, we take note of another study of lipid membrane water permeation (60), where volume changes in giant unilamellar vesicles (GUVs) of 15–60 _μ_m diameters were directly observed after exposure to osmotic stress imbalance. In that study (60), the flow permeability of the membrane, _P_f, was defined via the flux equation, as

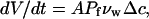graphic file with name M33.gif (A13)

where V and A are the volume and area of the GUV vesicle, Δ_c_ = (_c_–_c_∞) is the osmotic imbalance in moles per volume (the strength of the osmotic driving force), and _ν_w = 17 ml/mol is the molar volume of water. This flow permeation constant, _P_f, is reported to range from ∼30 to 40 _μ_m/s for mono- and di-mono-unsaturated PCs, to ∼100 _μ_m/s for diC18:2 and ∼170 _μ_m/s for diC18:3 at 18°C to 21°C (60). Despite many experimental differences between the two studies (57,60), these two sets of the diffusion permeation constant _P_f and P have similar magnitude and dependence on the lipid chain unsaturation. As already explained, brain CCVs contain an abundance of 20:4n-6 and 22:5n-3 lipid chains (58,59). Thus, it again seems reasonable to adopt an estimate that _P_f-CCV ≅ 100 _μ_m/s, based on this GUV data set (60).

It then follows from Eq. A13 that the time interval Δ_t_ for a volume reduction of Δ_V_/V at a constant driving force Δ_c_ is

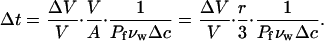graphic file with name M34.gif (A14)

For GUVs with diameters 2 · r =15–60 μ_m and experiencing Δ_c = 20 mM glucose, one can estimate the time required for each percent of initial volume reduction to be ∼0.5 s for small GUVs made up of unsaturated PCs, to ∼10 s for large GUVs containing saturated PCs (agreeing explicitly with Fig. 3 of (60)). In our AFM compression study, water is driven out of the inner, membrane-bounded vesicle by hydraulic pressure induced by the AFM tip force. However, the hydrostatic pressure is linked to the osmotic stress by Δ_p_ ∼ −Δ_π_ = −RT_Δ_c ≅ −0.025 (atm/mM)Δ_c_ (60,61), where R and T are the gas constant and temperature, respectively. Thus, from Eq. A13, we obtain an equation applicable to hydraulic flux and volume reduction time as

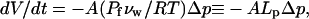graphic file with name M35.gif (A15)

where Δ_p_ is the hydraulic pressure buildup inside of the vesicle. The hydraulic permeation constant _L_p for CCVs is evaluated via the above definition, yielding 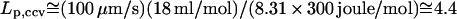Inline graphic _μ_m · s−1 · atm−1.

Now, following the principles leading to Eq. A11, we can postulate the force-balance relationship,

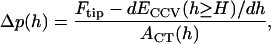graphic file with name M37.gif (A16)

where _dE_CCV (h ≥ H)/dh is the virtual force linked to the height reduction of the deforming vesicles, and _A_CT(h) is the applanation area of the inner vesicle upon which the AFM tip force is transmitted. Thus, a CCV approaches its equilibrium height h ≅ H only after being compressed for a period longer than the characteristic time for 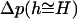Inline graphic to approach zero, i.e.,

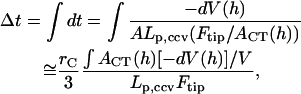graphic file with name M39.gif (A17)

where the integration is over the path of height reduction from h = 2_R_0 to H. It is rather complicated to evaluate the last quantity, 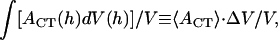Inline graphic since we do not have a full solution for vesicle shape under partial compression when there is an internal pressure buildup. However, we note that the applanation area is theoretically zero, i.e., _A_CT(h = 2_R_0) = 0, for an initially fully inflated membrane enclosure at the beginning of water outflow. Also, the bending-energy-minimized CMC shape for full compression has already been calculated for various heights H (see Fig. 4 B). At the outer edge of the CCV coat, the applanation area is simply the flat disk of radius _r_CF noted under Eq. A7. Although it is not known in detail how the forces that are applied to the CCV are transmitted to the inner vesicle, it is reasonable for present purposes to take the applanation area of the aqueous core to be located on the inner edge of the coat and use linear scaling, which leads to an applanation disk of radius _r_CT = _r_CF(H) · (_r_cr/_R_0) with an area of _A_CT (h = H) = π · _r_CT2. Therefore, in the integration in Eq. A17, we again project a linear approximation for _A_CT (h ≤ H) with respect to volume reduction and arrive at

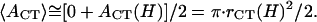graphic file with name M41.gif (A18)

Hence, Eq. A17 yields

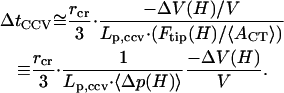graphic file with name M42.gif (A19)

This final estimate is analogous to the GUV result given by Eq. A14, and shows a linear proportionality with vesicle size, inverse proportionality with driving force, etc.

For numerical calculation, we now take the example shown in Fig. 4 A for compression to H = 70 nm, which is at the middle of our experimental data. First, we note that the radius of the aqueous core of the CCV, r_cr ≅ 23 nm, is ∼1000-times smaller than that of a typical GUV. Second, upon integrating over CMC shape, we find that the total volume reduction is only 4%, i.e., −Δ_V/V = 0.04 for this height. Third, the corresponding tip force is _F_tip ≅ 160 pN (Fig. 2 C), and the CMC contact disk radius is r_CT ≅ 10.6 nm (scaling from r_CF ≅ 23 nm on the outer surface in Fig. 4 B). Therefore, the average hydraulic pressure on the vesicle is 〈Δ_p(H)〉 ≅ 9 × 105 Pa [≅160 pN/1.8 × 10−16 m2], which is close to 20-times larger than the osmotic driving force of Δ_π ≅ 5 × 104 Pa arising in the GUV experiments (60) from an imbalance of 20 mM glucose. Accordingly, given that _L_p, ccv ≅ 4.4 _μ_m · s−1 · atm−1 (in correspondence with _P_f,CCV ≅ 100 _μ_m/s), Eq. A19 indicates

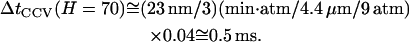graphic file with name M43.gif (A20)

In other words, the required CCV volume reduction would occur within a fraction of a millisecond, were simple water permeation the only mechanism relieving the hydraulic pressure induced by the AFM tip.

Additionally, we now consider membrane lysis. Membrane lysis can occur when the lateral surface tension τ increases beyond the limit _τ_ly, which is a material property that depends on lipid composition. The above mentioned GUV study (60) also reported bilayer _τ_ly values of ∼10 mN/m for mono- and di-mono-unsaturated PCs (18:0/1, 18:1/0, and diC18:1), dropping to ∼5 mN/m when one or both PC chains contained two _cis_-double bonds (C18:0/2 and diC18:2), and to an even lower value of ∼3 mN/m for diC18:3 at 21°C. The equation relating membrane tension and pressure buildup is the standard Laplace's Law (60,61), which for our spherical CCV core is

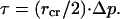graphic file with name M44.gif (A21)

Therefore, estimating _τ_lyCCV ≅ 5 mN/m for the mixture of CCV lipids, we obtain directly that Δ_p_lyCCV ≅ 4 × 105 Pa. Thus, during the initial moments of our AFM compression, CCV membrane tension may have somewhat exceeded the lysis limit. However, the lysis strength _τ_ly is reported from a long-time equilibrium limit, but the excessive tension in CCVs is short-lived. Due to the protective effect of the protein coat, the CCV vesicle may experience only a small amount of elevated leakage, or hyperpermeation, rather than membrane breakage. Such leakage/hyperpermeation would shorten the characteristic time of volume relaxation.

Likewise, one might consider the possible role of the initial hydration state of the CCV vesicle core as follows. Because our CCV sample is well equilibrated before adsorption onto the mica substrate, and our 100 mM MES-NaOH (pH = 6.5) buffer is partially nonionized and thus partially permeable (see Effect of Buffer Permeability on CCVs, below), it is less likely for CCV membranes to be under significant precompression tension. Any preexisting tension would be reduced by the expulsion of a small amount of buffer over hours and days. It is somewhat more probable that the CCV membrane contains a small amount of excess surface that can be released under initial intravesicle pressure buildup. This again shortens the time during which constraints on volume change arising from limited water flux may play a role.

In summary, we conclude that significant transient water pressure buildup inside the CCV membrane core is unlikely to last more than ∼1 ms. Because our AFM tip takes more than _t_V = 5 ms to move over each CCV at a scan rate of ∼1 line/s (Fig. 2 B), we infer that, on the timescale of our measurements, adjustments of vesicle volume are not constrained by slow water permeation, so water balance is satisfied for our rigidity calculation based on Eq. A11. The above calculations also clarify that, in other circumstances, water transport could be important. For examples, if the vesicles were to contain a large amount of cholesterol that reduces the effective permeability, or if the compression and volume reduction were much larger, or if the AFM scans were carried out at much higher rates, the characteristic time for water permeation/transport could became comparable to or even larger than the AFM force application time. In those circumstances, the effect of water pressure buildup must be treated more explicitly in the final analysis.

Furthermore, we have noted experimentally that images such as those shown in Figs. 1 and 2 sensitively depend on variations in force, but not scan rate. That is, we routinely vary the rate of our AFM imaging scan within the capability of the instrument, from a few lines per second to a few seconds per line (_t_V ∼2–15 ms per CCV), and see no difference in results (see Materials and Methods). If CCV volume changes were to be constrained by slow water permeation, the resistance to vesicle compression, under constant AFM force, would increase as the imaging scan rate increases, with a concomitant increase in apparent viscoelastic modulus. Since such behavior is not observed, the characteristic time Δ_t_CCV must be either <∼2 ms or >∼15 ms. This is consistent with our theoretically estimated characteristic time, Δ_t_CCV ≅ 0.5 ms. Therefore, we are confident that our data pertain to equilibrium CCV heights related solely to the elastic response of the composite coat.

Osmotic stress of buffer on CCVs

We also estimate, and find that we can neglect, osmotic stress resulting from CCV volume changes occurring during compression. Charged particles cannot pass through a lipid membrane during our AFM compressions, so it is possible that the ions in our 100 mM MES-NaOH (pH = 6.5) buffer increase in concentration, giving rise to an osmotic pressure contribution that elastically resists vesicle compression. To estimate the possible magnitude of the osmotic pressure imbalance, we note that the MES buffer is partially ionized and that its equivalent ionic strength at room temperature is ∼80 mM. The membrane permeabilities of these ionized and nonionized MES components are unknown, so we now estimate the maximal osmotic stress contribution by assuming that no buffer constituent escapes during our AFM compression. Again taking the example of Fig. 4 A for compression to 70 nm, we recall that the volume reduction is 4% for the CMC shape. Thus, the osmotic stress imbalance is <4 mM of higher internal MES concentration, which produces an outward osmotic pressure of ∼0.2 atm (60,61). This pressure is balanced by Laplace's force arising in the free-standing CCV surface associated with membrane surface tension (see Effect of Water Permeability on CCVs, above), which is too small to cause lysis or significant membrane area expansion in lipid membranes (60,61). This pressure would also act to counter AFM compression force over the flat part of the CCV in an elastic manner. The flat part of the CCV membrane is approximately, again, a disk of _r_CT ≅ 10.6 nm radius in Fig. 4 A. Therefore, the maximal osmotic stress force would be 12 pN [= 0.2 atm π(10 nm)2], which is <8% of the corresponding AFM compression force (see Fig. 2 C) and, at most, would change our rigidity estimation by a like amount. Moreover, because of the likely cross-membrane permeation of nonionized MES (especially during hyperpermeation), the actual effect of any osmotic imbalance on membrane surface tension and AFM compression probably is even less. Hence, we can discount any osmotic stress contribution in our model calculations.

Model approximations

The assumed symmetry between the planar mica substrate and the AFM tip plane is another approximation, in that the interaction energy ω, and hence the parameter factor ɛ, differ for the upper and lower contact surfaces. This assumption is necessary for analytic calculation of our CMC shapes, and is consistent with energy-minimization procedures only if the SiN surface tip is approximately flat and parallel to the mica surface, and if the adsorption energy between CCV surface and mica, _σ_CM, is the same as that between CCV and SiN tip surface, _σ_CS. The first condition is reasonable for a blunt tip (as is used by us (Fig 3)) and when CCV compression is small enough that the contact area is less than that blunt region. The second condition might be more problematic because interactions of the vesicle surfaces with mica and the AFM tip are not identical. However, when all likely interactions, e.g., electrostatic forces, hydrophobic and hydration forces, and van der Waals attraction forces are carefully considered (62), we conclude that this approximation is appropriate. For example, we infer that electrostatic forces are screened significantly, the Debye-Hückel length being ∼1.1 nm for our buffer of 100 mM MES-NaOH (63). The hydration and hydrophobic forces also are exponentially decaying, short-range forces. Hence, only the van der Waals attractive forces are long-range (i.e., power-law decay up to 10 nm), and thus are the main contributors to the adsorption energies _σ_CM and _σ_CS. Because the van der Waals force mainly depends on dielectric susceptibilities, the magnitude of the interaction between CCV surface and mica substrate is approximately the same as between CCV and SiN tip. Note also that a nonflat AFM-tip surface changes the energetic contributions in complicated ways, including a modification of the CCV-tip adsorption energy _σ_CS.

In addition, we recognize that real CCVs have significant thickness relative to their diameters, and that their coats feature discrete lattices. Hence, CCV distortions involve nanoscopic response beyond that of pure bending, possibly giving rise to macroscopic nonlinear elasticity (31–34). Indeed, we detected modest viscoelastic hysteresis in highly compressed CCVs, as well as irreversible collapse of reconstituted, membrane-free, clathrin-AP180 baskets (in other AFM measurements, not reported here). Nonlinear viscoelastic behavior needed to explain such response has been neglected in this calculation. Finally, nonaxial symmetric CCV shapes, which are relevant for off-center CCV compression, have not been discussed here.

References