A Combinatorial NMR and EPR Approach for Evaluating the Structural Ensemble of Partially Folded Proteins (original) (raw)

. Author manuscript; available in PMC: 2011 Jun 30.

Published in final edited form as: J Am Chem Soc. 2010 Jun 30;132(25):8657–8668. doi: 10.1021/ja100646t

Abstract

Partially folded proteins, characterized as exhibiting secondary structure elements with loose or absent tertiary contacts, represent important intermediates in both physiological protein folding and pathological protein misfolding. To aid in the characterization of the structural state(s) of such proteins, a novel structure calculation scheme is presented that combines structural restraints derived from pulsed EPR and NMR spectroscopy. The methodology is established for the protein α-synuclein (αS), which exhibits characteristics of a partially folded protein when bound to a micelle of the detergent sodium lauroyl sarcosinate (SLAS). By combining 18 EPR-derived interelectron spin label distance distributions with NMR-based secondary structure definitions and bond vector restraints, interelectron distances were correlated and a set of theoretical ensemble basis populations was calculated. A minimal set of basis structures, representing the partially folded state of SLAS-bound αS, was subsequently derived by back-calculating correlated distance distributions. A surprising variety of well-defined protein-micelle interactions was thus revealed in which the micelle is engulfed by two differently arranged anti-parallel αS helices. The methodology further provided the population ratios between dominant ensemble structural states, whereas limitation in obtainable structural resolution arose from spin label flexibility and residual uncertainties in secondary structure definitions. To advance the understanding of protein-micelle interactions, the present study concludes by showing that, in marked contrast to secondary structure stability, helix dynamics of SLAS-bound αS correlate with the degree of protein-induced departures from free micelle dimensions.

Introduction

The energy landscape theory of protein folding regards the transition from dynamically unstructured protein conformations to the native structure as the progressive organization of an ensemble of partially folded structures.1 Partially folded proteins may therefore be defined as exhibiting folded secondary structure elements with loose or absent tertiary contacts. Protein folding is not always successful and organisms of virtually all levels of complexity possess molecular chaperones that serve to prevent and resolve protein misfolding and aggregation.2,3 Nevertheless, particularly in organisms of increased age, certain proteins and fragments thereof misfold at levels that appear to be beyond the safeguarding capabilities of the chaperones present.4 This can lead to the formation of partially folded, metastable soluble oligomers whose cytotoxicity has been linked to the cellular demise characteristic of prevalent neurodegenerative diseases such as Alzheimer’s and Parkinson’s, as well as type II diabetes.5 For example, the misfolding of the protein α-synuclein underlies the pathogenesis of Parkinson’s disease.5 In light of the considerable biological and pathological significance of partially folded proteins, a detailed characterization of their structure (i.e., the range of structural states populated by these proteins) is desirable in order to better understand protein folding and misfolding.

Available methodology by which to study partially folded protein states employs site-specific diffusion and hydrogen-deuterium exchange experiments, the characterization of chemical shift patterns, and the analysis of, for example, 15N relaxation properties.6–15 These techniques have provided important insights into the structural and dynamic properties of mostly secondary structure elements within the context of the nascent protein fold. In addition, ensemble approaches using small-angle X-ray scattering data and ensemble-based interpretations of residual dipolar couplings (RDC) provide information on ensemble shape and composition.11,16,17 In favorable cases, a mimic of a partially folded state can be generated by mutagenesis, which enables a conventional structure determination.18 However, an experimental approach that could directly relate secondary structure elements to each other in space, and that could identify coexisting subpopulations within a structural ensemble, would further advance the capability to characterize partially folded proteins. Here, a combinatorial NMR and EPR spectroscopic approach is presented that permits the definition of the structural ensemble of metastable or trapped partially folded proteins. This method may also be applied to any other protein that exhibits large-amplitude dynamics between secondary structure elements, and is of value as well in characterizing protein domain-domain interactions and flexibility. To establish the methodology, the approach is demonstrated for a well-behaved model system: the 140-residue protein α-synuclein (αS) bound to a micelle of the detergent sodium lauroyl sarcosinate (SLAS).19

NMR observables provide linear and population-weighted averages, respectively, of the conformers underlying a structural ensemble in fast chemical exchange. In addition to NOE connectivity patterns,20 linearly-weighted, average chemical shifts and RDC define the effective conformational average of folded secondary structure elements.21,22 Global bond vector restraints may also be defined for protein segments that exhibit comparable degrees of alignment in anisotropic media.23 Valuable long-range distance information is encoded by paramagnetic relaxation enhancements (PRE) originating from a strategically placed paramagnetic center.24–30 In the present context, such information is perhaps most powerful when identifying transient long-range contacts31–33 or relative populations of a few, well-defined protein functional states.34 However, it is ambiguous to interpret the population-weighted average PRE in terms of an average distance or distance distribution when an a priori unknown range of structural states is populated. To capture the spatial distribution of secondary structure elements at average distances, the distribution of the value of an experimental parameter is required. Long-range distance information is most relevant and double electron-electron resonance (DEER) spectroscopy provides distance distributions up to 50–70 Å between a pair of unpaired electron spins residing on two strategically placed spin labels.35–38 The present study establishes a combinatorial EPR and NMR structure calculation scheme for partially folded proteins that identifies the preferred tertiary arrangement of dominant ensemble populations.

Experimental Section

NMR and EPR sample preparation

Human wild-type αS and 18 cysteine double mutants (Supplementary Fig. 1 and Fig. 1B) were prepared as described previously.39,40 The detergent sodium lauroyl sarcosinate (SLAS; Anatrace, Inc.) was present in all experiments at a saturating molar αS:SLAS ratio of 1:100.19 For NMR spectroscopy, 0.75 mM 2H/13C/15N-labeled αS samples were prepared in 25 mM NaH2PO4/Na2HPO4, pH 7.4, 0.02% NaN3 solution. To measure residual dipolar couplings (RDC), three different anisotropic environments were employed. The first anisotropic milieu was formed by G-tetrad liquid crystals employing 26 mg/ml d(GpG).41 The second one was based on a stretched, negatively charged polyacrylamide gel,42 polymerized in a 6.0 mm cylinder from a 4.6% w/v solution of acrylamide (AA), 2-acrylamido-2-methyl-1-propanesulfonate (AMPS) and bisacrylamide (BIS) at an AA:BIS ratio of 39:1 (w/w) and a molar ratio of AA to AMPS of 96:4. The third environment also employed a gel (6.0 mm, 5.2% w/v, AA:BIS=39:1 (w/w), [AA]:[AMPS]=95:5) that was reported previously.19 For EPR spectroscopy, cysteine double mutants were passed through 100 kDa cut-off filters and spin-labeled with [1-oxy-2,2,5,5 tetramethyl-Δ3-pyrroline-methyl] methanethiosulfonate, as described,39 resulting in a nitroxide side chain abbreviated R1 (Fig. 1A). To minimize intermolecular magnetic dipolar interactions, spin-labeled protein was combined with unlabeled wild-type αS at a molar ratio of 1:3. EPR samples were flash-frozen in 20 mM HEPES·NaOH, pH 7.4, 100 mM NaCl solution containing 30% sucrose to yield a final concentration of 50 μM spin-labeled αS.

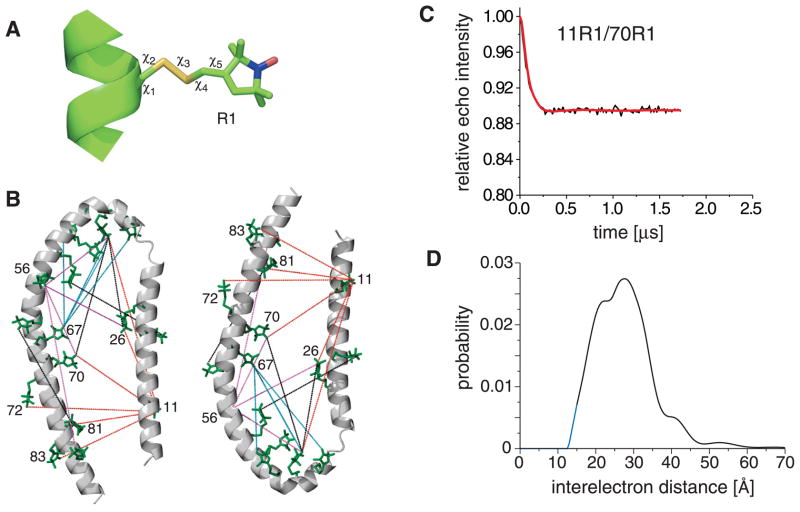
Figure 1.

Figure 1

Illustration of R1 spin label structure, incorporated R1 pairs and spin label interelectron distance distribution from 4-pulse DEER experiments. (A) Structure of the introduced nitroxide R1 side chain. Side chain dihedral angles, χ1-χ3, adopt canonical values, whereas χ4-χ5 float freely at surface sites.54 The nitroxide atoms are colored blue and red, respectively. (B) Residues 11, 22, 26, 37, 41, 44, 48, 52, 56, 63, 67, 70, 72, 81, 83 and 85 were R1 spin labeled. 11R1 is involved in six distance pairs, depicted in red. 56R1 is involved in four distance pairs, shown in violet. 67R1 is involved in four distance pairs, shown in cyan. The protein backbone structure depicts residues 1-93 of the subpopulation 93 C′N′/same average representative. (C) DEER dipolar evolution for the 11R1-70R1 spin label pair. The black traces denote background-corrected experimental data. The red curves depict fits using L-curve Tikhonov regularizations. (D) Resulting interelectron distance distribution. Due to the finite duration of microwave pulses, short distances become less accurate.48 To reach zero probability at distances below 15 Å, the distributions were extrapolated (blue curve). The distance distribution was integrated and assigned a probability of 1. Minor distribution peaks at low probabilities arise from imperfect background corrections and are unlikely to be of significance.

NMR and EPR measurements and analysis

Backbone chemical shift assignments of SLAS-bound αS were reported previously.19 N-H, C′-Cα and C′-N RDC were determined at 25 °C from 1_J_NH-scaled HNCO experiments43 and from quantitative _J_-correlation HNCO experiments44,45 of isotropic and aligned samples. A TXI cryoprobe-equipped Bruker Avance 700 spectrometer was used for data acquisition and data analysis employed the nmrPipe software package.46 Four-pulse DEER experiments35 were performed on a Bruker Elexsys E580 X-band spectrometer equipped with a 3 mm split-ring (MS-3) resonator, a continuous flow helium cryostat (CF935, Oxford Instruments, Inc.), and a temperature controller (ITC503S, Oxford Instruments, Inc.). Observer π/2 and π pulse lengths of 16 and 32 ns, respectively, were obtained and the observe frequency was set to the low-field absorption peak of the nitroxide EPR spectrum. The ELDOR pulse, at a length of 32 ns, was set to the maximum of the central absorption peak of the nitroxide EPR spectrum. A two-step phase cycle was employed to eliminate unwanted echoes. Measurements were performed at 78 K using a repetition rate of 500 Hz and a typical acquisition time of ~12 hr. The dipolar time evolution data were processed using a 3D background subtraction, and were then Fourier-transformed. Evolution times were optimized for the distance range studied and for the achievable signal-to-noise ratio, respectively (Supplementary Fig. 1). The interelectron distance distributions were obtained by Tikhonov regularization using L-curves as implemented in the DEERAnalysis2006 program.47 A regularization parameter of 100 was used for all spin pairs, except for 22R1-52R1, 11R1-41R1, 41R1-67R1 and 41R1-70R1, which were fitted with a parameter of 1,000. Due to the strongly reduced modulation depth of shorter distances in the time evolution data, distances below 15 Å cannot be clearly resolved using four-pulse DEER,48 and a few distributions were extrapolated at lower distances to reach zero probability (Fig. 1D and Supplementary Fig. 1).

Definition of structural constraints

Effective average backbone torsion angle intervals of SLAS-bound αS were obtained by molecular fragment replacement (MFR)21 employing three sets of N-H, C′-Cα and C′-N RDC and N, C′, Cα, Cβ chemical shifts, as described previously.19,49 Deuterium 13Cα and 13Cβ isotope effects were corrected for as outlined in the literature.50 A fragment length of seven residues was used for MFR, but the alignment tensor magnitude was essentially invariant for fragment lengths of 7, 9 and 11 residues (Supplementary Fig. 2). This resulted in two helices, termed helix-N′ (Asp2-Lys32) and helix-C′ (Ser42-Thr92; Supplementary Table 1), in analogy to SDS-bound αS.49 In accordance with the significant ps-ns timescale backbone dynamics of Thr33-Gly41 and Gly93-Ala140, respectively (Supplementary Fig. 3B), ambiguous fragments were found in these regions (data not shown). The weak helical tendency of Thr33-Gly41, as evidenced by their exclusively positive secondary 13Cα chemical shifts (Supplementary Fig. 3A),22,51 was taken into account by randomly defining one helix turn (φ= − 57 ± 35° and ψ= −47 ± 35°) per calculated structure within this region. No torsion restraints were defined for the dynamically unstructured tail (Gly93-Ala140), except for the proline-preceding residues Met127 and Glu137, which exhibited well-defined chemical shift patterns.52,53 The N-H, C′-Cα and C′-N bond vector orientations of residues 10-18 and 74-81, which exhibited comparable alignment tensor magnitudes (Supplementary Fig. 2), were related to a common tensor for each RDC dataset in order to implement translationally invariant bond vector restraints.23 Distance combinations from the 18 measured DEER distance distributions (Supplementary Fig. 1) were sampled, as described in Results and Discussion. Interelectron distance restraints were defined between the O atoms of the nitroxide side chains (Fig. 1A). The five documented χ1-χ3 spin label rotameric states of the R1 side chain in exposed α-helices (−60°, −60°, +90°), (−60°, −60°, −90°), (180°, −60°, −90°), (180°, +60°, +90°), and (180°, +60°, −90°) were randomly assigned with relative probabilities of 2:2:2:1:1 and intervals of ±30° around nominal values.54 The two higher dihedral angles of R1, χ4 and χ5, adopted a distribution of values at surface sites54 and were allowed to vary. Random numbers used throughout the present study were obtained from the Mersenne Twister generator MT19937.55

Simulated annealing structure calculations

For a chosen set of restraints, a structure was computed by simulated annealing starting at 3000 K and using the program XPLOR-NIH.56 Based on close 11R1-70R1, 11R1-72R1, 11R1-81R1 and 11R1-83R1 distances (Supplementary Fig. 1), initial coordinates defined helices-N′ and -C′ in an anti-parallel arrangement with ideal right-handed α-helical geometry (φ=−57°, ψ=−47°). To avoid the introduction of bias in helix orientations emanating from the initial coordinates, the orientation of the face of helix-C′ relative to helix-N′ was randomly incremented in 30° steps along the longitudinal helix-C′ axis, yielding 12 different, evenly distributed starting orientations. For each structure calculation, different initial random atom velocities were used. In addition to standard force field terms for covalent geometry (bonds, angles, and improper dihedrals) and nonbonded contacts (van der Waals repulsion), dihedral angle and interelectron spin label distance restraints were implemented using quadratic square-well potentials, and RDC restraints were incorporated using a harmonic potential. Also employed were a backbone-backbone hydrogen-bonding potential and a torsion angle potential of mean force.57,58 The final values for the force constants of the different terms in the simulated annealing target function were as follows: 1,000 kcal·mol−1·Å−2 for bond lengths; 500 kcal·mol−1·rad−2 for angles and improper dihedrals, which serve to maintain planarity and chirality; 4 kcal·mol−1·Å−4 for the quartic van der Waals repulsion term; 30 kcal·mol−1·Å−2 for interatom distance restraints; 500 kcal·mol−1·rad−2 for dihedral angle restraints; 0.3 kcal·mol−1·Hz−2 for the RDC restraints (normalized to a 1_D_NH tensor magnitude of 10 Hz); 1.0 for the torsion angle potential; and a directional force of 0.20 and a linearity force of 0.05 for the hydrogen-bonding potential. Structures violating any of the selected distance intervals by more than 0.5 Å, or any of the backbone torsion angle intervals by more than 5.0°, were excluded from ensembles. When fixing backbone coordinates in order to sample accessible spin label orientations, the force constant for interatom distance restraints was reduced to a final value of 0.4 kcal·mol−1·Å−2, and structures violating χ1-3 torsion angle intervals by more than 5.0° were excluded. Calculations were carried out on home-built quad-core Opteron and Xeon multiprocessor units. The average representatives of the detected ensemble subpopulations in C′N′/same and N′C′/same helix orders (Supplementary Table 5) have been deposited in the Protein Data Bank (accession number 2kkw).

Results and Discussion

In analogy to SDS-bound αS that had been studied earlier,49,59 the SLAS-bound αS model system employed herein was comprised of two anti-parallel helices: helix-N′ (Asp2-Lys32) and helix-C′ (Ser42-Thr92; Fig. 1B). In contrast to SDS-bound αS, however, no effective average conformation was discernible for the helix-helix connector (Thr33-Gly41) by molecular fragment replacement (MFR).21 This difference, which classifies SLAS-bound αS as partially folded, can be traced to a significantly reduced backbone order of the helix-helix connector in SLAS- compared to SDS-bound αS (Supplementary Fig. 3B). A structure calculation scheme must be established that relates two R1 spin-labeled secondary structure elements (Fig. 1A–B) to each other based mainly on 18 interelectron distance distributions (Fig. 1B–D and Supplementary Fig. 1). The scheme must account for the existence of distinct subpopulations of structures, whose presence is reflected by distributions exhibiting multiple maxima. In addition, R1 spin label flexibility contributes significantly to the appearance of interelectron distributions,60 which must be taken into account when translating interelectron into backbone interatom distances.

To arrive at the ensemble of structures underlying the DEER-derived interelectron distances, the present study sought to reproduce these distributions computationally based on a minimal set of basis structures that represented the partially folded protein state of SLAS-bound αS. First, the calculation of a structural ensemble based on distance combinations from entire distance distributions was explored directly so as to provide insight into the correlation of distance distributions. Second, structures involving distance combinations of distribution maxima only were calculated to obtain a theoretical set of ensemble basis structures. Third, in order to determine the minimal set of such structures (subpopulations), the basis structures were tested for their capacity to reconstruct the interelectron distance distributions. Fourth, the obtained basis structures were compared to the SLAS micelle dimension to learn more about the principles governing protein-micelle interactions.

Direct correlation of distance combinations

To calculate an ensemble of SLAS-bound αS structures, it was necessary to faithfully sample all 18 interelectron distance distributions (Fig. 1C–D and Supplementary Fig. 1). This amounts to selecting a specific distance from each distribution and forming distance combinations. When combining distances, however, it must be noted that individual distance probabilities are statistically not independent of each other if spin labels are linked among distributions. A pair of spin labels may be linked by sharing a common residue (e.g., 11R1-26R1 and 11R1-41R1), or, via an interconnecting R1 pair (e.g., 41R1-67R1 connects 11R1-41R1 and 44R1-67R1). In such cases, the selection of a distance in one distribution may alter the available distance combinations in linked distributions. In other words, the probability of a distance combination is conditional. Linked R1 pairs make structural restraints more stringent and can restrict the five degrees of freedom of each R1 spin label (Fig. 1A). A minimal number of residues should therefore be used when forming spin-labeled pairs at strategic sequence positions (Fig. 1B). When assuming statistical independence between distance choices, it is straightforward to calculate the probability of a distance combination, _P_i, as illustrated for all possible combinations of distribution maxima (Fig. 2A). In contrast, the calculation of conditional probabilities, _P_c, would require an a priori knowledge of the SLAS-bound αS structural ensemble. Given its obvious absence, only an approximation can be provided, which we based on two sequentially applied assumptions. First, for combinations of distance distribution maxima, _P_c > _P_i is assumed. If a spin label (e.g., 11R1 in Fig. 1B) must remain close to its average orientation encountered at a distribution maximum, the extreme difference in spin label orientations required to populate fringe interelectron distances in a linked distribution cannot be reached. Second, the NMR structural restraints must not be violated by any distance combination.

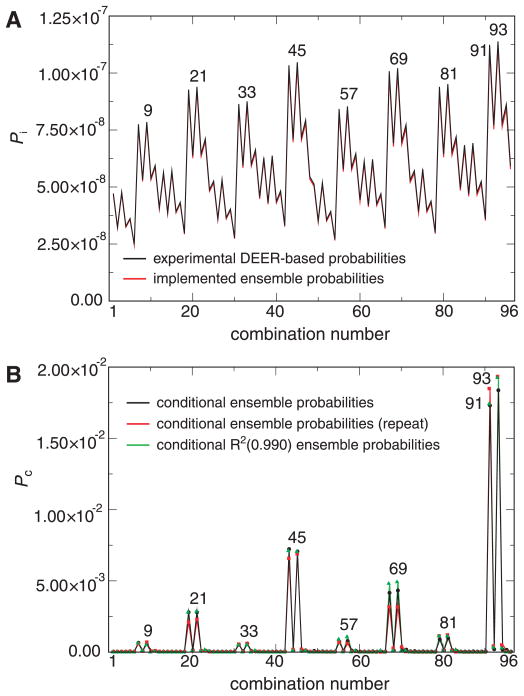
Figure 2.

Figure 2

Probabilities of encountering possible combinations of SLAS-bound αS interelectron distance distribution maxima (subpopulations). (A) The probability, _P_i, of encountering a selected distance combination was calculated as the product of the corresponding probabilities of the individual DEER-derived distances (Supplementary Fig. 1) or, alternatively, the computationally implemented ensemble probabilities. (B) The conditional probability, _P_c, of encountering a selected distance combination within the configuration space of the 60,000 structure ensemble, within an independent repeat configuration space, as well as within the R2(0.990) ensemble, was quantified by counting its frequency in the respective ensemble. The listed distance combinations, 1 to 96, represent all possible combinations of distribution maxima (Supplementary Table 2). For the evaluation of individual maxima probabilities and when counting ensemble structures, respectively, distance intervals of ±3.25 Å were employed around each distribution maximum. The two relatively close maxima of 37R1-67R1 at lower distances (Fig. 4B) gave rise to observed “doublet” patterns.

To implement the first assumption, conditional probabilities were defined as follows. Among the 18 distributions, a distance combination was randomly selected at a resolution of 0.5 Å, and each constituent distance was then removed from its respective distribution. This procedure was repeated until all available distance combinations were iteratively assigned to the desired number of total ensemble structures (Supplementary Fig. 4). This procedure allowed for the combination of any distribution distance, but favored combinations of distance maxima. In addition, as independent events, distance combinations were associated with a random combination of canonical spin label χ1-3 rotamers and a random starting structure (c.f. Experimental Procedures). For the configuration of 60,000 distance combinations, conditional probabilities were thus obtained for all possible combinations of distribution maxima (ensemble subpopulations) that were virtually independent of the distance selection sequence and, for the most probable maxima, were several orders of magnitude larger than the corresponding independent probabilities (Fig. 2).

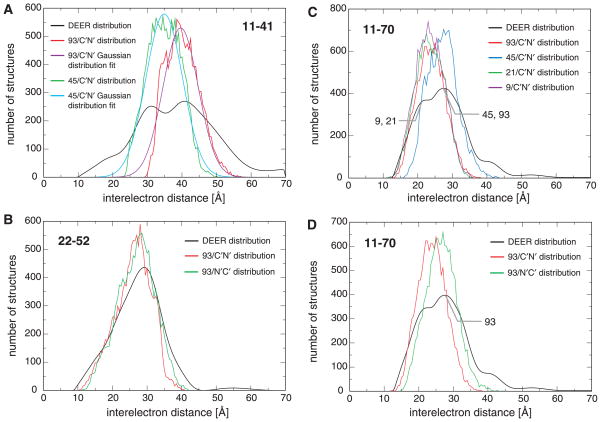
To implement the second assumption, we next performed simulated annealing structure calculations in order to determine whether a constraint configuration violated a structural restraint beyond grace margins. Each configuration was granted one attempt to succeed (no attempt was made to reevaluate failed structures by varying random initial atom velocities, starting helix orientation or chosen R1 rotamers). Of the 60,000 evaluated distance configurations of SLAS-bound αS, 23,954 were eliminated in this manner. This 39.9% portion of total configurations showed that the correlation among linked distance distributions was significant. Not unexpectedly, this approach left more structures at the most probable distances of individual distributions (Fig. 3A). The distributions were realigned by randomly eliminating surplus structures, which were required to improve the least-squares-fit between all experimental and calculated distance distributions, until a threshold correlation coefficient, R, was reached (Fig. 3B and Supplementary Figs. 5–6). For target R2 values of 0.985 and 0.990, this left 26,253 and 17,867 structures in the ensemble, respectively, and did not significantly change the conditional probabilities of subpopulations (Fig. 2B).

Figure 3.

Figure 3

Comparison of experimental and calculated distance distributions for the 11R1-81R1 spin label pair. (A) After eliminating from the initially sampled ensemble all structures that violated a structural restraint, the distribution expected for the number of remaining valid structures did not match the distance distribution of the ensemble. (B) The expected and obtained distance distributions were realigned by randomly removing surplus structures until a target correlation coefficient, R2, between the two distributions was reached for all measured spin label pairs (Supplementary Figs. 5–6).

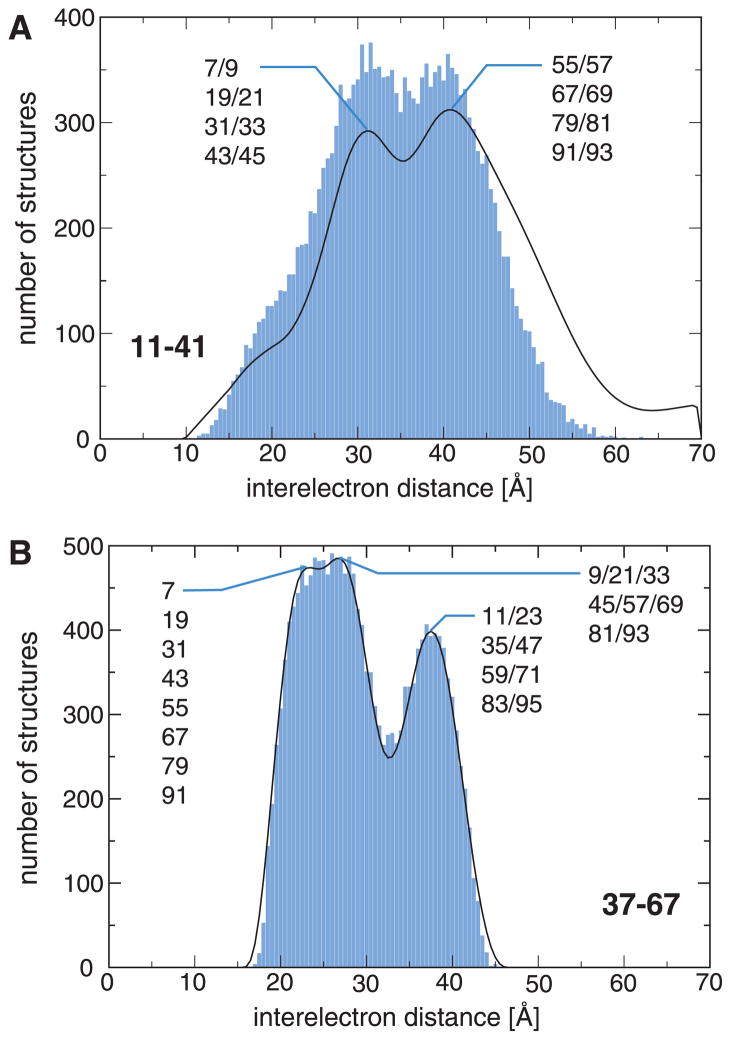
The obtained R2(0.990) ensemble can be immediately employed to test the self-consistency of distance distributions. The distribution containing the largest number of distances that could not be combined with entries from the other distributions exhibited the largest deviation between DEER-derived and ensemble back-calculated distance probabilities. This applied to 11R1-41R1 (Fig. 4A), whereas all other distributions exhibited close agreements between experimental and calculated distances (Fig. 4B and Supplementary Fig. 6). 11R1-41R1 represented the broadest of all distributions and contained distances in excess of 50 Å, which are close to the upper detection limit for current DEER measurements. In this context, we also note that a finite signal-to-noise ratio and dipolar evolution time may, in general, broaden distance distributions disproportionately, while the maxima of the distance distribution and immediately flanking distances are less sensitive to acquisition parameter.61

Figure 4.

Figure 4

Examples of distance distribution reproduction in the R2(0.990) ensemble. (A) The 11R1-41R1 distribution, which exhibits maxima at 31.0 and 40.5 Å, is not fully self-consistent with the other distributions. (B) As exemplified for 37R1-67R1, which exhibits distribution maxima at 23.5, 26.5 and 37.5 Å, all other distributions are in good agreement (Supplementary Fig. 6). Selected subpopulations associated with the distribution maxima are indicated.

Structural interpretation of the SLAS-bound αS R2(0.990) ensemble

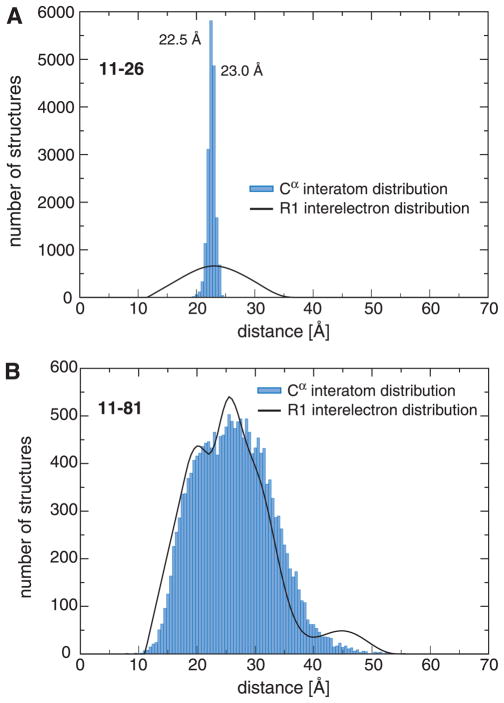
The R2(0.990) ensemble has been defined at the level of R1 spin label interelectron distances and, to yield useful structural information, must now be interpreted in terms of backbone interatom distances. The two cases of spin label pairs within the same secondary structure element (6 pairs) and across different secondary structure elements (12 pairs) can be differentiated. For the first case, the applied secondary structure definitions will limit backbone interatom distance variations, thereby aiding in the differentiation of backbone and spin label distance fluctuations. For example, for the 11R1-26R1 pair, whose spin labels were placed on the same helix-N′ face, a distribution maximum at an interelectron distance of 23 Å was obtained (Fig. 5A). This is within 0.5 Å of the expected distance for a 15-residue linear α-helix and, at the backbone level, the structural ensemble exhibited a sharp interresidue distribution peak at 22.5 Å between Cα atoms (Fig. 5A). In contrast, interelectron distance distributions across helix-N′ and -C′ resulted in broad interhelical distance distributions, as illustrated for the 11R1-81R1 pair (Fig. 5B). Consequently, spin label flexibility resulted in the convolution of interelectron and interhelical distances.

Figure 5.

Figure 5

Comparison of DEER-derived interelectron and R2(0.990)-ensemble backbone interatom distances for 11R1-26R1 and 11R1-81R1. Interatom distances were calculated between corresponding Cα atoms. 11R1-26R1 exhibits close interelectron and interatom distance maxima at 23.0 and 22.5 Å, respectively; this implies that, at the maximum, the 11R1/26R1 spin label orientations must have been similar. Outside of distribution maxima non-equivalent rotamer combinations will dominate. Due to the possibility of interhelical distance fluctuations (helix-N′ and -C′ nano- to millisecond timescale dynamics; Supplementary Fig. 2), equivalent 11R1/81R1 rotamers could, in theory, exhibit different interelectron distances.

In principle, an R1 orientation or ensemble thereof, could be defined independently of the DEER data by paramagnetic relaxation enhancements (PRE) originating from a single label.24,27 In practice, however, it was not possible to interpret 1HN transverse PRE, Γ2(1HN), originating from, for example, 27R1, within a single structure (data not shown). This implied the presence of multiple αS conformations in fast chemical exchange, in accordance with the multiple maxima exhibited by several interelectron distributions. Moreover, in the immediate vicinity of an examined spin label (±10 Å), where local backbone geometry remained unambiguous, Γ2(1HN) was prohibitively large. Thus, although the R2(0.990) ensemble provided valuable insight into the correlation of interelectron distribution distances, its use was limited by an overrepresentation of ensemble fringe regions at the backbone level (Fig. 5B). To compile the ensemble of SLAS-bound αS at the backbone level, a minimal set of backbone structures, capable of reconstructing all interelectron distance distributions, must be derived instead.

Theoretical basis set of subpopulation structures

Of the 18 measured distance distributions, six exhibited multiple maxima (Supplementary Fig. 1). In principle, different R1 rotamers could form defined subpopulations without affecting the ensemble at the backbone level. Such a scenario would require a substantial prejudice toward certain spin label rotameric states exerted by their surrounding structural environments. For SLAS-bound αS, the states and ratios of canonical R1 rotamers54 that had been defined in the initial configuration space were still intact in the R2(0.990) ensemble for all spin-labeled residues (Supplementary Table 3), indicating the absence of pronounced steric bias toward any particular rotameric state. It is further noted that spin label membrane immersion depths within the vesicle surface-bound αS amphiphilic helix faithfully followed a helical pattern of 3.67 residues per turn at all examined positions,39,62 demonstrating the absence of significant R1 partitioning preferences at the lipid-water interface. Thus, an unrestricted, canonical R1 rotamer distribution54 can indeed be assumed for SLAS-bound αS, implying a perhaps unexpected wealth of well-defined αS-SLAS protein-micelle interaction, and indicating that more than one structure will be required to successfully reconstruct the interelectron distance distributions.

From the multiple maxima of the measured distance distributions, a set of 96 theoretical subpopulations can be formed (Supplementary Table 2). For each subpopulation, a representative structure must be calculated in order to evaluate the match between experimental and reconstructed interelectron distance distributions. To calculate such structures, spin label orientations must be selected. For combinations of interelectron distribution maxima only, two principal ways of translating spin label interelectron into backbone interatom distances may be differentiated. First, at distribution maxima, where spin labels reside at their average orientation, R1 could be replaced by a fixed, uniform conformation. This introduces backbone interatom distance restraints and a representative structure, taking into account the uncertainty of distribution maxima, can be calculated in a standard manner. An analogous scheme was successfully applied to define the average structure of vesicle-bound αS, which consists of an elongated, uninterrupted α-helix.62 Moreover, such a scheme may be further expanded to attempt the selection of individual canonical R1 rotameric states.63 Second, the conformations of spin labels may be left to sample their canonical range in an ensemble calculation scheme restricted to combinations of distribution maxima. The subsequently calculated average backbone coordinates, which integrate all sampled and still-correlated rotamer combinations, then represent backbone interatom distances. For relatively simple structures, such as the linear α-helix of vesicle-bound αS, the second scheme would unnecessarily lower the precision of the structure calculation. Said scheme was preferred, however, for the non-trivial arrangement of two secondary structure elements in space. It can exploit the correlation of spin label orientations that partake in the measurements of linked distance pairs and thereby establish individual conformational preferences of spin labels.

Calculation of subpopulation structure representatives

Structures for the most probable subpopulations were present in the R2(0.990) ensemble (Fig. 2), but, to arrive at representative mean coordinates for a subpopulation, new ensembles, each consisting of 5,000 structures, were calculated. The permissive distance intervals around distribution maxima in these calculations need to correspond to measurement uncertainties rather than to measurement resolution. For 11R1-26R1, this uncertainty was determined to be 0.5 Å (Fig. 5A), but was larger for other distributions (e.g., 11R1-41R1). An estimate was obtained by evaluating the convergence of structures as a function of permissive distance intervals. For subpopulation 93 (Supplementary Table 2), distance intervals of ±1.5 Å resulted in ~3% larger r.m.s. deviations between the calculated structures and their mean coordinates compared to ±2.5 Å intervals. Subpopulations were therefore calculated with the latter interval. It is further noted that the implemented secondary structure definitions automatically restricted spin label pairs within the same secondary structure element to tighter intervals (e.g., 11R1-26R1; Fig. 5A), and the definition of individual distance intervals did not offer improvements in structure convergence (data not shown).

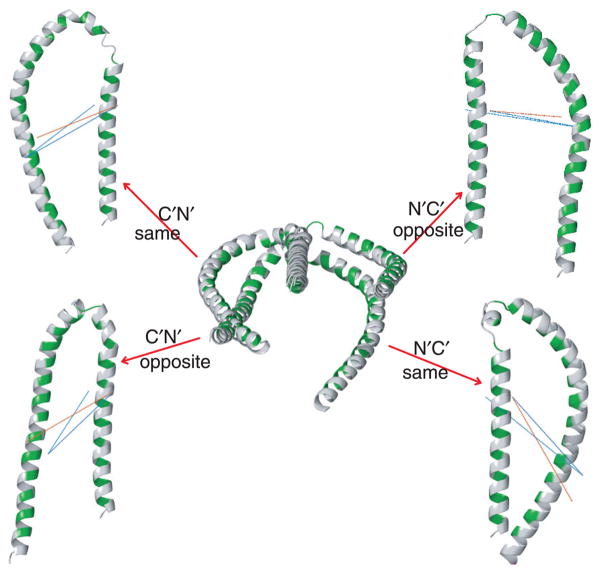
In the course of inspecting the range of generated structures in subpopulation calculations, structures were found that were unable to interact with the micelle; i.e., their hydrophobic helix faces pointed in opposite directions (Fig. 6). In the present case, RDC restraints were unable to unambiguously define the orientation of helix faces.64 Despite RDC measurements under three different anisotropic sample conditions, virtually identical SLAS-αS complex alignments were obtained (normalized tensor scalar products65 did not fall below 0.98). Another significant factor contributing to the encountered ambiguity, aside from spin label flexibility, was residual uncertainty in backbone torsion angles, which permitted spin label distance restraints to be fulfilled by distorting helix geometry (Fig. 6). Clearly, the requirement of the hydrophobic helix faces to bind to a common surface should be incorporated as an additional structural constraint, and similar criteria may also be obtainable for other proteins. In accordance with the alignment tensor orientation (data not shown), four principal configurations can be differentiated for the arrangement of helix-N′ and -C′ in space: helices in N′C′ or C′N′ order with their hydrophobic faces opposite of each other or on the same side, abbreviated as N′C′/opposite, C′N′/opposite, N′C′/same, and C′N′/same, respectively (Fig. 6). For subpopulation 93, which combines the most probable distances in all distributions (Fig. 2A and Supplementary Fig. 6), 62.2% of structures exhibited hydrophobic helix faces on the same side, of which 67.2% were in C′N′ order. Only such structures were considered further.

Figure 6.

Figure 6

Illustration of the four theoretical helix-N′ to -C′ configurations of SLAS-bound αS. The configurations followed from relative alignment tensor orientations between the two helices and were conveniently differentiated by using the following distance, d, selection criteria. C′N′/same: d[K10(Cβ)-T72(Cβ)] > d[K12(Cβ)-T72(Cβ)], d[K10(Cβ)-T72(Cβ)] > d[K10(Cβ)-V74(Cβ)]; N′C′/same: d[K10(Cβ)-T72(Cβ)] < d[K12(Cβ)-T72(Cβ)], d[K10(Cβ)-T72(Cβ)] < d[K10(Cβ)-V74(Cβ)]; C′N′/opposite: d[K10(Cβ)-T72(Cβ)] > d[K12(Cβ)-T72(Cβ)], d[K10(Cβ)-T72(Cβ)] < d[K10(Cβ)-V74(Cβ)]; N′C′/opposite: d[K10(Cβ)-T72(Cβ)] < d[K12(Cβ)-T72(Cβ)], d[K10(Cβ)-T72(Cβ)] > d[K10(Cβ)-V74(Cβ)]. The K10(Cβ)-T72(Cβ), K12(Cβ)-T72(Cβ) and K10(Cβ)-V74(Cβ) distances are indicated by cyan, blue and red lines, respectively. Shown are the average representatives of subpopulation 93 (residues 1-93) superimposed on helix-N′, with hydrophobic helix faces colored in green.

For subpopulation 93 C′N′/same structures, an ensemble r.m.s.d. of 4.6 Å to the mean coordinates was obtained. This relatively wide range was not unexpected, given considerable spin label flexibility coupled with uncertainties in secondary structure definitions. When calculating backbone mean coordinates over this r.m.s.d. range, covalent geometry became violated for some residues, especially in the helix-helix connector and within the unfolded tail region (data now shown). To preserve proper geometry, the structure closest to the helix-N′ and -C′ mean coordinates was selected as the average representative. To assess the precision of this structure, an independent repeat subpopulation structure calculation was performed, resulting in an average representative with an r.m.s.d. of 2.0 Å to the original one (Supplementary Fig. 7A). Similarly, a tightening of permissive χ1-3 intervals around their nominal values had little impact on the identity of the average representative (Supplementary Fig. 7B), indicating that averaging was robust; i.e., the spin label coordinates were centered around similar ensemble mean coordinates. In conclusion, with small bias from the structure calculation setup, a reproducible αS-SLAS subpopulation representative was obtained with a precision of 2.0 Å. The accuracy of this representative will invariably be tied to the number and quality of structural restraints, as well as to the difference between the average spin label side chain conformation present at the distribution maxima and its computed average conformation.

Description of average representatives of dominant subpopulations

Of the 96 theoretical subpopulations, the 24 subpopulations that could be formed with the high probability maxima of 11R1-41R1, 11R1-70R1, 11R1-81R1 and 37R1-67R1 (Fig. 2 and Supplementary Fig. 6) were initially evaluated. The remaining subpopulations, which involved combinations with the relatively low probability maxima of 26R1-56R1 and 48R1-67R1, were deemed of lesser significance in terms of reconstructing the interelectron distance distributions (Fig. 2). The average representatives that sampled the different 37R1-67R1 maxima (Fig. 4B) could not be distinguished in a meaningful manner (e.g., subpopulations 91, 93 and 95 in Supplementary Table 5). Residue 37R1 is located at the center of the disordered helix-helix linker (Supplementary Fig. 3B), and therefore had little influence on the helix-C′ to helix-N′ arrangement. Thus, the eight subpopulations involving 11R1-41R1, 11R1-70R1 and 11R1-81R1 maxima remained for a meaningful structural interpretation.

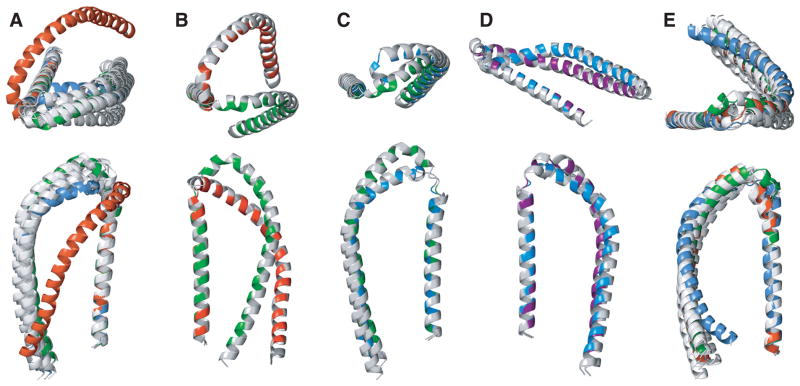
Among the eight C′N′/same subpopulation average representatives, we were able to differentiate four distinct structures (Table 1 and Fig. 7A). A conspicuous rotation of relative helix-C′ and -N′ orientations was obtained between subpopulations 93 and 45 (Fig. 7B). Between subpopulations 93 and 21, a change in helix-C′ to helix-N′ register was observed, leading to differences in helix-C′ curvature (Fig. 7C). Compared to subpopulation 21, the relative orientation of the hydrophobic helix faces was altered in subpopulation 9 (Fig. 7D). The average representatives in N′C′/same orientation exhibited greater uniformity (Fig. 7E), differing only slightly in helix-C′ curvatures and in relative orientation of helix faces. This indicated that, in N′C′/same configuration, different target spin label distances did not readily translate into different backbone conformations, but resulted instead in different average spin label conformations. In other words, the sum of structural constraints maintained a more uniform coordinate solution space. In total, the employed average representative structure calculation scheme identified five distinct helix-N′ and helix-C′ arrangement possibilities (theoretical set of basis structures).

Table 1.

Comparison of backbone r.m.s. deviations between subpopulation C′N′/same average representatives

Subpopulationa,b 9 21 33 45 57 69 81 93 r.m.s.d. to mean coordinatesc number of structuresd
9 0.0 1.9 2.2 2.9 2.5 1.0 2.7 2.0 4.5 1791
21 0.0 1.9 2.6 3.0 1.6 3.3 2.9 4.6 1680
33 0.0 2.8 2.3 1.8 2.6 1.9 4.8 1929
45 0.0 3.2 2.8 3.3 3.5 5.0 1762
57 0.0 2.6 1.7 1.8 4.1 2122
69 0.0 2.7 1.9 4.4 1966
81 0.0 2.0 4.3 2171
93 0.0 4.6 1974

Figure 7.

Figure 7

Comparison of putative SLAS micelle-bound αS structural states. (A) C′N′/same average representatives of subpopulations 9, 21, 33, 45, 57, 81, 91 and 93 superimposed on helix-N′. The backbones of representatives 21, 45 and 93 are colored in blue, red and green, respectively. (B) Comparison of subpopulation 93 and 45 representatives, shown in green and red, respectively. (C) Comparison of subpopulation 21 and 93 representatives, shown in blue and green, respectively. (D) Comparison of subpopulation 21 and 9 representatives, shown in blue and magenta, respectively. (E) N′C′/same average representatives of subpopulations 9, 21, 33, 45, 57, 81, 91 and 93 superimposed on helix-N′. The backbones of representatives 21, 45 and 93 are colored in blue, red and green, respectively. The dynamically unstructured αS tail residues (94–140) are omitted for clarity.

Reconstruction of interelectron distance distributions

To determine which of the average representatives described above actually existed, a reconstruction of the 18 interelectron distance distributions was performed from fixed backbone coordinates. For non-linked distributions, such as 22R1-52R1, a successful reconstruction of interelectron distances merely demonstrated the ability to place spin labels in canonical orientations within the structural context of the tested backbone structure. For linked distributions, this evaluation was expanded to test the self-consistency of all linked spin pairs and, thus, was more stringent. However, spin labels can, of course, be placed at the target interelectron distance maxima underlying the calculation of a specific average representative. To correlate spin label orientations more intricately, it is necessary to select combinations of interelectron distances from the entire distribution range of experimental distances. Stated differently, to reach meaningful reconstruction stringency, the question to be addressed is whether or not valid combinations of spin label orientations can be formed outside of distribution maxima.

The configuration space of the R2(0.990) ensemble provided an accurate, correlated sampling template for this effort (Supplementary Fig. 6). Its 17,867 distance combinations, together with their associated χ1-3 preferences, were probed in simulated annealing structure calculations for each putative basis subpopulation structure. In contrast to these calculations, some backbone dihedral angle variations were permitted during the deduction of the R2(0.990) ensemble (Supplementary Table 1). To achieve an efficient computational sampling of distributions, slight violations of target distances were therefore accepted, and were even encouraged by employing a relatively low force constant for interatom distance restraints (c.f. Experimental Procedures) as long as canonical χ1-3 combination could be maintained for all spin labels. Hence, if canonical spin label orientations were maintained, the closest obtained distance combination to a sought target distance combination was accepted. For over 75% of the simulated annealing calculations, distance combination with canonical spin label orientations could thus be achieved (Supplementary Figs. 8–9).

Upon offering a wide range of pairwise distances for linked distributions with multiple maxima, the obtained distributions nevertheless populated only one maximum and closely followed Gaussian distributions (Fig. 8A and Supplementary Fig. 8), attesting to the validity of the employed sampling scheme. For these distributions, standard deviations were on the order of 4–5 Å, indicating that distribution maxima, and thus subpopulations, can readily be differentiated. Moreover, obtainable distances were not limited to the range of offered target distances (e.g., 26R1-41R1; Supplementary Figs. 8–9), which revealed the strength of the sampling scheme. Conspicuously, the computationally reproduced distribution widths were consistently narrower than their DEER-derived counterparts (Supplementary Figs. 8–9). This applied as well to the non-linked 22R1-52R1 pair, which exhibited the largest standard deviation of all distributions of 5.3 Å (Fig. 8B). For 22R1-52R1, this may be ascribed to limited access to fringe distances by the implemented χ1-3 torsion intervals of ±30°. The inability of all other distributions containing a single maximum to match their DEER-based width (Supplementary Figs. 8–9) can be interpreted as an incompatibility of fringe distances with the other structural restraints. Consequently, these fringe distances may have merely resulted from the broadening of DEER distance distributions that arise from a finite signal-to-noise ratio and dipolar evolution time.61 This interpretation suggested that such a broadening is generally modest, albeit clearly limiting for 11R1-41R1, as already discussed. Finally, it is noted that, in addition to DEER acquisition parameter, distribution widths depend as well on the relative spatial orientation of spin labels.

Figure 8.

Figure 8

Examples of reconstructed interelectron distance distributions. (A) Results of 11R1-41R1 reconstruction for C′N′/same subpopulations 45 and 93, consisting of 15,435 and 13,510 structures, respectively. The reconstructions fit Gaussian distributions that encompass the same number of structures; subpopulation 93 exhibits a mean and standard deviation of 39.6 ± 5.1 Å, whereas, for subpopulation 45, these values are 34.9 ± 5.3 Å. The expected interelectron distribution for 15,483 structures is also shown. (B) Results of 22R1-52R1 reconstruction for subpopulation 93 in C′N′/same and N′C′/same orientation (13,510 and 14,488 structures, respectively). The expected interelectron distribution for 14,488 structures is also depicted. Of the 18 measured distance distributions, 22R1-52R1 is the only non-linked R1 pair. (C–D) Results of 11R1-70R1 reconstruction. 9/C′N′/same, 21/C′N′/same, 45/C′N′/same and 93/N′C′/same populate their correct target distance maximum, as indicated.

Interpretation of reconstructed interelectron distance distributions

To obtain a minimal set of basis structures, representing the partially folded state of SLAS-bound αS, it was necessary to identify the average representatives capable of reproducing their target distance maxima. First, the four C′N′/same average representatives of subpopulations 9, 21, 45 and 93 were evaluated, taking into account the ±2.5/0.5 Å distance interval/grace margin around distance maxima. The average representative of subpopulation 45 in C′N′/same orientation, abbreviated as 45/C′N′/same, failed to reproduce 11R1-72R1, whereas 21/C′N′/same failed to replicate 11R1-81R1, and 93/C′N′/same violated both 11R1-70R1 and 11R1-81R1 (Fig. 8C and Supplementary Fig. 8). However, 9/C′N′/same was capable of reconstructing all of its target maxima correctly, making it the first member of basis structures. To achieve agreement for 93/C′N′/same, greater 11R1-70R1/11R1-81R1 and shorter 11R1-72R1/11R1-83R1 distances, respectively, would be required (Fig. 8C and Supplementary Fig. 8). This could potentially be achieved by changing its helix topology to N′C′/same. Indeed, 93/N′C′/same populated all of its target distances correctly (Fig. 8D and Supplementary Figs. 8–9). For 11R1-41R1, its reconstructed distances fell in between the two distribution maxima (Supplementary Fig. 9); however, the average representative targeting the lower distance 11R1-41R1 minimum (45/N′C′/same) exhibited a virtually identical backbone structure (Fig. 7E). For the remaining N′C′/same or C′N′/same average representatives, similar interelectron distance reconstructions were anticipated based upon analogous backbone structures (Fig. 7), which would not match their target distance maxima. Thus, the 9/C′N′/same and 93/N′C′/same average representatives correctly populated all available distribution maxima in a complementary manner; i.e., they formed a self-consistent and minimal basis set of structures.

Finally, we note that a well-correlated sampling template, such as the R2(0.990) ensemble, will not be mandatory for the reconstruction of interelectron distributions. To achieve greatest computational efficiency in the assessment of future proteins, it appears sufficient to calculate subpopulation representatives from distance distribution maxima, and to subsequently reconstruct interelectron distributions from a sampling template whose configuration is solely based on _P_c > _P_i (Supplementary Fig. 4). Although this will make reconstructions somewhat less efficient than if R2(0.990) were used, an evaluation of the NMR restraints carried out for R2(0.990) already takes place during the calculation of subpopulation representatives.

Description of αS-SLAS micelle interactions

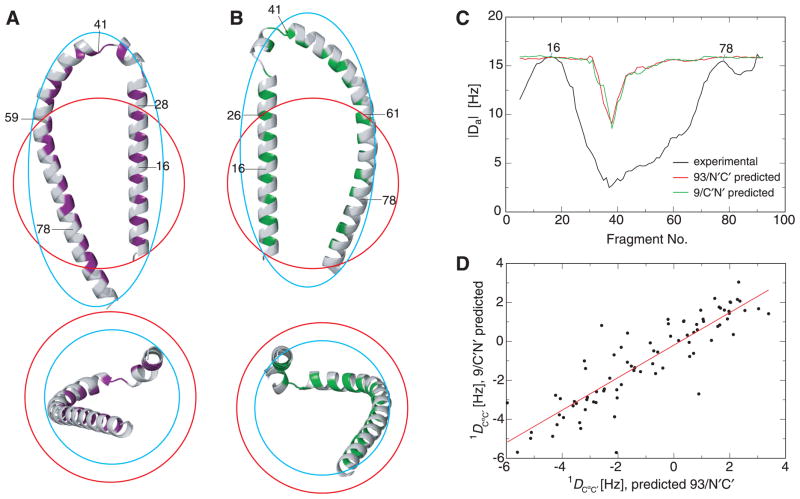
The distribution-based mean distances used in the calculation of subpopulation representatives have, for the first time, permitted a meaningful comparison with micelle dimension. The radius of a free unhydrated SLAS micelle is 22.2 Å (when assuming spherical geometry).19 An overlay of a sphere of such radius on the 93/N′C′/same and 9/C′N′/same basis structures could not immerse the entire lengths of helix-N′ (Asp2-Lys32) and helix-C′ (Ser42-Thr92) in the micelle (Fig. 9A–B). When centering the sphere on the backbone segments that exhibited the highest local alignment tensor magnitudes, Da (Fig. 9C), an asymmetrical mode of micelle binding was obtained. While keeping the micelle volume constant in the αS-bound state,19 adjustments from a spherical micelle shape toward a spheroidal form may be made in order to immerse the helices less deeply and to encompass the entire length of helix-C′ (Fig. 9A–B). Such a shape change will experience stabilizing contributions from the selective neutralization of detergent headgroup charges along the helix axes by the numerous lysine side chain charges.49,66 Although 93/N′C′/same and 9/C′N′/same exhibit a high degree of bilateral symmetry, somewhat different approaches to their micelle binding were noted. 9/C′N′/same maintained its helices closer than did 93/N′C′/same, which allowed the micelle to engage these helices from predominantly one direction. Nevertheless, even the 9/C′N′/same helices did not come to lie in a single plane. This was even more pronounced for 93/N′C′/same, which also altered the register between the two helices compared to 9/C′N′/same. The more distant lateral helix-N′ to helix-C′ arrangement of 93/N′C′/same also allowed a wrap around the micelle at different heights (Fig. 9A–B). Thus, αS possesses two distinct modes of SLAS micelle binding that use different relative secondary structure arrangements along and perpendicular to the helix axes. An additional gratification of the methodology presented herein is the ability to estimate relative subpopulation sizes based on the relative probabilities of associated distribution maxima. Based on the average peak probabilities of the maxima of 11R1-70R1 and 11R1-81R1 (Supplementary Fig. 6), the ratio of 93/N′C′/same to 9/C′N′/same was 0.55 to 0.45. A preference for N′C′/same orientations had been noted as well for SDS-bound αS.49,59 In sum, the amphiphilic region of αS is capable of folding into a wide variety of structural states, ranging from a fully extended helix,37,62 to the herein observed and related SDS-bound αS structures.49,59 A future task will be to explore the differences in free energies between these conformations relative to a common reference in order to assess the propensity of αS to interconvert between such conformations.

Figure 9.

Figure 9

Mode of αS-SLAS micelle binding and RDC averaging. (A–B) Comparison of SLAS micelle and αS dimensions. Free SLAS micelles exhibit an unhydrated radius of 22.2 Å.19 A sphere of such radius, shown in red, and a spheroid of equal volume, shown in cyan, were placed on the C′N′/same and N′C′/same average representatives of subpopulations 9 and 93, shown in magenta and green, respectively. The hydrophobic helix faces are colored to identify the micelle binding surfaces. Selected amino acid positions are indicated. The dynamically unstructured αS tail residues (94–140) are omitted for clarity. The two views depicted are related by a 90° rotation around the x-axis. The spheroid shown exhibits minor and major axes of 17.5 and 35.7 Å, respectively. The helices may immerse into an SDS micelle as deeply as detergent hydrocarbons 3 and 4.71,72 (C–D) Evaluation of RDC averaging. For predicted 9/C′N′/same and 93/N′C′/same 1_D_CαC′ couplings (see main text), a correlation coefficient, R, of 0.882 was obtained, which illustrates that averaging will improve 9/C′N′/same RDC fits to 93/N′C′/same coordinates and vice versa. Averaged RDC exhibit constant alignment tensor magnitude, Da, for fits to 7-residue backbone fragments of 9/C′N′/same or 93/N′C′/same, except for the helix-helix connector (residues 33–41). For comparison, Da values for experimental RDC are shown; these were obtained by MFR,21 as described previously.19,49 Fragments are denoted by their center residue.

For the 9/C′N′/same and 93/N′C′/same structures, it is interesting to briefly explore the linear averaging of RDC, which are central to defining the secondary structure of partially folded proteins by molecular fragment replacement (MFR).21 Starting with experimental RDC of the backbone segments of highest alignment tensor magnitudes (residues 10-18 and 74-81; Fig. 9C), complete sets of RDC can be back-calculated for each static 9/C′N′/same and 93/N′C′/same structure, then averaged. In this simple averaging mode, the quality of a fit of averaged RDC to helix-N′ and -C′ of 93/N′C′/same or 9/C′N′/same remained high, exhibiting q-factors67 below 0.2. In contrast, the quality of a fit to helical 93/N′C′/same coordinates with back-calculated 9/C′N′/same RDC and vice versa was poor, exhibiting a q-factor of 0.57 in both cases. The benefits of averaging can also be illustrated by directly correlating back-calculated RDC (Fig. 9D and Supplementary Fig. 10). However, averaging broke down for structurally more complex regions such as the helix-helix linker, where fits to 7-residue fragments exhibited q-factors in the range of 0.3–0.6. As a result of averaging, Da values in this region were also reduced substantially, which may have contributed to the low experimental Da values of this region (Fig. 9C). Thus, for partially folded proteins that exhibit distinct subpopulations, useful secondary structure definitions may be obtained from averaged RDC. As a threshold for structural interpretations, q-factors for 7-residue backbone fragments below 0.3 may be chosen.19

Dynamics of αS-SLAS micelle interactions

For αS regions not significantly affected by RDC averaging, variations in local alignment tensor magnitudes may be interpreted as global secondary structure dynamics (nano- to millisecond timescale dynamics).68 The experimental Da values at the end and beginning of helix-N′ and -C′, respectively, were significantly lower than for the segments engulfed by the free, unperturbed micelle and the predicted 9/C ′N′/same and 93/N′C′/same Da values (Fig. 9A–C), which showed that enhanced helix dynamics correlate with the deformation of the micelle. In turn, this implies the inherent difficulty of permanently deforming the micelle shape by surface-bound molecules; and we note that, outside of the 22.2 Å-radius sphere, helix-C′ geometry also changed from linear to curved (Fig. 9A–B). In other words, elevated helix dynamics have appeared as a manifestation of the struggle of the micelle against a deformation of its intrinsic shape. The higher helix dynamics of the sequence-rearranged αS variant SαS compared to the wild-type19 serve to further corroborate this statement. Nevertheless, the comparable order and content of helical secondary structure at the beginning and end of helix-C′ (Supplementary Fig. 3), which came into existence only by interacting with the micelle, showed that it is not possible for the micelle to separate itself from αS. The protein is aggressively engaging the micelle; thus, αS helix dynamics correlate well with the tertiary arrangement of SLAS-bound αS and the departure from free micelle dimensions.

Conclusions

For the purpose of determining and validating the structural ensemble of partially folded proteins, we have introduced a novel structure calculation scheme based on linearly weighted average NMR-based parameters and DEER-derived distance distributions. The methodology presented herein provides direct information concerning the existence and ratio of dominant ensemble subpopulations in partially folded proteins, as well as previously inaccessible preferences regarding the tertiary arrangement(s) of their secondary structure elements at mean distances. Populated ensemble subpopulations were successfully differentiated from mere theoretical possibilities by reconstructing interelectron distance distributions from (correlated) distance combinations, thereby reducing the ambiguity that arises from spin label flexibility. For SLAS-bound αS, we identified two dominant ensemble populations that yielded novel insight into protein-micelle interactions. Limitations to the attainable structural resolution of ensemble representatives arose from residual uncertainties in secondary structure definitions as well as rotamer ambiguity and spin label flexibility, which may be alleviated by advances in spin labeling strategies.69 While a partially folded intermediate state of proteins is generally transient in nature, defined amounts of denaturant, certain pH values, or protein engineering often can trap this state,7,8,11 allowing the acquisition of the NMR and EPR parameter employed herein. Finally, the presented methodology is well-suited to be combined with additional techniques, such as small-angle X-ray scattering.11,17,70

Supplementary Material

1_si_001

Acknowledgments

TSU acknowledges support from The John Douglas French Alzheimer’s Foundation, the National Institutes of Health (HL089726), and the American Heart Association. RL was supported by grants from the Larry L. Hillblom Foundation and the National Institutes of Health (AG027936).

Footnotes

Supporting Information Available: Backbone torsion angle intervals of SLAS-bound αS, subset combinations of spin label interelectron distance maxima (subpopulations), comparison of expected and actual R1 χ1-3 distributions, ratio of helix configurations in SLAS-bound αS subpopulations, comparison of subpopulation C′N′/same average representatives, interelectron distance distributions from 4-pulse DEER experiments, variation of alignment tensor magnitude with fragment length, structural and dynamic NMR parameter of SLAS-bound αS, flowchart of ensemble structure calculation scheme, correlation between expected and obtained ensemble structures, experimental and calculated ensemble distance distributions, comparison of subpopulation 93 C′N′/same average representatives, reconstruction of distance distributions from subpopulation structures, and expected RDC for 9/C′N′/same and 93/N′C′/same structures. This material is available free of charge via the Internet at http://pubs.acs.org.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1_si_001