Normalizing bead-based microRNA expression data: a measurement error model-based approach (original) (raw)
Abstract
Motivation: Compared with complementary DNA (cDNA) or messenger RNA (mRNA) microarray data, microRNA (miRNA) microarray data are harder to normalize due to the facts that the total number of miRNAs is small, and that the majority of miRNAs usually have low expression levels. In bead-based microarrays, the hybridization is completed in several pools. As a result, the number of miRNAs tested in each pool is even smaller, which poses extra difficulty to intrasample normalization and ultimately affects the quality of the final profiles assembled from various pools. In this article, we consider a measurement error model-based method for bead-based microarray intrasample normalization.
Results: In this study, results from quantitative real-time PCR (qRT-PCR) assays are used as ‘gold standards’ for validation. The performance of the proposed measurement error model-based method is evaluated via a simulation study and real bead-based miRNA expression data. Simulation results show that the new method performs well to assemble complete profiles from subprofiles from various pools. Compared with two intrasample normalization methods recommended by the manufacturer, the proposed approach produces more robust final complete profiles and results in better agreement with the qRT-PCR results in identifying differentially expressed miRNAs, and hence improves the reproducibility between the two microarray platforms. Meaningful results are obtained by the proposed intrasample normalization method, together with quantile normalization as a subsequent complemental intersample normalization method.
Availability: Datasets and R package are available at http://gauss.usouthal.edu/publ/beadsme/.
Contact: bwang@jaguar1.usouthal.edu
1 INTRODUCTION
MiRNAs are short, non-coding RNA molecules that modulate gene expression by base pairing with the 3′ untranslated region of their target mRNAs. It has been shown that miRNAs regulate about 30% of all transcripts in mammalian genomes. Each miRNA can regulate the expression level of hundreds of different mRNAs (Lewis et al., 2005). As regulators of gene expression, potential therapeutic targets and biomarkers, miRNAs were extensively studied in the past few years. As the number of annotated miRNAs continues to increase, several large-scale miRNA expression profiling microarrays have been developed, including quantitative PCR and sequencing. As an alternative arraying strategy to planar substrates that are widely used in microarrays, bead-based microarrays (beads arrays hereafter) have been developed either by impregnating beads with different concentrations of fluorescent dye or by some type of barcoding technology. The beads are addressable and used to identify specific binding events that occur on their surface. Bead-based arrays allow for the inclusion of many combinations of miRNA capture beads into a single pool, and provide greater flexibility over time as miRNAs are discovered and corresponding beads are created. In addition, beads arrays are expected to have increased specificity over the traditional glass-based microarrays (Lu et al., 2005).
Normalization is a crucial process of removing systematic bias as a result of the experimental artifacts from the data. Many existing normalization methods assume that the majority genes are not differentially expressed in the control and treated samples. Such an assumption might not hold true for miRNA arrays due to the facts that the total number of miRNAs is small (less than 1000), and the current miRNA microarray platforms possibly do not include enough miRNAs that are stably expressed (Davison et al., 2006). As a result, methods such as normalizing by mean or median might not work well for miRNA microarray data analyses. In addition, because of the capacity limit of the pools in beads arrays, the miRNAs are divided into small subsets and the tests are finished in various pools separately. The subprofiles of the miRNAs from different pools need to be normalized to assemble a complete profile. Such a normalization procedure is called intrasample normalization. Because the miRNA sets in different pools are different, and the numbers of miRNAs in different pools are small, intrasample normalization is difficult. Furthermore, most of the existing normalization methods are not applicable. In this study, we investigate a measurement error model-based approach to improve beads array intrasample normalization.
2 MATERIALS AND METHODS
2.1 MiRNAs profiling analysis and beads array data
Ten human osterosarcoma xenografts specimens are collected. For each specimen, four samples are prepared as follows: one sample is treated with saline and used as control (Ctrl); three samples are treated with each of the three chemotherapeutic treatments: cisplatin (Cis), doxorubicin (Dox) and ifosfamide (Ifo). Thus, a total of 40 samples are employed for this study. The total RNAs are isolated following the established protocols (Bruheim et al., 2009; Xi et al., 2007). Luminex FlexmiR MicroRNA Human Panel (Luminex Corp., TX, USA) is employed for miRNA profiling analysis. All procedures are conducted by strictly following the manufacturer's instructions. In brief, 5 μg of total RNA per sample is 3′-biotinylated and hybridized to oligonucleotide-capture probes coupled to the carboxylated 5-μ polystyrene xMAP beads. The intensities are captured with a Luminex-200 instrument. For each sample, a total of 319 human miRNAs are tested by beads array in five human pools. The numbers of miRNAs in the five pools are 60, 64, 64, 65 and 66, respectively. In each human pool, four microspheres (regions 72, 73, 74 and 76) are included for the purpose of data normalization. Each normalization microsphere (normalizer hereafter) contains a unique capture probe designed to target specifically a ubiquitously expressed human small nucleolar RNA (snoRNA).
2.2 MiRNAs expression validation
The experimental results from beads array are validated using Taqman-based quantitative real-time polymerase chain reaction (qRT-PCR) miRNA assays. QRT-PCR is a prevalent molecular analysis technique for amplification and simultaneous quantification of a target molecule. In recent years, the development of novel chemistries and instrumentation platforms enabling detection of PCR products on a real-time basis have led to widespread adoption of qRT-PCR as a preferred validation method (Schmittgen et al., 2008). TaqMan Low Density Array (TLDA) Human MicroRNA Panel v2.0 (Applied Biosystems, CA, USA), containing pre-loaded PCR primer/probe set for 664 miRNAs and controls, is applied for miRNA expression validation by following the manufacturer's operating manual and instructions. After reverse transcription, the mixture is loaded onto TLDA cards and incubated on Applied Biosystems 7900 HT Real-Time PCR system. The data are collected and processed using the software endorsed by Applied Biosystems. Relative Quantification (RQ) values are calculated using the standard formula (Livak and Schmittgen, 2001). An RQ value shows the fold-change (FC) of a specific miRNA in two cell populations. RQ=1 indicates that a specific miRNA is non-differentially expressed in the control and the treated samples. Otherwise, if the RQ value is significantly different from one, the miRNA is differentially expressed in the two samples. Among all 319 miRNAs being profiled by beads array, 231 of them are also profiled by TLDA. Throughout this study, the qRT-PCR results are used as ‘gold standards’ to assess the performances of normalization methods.
2.3 A measurement error model for miRNA data
Just as with other cDNA or oligonucleotide arrays, measurement errors exist in miRNA arrays. The measurement errors are usually produced from various sources including sample preparation, dying, image intensity and microarray hybridization, scanning and equipment errors among many others. In this study, we consider the following measurement error model for miRNA beads arrays,
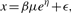 |
(1) |
|---|
where x is the net median fluorescent intensity (nMFI), which is the background-subtracted response at concentration μ. In beads arrays, the background noise is estimated by a spare unit for each molecular unit. In model (1), η represents the multiplicative error that always exists but is noticeable at concentrations significantly above zero; ε represents the additive error that always exists but is noticeable mainly for near-zero concentrations. For gene expression arrays, the actual expression level in molecular units is hard to be discerned due to the lack of calibration data. In model (1), β is a relative expression level that can be adjusted to calibrate data from different pools or samples to close expression levels for direct comparisons.
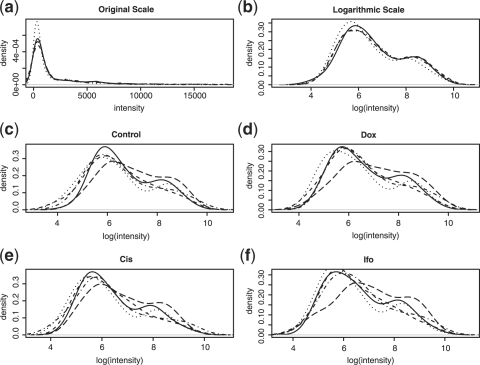
It is unpleasant to work with the gene expression data at the original scales due to the fact that the distributions of gene expression data are usually right-skewed. Figure 1a shows the intensity distributions of the four samples of a specimen. After the natural logarithmic transformation, the distributions become less skewed (Figure 1b). Figure 1c shows the intensity distributions of the five subprofiles for the sample used as a control, while Figure 1d through Figure 1f show the distributions of the subprofiles for the three treated samples, respectively. We find that the similarity among the distributions of the subprofiles for the same pool for different samples are higher than those across pools, which is reasonable because the miRNAs tested in the same pools for different samples are the same.
Fig. 1.
All results are based on the experimental data for one specimen. Plot (a) shows the original intensity distributions of the four samples (before normalization). Plot (b) shows the logarithmic intensity distributions of the four samples (before normalization). Each of plots (c) through (f) shows the logarithmic intensity distributions of the five subprofiles of the four samples.
Applying a Taylor expansion to the logarithm of x for the miRNAs that are highly expressed, we get the following measurement error model for log-scale expressions,
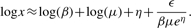 |
(2) |
|---|
The last term to the right-hand-side of (2) is negligible for large μ's (Ideker et al. 2000; Rocke and Durbin, 2001; Rocke and Lorenzato, 1995). For convenience, we assume the following model throughout this study,
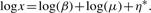 |
(3) |
|---|
where the last term in (2) is absorbed in η*, which is assumed to be a heteroscedastic normal error term with mean zero and variance σ2η*.
2.4 A maximum likelihood-based iterative normalization method
To serve the purpose of data normalization, the four normalizers are supposed to be strongly expressed across pools and samples, and have no biological interactions with the assayed samples. Let x ijk be the nMFI of normalizer i in pool k for sample j, and μ_i_ be the corresponding true concentrations. We have
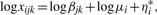 |
(4) |
|---|
for _i_=1,…,4; _j_=1,…,4; and k_=1,…,5. Our objective is to estimate β_jk's to commit the intrasample normalization. Now we have
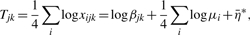
where 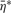 is normally distributed with mean zero and variance
is normally distributed with mean zero and variance 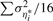 . If the concentrations of each normalizer can be assumed to remain unchanged across samples and across pools, we have
. If the concentrations of each normalizer can be assumed to remain unchanged across samples and across pools, we have
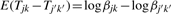
for any two pools with _i_≠_i_′ or _j_≠_j_′, or both. Without loss of generality, we take pool k for sample j as a reference pool and set β_jk_=1. Then we can estimate the correction factor for pool _k_′ for sample _j_′ by
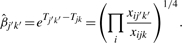 |
(5) |
|---|
To normalize a subprofile, we simply divide all nMFIs in the subprofile in pool _k_′ for sample _j_′ by 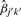 . Let
. Let 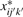 be the nMFI after the initial intrasample normalization. From (4) we have
be the nMFI after the initial intrasample normalization. From (4) we have
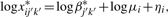
where 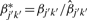 . We can further refine the normalization by finding an estimate for the new correction factor
. We can further refine the normalization by finding an estimate for the new correction factor 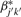 , which can be found by maximizing the likelihood based on each pool. The log-likelihood for pool k for sample j can be expressed as
, which can be found by maximizing the likelihood based on each pool. The log-likelihood for pool k for sample j can be expressed as
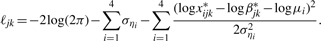
By equating the first derivative of the above log-likelihood to zero, and solving the equations with some algebra, we obtain the following estimator
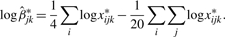
The refinement process can be iterated until the overall likelihood, l_=∑_j_∑_k l jk, is maximized.
3 RESULTS AND DISCUSSION
3.1 Performance comparisons of intrasample normalization methods
The following two normalization methods are recommended by the manufacturer:
3.1.1 nmean
In (5), the correction factor is computed by taking the geometric mean of the ratios of the nMFIs of the four normalizers in two different pools. The FlexmiR TM _MicroRNA Human Panel Instruction Manual Version A_-2 suggests to compute the correction factor by taking the arithmetic mean instead (BG-FMIR-H20-8.0A-2, 2007),
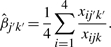 |
(6) |
|---|
3.1.2 nmed
Similar to the maximum likelihood-based estimator in (5) and nmean in (6), a median of the ratios of the nMFIs of the four normalizers is suggested in the FlexmiR TM MicroRNA Human Panel Instruction Manual (Version B) (BG-FMIR-H20-8.0B, 2008),
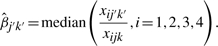 |
(7) |
|---|
All the above three intrasample normalization methods work under the assumptions that (i) the normalization beads have intensities significantly different from the background noises; (ii) the normalizers have stable measurements: they have no biological interaction with the assayed samples. To select the qualified normalizers, we screen the normalization microspheres with 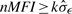 , where σε is estimated by using the probes that have intensities close to the mean background. Because the intensity measures for the normalization beads are usually large, the selection of k is not that crucial. The results based on the 40 samples show that _k_=3 is sufficient. We also screen the normalization beads based on their stability by performing a χ2-test: we first compute σ2η by pooling the estimated variances for the various normalization beads under an assumption of homoscedastic multiplicative errors. Second, we perform a χ2-test with a null hypothesis _H_0:σ2_i_=σ2η to check whether the variance of normalizer-i equals to σ2η. As an alternative, one can also perform pairwise _F_-tests to check the stability of the normalizers. By controlling the significance level, we can control the quality of the beads used for normalization. In this study, we choose α=0.05. Based on the experiment results, the results are petty stable by varying the significance levels from 0.01 to 0.1.
, where σε is estimated by using the probes that have intensities close to the mean background. Because the intensity measures for the normalization beads are usually large, the selection of k is not that crucial. The results based on the 40 samples show that _k_=3 is sufficient. We also screen the normalization beads based on their stability by performing a χ2-test: we first compute σ2η by pooling the estimated variances for the various normalization beads under an assumption of homoscedastic multiplicative errors. Second, we perform a χ2-test with a null hypothesis _H_0:σ2_i_=σ2η to check whether the variance of normalizer-i equals to σ2η. As an alternative, one can also perform pairwise _F_-tests to check the stability of the normalizers. By controlling the significance level, we can control the quality of the beads used for normalization. In this study, we choose α=0.05. Based on the experiment results, the results are petty stable by varying the significance levels from 0.01 to 0.1.
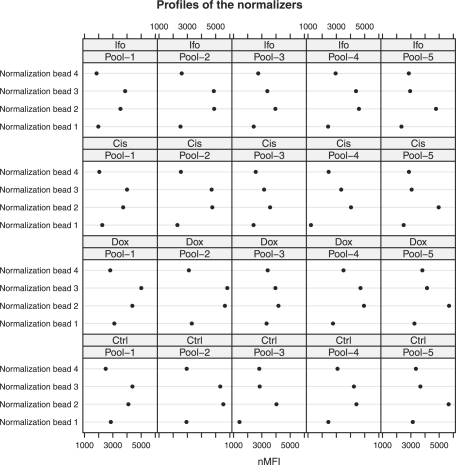
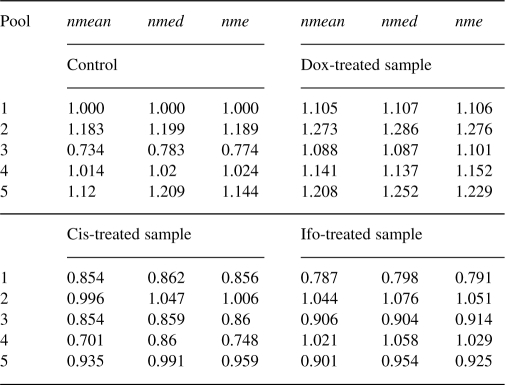
Figure 2 shows the profiles of the four normalizers for one specimen. We see that the profiles show similar pattern across samples and pools. Normalizers 2 and 3 have relatively higher expression levels, while the expression level of normalizer 1 is smaller than the others. By applying the three intrasample normalization methods, we estimate the correction factors for the different pools (Table 1). In Table 1, pool 1 for the control sample is used as the reference pool. We find that the estimated correction factors by the three methods for the same pool are very close for the same samples. The overall expression levels of the subprofiles for different pools and different samples are also close, except pool 3 for the control and pool 1 for the Ifo-treated sample.
Fig. 2.
Profiles of the four normalizers in the five pools (in columns) for the four samples (in rows) for 1 of the 10 specimens. Original scale nMFIs are shown in the _x_-axis.
Table 1.
Correction factors estimation for intrasample normalization based on one specimen
To compare the performance of nme, nmed and mean, a simulation study is performed as follows: first, based on the data after intranormalization (with any of the three methods, we choose nmed here), estimate μ, η and ε of the four normalizers. Second, randomly choose β_jk_~_Uniform_[0.6, 1.3] for _j_=1,…,4 and _k_=1,…,5, and generate data X as in model (1). Third, based on X, estimate β with the three methods, respectively. Fourth, compute the distance between β and each 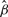 as
as
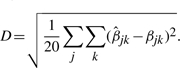
Last, repeat the above three steps for M times and compare the performances of the intrasample normalization methods based on the D's.
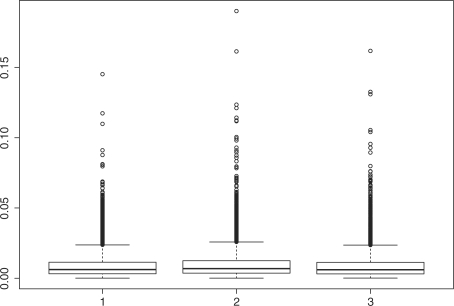
Figure 3 shows the boxplot of the D's for nmean (left), nmed (middle) and nme (right), respectively. In this simulation, the following parameters are used,
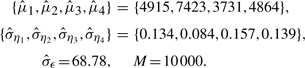
Simulation results show that nme has the smallest median value (6.05e−3) and mean value (8.86e−3) of D with SD 9.16e−3. Method nmed has the largest median D value (=6.84e−3) and mean value (9.75e−3) with SD (9.94e−3), which is larger than those for nme and nmean. The performance of nmean is close to that of nme with a larger median (6.20e−3), but a smaller mean (8.84e−3), and with the smallest SD (8.70e−3). Based on each generated sample, D values are computed with the three methods, respectively. Thus, the three sets of D values are paired. To further compare the D's, we perform a paired Wilcoxon rank test for any two sets of D's. Results show that the mean of D by nme is smaller than that by nmed with P<0.00001, and is smaller than that by nmean as well, with _P_=0.00003. Meanwhile, nmean attains smaller mean of D than nmed (P<0.00001).
Fig. 3.
Box-plots of the D's based on 10 000 repeats: left, nmean; middle, nmed; right, nme.
In the analysis of this study, the iterative procedure for nme converges within three steps for all samples for stopping criteria Δℓ/ℓ<1.0e−6 and Δℓ<1.0e−6. In addition, there are only 80 intensity measures (four normalizers in each of the five pools for the four samples) involved in computing the correction factors; the computation burden is pretty light. The simulation with 10 000 repeats takes <2 min on a Mac Book Pro with Intel Core 2 Duo at 2.33 GHz and 3 GB 667 MHz RAM, so the speed of the algorithm shall not be a concern.
3.2 Performance comparisons of intersample normalization methods
All three intrasample normalization methods can also be applied to normalize the subprofiles (or the assembled profiles) for different samples. However, the above three intrasample normalization methods are linear rescaling methods. Their uses could be very limited mainly due to the fact that the relationship between two profiles are usually non-linear, especially for miRNAs with very high or very low expression levels. Instead of using the information of the four normalizers alone, some global information can also be utilized to normalize the assembled complete profiles by considering the following non-linear normalization methods.
3.2.1 Loess
Let Y and X be the nMFIs in the treated sample and in the control sample, respectively. The cyclic loess method is a method based on the idea of the M versus A plot, where _M_=log(Y/X) is the difference in log expression values, and _A_=log(Y*X)/2 is the average of the log expression values. A normalization curve is fitted to the M versus A plot using local regression. Let 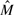 be the fitted values. Thus, we set
be the fitted values. Thus, we set 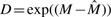 and justify the fold change by multiplying D (Dudoit et al., 2002; Mascellani et al., 2008). The cyclic loess normalization has been implemented in an R packages codelink and affy as well.
and justify the fold change by multiplying D (Dudoit et al., 2002; Mascellani et al., 2008). The cyclic loess normalization has been implemented in an R packages codelink and affy as well.
3.2.2 LoessM
This is a modification of the traditional loess normalization (Risso et al., 2009). In loessM, the median of M on the microarray experiment is subtracted from the loess fit to the MA-plot D. In miRNA data analysis, such a modification could be important due to the possible violation of the following two assumptions (i) the majority of miRNAs are equally expressed and that (ii) the distribution of the log-intensity ratio of deregulated miRNAs is roughly symmetric about zero (Yang et al., 2002).
3.2.3 Qnorm
The quantile normalization method is proposed firstly in (Bolstad et al., 2003), which is based upon the concept of quantile–quantile plot extended to _n_-dimensions. This method forces the distribution of all the replicate arrays to follow a common distribution by replacing the intensities with a certain quantile level with the average of all intensity measures with the same quantile level (Garzon et al., 2008; Northcott et al., 2009). The quantile normalization method has been implemented in R package affy.
In this study, there are no replicated samples tested, as a result some existing statistical test-based methods to identify the differentially expressed miRNAs (genes) are not applicable. We use the fold changes to identify whether the miRNAs are differentially expressed in the drug-treated sample compared with the untreated sample (control). The FC value of miRNA-i is computed by FC _i_=x _i_1/x _i_0, where x _i_1 and x _i_0 are the normalized nMFIs of miRNA-i in the drug-treated sample and control, respectively. If an miRNA has an FC value larger than the predetermined cutoff, we classify it as ‘upregulated’; if its FC value is smaller than 1/cutoff, it is classified as downregulated; otherwise, it is classified as non-differentially expressed. The same rule is applied to the qRT-PCR results by using the RQ values instead of the FC values.
Let (_z_1,_z_2) be a pair of classification results based on the bead-based array and qRT-PCR results, respectively. Each of _z_1 and _z_2 may have three possible results: 0 if non-differentially expressed, −1 if downregulated and 1 if upregulated. Table 2 shows a three-way classification table to identify differentially expressed miRNAs. In Table 2, DR is referred as ‘downregulated’, NDE as ‘non-differentially expressed’, UR as ‘upregulated’, n ij is the number of miRNAs classified as _z_1 based on the beads array results and _z_2 based on the qRT-PCR results. For illustration purposes, Table 3 shows the identification results based on the experimental results for the control and Ifo-treated sample for specimen #8, by using nme, nmean and nmed for both intra- and intersample normalizations. The same cutoff 2.0 is used for both qRT-PCR results and computed FCs, and only the miRNAs that are not weakly expressed are used. In this study, we filter the weakly expressed miRNAs by choosing those with 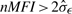 . We find that all three methods are too conservative: nmean claims all miRNAs are non-differentially expressed, while nme and nmed claim one as upregulated and the all others as non-differentially expressed. None of them can identify any of the 50 upregulated miRNAs and the 7 downregulated miRNAs.
. We find that all three methods are too conservative: nmean claims all miRNAs are non-differentially expressed, while nme and nmed claim one as upregulated and the all others as non-differentially expressed. None of them can identify any of the 50 upregulated miRNAs and the 7 downregulated miRNAs.
Table 2.
Three way-classification table for differentially expressed miRNAs
| Beads array results | ||||
|---|---|---|---|---|
| DR | NDE | UR | ||
| DR | _n_11 | _n_12 | _n_13 | |
| qRT-PCR | NDE | _n_21 | _n_22 | _n_23 |
| results | UR | _n_31 | _n_32 | _n_33 |
Table 3.
Performance comparisons for identifying differentially expressed miRNAs (cutoff=2.0)
| nmean | nmed | nme | |||||||
|---|---|---|---|---|---|---|---|---|---|
| DR | NDE | UR | DR | NDE | UR | DR | NDE | UR | |
| DR | 0 | 50 | 0 | 0 | 49 | 1 | 0 | 49 | 1 |
| NDE | 0 | 48 | 0 | 0 | 48 | 0 | 0 | 48 | 0 |
| UR | 0 | 7 | 0 | 0 | 7 | 0 | 0 | 7 | 0 |
Sensitivity and specificity are two statistical measures of the performance of a binary classification test, which can be computed as follows,
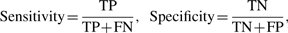
where TP=_n_11+_n_33 is the number of true positives, FN=_n_12+_n_32 is the number of false negatives, TN=_n_22 is the number of true negatives and FP=_n_13+_n_21+_n_23+_n_31 is the number of false positives. The sensitivity measures the proportion of actual positives which are correctly identified as such, and the specificity measures the proportion of negatives which are correctly identified. In Table 3, all three methods have specificity zero. The sensitivity for both nmean and nme is 0.980, and 1.0 for nmed. A more aggressive strategy can be taken by lowering the cutoff, so that more miRNAs will be classified as up- or downregulated based on the FC values. Table 4 shows the results by choosing different cutoff values. We see that when the cutoff is 1.8, both the sensitivity and the specificity do not change much. When the cutoff is 1.5, the specificity is reduced by about 0.2, while the sensitivity is increased no more than 0.025. The sensitivities can be improved at a cost of dramatic drop of specificities. When the cutoff is reduced to 1.3, the specificity is decreased more than half, while the sensitivity is barely increased to about 0.1 (only 0.075 for nmed). In practice, a cutoff shall not be chosen to be too close to 1.00. Otherwise, the classification strategy will be too aggressive and the specificity will be sacrificed.
Table 4.
Performance comparisons for identifying differentially expressed miRNAs with different cutoffs
| Cutoff | Method | Sensitivity | Specificity |  |
_P_-value |
|---|---|---|---|---|---|
| 1.1 | nmean | 0.500 | 0.022 | −0.001 | 0.981 |
| nmed | 0.441 | 0.000 | −0.009 | 0.871 | |
| nme | 0.467 | 0.022 | −0.007 | 0.898 | |
| 1.3 | nmean | 0.115 | 0.407 | 0.025 | 0.640 |
| nmed | 0.075 | 0.400 | 0.009 | 0.859 | |
| nme | 0.090 | 0.407 | 0.013 | 0.791 | |
| 1.5 | nmean | 0.025 | 0.792 | 0.019 | 0.597 |
| nmed | 0.024 | 0.826 | 0.027 | 0.418 | |
| nme | 0.025 | 0.792 | 0.019 | 0.597 | |
| 1.8 | nmean | 0.000 | 0.950 | 0.000 | 0.991 |
| nmed | 0.015 | 0.950 | 0.014 | 0.644 | |
| nme | 0.015 | 0.950 | 0.014 | 0.644 |
As illustrated in Table 4, specificity and sensitivity are not good measures to assess the three-way classification. For binary classifications, a completely random classification strategy will result in an expected value 1/2 for both sensitivity and specificity, and a naive strategy by claiming all negative will result in _sensitivity_=0.0 and _specificity_=1.0. In three-way classifications as in this study, an miRNA could be classified as upregulated, downregulated or non-differentially expressed. When a strategy other than the naive classification is taken, the gain in sensitivity may not be able to compensate the loss in specificity, and vice versa. A completely random strategy will result in an expected value 1/3 for both sensitivity and specificity, which make the performance comparisons difficult. To address this issue, we adopt the following weighed kappa coefficient, which is a measure of agreement between two qualitative classification schemes:
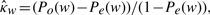 |
(8) |
|---|
where P o(w)=∑i_∑_j w ij p ij, P e(w)=∑i_∑_j w ij_p_i.p.j, p ij_=n ij/∑_i_∑_j n ij, p i.=n ij/∑j n ij and p.j_=n ij/∑_i n ij. The weights w ij are constructed so that 0≤w ij<1 for all i_≠_j, w _ii_=1 for all i, and w _ij_=w ji. We define a distance C _ij_=|_z_1−_z_2| to quantify the relative difference between categories, and use the Fleiss–Cohen weighting scheme to compute w ij_=1−_C _ij_2/4 (Cohen, 1960; Fleiss, 1969; Fless, 1981; Fleiss and Cohen, 1973; Wang et al., 2010a).
In Table 4, we compute the weighted kappa coefficients (column 5), and the _P_-values of testing a null hypothesis that the weight kappa equals zero (column 6). The results by all three methods indicate no agreement between the beads array and qRT-PCR results at significance level α=0.05. From Table 3, we see that more than 50% of the miRNA are differentially expressed by the qRT-PCR results, which also indicates that the cutoff for RQ is already reasonably large. By fixing the RQ cutoff, varying the FC cutoff does not improve the results. A non-linear normalization is needed for intersample normalization. Now we apply the three non-linear normalization methods to the profiles assembled by either of the three intrasample normalization methods. The results are shown in Table 5. We find that the combination of nme and Qnorm leads to a weighted kappa coefficient 0.195 with _P_-value of 0.016, which reveals slight-to-fair agreement according to the interpretation by (Landis and Koch, 1977). The combination of nmed and Qnorm also produces a reasonably large weighted kappa coefficient of 0.144 with _P_=0.075, which is not significant at level 0.05.
Table 5.
Performance comparisons for identifying differentially expressed miRNAs together with non-linear intersample normalization (cutoff=2.0)
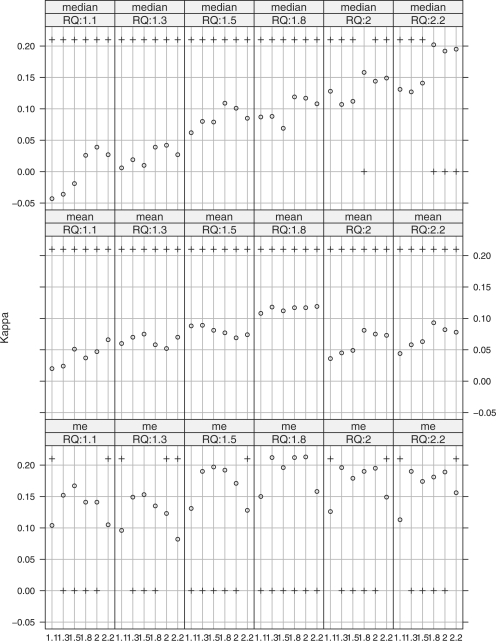
It is also worth noting that when Qnorm is used for intersample normalization, the profiles assembled by nme for this specimen is very robust to the cutoff selection. In Figure 4, the kappa coefficients are computed for different combinations of the FC cutoffs (shown in the _x_-axis in each small panel) and RQ cutoffs (for panels in different columns). For all panels, Qnorm is used for intersample normalization based on the complete profiles assembled by nmed (row 1), nmean (row 2) and nme (row 3). The _y_-values of the circles represent the values of the kappa coefficients. A plus sign (‘+’) at the bottom indicates that the corresponding kappa coefficient is significant at level α=0.05, and not significant if the plus sign is on the top. We see that based on the profiles assembled by nmed, the coefficients are significant only when in the fifth panel (RQ cutoff is 2.0) and FC cutoff is 1.8, and in the sixth panel (RQ cutoff is 2.2) and FC cutoffs are 1.8, 2.0 and 2.2, respectively. All coefficients based on the profiles assembled by nmean are not significant at level 0.05. Meanwhile, most of the weighted kappa coefficients are significantly different from zero based on the profiles assembled by nme.
Fig. 4.
Weighted Kappa coefficient comparisons for different intrasample normalization methods, under various FC and RQ cutoffs, and with Qnorm as intersample normalization method.
Overall, the performances of the three intrasample normalization methods are similar. A study showed that although the intraplatform reproducibilities for beads array and TLDA arrays are high, the interplatform reproducibility between them is poor (Wang et al., 2011). In terms of the Spearman's correlation coefficient between the beads array FCs and qRT-PCR RQs, the median coefficient is 0.1060 with a SD of 0.0391 based on all 40 samples. As a consequence, the three methods agree with each other most of the time, revealing weak agreement between the results from the two platforms.
4 CONCLUSIONS
For beads arrays, there are not many options for intrasample normalization due to the facts that the number of miRNAs in each pool is small, and the miRNA sets in different pools are different. The selection of reliable controls as normalizers is crucial. The ideal controls should be consistently stable and highly abundant despite tissue types or treatments. In one of our ongoing projects, we found that some ncRNAs were influenced by chemo drug treatments, such as 5-fluorouracil, cisplatin or doxorubicin. Thus, it is recommended that the stability of normalization beads should be checked. We need to be aware of the stability of normalization controls across a relatively wide variety of tissues, cell lines and conditions.
Although the common distribution assumption by Qnorm is of concern in miRNA data normalization, the literature showed that the quantile method is one of the best normalization methods compared with some existing one-color miRNA microarray normalization techniques (Pradervand et al., 2009; Wang et al., 2010a). In this study, results also show that the quantile method works well even when the number of usable miRNAs reduces to about 100.
The selection of either the fold change cutoff or RQ cutoff is always a problem in practice. Even if the expression levels can be measured without any measurement errors, it is a concern about how to select an appropriate cutoff to classify the differentially expressed miRNAs. Another concern in miRNA data analysis is that the expression levels of the majority of miRNAs are much lower compared with mRNA or cDNA microarray expression data. Consequently, the measurement error can greatly affect the FC values. When the basal level is not high, the measurement error could even dominate an FC value. In this study, we proposed a measurement error model-based approach for intrasample normalization by taking the measurement errors in the measures of the normalizers into consideration. Advanced errors-in-variables smoothing or regression techniques can also be applied to improve the subsequent intersample normalization (Wang and Wang, 2011; Wang et al., 2010b). We will further investigate how to calibrate the measurement errors based on the model in (1) for intersample normalization, and develop a statistical test for identify the differentially expressed miRNAs.
ACKNOWLEDGEMENTS
We are grateful to the reviewers for their invaluable comments. Special thanks must go to the editor and associate editor for allowing us to improve significantly the manuscript and present our work here. We also thank Dr Cynthia Schneider for her help in revising this article.
Funding: NIH (grant UL1 RR024989 to X.-F.W., in part).
Conflict of Interest: none declared.
REFERENCES
- Bolstad B.M., et al. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics. 2003;19:185–193. doi: 10.1093/bioinformatics/19.2.185. [DOI] [PubMed] [Google Scholar]
- Bruheim S., et al. Gene expression profiles classify human osteosarcoma xenografts according to sensitivity to doxorubicin, cisplatin, and ifosfamide. Clin. Cancer Res. 2009;15:7161–7169. doi: 10.1158/1078-0432.CCR-08-2816. [DOI] [PubMed] [Google Scholar]
- Cohen J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960;20:37–46. [Google Scholar]
- Davison T.S., et al. Analyzing micro-RNA expression using microarrays. Methods Enzymol. 2006;411:14–34. doi: 10.1016/S0076-6879(06)11002-2. [DOI] [PubMed] [Google Scholar]
- Dudoit S., et al. Statistical methods for identifying genes with differential expression in replicated cDNA microarray experiments. Stat. Sin. 2002;12:111–139. [Google Scholar]
- Fleiss J.L. Statistical Methods for Rates and Proportions. New York: Wiley; 1981. pp. 38–46. [Google Scholar]
- Fleiss J.L., Cohen J. The equivalence of weighted kappa and the intraclass correlation coefficient as measures of reliability. Educ. Psychol. Meas. 1973;33:613–619. [Google Scholar]
- Fleiss J.L., et al. Large sample standard errors of kappa and weighted kappa. Psychol. Bull. 1969;72:323–327. [Google Scholar]
- FlexmiRTMMicroRNA Assay, MicroRNA Human Panel Instruction Manual for product # BG-FMIR-H20-8.0, Version A-2 (December 2007), pp. 18–20. Availabe at http://gauss.usouthal.edu/~bwang/pub/supp/beadsme/refs/FlexmiR_Human_Panel_Instructions-revA-2.pdf. [Google Scholar]
- FlexmiRTMMicroRNA Assay, MicroRNA Human Panel Instruction Manual for product # BG-FMIR-H20-8.0, Version B (March 2008), pp. 20–23. Availabe at http://gauss.usouthal.edu/~bwang/pub/supp/beadsme/refs/FlexmiR.pdf. [Google Scholar]
- Garzon R., et al. Distinctive microRNA signature of acute myeloid leukemia bearing cytoplasmic mutated nucleophosmin. Proc. Natl Acad. Sci. USA. 2008;105:3945–3950. doi: 10.1073/pnas.0800135105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ideker T., et al. Testing for differentially-expressed genes by maximum likelihood analysis of microarray data. J. Comput. Biol. 2000;7:805–817. doi: 10.1089/10665270050514945. [DOI] [PubMed] [Google Scholar]
- Landis J.R., Koch G.G. The measurement of observer agreement for categorical data. Biometrics. 1973;33:159–174. [PubMed] [Google Scholar]
- Lewis B.P., et al. Conserved seed pairing, often flanked by adenosines indicates that thousands of human genes are microRNA targets. Cell. 2005;120:15–20. doi: 10.1016/j.cell.2004.12.035. [DOI] [PubMed] [Google Scholar]
- Livak K.J., Schmittgen T.D. Analysis of relative gene expression data using real-time quantitative PCR and the 2(-Delta Delta C(T)) Method. Methods. 2001;25:402–408. doi: 10.1006/meth.2001.1262. [DOI] [PubMed] [Google Scholar]
- Lu J., et al. MicroRNA expression profiles classify human cancers. Nature. 2005;435:834–838. doi: 10.1038/nature03702. [DOI] [PubMed] [Google Scholar]
- Mascellani N., et al. Using miRNA expression data for the study of human cancer. MINERVA BIOTEC. 2008;20:23–30. [Google Scholar]
- Northcott P.A., et al. The miR-17/92 polycistron is up-regulated in sonic hedgehogdriven medulloblastomas and induced by N-myc in sonic hedgehogtreated cerebellar neural precursors. Cancer Res. 2009;69:3249–3255. doi: 10.1158/0008-5472.CAN-08-4710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pradervand S., et al. Impact of normalization on miRNA microarray expression profiling. RNA. 2009;15:493–501. doi: 10.1261/rna.1295509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risso D., et al. A modified LOESS normalization applied to microRNA arrays: a comparative evaluation. Bioinformatics. 2009;25:2685–2691. doi: 10.1093/bioinformatics/btp443. [DOI] [PubMed] [Google Scholar]
- Rocke D.M., Durbin B. A model for measurement error for gene expression arrays. J. Comput. Biol. 2001;8:557–569. doi: 10.1089/106652701753307485. [DOI] [PubMed] [Google Scholar]
- Rocke D.M., Lorenzato S. A two-component model for measurement error in analytical chemistry. Technometrics. 1995;37:176–184. [Google Scholar]
- Schmittgen T.D., et al. Real-time PCR quantification of precursor and mature microRNA. Methods. 2008;44:31–38. doi: 10.1016/j.ymeth.2007.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang B., et al. A personalized microRNA microarray normalization method using a logistic regression model. Bioinformatics. 2010a;26:228–234. doi: 10.1093/bioinformatics/btp655. [DOI] [PubMed] [Google Scholar]
- Wang X.F., et al. Estimating smooth distribution function in the presence of heteroscedastic measurement errors. Comput. Stat. Data Anal. 2010b;54:25–36. doi: 10.1016/j.csda.2009.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang B., et al. Systematic evaluation of three microRNA profiling platforms: microarray, beads array, and quantitative real-time PCR array. PLoS One. 2011;6:e17167. doi: 10.1371/journal.pone.0017167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X., Wang B. Deconvolution estimation in measurement error models: The r package decon. J. Stat. Softw. 2011;39:1–24. [PMC free article] [PubMed] [Google Scholar]
- Xi Y., et al. Systematic analysis of microRNA expression of RNA extracted from fresh frozen and formalin-fixed paraffin-embedded samples. RNA. 2007;13:1668–1674. doi: 10.1261/rna.642907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y.H., et al. Normalization for cDNA microarray data: a robust composite method addressing single and multiple slide systematic variation. Nucleic Acids Res. 2002;30:e15. doi: 10.1093/nar/30.4.e15. [DOI] [PMC free article] [PubMed] [Google Scholar]