The Intrinsic Connectivity Distribution: A Novel Contrast Measure Reflecting Voxel Level Functional Connectivity (original) (raw)
. Author manuscript; available in PMC: 2013 Sep 1.
Abstract
Resting-state fMRI (rs-fMRI) holds promise as a clinical tool to characterize and monitor the phenotype of different neurological and psychiatric disorders. The most common analysis approach requires the definition of one or more regions-of-interest (ROIs). However this need for a priori ROI information makes rs-fMRI inadequate to survey functional connectivity differences associated with a range of neurological disorders where the ROI information may not be available. A second problem encountered in fMRI measures of connectivity is the need for an arbitrary correlation threshold to determine whether or not two areas are connected. This is problematic because in many cases the differences in tissue connectivity between disease groups and/or control subjects are threshold dependent. In this work we propose a novel voxel-based contrast mechanism for rs-fMRI, the Intrinsic Connectivity Distribution (ICD), that neither requires a priori information to define a ROI, nor an arbitrary threshold to define a connection. We show the sensitivity of previous methods to the choice of connection thresholds and evaluate ICD using a survey study comparing young adults born prematurely to healthy term control subjects. Functional connectivity differences were found in hypothesized language processing areas in the left temporal-parietal areas. In addition, significant clinically-relevant differences were found between preterm and term control subjects, highlighting the importance of whole brain surveys independent of a priori information.
Keywords: Functional Connectivity, Network theory, Preterm, Resting-state fMRI
Introduction
Functional magnetic resonance imaging (fMRI) is a powerful tool commonly used to phenotype a wide range of neurological and psychiatric disorders. These phenotypes are often characterized by altered functional networks as detected by functional connectivity fMRI (fc-fMRI) and can be vital in diagnosing and monitoring disorders or evaluating treatments. An important first step in characterizing any disease is a survey study in which differences across all brain regions between two populations are probed in order to form further testable hypothesizes. However, the ability to perform whole brain survey studies using fMRI without a priori information remains elusive. Task-based fMRI, the foundation of much fMRI based research, can only highlight regions differentially involved in the execution of a specific task, as different Task/Control conditions cause local changes in the blood oxygenation level dependent (BOLD) signal (Ogawa et al., 1990; Ogawa et al., 1992). This limits the number of regions that can be surveyed with task-based fMRI paradigms because only a very few cortical regions typically show differential activation to any given task, and the number of tasks that can be run in a reasonable time with sufficient statistical power is low.
In contrast, resting state fMRI (rs-fMRI) can reveal changes in functional networks using task-free time courses between cortical regions based on spontaneous fluctuations in the BOLD signal (Biswal et al., 1995; Lowe et al., 1998). Substantial evidence suggests that these temporal correlations reflect intrinsic functional connections in that they are present when subjects are both awake and under anesthesia (Martuzzi et al., 2010; Martuzzi et al., 2011; Vincent et al., 2007). Importantly, these correlations are highly reproducible (Shehzad et al., 2009). This intrinsic brain activity has been shown to be both related to behavioral variables (Hampson et al., 2010; Hampson et al., 2006a; Hampson et al., 2006b; Rogers et al., 2010; Schafer and Constable, 2009) and altered in numerous clinical conditions ranging from schizophrenia and depression to autism and epileptic disorders (Irwin et al., 2004; Killory et al., 2011; Lowe et al., 2002; Waites et al., 2006). Overall, resting-state functional connectivity mapping has significant potential to elucidate how and where functional networks may be altered in the presence of different diseases or disorders using a whole brain survey study.
Most connectivity analysis follows the resting state region of interest (ROI)-based approach that was first presented in 1995 by Biswal et al (Biswal et al., 1995). In this approach, either a single ROI is chosen and the connectivity between that ROI and the rest of the brain is calculated, or multiple ROIs are chosen and connectivity between different combinations is assessed. In either case, the choice of the ROI is critical. If an ROI contains multiple time-courses then the average time-course from the ROI may not properly represent any of the independent time-courses within that region and the results may therefore be erroneous. Approaches to defining ROIs have centered on several different methods. Defining ROIs based on results from task-based fMRI is limited by the number of regions that differentially activate during the given task (the same weakness of task-based fMRI) and whole-brain assessment is not possible. Anatomic ROI definitions are sufficient in areas with clear anatomical distinction, such as the hippocampus, but are problematic where anatomic boundaries are not well defined, such as in the frontal or parietal lobes. ROIs in these areas, along with spherical ROIs, arbitrary parcellation of the cortex into a large number of subunits, and the use of an atlas (such as the Brodmann areas), all suffer from the problem of potentially mixing several distinct time-courses. Further, even if one of these ROI approaches were proven to be effective in healthy normal controls, the ROI definitions may not be applicable in the presence of a neurologic disease or disorder in which functional networks may be altered such as prematurely born infants.
To potentially overcome this problem, voxel-based analyses have been introduced in which network measures such as degree can be calculated for each voxel (Rubinov & Sporns 2010). In these analyses, the term “degree” represents a count of the number of connections to a given voxel that exceeds a specific correlation threshold. While intuitive, the degree measure applied to rs-fMRI is a fundamentally flawed descriptor due to its dependence on the choice of threshold for which there is no principled method of selection. A large range of thresholds have been used to determine if two voxels are connected ranging from a correlation of 0.1 (supplementary analysis from Buckner et al (Buckner et al., 2009)) to a correlation of 0.8 (supplementary analysis from Tomasi and Volkow (Tomasi and Volkow, 2010)). These thresholds are frequently chosen to be large enough to prevent false positive results but small enough to maintain the important connections. This approach is often justified by presenting results produced by a range of thresholds highlighting the robustness of the results to the chosen threshold. However, the range of thresholds used to highlight the robustness of the results is relatively small (typically a correlation range of 0.2 to 0.4) compared to the total range of available thresholds. Others have chosen thresholds such that the overall network maintains specific properties such as sparseness (Achard et al., 2006). However, these network properties have not been shown to be important or necessary in discriminating group differences in functional connectivity. Thesholding based on significance level is a potential method that could be used to select a threshold. However, this method is limited by issues surrounding multiple comparisons (each voxel is correlated with ~10,000 other voxels and this procedure is then repeated for all of the ~10,000 voxels), experimental parameters (scan length, number of scans, and repetition time) controlling the number of time points collected as significance in correlation is a function of the number of samples (it is unclear how differing amount resting data affects group comparisons), and preprocessing steps such as removal of global mean which make quantitative interpretation of the correlations ambiguous (Buckner et al., 2009). Several studies have proposed methods that are not reliant on this threshold (Cole et al., 2010; Martuzzi et al., 2011; Rubinov and Sporns, 2011). However, to date, there have been no publications highlighting the sensitivity to between-group differences due to threshold effects.
The focus of this work is the introduction of a voxel-based measure that characterizes the entire degree curve, the distribution of connections across all thresholds, and eliminates the need for a specific threshold to be chosen. In the conventional degree calculation, the distribution of all correlations between a voxel’s time-course and every other time-course is calculated. This distribution is then integrated to extract a single parameter: degree. Many potential correlation distributions could have the same integral, but could have different shapes. Hence, much of the information and the sensitivity to small changes could be lost. In this work, we present a novel method to estimate the entire degree function d(x,τ), where d(x, τ) is defined as the number of connections stronger than the threshold τ at voxel x. We label the function d(x, τ) the intrinsic connectivity distribution (ICD), as it captures information about all connections (weak to strong) as opposed to simply the number of some arbitrarily strong ones. By parameterizing the degree function with a small number of parameters, statistical differences in intrinsic, threshold-free voxel-wise connectivity can be established between groups, or for an individual compared to a group.
To assess our ICD measure, we performed a whole-brain survey study using rs-fMRI to compare study subjects that were born prematurely (the preterm group) and those that were born full term (the term group) all of whom are now 20 years old. Using subjects from this same cohort, several studies have identified group differences in language processing areas (Constable et al., 2008; Gozzo et al., 2009; Mullen et al., 2011; Myers et al., 2010). ROI-based methods have revealed that preterm subjects, when compared to term subjects, show increased functional connectivity between ROIs in the left temporal and parietal lobe for subjects at ages 8 and 16 years (Gozzo et al., 2009; Myers et al., 2010). Similarly, diffusion tensor imaging has shown that fractional anisotropy in the left arcuate fasciculus (a pathway connecting the temporoparietal junction) is correlated with neuropsychological language testing for preterm subjects (Constable et al., 2008; Mullen et al., 2011). From this previous work, we hypothesized that preterm subjects would continue to show differences relative to term controls in functional connectivity in the language processing areas of the left temporal and parietal lobes. Second we hypothesized that use of intrinsic connectivity distribution (ICD) compared to other network theory measures would improve the sensitivity of rs-fMRI while eliminating the need for threshold or a priori ROI definitions.
Theory
A need exists for a voxel-based measure that reflects tissue functional connectivity without the need for a priori information to define an ROI, or to define a threshold. Here we review intrinsic connectivity contrast (ICC) based on the network theory measure degree using the terminology in Martuzzi et al (Martuzzi et al., 2011), review similar weighted degree metric (weight Global Brain Connectivity (wGBC)) (Cole et al., 2010), and develop our new measure, the intrinsic connectivity distribution (ICD).
Degree is a common network theory measure used to analyze rs-fMRI that characterizes the number of connections between a given ROI or voxel and every other ROI or voxel (Rubinov and Sporns, 2010)). This metric has been used to analyze fMRI connectivity using both un-weighted (ICC-dτ) and weighted connections (ICC-pτ, where p stands for power, and wGBC) metrics. ICC-dτ for any voxel x can be calculated from distribution of connection strength, f(x,r). First, f(x,r) is defined as the distribution of the correlations (r) for the time-course at voxel x to the time-course at every other voxel in the brain. ICC-dτ(x) is then defined as the integral, ∫τ1f(x,r)dr. ICC-pτ and wGBC for any voxel x can be calculated from a weighted distribution of connection strength, g(x, r, w) = w(r)f(x, r), and is defined as the integral ∫τ1g(x,r,w)dr. For ICC-pτ, the weighting is the square of the correlation (_w(r)_=_r_2). For wGBC, the weighting is the Fisher transform of the correlation (w(r)=12ln1+r1−r). These degree metrics are simply the sum of the number, or of the weights of connections above a threshold. While ICC-dτ is completely dependent on threshold (without a threshold ICC-dτ is equal to the number of voxels in the image), ICC-pτ and wGBC can be performed independent of a threshold. However, these weighting are designed to minimize the contribution of weak connections either by suppressing the weak connections (_w(r) = r_2) or to emphasize the strong connections (w(r)=12ln1+r1−r).
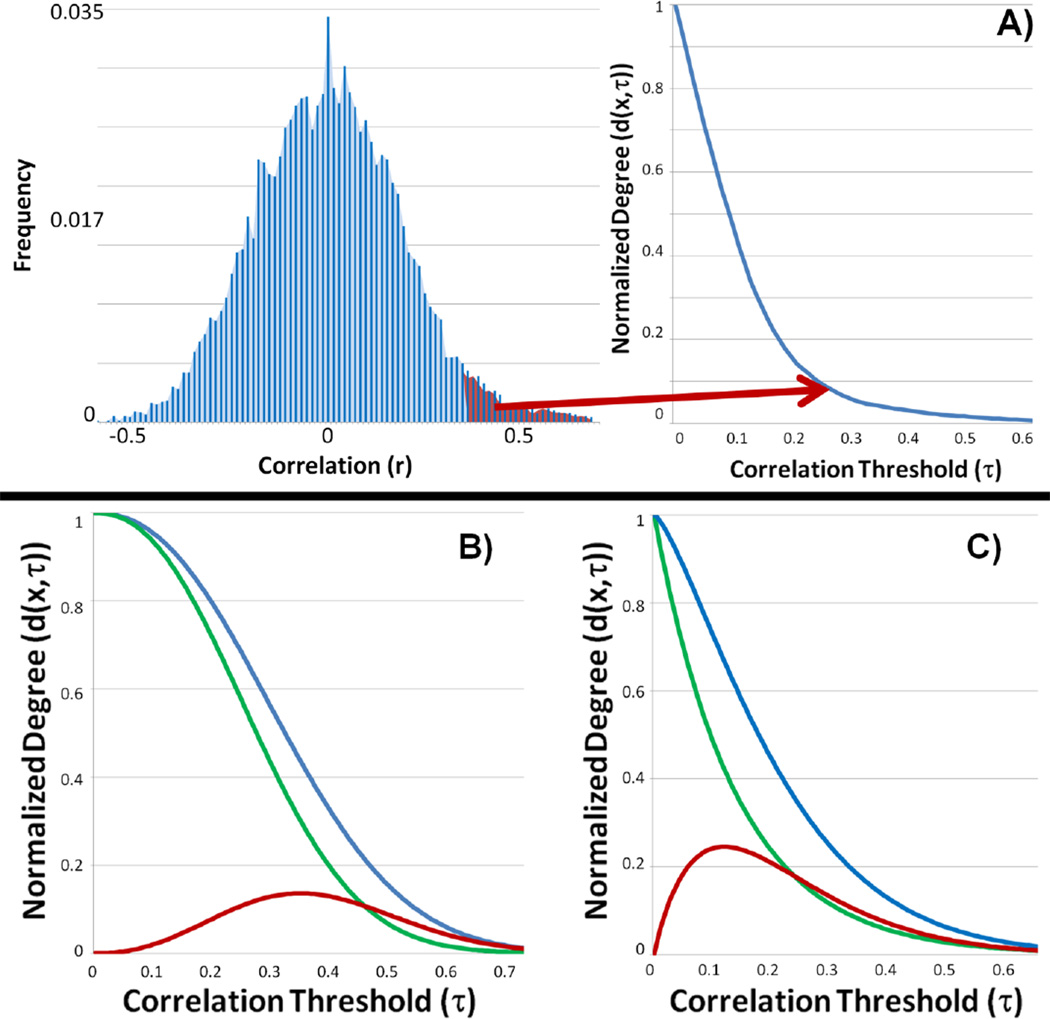
Instead of simply integrating the strength of all connections for a particular voxel, as is performed in the degree metrics, ICD models the distribution of the connection strength. To obtain the ICD measure, the distribution of the connection strengths (f(x,r)) is estimated in the same manner as the degree metrics. Next, we define our ICD measure (d(x, τ)) as the survival function corresponding to f(x,r)) noting that d(x, τ) at any value τ is the same as the ICC-dτ_(x)_ measure with a threshold equal to τ. An example distribution of the connection strength and its corresponding survival function is shown in Figure 1A. The survival function is modeled as a stretched exponential with unknown variance parameter (α) and shape parameter (β) as: d(τ, x, α(x), β(x))=e−α(x)τβ(x) (1). The parameterization in equation (1) is flexible to a wide range of survival functions (examples are shown in Figure 1) and guarantees the fitted curve is monotonically decreasing (an important property of survival functions) when α and β are restricted to positive numbers. A smaller α indicates a larger spread in the survival of strong connections as shown in Figure 1B where the blue curve has a smaller α (but the same β) and a larger degree metric at any threshold compared to the green curve. A larger β indicates a shallower decay from the number of voxels showing weak connections to the number showing strong connections as shown in Figure 1C where the blue curve has a smaller β (but the same α) and a larger degree metric at any threshold compared to the green curve. These examples illustrate a smaller α and a larger β represent a relatively larger amount of strong connections and higher connectivity.
Figure 1.
A) An example distribution of connection strengths and its corresponding survival curve. The red area of the connection strengths distribution represents ICC-d at an arbitrary threshold. This area maps to a single point on survival curve, d(x,τ). ICD parameterizes the survival curve eliminating the need for thresholds. B-C) The ICD parameterization is monotonically decreasing (an important property of any survival curve) and is capable of capturing a variety of shapes with only two parameters (α and β). The varied shape of the curves illustrates the sensitivity to threshold for degree based measures. B) The blue and green survival curves have the same β parameter but the blue curve has a smaller α parameter and a larger degree metric at any threshold. The red curve represents the difference between the survival curves and peaks at approximately τ=0.35. C) The blue and green survival curves have the same α parameter but the blue curve has a larger β parameter and a larger degree metric at any threshold. The red curve represents the difference between the survival curves and peaks at approximately τ=0.13.
ICD represents a generalization of the degree metric incorporating information about the survival of the distribution of the connection strength instead of just the area under the curve. ICD represents the curve of the ICC-dτ measure versus the threshold used to calculate ICC-dτ. The curve of ICC-p or wGBC versus threshold is the survival function of a related distribution of connection strengths, g(x, r, w). The approaches used to date typically examine only a single point on these survival functions. Viewing ICC-d and ICC-p as single points on a curve reveals potential flaws in these measures. The threshold τ at which the degree calculation is performed can have a significant influence on the interpretation of the results. The two pairs of example survival functions (d(x, τ)) along with the difference between the pairs shown in Figure 1B and Figure 1C help elucidate this influence. The maximum difference between each d(x, τ) pair occurs at two different thresholds (approximately τ=0.35 for the example in Figure 1B and τ=0.13 for the example in Figure 1C). A threshold of τ=0.15 may produce significant differences for the example in Figure 1C but not for the example in Figure 1B. A threshold of τ=0.25 may produce significant differences in both examples. Further, if two population survival curves cross, picking a single threshold point for comparisons may produce no meaningful information about the differences in functional connectivity. A threshold point can be chosen to show an increase, a decrease, or no changes in connectivity. Furthermore, neither ICC metric provides insight into the underlying information regarding the composition of the connections that make up a network. For example, if different thresholds are to be used, the ICC metric will need to be recalculated for each threshold. The ICD metric allows all of the connectivity information to be captured with only a few parameters, and eliminates the need for setting arbitrary thresholds.
The parameters (α and β) can be estimated using standard non-linear regression algorithms such as the Levenberg–Marquardt algorithm used in this work. Unlike linear regression, nonlinear regression does not guarantee an unbiased minimum variance estimate. However, the bias in the estimates can be assumed to be small and the estimate approaches minimum variance, since the number of samples for the distribution of a voxel’s correlations is large (50–250 histogram bins or ~10000 or more voxels). Using these asymptotic assumptions, group comparisons of the parameters can be made in a manner similar to the parameters estimated from a GLM, creating t-maps for each parameter.
Methods
This study was performed at Yale University School of Medicine, New Haven, CT, and Warren Alpert Brown Medical School, Providence RI. The protocols were reviewed and approved by institutional review boards at each location. Informed consent was obtained. All scans were obtained and analyzed at Yale University.
Subjects
The preterm cohort consisted of 21 young adults with no evidence for intraventricular hemorrhage (IVH), periventricular leukomalacia and/or low pressure ventriculomegaly. Subjects had normal findings on conventional MRI. They had no contraindications to MRI. All preterm subjects enrolled in the follow-up component of the “Multicenter Randomized Indomethacin IVH Prevention Trial” (Ment et al., 1994) were sequentially recruited for the MRI study when they reached 20 years of age. These subjects are representative of the cohort of subjects with no evidence of neonatal brain injury with respect to gender, handedness, FSIQ scores, minority status, and maternal education. Nineteen healthy term young adults, aged 20 years, were recruited from the local community and group-matched with the preterm subjects as previously described. The assessments of neonatal health status and neurologic outcome of the preterm subjects have been previously reported (Peterson et al., 2000).
Imaging Parameters
Subjects were scanned in a Siemens 3T Tim Trio scanner and instructed to keep their eyes-open, not think of anything in particular, and not to fall asleep. No fixation cross was used. After a first localizing scan, a high resolution 3D volume was collected using a magnetization prepared rapid gradient echo (MPRAGE) sequence (176 contiguous sagittal slices, slice thickness 1 mm, matrix size 256×256, FoV = 256mm, TR = 2530 ms, TE = 2.77 ms, flip angle = 7°). Next, a T1-weighted anatomical scan (TR = 300 ms, TE = 2.55 ms, FoV = 220 mm, matrix size 256x256, thickness = 6 mm thick, gap = 1mm) was collected with 25 AC-PC aligned axial-oblique slices. After these structural images, acquisition of functional data began in the same slice locations as the axial-oblique T1-weighted data. Functional images were acquired using a T2* sensitive gradient-recalled single shot echo-planar pulse sequence (TR = 1550ms, TE = 30ms, flip angle = 80°, Bandwidth = 2056 Hz/pixel, 64*64 matrix, field of view: 220mm×220mm, interleaved acquisition). Functional runs consisted of 190 volumes (approximately 5 minute scan length) with the first four volumes discarded to allow the magnetization to reach the steady-state.
Preprocessing
Images were slice time corrected using sinc interpolation and motion corrected using SPM5 (http://www.fil.ion.ucl.ac.uk/spm/software/spm5/). All further analysis was performed using BioImage Suite (http://bioimagesuite.org). Several covariates of no interest were regressed from the data including linear and quadratic drift, six rigid-body motion parameters, mean cerebral-spinal fluid (CSF), and mean white matter signals. The white matter and CSF areas were defined on a template brain (Holmes et al., 1998), eroded to ensure only white matter or CSF signal would be included, and warped to subject’s space using a series of transformations described below. The overall volume mean was removed for each individual volume in the 4D sequence. Finally, the data were temporally smoothed with a zero mean unit variance Gaussian filter (approximate cutoff frequency=0.12Hz).
Degree and ICD estimation
After preprocessing, the two resting state runs were concatenated and the distribution of connections for each voxel was then calculated in each subject’s individual space. First, a gray matter mask was applied to the data so only voxels in the gray matter were used in the calculation. The gray matter mask was defined on a template brain (Holmes et al., 1998), dilated to ensure full coverage of the gray matter, and warped to the individual subject’s space using a series of transformations described below. Next, f(x,r) was calculated for each voxel×by correlating its time-course with every other time-course in the gray matter. A 201 bin histogram was used to estimate f(x,r). Because the removal of the global mean makes the signs of the correlation ambiguous, we only focus on the positive correlation as in Buckner et al (Buckner et al., 2009). ICC-d was calculated using a range of thresholds from 0.05 to 1 in 0.05 increments and ICC-p and wGBC were calculated using a range of thresholds from 0 to 1 in 0.05 increments. (We note that wGBC was originally formulated without a threshold term. We have added this term to make wGBC comparable to ICC-d and ICC-p and to investigate wGBC sensitivity to threshold.) Each subject’s map was then normalized by subtracting the mean across all voxels and dividing by the standard deviation across all voxels. This normalization does not change the underlying connectivity pattern but ensures all subject maps are consistently scaled. To estimate the ICD parameters, the connection strength distribution of the positive correlations was normalized to form a proper probability density and the corresponding survival function (d(x, τ)) was estimated. Equation (1) was then fitted to the survival function using the Levenberg–Marquardt algorithm to estimate the ICD parameters, α and β. While restricting the analysis to only the positive correlations does introduce a threshold for this study, the overall ICD method can be generalized to include the entire distribution. To assess the fit of ICD, the coefficient of determination (as known as R2, but we refer to this statistic as the coefficient of determination to avoid confusion with the weighting of ICC-p) was calculated and, in common space, averaged across subjects for each voxel. The results here are shown only for the α measure, but the methodology is the same for the β parameter of this distribution.
To facilitate group statistics, all single subject results (wGDC,ICC-p, ICC-d, ICD-α) were first spatially smoothed with a 6mm Gaussian filter and warped to a common template space through the concatenation of a series of linear and non-linear registrations. The functional series were linearly registered to the T1 axial-oblique (2D anatomical) image. The 2D anatomical image was linearly registered to the MPRAGE (3D anatomical) image. The 3D anatomical image was non-linearly registered to the template brain. All transformation pairs were calculated independently and combined into a single transform warping the single subject results into common space. This single transformation allows the single subject images to be transformed to common space with only one transformation reducing interpolation error. All transformations were visually inspected for accuracy and were estimated using the intensity-only component of the method implemented by BioImage Suite as previously reported in Papademetris et al (Papademetris et al., 2004). Differences between preterm and term subjects for each measure were identified using a t-test with significance accessed at p=0.05. AFNI AlphaSim (http://afni.nimh.nih.gov/afni) was used to correct for multiple statistical comparisons across the cortex with a cluster size=8,297 (1mm3) voxels. The Monte Carlo simulation was run with a smoothing kernel estimated using AFNI 3dFWHMx, an uncorrected p-value=0.05, and 10000 iterations. Brodmann areas (BA) locations were identified using BioImage Suite’s digital Brodmann atlas.
Results
To show the efficacy of our new ICD measure, we employed a whole-brain survey rs-fMRI study to explore group differences between the preterm and term subject groups at age twenty years. The data were analyzed with our ICD measure as well as two previously described methods based on the network theory measure degree. Both ICC-p and ICC-d employed thresholds to determine which voxels are functionally connected for the calculation of the degree metric. Thus, we performed these measures over a large range of thresholds. ICC-d is completely reliant on this threshold and, while ICC-p can be used without a threshold, previous results suggest that using a threshold increases sensitivity in ICC-p (Martuzzi et al., 2011).
Sensitivity to Degree Threshold
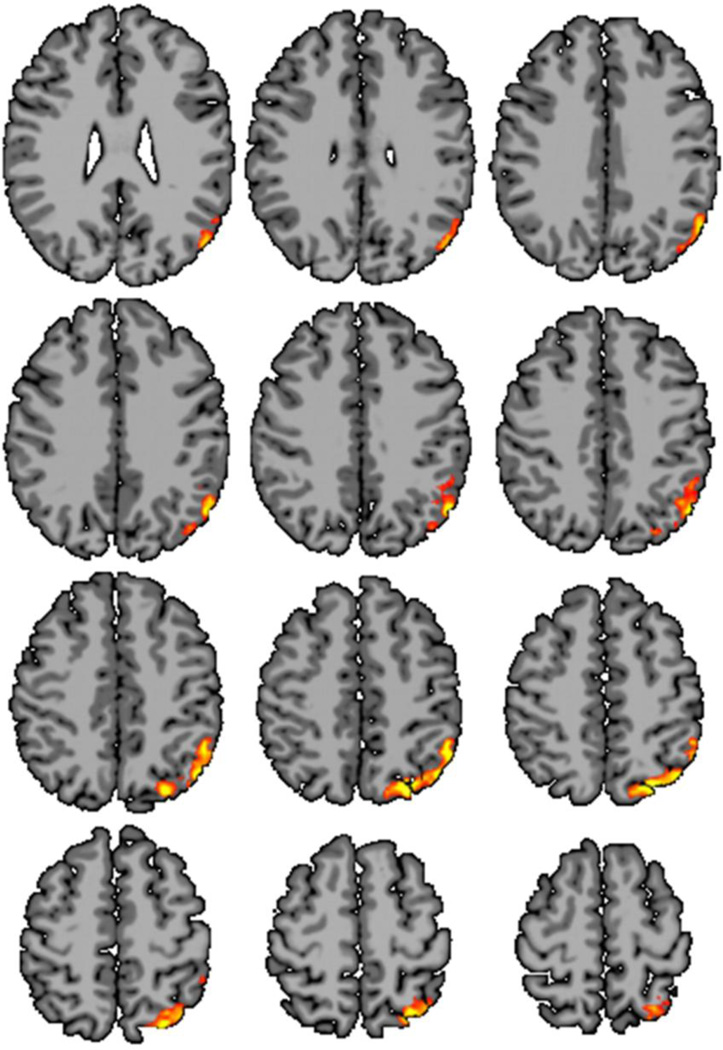
The three degree metrics revealed differences in the hypothesized temporal-parietal region over a range of thresholds. However, the extent of the clusters varied by threshold with different sub-areas detected at different thresholds. ICC-d results from 8 different thresholds are shown in Figure 2. ICC-d revealed significant differences in BA 40 at a threshold τ<0.35 and reveals significant differences in BA 19 only at a threshold of τ>0.55. In addition, ICC-d detected greater changes in connectivity in the superior portions of the temporal-parietal cluster as the threshold was increased. A similar trend appeared for additional clusters detected in the right and left inferior temporal lobe. The right cluster is only detected at a threshold of τ=0.15 and the left cluster is only detected at a threshold of τ<=0.35. ICC-p showed even greater sensitivity to threshold as ICC-d (Figure 3) as connectivity differences in the temporal-parietal area were only detected at thresholds between τ=0.55 and τ=0.60. WGBC showed a similar trend with threshold effects as ICC-d as shown in Figure 4. Like ICC-d, wGBC revealed changes in BA 40 at a threshold τ<0.30 and BA 19 at a threshold τ>0.55. The left inferior temporal lobe cluster was detected with a threshold t<0.35.
Figure 2.
ICC-d revealed group differences between preterm and term subjects in the temporal-parietal area. Results from a range of threshold from τ=0.15 to τ=0.7 are shown. While the temporal-parietal area consistently showed group differences, specific regions (such as BA 40 and BA 19) were inconsistent over the different thresholds. Additionally, the clusters in the right and left inferior temporal lobe are not detected at higher thresholds. The circles highlight regions that show changes when the threshold is increased by 0.05.
Figure 3.
ICC-p revealed group difference between preterm and term subjects in the hypothesized temporal-parietal lobe only at thresholds between τ=0.55 (not shown) and τ=0.60 (shown). ICC-p did detect group differences in the inferior temporal lobes or medial frontal lobes at any threshold.
Figure 4.
Weighted Global Brain Connectivity (shown at three different thresholds) performed similarly to ICC-p in detecting group difference but was less sensitive to threshold effects. However, wGBC detected fewer group differences then ICC-d (over a variety of thresholds) and ICD-α.
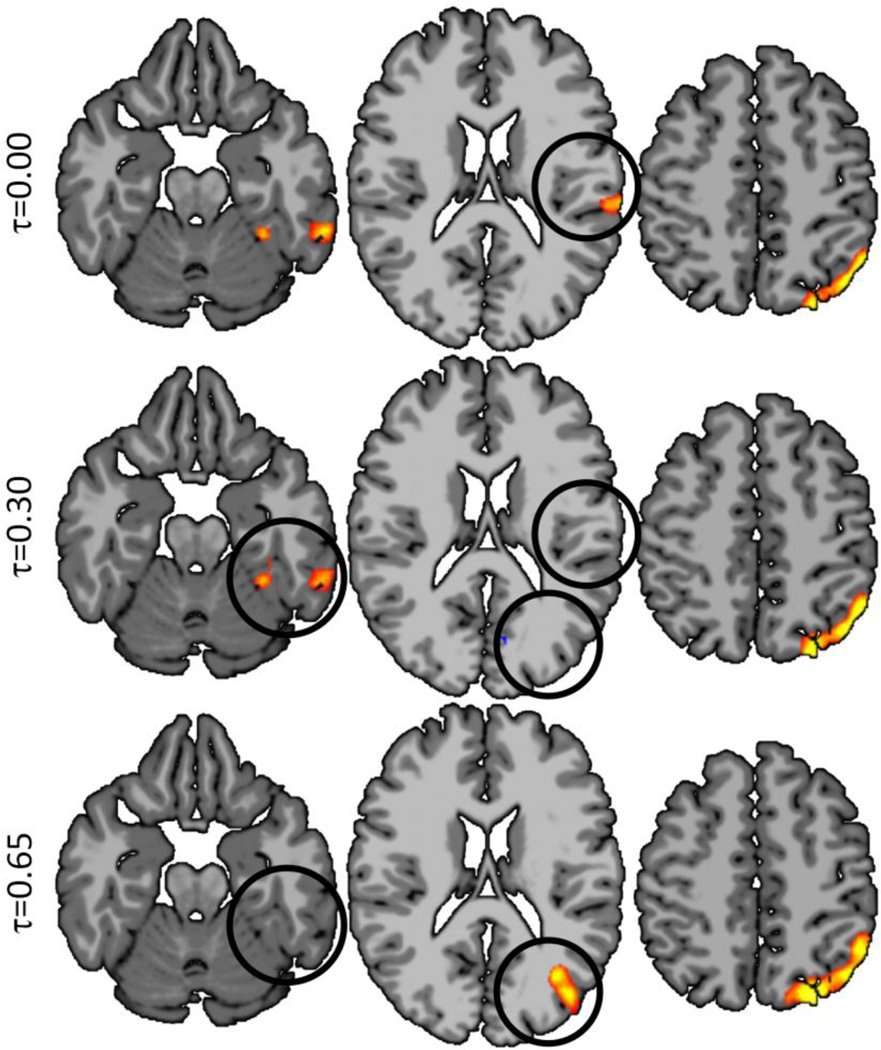
The ICC-d maps at reduced significance levels (p<0.05 uncorrected) highlight the difficult problem with metrics based on a threshold to evaluate functional connectivity instead of modeling the entire distribution of connections. The average survival functions (d(x, τ)) from an ROI (white circle in Figure 5b-c) in the right frontal lobe for both term and preterm subjects are shown in Figure 5a. The two curves cross at approximately τ=0.15 leading to ambiguous results. A threshold can be chosen to show decreases (Figure 5b), no changes (Figure 5c), or increases (Figure 5d) in functional connectivity as measured by ICC-d between preterm and term subjects. ICD detects no significant connectivity differences in this region. However, from the ICD parameters, the survival curves can be reconstructed allowing for graphical and qualitative interpretations such as preterm subjects showing more strong connections but term subjects showing a larger amount of total connections.
Figure 5.
The threshold dependency of ICC-d can cause ambiguous results if the survival functions from two populations cross. The average survival functions from the white circle in (B-D) are shown in (A). These curves cross at approximately τ=0.15. Group results as produced by ICC-d at p<0.05 uncorrected using threshold (B) τ=0.05, (C) τ=0.15, and (D) τ=0.55 are shown. The direction of the differences changes as predicted by the survival functions.
Evaluation of ICD
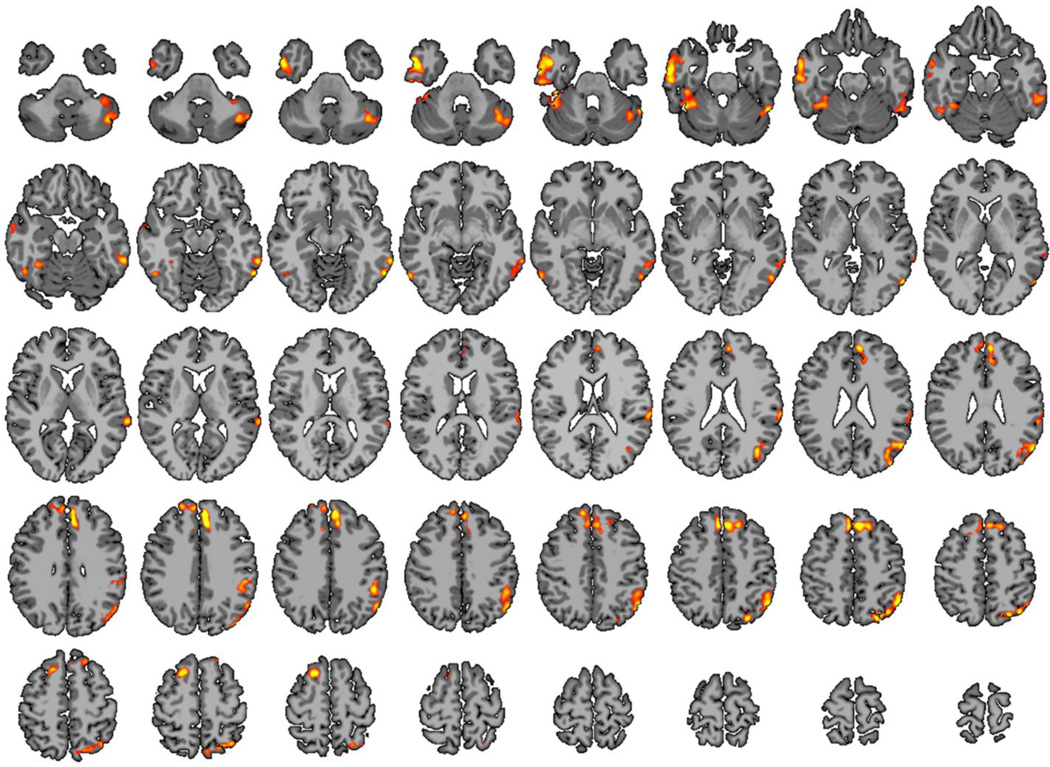
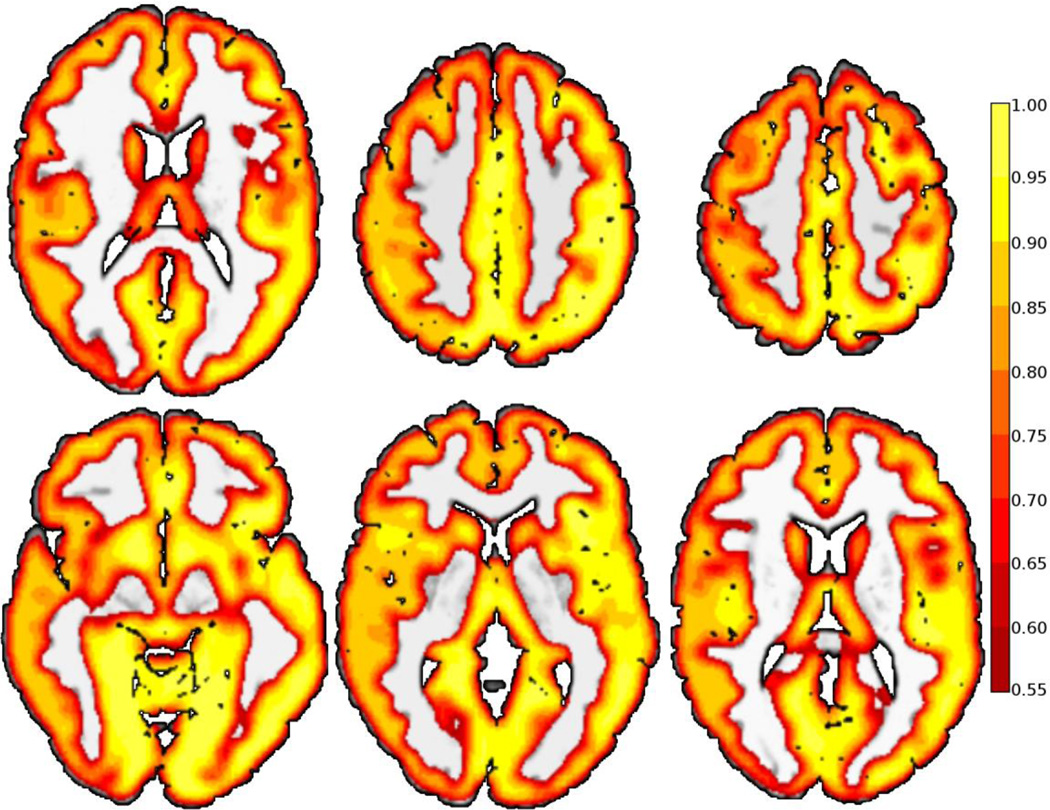
Significant differences were found between preterm and term subjects, and all methods detected differences in the left temporal-parietal area initially hypothesized. The ICD-α measure (Figure 6) revealed five clusters of increased connectivity for the preterm group centered in the left temporal-parietal area, the right inferior temporal lobe, the left inferior temporal lobe, the left cerebellum, and bilateral medial frontal lobes compared to the term group. The left temporal-parietal area cluster was comprised mainly of BA 39 and BA 40, but also included BA7, BA 19, BA 21, and BA 22. The right inferior temporal lobe cluster was comprised of BA21 and fusiform gyrus. The left inferior temporal lobe cluster was comprised of the left fusiform gyrus, but also included BA 19 and BA 21. The medial frontal lobe cluster included right BA 6, bilateral BA 8, bilateral BA 9, and left BA32. The left cerebellar region included the biventer, inferior semilunar, superior semilunar, and the quadrangular lobules. As shown in Figure 7, ICD fitted the survival curves equally well in both cortical and sub-cortical structures with a mean coefficient of determination of 0.78 with a standard deviation of 0.17 throughout the gray matter.
Figure 6.
The proposed ICD-α revealed significant difference between preterm and tern subject at age 20 using resting state fMRI in a whole-brain survey study. This method detected four clusters increased functional connectivity for the preterm group when compared to the term group. The first cluster is centered in the left temporal-parietal area in known language processing areas including BA 39 and BA 40. The second and third clusters are located in the right and left inferior temporal lobe. The fourth cluster is located in the medial frontal lobe.
Figure 7.
Coefficient of Determination (R2) illustrating that ICD provides a good fit of the degree curve throughout both cortical and sub-cortical gray matter. The mean coefficient of determination is 0.78 with a standard deviation of 0.17 in the gray matter.
All degree metrics measures revealed similar clusters to ICD-α in the left temporal-parietal area. The general area of the cluster was robust to several threshold levels. ICC-d detected differences in the temporal-parietal area over a threshold range from τ=0.15 to τ=0.75, ICC-p detected differences over a threshold range from τ=0.55 to τ=0.60, and wGBC detected differences over a range from τ=0.00 to τ=0.75. Additionally, ICC-d revealed similar clusters as ICD-α in the right and left inferior temporal lobe. WGBC detected only the cluster in the left inferior temporal lobe while ICC-p did not detect these clusters. Finally, all degree metrics detected differences in the occipital lobe not detected by ICD-α and no degree metric detected significant differences in the medial frontal lobe.
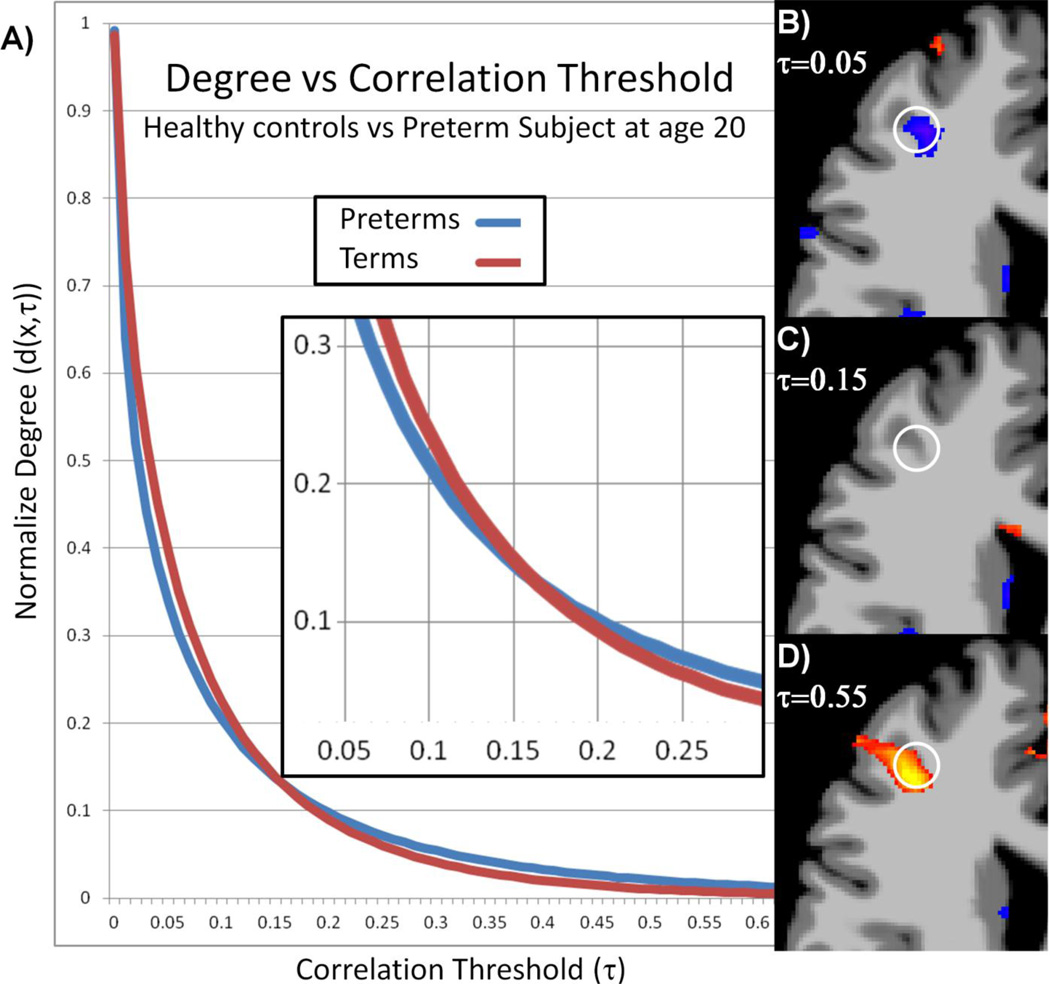
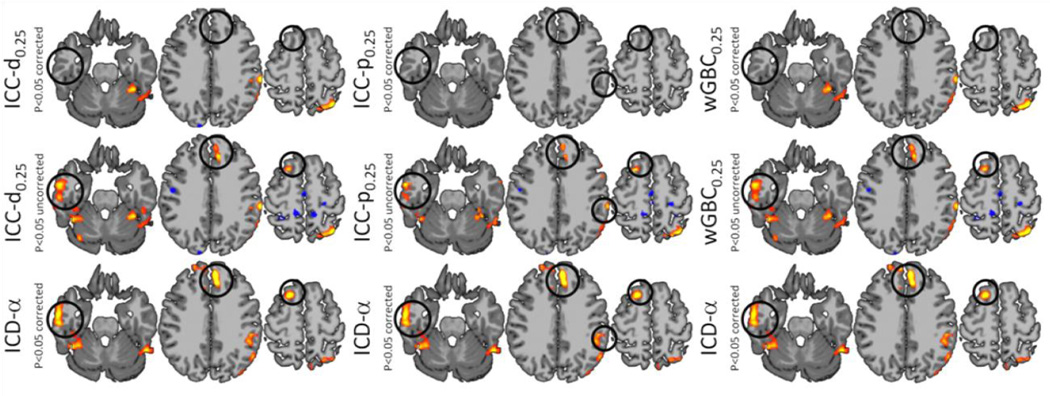
When the significance level was reduced by not correcting for multiple statistical comparisons (cluster size=500), ICC-d, ICC-p, and wGBC detected a frontal lobe cluster and produced results similar to ICD-α as shown in Figure 8. Also, these metrics detected differences in visual processing areas of the occipital lobe over several thresholds. However, ICD-α only detected differences in the occipital cortex when the significance level was reduced and these differences had much lower spatial extent.
Figure 8.
ICC-d, ICC-p, wGBC, and ICD-α results shown on the same axial slices with a τ=0.25 for ICC-d, ICC-p, and wGBC. The regions highlighted by the black circle are detected at p<0.05 corrected only for ICD-α. However, when the significance level is relaxed, all show similar results in these areas.
Discussion
We present a network theory-based measure that models the distribution of all connections to a voxel called the intrinsic connectivity distribution (ICD). Using a whole-brain survey study, ICD-α not only revealed functional connectivity differences between preterm and term subjects in hypothesized language processing areas of the brain identified in earlier studies (Gozzo et al., 2009; Myers et al., 2010) but also demonstrated important differences in both frontal executive function regions and the left cerebellar hemisphere, recently also identified as subserving language. The sensitivity to thresholds of other voxel-based approaches based on the network theory measure degree was shown. ICC-p requires a threshold to determine if two voxels are connected. Changing this threshold can change which areas of the brain show between group differences and even cause results that are ambiguous in terms of the direction of the difference. ICC-p and wGBC also showed sensitivity to thresholds and detected different regions if certain thresholds were used.
ICD-α shows similar results to ICC-d, ICC-p, and wGBC as all metrics detect differences in the hypothesized temporal-parietal area. The specific regions in the temporal-parietal area that show group differences using the degree based metrics were sensitive to threshold with some of these regions showing significant differences at one connection threshold but not another. In the temporal-parietal area and bilateral inferior temporal lobes, all significant regions detected by the degree based metrics at any threshold were identified by ICD-α in a single map suggesting increased sensitivity of the proposed method. Further, ICD-α detected additional connectivity differences in the medial frontal lobe that were not part of the initial hypothesis. While overall these results suggest an increased sensitivity of by ICD-α, ICD-α did not detect the same occipital lobe cluster as the degree based metrics. This result may suggest that ICD-α is better at detecting certain connectivity patterns than others. A proper specificity and sensitivity study with a larger sample is warranted before exact claims about sensitivity can be made.
As hypothesized, preterm subjects show an increase in functional connectivity in the left temporal-parietal area when compared to term subjects. These results are consistent with previous ROI based results and suggest that preterm subjects continue to exhibit altered language networks into early adulthood. We also found statistical evidence of increased functional connectivity in the right temporal lobe. However, these changes in connectivity are located in different areas (BA 21) than connectivity changes previously found in the right hemisphere when comparing preterm and term subjects. At younger ages, this cohort showed increased connectivity between left Wernicke’s area and the right homologues of Broca’s and Wernicke’s area (Gozzo et al., 2009; Myers et al., 2010). This finding may suggest age-related changes in the language networks of preterm subjects or may be due to differences in sensitivity when incorporating a priori information (ROI definitions) into the connectivity analysis. This survey study also revealed connectivity differences in the medial frontal lobes and the left cerebellum that were not hypothesized before the study as previous work investigating this cohort did not examine ROI based changes in either of these regions. Since the frontal lobes subserve executive function, an area of reported deficits for the prematurely-born, and the cerebellar hemispheres contribute to language in typically developing subjects, these clinically relevant findings highlight one of the primary translational benefits of our work: changes throughout the entire brain volume (not just previously hypothesized areas) can be detected.
Several works have investigated the degree distribution over the whole brain and have found several distribution classes that provide reasonable fits including the exponential distribution, the truncated exponential distribution, and the power law distribution (Achard et al., 2006; Tomasi and Volkow, 2010). Our ICD approach can be viewed as modeling the degree distribution of a weighted sub-network centered at a voxel. This sub-network is defined by removing all voxels not connected to the target voxel resulting in a star graph with all connections passing through the center voxel. Unlike studies examining whole brain networks, we weight the connections by the correlation, instead of using a threshold, to form an un-weighted network and model the cumulative distribution (survival function) instead of the probability density function. An noted by Li (Li et al., 2005), this approach is more robust to measurement errors and noise. Initially, the survival curve was modeled with a power-law distribution and exponential distribution with a fixed shape (β=1,2). However, neither distribution was able to properly fit the varied shapes of the distribution across different brain regions.
As ICD can be viewed as modeling the degree distribution, ICD generalizes current approaches based on degree. Instead of calculating degree at a predetermined threshold as introduced in Buckner et al (Buckner et al., 2009), ICD calculates degree at all thresholds and then models the change of degree with the change of threshold. This function of degree can also be expressed as the survival function of the underlying distribution of connection strength for a particular voxel. By modeling all values of degree, ICD does not require a threshold and, by modeling a survival function, ICD can be parameterized with simple monotonically decreasing distributions. As a threshold-free method, ICD takes a differing approach than that of Martuzzi et al (Martuzzi et al., 2011) and Cole et al (Cole et al., 2010) and does not employ a variance stabilizing transformation. ICC-p and wGBC transform the correlation distribution in order to reduce the contribution of weak connections as oppose to removing the contribution of weak connections by thresholding as in ICC-d. ICD weights all data equally. While weights based on correlation are intuitive, empirically, these weighting methods do not perform as well as ICC-d as shown in Martuzzi et al (Martuzzi et al., 2011) and echoed by the presented results. ICD (with the model proposed in this work) requires a model with two free parameters. In this manuscript, we decided a priori to only investigate ICD-α. An alternative and more common parameterization of a stretch exponential is d(τ) = e_−(τ/λ)k. The α parameter captures both the shape and decay rate of the more common parameterization as α = λ−_k. The a priori hypothesis was that ICD-α would be the best parameter to test against due to its interpretation in comparison to the classical parameterization. Independent work also suggests that ICD-α is more sensitivity to group differences (not presented in this work). We are currently investigating nonparametric multivariate statistics to simultaneously test both parameters.
Although voxel-based methods eliminate the need of a priori information to define ROIs, several weaknesses exist. These methods can be viewed as a generalization of ROI-based methods where each voxel is really an ROI. This approach results in large connectivity matrices (~10,000 parameters per voxel) that are difficult to interpret and use for statistical inferences. To simplify inferences, network theory methods essentially work as compression mechanisms to reduce these large connectivity matrices to a few parameters per voxel. As a consequence, network theory measures lose any spatial information about the connectivity changes to a specific voxel. Further analyses, usually in the form of ROI-based methods, are needed to specify which regions are responsible for these changes in connectivity. Voxel-based and ROI-based methods often form complementary pairs. Voxel-based methods can be used to survey regions of altered connectivity and ROI-based methods can be used to test specific hypothesis about these regions.
Investigations over the past decade have suggested numerous clinically important disorders of connectivity, yet the translational technology for evaluating diseases using fc-fMRI remains elusive mainly due to the need for a priori information in many conventional approaches. We present a novel contrast mechanism for resting state functional connectivity that requires no a priori information to define an ROI nor does it require a connection strength threshold. Our measure, ICD, examines the distribution of connections to a voxel instead of investigating only a few strong connections as in the network theory measure degree. Moreover, we highlighted the sensitivity of the degree-based metric to the threshold used to define which voxels are connected. ICD was applied to rs-fMRI data from a cohort of young adults born prematurely versus age-matched controls and revealed connectivity differences in hypothesized language processing areas in the left temporal-parietal lobe. Additional clinically-relevant areas of functional connectivity differences were detected with the ICD measure highlighting both an improved sensitivity of ICD over previous methods and the importance of whole brain survey studies that do not require a priori information. Consequently, ICD holds promise as a survey study method aimed at evaluating clinical conditions and treatments using functional connectivity and could potentially fill this important void left by conventional approaches.
Highlights.
We devised a novel metric to detect differences in functional connectivity.
Intrinsic Connectivity Distribution (ICD) models voxel connection distributions.
Unlike the network measure degree, ICD does not require a connection threshold.
ICD can be used as an exploratory tool for investigating local tissue connectivity and functional organization.
ICD revealed differences between preterm and term subjects not identified by degree.
Acknowledgements
This study was funded in part by R01 EB006494, RO1 EB009666, R01 NS051622, R01 NS027116-20, R03 EB012969.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E. A Resilient, Low-Frequency, Small- World Human Brain Functional Network with Highly Connected Association Cortical Hubs. The Journal of Neuroscience. 2006;26:63–72. doi: 10.1523/JNEUROSCI.3874-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Zerrin Yetkin F, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar mri. Magnetic Resonance in Medicine. 1995;34:537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Buckner RL, Sepulcre J, Talukdar T, Krienen FM, Liu H, Hedden T, Andrews-Hanna JR, Sperling RA, Johnson KA. Cortical Hubs Revealed by Intrinsic Functional Connectivity: Mapping, Assessment of Stability, and Relation to Alzheimer's Disease. The Journal of Neuroscience. 2009;29:1860–1873. doi: 10.1523/JNEUROSCI.5062-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Pathak S, Schneider W. Identifying the brain's most globally connected regions. NeuroImage. 2010;49:3132–3148. doi: 10.1016/j.neuroimage.2009.11.001. [DOI] [PubMed] [Google Scholar]
- Constable RT, Ment LR, Vohr BR, Kesler SR, Fulbright RK, Lacadie C, Delancy S, Katz KH, Schneider KC, Schafer RJ, Makuch RW, Reiss AR. Prematurely Born Children Demonstrate White Matter Microstructural Differences at 12 Years of Age, Relative to Term Control Subjects: An Investigation of Group and Gender Effects. Pediatrics. 2008;121:306–316. doi: 10.1542/peds.2007-0414. [DOI] [PubMed] [Google Scholar]
- Gozzo Y, Vohr B, Lacadie C, Hampson M, Katz KH, Maller-Kesselman J, Schneider KC, Peterson BS, Rajeevan N, Makuch RW, Constable RT, Ment LR. Alterations in neural connectivity in preterm children at school age. NeuroImage. 2009;48:458–463. doi: 10.1016/j.neuroimage.2009.06.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hampson M, Driesen N, Roth JK, Gore JC, Constable RT. Functional connectivity between task-positive and task-negative brain areas and its relation to working memory performance. Magnetic resonance imaging. 2010;28:1051–1057. doi: 10.1016/j.mri.2010.03.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hampson M, Driesen NR, Skudlarski P, Gore JC, Constable RT. Brain Connectivity Related to Working Memory Performance. The Journal of Neuroscience. 2006a;26:13338–13343. doi: 10.1523/JNEUROSCI.3408-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hampson M, Tokoglu F, Sun Z, Schafer RJ, Skudlarski P, Gore JC, Constable RT. Connectivity-behavior analysis reveals that functional connectivity between left BA39 and Broca's area varies with reading ability. NeuroImage. 2006b;31:513–519. doi: 10.1016/j.neuroimage.2005.12.040. [DOI] [PubMed] [Google Scholar]
- Holmes CJ, Hoge R, Collins L, Woods R, Toga AW, Evans AC. Enhancement of MR Images Using Registration for Signal Averaging. Journal of Computer Assisted Tomography. 1998;22:324–333. doi: 10.1097/00004728-199803000-00032. [DOI] [PubMed] [Google Scholar]
- Irwin W, Anderle MJ, Abercrombie HC, Schaefer SM, Kalin NH, Davidson RJ. Amygdalar interhemispheric functional connectivity differs between the non-depressed and depressed human brain. NeuroImage. 2004;21:674–686. doi: 10.1016/j.neuroimage.2003.09.057. [DOI] [PubMed] [Google Scholar]
- Killory BD, Bai X, Negishi M, Vega C, Spann MN, Vestal M, Guo J, Berman R, Danielson N, Trejo J, Shisler D, Novotny EJ, Jr, Constable RT, Blumenfeld H. Impaired attention and network connectivity in childhood absence epilepsy. NeuroImage. 2011;56:2209–2217. doi: 10.1016/j.neuroimage.2011.03.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li L, Alderson D, Doyle JC, Willinger W. Towards a theory of scale-free graphs: Definition, properties, and implications. Internet Mathematics. 2005;2:431–523. [Google Scholar]
- Lowe MJ, Mock BJ, Sorenson JA. Functional Connectivity in Single and Multislice Echoplanar Imaging Using Resting-State Fluctuations. NeuroImage. 1998;7:119–132. doi: 10.1006/nimg.1997.0315. [DOI] [PubMed] [Google Scholar]
- Lowe MJ, Phillips MD, Lurito JT, Mattson D, Dzemidzic M, Mathews VP. Multiple Sclerosis: Low-Frequency Temporal Blood Oxygen Level–Dependent Fluctuations Indicate Reduced Functional Connectivity—Initial Results1. Radiology. 2002;224:184–192. doi: 10.1148/radiol.2241011005. [DOI] [PubMed] [Google Scholar]
- Martuzzi R, Ramani R, Qiu M, Rajeevan N, Constable RT. Functional connectivity and alterations in baseline brain state in humans. NeuroImage. 2010;49:823–834. doi: 10.1016/j.neuroimage.2009.07.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martuzzi R, Ramani R, Qiu M, Shen X, Papademetris X, Constable RT. A whole-brain voxel based measure of intrinsic connectivity contrast reveals local changes in tissue connectivity with anesthetic without a priori assumptions on thresholds or regions of interest. NeuroImage. 2011;58:1044–1050. doi: 10.1016/j.neuroimage.2011.06.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ment LR, Ehrenkranz RA, Duncan CC, Scott DT, Taylor KJW, Katz KH, Schneider KC, Makuch RW, Oh W, Vohr B, Philip AGS, Allan W. Low-Dose Indomethacin and Prevention of Intraventricular Hemorrhage: A Multicenter Randomized Trial. Pediatrics. 1994;93:543–550. [PubMed] [Google Scholar]
- Mullen KM, Vohr BR, Katz KH, Schneider KC, Lacadie C, Hampson M, Makuch RW, Reiss AL, Constable RT, Ment LR. Preterm birth results in alterations in neural connectivity at age 16 years. NeuroImage. 2011;54:2563–2570. doi: 10.1016/j.neuroimage.2010.11.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers EH, Hampson M, Vohr B, Lacadie C, Frost SJ, Pugh KR, Katz KH, Schneider KC, Makuch RW, Constable RT, Ment LR. Functional connectivity to a right hemisphere language center in prematurely born adolescents. NeuroImage. 2010;51:1445–1452. doi: 10.1016/j.neuroimage.2010.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa S, Lee TM, Kay AR, Tank DW. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proceedings of the National Academy of Sciences. 1990;87:9868–9872. doi: 10.1073/pnas.87.24.9868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa S, Tank DW, Menon R, Ellermann JM, Kim SG, Merkle H, Ugurbil K. Intrinsic signal changes accompanying sensory stimulation: functional brain mapping with magnetic resonance imaging. Proceedings of the National Academy of Sciences. 1992;89:5951–5955. doi: 10.1073/pnas.89.13.5951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papademetris X, Jackowski A, Schultz R, Staib L, Duncan J, Barillot C, Haynor D, Hellier P. Medical Image Computing and Computer- Assisted Intervention-MICCAI 2004. Berlin / Heidelberg: Springer; 2004. Integrated Intensity and Point-Feature Nonrigid Registration; pp. 763–770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterson BS, Vohr B, Staib LH, Cannistraci CJ, Dolberg A, Schneider KC, Katz KH, Westerveld M, Sparrow S, Anderson AW, Duncan CC, Makuch RW, Gore JC, Ment LR. Regional brain volume abnormalities and long-term cognitive outcome in preterm infants. Jama. 2000;284:1939–1947. doi: 10.1001/jama.284.15.1939. [DOI] [PubMed] [Google Scholar]
- Rogers B, Avery S, Heckers S. Internal representation of hierarchical sequences involves the default network. BMC Neuroscience. 2010;11:54. doi: 10.1186/1471-2202-11-54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov M, Sporns O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage. 2010;52:1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
- Rubinov M, Sporns O. Weight-conserving characterization of complex functional brain networks. NeuroImage. 2011;56:2068–2079. doi: 10.1016/j.neuroimage.2011.03.069. [DOI] [PubMed] [Google Scholar]
- Schafer RJ, Constable T. Modulation of functional connectivity with the syntactic and semantic demands of a Noun Phrase Formation Task: A possible role for the Default Network. NeuroImage. 2009;46:882–890. doi: 10.1016/j.neuroimage.2009.02.017. [DOI] [PubMed] [Google Scholar]
- Shehzad Z, Kelly AMC, Reiss PT, Gee DG, Gotimer K, Uddin LQ, Lee SH, Margulies DS, Roy AK, Biswal BB, Petkova E, Castellanos FX, Milham MP. The Resting Brain: Unconstrained yet Reliable. Cerebral Cortex. 2009;19:2209–2229. doi: 10.1093/cercor/bhn256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomasi D, Volkow ND. Functional connectivity density mapping. Proceedings of the National Academy of Sciences. 2010;107:9885–9989. doi: 10.1073/pnas.1001414107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vincent JL, Patel GH, Fox MD, Snyder AZ, Baker JT, Van Essen DC, Zempel JM, Snyder LH, Corbetta M, Raichle ME. Intrinsic functional architecture in the anaesthetized monkey brain. Nature. 2007;447:83–86. doi: 10.1038/nature05758. [DOI] [PubMed] [Google Scholar]
- Waites AB, Briellmann RS, Saling MM, Abbott DF, Jackson GD. Functional connectivity networks are disrupted in left temporal lobe epilepsy. Annals of Neurology. 2006;59:335–343. doi: 10.1002/ana.20733. [DOI] [PubMed] [Google Scholar]