Understanding the Role of Amphipathic Helices in N-BAR Domain Driven Membrane Remodeling (original) (raw)
Abstract
Endophilin N-BAR (N-terminal helix and Bin/amphiphysin/Rvs) domain tubulates and vesiculates lipid membranes in vitro via its crescent-shaped dimer and four amphipathic helices that penetrate into membranes as wedges. Like F-BAR domains, endophilin N-BAR also forms a scaffold on membrane tubes. Unlike F-BARs, endophilin N-BARs have N-terminal H0 amphipathic helices that are proposed to interact with other N-BARs in oligomer lattices. Recent cryo-electron microscopy reconstructions shed light on the organization of the N-BAR lattice coats on a nanometer scale. However, because of the resolution of the reconstructions, the precise positioning of the amphipathic helices is still ambiguous. In this work, we applied a coarse-grained model to study various membrane remodeling scenarios induced by endophilin N-BARs. We found that H0 helices of N-BARs prefer to align in an antiparallel manner at two ends of the protein to form a stable lattice. The deletion of H0 helices causes disruption of the lattice. In addition, we analyzed the persistence lengths of the protein-coated tubes and found that the stiffness of endophilin N-BAR-coated tubules qualitatively agrees with previous experimental work studying N-BAR-coated tubules. Large-scale simulations on membrane liposomes revealed a systematic relation between H0 helix density and local membrane curvature fluctuations. The data also suggest that the H0 helix is required for BARs to form organized structures on the liposome, further illustrating its important function.
Introduction
Plasma membranes play a key role in cells as boundaries that separate cells and the outer environment. Protein-mediated deformation of the plasma membrane is an essential part of all endocytotic and exocytotic pathways. In this work, we focus on the Bin/amphiphysin/Rvs (BAR) domains, which are important agents in clathrin-mediated endocytosis (1–3). Crescent shaped and positively charged on the concave surface, the BAR domain dimers naturally are excellent scaffolding proteins for remodeling the membrane shape (4,5). BAR domains sense and bind to curved membranes and recruit proteins such as dynamins to complete endocytosis (6). Understanding how BAR domain proteins organize on the membrane surface to form and stabilize tubules (necks of budding vesicles) can bring new insight to the important processes required for clathrin-mediated endocytosis (7). In addition to clathrin-mediated endocytosis, BAR domains are also involved in other processes that result in exotic shapes, such as T-tubule biogenesis and filopodia (8,9). BAR domains alone can tubulate and vesiculate lipid membranes depending on protein concentration in vitro (4,10–12).
BAR domains have been subdivided into families such as N-BAR domains, which contain N-terminal amphipathic helices (13). The role of the amphipathic helices as both sensors and generators of curvature is the subject of several recent experimental and theoretical investigations (14–18). Despite these efforts, how the scaffolding and the amphipathic helices collaborate to remodel the membrane is poorly understood. Several experiments have tried to directly image protein-coated membranes to understand the remodeling mechanism (12,19,20). Recent efforts based on cryo-electron microscopy (cryo-EM) have demonstrated a significant improvement in resolution, which allowed the visualization of detailed BAR domain-coated membrane at the nanometer level (12,20,21). For instance, Frost et al. (12) considered F-BAR domains that assemble as a helical lattice onto membranes. Multiple lateral contacts between F-BARs were shown to drive the oligomerization of the proteins and form a rigid tube.
Recently a cryo-EM reconstruction of endophilin N-BARs was published (20). As for F-BARs, endophilin N-BARs are found to assemble on the membrane in a helical pattern. Unlike F-BAR protein coats, endophilin N-BAR scaffolds expose large membrane areas. The N-BAR lattice is connected via N-terminal amphipathic helix dimers and these helix interactions are proposed to be critical in stabilizing oligomers. Along with these new discoveries, new questions also arise. For example, the amphipathic H0 helices, which are buried in the lipid headgroups, were not explicitly resolved in the EM images, but some positional information was available from the reconstructions. Exploiting these experimental constraints, the problem of how the H0 helix acts to maintain the endophilin N-BAR scaffold seemed to be an ideal target for computer simulations (20,22–24). In particular, coarse-grained (CG) simulations together with the cryo-EM data offer a means to connect large-scale phenomena, such as the organization of the protein coat, with modifications on a molecular level, such as point mutations in the wild-type sequence. Much recent work shows the use of simulation and theory for understanding the membrane remodeling process from various aspects and scales (18,25–32).
In this work, we present the results of CG molecular dynamics (MD) simulations of endophilin N-BAR-coated membranes. Starting from the lattice structure of endophilin BARs on membrane tubes, several N-BAR models were simulated to study how H0 helix geometries contribute to the overall oligomer pattern. We also calculate the persistence lengths of the protein-coated membrane tubes to study the effect of N-BARs on membrane stiffness, because the experimental persistence lengths of N-BAR and F-BAR tubules are quite different. Simulation results for endophilin N-BAR on membrane liposome are further presented to address the relationship between H0 densities and local membrane curvatures.
Methods
Simulation methods
The modeling procedure in this work follows a systematic multiscale approach in which information from the atomic scale is used as input for a longer lengthscale, CG simulation (29,31,33,34). Endophilin N-BAR is first coarse-grained into a sequence-based 26-site model (see Fig. 1 a) based on a membrane bound all atom (AA) simulation trajectory (24), with two CG sites on each H0 helix (blue CG beads) and one CG site on each of the so-called insert helices (white CG beads). The AA to CG mapping is defined using the essential dynamics coarse-graining method (35), which is designed to capture the longest lengthscale motions in the protein. The intraprotein interactions are then modeled by a heterogeneous elastic network (36), in which each pair of CG sites are connected with an effective harmonic bond. Bond strength is parameterized to reproduce the fluctuations observed at AA scales. Both steps are based on a 75 ns membrane-bound endophilin N-BAR atomistic trajectory that was reported in a previous publication (24).
Figure 1.
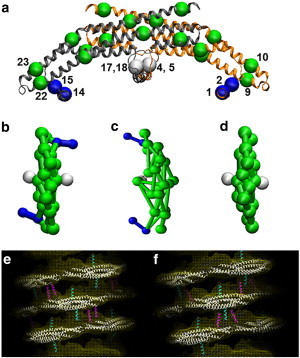
CG model of endophilin N-BARs is shown in panel a. The BAR domain main arch CG sites are colored in green, H0 helices are colored in blue, and the insert helices in white. The sites are assigned based on essential dynamics coarse-graining calculations. Panels b to d show top views of zigzag N-BAR, triad N-BAR, and BAR domain, respectively. Panels e and f show the zigzag model and the triad model fitted into the cryo-EM map, respectively.
Each phospholipid was modeled as a Gay-Berne ellipsoidal particle using a hybrid analytic-systematic approach (37,38). The hybrid approach also employs the multiscale coarse-graining method (MS-CG) (39–41) to model the in-plane potential to capture correctly properties like lipid lateral diffusion and radial distribution functions. A 6 ns atomistic trajectory of 50/50 DOPC/PS (dioleoylphosphatidylserine/phosphatidylcholine) lipid mixture was used as input for MS-CG. When modeling lipids that are close in distance (<0.5 nm) or that are out of plane where MS-CG suffers from poor sampling, the analytical Gay-Berne functional form was used with an aspect ratio of 3:1, ε = 3.3kcal/mol and σ = 0.76 nm to obtain correct phase behavior (37). Additionally, a spherically symmetric correction term is used for distances larger than the Gay-Berne cutoff to ensure that the potential and forces are continuous (37). This CG lipid model was found to reasonably reproduce elastic properties of the membrane, specifically the bending and expansion moduli, and has previously been used to study the structure of immature HIV virions (34).
It should be noted that resolution in the present model is very coarse to efficiently simulate and analyze the experimentally relevant systems. Because of the highly CG nature of our model, the use of a more systematically derived MS-CG approach is unfeasible. To this end, we have used a combination of bottom-up and top-down approaches to develop the cross-interactions in the model. Lipid-protein interactions and protein-protein interactions were modeled through screened electrostatic interactions between the CG sites, as well as a 6–12 Lennard-Jones (LJ) potential (31,34). The LJ potential was used mainly to reproduce the volumes of CG sites in the molecules, so a shallow attractive potential was used: ε = 0.12 kcal/mol for lipid-protein σ = 0.76 nm, and for protein-protein σ = 1.5 nm; for lipids the interaction site was placed at the headgroup that is 0.38 nm above the ellipsoid center along the long axis). Using a similar technique as previous work (34), the Debye-Hückel approximation to the screened electrostatic potential was employed. Charges from underlying residues in proteins were lumped to each CG site, whereas charges from the lipids were modeled by one negative point charge on the 1,2-dioleoyl-3-_sn_-phosphatidylserine (DOPS) CG site. To determine the decay constant in a bottom-up approach from atomistic information was not straightforward. It should include contributions from two parts: one is from counter ion screening; the other is due to the screened implicit from the coarse-graining. The decay constant was set to 2.6 nm−1 by a parameter sweeping from 1 to 8 nm−1, to allow the protein to bind to the membrane without aggregating with other proteins. (Current work is focusing on developing a bottom-up method that can capture the atomistic-level electrostatic potential surface at the CG scale.) The interactions between the amphipathic H0 helix with the membrane were modeled by a LJ interaction with ε = 4.8kcal/mol and σ = 0.76 nm. Each H0 helix has two such LJ sites, whereas the insert helix has just one (cf. Fig. 1). This helix-membrane interaction was determined by a combination of two computations: an atomistic resolution peptide folding free energy calculation (18) and an empirical peptide binding calculation from the Membrane Protein Explorer (http://blanco.biomol.uci.edu/mpex/). The H0 peptide binding free energy is ∼6 kcal/mole per helix from the latter calculation and the folding into the membrane is ∼3–4 kcal/mol as found from the atomistic folding calculation. The combined result for a single H0 is thus 9–10 kcal/mol and so the LJ attraction parameter was given the value as stated previously (there are two such LJ CG sites per H0 and one CG site per shorter insert helix as mentioned earlier). The use of free energy in determining these lipid-protein CG interaction terms also allows us to implicitly include both enthalpic and entropic terms when specifying these nontrivial cross-interaction potentials.
All simulations were performed with an in-house MD program Tantalus (31,34,37), with a velocity Verlet integrator and Nosé-Hoover thermostat. The simulation was performed with a timestep of 0.005 psec (the timescale is an arbitrary, CG timescale) and at 300 K. Initial configurations for membrane tube simulations were based on the cryo-EM reconstruction data (20). Atomistic endophilin N-BARs (PDB entry 1X03) was first fit into an EM electron density map, and then coarse-grained into CG N-BARs. These CG N-BARs were then periodically rotated and replicated according to EM images to form 120 and 160 nm long protein coats. HAS lipids were then placed inside the coat with a radius of 8.9 nm. The initial configuration in the liposome simulations was built by randomly generating 1000 N-BARs with uniform distribution on liposomes with diameters of 200 nm. It should also be noted that all simulations were performed without the use of periodic boundary conditions, resulting in no axial tension on any of the tubules. Control simulations of pure (uncoated) CG membrane tubules under periodic boundary conditions and fixed length were also simulated (results not shown) and found to be stable on the timescale of the CG MD simulation.
Experimental methods
Protein purification
cDNA fragments encoding rat endophilin A1 (1-247) were subcloned into pGEX6P-1 (Amersham Biosciences, Piscataway, NJ) via polymerase chain reaction. cDNA for Rat endophilin A1 were kindly provided by P. DeCamilli, Yale University. Fusion proteins were bacterially expressed and purified first on a GST-glutathione affinity column (GE Health Care, Piscataway, NJ). The GST tag was cleaved by PreScission protease, followed by gel filtration chromatography. Aliquots of 4 mg/mL (endophilin NBAR) protein were stored at −80°C.
Liposome preparation and tubulation in vitro
For all experiments, synthetic lipids were used (Avanti, Alabaster, AL). For the imaged sample we prepared lipids with the following composition (w/w): 50% DOPS, 45% 1,2-dioleoyl-3-sn-phosphatidylethanolamine (DOPE), 5% Cholesterol (endophilin). These mixtures were dried under a stream of dry argon with gentle vortexing in glass vials, dissolved in absolute hexane, dried with argon again, and desiccated under high vacuum for 1 h. Lipids were then hydrated with buffer A (50 mM K-Aspartate,10 mM Tris/HCl 1 mM EGTA, pH 7.5), sonicated, and used immediately or stored in aliquots at −80°C. The in vitro tubulation was performed with liposomes (0.1–0.25 mg/mL) equilibrated at room temperature before adding the protein at a lipid/protein ratio (w/w) of 1.4:1 (endophilin N-BAR).
Electron microscopy imaging and processing
The tubulation reaction was screened using 1% uranyl acetate-stained samples and a Tecnai 12 microscope (Philips; FEI, Eindhoven, The Netherlands) operating at 120 kV. Vitrification required holey carbon grids (Electron Microscopy Sciences, Hatfield, PA) that were plasma cleaned for 30 s (Solarus Gatan, Warrendale, PA) before use. The sample was applied on both sides of the grid and blotted at 4°C using a Vitrobot (FEI). Images of unstained samples were acquired at a sample temperature of −170°C on a Tecnai F20 Twin transmission electron microscope operating at 120 kV, and recorded with a Tietz F415 4 k × 4 k pixel charge-coupled device camera (Tietz Video and Image Processing Systems, Gauting, Germany) using the Leginon data collection software (42) at nominal magnifications of 29 kx, and defocus values of –1.5 to –2 _μ_m. Electron cryo micrographs used in the figures were contrast enhanced to increase visibility of fine molecular features. The images were processed with ImageJ to obtain the data for the persistence length calculation.
Results
Comparing two N-BAR models
High-resolution cryo-EM reconstruction provided the first insight into N-BAR lattice coats on membranes (20). However, the amphipathic helices were not individually resolved in the image reconstructions. Previous experiments suggested that H0 helices stay parallel to the membrane surface (11). The orientation of the helices with regard to the BAR domain main axis is, however, not clear. Based on the observed cryo-EM electron density of the tubule with diameter of 28 nm (20), two N-BAR models, the zigzag model, and the triad model are permissible (shown in Fig. 1 b and c). Both of them fit into the cryo-EM electron density map _(_zigzag in Fig. 1 e and triad in Fig. 1 f). We modeled these two structures by building a protein lattice of each type that wraps around the membrane tube based on the reconstruction of BAR domain main arch. CG MD simulations show that these two lattices have different stabilities, with the triad lattice becoming significantly more disordered than the zigzag model (Fig. 2, panels a–d) when simulated at room temperature.
Figure 2.

CG simulation snapshots of membrane tubes coated by zigzag N-BARs and triad N-BARs. Panels a and b show the initial and final configurations of zigzag simulation and panels c and d show the initial and final configurations of the triad system. The lattice structure remains more organized in the zigzag system.
A local orientation order parameter was calculated to quantitatively analyze the uniformity of the protein orientation on the lattice (Fig. 3 a shows the definition of this order parameter.) The orientation of the BAR domain is estimated by a vector obtained by fitting CG sites 9, 10, 22, 23 with a line. The local orientation order parameter is calculated by averaging the overall tilt angle similarity (dot product of vectors) between all N-BAR pairs that are within 12 nm, normalized to 1.0 for a lattice that matches exactly the cryo-EM structure. This parameter is defined by
| Ol=1Npairs∑i∑j<iμ→i⋅μ→j, | (1) |
|---|
where μ→ is the vector corresponding to the direction of the N-BAR protein along its long axis as defined previously (cf. Fig. 3 a).
Figure 3.
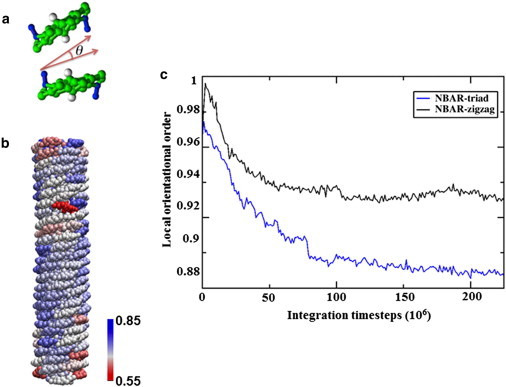
Order of the N-BAR protein coats. Panel a illustrates the local orientation order parameter, defined by the cosine of the orientational difference between two BARs. Panel b shows a snapshot of the protein lattice, colored from blue to red as the order parameter decreases. Panel c plots the order parameters of the zigzag N-BAR system and the triad N-BAR system as functions of time. The lattice of the triad system is significantly disrupted at the end of the simulation.
Fig. 3 b shows a snapshot of the zigzag system at the end of the simulation, with proteins colored corresponding to their order parameters. The majority of the proteins stay highly organized throughout the simulation, whereas proteins at the ends of the tube are more disordered because of reduced packing. Fig. 3 c compares the order parameter between the zigzag system and the triad system. The order parameter for the triad model both decays faster and equilibrates to a smaller value, indicating a more loosely packed pattern. Overall, this order parameter calculation suggests that the zigzag N-BAR model better maintains the lattice. This may be due to the more symmetric structure of the zigzag N-BAR, where the main arch of the BAR domain is balanced by both amphipathic helices.
Role of H0 helix in stabilizing tubules
Simulations further suggest that the H0 helix pairing in the N-BAR oligomer structure is necessary for proper protein packing and oligomer formation. One of the strengths of simulation is that conditions may be explored that are inaccessible experimentally; here we consider a lattice as observed by cryo-EM but without the H0 helices. A BAR domain-coated tube, built by duplicating the N-BAR system but with the H0 helix sites and bonds connecting them deleted (shown in 1_d_), is presented in Fig. 4 a. Panel b in Fig. 4 shows a snapshot of the BAR system after a 50 million timestep CG MD simulation. The lattice structure was greatly disturbed after the simulation, quantitatively described in Fig. 4 b. The average local orientational order decreased significantly in the BAR lattice case, compared to the N-BAR case. Overall, the simulation confirmed that the lattice without H0 helix dimers is unstable. Interestingly, the membrane tube also undulates more for the BAR system, as shown in Fig. 4 a, suggesting that on longer simulation timescales the lattice is unstable without the H0 helix.
Figure 4.
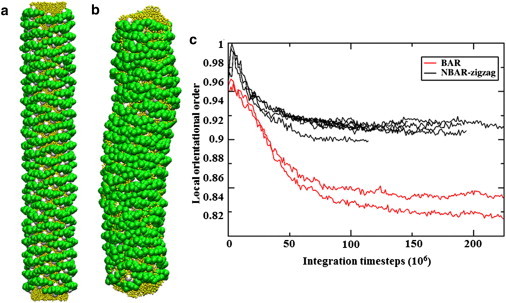
Simulation snapshots of BAR domain-coated membrane are shown; panel a is the initial configuration and panel b is the final state of the simulation. Panel c shows the local orientational order parameters calculated for multiple trajectories in the N-BAR system and BAR system. The N-BAR system stays much more organized after the simulation compared to the BAR system with H0 helices deleted.
Persistence length of the protein-coated tubes
The persistence length (_s_0) is the distance over which the tube loses memory of its direction, defined by the linear coefficient between distance along the contour (s) and the logarithm of angle (θ) correlation (s0=−s/ln〈cos(θ)〉). It measures how fast the tangents at two points in a polymer lose correlation as the distance between these two points increases. The lipid particles were equally grouped into 20 segments and the centers of mass of these segments were used to represent the tube geometry. Similar to previous work on actin filament persistence length calculations (43), the tangent direction at one segment is defined as a vector that connects the centers of mass of its neighboring two segments; the angular correlation is the absolute value of the dot product between tangent vectors. The contour length is defined as the averaged segment length multiplied by the number of segments between two points. Fig. 5 a shows an example of this regression of a 120 nm long protein-coated tube. A time-dependent relationship between the persistence length and the simulation time is plotted in Fig. 5 b, showing convergence after 50 million timesteps. Table 1 compares persistence lengths of BAR-coated tubes of two different lengths. The data suggest that the persistence length varies little for different length tubules. This observation agrees with experimental work showing that N-BAR-coated tubules are formed within these length ranges (21). In contrast, a membrane tube without protein oligomer shows a significantly shorter persistence length. In fact, the membrane tube alone is not stable over a longer simulation time, which implies the importance of protein lattice in fortifying the tubular geometry. The persistence length obtained by CG simulation (shown in Table 1) is also consistent with that obtained from analysis of experimental cryo-EM images of amphiphysin tubules (12), confirming that our model reasonably captures the stiffness of N-BAR-coated tubules. Examples of the experimental images are shown in Fig. 5, c and d. We note that the diameter of endophilin-coated tubules are about a factor to two below that of amphiphysin tubules (10) and that the persistence length may approximately be some nonlinear function of tubule diameter (F-BAR tubules are about four times larger in radius than amphiphysin with a persistence length more than an order of magnitude greater (12)). It is thus possible that the experimental endophilin persistence length should be around a factor of two below that of amphiphysin, as suggested by our calculations, but this requires confirmation.
Figure 5.
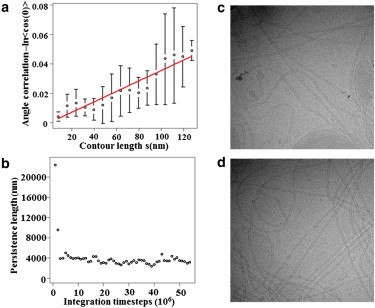
Persistence length calculations. Panel a shows an example of the regression used to compute the persistence length for one membrane tube at one time frame; error bars show the standard deviations of the value of angle correlation for segments that have the same contour lengths. Panel b plots the persistence length for one tube over the simulation as a function of simulation time, demonstrating that the persistence length converges after 50 million CG MD time steps. Panels c and d show representative experimental EM images of endophilin N-BAR-coated tubes.
Table 1.
Computed persistence lengths for different BAR systems and experimental amphiphysin values (12)
| Simulation | Persistence length (nm) | Experiment | Persistence length (nm) |
|---|---|---|---|
| 120 nm Endophilin tube | 3178 (609) | Amphiphysin (12) | 9100 (600) |
| 160 nm Endophilin tube | 3000 (380) | ||
| No protein (unstable) | 563 (142) |
Liposome membrane interactions
Here, we consider the initial stage of membrane remodeling by endophilin N-BARs. Compared to previous simulations that used a single-component dimyristoylphosphatidylcholine (DMPC) liposome, we have improved the model by using a multicomponent lipid membrane with 1:1 DOPC:DOPS. Fig. S1 in the Supporting Material shows a snapshot of a protein-coated membrane liposome after 5 million timesteps. By comparing the regions of local convex curvature to the H0 density on the right, it is clear that the local membrane curvature and the H0 helix density are correlated. Although local membrane curvatures under individual N-BARs are often positive (22–24), negatively curved regions more frequently have multiple N-BAR domains in their vicinity. This behavior may be important for the early stages of membrane remodeling in endocytosis as membrane buds are formed through the membrane interaction with other proteins.
A key role of the H0 helix has also been illustrated by comparing CG MD configurations of N-BARs to BARs with H0 deleted on the liposome surface. Fig. 6 shows representative snapshots of the two systems, with the proteins colored by a local packing order parameter. This parameter was defined similarly to the orientational order parameter that was used in the tubule analysis (e.g., in Fig. 3). However, in this case, instead of using the averaged dot product of the neighboring protein orientations, we divide the total dot product of neighboring orientations by square root of the number of the neighbors, as this choice strikes a balance between measuring packing density and alignment. In this way, we consider not only how significantly a group of proteins align in the same direction, but also the protein density in that group. Thus, we can capture both the orientational packing and the spatial packing on the liposome.
Figure 6.
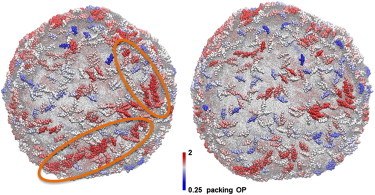
Representative snapshots of the N-BAR system (left) and the BAR-coated liposome systems (right) after 5 million CG MD timestep simulations. The proteins are colored by a packing order parameter that is explained in the main text. Circles in the left panel highlight the region where proteins gather into structures that have similar orientations. This kind of clustering is missing in the BAR domain system in the right panel. The data are consistent with the hypothesis that BAR domains require H0 helices to form arrays and strings on the liposome.
The results shown in Fig. 6 provide an interesting insight: H0 helices are necessary to form spatially contiguous BAR domain strings or arrays on the liposome. In Fig. 6, N-BARs that are both oriented similarly with their neighbors, and have more neighbors than average, are colored red. Compared to the BAR domains, we observe the N-BAR domains have both a higher local density, as well as more local ordering on the liposome, perhaps offering a hint as to why N-BAR domains are much more efficient tubulation agents than BAR domains. Similarly aligned arrays of protein are found experimentally in vitro before tubulation, an example of which is highlighted in Fig. 7. It should be noted that these structures are rare and were observed in only 2 out of 80 cryo-EM images. Therefore, it is tempting to speculate that these structures represent a transition state during the initial stage of membrane remodeling by N-BAR domains.
Figure 7.
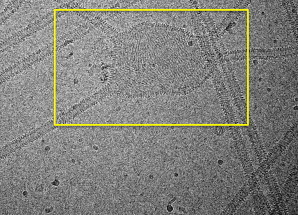
EM image showing aligned arrays of endophilin N-BARs on a liposome surface in an area that is not yet tubulated.
Discussion and Conclusions
By combining CGMD with cryo-EM reconstructions of N-BAR-coated tubules, we have extended the static structures provided by the structural data into the time domain. In this way, we have investigated the stability of the lattice structure at room temperature under different configurations of the N-terminal amphipathic helices—a detail not resolved in our recently published structure of the protein coat (19). Although our previously reported data showed an essential role for the H0 helix in determining the structure of the lattice (19), the observed electron density for the membrane-associated regions did not admit unambiguous determination of how the helices are associated. We therefore examined by simulation two configurations that are both consistent with the experimental data: the zigzag, in which pairs of H0 helices from different turns dimerize in an antiparallel configuration, and the triad, in which H0 helices from neighboring N-BARs in the same helical turn oligomerize with an antiparallel insert helix from the neighboring turn interposed. The data indicate that the zigzag configuration yields more ordered tubules that are more consistent with the experimental data.
The present simulations provide clues to explain the molecular mechanism of N-BAR lattice formation. Based on cryo-EM reconstructions and in vivo studies, it was previously shown that F-BAR domains contain a second lipid-binding interface that allows these domains to engage flat bilayer surfaces (11). Intriguingly, this binding mode allows F-BAR domains to exist as curvature neutral storage arrays until a cooperative reorientation of multiple F-BAR induces (or conforms to) curvature on a macroscopic scale. In the case of the N-BAR domain of endophilin, no such alternate mode of membrane binding has yet been identified, raising the question how macroscopic curvature induction is accomplished (19). Our calculations also suggest that the antiparallel interactions between H0 helices in the zigzag model of the N-BAR-coated tubules can form spontaneously on liposome membrane surfaces, causing N-BAR domains to first aggregate into strings of locally aligned modules before curvature induction. Notably, if the formation of such strings were a mandatory intermediate in the assembly of N-BAR scaffolds they could explain why experimentally H0:H0 interactions were found to be very promiscuous, involving both lateral surfaces of H0 (19), because in the context of a string, where higher order lattice constraints are missing, weak lateral interactions between H0 helices do not require a precise alignment. In line with this mechanistic model, the calculated order parameter also indicated that even fully assembled endophilin lattices on tubules are highly dynamic and display a high degree of plasticity.
Our results also speak to the mechanism of curvature induction, in a setting designed to mimic a tubulation assay. Simulations of N-BARs on liposome surfaces suggest that the N-BARs generate local curvature fluctuations in a density-dependent manner—it is found that regions with higher H0 concentration usually have higher curvature (14,15). Both atomistic analysis on membrane defects and continuum simulations of large-scale membrane remodeling imply a sensing mechanism of N-BARs for curved membranes (18,24,32). Nevertheless, N-BAR domains are mostly found on the neck of vesicles where the curvature is already significant (6). The two different modes of N-BAR, sensing and induction, suggest a mechanism in which initial curvature fluctuations increase the local density of bound protein, in turn driving higher curvature, which then recruits more protein, and so on. A CG level study of this sensing mechanism, which could follow the process from adsorption of the first N-BAR domains through local curvature generation and recruitment of more protein, will therefore be of great interest; this effort is underway. Additional future work will focus on the effect of liposome size on membrane remodeling. Preliminary simulation results suggest that the membrane curvature fluctuations of 100 nm diameter N-BAR-coated liposomes are less than those of 200 nm liposome systems, consistent with the reduced curvature stress in larger liposomes. This is interesting in light of the experimental observation that liposomes smaller than 400 nm in diameter are incompatible with full tubulation.
Acknowledgments
This work was funded by GM063796 (to G.A.V.) and GM094479 (to V.M.U.) from the National Institutes of Health, as well as the Deutsche Forschungsgemeinschaft (to C.M.), the Cancer Research Institute (to C.M.), and Public Health Service (PHS) grants DA24101 (V.M.U.). The research was supported by an allocation of advanced computing resources provided by the National Science Foundation. The computations were performed on Kraken at the National Institute for Computational Sciences. Experimental data for this work were collected at the National Resource for Automated Molecular Microscopy, which is supported by the National Institutes of Health through the National Center for Research Resources’ P41 program (RR017573).
Supporting Material
Document S1. Two tables, one figure, and membrane liposome and H0 interactions section
References
- 1.McMahon H.T., Gallop J.L. Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature. 2005;438:590–596. doi: 10.1038/nature04396. [DOI] [PubMed] [Google Scholar]
- 2.Slepnev V.I., De Camilli P. Accessory factors in clathrin-dependent synaptic vesicle endocytosis. Nat. Rev. Neurosci. 2000;1:161–172. doi: 10.1038/35044540. [DOI] [PubMed] [Google Scholar]
- 3.Zimmerberg J., Kozlov M.M. How proteins produce cellular membrane curvature. Nat. Rev. Mol. Cell Biol. 2006;7:9–19. doi: 10.1038/nrm1784. [DOI] [PubMed] [Google Scholar]
- 4.Peter B.J., Kent H.M., McMahon H.T. BAR domains as sensors of membrane curvature: the amphiphysin BAR structure. Science. 2004;303:495–499. doi: 10.1126/science.1092586. [DOI] [PubMed] [Google Scholar]
- 5.Weissenhorn W. Crystal structure of the endophilin-A1 BAR domain. J. Mol. Biol. 2005;351:653–661. doi: 10.1016/j.jmb.2005.06.013. [DOI] [PubMed] [Google Scholar]
- 6.Ringstad N., Gad H., De Camilli P. Endophilin/SH3p4 is required for the transition from early to late stages in clathrin-mediated synaptic vesicle endocytosis. Neuron. 1999;24:143–154. doi: 10.1016/s0896-6273(00)80828-4. [DOI] [PubMed] [Google Scholar]
- 7.Kukulski W., Schorb M., Briggs J.A. Plasma membrane reshaping during endocytosis is revealed by time-resolved electron tomography. Cell. 2012;150:508–520. doi: 10.1016/j.cell.2012.05.046. [DOI] [PubMed] [Google Scholar]
- 8.Lee E., Marcucci M.J., De Camilli P. Amphiphysin 2 (bin1) and t-tubule biogenesis in muscle. Science. 2002;297:1193–1196. doi: 10.1126/science.1071362. [DOI] [PubMed] [Google Scholar]
- 9.Saarikangas J., Zhao H.X., Lappalainen P. Molecular mechanisms of membrane deformation by I-BAR domain proteins. Curr. Biol. 2009;19:95–107. doi: 10.1016/j.cub.2008.12.029. [DOI] [PubMed] [Google Scholar]
- 10.Masuda M., Takeda S., Mochizuki N. Endophilin BAR domain drives membrane curvature by two newly identified structure-based mechanisms. EMBO J. 2006;25:2889–2897. doi: 10.1038/sj.emboj.7601176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gallop J.L., Jao C.C., McMahon H.T. Mechanism of endophilin N-BAR domain-mediated membrane curvature. EMBO J. 2006;25:2898–2910. doi: 10.1038/sj.emboj.7601174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Frost A., Perera R., Unger V.M. Structural basis of membrane invagination by F-BAR domains. Cell. 2008;132:807–817. doi: 10.1016/j.cell.2007.12.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Farsad K., Ringstad N., De Camilli P. Generation of high curvature membranes mediated by direct endophilin bilayer interactions. J. Cell Biol. 2001;155:193–200. doi: 10.1083/jcb.200107075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hatzakis N.S., Bhatia V.K., Stamou D. How curved membranes recruit amphipathic helices and protein anchoring motifs. Nat. Chem. Biol. 2009;5:835–841. doi: 10.1038/nchembio.213. [DOI] [PubMed] [Google Scholar]
- 15.Bhatia V.K., Madsen K.L., Stamou D. Amphipathic motifs in BAR domains are essential for membrane curvature sensing. EMBO J. 2009;28:3303–3314. doi: 10.1038/emboj.2009.261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fernandes F., Loura L.M.S., Prieto M. Role of helix 0 of the N-BAR domain in membrane curvature generation. Biophys. J. 2008;94:3065–3073. doi: 10.1529/biophysj.107.113118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Campelo F., McMahon H.T., Kozlov M.M. The hydrophobic insertion mechanism of membrane curvature generation by proteins. Biophys. J. 2008;95:2325–2339. doi: 10.1529/biophysj.108.133173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cui H.S., Lyman E., Voth G.A. Mechanism of membrane curvature sensing by amphipathic helix containing proteins. Biophys. J. 2011;100:1271–1279. doi: 10.1016/j.bpj.2011.01.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mizuno N., Jao C.C., Steven A.C. Multiple modes of endophilin-mediated conversion of lipid vesicles into coated tubes: implications for synaptic endocytosis. J. Biol. Chem. 2010;285:23351–23358. doi: 10.1074/jbc.M110.143776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mim C., Cui H., Unger V.M. Structural basis of membrane bending by the n-bar protein endophilin. Cell. 2012;149:9–10. doi: 10.1016/j.cell.2012.01.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shimada A., Niwa H., Yokoyama S. Curved EFC/F-BAR-domain dimers are joined end to end into a filament for membrane invagination in endocytosis. Cell. 2007;129:761–772. doi: 10.1016/j.cell.2007.03.040. [DOI] [PubMed] [Google Scholar]
- 22.Blood P.D., Voth G.A. Direct observation of Bin/amphiphysin/Rvs (BAR) domain-induced membrane curvature by means of molecular dynamics simulations. Proc. Natl. Acad. Sci. USA. 2006;103:15068–15072. doi: 10.1073/pnas.0603917103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Blood P.D., Swenson R.D., Voth G.A. Factors influencing local membrane curvature induction by N-BAR domains as revealed by molecular dynamics simulations. Biophys. J. 2008;95:1866–1876. doi: 10.1529/biophysj.107.121160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cui H.S., Ayton G.S., Voth G.A. Membrane binding by the endophilin N-BAR domain. Biophys. J. 2009;97:2746–2753. doi: 10.1016/j.bpj.2009.08.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ayton G.S., Blood P.D., Voth G.A. Membrane remodeling from N-BAR domain interactions: insights from multi-scale simulation. Biophys. J. 2007;92:3595–3602. doi: 10.1529/biophysj.106.101709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Arkhipov A., Yin Y., Schulten K. Four-scale description of membrane sculpting by BAR domains. Biophys. J. 2008;95:2806–2821. doi: 10.1529/biophysj.108.132563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Arkhipov A., Yin Y., Schulten K. Membrane-bending mechanism of amphiphysin N-BAR domains. Biophys. J. 2009;97:2727–2735. doi: 10.1016/j.bpj.2009.08.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yin Y., Arkhipov A., Schulten K. Simulations of membrane tubulation by lattices of amphiphysin N-BAR domains. Structure. 2009;17:882–892. doi: 10.1016/j.str.2009.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lyman E., Cui H.S., Voth G.A. Reconstructing protein remodeled membranes in molecular detail from mesoscopic models. Phys. Chem. Chem. Phys. 2011;13:10430–10436. doi: 10.1039/c0cp02978e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lyman E., Cui H.S., Voth G.A. Water under the BAR. Biophys. J. 2010;99:1783–1790. doi: 10.1016/j.bpj.2010.06.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ayton G.S., Lyman E., Voth G.A. Hierarchical coarse-graining strategy for protein-membrane systems to access mesoscopic scales. Faraday Discuss. 2010;144:347–357. doi: 10.1039/b901996k. discussion 445–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ayton G.S., Lyman E., Voth G.A. New insights into BAR domain-induced membrane remodeling. Biophys. J. 2009;97:1616–1625. doi: 10.1016/j.bpj.2009.06.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ayton G.S., Voth G.A. Multiscale simulation of protein mediated membrane remodeling. Semin. Cell Dev. Biol. 2010;21:357–362. doi: 10.1016/j.semcdb.2009.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ayton G.S., Voth G.A. Multiscale computer simulation of the immature HIV-1 virion. Biophys. J. 2010;99:2757–2765. doi: 10.1016/j.bpj.2010.08.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhang Z.Y., Pfaendtner J., Voth G.A. Defining coarse-grained representations of large biomolecules and biomolecular complexes from elastic network models. Biophys. J. 2009;97:2327–2337. doi: 10.1016/j.bpj.2009.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lyman E., Pfaendtner J., Voth G.A. Systematic multiscale parameterization of heterogeneous elastic network models of proteins. Biophys. J. 2008;95:4183–4192. doi: 10.1529/biophysj.108.139733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ayton G.S., Voth G.A. Hybrid coarse-graining approach for lipid bilayers at large length and time scales. J. Phys. Chem. B. 2009;113:4413–4424. doi: 10.1021/jp8087868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gay J.G., Berne B.J. Modification of the overlap potential to mimic a linear site-site potential. J. Chem. Phys. 1981;74:3316–3319. [Google Scholar]
- 39.Izvekov S., Voth G.A. A multiscale coarse-graining method for biomolecular systems. J. Phys. Chem. B. 2005;109:2469–2473. doi: 10.1021/jp044629q. [DOI] [PubMed] [Google Scholar]
- 40.Noid W.G., Chu J.W., Andersen H.C. The multiscale coarse-graining method. I. A rigorous bridge between atomistic and coarse-grained models. J. Chem. Phys. 2008;128 doi: 10.1063/1.2938860. 244114-1–244114-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Noid W.G., Chu J.W., Voth G.A. Multiscale coarse-graining and structural correlations: connections to liquid-state theory. J. Phys. Chem. B. 2007;111:4116–4127. doi: 10.1021/jp068549t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Suloway C., Pulokas J., Carragher B. Automated molecular microscopy: the new Leginon system. J. Struct. Biol. 2005;151:41–60. doi: 10.1016/j.jsb.2005.03.010. [DOI] [PubMed] [Google Scholar]
- 43.Chu J.W., Voth G.A. Allostery of actin filaments: molecular dynamics simulations and coarse-grained analysis. Proc. Natl. Acad. Sci. USA. 2005;102:13111–13116. doi: 10.1073/pnas.0503732102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Document S1. Two tables, one figure, and membrane liposome and H0 interactions section